Cell State Transition Models Stratify Breast Cancer Cell Phenotypes and Reveal New Therapeutic Targets
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Pre-Processing the CYTOF Data
2.2. Building the STVs and Calculating the DPD Scores
2.3. Reconstruction of Core Networks
2.4. Model Construction and Simulation
2.5. Parameter Estimation of Cell Line-Specific Models
2.6. Construction of Waddington’s Landscape
3. Results
3.1. Combining Machine Learning, Network Reconstruction and Mechanistic Modeling to Understand and Manipulate Cell States—The cSTAR Approach in Action
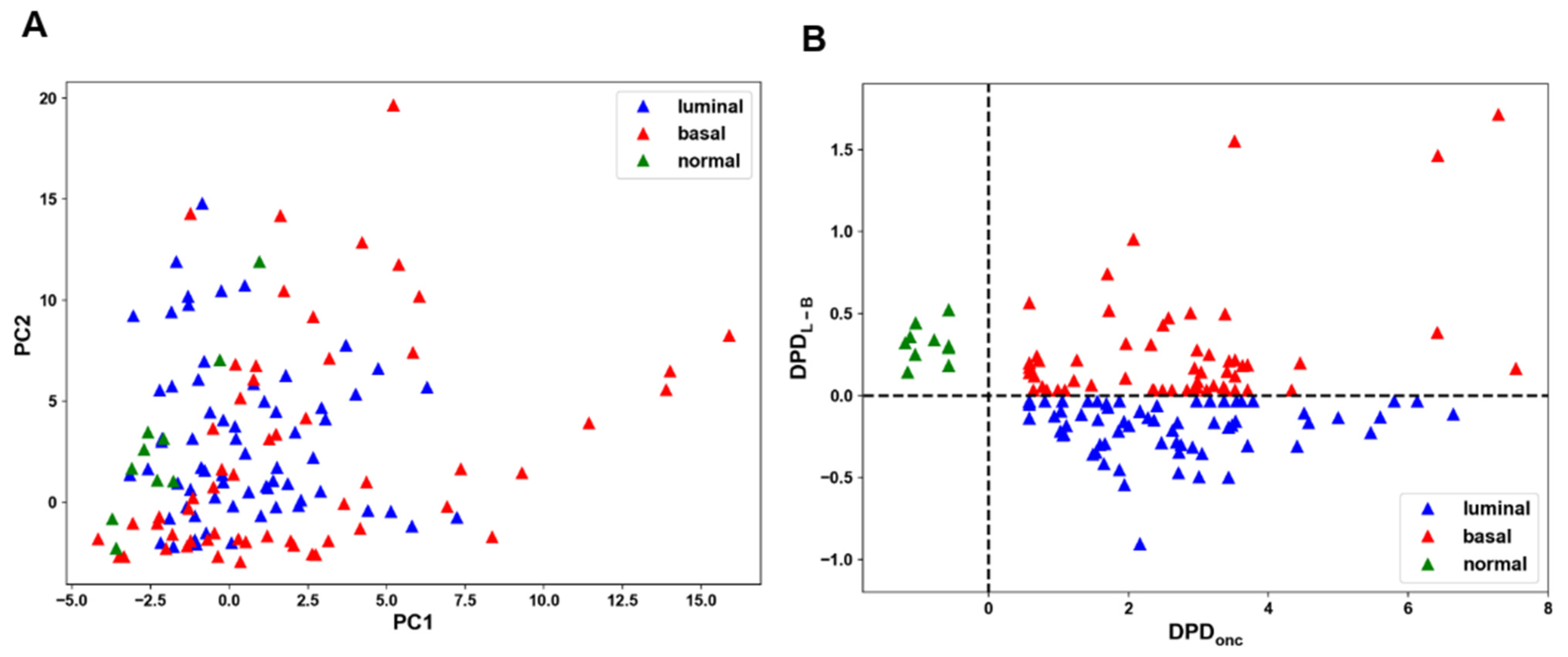
3.2. Applying Supervised ML to Separate Distinct States of BC and Non-Malignant Breast Cells
3.3. Testing the Robustness of the cSTAR Predictions
3.4. The Accuracy of BC Cell State Classification Using Total Proteomics Data
3.5. Building the State Transition Vector (STV)
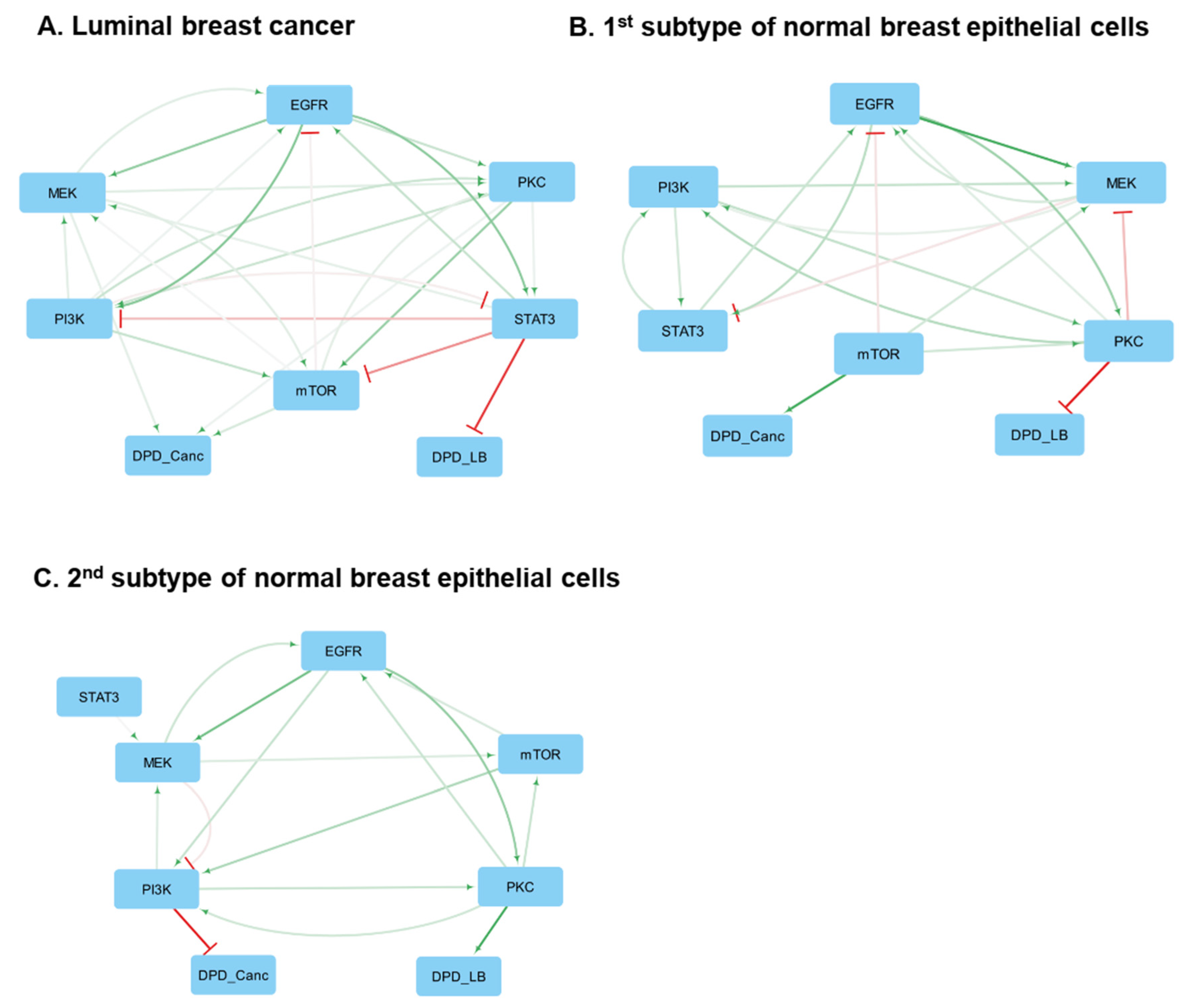
3.6. Determining Components of a Core Controlling Network
3.7. Mechanistic Insights Coming from Core Network Reconstruction Explain Predictions and DPD Scores
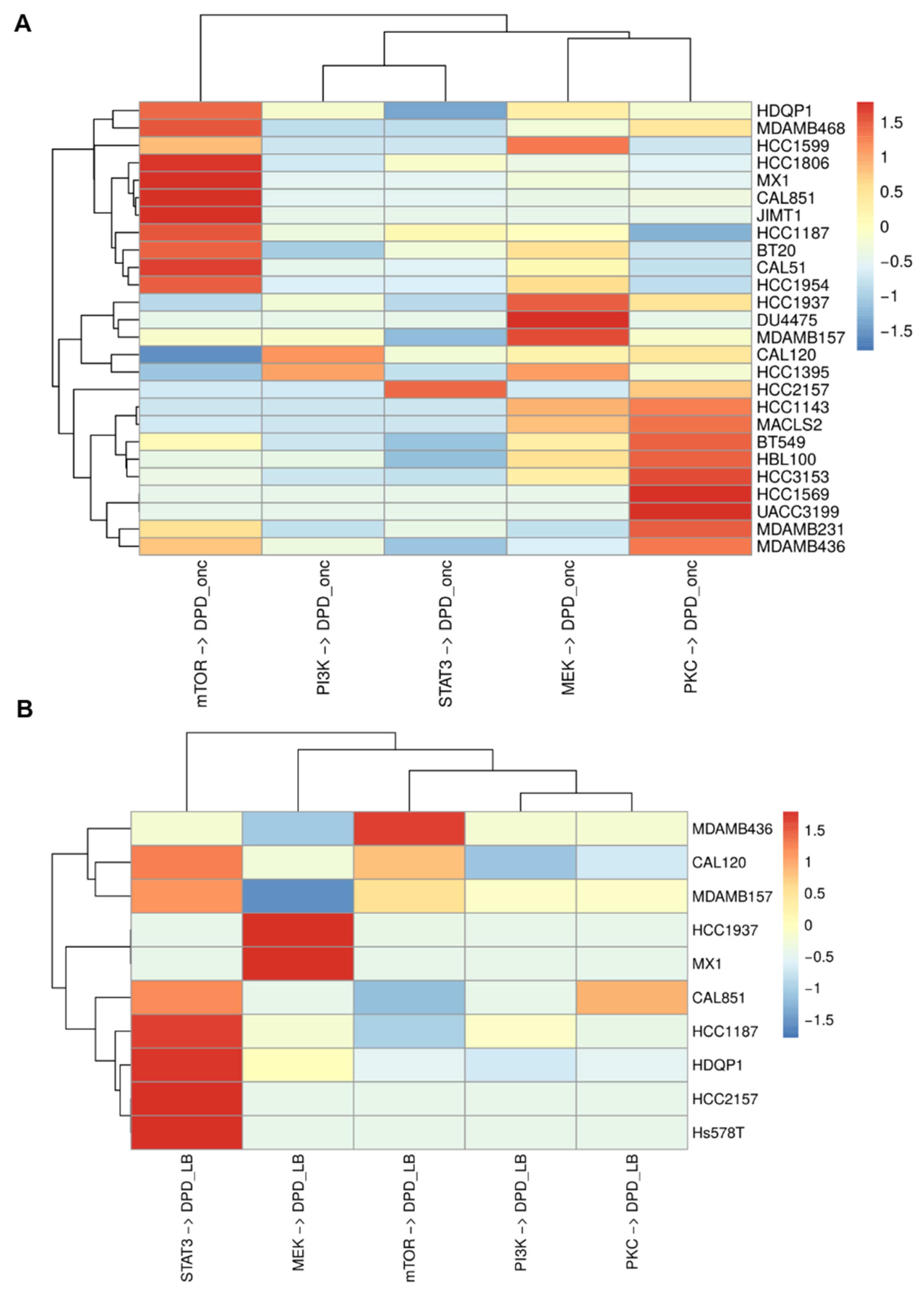
3.8. Modular Response Analysis of Cell Function
3.9. Reconstruction of Core Networks in BC and Normal Breast Tissue Derived Cell Lines
3.10. Luminal BC Cell Lines
3.11. Basal BC Cell Lines
3.12. Normal Breast Tissue-Derived Cell Lines
3.13. MRA Predicts Phenotypic Effects of Drug Responses That Correlate with Available Data
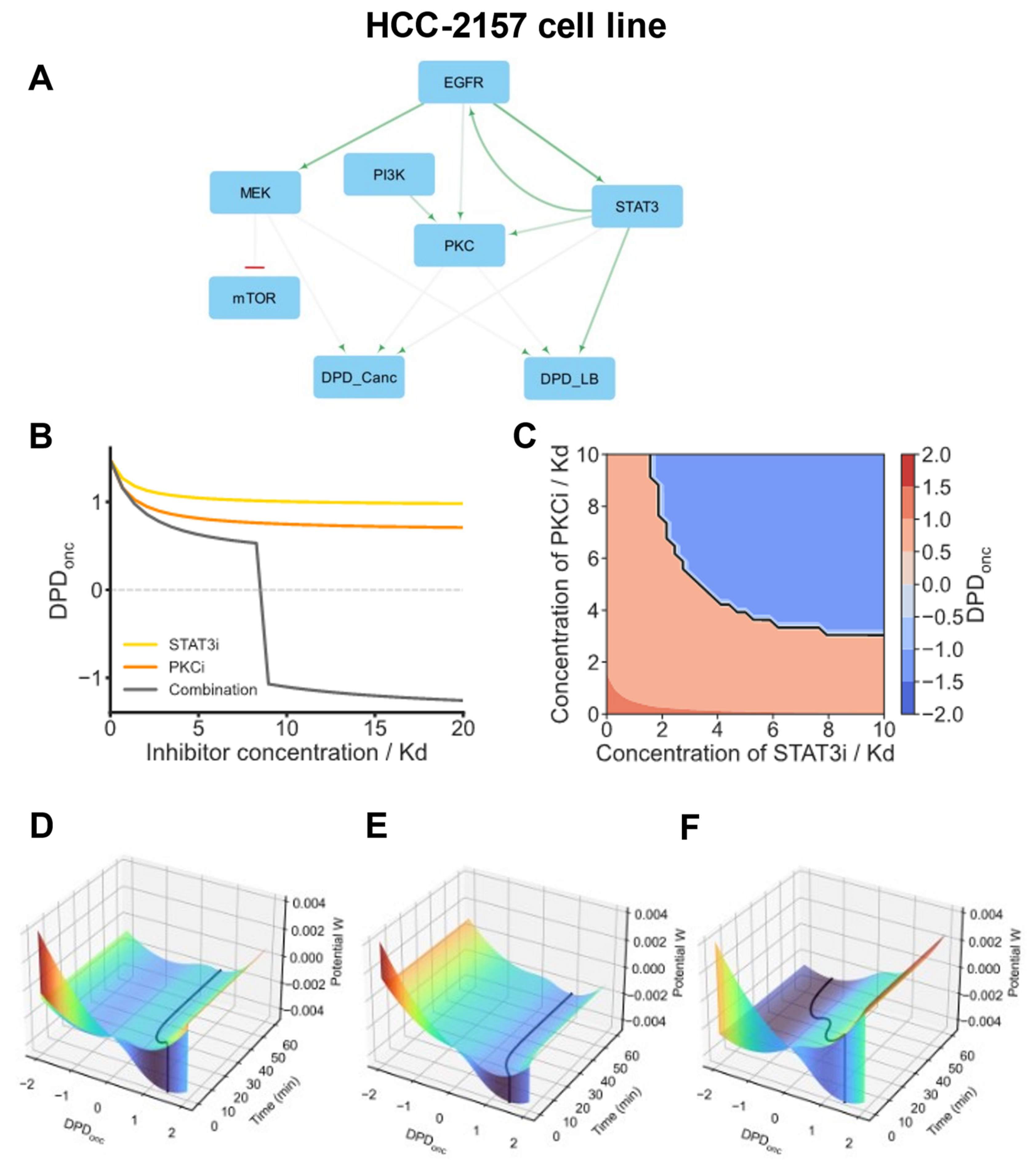
3.14. Building cSTAR Models: Digital Cell Twins
3.15. cSTAR Model of the MDA-MB-468 Cell Line Suggests Experimental Interventions Normalizing Phosphoproteomic Patterns of the First Group of Basal BC Cells
3.16. STAT3-Driven Basal BC Cells
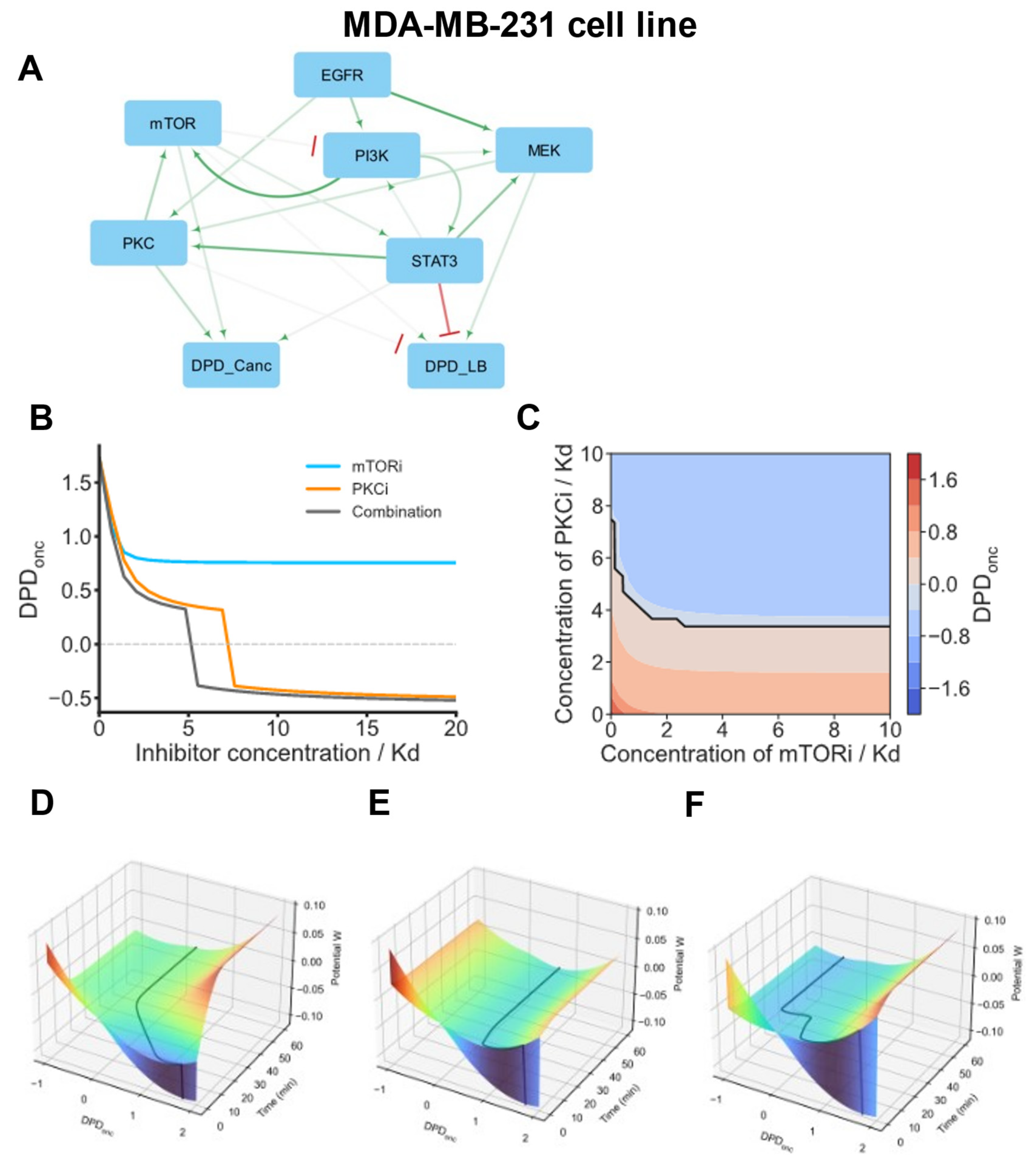
3.17. cSTAR Model of the MDA-MB-231 Cell Line of the Fourth Basal BC Cell Group
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- La Manno, G.; Soldatov, R.; Zeisel, A.; Braun, E.; Hochgerner, H.; Petukhov, V.; Lidschreiber, K.; Kastriti, M.E.; Lönnerberg, P.; Furlan, A.; et al. RNA Velocity of Single Cells. Nature 2018, 560, 494–498. [Google Scholar] [CrossRef] [PubMed]
- Schiebinger, G.; Shu, J.; Tabaka, M.; Cleary, B.; Subramanian, V.; Solomon, A.; Gould, J.; Liu, S.; Lin, S.; Berube, P.; et al. Optimal-Transport Analysis of Single-Cell Gene Expression Identifies Developmental Trajectories in Reprogramming. Cell 2019, 176, 928–943.e22. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Zhang, Y.; Martin-Rufino, J.D.; Weng, C.; Hosseinzadeh, S.; Yang, D.; Pogson, A.N.; Hein, M.Y.; Hoi (Joseph) Min, K.; Wang, L.; et al. Mapping Transcriptomic Vector Fields of Single Cells. Cell 2022, 185, 690–711.e45. [Google Scholar] [CrossRef] [PubMed]
- Yeo, G.H.T.; Saksena, S.D.; Gifford, D.K. Generative Modeling of Single-Cell Time Series with PRESCIENT Enables Prediction of Cell Trajectories with Interventions. Nat. Commun. 2021, 12, 3222. [Google Scholar] [CrossRef] [PubMed]
- Rukhlenko, O.S.; Halasz, M.; Rauch, N.; Zhernovkov, V.; Prince, T.; Wynne, K.; Maher, S.; Kashdan, E.; MacLeod, K.; Carragher, N.O.; et al. Control of Cell State Transitions. Nature 2022, 609, 975–985. [Google Scholar] [CrossRef] [PubMed]
- Tognetti, M.; Gabor, A.; Yang, M.; Cappelletti, V.; Windhager, J.; Rueda, O.M.; Charmpi, K.; Esmaeilishirazifard, E.; Bruna, A.; de Souza, N.; et al. Deciphering the Signaling Network of Breast Cancer Improves Drug Sensitivity Prediction. Cell Syst. 2021, 12, 401–418.e12. [Google Scholar] [CrossRef] [PubMed]
- Waddington, C.H. Organisers and Genes; The University Press: Cambridge, UK, 1940. [Google Scholar]
- Tognetti, M.; Gabor, A.; Yang, M.; Cappelletti, V.; Windhager, J.; Rueda, O.M.; Charmpi, K.; Esmaeilishirazifard, E.; Bruna, A.; de Souza, N.; et al. Deciphering the Signaling Network Landscape of Breast Cancer Improves Drug Sensitivity Prediction. Mendeley Data 2021, V1. [Google Scholar] [CrossRef]
- Lill, D.; Rukhlenko, O.S.; Mc Elwee, A.J.; Kashdan, E.; Timmer, J.; Kholodenko, B.N. Mapping Connections in Signaling Networks with Ambiguous Modularity. NPJ Syst. Biol. Appl. 2019, 5, 19. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N.; Kiyatkin, A.; Bruggeman, F.J.; Sontag, E.; Westerhoff, H.V.; Hoek, J.B. Untangling the Wires: A Strategy to Trace Functional Interactions in Signaling and Gene Networks. Proc. Natl. Acad. Sci. USA 2002, 99, 12841–12846. [Google Scholar] [CrossRef]
- Lopez, C.F.; Muhlich, J.L.; Bachman, J.A.; Sorger, P.K. Programming Biological Models in Python Using PySB. Mol. Syst. Biol. 2013, 9, 646. [Google Scholar] [CrossRef]
- Tsyganov, M.A.; Kolch, W.; Kholodenko, B.N. The Topology Design Principles That Determine the Spatiotemporal Dynamics of G-Protein Cascades. Mol. Biosyst. 2012, 8, 730–743. [Google Scholar] [CrossRef] [PubMed]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 99–104. [Google Scholar] [CrossRef]
- Waskom, M. Seaborn: Statistical Data Visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Plischke, M.; Bergersen, B. Equilibrium Statistical Physics, 3rd ed.; World Scientific: Singapore, 2006; ISBN 9789812774811. [Google Scholar]
- Koboldt, D.C.; Fulton, R.S.; McLellan, M.D.; Schmidt, H.; Kalicki-Veizer, J.; McMichael, J.F.; Fulton, L.L.; Dooling, D.J.; Ding, L.; Mardis, E.R.; et al. Comprehensive Molecular Portraits of Human Breast Tumours. Nature 2012, 490, 61–70. [Google Scholar] [CrossRef]
- Curtis, C.; Shah, S.P.; Chin, S.F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The Genomic and Transcriptomic Architecture of 2000 Breast Tumours Reveals Novel Subgroups. Nature 2012, 486, 346–352. [Google Scholar] [CrossRef]
- Chin, K.; DeVries, S.; Fridlyand, J.; Spellman, P.T.; Roydasgupta, R.; Kuo, W.-L.; Lapuk, A.; Neve, R.M.; Qian, Z.; Ryder, T.; et al. Genomic and Transcriptional Aberrations Linked to Breast Cancer Pathophysiologies. Cancer Cell 2006, 10, 529–541. [Google Scholar] [CrossRef]
- Porta-Pardo, E.; Valencia, A.; Godzik, A. Understanding Oncogenicity of Cancer Driver Genes and Mutations in the Cancer Genomics Era. FEBS Lett. 2020, 594, 4233–4246. [Google Scholar] [CrossRef]
- Martincorena, I.; Campbell, P.J. Somatic Mutation in Cancer and Normal Cells. Science 2015, 349, 1483–1489. [Google Scholar] [CrossRef]
- Magwene, P.M.; Lizardi, P.; Kim, J. Reconstructing the Temporal Ordering of Biological Samples Using Microarray Data. Bioinformatics 2003, 19, 842–850. [Google Scholar] [CrossRef] [PubMed]
- Cacchiarelli, D.; Qiu, X.; Srivatsan, S.; Manfredi, A.; Ziller, M.; Overbey, E.; Grimaldi, A.; Grimsby, J.; Pokharel, P.; Livak, K.J.; et al. Aligning Single-Cell Developmental and Reprogramming Trajectories Identifies Molecular Determinants of Myogenic Reprogramming Outcome. Cell Syst. 2018, 7, 258–268.e3. [Google Scholar] [CrossRef]
- Murtagh, F.; Contreras, P. Algorithms for Hierarchical Clustering: An Overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 86–97. [Google Scholar] [CrossRef]
- Comon, P.; Jutten, C. Handbook of Blind Source Separation: Independent Component Analysis and Applications; Academic Press: Cambridge, MA, USA, 2010; ISBN 9780123747266. [Google Scholar]
- Gordonov, S.; Hwang, M.K.; Wells, A.; Gertler, F.B.; Lauffenburger, D.A.; Bathe, M. Time Series Modeling of Live-Cell Shape Dynamics for Image-Based Phenotypic Profiling. Integr. Biol. 2016, 8, 73–90. [Google Scholar] [CrossRef] [PubMed]
- Cook, D.P.; Vanderhyden, B.C. Context Specificity of the EMT Transcriptional Response. Nat. Commun. 2020, 11, 2142. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortez, P. Data Mining with Neural Networks and Support Vector Machines Using the R/Rminer Tool. In Advances in Data Mining: Applications and Theoretical Aspects; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6171 LNAI, pp. 572–583. [Google Scholar]
- Bzdok, D.; Krzywinski, M.; Altman, N. Points of Significance: Machine Learning: Supervised Methods. Nat. Methods 2018, 15, 5–6. [Google Scholar] [CrossRef]
- Kolch, W.; Halasz, M.; Granovskaya, M.; Kholodenko, B.N. The Dynamic Control of Signal Transduction Networks in Cancer Cells. Nat. Rev. Cancer 2015, 15, 515–527. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 27, ISBN 9780387848570. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Kolch, W.; Rukhlenko, O.S. Reversing Pathological Cell States: The Road Less Travelled Can Extend the Therapeutic Horizon. Trends Cell Biol. 2023, 33, 913–923. [Google Scholar] [CrossRef]
- Yabaji, S.M.; Rukhlenko, O.S.; Chatterjee, S.; Bhattacharya, B.; Wood, E.; Kasaikina, M.; Kholodenko, B.N.; Gimelbrant, A.A.; Kramnik, I. Cell State Transition Analysis Identifies Interventions That Improve Control of Mycobacterium Tuberculosis Infection by Susceptible Macrophages. Sci. Adv. 2023, 9, eadh4119. [Google Scholar] [CrossRef] [PubMed]
- Haken, H. Synergetics Introduction and Advanced Topics; Springer: New York, NY, USA, 2004; ISBN 3-540-40824-X. [Google Scholar]
- Santra, T.; Rukhlenko, O.; Zhernovkov, V.; Kholodenko, B.N. Reconstructing Static and Dynamic Models of Signaling Pathways Using Modular Response Analysis. Curr. Opin. Syst. Biol. 2018, 9, 11–21. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Westerhoff, H.V. The Macroworld versus the Microworld of Biochemical Regulation and Control. Trends Biochem. Sci. 1995, 20, 52–54. [Google Scholar] [CrossRef] [PubMed]
- Peterson, A.F.; Ingram, K.; Huang, E.J.; Parksong, J.; McKenney, C.; Bever, G.S.; Regot, S. Systematic Analysis of the MAPK Signaling Network Reveals MAP3K-Driven Control of Cell Fate. Cell Syst. 2022, 13, 885–894.e4. [Google Scholar] [CrossRef] [PubMed]
- Hanson, R.L.; Batchelor, E. Coordination of MAPK and P53 Dynamics in the Cellular Responses to DNA Damage and Oxidative Stress. Mol. Syst. Biol. 2022, 18, e11401. [Google Scholar] [CrossRef] [PubMed]
- Santos, S.D.M.; Verveer, P.J.; Bastiaens, P.I.H. Growth Factor-Induced MAPK Network Topology Shapes Erk Response Determining PC-12 Cell Fate. Nat. Cell Biol. 2007, 9, 324–330. [Google Scholar] [CrossRef]
- Nakakuki, T.; Birtwistle, M.R.; Saeki, Y.; Yumoto, N.; Ide, K.; Nagashima, T.; Brusch, L.; Ogunnaike, B.A.; Okada-Hatakeyama, M.; Kholodenko, B.N. Ligand-Specific c-Fos Expression Emerges from the Spatiotemporal Control of ErbB Network Dynamics. Cell 2010, 141, 884–896. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N.; Hoek, J.B.; Westerhoff, H.V.; Brown, G.C. Quantification of Information Transfer via Cellular Signal Transduction Pathways. FEBS Lett. 1997, 414, 430–434. [Google Scholar] [CrossRef]
- Sontag, E.; Kiyatkin, A.; Kholodenko, B.N. Inferring Dynamic Architecture of Cellular Networks Using Time Series of Gene Expression, Protein and Metabolite Data. Bioinformatics 2004, 20, 1877–1886. [Google Scholar] [CrossRef]
- Yalamanchili, N.; Zak, D.E.; Ogunnaike, B.A.; Schwaber, J.S.; Kriete, A.; Kholodenko, B.N. Quantifying Gene Network Connectivity In Silico: Scalability and Accuracy of a Modular Approach. Syst. Biol. 2006, 153, 236–246. [Google Scholar] [CrossRef][Green Version]
- Bastiaens, P.; Birtwistle, M.R.; Blüthgen, N.; Bruggeman, F.J.; Cho, K.H.; Cosentino, C.; De La Fuente, A.; Hoek, J.B.; Kiyatkin, A.; Klamt, S.; et al. Silence on the Relevant Literature and Errors in Implementation. Nat. Biotechnol. 2015, 33, 336–339. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N. Untangling the Signalling Wires. Nat. Cell Biol. 2007, 9, 247–249. [Google Scholar] [CrossRef] [PubMed]
- Mekedem, M.; Ravel, P.; Colinge, J. Application of Modular Response Analysis to Medium- to Large-Size Biological Systems. PLoS Comput. Biol. 2022, 18, e1009312. [Google Scholar] [CrossRef] [PubMed]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring Regulatory Networks from Expression Data Using Tree-Based Methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context. BMC Bioinform. 2006, 7, S7. [Google Scholar] [CrossRef] [PubMed]
- Thomaseth, C.; Fey, D.; Santra, T.; Rukhlenko, O.S.; Radde, N.E.; Kholodenko, B.N. Impact of Measurement Noise, Experimental Design, and Estimation Methods on Modular Response Analysis Based Network Reconstruction. Sci. Rep. 2018, 8, 16217. [Google Scholar] [CrossRef] [PubMed]
- Santra, T.; Kolch, W.; Kholodenko, B.N. Integrating Bayesian Variable Selection with Modular Response Analysis to Infer Biochemical Network Topology. BMC Syst. Biol. 2013, 7, 57. [Google Scholar] [CrossRef] [PubMed]
- Halasz, M.; Kholodenko, B.N.; Kolch, W.; Santra, T. Integrating Network Reconstruction with Mechanistic Modeling to Predict Cancer Therapies. Sci. Signal. 2016, 9, ra114. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, M.J.; Perrone, M.C.; Riggio, M.; Palafox, M.; Salinas, V.; Elia, A.; Salgueiro, N.D.; Werbach, A.E.; Marks, M.P.; Kauffman, M.A.; et al. Targeting MTOR to Overcome Resistance to Hormone and CDK4/6 Inhibitors in ER-Positive Breast Cancer Models. Sci. Rep. 2023, 13, 2710. [Google Scholar] [CrossRef]
- Rotundo, M.S.; Galeano, T.; Tassone, P.; Tagliaferri, P. MTOR Inhibitors, a New Era for Metastatic Luminal HER2-Negative Breast Cancer? A Systematic Review and a Meta-Analysis of Randomized Trials. Oncotarget 2016, 7, 27055–27066. [Google Scholar] [CrossRef]
- Hollestelle, A.; Nagel, J.H.A.; Smid, M.; Lam, S.; Elstrodt, F.; Wasielewski, M.; Ng, S.S.; French, P.J.; Peeters, J.K.; Rozendaal, M.J.; et al. Distinct Gene Mutation Profiles among Luminal-Type and Basal-Type Breast Cancer Cell Lines. Breast Cancer Res. Treat. 2010, 121, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Cheng, H.; Bai, Z.; Li, J. Breast Cancer Cell Line Classification and Its Relevance with Breast Tumor Subtyping. J. Cancer 2017, 8, 3131–3141. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Soares, J.; Greninger, P.; Edelman, E.J.; Lightfoot, H.; Forbes, S.; Bindal, N.; Beare, D.; Smith, J.A.; Thompson, I.R.; et al. Genomics of Drug Sensitivity in Cancer (GDSC): A Resource for Therapeutic Biomarker Discovery in Cancer Cells. Nucleic Acids Res. 2013, 41, 955–961. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N.; Rauch, N.; Kolch, W.; Rukhlenko, O.S. A Systematic Analysis of Signaling Reactivation and Drug Resistance. Cell Rep. 2021, 35, 109157. [Google Scholar] [CrossRef] [PubMed]
- Sturm, O.E.; Orton, R.; Grindlay, J.; Birtwistle, M.; Vyshemirsky, V.; Gilbert, D.; Calder, M.; Pitt, A.; Kholodenko, B.; Kolch, W. The Mammalian MAPK/ERK Pathway Exhibits Properties of a Negative Feedback Amplifier. Sci. Signal. 2010, 3, ra90. [Google Scholar] [CrossRef] [PubMed]
- Neve, R.M.; Chin, K.; Fridlyand, J.; Yeh, J.; Baehner, F.L.; Fevr, T.; Clark, L.; Bayani, N.; Coppe, J.P.; Tong, F.; et al. A Collection of Breast Cancer Cell Lines for the Study of Functionally Distinct Cancer Subtypes. Cancer Cell 2006, 10, 515–527. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N.; Demin, O.V.; Moehren, G.; Hoek, J.B. Quantification of Short Term Signaling by the Epidermal Growth Factor Receptor. J. Biol. Chem. 1999, 274, 30169–30181. [Google Scholar] [CrossRef] [PubMed]
- Bruggeman, F.J.; Westerhoff, H.V.; Hoek, J.B.; Kholodenko, B.N. Modular Response Analysis of Cellular Regulatory Networks. J. Theor. Biol. 2002, 218, 507–520. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, P.; Kofia, V.; Maru, A.; Freeman, M.; Ho, C.; El-Hachem, N.; Adam, G.A.; Ba-Alawi, W.; Safikhani, Z.; Haibe-Kains, B. PharmacoDB: An Integrative Database for Mining in Vitro Anticancer Drug Screening Studies. Nucleic Acids Res. 2018, 46, D994–D1002. [Google Scholar] [CrossRef]
- Rukhlenko, O.S.; Khorsand, F.; Krstic, A.; Rozanc, J.; Alexopoulos, L.G.; Rauch, N.; Erickson, K.E.; Hlavacek, W.S.; Posner, R.G.; Gómez-Coca, S.; et al. Dissecting RAF Inhibitor Resistance by Structure-Based Modeling Reveals Ways to Overcome Oncogenic RAS Signaling. Cell Syst. 2018, 7, 161–179.e14. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Sontag, E.D. Determination of Functional Network Structure from Local Parameter Dependence Data. arXiv 2002, arXiv:physics/0205003v1. [Google Scholar]
- Bolado-Carrancio, A.; Rukhlenko, O.S.; Nikonova, E.; Tsyganov, M.A.; Wheeler, A.; Garcia-Munoz, A.; Kolch, W.; von Kriegsheim, A.; Kholodenko, B.N. Periodic Propagating Waves Coordinate Rhogtpase Network Dynamics at the Leading and Trailing Edges during Cell Migration. Elife 2020, 9, e58165. [Google Scholar] [CrossRef] [PubMed]
- Aksamitiene, E.; Kiyatkin, A.; Kholodenko, B.N. Cross-Talk between Mitogenic Ras/MAPK and Survival PI3K/Akt Pathways: A Fine Balance. Biochem. Soc. Trans. 2012, 40, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Molinelli, E.J.; Korkut, A.; Wang, W.; Miller, M.L.; Gauthier, N.P.; Jing, X.; Kaushik, P.; He, Q.; Mills, G.; Solit, D.B.; et al. Perturbation Biology: Inferring Signaling Networks in Cellular Systems. PLoS Comput. Biol. 2013, 9, e1003290. [Google Scholar] [CrossRef] [PubMed]
- Meunier, P.Y.; Raynaud, C.; Guimaraes, E.; Gueyffier, F.; Letrilliart, L. Barriers and Facilitators to the Use of Clinical Decision Support Systems in Primary Care: A Mixed-Methods Systematic Review. Ann. Fam. Med. 2023, 21, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N.; Cascante, M.; Hoek, J.B.; Westerhoff, H.V.; Schwaber, J. Metabolic Design: How to Engineer a Living Cell to Desired Metabolite Concentrations and Fluxes. Biotechnol. Bioeng. 1998, 59, 239–247. [Google Scholar] [CrossRef]
- Takahashi, K.; Yamanaka, S. Induction of Pluripotent Stem Cells from Mouse Embryonic and Adult Fibroblast Cultures by Defined Factors. Cell 2006, 126, 663–676. [Google Scholar] [CrossRef]
- Jia, D.; Jolly, M.K.; Kulkarni, P.; Levine, H. Phenotypic Plasticity and Cell Fate Decisions in Cancer: Insights from Dynamical Systems Theory. Cancers 2017, 9, 70. [Google Scholar] [CrossRef]
- Moris, N.; Pina, C.; Arias, A.M. Transition States and Cell Fate Decisions in Epigenetic Landscapes. Nat. Rev. Genet. 2016, 17, 693–703. [Google Scholar] [CrossRef]
- Hafner, A.; Bulyk, M.L.; Jambhekar, A.; Lahav, G. The Multiple Mechanisms That Regulate P53 Activity and Cell Fate. Nat. Rev. Mol. Cell Biol. 2019, 20, 199–210. [Google Scholar] [CrossRef]
- Patel, R.; Islam, S.A.; Bommareddy, R.R.; Smalley, T.; Acevedo-Duncan, M. Simultaneous Inhibition of Atypical Protein Kinase-C and MTOR Impedes Bladder Cancer Cell Progression. Int. J. Oncol. 2020, 56, 1373–1386. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rukhlenko, O.S.; Imoto, H.; Tambde, A.; McGillycuddy, A.; Junk, P.; Tuliakova, A.; Kolch, W.; Kholodenko, B.N. Cell State Transition Models Stratify Breast Cancer Cell Phenotypes and Reveal New Therapeutic Targets. Cancers 2024, 16, 2354. https://doi.org/10.3390/cancers16132354
Rukhlenko OS, Imoto H, Tambde A, McGillycuddy A, Junk P, Tuliakova A, Kolch W, Kholodenko BN. Cell State Transition Models Stratify Breast Cancer Cell Phenotypes and Reveal New Therapeutic Targets. Cancers. 2024; 16(13):2354. https://doi.org/10.3390/cancers16132354
Chicago/Turabian StyleRukhlenko, Oleksii S., Hiroaki Imoto, Ayush Tambde, Amy McGillycuddy, Philipp Junk, Anna Tuliakova, Walter Kolch, and Boris N. Kholodenko. 2024. "Cell State Transition Models Stratify Breast Cancer Cell Phenotypes and Reveal New Therapeutic Targets" Cancers 16, no. 13: 2354. https://doi.org/10.3390/cancers16132354
APA StyleRukhlenko, O. S., Imoto, H., Tambde, A., McGillycuddy, A., Junk, P., Tuliakova, A., Kolch, W., & Kholodenko, B. N. (2024). Cell State Transition Models Stratify Breast Cancer Cell Phenotypes and Reveal New Therapeutic Targets. Cancers, 16(13), 2354. https://doi.org/10.3390/cancers16132354





