Figure 1.
Eash WSI is represented in the context of tumor heterogeneity for biomarker discovery: (a) a WSI is partitioned to patches of 224-by-224, where each patch is analyzed for pen marks or other aberrations; (b) nuclei are segmented in patches; (c) H&E optical density is normalized in each patch; (d) nuclei organization is quantified in each patch; (e,f) computed indices from nuclei and their organizations are used for the dictionary- and PDF-based representations. (g) Predictive morphometric indices of survival are identified.
Figure 1.
Eash WSI is represented in the context of tumor heterogeneity for biomarker discovery: (a) a WSI is partitioned to patches of 224-by-224, where each patch is analyzed for pen marks or other aberrations; (b) nuclei are segmented in patches; (c) H&E optical density is normalized in each patch; (d) nuclei organization is quantified in each patch; (e,f) computed indices from nuclei and their organizations are used for the dictionary- and PDF-based representations. (g) Predictive morphometric indices of survival are identified.
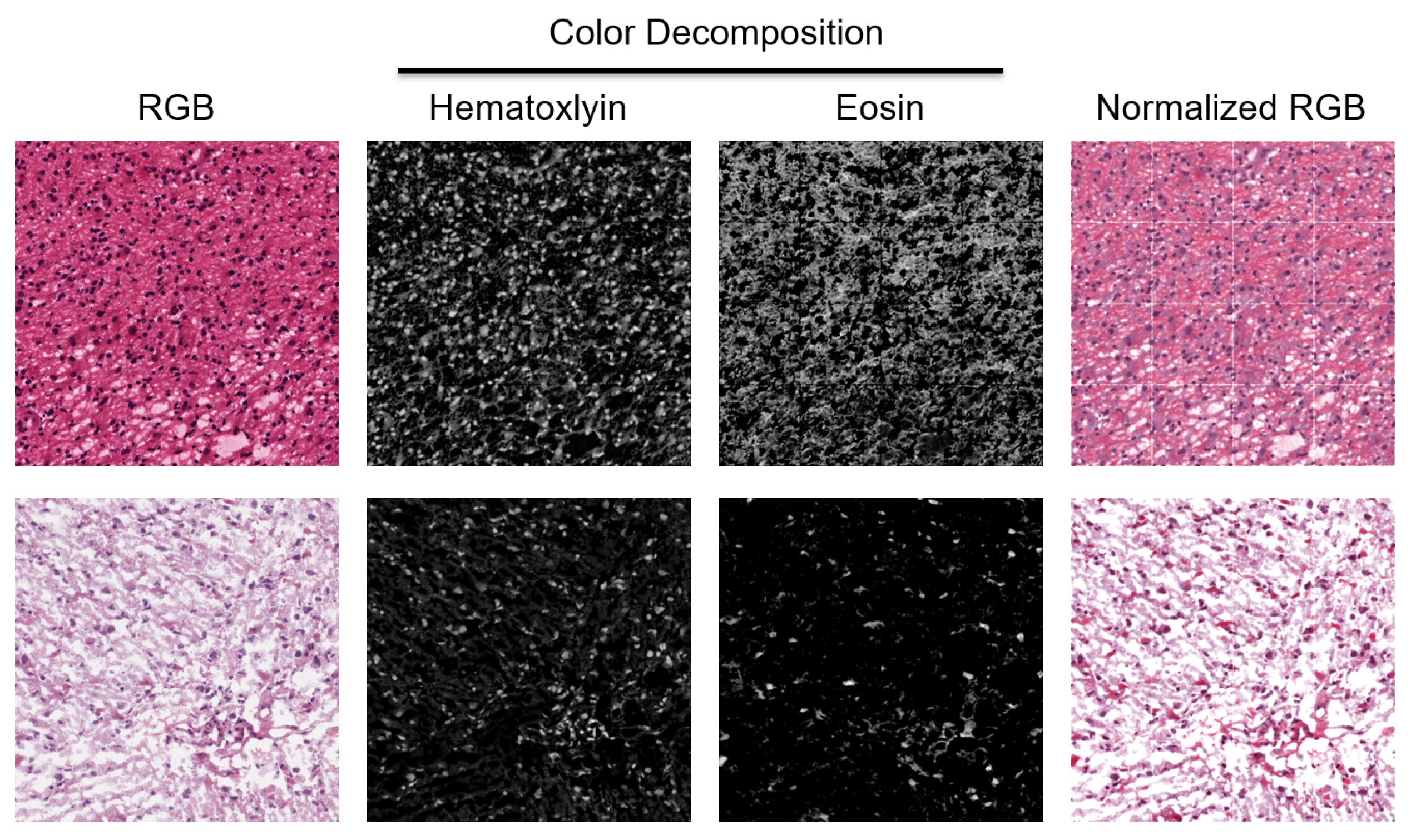
Figure 2.
H&E stain is heterogeneous between patients. Two patches from two WSIs indicate a diverse staining signature. They are normalized for quantifying HOD and visualized in the RGB space.
Figure 2.
H&E stain is heterogeneous between patients. Two patches from two WSIs indicate a diverse staining signature. They are normalized for quantifying HOD and visualized in the RGB space.
Figure 3.
Dictionary-based learning identified two and three subpopulation (e.g., clusters) of patients based on cellularity and eccentricity indices, respectively. (top row): Computed similarity matrices; (middle row) the cumulative Density Function (CDF) of similarity matrices shows the quality of the number of clusters for each index (e.g., a flat horizontal line indicates a low number of misclassified samples between clusters). (bottom row) Silhouette plots of 800,000 randomly sampled nuclei show the similarity of patients within a cluster (e.g., a silhouette score less than 1) and a red dashed indicating the average silhouette score.
Figure 3.
Dictionary-based learning identified two and three subpopulation (e.g., clusters) of patients based on cellularity and eccentricity indices, respectively. (top row): Computed similarity matrices; (middle row) the cumulative Density Function (CDF) of similarity matrices shows the quality of the number of clusters for each index (e.g., a flat horizontal line indicates a low number of misclassified samples between clusters). (bottom row) Silhouette plots of 800,000 randomly sampled nuclei show the similarity of patients within a cluster (e.g., a silhouette score less than 1) and a red dashed indicating the average silhouette score.
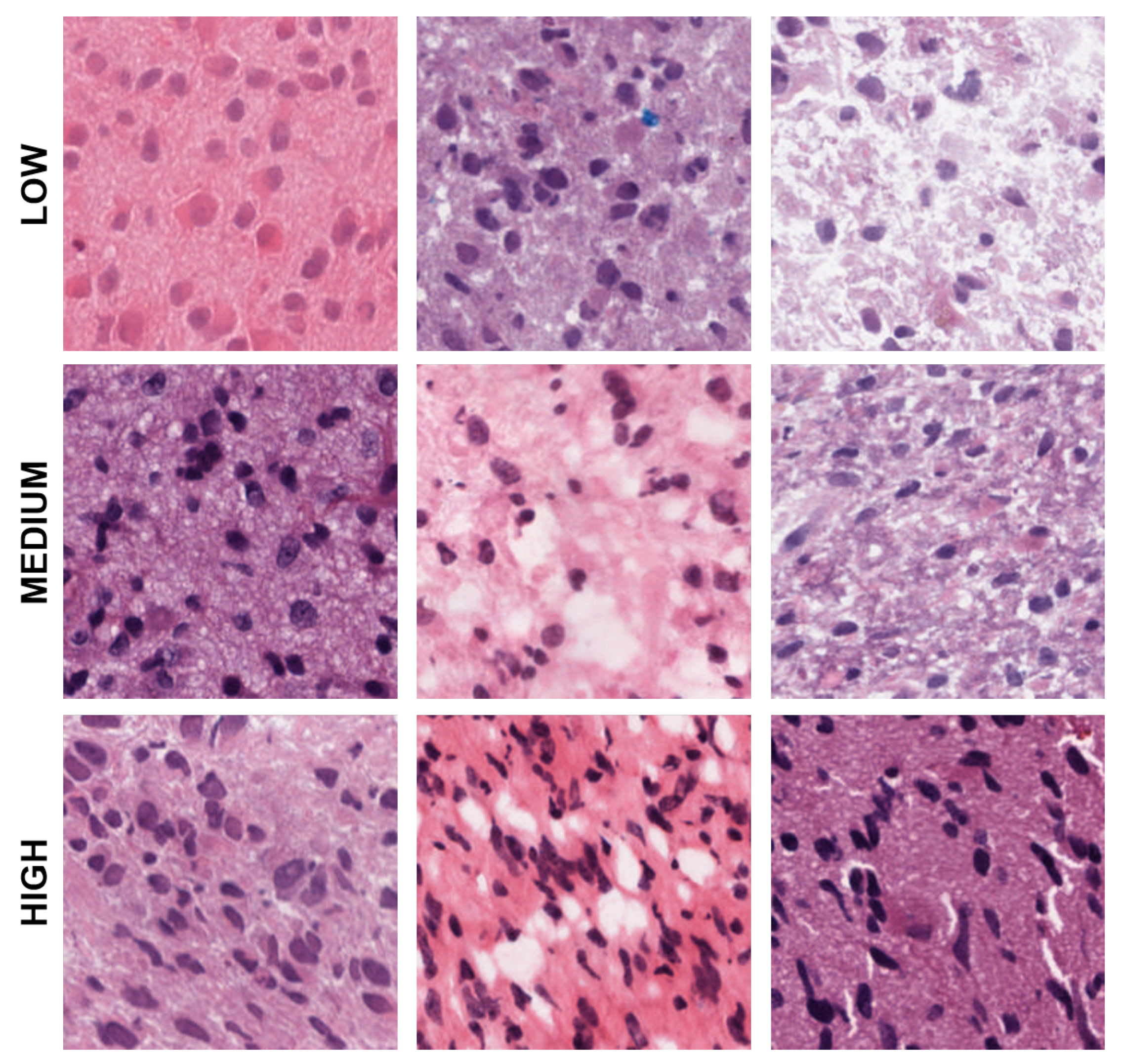
Figure 4.
Representative patches showing low, medium, and high eccentricities corresponding to clusters 1, 2, and 3 from the dictionary-based method.
Figure 4.
Representative patches showing low, medium, and high eccentricities corresponding to clusters 1, 2, and 3 from the dictionary-based method.
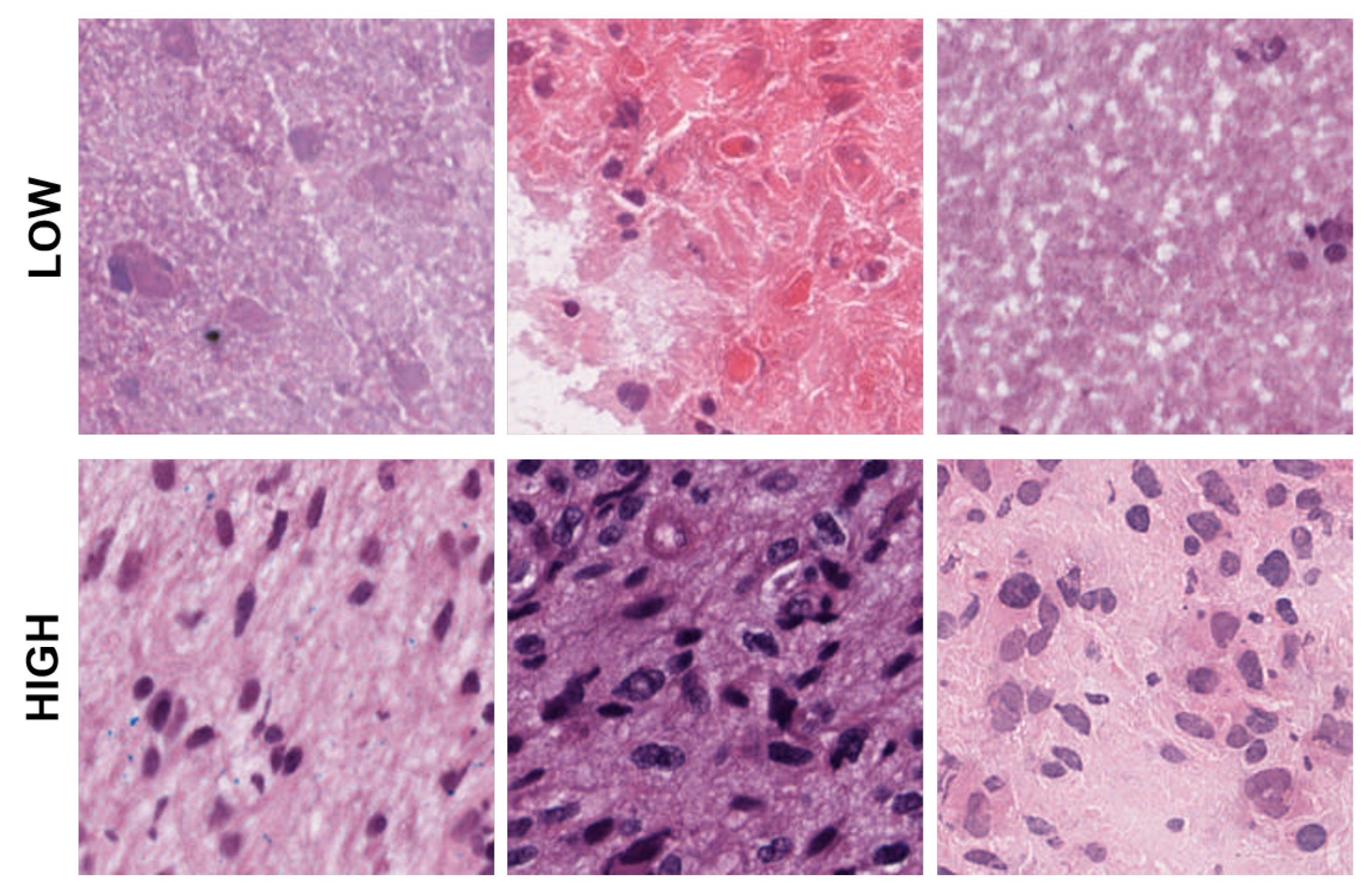
Figure 5.
Representative patches showing low, and high cellularities corresponding to clusters 1 and 2 from the dictionary-method.
Figure 5.
Representative patches showing low, and high cellularities corresponding to clusters 1 and 2 from the dictionary-method.
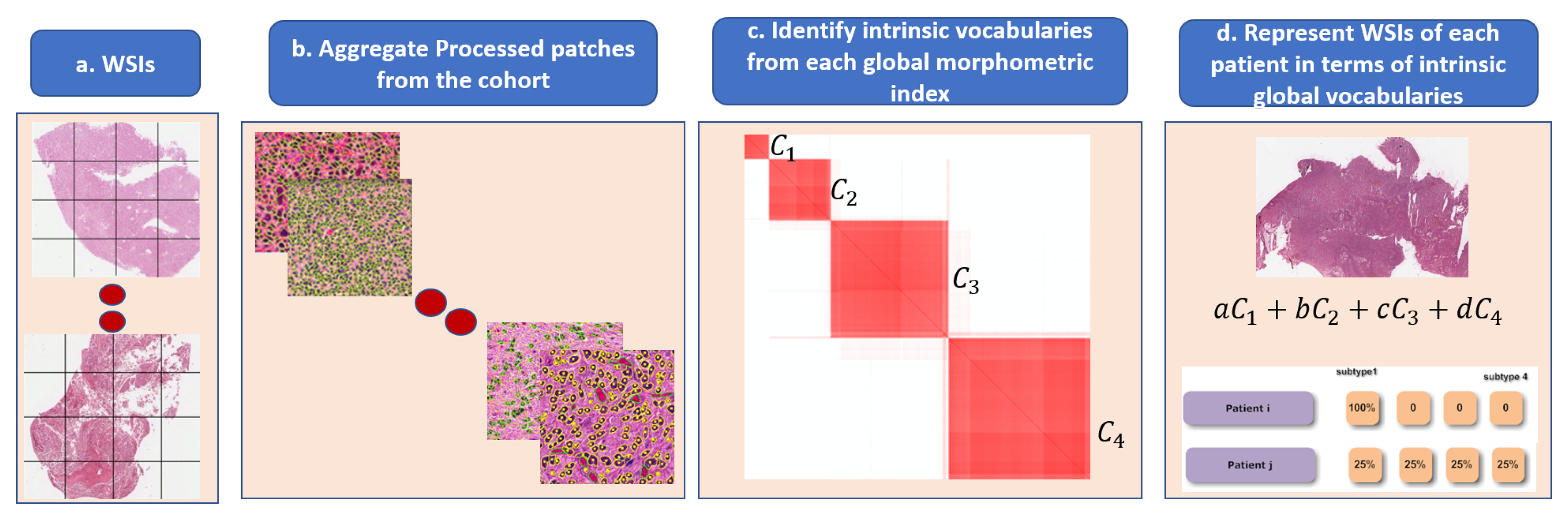
Figure 6.
Steps in the dictionary-based method for representing heterogeneity: (a) each WSI is partitioned into patches; (b) each patch is quantified in terms of nuclear indices and organization; (c) each computed index (e.g., HOD content, nuclear size) is aggregated across the entire cohort for dictionary-based learning (e.g., alphabets, which are four in this example); and (d) each WSI is then represented as a composition of learned alphabets.
Figure 6.
Steps in the dictionary-based method for representing heterogeneity: (a) each WSI is partitioned into patches; (b) each patch is quantified in terms of nuclear indices and organization; (c) each computed index (e.g., HOD content, nuclear size) is aggregated across the entire cohort for dictionary-based learning (e.g., alphabets, which are four in this example); and (d) each WSI is then represented as a composition of learned alphabets.
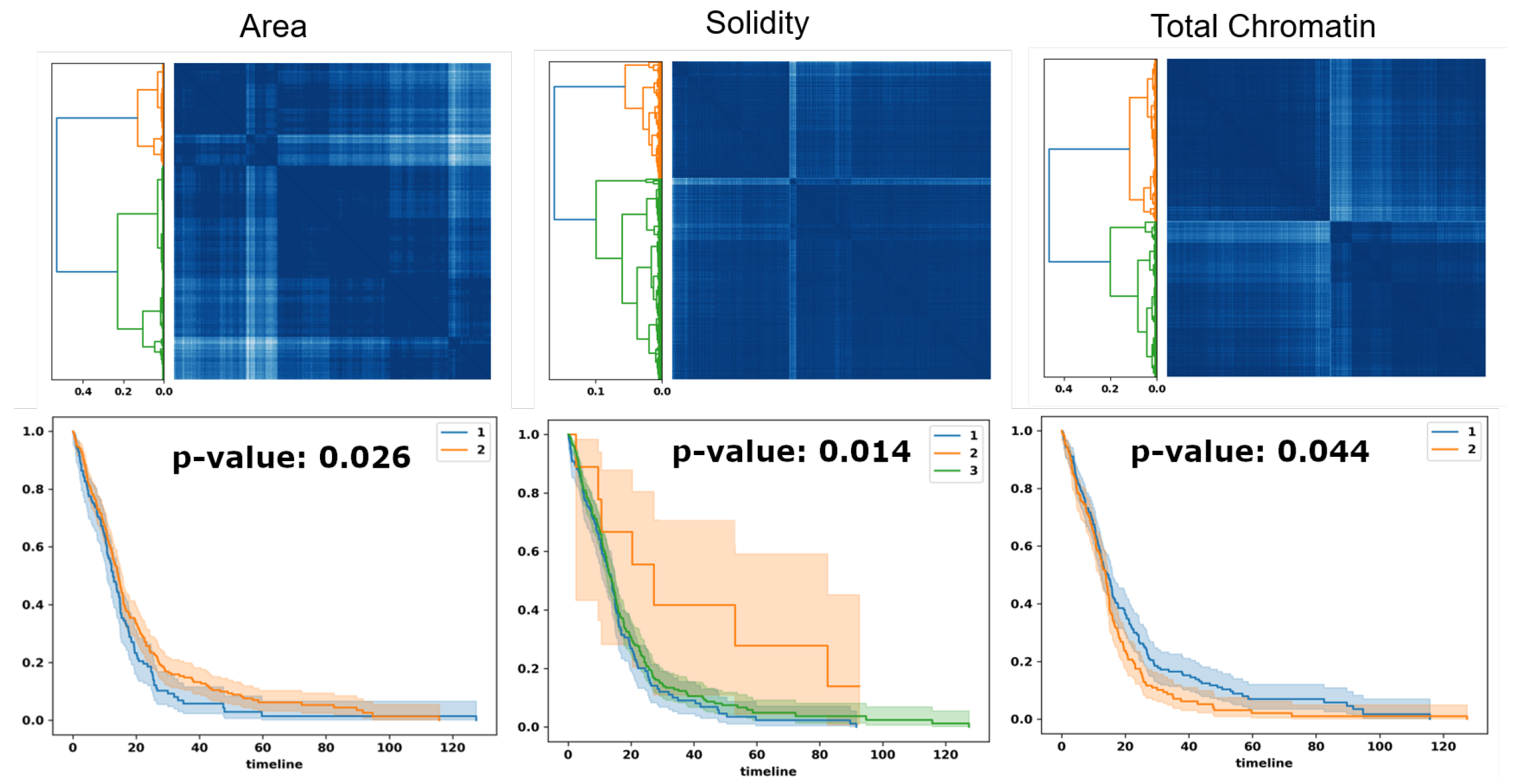
Figure 7.
Optimal transport identifies subpopulations of patients, based on PDF representation, for survival analysis. Top row: similarity matrices identified by linkage analysis; Bottom row: Kaplan–Meier plots, hazard ratio, and computed p-values for three computed morphometric indices of nuclear size, solidity, and total chromatin.
Figure 7.
Optimal transport identifies subpopulations of patients, based on PDF representation, for survival analysis. Top row: similarity matrices identified by linkage analysis; Bottom row: Kaplan–Meier plots, hazard ratio, and computed p-values for three computed morphometric indices of nuclear size, solidity, and total chromatin.
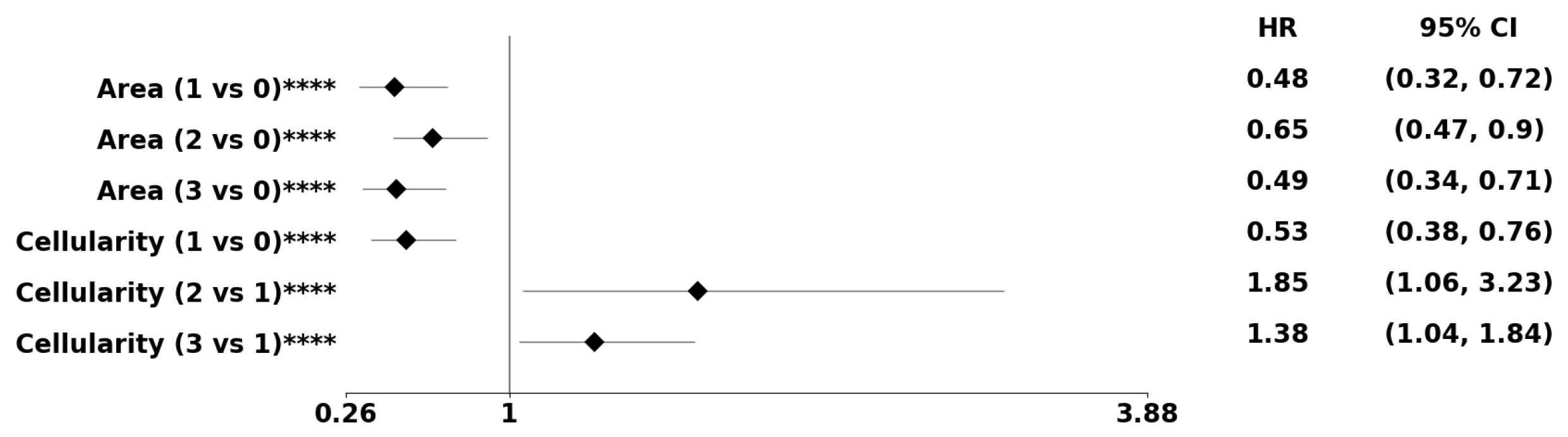
Figure 8.
The forest plot indicates biomarkers associated with the subpopulation at risk using the PDF-based representation without any genomic preconditioning. The asterisks **, ***, and **** denote the number of stratifications per morphometric index.
Figure 8.
The forest plot indicates biomarkers associated with the subpopulation at risk using the PDF-based representation without any genomic preconditioning. The asterisks **, ***, and **** denote the number of stratifications per morphometric index.
Figure 9.
Using the PDF method, pre-conditioned on the classical subtype, the forest plot indicates the subpopulation at risk. The asterisks **, ***, and **** denote the number of stratifications per morphometric index.
Figure 9.
Using the PDF method, pre-conditioned on the classical subtype, the forest plot indicates the subpopulation at risk. The asterisks **, ***, and **** denote the number of stratifications per morphometric index.
Figure 10.
Using the PDF method, pre-conditioned on a high EGFR expression, the forest plot indicates the subpopulation at risk. For example, Area cluster two has an 52% decreased risk of death compared to Area cluster zero. The asterisks **** denote the number of stratifications per morphometric index.
Figure 10.
Using the PDF method, pre-conditioned on a high EGFR expression, the forest plot indicates the subpopulation at risk. For example, Area cluster two has an 52% decreased risk of death compared to Area cluster zero. The asterisks **** denote the number of stratifications per morphometric index.
Table 1.
Predicted morphometric biomarkers and their p-values from patients in the TCGA-GBM cohort.
Table 1.
Predicted morphometric biomarkers and their p-values from patients in the TCGA-GBM cohort.
| | Morphometric Index | Number of Clusters | p-Value |
|---|
| (a) PDF model | | | |
| | Area | 2 | 0.026 |
| | Area | 3 | 0.016 |
| | Area | 4 | 0.013 |
| | Mean HOD | 3 | 0.016 |
| | Mean HOD | 4 | 0.006 |
| | Solidity | 3 | 0.014 |
| | Solidity | 4 | 0.007 |
| | Total HOD | 2 | 0.044 |
| | Total HOD | 3 | 0.037 |
| | Total HOD | 4 | 0.025 |
| (b) Dictionary model | | | |
| | Cellularity | 2 | 0.008 |
| | Cellularity | 3 | 0.040 |
| | Eccentricity | 2 | 0.002 |
| | Eccentricity | 3 | 0.005 |
| | Eccentricity | 4 | 0.011 |
| | Mean HOD | 2 | 0.019 |
Table 2.
Predicted morphometric biomarkers and their p-values for the combined model without genomic preconditioning.
Table 2.
Predicted morphometric biomarkers and their p-values for the combined model without genomic preconditioning.
| Nuclear Morphometric Index | Number of Clusters | p-Value |
|---|
| Cellularity | 2 | 0.025 |
| Eccentricity | 2 | 0.007 |
| Eccentricity | 3 | 0.013 |
| Eccentricity | 4 | 0.019 |
| Mean HOD | 4 | 0.028 |
Table 3.
Predicted morphometric biomarkers for the PDF- and dictionary-based models preconditioned on genomic subtypes.
Table 3.
Predicted morphometric biomarkers for the PDF- and dictionary-based models preconditioned on genomic subtypes.
| Nuclear Morphometric Index | Number of Clusters | p-Value |
|---|
| Neural | Proneural | Mesenchymal | Classical |
|---|
| (a) PDF method | | | | | |
| Area | 2 | 0.021 | - | - | - |
| Area | 3 | 0.020 | - | - | 0.009 |
| Area | 4 | 0.018 | - | - | 0.006 |
| Mean HOD | 4 | 0.024 | - | - | - |
| Solidity | 3 | 0.006 | - | - | - |
| Solidity | 4 | <0.001 | - | 0.009 | - |
| Total HOD | 2 | - | - | - | 0.019 |
| Total HOD | 3 | - | - | - | 0.008 |
| Total HOD | 4 | - | - | - | 0.008 |
| (b) Dictionary method | | | | | |
| Area | 4 | - | - | - | 0.040 |
| Total HOD | 2 | <0.001 | - | - | - |
| Total HOD | 3 | 0.008 | - | - | - |
| Total HOD | 4 | 0.003 | - | - | - |
Table 4.
Predicted morphometric biomarkers and their p-values for the combined model preconditioned on genomic subtypes.
Table 4.
Predicted morphometric biomarkers and their p-values for the combined model preconditioned on genomic subtypes.
| Nuclear Morphometric Index | Number of Clusters | p-Value |
|---|
| Neural | Proneural | Mesenchymal | Classical |
|---|
| Area | 2 | 0.04 | - | - | - |
| Area | 4 | - | - | - | 0.043 |
| Mean HOD | 4 | - | 0.031 | - | - |
| Solidity | 3 | 0.010 | - | - | - |
| Solidity | 4 | 0.004 | - | 0.048 | - |
| Total HOD | 2 | 0.001 | - | - | - |
| Total HOD | 3 | 0.012 | - | - | - |
| Total HOD | 4 | 0.004 | - | - | 0.036 |
Table 5.
Predicted morphometric biomarkers for the PDF- and dictionary-based models preconditioned on patients with high EGFR expression.
Table 5.
Predicted morphometric biomarkers for the PDF- and dictionary-based models preconditioned on patients with high EGFR expression.
| | Nuclear Morphometric Index | Number of Clusters | p-Value |
|---|
| (a) PDF model | | | |
| | Total HOD | 4 | 0.048 |
| (b) Dictionary model | | | |
| | Area | 2 | 0.007 |
| | Area | 3 | 0.009 |
| | Area | 4 | 0.025 |
Table 6.
Predicted morphometric biomarkers for the PDF- and dictionary-based models preconditioned on patients with low EGFR expression.
Table 6.
Predicted morphometric biomarkers for the PDF- and dictionary-based models preconditioned on patients with low EGFR expression.
| | Nuclear Morphometric Index | Number of Clusters | p-Value |
|---|
| (a) PDF model | | | |
| | Area | 4 | 0.031 |
| | Cellularity | 4 | 0.018 |
| (b) Dictionary model | | | |
| | Cellularity | 2 | 0.035 |
| | Total HOD | 2 | 0.001 |
| | Total HOD | 3 | 0.003 |
| | Total HOD | 4 | 0.009 |
Table 7.
Predicted morphometric biomarkers and their p-values for the combined model preconditioned on the EGFR transcript.
Table 7.
Predicted morphometric biomarkers and their p-values for the combined model preconditioned on the EGFR transcript.
| | Nuclear Morphometric Index | Number of Clusters | p-Value |
|---|
| (a) Biomarkers for patients with matched transcriptome data |
| | Cellularity | 2 | 0.047 |
| | Cellularity | 3 | 0.033 |
| | Cellularity | 4 | 0.019 |
| | Eccentricity | 2 | 0.040 |
| | Mean HOD | 3 | 0.010 |
| | Mean HOD | 4 | 0.004 |
| (b) Biomarkers of patients stratified with high EGFR expression |
| | Area | 3 | 0.004 |
| | Area | 4 | 0.005 |
| | Cellularity | 3 | 0.031 |
| | Cellularity | 4 | 0.009 |
| (c) Biomarkers of patients with low EGFR expression |
| | Cellularity | 2 | 0.034 |
| | Cellularity | 4 | 0.018 |
| | Mean HOD | 3 | 0.015 |
| | Mean HOD | 4 | 0.021 |
| | Total HOD | 2 | 0.001 |
| | Total HOD | 3 | 0.002 |