Impact of Aggregation Methods for Texture Features on Their Robustness Performance: Application to Nasopharyngeal 18F-FDG PET/CT
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Patients and PET/CT Imaging
2.2. Tumor Delination, Partial Volume Correction and Intensity Discretization
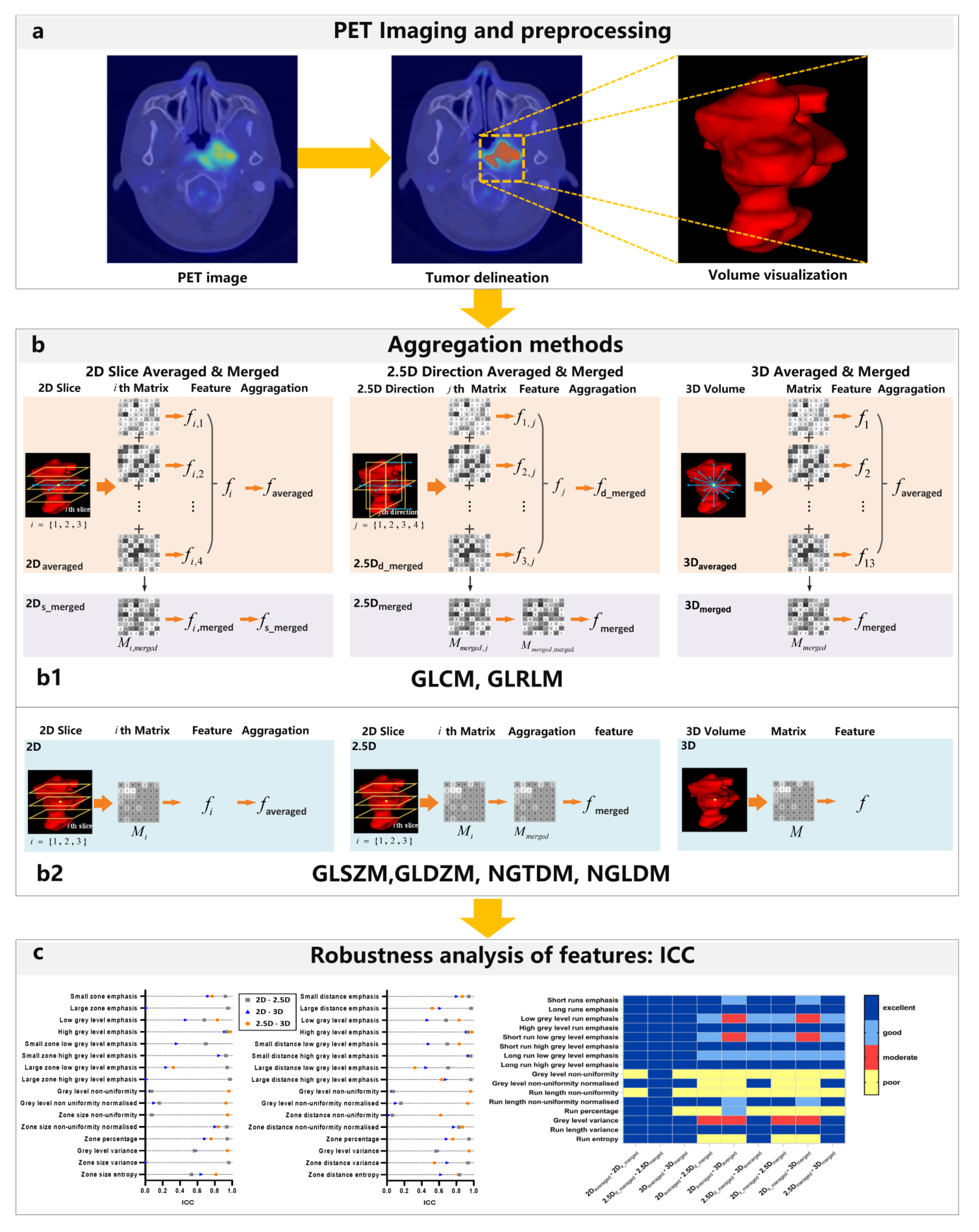
2.3. Matrix Construction with Different Aggregation Methods
- Features are computed from each 2D directional matrix and then averaged over 2D directions and slices, namely 2Daveraged;
- Features are computed from a single matrix after merging 2D directional matrices per slice, and then averaged over slices, namely 2Ds-meraged;
- Features are computed from a single matrix after merging 2D directional matrices per direction, and then averaged over directions, namely 2Dd-meraged;
- The feature is computed from a single matrix after merging all 2D directional matrices, namely 2Dmeraged;
- Features are computed from each 3D directional matrix and averaged over the 3D directions, namely 3Daveraged;
- The feature is computed from a single matrix after merging all 3D directional matrices, namely 3Dmeraged.
- Features are computed from 2D matrices and averaged over slices, namely 2D;
- The feature is computed from a single matrix after merging all 2D matrices, namely 2.5D;
- The feature is computed from a 3D matrix, namely 3D.
2.4. Feature Extraction
| Characteristic | All Patients |
|---|---|
| Patient No. | 128 |
| Age (year), mean SD | 47.7 ± 13.2 |
| Sex, no.(%) | |
| Male | 103 (80.5%) |
| Female | 25 (19.5%) |
| AJCC stage, no.(%) | |
| I | 4 (3.1%) |
| II | 11 (8.6%) |
| III | 49 (38.3%) |
| IV | 64 (50%) |
| MATV | 50.9 ± 86.4 |
| SUVmax | 15.4 ± 7.77 |
| SUVmean | 7.95 ± 3.75 |
| CTmean | 50.4 ± 55.1 |
2.5. Robustness Evaluation by Intra-Class Coefficient (ICC)
3. Results
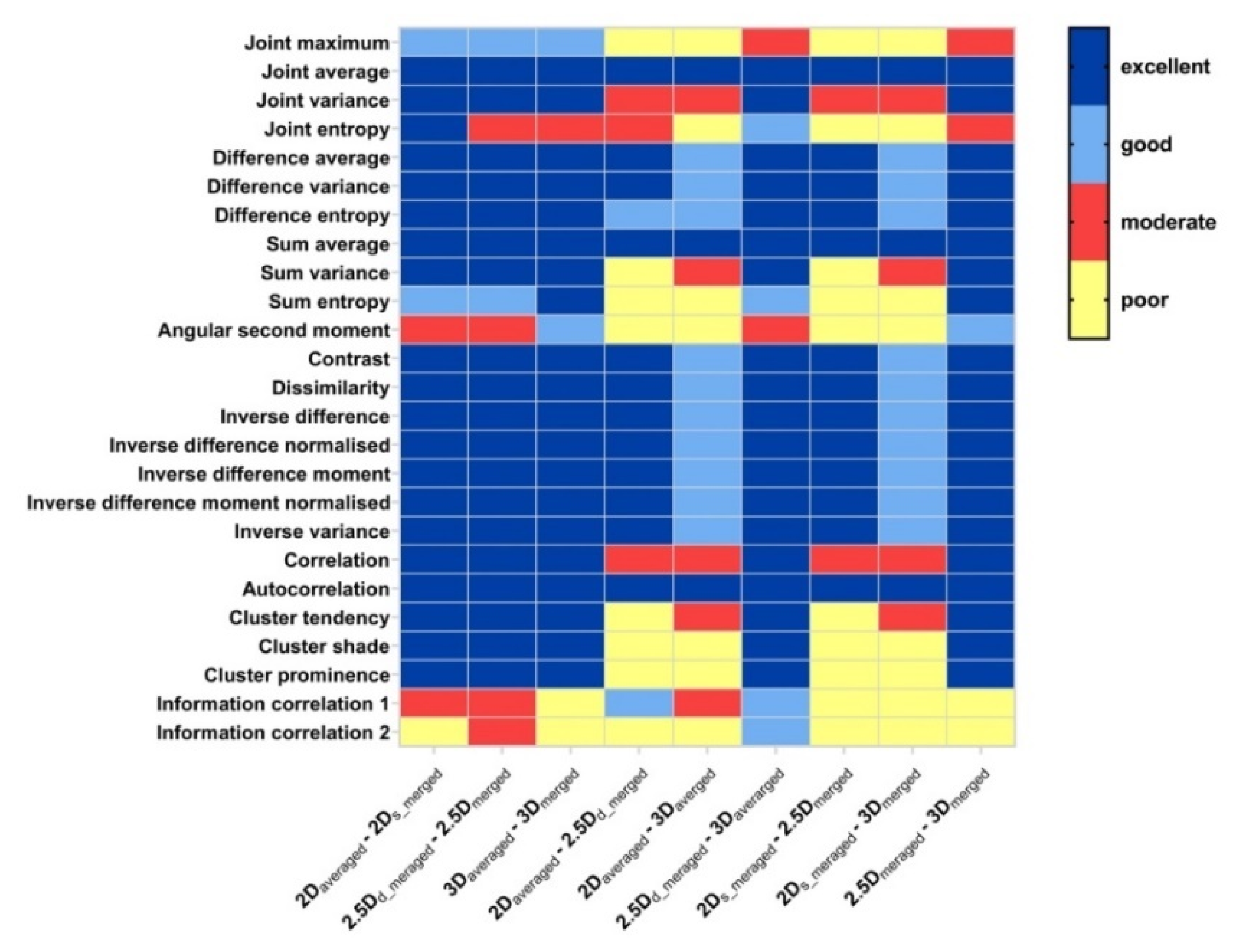
3.1. Robustness of GLCM Features Affected by Aggregation Methods
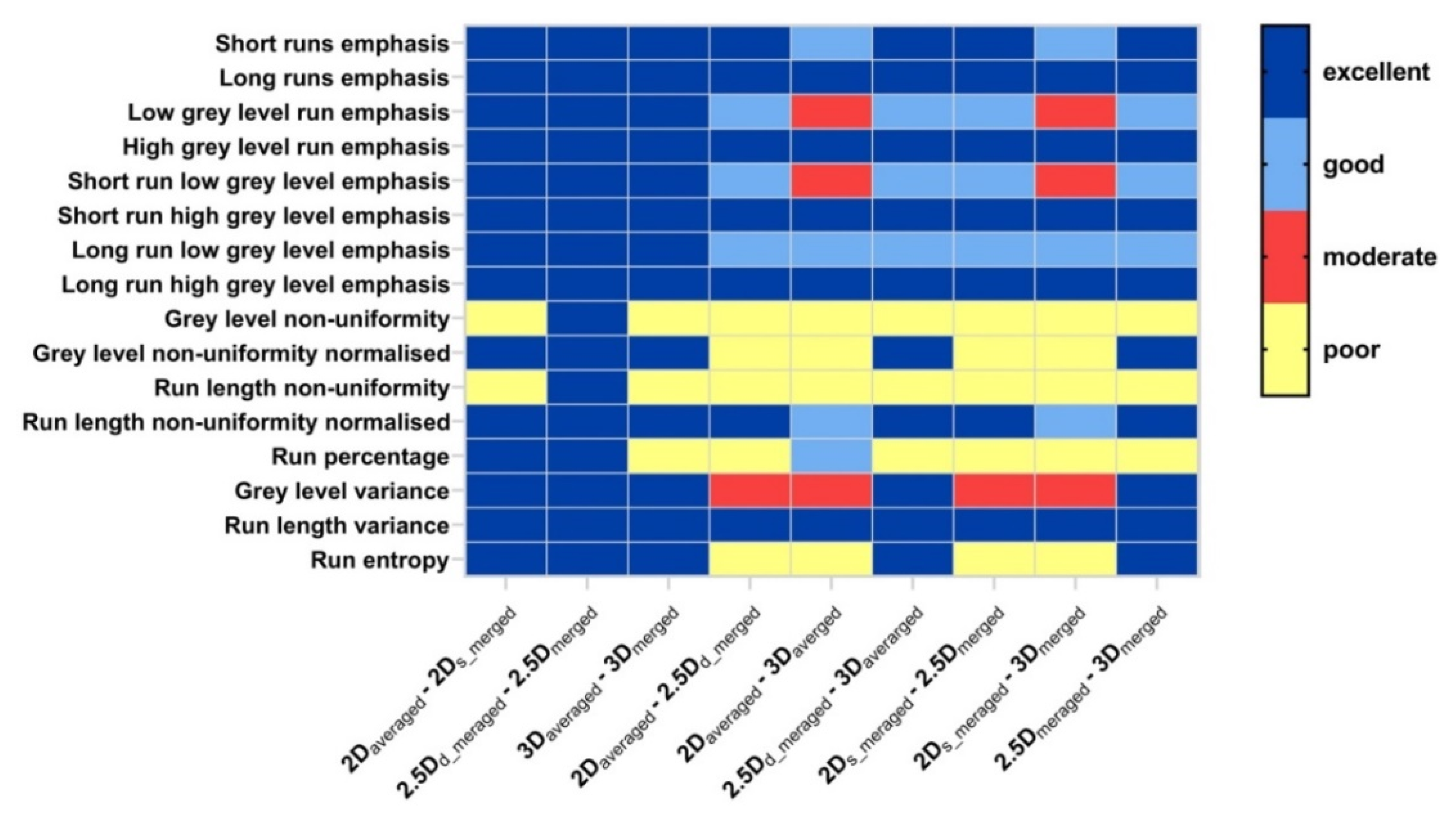
3.2. Robustness of GLRLM Features Affected by Aggregation Methods
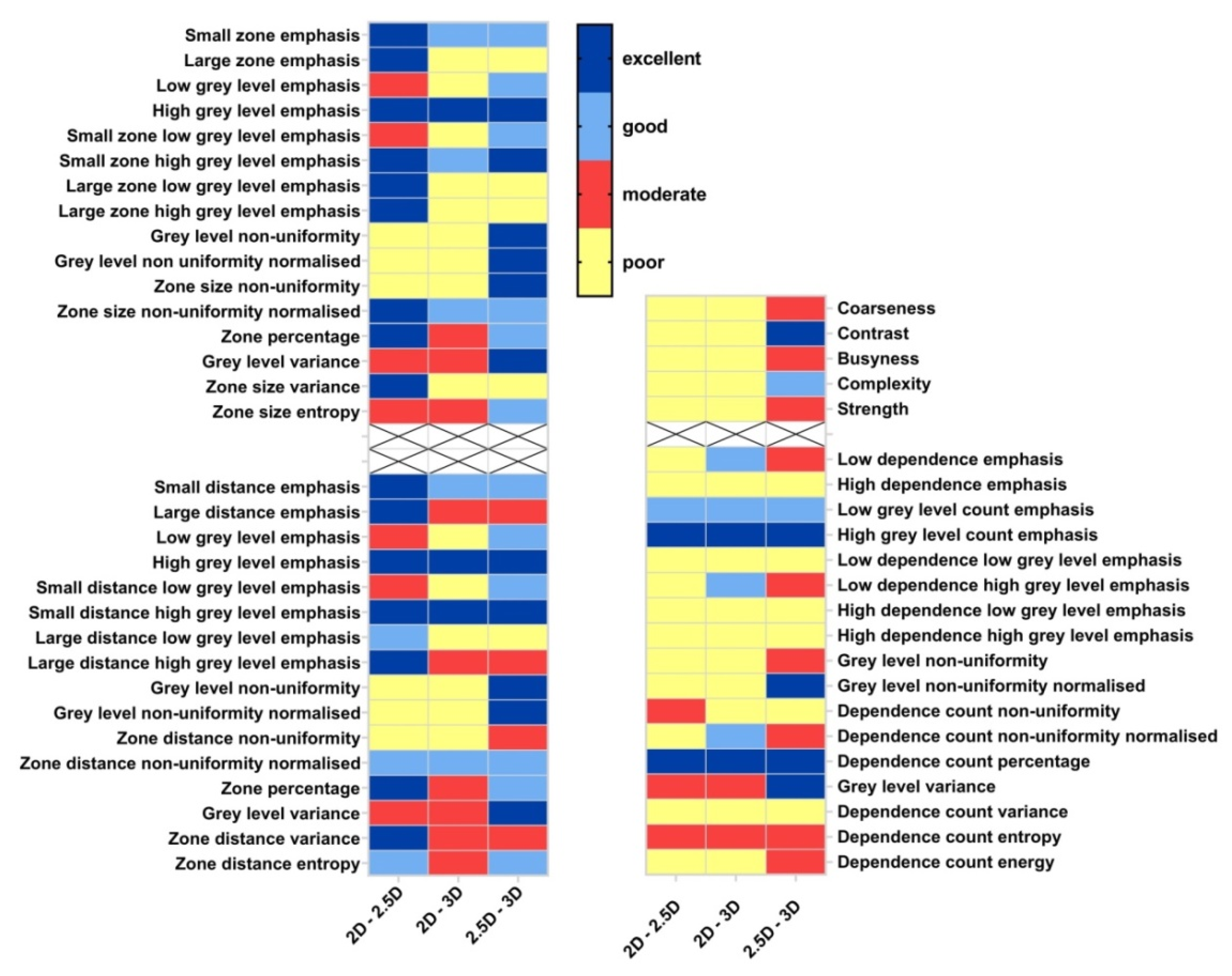
3.3. Robustness of GLSZM, GLDZM, NGLDM, NGTDM Features Affected by Aggregation Methods
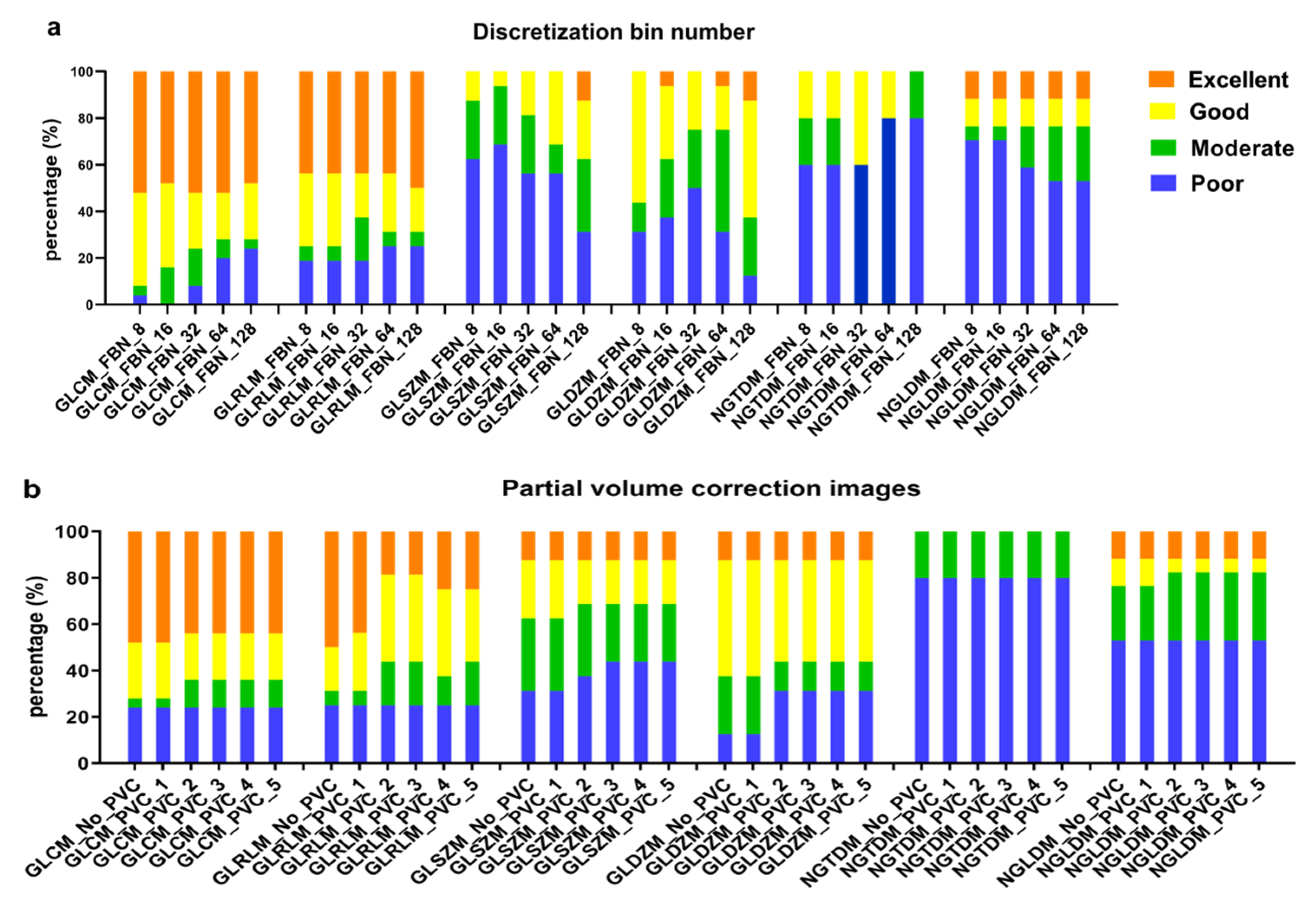
3.4. Effect of Discretization and Partial Volume Correction on Feature’s Robustness
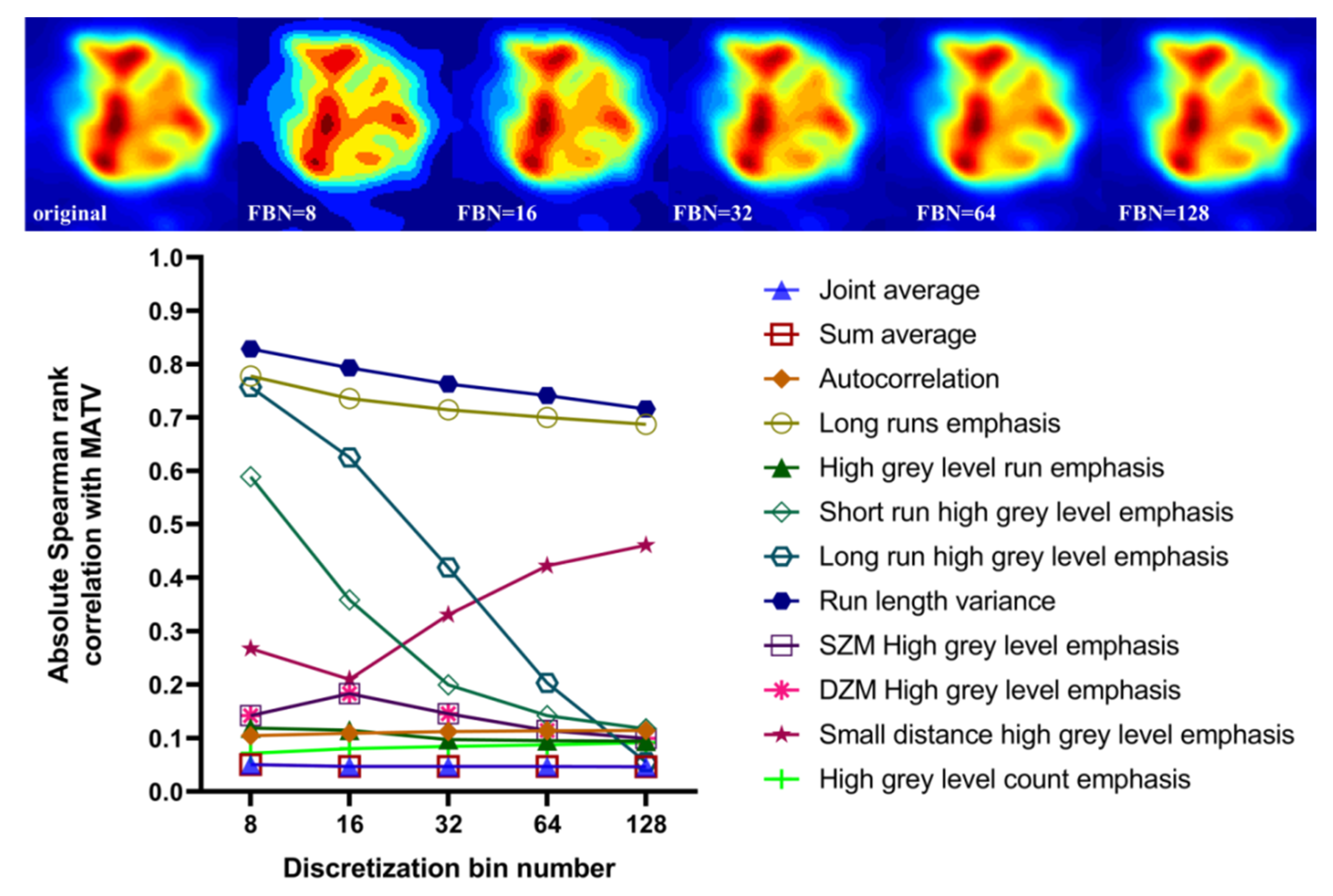
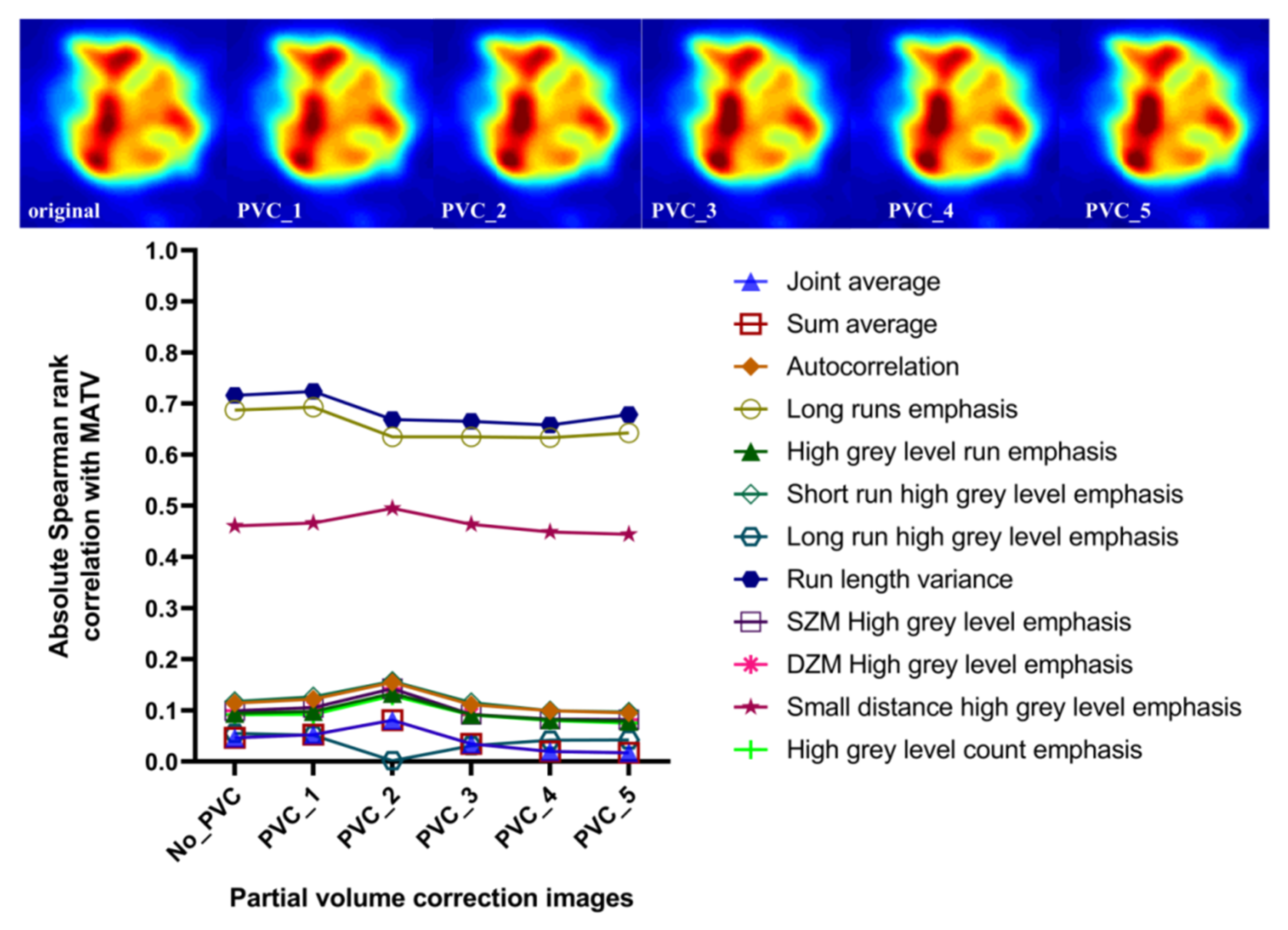
3.5. Effect of Discretization and Partial Volume Correction on Correlation between Features with Excellent Robustness and MATV
4. Discussion
4.1. The Research Value of This Study
4.2. The Effect of Different Aggregation Methods and Feature Dimension on the Feature’s Robustness
4.3. Statistical Metric and Cutoff Values
4.4. The Effect of Discretization and Partial Volume Corrections on the Percent of ICC Categories of All Texture Features
4.5. Robustness and Discriminability of Features
4.6. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boellaard, R.; Delgado-Bolton, R.; Oyen, W.J.; Giammarile, F.; Tatsch, K.; Eschner, W.; Verzijlbergen, F.J.; Barrington, S.F.; Pike, L.C.; Weber, W.A. FDG PET/CT: EANM procedure guidelines for tumour imaging: Version 2.0. Eur. J. Nucl. Med. Mol. I. 2015, 42, 328–354. [Google Scholar] [CrossRef] [PubMed]
- Lodge, M.A. Repeatability of SUV in oncologic 18F-FDG PET. J. Nucl. Med. 2017, 58, 523–532. [Google Scholar] [CrossRef] [PubMed]
- Boellaard, R. Standards for PET image acquisition and quantitative data analysis. J. Nucl. Med. 2009, 50, 11S–20S. [Google Scholar] [CrossRef] [PubMed]
- Tomaszewski, M.R.; Gillies, R.J. The biological meaning of radiomic features. Radiology 2021, 298, 505–516. [Google Scholar] [CrossRef]
- Kumar, V.; Gu, Y.; Basu, S.; Berglund, A.; Eschrich, S.A.; Schabath, M.B.; Forster, K.; Aerts, H.J.; Dekker, A.; Fenstermacher, D. Radiomics: The process and the challenges. Magn. Reson. Imaging 2012, 30, 1234–1248. [Google Scholar] [CrossRef]
- Lambin, P.; Rios-Velazquez, E.; Leijenaar, R.; Carvalho, S.; Van Stiphout, R.G.; Granton, P.; Zegers, C.M.; Gillies, R.; Boellard, R.; Dekker, A. Radiomics: Extracting more information from medical images using advanced feature analysis. Eur. J. Cancer 2012, 48, 441–446. [Google Scholar] [CrossRef]
- Aerts, H.J.; Velazquez, E.R.; Leijenaar, R.T.; Parmar, C.; Grossmann, P.; Carvalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; Rietveld, D. Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nat. Commun. 2014, 5, 4006. [Google Scholar] [CrossRef]
- Mayerhoefer, M.E.; Materka, A.; Langs, G.; Häggström, I.; Szczypiński, P.; Gibbs, P.; Cook, G. Introduction to radiomics. J. Nucl. Med. 2020, 61, 488–495. [Google Scholar] [CrossRef]
- Welch, M.L.; Mcintosh, C.; Haibe-Kains, B.; Milosevic, M.F.; Wee, L.; Dekker, A.; Huang, S.H.; Purdie, T.G.; O’Sullivan, B.; Aerts, H.J. Vulnerabilities of radiomic signature development: The need for safeguards. Radiother. Oncol. 2019, 130, 2–9. [Google Scholar] [CrossRef]
- Zwanenburg, A. Radiomics in nuclear medicine: Robustness, reproducibility, standardization, and how to avoid data analysis traps and replication crisis. Eur. J. Nucl. Med. Mol. Imaging 2019, 46, 2638–2655. [Google Scholar] [CrossRef]
- Hatt, M.; Krizsan, A.K.; Rahmim, A.; Bradshaw, T.J.; Costa, P.F.; Forgacs, A.; Seifert, R.; Zwanenburg, A.; El Naqa, I.; Kinahan, P. Joint EANM/SNMMI Guideline on Radiomics in Nuclear Medicine. Eur. J. Nucl. Med. Mol. Imaging 2022, 50, 352–373. [Google Scholar] [CrossRef]
- Xu, H.; Lv, W.; Zhang, H.; Ma, J.; Zhao, P.; Lu, L. Evaluation and optimization of radiomics features stability to respiratory motion in 18F-FDG 3D PET imaging. Med. Phys. 2021, 48, 5165–5178. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Shiri, I.; Hajianfar, G.; Bahadorzadeh, B.; Ghafarian, P.; Zaidi, H.; Ay, M.R. Synergistic impact of motion and acquisition/reconstruction parameters on 18F-FDG PET radiomic features in non-small cell lung cancer: Phantom and clinical studies. Med. Phys. 2022, 49, 3783–3796. [Google Scholar] [CrossRef]
- Carles, M.; Torres-Espallardo, I.; Alberich-Bayarri, A.; Olivas, C.; Bello, P.; Nestle, U.; Martí-Bonmatí, L. Evaluation of PET texture features with heterogeneous phantoms: Complementarity and effect of motion and segmentation method. Phys. Med. Biol. 2016, 62, 652–668. [Google Scholar] [CrossRef]
- Galavis, P.E.; Hollensen, C.; Jallow, N.; Paliwal, B.; Jeraj, R. Variability of textural features in FDG PET images due to different acquisition modes and reconstruction parameters. Acta. Oncol. 2010, 49, 1012–1016. [Google Scholar] [CrossRef]
- Yan, J.; Chu-Shern, J.L.; Loi, H.Y.; Khor, L.K.; Sinha, A.K.; Quek, S.T.; Tham, I.W.K.; Townsend, D. Impact of image reconstruction settings on texture features in 18F-FDG PET. J. Nucl. Med. 2015, 56, 1667–1673. [Google Scholar] [CrossRef]
- Van Velden, F.H.; Kramer, G.M.; Frings, V.; Nissen, I.A.; Mulder, E.R.; de Langen, A.J.; Hoekstra, O.S.; Smit, E.F.; Boellaard, R. Repeatability of radiomic features in non-small-cell lung cancer [18F] FDG-PET/CT studies: Impact of reconstruction and delineation. Mol. Imaging Biol. 2016, 18, 788–795. [Google Scholar] [CrossRef]
- Shiri, I.; Rahmim, A.; Ghaffarian, P.; Geramifar, P.; Abdollahi, H.; Bitarafan-Rajabi, A. The impact of image reconstruction settings on 18F-FDG PET radiomic features: Multi-scanner phantom and patient studies. Eur. Radiol. 2017, 27, 4498–4509. [Google Scholar] [CrossRef]
- Hatt, M.; Tixier, F.; Cheze Le Rest, C.; Pradier, O.; Visvikis, D. Robustness of intratumour 18F-FDG PET uptake heterogeneity quantification for therapy response prediction in oesophageal carcinoma. Eur. J. Nucl. Med. Mol. Imaging 2013, 40, 1662–1671. [Google Scholar] [CrossRef]
- Pfaehler, E.; Beukinga, R.J.; de Jong, J.R.; Slart, R.H.; Slump, C.H.; Dierckx, R.A.; Boellaard, R. Repeatability of 18F-FDG PET radiomic features: A phantom study to explore sensitivity to image reconstruction settings, noise, and delineation method. Med. Phys. 2019, 46, 665–678. [Google Scholar] [CrossRef]
- Yip, S.S.; Parmar, C.; Kim, J.; Huynh, E.; Mak, R.H.; Aerts, H.J. Impact of experimental design on PET radiomics in predicting somatic mutation status. Eur. J. Radiol. 2017, 97, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Leijenaar, R.T.; Nalbantov, G.; Carvalho, S.; Van Elmpt, W.J.; Troost, E.G.; Boellaard, R.; Aerts, H.J.; Gillies, R.J.; Lambin, P. The effect of SUV discretization in quantitative FDG-PET Radiomics: The need for standardized methodology in tumor texture analysis. Sci. Rep. 2015, 5, 11075. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Lv, W.; Jiang, J.; Ma, J.; Feng, Q.; Rahmim, A.; Chen, W. Robustness of radiomic features in [11C] choline and [18F] FDG PET/CT imaging of nasopharyngeal carcinoma: Impact of segmentation and discretization. Mol. Imaging Biol. 2016, 18, 935–945. [Google Scholar] [CrossRef] [PubMed]
- Zwanenburg, A.; Vallières, M.; Abdalah, M.A.; Aerts, H.J.; Andrearczyk, V.; Apte, A.; Ashrafinia, S.; Bakas, S.; Beukinga, R.J.; Boellaard, R. The image biomarker standardization initiative: Standardized quantitative radiomics for high-throughput image-based phenotyping. Radiology 2020, 295, 328–338. [Google Scholar] [CrossRef] [PubMed]
- Yip, S.S.; Aerts, H.J. Applications and limitations of radiomics. Phys. Med. Biol. 2016, 61, R150. [Google Scholar] [CrossRef]
- Hatt, M.; Tixier, F.; Pierce, L.; Kinahan, P.E.; Le Rest, C.C.; Visvikis, D. Characterization of PET/CT images using texture analysis: The past, the present… any future? Eur. J. Nucl. Med. Mol. Imaging 2017, 44, 151–165. [Google Scholar] [CrossRef]
- Hatt, M.; Majdoub, M.; Vallières, M.; Tixier, F.; Le Rest, C.C.; Groheux, D.; Hindié, E.; Martineau, A.; Pradier, O.; Hustinx, R. 18F-FDG PET uptake characterization through texture analysis: Investigating the complementary nature of heterogeneity and functional tumor volume in a multi–cancer site patient cohort. J. Nucl. Med. 2015, 56, 38–44. [Google Scholar] [CrossRef]
- Lv, W.; Yuan, Q.; Wang, Q.; Ma, J.; Jiang, J.; Yang, W.; Feng, Q.; Chen, W.; Rahmim, A.; Lu, L. Robustness versus disease differentiation when varying parameter settings in radiomics features: Application to nasopharyngeal PET/CT. Eur. Radiol. 2018, 28, 3245–3254. [Google Scholar] [CrossRef]
- Reiazi, R.; Abbas, E.; Famiyeh, P.; Rezaie, A.; Kwan, J.Y.; Patel, T.; Bratman, S.V.; Tadic, T.; Liu, F.; Haibe-Kains, B. The impact of the variation of imaging parameters on the robustness of computed tomography radiomic features: A review. Comput. Biol. Med. 2021, 133, 104400. [Google Scholar] [CrossRef]
- Zhao, B.; Tan, Y.; Tsai, W.; Qi, J.; Xie, C.; Lu, L.; Schwartz, L.H. Reproducibility of radiomics for deciphering tumor phenotype with imaging. Sci. Rep. 2016, 6, 1–7. [Google Scholar] [CrossRef]
- Meng, L.; Dong, D.; Chen, X.; Fang, M.; Wang, R.; Li, J.; Liu, Z.; Tian, J. 2D and 3D CT radiomic features performance comparison in characterization of gastric cancer: A multi-center study. IEEE J. Biomed. Health 2020, 25, 755–763. [Google Scholar] [CrossRef]
- Leijenaar, R.T.; Carvalho, S.; Velazquez, E.R.; Van Elmpt, W.J.; Parmar, C.; Hoekstra, O.S.; Hoekstra, C.J.; Boellaard, R.; Dekker, A.L.; Gillies, R.J. Stability of FDG-PET radiomics features: An integrated analysis of test-retest and inter-observer variability. Acta Oncol. 2013, 52, 1391–1397. [Google Scholar] [CrossRef]
- Teo, B.; Seo, Y.; Bacharach, S.L.; Carrasquillo, J.A.; Libutti, S.K.; Shukla, H.; Hasegawa, B.H.; Hawkins, R.A.; Franc, B.L. Partial-volume correction in PET: Validation of an iterative postreconstruction method with phantom and patient data. J. Nucl. Med. 2007, 48, 802–810. [Google Scholar]
- Bartko, J.J. The intraclass correlation coefficient as a measure of reliability. Psychol. Rep. 1966, 19, 3–11. [Google Scholar] [CrossRef]
- Foy, J.J.; Robinson, K.R.; Li, H.; Giger, M.L.; Al-Hallaq, H.; Armato, S.G. Variation in algorithm implementation across radiomics software. J. Med. Imaging 2018, 5, 44505. [Google Scholar] [CrossRef]
- Suarez-Ibarrola, R.; Basulto-Martinez, M.; Heinze, A.; Gratzke, C.; Miernik, A. Radiomics applications in renal tumor assessment: A comprehensive review of the literature. Cancers 2020, 12, 1387. [Google Scholar] [CrossRef]
- Sollini, M.; Antunovic, L.; Chiti, A.; Kirienko, M. Towards clinical application of image mining: A systematic review on artificial intelligence and radiomics. Eur. J. Nucl. Med. Mol. Imaging 2019, 46, 2656–2672. [Google Scholar] [CrossRef]
- Khorrami, M.; Bera, K.; Thawani, R.; Rajiah, P.; Gupta, A.; Fu, P.; Linden, P.; Pennell, N.; Jacono, F.; Gilkeson, R.C. Distinguishing granulomas from adenocarcinomas by integrating stable and discriminating radiomic features on non-contrast computed tomography scans. Eur. J. Cancer 2021, 148, 146–158. [Google Scholar] [CrossRef]
- Bogowicz, M.; Riesterer, O.; Bundschuh, R.A.; Veit-Haibach, P.; Hüllner, M.; Studer, G.; Stieb, S.; Glatz, S.; Pruschy, M.; Guckenberger, M. Stability of radiomic features in CT perfusion maps. Phys. Med. Biol. 2016, 61, 8736. [Google Scholar] [CrossRef]
- Somasundaram, A.; García, D.V.; Pfaehler, E.; Jauw, Y.W.; Zijlstra, J.M.; van Dongen, G.A.; Huisman, M.C.; de Vries, E.G.; Boellaard, R. Noise sensitivity of 89Zr-Immuno-PET radiomics based on count-reduced clinical images. EJNMMI Phys. 2022, 9, 16. [Google Scholar] [CrossRef]
- Tixier, F.; Hatt, M.; Le Rest, C.C.; Le Pogam, A.; Corcos, L.; Visvikis, D. Reproducibility of tumor uptake heterogeneity characterization through textural feature analysis in 18F-FDG PET. J. Nucl. Med. 2012, 53, 693–700. [Google Scholar] [CrossRef] [PubMed]
- Lovinfosse, P.; Visvikis, D.; Hustinx, R.; Hatt, M. FDG PET radiomics: A review of the methodological aspects. Clin. Transl. Imaging 2018, 6, 379–391. [Google Scholar] [CrossRef]
- Lv, W.; Yuan, Q.; Wang, Q.; Ma, J.; Feng, Q.; Chen, W.; Rahmim, A.; Lu, L. Radiomics analysis of PET and CT components of PET/CT imaging integrated with clinical parameters: Application to prognosis for nasopharyngeal carcinoma. Mol. Imaging Biol. 2019, 21, 954–964. [Google Scholar] [CrossRef] [PubMed]
- Crandall, J.P.; Fraum, T.J.; Lee, M.; Jiang, L.; Grigsby, P.; Wahl, R.L. Repeatability of 18F-FDG PET radiomic features in cervical cancer. J. Nucl. Med. 2021, 62, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Cysouw, M.C.; Kramer, G.M.; Schoonmade, L.J.; Boellaard, R.; de Vet, H.C.; Hoekstra, O.S. Impact of partial-volume correction in oncological PET studies: A systematic review and meta-analysis. Eur. J. Nucl. Med. Mol. Imaging 2017, 44, 2105–2116. [Google Scholar] [CrossRef]
- Erlandsson, K.; Buvat, I.; Pretorius, P.H.; Thomas, B.A.; Hutton, B.F. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys. Med. Biol. 2012, 57, R119–R159. [Google Scholar] [CrossRef]
- Tohka, J.; Reilhac, A. Deconvolution-based partial volume correction in Raclopride-PET and Monte Carlo comparison to MR-based method. Neuroimage 2008, 39, 1570–1584. [Google Scholar] [CrossRef]
- Lu, L.; Hu, D.; Han, Y.; Gu, C.; Rahmim, A.; Ma, J.; Chen, W. Partial volume correction in small animal PET imaging incorporating total variation regularization. J. Nucl. Med. 2014, 55 (Suppl. 1), 374. [Google Scholar]
- Boussion, N.; Cheze Le Rest, C.; Hatt, M.; Visvikis, D. Incorporation of wavelet-based denoising in iterative deconvolution for partial volume correction in whole-body PET imaging. Eur. J. Nucl. Med. Mol. I. 2009, 36, 1064–1075. [Google Scholar] [CrossRef]
- Golla, S.S.V.; Lubberink, M.; van Berckel, B.N.M.; Lammertsma, A.A.; Boellard, R. Partial volume correction of brain PET studies using iterative deconvolution in combination with HYPR denoising. EJNMMI Res. 2015, 7, 36. [Google Scholar] [CrossRef]
- Yan, J.; Chu-Shern, J.L.; Townsend, D. MRI-guided brain PET image filtering and partial volume correction. Phys. Med. Biol. 2015, 60, 961–976. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, Y.; Bilgel, M.; Ashrafinia, S.; Lu, L.; Rahmim, A. Voxel-based partial volume correction of PET images via subtle MRI guided non-local means regularization. Phys. Med. 2021, 89, 129–139. [Google Scholar] [CrossRef]
- Zhu, Y.; Bilgel, M.; Gao, Y.; Rousset, O.G.; Resnick, S.M.; Wong, D.F.; Rahmim, A. Deconvolution-based partial volume correction of PET images with parallel level set regularization. Phys. Med. Biol. 2021, 66, 145003. [Google Scholar] [CrossRef]
- Du, D.; Feng, H.; Lv, W.; Ashrafinia, S.; Yuan, Q.; Wang, Q.; Yang, W.; Feng, Q.; Chen, W.; Rahmim, A.; et al. Machine learning methods for optimal radiomics-based differentiation between recurrence and inflammation: Application to nasopharyngeal carcinoma post-therapy PET/CT images. Mol. Imaging Biol. 2020, 22, 730–738. [Google Scholar] [CrossRef]
- Patel, V.K.; Savsani, V.J. Heat transfer search (HTS): A novel optimization algorithm. Inf. Sci. 2015, 324, 217–246. [Google Scholar] [CrossRef]
- Vakharia, V.; Shah, M.; Suthar, V.; Patel, V.K.; Solanki, A. Hybrid Perovskites Thin Films Morphology Identification by adapting Multiscale-SinGAN architecture, Heat Transfer Search optimized feature selection and Machine Learning Algorithms. Physica Scripta. Heat transfer search (HTS): A novel optimization algorithm. Phys. Scr. 2023, 98, 025203. [Google Scholar]




| Feature Family | Count | Aggregation Methods |
|---|---|---|
| GLCM | 25 | 6 |
| GLRLM | 16 | 6 |
| GLSZM | 16 | 3 |
| GLDZM | 16 | 3 |
| NGTDM | 5 | 3 |
| NGLDM | 17 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, L.; Xu, H.; Lv, W.; Lu, L.; Chen, W. Impact of Aggregation Methods for Texture Features on Their Robustness Performance: Application to Nasopharyngeal 18F-FDG PET/CT. Cancers 2023, 15, 932. https://doi.org/10.3390/cancers15030932
Peng L, Xu H, Lv W, Lu L, Chen W. Impact of Aggregation Methods for Texture Features on Their Robustness Performance: Application to Nasopharyngeal 18F-FDG PET/CT. Cancers. 2023; 15(3):932. https://doi.org/10.3390/cancers15030932
Chicago/Turabian StylePeng, Lihong, Hui Xu, Wenbing Lv, Lijun Lu, and Wufan Chen. 2023. "Impact of Aggregation Methods for Texture Features on Their Robustness Performance: Application to Nasopharyngeal 18F-FDG PET/CT" Cancers 15, no. 3: 932. https://doi.org/10.3390/cancers15030932
APA StylePeng, L., Xu, H., Lv, W., Lu, L., & Chen, W. (2023). Impact of Aggregation Methods for Texture Features on Their Robustness Performance: Application to Nasopharyngeal 18F-FDG PET/CT. Cancers, 15(3), 932. https://doi.org/10.3390/cancers15030932







