A Series-Based Deep Learning Approach to Lung Nodule Image Classification
Abstract
Simple Summary
Abstract
1. Introduction
Related Works
2. Methodology
2.1. Series by Radial Scanning
2.2. 3D Nodule Segmentation
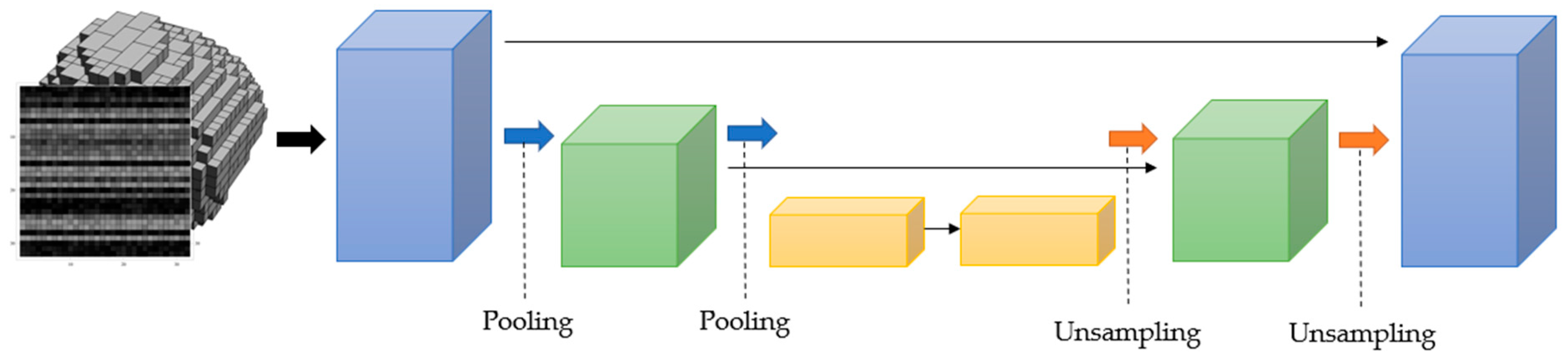
2.3. Classification with U-Net
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rowland, J.H.; Bellizzi, K.M. Cancer survivors and survivorship research: A reflection on today’s successes and tomorrow’s challenges. Hematol. Oncol. Clin. N. Am. 2008, 22, 181–200. [Google Scholar] [CrossRef] [PubMed]
- Elmore, L.W.; Greer, S.F.; Daniels, E.C.; Saxe, C.C.; Melner, M.H.; Krawiec, G.M.; Phelps, W.C. Blueprint for cancer research: Critical gaps and opportunities. CA Cancer J. Clin. 2021, 71, 107–139. [Google Scholar] [CrossRef] [PubMed]
- Benning, L.; Peintner, A.; Peintner, L. Advances in and the applicability of machine learning-based screening and early detection approaches for cancer: A primer. Cancers 2022, 14, 623. [Google Scholar] [CrossRef] [PubMed]
- Nanavaty, P.; Alvarez, M.S.; Alberts, W.M. Lung cancer screening: Advantages, controversies, and applications. Cancer Control 2014, 21, 9–14. [Google Scholar] [CrossRef]
- Khawaja, A.; Bartholmai, B.J.; Rajagopalan, S.; Karwoski, R.A.; Varghese, C.; Maldonado, F.; Peikert, T. Do we need to see to believe?—Radiomics for lung nodule classification and lung cancer risk stratification. J. Thorac. Dis. 2020, 12, 3303. [Google Scholar] [CrossRef]
- Parekh, V.; Jacobs, M.A. Radiomics: A new application from established techniques. Expert Rev. Precis. Med. Drug Dev. 2016, 1, 207–226. [Google Scholar] [CrossRef]
- Oliveira, S.P.; Neto, P.C.; Fraga, J.; Montezuma, D.; Monteiro, A.; Monteiro, J.; Cardoso, J.S. CAD systems for colorectal cancer from WSI are still not ready for clinical acceptance. Sci. Rep. 2021, 11, 14358. [Google Scholar] [CrossRef]
- Yanase, J.; Triantaphyllou, E. A systematic survey of computer-aided diagnosis in medicine: Past and present developments. Expert Syst. Appl. 2019, 138, 112821. [Google Scholar] [CrossRef]
- Yan, Y.; Yao, X.J.; Wang, S.H.; Zhang, Y.D. A survey of computer-aided tumor diagnosis based on convolutional neural network. Biology 2021, 10, 1084. [Google Scholar] [CrossRef]
- Chambara, N.; Ying, M. The diagnostic efficiency of ultrasound computer-aided diagnosis in differentiating thyroid nodules: A systematic review and narrative synthesis. Cancers 2019, 11, 1759. [Google Scholar] [CrossRef]
- Ding, J.; Li, A.; Hu, Z.; Wang, L. Accurate pulmonary nodule detection in computed tomography images using deep convolutional neural networks. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2017; pp. 559–567. [Google Scholar]
- Wang, S.; Zhou, M.; Liu, Z.; Liu, Z.; Gu, D.; Zang, Y.; Tian, J. Central focused convolutional neural networks: Developing a data-driven model for lung nodule segmentation. Med. Image Anal. 2017, 40, 172–183. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Zhou, Z.; Wang, J.; Wang, Y. Joint learning for pulmonary nodule segmentation, attributes and malignancy prediction. In 2018 IEEE 15th International Symposium on Biomedical Imaging; Curran Associates: Washington, DC, USA, 2018; pp. 1109–1113. [Google Scholar]
- Shen, S.; Han, S.X.; Aberle, D.R.; Bui, A.A.; Hsu, W. An interpretable deep hierarchical semantic convolutional neural network for lung nodule malignancy classification. Expert Syst. Appl. 2019, 128, 84–95. [Google Scholar] [CrossRef] [PubMed]
- Ferreira-Junior, J.R.; Koenigkam-Santos, M.; Magalhaes Tenorio, A.P.; Faleiros, M.C.; Garcia Cipriano, F.E.; Fabro, A.T.; de Azevedo-Marques, P.M. CT-based radiomics for prediction of histologic subtype and metastatic disease in primary malignant lung neoplasms. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Firmino, M.; Angelo, G.; Morais, H.; Dantas, M.R.; Valentim, R. Computer-aided detection (CADe) and diagnosis (CADx) system for lung cancer with likelihood of malignancy. Biomed. Eng. OnLine 2016, 15, 2. [Google Scholar] [CrossRef] [PubMed]
- Choy, G.; Khalilzadeh, O.; Michalski, M.; Do, S.; Samir, A.E.; Pianykh, O.S.; Dreyer, K.J. Current applications and future impact of machine learning in radiology. Radiology 2018, 288, 318. [Google Scholar] [CrossRef]
- Ferreira, J.R.; Oliveira, M.C.; de Azevedo-Marques, P.M. Characterization of pulmonary nodules based on features of margin sharpness and texture. J. Digit. Imaging 2018, 31, 451–463. [Google Scholar] [CrossRef]
- Dhara, A.K.; Mukhopadhyay, S.; Dutta, A.; Garg, M.; Khandelwal, N. A combination of shape and texture features for classification of pulmonary nodules in lung CT images. J. Digit. Imaging 2016, 29, 466–475. [Google Scholar] [CrossRef]
- Felix, A.; Oliveira, M.; Machado, A.; Raniery, J. Using 3D texture and margin sharpness features on classification of small pulmonary nodules. In 2016 29th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI); Curran Associates: Washington, DC, USA, 2016; pp. 394–400. [Google Scholar]
- Beig, N.; Khorrami, M.; Alilou, M.; Prasanna, P.; Braman, N.; Orooji, M.; Madabhushi, A. Perinodular and intranodular radiomic features on lung CT images distinguish adenocarcinomas from granulomas. Radiology 2019, 290, 783. [Google Scholar] [CrossRef]
- Uthoff, J.; Stephens, M.J.; Newell Jr, J.D.; Hoffman, E.A.; Larson, J.; Koehn, N.; Sieren, J.C. Machine learning approach for distinguishing malignant and benign lung nodules utilizing standardized perinodular parenchymal features from CT. Med. Phys. 2019, 46, 3207–3216. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Z. Usage of intelligent medical aided diagnosis system under the deep convolutional neural network in lumbar disc herniation. Appl. Soft Comput. 2021, 111, 107674. [Google Scholar] [CrossRef]
- Bakheet, S.; Al-Hamadi, A. Computer-aided diagnosis of malignant melanoma using Gabor-based entropic features and multilevel neural networks. Diagnostics 2020, 10, 822. [Google Scholar] [CrossRef] [PubMed]
- Maqsood, S.; Damaševičius, R.; Maskeliūnas, R. TTCNN: A breast cancer detection and classification towards computer-aided diagnosis using digital mammography in early stages. Appl. Sci. 2022, 12, 3273. [Google Scholar] [CrossRef]
- Campanella, G.; Hanna, M.G.; Geneslaw, L.; Miraflor, A.; Werneck Krauss Silva, V.; Busam, K.J.; Fuchs, T.J. Clinical-grade computational pathology using weakly supervised deep learning on whole slide images. Nat. Med. 2019, 25, 1301–1309. [Google Scholar] [CrossRef]
- Chlebus, G.; Schenk, A.; Moltz, J.H.; van Ginneken, B.; Hahn, H.K.; Meine, H. Automatic liver tumor segmentation in CT with fully convolutional neural networks and object-based postprocessing. Sci. Rep. 2018, 8, 15497. [Google Scholar] [CrossRef] [PubMed]
- De Fauw, J.; Ledsam, J.R.; Romera-Paredes, B.; Nikolov, S.; Tomasev, N.; Blackwell, S.; Ronneberger, O. Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat. Med. 2018, 24, 1342–1350. [Google Scholar] [CrossRef]
- Dash, M.; Londhe, N.D.; Ghosh, S.; Semwal, A.; Sonawane, R.S. PsLSNet: Automated psoriasis skin lesion segmentation using modified U-Net-based fully convolutional network. Biomed. Signal Process. Control 2019, 52, 226–237. [Google Scholar] [CrossRef]
- Xie, F.; Yang, J.; Liu, J.; Jiang, Z.; Zheng, Y.; Wang, Y. Skin lesion segmentation using high-resolution convolutional neural network. Comput. Methods Programs Biomed. 2020, 186, 105241. [Google Scholar] [CrossRef]
- Abdoulaye, I.B.C.; Demir, Ö. Mamografi görüntülerinden kitle tespiti amacıyla öznitelik çıkarımı. In Ulusal Biyomedikal Cihaz Tasarımı ve Üretmi Sempozyumu; UBICTÜS: Istanbul, Turkey, 2017; Volume 1, pp. 33–36. [Google Scholar]
- Wang, P.; Hu, X.; Li, Y.; Liu, Q.; Zhu, X. Automatic cell nuclei segmentation and classification of breast cancer histopathology images. Signal Process. 2016, 122, 1–13. [Google Scholar] [CrossRef]
- Jiang, H.; Li, Z.; Li, S.; Zhou, F. An effective multi-classification method for NHL pathological images. In 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC); Curran Associates: Washington, DC, USA, 2018; pp. 763–768. [Google Scholar]
- Muhammad, W.; Hart, G.R.; Nartowt, B.; Farrell, J.J.; Johung, K.; Liang, Y.; Deng, J. Pancreatic cancer prediction through an artificial neural network. Front. Artif. Intell. 2019, 2, 2. [Google Scholar] [CrossRef]
- Busnatu, Ș.; Niculescu, A.G.; Bolocan, A.; Petrescu, G.E.; Păduraru, D.N.; Năstasă, I.; Martins, H. Clinical applications of artificial intelligence—An updated overview. J. Clinic. Med. 2022, 11, 2265. [Google Scholar] [CrossRef]
- Hunter, B.; Hindocha, S.; Lee, R.W. The role of artificial intelligence in early cancer diagnosis. Cancers 2022, 14, 1524. [Google Scholar] [CrossRef] [PubMed]
- Iakovidis, D.K.; Tsevas, S.; Savelonas, M.A.; Papamichalis, G. Image analysis framework for infection monitoring. IEEE Trans. Biomed. Eng. 2012, 59, 1135–1144. [Google Scholar] [CrossRef] [PubMed]
- Baur, B.; Bozdag, S. A canonical correlation analysis-based dynamic Bayesian network prior to infer gene regulatory networks from multiple types of biological data. J. Comput. Biol. 2015, 22, 289–299. [Google Scholar] [CrossRef]
- Guo, S.; Jiang, Q.; Chen, L.; Guo, D. Gene regulatory network inference using PLS-based methods. BMC Bioinform. 2016, 17, 545. [Google Scholar] [CrossRef]
- Penfold, C.A.; Shifaz, A.; Brown, P.E.; Nicholson, A.; Wild, D.L. CSI: A nonparametric Bayesian approach to network inference from multiple perturbed time series gene expression data. Stat. Appl. Genet. Mol. Biol. 2015, 14, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Isci, S.; Dogan, H.; Ozturk, C.; Otu, H.H. Bayesian network prior: Network analysis of biological data using external knowledge. Bioinformatics 2014, 30, 860–867. [Google Scholar] [CrossRef]
- Schlitt, T. Approaches to modeling gene regulatory networks: A gentle introduction. Methods Mol. Biol. 2013, 1021, 13–35. [Google Scholar]
- Murphy, K.; Mian, S. Modelling Gene Expression Data Using Dynamic Bayesian Networks; Technical Report; Computer Science Division, University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Ni, Y.; Müller, P.; Wei, L.; Ji, Y. Bayesian graphical models for computational network biology. BMC Bioinform. 2018, 19, 59–69. [Google Scholar] [CrossRef]
- Kim, S.Y.; Imoto, S.; Miyano, S. Inferring gene networks from time series microarray data using dynamic Bayesian networks. Brief. Bioinform. 2003, 4, 228–235. [Google Scholar] [CrossRef]
- Kourou, K.; Rigas, G.; Papaloukas, C.; Mitsis, M.; Fotiadis, D.I. Cancer classification from time series microarray data through regulatory dynamic Bayesian networks. Comput. Biol. Med. 2020, 116, 103577. [Google Scholar] [CrossRef]
- Imani, F.; Daoud, M.; Moradi, M.; Abolmaesumi, P.; Mousavi, P. Tissue classification using depth-dependent ultrasound time series analysis: In-vitro animal study. In Medical Imaging 2011: Ultrasonic Imaging, Tomography, and Therapy; SPIE Medical Imaging: Lake Buena Vista, FL, USA, 2011; Volume 7968, pp. 120–126. [Google Scholar]
- Shen, W.; Zhou, M.; Yang, F.; Yu, D.; Dong, D.; Yang, C.; Tian, J. Multi-crop convolutional neural networks for lung nodule malignancy suspiciousness classification. Pattern Recognit. 2017, 61, 663–673. [Google Scholar] [CrossRef]
- Al-Shabi, M.; Lee, H.K.; Tan, M. Gated-dilated networks for lung nodule classification in CT scans. IEEE Access 2019, 7, 178827–178838. [Google Scholar] [CrossRef]
- Ren, Y.; Tsai, M.Y.; Chen, L.; Wang, J.; Li, S.; Liu, Y.; Shen, C. A manifold learning regularization approach to enhance 3D CT image-based lung nodule classification. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Tsai, M.Y.; Chen, L.; Li, S.; Nguyen, D.; Wang, J.; Jia, X. On the robustness of deep learning-based lung-nodule classification for CT images with respect to image noise. Phys. Med. Biol. 2020, 65, 245037. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Gao, F.; Xu, X.; Huang, F.; Zhu, S. Attentive and ensemble 3D dual path networks for pulmonary nodules classification. Neurocomputing 2020, 398, 422–430. [Google Scholar] [CrossRef]
- Al-Shabi, M.; Lan, B.L.; Chan, W.Y.; Ng, K.H.; Tan, M. Lung nodule classification using deep local-global networks. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1815–1819. [Google Scholar] [CrossRef]
- Al-Shabi, M.; Shak, K.; Tan, M. 3D axial-attention for lung nodule classification. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 1319–1324. [Google Scholar] [CrossRef]
- Bosch, C.M.; Baumann, C.; Dehghani, S.; Sommersperger, M.; Johannigmann-Malek, N.; Kirchmair, K.; Nasseri, M.A. A tool for high-resolution volumetric optical coherence tomography by compounding radial-and linear acquired B-scans using registration. Sensors 2022, 22, 1135. [Google Scholar] [CrossRef]
- Murad, M.; Jalil, A.; Bilal, M.; Ikram, S.; Ali, A.; Khan, B.; Mehmood, K. Radial undersampling-based interpolation scheme for multislice CSMRI reconstruction techniques. BioMed Res. Int. 2021, 2021, 6638588. [Google Scholar] [CrossRef]
- Mendoza, L.; Christopher, M.; Brye, N.; Proudfoot, J.A.; Belghith, A.; Bowd, C.; Zangwill, L.M. Deep learning predicts demographic and clinical characteristics from optic nerve head OCT circle and radial scans. Investig. Ophthalmol. Vis. Sci. 2021, 62, 2120. [Google Scholar]
- Deng, C.X.; Wang, G.B.; Yang, X.R. Image edge detection algorithm based on improved canny operator. In 2013 International Conference on Wavelet Analysis and Pattern Recognition; Curran Associates: Washington, DC, USA, 2013; pp. 168–172. [Google Scholar]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geograph. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Sato, Y. Piecewise linear approximation of plane curves by perimeter optimization. Pattern Recognit. 1992, 25, 1535–1543. [Google Scholar] [CrossRef]
- Aresta, G.; Jacobs, C.; Araújo, T.; Cunha, A.; Ramos, I.; van Ginneken, B.; Campilho, A. iW-Net: An automatic and minimalistic interactive lung nodule segmentation deep network. Sci. Rep. 2019, 9, 11591. [Google Scholar] [CrossRef] [PubMed]
- Aresta, G.; Araújo, T.; Jacobs, C.; Ginneken, B.V.; Cunha, A.; Ramos, I.; Campilho, A. Towards an automatic lung cancer screening system in low dose computed tomography. In Image Analysis for Moving Organ, Breast, and Thoracic Images; Springer: Cham, Switzerland, 2018; pp. 310–318. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2016; pp. 424–432. [Google Scholar]
- Giannopoulos, M.; Tsagkatakis, G.; Tsakalides, P. 4D U-nets for multi-temporal remote sensing data classification. Remote Sens. 2022, 14, 634. [Google Scholar] [CrossRef]
- Armato III, S.G.; McLennan, G.; Bidaut, L.; McNitt-Gray, M.F.; Meyer, C.R.; Reeves, A.P.; Clarke, L.P. The lung image database consortium (LIDC) and image database resource initiative (IDRI): A completed reference database of lung nodules on CT scans. Med. Phys. 2011, 38, 915–931. [Google Scholar] [CrossRef]
- Ferreira Junior, J.R.; Oliveira, M.C.; de Azevedo-Marques, P.M. Cloud-based NoSQL open database of pulmonary nodules for computer-aided lung cancer diagnosis and reproducible research. J. Digit. Imaging 2016, 29, 716–729. [Google Scholar] [CrossRef] [PubMed]
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Kirby, J.; Koppel, P.; Prior, F. The Cancer Imaging Archive (TCIA): Maintaining and operating a public information repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef]
- Wormanns, D.; Hamer, O.W. Glossary of terms for thoracic imaging-German version of the Fleischner Society recommendations. RoFo 2015, 187, 638–661. [Google Scholar]
- Calheiros, J.L.L.; de Amorim, L.B.V.; de Lima, L.L.; de Lima Filho, A.F.; Ferreira Júnior, J.R.; de Oliveira, M.C. The effects of perinodular features on solid lung nodule classification. J. Digit. Imaging 2021, 34, 798–810. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Y.; Chen, L.; Wang, J. U-net-based deformation vector field estimation for motion-compensated 4D-CBCT reconstruction. Med. Phys. 2020, 47, 3000–3012. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Zhao, Y.; Huang, Q.; Gao, H. 4D-AirNet: A temporally-resolved CBCT slice reconstruction method synergizing analytical and iterative method with deep learning. Phys. Med. Biol. 2020, 65, 175020. [Google Scholar] [CrossRef] [PubMed]
- Choy, C.; Gwak, J.; Savarese, S. 4D spatio-temporal convnets: Minkowski convolutional neural networks. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. 2019, 3075–3084. [Google Scholar]
- Liu, T.; Meng, Q.; Huang, J.J.; Vlontzos, A.; Rueckert, D.; Kainz, B. Video summarization through reinforcement learning with a 3D spatio-temporal U-net. IEEE Trans. Image Process. 2022, 31, 1573–1586. [Google Scholar] [CrossRef] [PubMed]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Abanda, A.; Mori, U.; Lozano, J.A. A review on distance-based time series classification. Data Min. Knowl. Discov. 2019, 33, 378–412. [Google Scholar] [CrossRef]
- Iwana, B.K.; Uchida, S. An empirical survey of data augmentation for time series classification with neural networks. PLoS ONE 2021, 16, e0254841. [Google Scholar] [CrossRef]


| Depth | No. of Filters | Recall | Precision | Accuracy | Time |
|---|---|---|---|---|---|
| 3 | 4 | 80.13 | 81.54 | 83.45 | 469.92 |
| 8 | 92.41 | 92.63 | 92.84 | 661.8 | |
| 4 | 4 | 80.04 | 79.63 | 81.22 | 477.74 |
| 8 | 87.19 | 88.01 | 88.73 | 668.4 |
| Method | AUC | Recall | Precision | Accuracy | F1 |
|---|---|---|---|---|---|
| HSCNN [14] | 85.6 | 70.5 | N/A | 84.2 | N/A |
| Multi-Crop [48] | 93.0 | 77.0 | N/A | 87.14 | N/A |
| Local-Global [52] | 95.62 | 88.66 | 87.38 | 88.46 | 88.01 |
| Gated-Dilated [49] | 95.14 | 92.21 | 91.85 | 92.57 | 92.03 |
| 3D DPN [53] | N/A | 92.04 | N/A | 90.24 | N/A |
| MRC-DNN [50] | N/A | 81.00 | N/A | 90.00 | N/A |
| Perturbated DNN [51] | 91.0 | 90.0 | N/A | 83.0 | N/A |
| 3D Axial-Attention [54] | 96.17 | 92.36 | 92.59 | 92.81 | 92.47 |
| Our method | 96.19 | 92.41 | 92.63 | 92.84 | 92.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balcı, M.A.; Batrancea, L.M.; Akgüller, Ö.; Nichita, A. A Series-Based Deep Learning Approach to Lung Nodule Image Classification. Cancers 2023, 15, 843. https://doi.org/10.3390/cancers15030843
Balcı MA, Batrancea LM, Akgüller Ö, Nichita A. A Series-Based Deep Learning Approach to Lung Nodule Image Classification. Cancers. 2023; 15(3):843. https://doi.org/10.3390/cancers15030843
Chicago/Turabian StyleBalcı, Mehmet Ali, Larissa M. Batrancea, Ömer Akgüller, and Anca Nichita. 2023. "A Series-Based Deep Learning Approach to Lung Nodule Image Classification" Cancers 15, no. 3: 843. https://doi.org/10.3390/cancers15030843
APA StyleBalcı, M. A., Batrancea, L. M., Akgüller, Ö., & Nichita, A. (2023). A Series-Based Deep Learning Approach to Lung Nodule Image Classification. Cancers, 15(3), 843. https://doi.org/10.3390/cancers15030843






