A Systematic Review and Critical Assessment of Breast Cancer Risk Prediction Tools Incorporating a Polygenic Risk Score for the General Population
Abstract
:Simple Summary
Abstract
1. Introduction
2. Methods
2.1. Protocol and Registration
2.2. Search Strategy
2.3. Eligibility Criteria
2.4. Study Selection
2.5. Data Extraction Process and Analysis
2.6. Risk of Bias of Individual Studies
3. Results
3.1. Study Selection
3.2. Characteristics of Included Studies
3.3. Characteristics of Risk Prediction Models
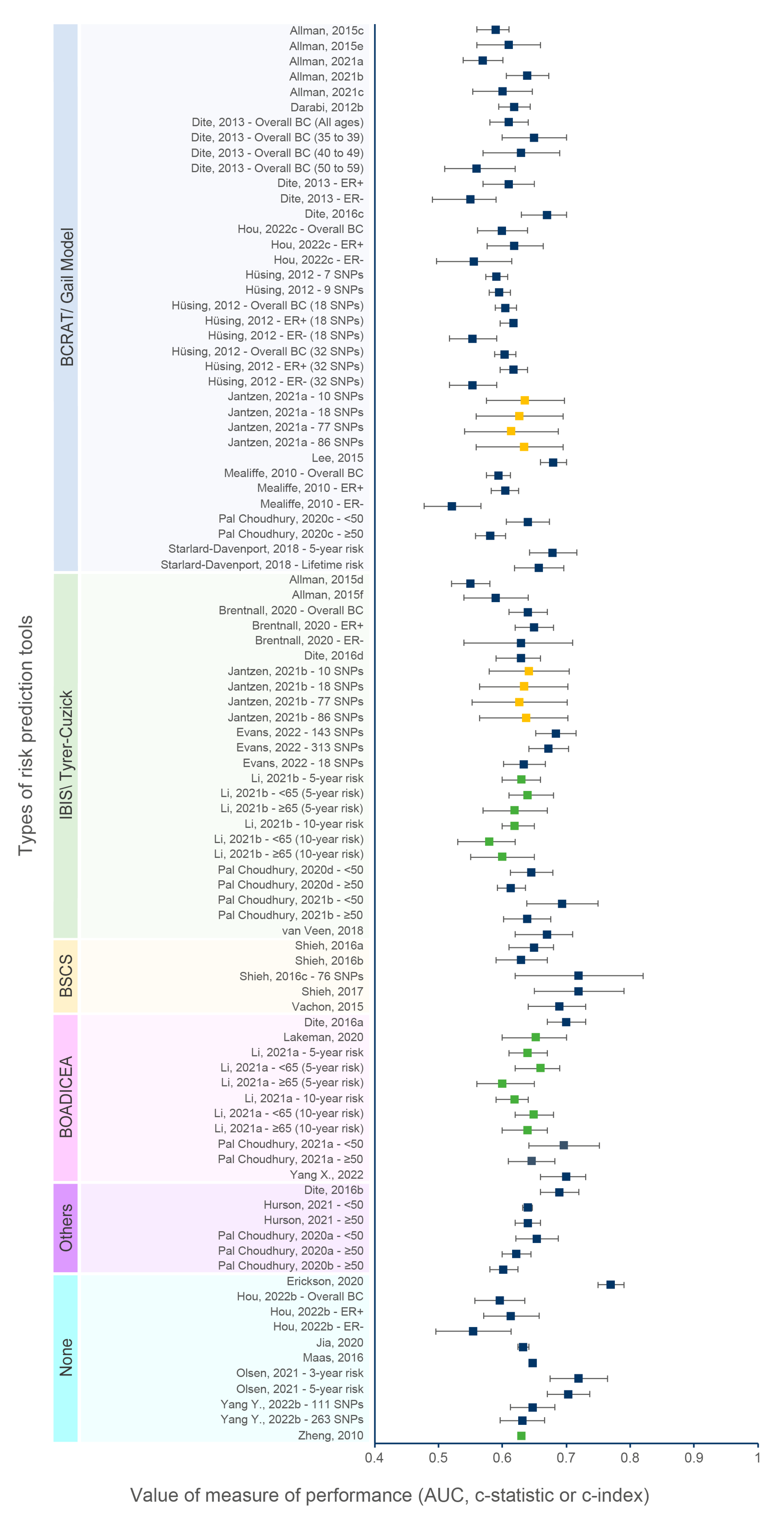
3.4. Discriminatory Accuracy
3.5. Calibration Accuracy
3.6. Net Reclassification Improvement
3.7. Sensitivity Analysis
3.7.1. Effect of Number of SNPs
3.7.2. Effect of Age
3.7.3. Effect of Combining a PRS and Genetic and Non-Genetic Risk Factors
3.7.4. Effect of Ethnicity
3.7.5. Effect of Prediction Time Frame
3.7.6. Effect of the Type of Risk Prediction Tools
3.7.7. Effect of Breast Cancer Subtypes
3.8. Quality of Reporting
3.9. Risk of Bias within Studies
4. Discussion
5. Strengths and Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- WHO. Cancer n.d. Available online: https://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 26 September 2019).
- Jin, J. Breast Cancer Screening: Benefits and Harms. JAMA 2014, 312, 2585. [Google Scholar] [CrossRef] [PubMed]
- Dibden, A.; Offman, J.; Duffy, S.W.; Gabe, R. Worldwide Review and Meta-Analysis of Cohort Studies Measuring the Effect of Mammography Screening Programmes on Incidence-Based Breast Cancer Mortality. Cancers 2020, 12, 976. [Google Scholar] [CrossRef] [PubMed]
- Klarenbach, S.; Sims-Jones, N.; Lewin, G.; Singh, H.; Thériault, G.; Tonelli, M.; Doull, M.; Courage, S.; Garcia, A.J.; Thombs, B.D. Recommendations on screening for breast cancer in women aged 40–74 years who are not at increased risk for breast cancer. CMAJ 2018, 190, E1441–E1451. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Chen, M.; Qiao, Y.; Zhao, F. Global guidelines for breast cancer screening: A systematic review. Breast Off. J. Eur. Soc. Mastology 2022, 64, 85–99. [Google Scholar] [CrossRef] [PubMed]
- Łukasiewicz, S.; Czeczelewski, M.; Forma, A.; Baj, J.; Sitarz, R.; Stanisławek, A. Breast Cancer—Epidemiology, Risk Factors, Classification, Prognostic Markers, and Current Treatment Strategies—An Updated Review. Cancers 2021, 13, 4287. [Google Scholar] [CrossRef] [PubMed]
- Shieh, Y.; Eklund, M.; Madlensky, L.; Sawyer, S.D.; Thompson, C.K.; Stover Fiscalini, A.; Ziv, E.; Van’t Veer, L.J.; Esserman, L.J.; Tice, J.A.; et al. Breast Cancer Screening in the Precision Medicine Era: Risk-Based Screening in a Population-Based Trial. J. Natl. Cancer Inst. 2017, 109, djw290. [Google Scholar] [CrossRef] [PubMed]
- Pashayan, N.; Antoniou, A.C.; Ivanus, U.; Esserman, L.J.; Easton, D.F.; French, D.; Sroczynski, G.; Hall, P.; Cuzick, J.; Evans, D.G.; et al. Personalized early detection and prevention of breast cancer: ENVISION consensus statement. Nat. Rev. Clin. Oncol. 2020, 17, 687–705. [Google Scholar] [CrossRef] [PubMed]
- Clift, A.K.; Dodwell, D.; Lord, S.; Petrou, S.; Brady, S.M.; Collins, G.S.; Hippisley-Cox, J. The current status of risk-stratified breast screening. Br. J. Cancer 2022, 126, 533–550. [Google Scholar] [CrossRef]
- Michailidou, K.; Lindström, S.; Dennis, J.; Beesley, J.; Hui, S.; Kar, S.; Lemaçon, A.; Soucy, P.; Glubb, D.; Rostamianfar, A.; et al. Association analysis identifies 65 new breast cancer risk loci. Nature 2017, 551, 92–94. [Google Scholar] [CrossRef]
- Roberts, E.; Howell, S.; Evans, D.G. Polygenic risk scores and breast cancer risk prediction. Breast Off. J. Eur. Soc. Mastology 2023, 67, 71–77. [Google Scholar] [CrossRef]
- Mavaddat, N.; Michailidou, K.; Dennis, J.; Lush, M.; Fachal, L.; Lee, A.; Tyrer, J.P.; Chen, T.-H.; Wang, Q.; Bolla, M.K.; et al. Polygenic Risk Scores for Prediction of Breast Cancer and Breast Cancer Subtypes. Am. J. Hum. Genet. 2019, 104, 21–34. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.; Mavaddat, N.; Wilcox, A.N.; Cunningham, A.P.; Carver, T.; Hartley, S.; Babb de Villiers, C.; Izquierdo, A.; Simard, J.; Schmidt, M.K.; et al. BOADICEA: A comprehensive breast cancer risk prediction model incorporating genetic and nongenetic risk factors. Genet. Med. 2019, 21, 1708–1718. [Google Scholar] [CrossRef] [PubMed]
- Mavaddat, N.; Ficorella, L.; Carver, T.; Lee, A.; Cunningham, A.P.; Lush, M.; Dennis, J.; Tischkowitz, M.; Downes, K.; Hu, D.; et al. Incorporating alternative Polygenic Risk Scores into the BOADICEA breast cancer risk prediction model. Cancer Epidemiol. Biomark. Prev. 2023, 32, 422–427. [Google Scholar] [CrossRef] [PubMed]
- Yanes, T.; Young, M.-A.; Meiser, B.; James, P.A. Clinical applications of polygenic breast cancer risk: A critical review and perspectives of an emerging field. Breast Cancer Res. 2020, 22, 21. [Google Scholar] [CrossRef] [PubMed]
- Zeinomar, N.; Chung, W.K. Cases in Precision Medicine: The Role of Polygenic Risk Scores in Breast Cancer Risk Assessment. Ann. Intern. Med. 2021, 174, 408–412. [Google Scholar] [CrossRef] [PubMed]
- Louro, J.; Posso, M.; Hilton Boon, M.; Román, M.; Domingo, L.; Castells, X.; Sala, M. A systematic review and quality assessment of individualised breast cancer risk prediction models. Br. J. Cancer 2019, 121, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Usher-Smith, J.; Emery, J.; Hamilton, W.; Griffin, S.J.; Walter, F.M. Risk prediction tools for cancer in primary care. Br. J. Cancer 2015, 113, 1645–1650. [Google Scholar] [CrossRef] [PubMed]
- Gail, M.H.; Brinton, L.A.; Byar, D.P.; Corle, D.K.; Green, S.B.; Schairer, C.; Mulvihill, J.J. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J. Natl. Cancer Inst. 1989, 81, 1879–1886. [Google Scholar] [CrossRef]
- Tyrer, J.; Duffy, S.W.; Cuzick, J. A breast cancer prediction model incorporating familial and personal risk factors. Stat. Med. 2004, 23, 1111–1130. [Google Scholar] [CrossRef]
- Mazzola, E.; Blackford, A.; Parmigiani, G.; Biswas, S. Recent Enhancements to the Genetic Risk Prediction Model BRCAPRO. Cancer Inform. 2015, 14, 147–157. [Google Scholar] [CrossRef]
- Lee, A.; Mavaddat, N.; Cunningham, A.; Carver, T.; Ficorella, L.; Archer, S.; Walter, F.M.; Tischkowitz, M.; Roberts, J.; Usher-Smith, J.; et al. Enhancing the BOADICEA cancer risk prediction model to incorporate new data on RAD51C, RAD51D, BARD1 updates to tumour pathology and cancer incidence. J. Med. Genet. 2022, 59, 1206–1218. [Google Scholar] [CrossRef]
- Yang, X.; Eriksson, M.; Czene, K.; Lee, A.; Leslie, G.; Lush, M.; Wang, J.; Dennis, J.; Dorling, L.; Carvalho, S.; et al. Prospective validation of the BOADICEA multifactorial breast cancer risk prediction model in a large prospective cohort study. J. Med. Genet. 2022, 59, 1196–1205. [Google Scholar] [CrossRef] [PubMed]
- Lakeman, I.M.M.; Rodríguez-Girondo, M.; Lee, A.; Ruiter, R.; Stricker, B.H.; Wijnant, S.R.A.; Kavousi, M.; Antoniou, A.C.; Schmidt, M.K.; Uitterlinden, A.G.; et al. Validation of the BOADICEA model and a 313-variant polygenic risk score for breast cancer risk prediction in a Dutch prospective cohort. Genet. Med. Off. J. Am. Coll. Med. Genet. 2020, 22, 1803–1811. [Google Scholar] [CrossRef] [PubMed]
- Pal Choudhury, P.; Brook, M.N.; Hurson, A.N.; Lee, A.; Mulder, C.V.; Coulson, P.; Schoemaker, M.J.; Jones, M.E.; Swerdlow, A.J.; Chatterjee, N.; et al. Comparative validation of the BOADICEA and Tyrer-Cuzick breast cancer risk models incorporating classical risk factors and polygenic risk in a population-based prospective cohort of women of European ancestry. Breast Cancer Res. 2021, 23, 22. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Hou, K.; Burch, K.S.; Lapinska, S.; Privé, F.; Vilhjálmsson, B.; Sankararaman, S.; Pasaniuc, B. Large uncertainty in individual polygenic risk score estimation impacts PRS-based risk stratification. Nat. Genet. 2022, 54, 30–39. [Google Scholar] [CrossRef]
- Debray, T.P.A.; Damen, J.A.A.G.; Snell, K.I.E.; Ensor, J.; Hooft, L.; Reitsma, J.B.; Riley, R.D.; Moons, K.G.M. A guide to systematic review and meta-analysis of prediction model performance. BMJ 2017, 356, i6460. [Google Scholar] [CrossRef] [PubMed]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Moons, K.G.M.; de Groot, J.A.H.; Bouwmeester, W.; Vergouwe, Y.; Mallett, S.; Altman, D.G.; Reitsma, J.B.; Collins, G.S. Critical appraisal and data extraction for systematic reviews of prediction modelling studies: The CHARMS checklist. PLoS Med. 2014, 11, e1001744. [Google Scholar] [CrossRef] [PubMed]
- Collins, G.S.; Reitsma, J.B.; Altman, D.G.; Moons, K.G. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): The TRIPOD Statement. BMC Med. 2015, 13, 1. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Vickers, A.J.; Cook, N.R.; Gerds, T.; Gonen, M.; Obuchowski, N.; Pencina, M.J.; Kattan, M.W. Assessing the performance of prediction models: A framework for some traditional and novel measures. Epidemiology 2010, 21, 128–138. [Google Scholar] [CrossRef]
- Zou, K.H.; O’Malley, A.J.; Mauri, L. Receiver-Operating Characteristic Analysis for Evaluating Diagnostic Tests and Predictive Models. Circulation 2007, 115, 654–657. [Google Scholar] [CrossRef] [PubMed]
- Kerr, K.F.; Wang, Z.; Janes, H.; McClelland, R.L.; Psaty, B.M.; Pepe, M.S. Net Reclassification Indices for Evaluating Risk-Prediction Instruments: A Critical Review. Epidemiol. Camb. Mass 2014, 25, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Pencina, M.J.; D’Agostino, R.B.; D’Agostino, R.B.; Vasan, R.S. Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Stat. Med. 2008, 27, 157–172; discussion 207–212. [Google Scholar] [CrossRef] [PubMed]
- Wolff, R.F.; Moons, K.G.M.; Riley, R.D.; Whiting, P.F.; Westwood, M.; Collins, G.S.; Reitsma, J.B.; Kleijnen, J.; Mallett, S.; PROBAST Group. PROBAST: A Tool to Assess the Risk of Bias and Applicability of Prediction Model Studies. Ann. Intern. Med. 2019, 170, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Rosner, B.; Tamimi, R.M.; Kraft, P.; Gao, C.; Mu, Y.; Scott, C.; Winham, S.J.; Vachon, C.M.; Colditz, G.A. Simplified Breast Risk Tool Integrating Questionnaire Risk Factors, Mammographic Density, and Polygenic Risk Score: Development and Validation. Cancer Epidemiol. Biomarkers Prev. 2021, 30, 600–607. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Rice, M.; Tworoger, S.S.; Rosner, B.A.; Eliassen, A.H.; Tamimi, R.M.; Joshi, A.D.; Lindstrom, S.; Qian, J.; Colditz, G.A.; et al. Addition of a polygenic risk score, mammographic density, and endogenous hormones to existing breast cancer risk prediction models: A nested case–control study. PLoS Med. 2018, 15, e1002644. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.; Brentnall, A.R.; Byers, H.; Harkness, E.; Stavrinos, P.; Howell, A.; Newman, W.; Cuzick, J. The impact of a panel of 18 single nucleotide polymorphisms on breast cancer risk in women attending a UK familial-screening clinic: A case-control study. J. Med. Genet. 2017, 54, 111–113. [Google Scholar] [CrossRef]
- Lello, L.; Raben, T.G.; Hsu, S.D.H. Sibling validation of polygenic risk scores and complex trait prediction. Sci. Rep. 2020, 10, 13190. [Google Scholar] [CrossRef]
- Kramer, I.; Hooning, M.J.; Mavaddat, N.; Hauptmann, M.; Keeman, R.; Steyerberg, E.W.; Giardiello, D.; Antoniou, A.C.; Pharoah, P.D.P.; Canisius, S.; et al. Breast Cancer Polygenic Risk Score and Contralateral Breast Cancer Risk. Am. J. Hum. Genet. 2020, 107, 837–848. [Google Scholar] [CrossRef]
- Giardiello, D.; Hooning, M.J.; Hauptmann, M.; Keeman, R.; Heemskerk-Gerritsen, B.A.M.; Becher, H.; Blomqvist, C.; Bojesen, S.E.; Bolla, M.K.; Camp, N.J.; et al. PredictCBC-2.0: A contralateral breast cancer risk prediction model developed and validated in ~ 200,000 patients. Breast Cancer Res. 2022, 24, 69. [Google Scholar] [CrossRef]
- Borde, J.; Ernst, C.; Wappenschmidt, B.; Niederacher, D.; Weber-Lassalle, K.; Schmidt, G.; Hauke, J.; Quante, A.S.; Weber-Lassalle, N.; Horváth, J.; et al. Performance of Breast Cancer Polygenic Risk Scores in 760 Female CHEK2 Germline Mutation Carriers. J. Natl. Cancer Inst. 2021, 113, 893–899. [Google Scholar] [CrossRef] [PubMed]
- Allman, R.; Dite, G.S.; Hopper, J.L.; Gordon, O.; Starlard-Davenport, A.; Chlebowski, R.; Kooperberg, C. SNPs and breast cancer risk prediction for African American and Hispanic women. Breast Cancer Res. Treat. 2015, 154, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Allman, R.; Spaeth, E.; Lai, J.; Gross, S.J.; Hopper, J.L. A streamlined model for use in clinical breast cancer risk assessment maintains predictive power and is further improved with inclusion of a polygenic risk score. PLoS ONE 2021, 16, e0245375. [Google Scholar] [CrossRef] [PubMed]
- Brentnall, A.R.; van Veen, E.M.; Harkness, E.F.; Rafiq, S.; Byers, H.; Astley, S.M.; Sampson, S.; Howell, A.; Newman, W.G.; Cuzick, J.; et al. A case-control evaluation of 143 single nucleotide polymorphisms for breast cancer risk stratification with classical factors and mammographic density. Int. J. Cancer 2020, 146, 2122–2129. [Google Scholar] [CrossRef] [PubMed]
- Darabi, H.; Czene, K.; Zhao, W.; Liu, J.; Hall, P.; Humphreys, K. Breast cancer risk prediction and individualised screening based on common genetic variation and breast density measurement. Breast Cancer Res. BCR 2012, 14, R25. [Google Scholar] [CrossRef] [PubMed]
- Dite, G.S.; Mahmoodi, M.; Bickerstaffe, A.; Hammet, F.; Macinnis, R.J.; Tsimiklis, H.; Dowty, J.G.; Apicella, C.; Phillips, K.-A.; Giles, G.G.; et al. Using SNP genotypes to improve the discrimination of a simple breast cancer risk prediction model. Breast Cancer Res. Treat. 2013, 139, 887–896. [Google Scholar] [CrossRef]
- Dite, G.S.; MacInnis, R.J.; Bickerstaffe, A.; Dowty, J.G.; Allman, R.; Apicella, C.; Milne, R.L.; Tsimiklis, H.; Phillips, K.-A.; Giles, G.G.; et al. Breast Cancer Risk Prediction Using Clinical Models and 77 Independent Risk-Associated SNPs for Women Aged Under 50 Years: Australian Breast Cancer Family Registry. Cancer Epidemiol. Biomark. Prev. 2016, 25, 359–365. [Google Scholar] [CrossRef]
- Du, Z.; Gao, G.; Adedokun, B.; Ahearn, T.; Lunetta, K.L.; Zirpoli, G.; Troester, M.A.; Ruiz-Narváez, E.A.; Haddad, S.A.; PalChoudhury, P.; et al. Evaluating Polygenic Risk Scores for Breast Cancer in Women of African Ancestry. J. Natl. Cancer Inst. 2021, 113, 1168–1176. [Google Scholar] [CrossRef]
- Ho, W.-K.; Tan, M.-M.; Mavaddat, N.; Tai, M.-C.; Mariapun, S.; Li, J.; Ho, P.-J.; Dennis, J.; Tyrer, J.P.; Bolla, M.K.; et al. European polygenic risk score for prediction of breast cancer shows similar performance in Asian women. Nat. Commun. 2020, 11, 3833. [Google Scholar] [CrossRef]
- Hurson, A.N.; Pal Choudhury, P.; Gao, C.; Hüsing, A.; Eriksson, M.; Shi, M.; Jones, M.E.; Evans, D.G.R.; Milne, R.L.; Gaudet, M.M.; et al. Prospective evaluation of a breast-cancer risk model integrating classical risk factors and polygenic risk in 15 cohorts from six countries. Int. J. Epidemiol. 2021, 50, 1897–1911. [Google Scholar] [CrossRef]
- Hüsing, A.; Canzian, F.; Beckmann, L.; Garcia-Closas, M.; Diver, W.R.; Thun, M.J.; Berg, C.D.; Hoover, R.N.; Ziegler, R.G.; Figueroa, J.D.; et al. Prediction of breast cancer risk by genetic risk factors, overall and by hormone receptor status. J. Med. Genet. 2012, 49, 601–608. [Google Scholar] [CrossRef] [PubMed]
- Jantzen, R.; Payette, Y.; de Malliard, T.; Labbé, C.; Noisel, N.; Broët, P. Validation of breast cancer risk assessment tools on a French-Canadian population-based cohort. BMJ Open 2021, 11, e045078. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.P.L.; Choi, H.; Soo, K.C.; Tan, M.-H.; Chay, W.Y.; Chia, K.S.; Liu, J.; Li, J.; Hartman, M. Mammographic Breast Density and Common Genetic Variants in Breast Cancer Risk Prediction. PLoS ONE 2015, 10, e0136650. [Google Scholar] [CrossRef] [PubMed]
- Maas, P.; Barrdahl, M.; Joshi, A.D.; Auer, P.L.; Gaudet, M.M.; Milne, R.L.; Schumacher, F.R.; Anderson, W.F.; Check, D.; Chattopadhyay, S.; et al. Breast Cancer Risk from Modifiable and Nonmodifiable Risk Factors Among White Women in the United States. JAMA Oncol. 2016, 2, 1295–1302. [Google Scholar] [CrossRef] [PubMed]
- Mavaddat, N.; Pharoah, P.D.P.; Michailidou, K.; Tyrer, J.; Brook, M.N.; Bolla, M.K.; Wang, Q.; Dennis, J.; Dunning, A.M.; Shah, M.; et al. Prediction of breast cancer risk based on profiling with common genetic variants. J. Natl. Cancer Inst. 2015, 107, djv036. [Google Scholar] [CrossRef] [PubMed]
- Mealiffe, M.E.; Stokowski, R.P.; Rhees, B.K.; Prentice, R.L.; Pettinger, M.; Hinds, D.A. Assessment of clinical validity of a breast cancer risk model combining genetic and clinical information. J. Natl. Cancer Inst. 2010, 102, 1618–1627. [Google Scholar] [CrossRef] [PubMed]
- Pal Choudhury, P.; Wilcox, A.N.; Brook, M.N.; Zhang, Y.; Ahearn, T.; Orr, N.; Coulson, P.; Schoemaker, M.J.; Jones, M.E.; Gail, M.H.; et al. Comparative Validation of Breast Cancer Risk Prediction Models and Projections for Future Risk Stratification. J. Natl. Cancer Inst. 2020, 112, 278–285. [Google Scholar] [CrossRef] [PubMed]
- Shieh, Y.; Hu, D.; Ma, L.; Huntsman, S.; Gard, C.C.; Leung, J.W.T.; Tice, J.A.; Vachon, C.M.; Cummings, S.R.; Kerlikowske, K.; et al. Breast cancer risk prediction using a clinical risk model and polygenic risk score. Breast Cancer Res. Treat. 2016, 159, 513–525. [Google Scholar] [CrossRef]
- Shieh, Y.; Hu, D.; Ma, L.; Huntsman, S.; Gard, C.C.; Leung, J.W.T.; Tice, J.A.; Ziv, E.; Kerlikowske, K.; Cummings, S.R. Joint relative risks for estrogen receptor-positive breast cancer from a clinical model, polygenic risk score, and sex hormones. Breast Cancer Res. Treat. 2017, 166, 603–612. [Google Scholar] [CrossRef]
- Starlard-Davenport, A.; Allman, R.; Dite, G.S.; Hopper, J.L.; Spaeth Tuff, E.; Macleod, S.; Kadlubar, S.; Preston, M.; Henry-Tillman, R. Validation of a genetic risk score for Arkansas women of color. PLoS ONE 2018, 13, e0204834. [Google Scholar] [CrossRef]
- van Veen, E.M.; Brentnall, A.R.; Byers, H.; Harkness, E.F.; Astley, S.M.; Sampson, S.; Howell, A.; Newman, W.G.; Cuzick, J.; Evans, D.G.R. Use of Single-Nucleotide Polymorphisms and Mammographic Density Plus Classic Risk Factors for Breast Cancer Risk Prediction. JAMA Oncol. 2018, 4, 476–482. [Google Scholar] [CrossRef]
- Vachon, C.M.; Pankratz, V.S.; Scott, C.G.; Haeberle, L.; Ziv, E.; Jensen, M.R.; Brandt, K.R.; Whaley, D.H.; Olson, J.E.; Heusinger, K.; et al. The contributions of breast density and common genetic variation to breast cancer risk. J. Natl. Cancer Inst. 2015, 107, dju397. [Google Scholar] [CrossRef] [PubMed]
- Wen, W.; Shu, X.-O.; Guo, X.; Cai, Q.; Long, J.; Bolla, M.K.; Michailidou, K.; Dennis, J.; Wang, Q.; Gao, Y.-T.; et al. Prediction of breast cancer risk based on common genetic variants in women of East Asian ancestry. Breast Cancer Res. BCR 2016, 18, 124. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Wen, W.; Gao, Y.-T.; Shyr, Y.; Zheng, Y.; Long, J.; Li, G.; Li, C.; Gu, K.; Cai, Q.; et al. Genetic and Clinical Predictors for Breast Cancer Risk Assessment and Stratification Among Chinese Women. JNCI J. Natl. Cancer Inst. 2010, 102, 972–981. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, M.; Czene, K.; Strand, F.; Zackrisson, S.; Lindholm, P.; Lång, K.; Förnvik, D.; Sartor, H.; Mavaddat, N.; Easton, D.; et al. Identification of Women at High Risk of Breast Cancer Who Need Supplemental Screening. Radiology 2020, 297, 327–333. [Google Scholar] [CrossRef] [PubMed]
- Gao, G.; Zhao, F.; Ahearn, T.U.; Lunetta, K.L.; Troester, M.A.; Du, Z.; Ogundiran, T.O.; Ojengbede, O.; Blot, W.; Nathanson, K.L.; et al. Polygenic risk scores for prediction of breast cancer risk in women of African ancestry: A cross-ancestry approach. Hum. Mol. Genet. 2022, 31, 3133–3143. [Google Scholar] [CrossRef] [PubMed]
- Ho, W.-K.; Tai, M.-C.; Dennis, J.; Shu, X.; Li, J.; Ho, P.J.; Millwood, I.Y.; Lin, K.; Jee, Y.-H.; Lee, S.-H.; et al. Polygenic risk scores for prediction of breast cancer risk in Asian populations. Genet. Med. Off. J. Am. Coll. Med. Genet. 2022, 24, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.G.R.; van Veen, E.M.; Harkness, E.F.; Brentnall, A.R.; Astley, S.M.; Byers, H.; Woodward, E.R.; Sampson, S.; Southworth, J.; Howell, S.J.; et al. Breast cancer risk stratification in women of screening age: Incremental effects of adding mammographic density, polygenic risk, and a gene panel. Genet. Med. 2022, 24, 1485–1494. [Google Scholar] [CrossRef]
- Hou, C.; Xu, B.; Hao, Y.; Yang, D.; Song, H.; Li, J. Development and validation of polygenic risk scores for prediction of breast cancer and breast cancer subtypes in Chinese women. BMC Cancer 2022, 22, 374. [Google Scholar] [CrossRef]
- Olsen, M.; Fischer, K.; Bossuyt, P.M.; Goetghebeur, E. Evaluating the prognostic performance of a polygenic risk score for breast cancer risk stratification. BMC Cancer 2021, 21, 1351. [Google Scholar] [CrossRef]
- Yang, Y.; Tao, R.; Shu, X.; Cai, Q.; Wen, W.; Gu, K.; Gao, Y.-T.; Zheng, Y.; Kweon, S.-S.; Shin, M.-H.; et al. Incorporating Polygenic Risk Scores and Nongenetic Risk Factors for Breast Cancer Risk Prediction Among Asian Women. JAMA Netw. Open 2022, 5, e2149030. [Google Scholar] [CrossRef]
- Li, S.X.; Milne, R.L.; Nguyen-Dumont, T.; Wang, X.; English, D.R.; Giles, G.G.; Southey, M.C.; Antoniou, A.C.; Lee, A.; Li, S.; et al. Prospective Evaluation of the Addition of Polygenic Risk Scores to Breast Cancer Risk Models. JNCI Cancer Spectr. 2021, 5, pkab021. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zeinomar, N.; Chung, W.K.; Kiryluk, K.; Gharavi, A.G.; Hripcsak, G.; Crew, K.D.; Shang, N.; Khan, A.; Fasel, D.; et al. Generalizability of Polygenic Risk Scores for Breast Cancer Among Women with European, African, and Latinx Ancestry. JAMA Netw. Open 2021, 4, e2119084. [Google Scholar] [CrossRef] [PubMed]
- Jia, G.; Lu, Y.; Wen, W.; Long, J.; Liu, Y.; Tao, R.; Li, B.; Denny, J.C.; Shu, X.-O.; Zheng, W. Evaluating the Utility of Polygenic Risk Scores in Identifying High-Risk Individuals for Eight Common Cancers. JNCI Cancer Spectr. 2020, 4, pkaa021. [Google Scholar] [CrossRef] [PubMed]
- Márquez-Luna, C.; Loh, P.-R.; South Asian Type 2 Diabetes (SAT2D) Consortium; SIGMA Type 2 Diabetes Consortium; Price, A.L. Multiethnic polygenic risk scores improve risk prediction in diverse populations. Genet. Epidemiol. 2017, 41, 811–823. [Google Scholar] [CrossRef] [PubMed]
- Khera, A.V.; Chaffin, M.; Aragam, K.G.; Haas, M.E.; Roselli, C.; Choi, S.H.; Natarajan, P.; Lander, E.S.; Lubitz, S.A.; Ellinor, P.T.; et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 2018, 50, 1219–1224. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Qian, F.; Zheng, Y.; Ogundiran, T.; Ojengbede, O.; Zheng, W.; Blot, W.; Nathanson, K.L.; Hennis, A.; Nemesure, B.; et al. Genetic variants demonstrating flip-flop phenomenon and breast cancer risk prediction among women of African ancestry. Breast Cancer Res. Treat. 2018, 168, 703–712. [Google Scholar] [CrossRef] [PubMed]
- Shieh, Y.; Fejerman, L.; Lott, P.C.; Marker, K.; Sawyer, S.D.; Hu, D.; Huntsman, S.; Torres, J.; Echeverry, M.; Bohórquez, M.E.; et al. A Polygenic Risk Score for Breast Cancer in US Latinas and Latin American Women. J. Natl. Cancer Inst. 2020, 112, 590–598. [Google Scholar] [CrossRef]
- Chang, C.C.; Chow, C.C.; Tellier, L.C.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-generation PLINK: Rising to the challenge of larger and richer datasets. GigaScience 2015, 4, 7. [Google Scholar] [CrossRef]
- Pashayan, N.; Duffy, S.W.; Chowdhury, S.; Dent, T.; Burton, H.; Neal, D.E.; Easton, D.F.; Eeles, R.; Pharoah, P. Polygenic susceptibility to prostate and breast cancer: Implications for personalised screening. Br. J. Cancer 2011, 104, 1656–1663. [Google Scholar] [CrossRef]
- Wacholder, S.; Hartge, P.; Prentice, R.; Garcia-Closas, M.; Feigelson, H.S.; Diver, W.R.; Thun, M.J.; Cox, D.G.; Hankinson, S.E.; Kraft, P.; et al. Performance of Common Genetic Variants in Breast-Cancer Risk Models. N. Engl. J. Med. 2010, 362, 986–993. [Google Scholar] [CrossRef] [PubMed]
- Läll, K.; Lepamets, M.; Palover, M.; Esko, T.; Metspalu, A.; Tõnisson, N.; Padrik, P.; Mägi, R.; Fischer, K. Polygenic prediction of breast cancer: Comparison of genetic predictors and implications for risk stratification. BMC Cancer 2019, 19, 557. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Ahearn, T.U.; Lecarpentier, J.; Barnes, D.; Beesley, J.; Qi, G.; Jiang, X.; O’Mara, T.A.; Zhao, N.; Bolla, M.K.; et al. Genome-wide association study identifies 32 novel breast cancer susceptibility loci from overall and subtype-specific analyses. Nat. Genet. 2020, 52, 572–581. [Google Scholar] [CrossRef] [PubMed]
- Benichou, J.; Gail, M.H. Methods of inference for estimates of absolute risk derived from population-based case-control studies. Biometrics 1995, 51, 182–194. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G.; Royston, P. What do we mean by validating a prognostic model? Stat. Med. 2000, 19, 453–473. [Google Scholar] [CrossRef]
- Courvoisier, D.S.; Combescure, C.; Agoritsas, T.; Gayet-Ageron, A.; Perneger, T.V. Performance of logistic regression modeling: Beyond the number of events per variable, the role of data structure. J. Clin. Epidemiol. 2011, 64, 993–1000. [Google Scholar] [CrossRef] [PubMed]
- Ogundimu, E.O.; Altman, D.G.; Collins, G.S. Adequate sample size for developing prediction models is not simply related to events per variable. J. Clin. Epidemiol. 2016, 76, 175–182. [Google Scholar] [CrossRef]
- Austin, P.C.; Steyerberg, E.W. Events per variable (EPV) and the relative performance of different strategies for estimating the out-of-sample validity of logistic regression models. Stat. Methods Med. Res. 2017, 26, 796–808. [Google Scholar] [CrossRef]
- Anderssen, E.; Dyrstad, K.; Westad, F.; Martens, H. Reducing over-optimism in variable selection by cross-model validation. Chemom. Intell. Lab. Syst. 2006, 84, 69–74. [Google Scholar] [CrossRef]
- Wu, C.; Ma, S. A selective review of robust variable selection with applications in bioinformatics. Brief. Bioinform. 2015, 16, 873–883. [Google Scholar] [CrossRef]
- Brentnall, A.R.; Cuzick, J. Use of the concordance index for predictors of censored survival data. Stat. Methods Med. Res. 2018, 27, 2359–2373. [Google Scholar] [CrossRef] [PubMed]
- Verbakel, J.Y.; Steyerberg, E.W.; Uno, H.; Cock, B.D.; Wynants, L.; Collins, G.S.; Calster, B.V. ROC curves for clinical prediction models part 1. ROC plots showed no added value above the AUC when evaluating the performance of clinical prediction models. J. Clin. Epidemiol. 2020, 126, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Aarts, A.; Duffy, S.; Geurts, S.; Vulkan, D.; Otten, J.; Hsu, C.-Y.; Chen, T.; Verbeek, A.; Broeders, M. Test sensitivity of mammography and mean sojourn time over 40 years of breast cancer screening in Nijmegen (The Netherlands). J. Med. Screen. 2019, 26, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Costantino, J.P.; Gail, M.H.; Pee, D.; Anderson, S.; Redmond, C.K.; Benichou, J.; Wieand, H.S. Validation Studies for Models Projecting the Risk of Invasive and Total Breast Cancer Incidence. JNCI J. Natl. Cancer Inst. 1999, 91, 1541–1548. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.R.; Kanai, M.; Kamatani, Y.; Okada, Y.; Neale, B.M.; Daly, M.J. Current clinical use of polygenic scores will risk exacerbating health disparities. Nat. Genet. 2019, 51, 584–591. [Google Scholar] [CrossRef] [PubMed]
- McClellan, K.A.; Avard, D.; Simard, J.; Knoppers, B.M. Personalized medicine and access to health care: Potential for inequitable access? Eur. J. Hum. Genet. 2013, 21, 143–147. [Google Scholar] [CrossRef] [PubMed]
- Duncan, L.; Shen, H.; Gelaye, B.; Meijsen, J.; Ressler, K.; Feldman, M.; Peterson, R.; Domingue, B. Analysis of polygenic risk score usage and performance in diverse human populations. Nat. Commun. 2019, 10, 3328. [Google Scholar] [CrossRef] [PubMed]
- Lewis, C.M.; Vassos, E. Polygenic risk scores: From research tools to clinical instruments. Genome Med. 2020, 12, 44. [Google Scholar] [CrossRef]
- Fatumo, S.; Chikowore, T.; Choudhury, A.; Ayub, M.; Martin, A.R.; Kuchenbaecker, K. A roadmap to increase diversity in genomic studies. Nat. Med. 2022, 28, 243–250. [Google Scholar] [CrossRef]
- Terry, M.B.; Liao, Y.; Whittemore, A.S.; Leoce, N.; Buchsbaum, R.; Zeinomar, N.; Dite, G.S.; Chung, W.K.; Knight, J.A.; Southey, M.C.; et al. 10-year performance of four models of breast cancer risk: A validation study. Lancet Oncol. 2019, 20, 504–517. [Google Scholar] [CrossRef]
- Moorthie, S.; Hall, A.; Janus, J.; Brigden, T.; Babb de Villiers, C.; Blackburn, L.; Johnson, E.; Kroese, M. Polygenic Scores and Clinical Utility; PHG Foundation: Cambridge, UK, 2021; 53p. [Google Scholar]



| Author, Year | Country | Type of BC | Number of SNPs | Selection of SNPs | Method of Development of GRS or PRS | Selection of Risk Factors | Method of Development of Combined Model | TRIPOD Level |
|---|---|---|---|---|---|---|---|---|
| Models based on genetic risk factors alone | ||||||||
| Du, 2021 [49] | Various (USA, Ghana, Nigeria and Barbados) | Overall BC, ER-positive, ER-negative | 179 and 313 SNPs | SNPs that reached genome-wide statistical significance in GWAS analyses and SNPs from a previously published study [12]. | Cumulative effect at a risk locus of the weights of each SNP multiplied by the risk allele dosage of each SNP. | __ | __ | 2a |
| Gao, 2022 [67] | Various (Barbados, Ghana, USA) | Overall BC, ER-positive, ER-negative | 307 SNPs | Modified version of the hard-thresholding based on stepwise forward logistic regression outlined by Mavaddat et al. [12]. | Three methods were evaluated: (1) Cumulative effect of the per-allele log OR for BC associated with each SNP multiplied by the allele dosage for each SNP from genome-wide data in women of African Ancestry, (2) the 313 SNPs PRS using the effect size from Mavaddat et al. [12] and (3) the joint and hybrid PRS as a weighted linear combination of the two previous PRS (adapted method from Márquez-Luna et al. [76]). | __ | __ | 2a |
| Ho, 2020 [50] | Various (China, Malaysia, India) | Invasive BC, ER-positive, ER-negative | 287 SNPs | Available race-specific derived SNPs from Mavaddat et al. [12] based on an imputation accuracy score. | Cumulative effect of the weights of each SNP multiplied by the dosage of risk allele for each SNP. | __ | __ | 4 |
| Ho, 2022 [68] | Various (China, India, Taiwan, Singapore, Korea, Japan, Malaysia) | Invasive BC | 46, 287 and 2985 SNPs | Multiple approaches: (1) Clumping and threshold approach, (2) lasso penalized regression, (3) linear combination of European and Asian PRS, (4) integration of Asian weights into European PRS, (5) Bayesian polygenic prediction approach and (6) South Asian specific SNPs. | Cumulative effect of the weights of each SNP multiplied by the risk allele dosage of each SNP. | __ | __ | 3 |
| Liu, 2021 [74] | USA | Overall BC | 313, 3820 or 5218 SNPs (European ancestry), 34 or 75 SNPs (African ancestry), 71 or 180 SNPs (Latinx ancestry) | Previously identified SNPs from published studies (2 studies in women of European ancestry [12,77], 2 in women of African ancestry [43,78] and 2 in women from Latinx ancestry [43,79]. | Weighted sum of each variant effect size using the PLINK version 1.9 [80] to reconstruct seven previously developed and tested PRS with European, African and Latinx ancestries. Ambiguous variants, variants with allele mismatches, and variants with more than 3+ alleles from each PRS model were excluded. | __ | __ | 4 |
| Mavaddat, 2015 [56] | Various (Europe, Australia, USA) | Overall BC | 77 SNPs | SNPs associated at p < 5 × 10−8 with overall or ER-negative BC by the COGS or previous publications. | Cumulative effect of the per-allele log OR multiplied by the number of alleles for the same SNP, ignoring departures from a multiplicative model. | __ | __ | 2b |
| Mavaddat, 2019 [12] | Various (Europe, Australia, USA) | Overall BC, ER-positive, ER-negative | 77, 313 and 3820 SNPs | Hard-thresholding based on stepwise forward regression that retained SNPs significantly association with overall or subtype-specific BC or lasso penalized regression. | For overall BC: Cumulative effect of the per-allele log OR for BC associated with each SNP and multiplied by the allele dosage for each SNP. For BC subtypes, four methods were evaluated: (1) using effect sizes for overall BC; (2) using effect sizes for subtype-specific BC; (3) using a hybrid method; (4) deriving subtypes-specific estimates using case-only ORs case-only ORs estimated by lasso combining with overall BC ORs. | __ | __ | 3 |
| Wen, 2016 [64] | Various (China, Japan, South Korea, Thailand, and Malaysia) | Overall BC | 44 SNPs | SNPs associated with overall BC at p < 0.05 (one-sided). | Cumulative effect of the per-allele log OR for BC associated with the risk allele for each SNP. | __ | __ | 1a |
| Models based on genetic risk factors and non-genetic risk factors | ||||||||
| Allman, 2015 [43] | USA | Overall BC | 75 SNPs (African American), 71 SNPs (Hispanics) | Race-specific derived SNPs identified as being associated with BC from studies of White women [56] for which imputed genotypes were available. | Mealiffe et al. [57] approach. SNP-based relative risk score using ORs per-allele and risk allele frequency assuming independent and additive risks on the log-OR scale. Then, multiplying the adjusted risk values for each SNP. | From existing models (BCRAT and IBIS). | Log-transformed combined score (SNP-based score multiplied by model’s predicted 5-year risk) and age-adjusted using logistic regression. | 1a |
| Allman, 2021 [44] | USA | Overall BC | 77 SNPs (European ancestry), 75 SNPs (African American), 71 SNPs (Hispanics) | Race-specific derived SNPs from published GWAS. | Mealiffe et al. [57] approach. SNP-based relative risk score using ORs per-allele and risk allele frequency assuming independent and additive risks on the log-OR scale. Then, multiplying the adjusted risk values for each SNP. | From real-world clinical practice factors based on the BCRAT. | Log-transformed combined score (SNP-based score multiplied by model’s predicted 5-year risk) and age-adjusted using logistic regression. | 4 |
| Brentmall, 2020 [45] | UK | Overall BC (invasive or ductal carcinoma in situ), ER-positive, ER-negative | 143 SNPs | Previously identified SNPs associated with BC from Michailidou et al. [10] and available in the dataset. | Multiplying the per-allele OR for each SNP, normalized by the average risk expected in the populations based on the assumed allele frequency. | From an existing model (Tyrer–Cuzick). | Regressing the PRS on adjustment factors (age, the natural logarithm of 10-year risk from the Tyrer–Cuzick model and mammographic density) in controls. | 4 |
| Darabi, 2012 [46] | Sweden | Overall BC | 18 SNPs | Previously identified SNPs from Pashayan et al. [81]. | Weighted average of effect estimates from separate studies obtained by the inverse variance method or multiplicative penetrance model for BC-associated SNPs. | From an existing model (Gail). | Method by Gail et al. [19] to estimate the probability of a woman with a particular risk profile developing BC in a specific time interval. | 1a |
| Dite, 2013 [47] | Australia | Invasive BC, ER-positive, ER-negative | 7 SNPs | Statistically significant SNPs associated with BC in GWAS and identified in the study by Mealiffe et al. [57] | Mealiffe et al. [57] approach. SNP-based relative risk score using ORs and risk allele frequency assuming independence of additive risks on the log-OR scale. Then, multiplying the adjusted risk values for each SNP. | From an existing model (BCRAT). | Multiplying the SNP risk score and the BCRAT risk score under the assumption of independence. | 1a |
| Dite, 2016 [48] | Australia | Invasive BC, ER-positive, ER-negative | 77 SNPs | Previously identified SNPs from Mavaddat et al. [56]. | Mealiffe et al. approach [57]. SNP-based relative risk score using ORs per-allele and risk allele frequency assuming independence of additive risks on the log-OR scale. Then, multiplying the adjusted risk values for each SNP. | From existing models (BOADICEA, BRCAPRO, BCRAT, IBIS). | Multiplying the SNP-based score by model’s predicted 5-year absolute risk of BC (all risk factors were age-adjusted log 5-year risks). | 1a |
| Eriksson, 2020 [66] | Sweden | Overall BC | 313 SNPs | Previously identified SNPs from Mavaddat et al. [12]. | Per-allele log OR for each SNP in a log-additive model. | Not specified—All considered were included. | Unconditional logistic regression stratified by age. | 1a |
| Evans, 2022 [69] | UK | Overall BC (invasive or ductal carcinoma in situ) | 18, 143 and 313 SNPs | Previously identified SNPs from two studies [45,63]. | PRS143: Per-allele OR derived from published OR and allele frequency normalized around a relative risk of 1.0. PRS313: Cumulative effect of the log OR for each SNP multiplied by the corresponding number of minor alleles. | From existing model (Tyrer–Cuzick). | Regressing the PRS on adjustment factors. | 4 |
| Hou, 2022 [70] | China | Overall BC, ER-positive, ER-negative | 24 SNPs | Previously identified SNPs from GWAS or meta-analyses found to be associated with BC risk in Chinese women. | Three different approaches, the first two based on the cumulative effect size, calculated as the per-allele log OR for BC associated with each SNP, multiplied by the number of effect alleles: (1) repeated logistic regression (RLR) (2) logistic ridge regression (LRR), (3) artificial neural network (ANN)-based approach. | Established BC risk factors. | Regressed the PRS against non-genetic risk factors or absolute risks predicted by the Gail-2 model. | 3 * |
| Hurson, 2021 [51] | Various (Australia, Germany, Netherlands, Sweden, UK, USA) | Overall BC (In situ or invasive BC) | 313 SNPs | Previously identified SNPs from Mavaddat et al. [12]. | Cumulative effect of the per-allele log OR for BC associated with each SNP and multiplied by the allele dosage for each SNP. | From an existing model (iCARE-Lit). | Use of iCARE tool to incorporate risk factors and the PRS assuming a multiplicative joint association with disease risk, accounting for the correlation of PRSs with family history. | 4 |
| Husing, 2012 [52] | Various (USA, Europe) | Invasive BC, ER-positive, ER-negative | 7, 9, 18 and 32 SNPs | Statistically significant SNPs in at least one GWAS at a genome-wide significance level (p < 10−7). | Log-additive model with individually weighted per-allele effects for each SNP. | Available factors from an existing model (BCRAT) selected using a backwards selection process. | Unconditional logistic regression with BC status as the outcome combining genetic effects and covariate model. | 2a |
| Jantzen, 2021 [53] | Canada | Invasive BC | 10, 18, 77 and 86 SNPs | Previously identified SNPs from 4 published studies [38,56,59,82]. | Linear combinations of the risk-conferring variant alleles weighted by their effect sizes. | Available factors from existing models (BCRAT and IBIS). | Use of the iCARE package to sum the PRS and BCRAT score (relative hazard regression score). Use of the IBIS tool to incorporate shifted PRS scores. | 4 |
| Jia, 2020 [75] | UK | Overall BC | 282 SNPs | Available SNPs in dataset from the 313 SNPs previously identified by Mavaddat et al. [12]. | Sum of the product of the weight and the number of risk alleles for each risk variant across all selected risk variants per individual. | Not specified—Only family history of cancer in first-degree relatives was included. | Logistical models adjusted for genotype array types. | 4 |
| Lakeman, 2020 [24] | The Netherlands | Overall BC (In situ or invasive BC) | 313 SNPs | Previously identified SNPS from Mavaddat et al. [12]. | Cumulative effect of per- allele log OR (obtained from the BCAC) for BC associated with each SNP and multiplied by the number of risk alleles. | Available factors from an existing model (BOADICEA). | Use of BOADICEA version 5. | 4 |
| Lee, 2015 [54] | Singapore | Overall BC (In situ or invasive BC) | 75 SNPs | SNPs identified in GWAS or in BCAC from the Asian populations assuming no interaction between SNPs, mammographic density and other risk factors. | Cumulative effect of log OR for each SNP multiplied by the number of risk alleles. | From an existing model (Gail) + predictors relevant to their population. | Cox proportional hazards model. | 1a |
| Li, 2021 [73] | Australia | Invasive BC | 313 SNPs | Previously identified SNPs based on GWAS published by the BCAC [10,12]. | BOADICEA: Sum of the per allele log-OR multiplied by the allele counts for each SNP across variants and then normalized using population-based risk and allele frequency. IBIS: Multiplying the SNP-specific relative risk by the genotype-specific relative risk of BC, which estimates the average population relative risk accounting for the population-based risk and the allele frequency for the women’s genotype. | From existing models (BOADICEA v5.0.0 and IBIS V8b). | Use of BOADICEA version 5.0.0 and the Tyler-Cuzick model v.8b. | 4 |
| Maas, 2016 [55] | Various (Australia, Europe, USA) | Invasive BC | 92 SNPs | SNPs identified in the BPC3 study and previously published SNPs. | Combination of a PRS24 assuming additive associations on the log scale after adjustments and a simulated PRS68 conditional on case-control status and family history, using the model estimates of the log-OR and the allele frequencies for the SNPs with an estimate of the log-OR for family history. | Established BC risk factors. | Multivariate logistic regression. | 1a |
| Mealiffe, 2010 [57] | USA | Invasive BC, ER-positive, ER-negative | 7 SNPs | Statistically significant SNPs in GWAS with correction for multiple testing and confirmed in an independent set of case controls. | Product of genotype relative risk value for each SNP based on a log-additive model. | Available factors from an existing model (BCRAT). | Multiplying 5-year Gail absolute risk estimates by SNP risk score. | 1b |
| Olsen, 2021 [71] | Estonia | Overall BC | 973 SNPs | Previously identified SNPs from Läll et al. [83]. | Weighted average of the two strongest associated PRS (named metaGRS2), each PRS obtained by a linear combination of SNPs effect weighted by their log beta-coefficients. | Statistically significant predictors from a fully adjusted Cox model. | Cox proportional hazards model adjusted for age. | 2a |
| Pal Choudhury, 2020 [58] | UK and USA | Overall BC | 313 SNPs | Previously identified SNPS from Mavaddat et al. [12]. | Cumulative effect for the total number of SNPS per allele OR associated with SNPs multiplied by allele dosage for SNPs. | From existing models (iCARE-Lit, iCARE-BPC3, BCRAT, IBIS). | Use of the iCARE, BCRAT and IBIS v8 models. | 4 |
| Pal Choudhury, 2021 [25] | UK | Overall BC | 313 SNPs | Previously identified SNPS from Mavaddat et al. [12]. | Cumulative effect for the total number of SNPS per allele OR associated with SNPs multiplied by allele dosage for SNPs. | From existing models (BOADICEA and Tyrer–Cuzick). | Use of BOADICEA version 5 as described by Lee et al. [13] and the IBIS tool (v.8) as described by Brentnall et al. [45] | 4 |
| Shieh, 2016 [59] | USA | Invasive BC | 76 (Asian) and 83 SNPs | GWAS significant SNPs (p < 5 × 10−8) associated with invasive BC in White, Asian or Hispanic women. | Bayesian approach of the composite likelihood ratio representing the individual effects of each SNP assuming independence and no interaction between them. | From an existing model (fitted-BCSC). | Use version 2.0 of the BCSC model for multivariable regression analysis. | 2a |
| Shieh, 2017 [60] | USA | ER-positive | 83 SNPs | GWAS significant SNPs (p < 5 × 10−8) associated with invasive BC in White, Asian or Hispanic women. | Bayesian approach of the composite likelihood ratio representing the individual effects of each SNP assuming independence and no interaction between them. | From an existing model (BCSC v1). | Conditional logistic regression using a multivariable model. | 2a |
| Starlard-Davenport, 2018 [61] | USA | Overall BC | 75 SNPs | Previously identified SNPs from Mavaddat et al. [56] | Mealiffe et al. approach [57]. SNP-based relative risk score using ORs per-allele and risk allele frequency assuming independence of additive risks on the log-OR scale. Then, multiplying the adjusted risk values for each SNP. | From an existing model (BCRAT). | Multiplying the SNP-based score by the model’s predicted 5-year and lifetime absolute risk of BC. | 4 |
| Vachon, 2015 [63] | USA and Germany | Overall BC, invasive BC | 76 SNPs | Previously identified SNPS from published studies. | Cumulative effect of the log OR for each SNP multiplied by the corresponding number of minor alleles. | From an existing model (BCSC). | Logistic regression. | 1b |
| van Veen, 2018 [62] | UK | Overall BC (Invasive and ductal carcinoma in-situ) | 18 SNPs | SNPs associated with BC in GWAS. | Multiplying the per-allele OR for each SNP and normalizing the risk by the average risk expected in the population using published minor allele frequencies. | From an existing model (Tyrer–Cuzick). | Multiplying Tyrer–Cuzick 10-year absolute risk by density residual and PRS assuming independence. | 1a |
| Yang X., 2022 [23] | Sweden | Invasive BC | 313 SNPs | Previously identified SNPs from Mavaddat et al. [12]. | SNP was given a per-allele log OR in a log-additive model and derived and standardized by the mean and standard deviation. | From existing model (BOADICEA v.6) | Used BOADICEA V.6 with Swedish age-specific and calendar period-specific population incidences for invasive BC. | 4 |
| Yang Y., 2022 [72] | Various (China, Japan, Korea Shanghai) | Overall BC | 111 and 263 SNPs | Race-specific SNPs from two published studies [12,84]. | Three different approaches based on the cumulative effect of the allelic dosage multiplied by the corresponding weight of each SNP: (1) reported European PRS, (2) PRS based on SNPs identified by fine-mapping of GWAS-identified risk loci and (3) PRS-based on genome-wide risk prediction algorithms. | Established BC risk factors. | An integrated risk prediction model included the PRS and the non-genetic risk score (weighted value of each risk factor plus the weight of the interaction between BMI and menopause status) as independent predictors of BC (BC~PRS + NgRS). | 3 |
| Zheng, 2010 [65] | China | Overall BC | 9 SNPs | Statistically significant SNPs associated with BC in GWAS. | Cumulative effect of the OR for each SNP multiplied by the number of SNPs replicated in the study. | Established BC risk factors. | Similar approach to Gail et al. [81] to estimate the absolute risk of C according to the risk factors that a woman carried [85]. | 1b |
| Author, Year | Age | Age at Mena-Rche | Age at Meno- Pause | Age at First Live Birth | No of Live Births | Parity | Family History of BC | No of Relatives with BC | Breast Biopsy | No of Biopsies | Breast Density | Meno- Pausal Status | HRT Use | OC Use | History of BBD | BMI | Alcohol Use | Smoking Status | Race/ Ethnicity | Atypical Hyper-Plasia | Heig-Ht |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Allman, 2015 [43] BCRAT | X | X | X | X 1 | X Ⴕ | NA | |||||||||||||||
| Allman, 2015 [43] a IBIS | X | X | X | NA | X 1 | X Ⴕ | |||||||||||||||
| Allman, 2021 [44] | X | X 1 | X Ⴕ | ||||||||||||||||||
| Brentnall, 2021 [45] | X | X | X | X 1 | X b | X | X | ||||||||||||||
| Darabi, 2012 [46] | X | X | X 1 | NA | X b | X | X | ||||||||||||||
| Dite, 2013 [47] | X ‡ | X | X | X 1 | NA | X | NA | ||||||||||||||
| Dite, 2016 [48] BOADICEA | X | X | X 1 | ||||||||||||||||||
| Dite, 2016 [48] BRCAPRO | X | X 1 | |||||||||||||||||||
| Dite, 2016 [48] BCRAT | X | X | X | X 1 | NA | NA | |||||||||||||||
| Dite, 2016 [48] IBIS | X | X | X | NA | |||||||||||||||||
| Eriksson, 2020 [66] c | X | X 1 | X | X | X | X | X | X | |||||||||||||
| Evans, 2022 [69] d | X | X | X 1,2,ႵႵ | X | X | X | |||||||||||||||
| Hou, 2022 [70] | X | X | X | X | X | X | |||||||||||||||
| Hurson, 2021 [51] <50 years old | X ‡ | X | X | X | X | X | X | X | X | X | |||||||||||
| Hurson, 2021 [51] ≥50 years | X ‡ | X | X | X | X | X | X e | X | X | NA | X | X | |||||||||
| Husing, 2012 [52] | X | X | X | X | X f | X | X f | X | X | ||||||||||||
| Jantzen, 2021 [53] BCRAT | X | X | X | X 1 | X | X | |||||||||||||||
| Jantzen, 2021 [53] g IBIS V.8.0.b | X | X | X | X | X | X | NA | X | X | X | |||||||||||
| Jia, 2020 [75] | X 1 | ||||||||||||||||||||
| Lakeman, 2020 [24] | X | X | X | X | X | X | X | X | X | X | |||||||||||
| Lee, 2015 [54] | X | X | X | X 1 | X | X | X | X | |||||||||||||
| Li, 2021 [73] h BOADICEA | X | X | X | X | X | X | X 1,2 | NA | X | X | X | X | X | X | |||||||
| Li, 2021 [73] i IBIS | X | X | X | X | X 1,2 | NA | NA | X | X | X | X | NA | X | ||||||||
| Maas, 2016 [55] | X | X | X | X | X | X | X | X | X | X | X | ||||||||||
| Mealiffe, 2010 [57] | X | X | X | X 1 | X | X | NA | ||||||||||||||
| Olsen, 2021 [71] | X | ||||||||||||||||||||
| Pal Choudhury, 2020 [58] iCARE-Lit | X ‡ | X | X | X | X | X 1 | X | X | X | X | X | X | |||||||||
| Pal Choudhury, 2020 [58] iCARE-BPC3 | X ‡ | X | X | X | X | X 1 | X | X | X | X | X | ||||||||||
| Pal Choudhury, 2020 [58] BCRAT | X ‡ | X | X | X 1 | X 1 | X | X | X | |||||||||||||
| Pal Choudhury, 2020 [58] IBIS j | X ‡ | X | X | X | X | X 1,2,3 | X 1,2,3 | X | X | X | X | X | |||||||||
| Pal Choudhury, 2021 [25] BOADICEA k | X ‡ | X | X | X | X | X 1 | X | X | X | X | X | ||||||||||
| Pal Choudhury, 2021 [25] Tyrer–Cuzick | X ‡ | X | X | X | X | X 1 | X | X e | X | X | X | ||||||||||
| Shieh, 2016 [59] | X | X 1 | X | X | X | X Ⴕ | |||||||||||||||
| Shieh, 2017 [60] l | X | X 1 | X | X | X | ||||||||||||||||
| Starlard-Davenport, 2018 [61] | X | X | X | X 1 | NA | NA | |||||||||||||||
| Vachon, 2015 [63] | X | X | X | ||||||||||||||||||
| van Veen, 2018 [62] | X | X | X | X 1 | X | X | X | ||||||||||||||
| Yang X., 2022 [23] | X | X | X | X | X | X 1 | X | X | X | X | X | X | X | ||||||||
| Yang Y., 2022 [72] f,m | X | X | X | X | X | ||||||||||||||||
| Zheng, 2010 [65]m | X | X | X | X 1 | X | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mbuya-Bienge, C.; Pashayan, N.; Kazemali, C.D.; Lapointe, J.; Simard, J.; Nabi, H. A Systematic Review and Critical Assessment of Breast Cancer Risk Prediction Tools Incorporating a Polygenic Risk Score for the General Population. Cancers 2023, 15, 5380. https://doi.org/10.3390/cancers15225380
Mbuya-Bienge C, Pashayan N, Kazemali CD, Lapointe J, Simard J, Nabi H. A Systematic Review and Critical Assessment of Breast Cancer Risk Prediction Tools Incorporating a Polygenic Risk Score for the General Population. Cancers. 2023; 15(22):5380. https://doi.org/10.3390/cancers15225380
Chicago/Turabian StyleMbuya-Bienge, Cynthia, Nora Pashayan, Cornelia D. Kazemali, Julie Lapointe, Jacques Simard, and Hermann Nabi. 2023. "A Systematic Review and Critical Assessment of Breast Cancer Risk Prediction Tools Incorporating a Polygenic Risk Score for the General Population" Cancers 15, no. 22: 5380. https://doi.org/10.3390/cancers15225380
APA StyleMbuya-Bienge, C., Pashayan, N., Kazemali, C. D., Lapointe, J., Simard, J., & Nabi, H. (2023). A Systematic Review and Critical Assessment of Breast Cancer Risk Prediction Tools Incorporating a Polygenic Risk Score for the General Population. Cancers, 15(22), 5380. https://doi.org/10.3390/cancers15225380






