A Study on Survival Analysis Methods Using Neural Network to Prevent Cancers
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Characteristics, Biomarkers, and Events
- Demographic: AGE—age, years; SEX—sex, 1 as male and 2 as female.
- Metabolic characteristics: WT—weight, kilograms; HT—height, centimeters; and BMI—body mass index = weight/height2 (kg/m2); WC—waist circumference, centimeters; SBP—systolic blood pressure, mmHg; DBP—diastolic blood pressure, mmHg; CHO total cholesterol, mg/dL; HDL—high-density cholesterol, mg/dL; TG—triglycerides, mg/dL; LDL—low-density cholesterol, mg/dL; GLU—glucose, mg/dL; PP—pulse pressure = systolic blood pressure − diastolic blood pressure, mmHg.
- Liver function: ALB—albumin, g/dL; GLOBULIN—globulin, g/dL; AGR—albumin globulin rate; BIL—total bilirubin, mg/dL; DBIL—direct bilirubin, mg/dL; ALP—alkaline phosphatase, units/L; AST—aspartate aminotransferase, units/L; ALT—alanine aminotransferase, units/L; GGTP—gamma-glutamyl transpeptidase, units/L.
- Kidney function: CREAT—creatinine, mg/dL; BUN—blood urea nitrogen, mg/dL; SG—specific gravity; PH—urine pH; CCR—creatinine clearance rate = (140 − Age) × Weight/(Creatinine × 72) for Men OR ((140 − Age) × Weight/(Creatinine × 72)) × 0.85 for Women.
- Pancreas function: AMYLASE—amylase, units/L.
- Pulmonary function: FVC—forced lung capacity, measured in liters; FEV1—forced expiratory volume, measured in liters.
2.3. Project Pipeline
2.4. Model Description
2.4.1. Cox PH Regression
- t is the survival time
- h(t) is the hazard function
- xi is the vector of covariates
- h0(t) is the baseline hazard when all the xi are equal to zero.
- β is the vector of coefficients of xi
- Ei, Ti, and xi are event indicator, survival time, and baseline covariates of the ith observation.
- The likelihood is defined in non-censored observations (Ei = 1).
- R(t) = {i: Ti >= t} is the set of participants at risk of event at time t.
2.4.2. DeepSurv
2.4.3. DeepHit
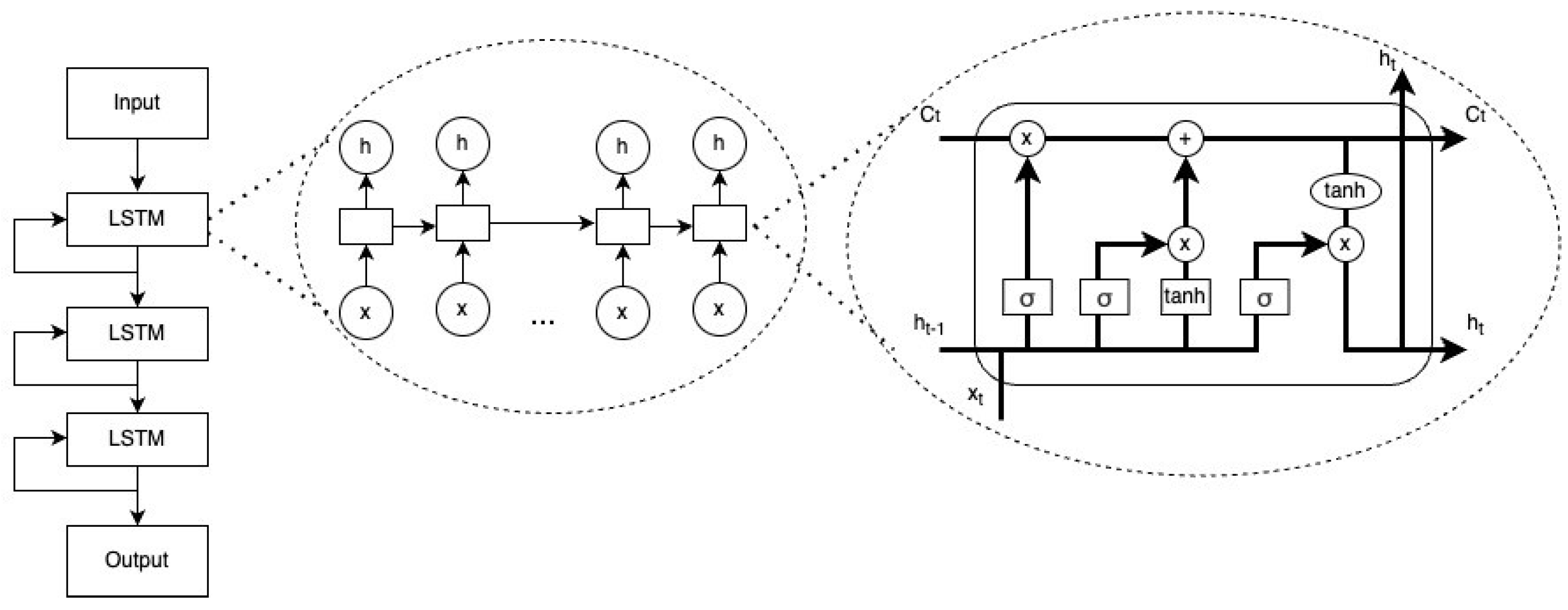
2.4.4. nDeep
- The initial values c0 = 0 and h0 = 0
- xt ∈ Rd: vector of input
- ft ∈ (0, 1)h: vector of forget gate’s activation
- it ∈ (0, 1)h: vector of input/update gate’s activation
- ot ∈ (0, 1)h: vector of output gate’s activation
- ht ∈ (−1, 1)h: vector of hidden state, also output
- ∈ (−1, 1)h: vector of cell input activation
- ct ∈ Rh: vector of cell state
- W ∈ Rhxd, U ∈ Rhxd and b ∈ Rh: vectors of weight matrices and bias
- ⊙: element-wise product (Hadamard product)
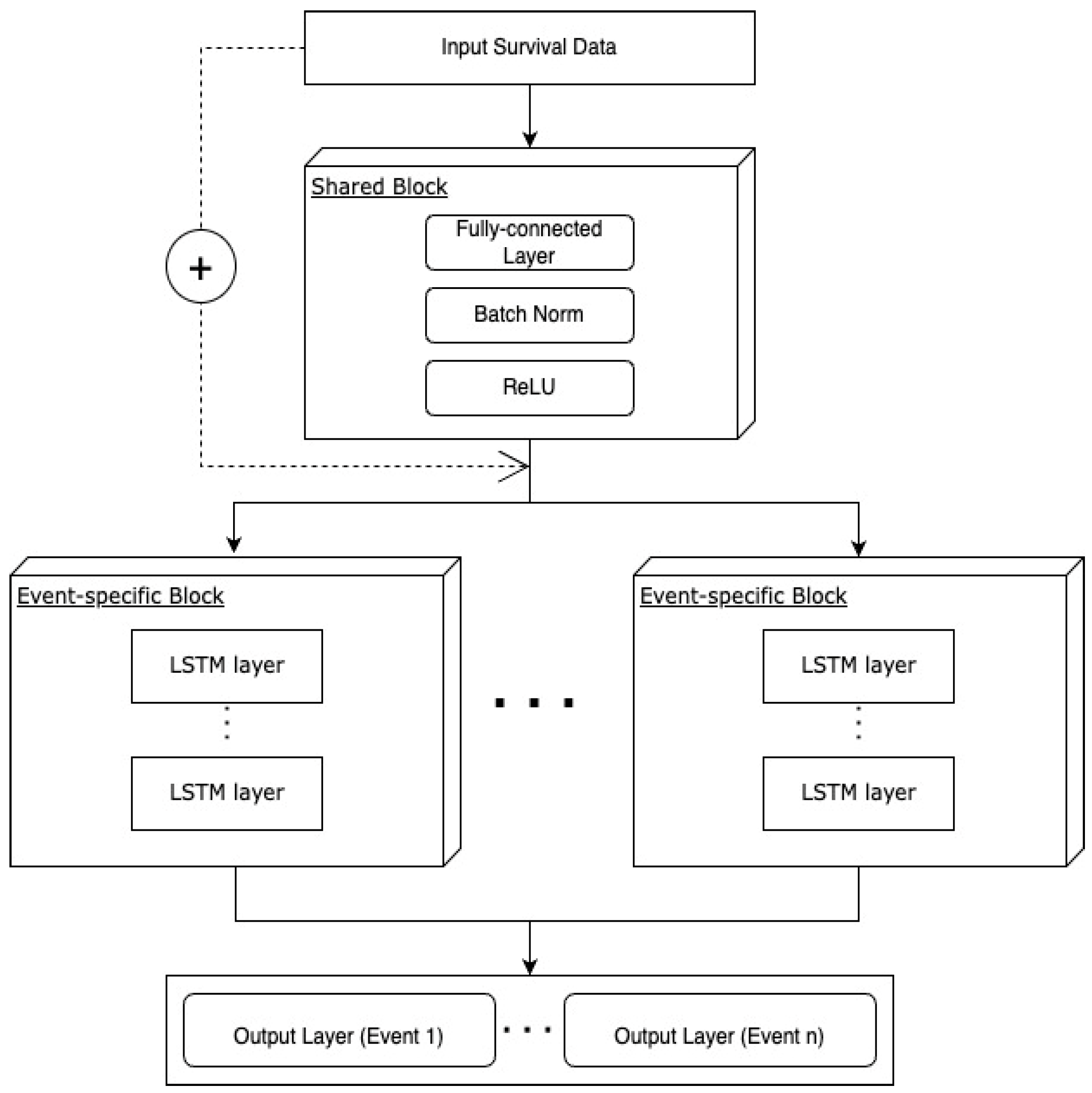
2.4.5. Multi-nDeep
2.4.6. Hyperparameters of DNN Models
2.5. Model Learning
- N: number of subjects
- I: indicator function (1: death, 0: otherwise)
- θ: weights of the network
- : estimated hazard function
- xi, xj: vectors of covariates
- R(ti): set of subjects at risk at time ti
- : convex loss function
- : estimated cumulative incidence function
- s: time
- x: covariate
2.6. Performance Metric
2.7. Feature Importance
2.8. Ethical Considerations
3. Results
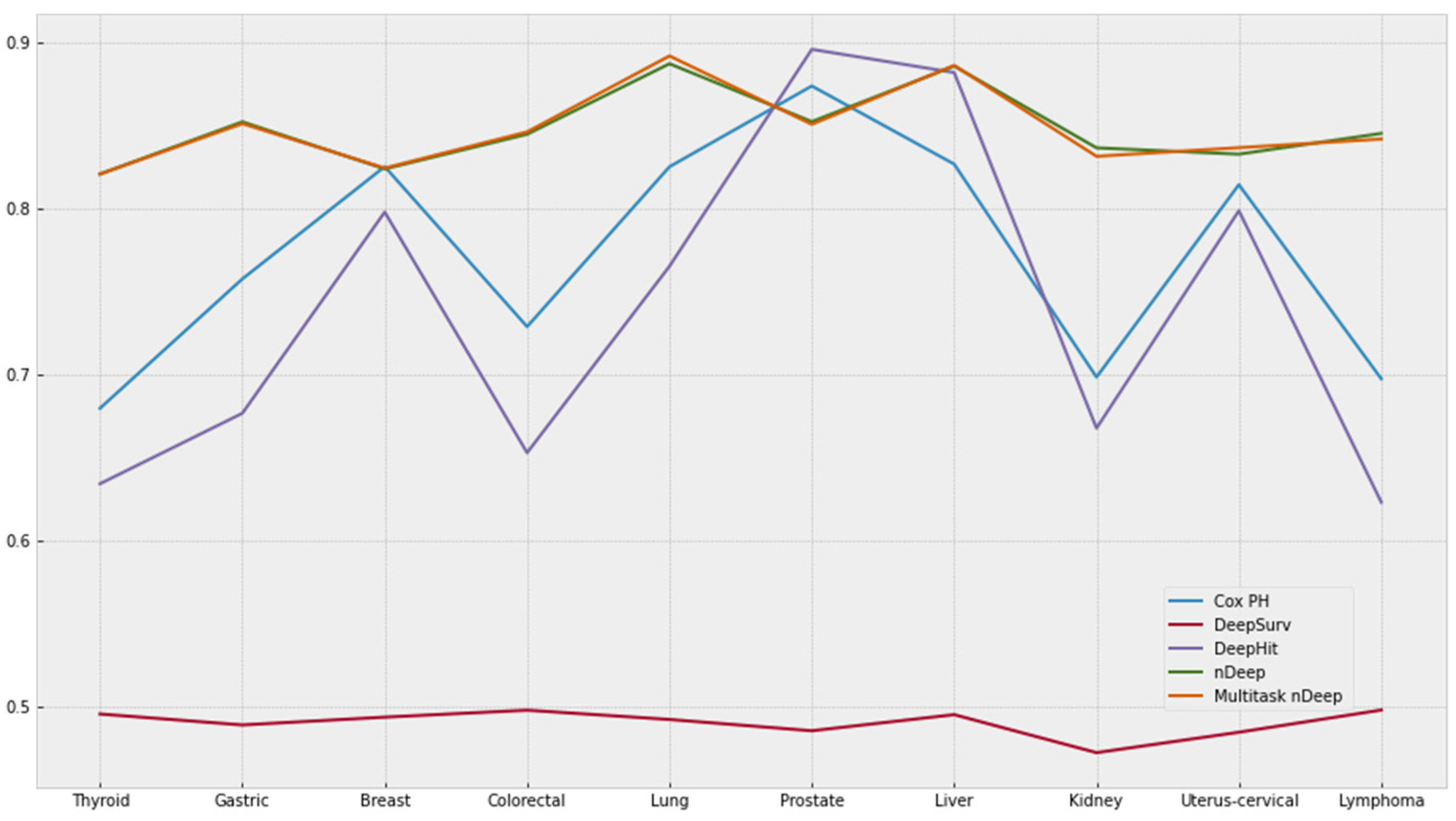
3.1. Comparing c-Index of Each Model
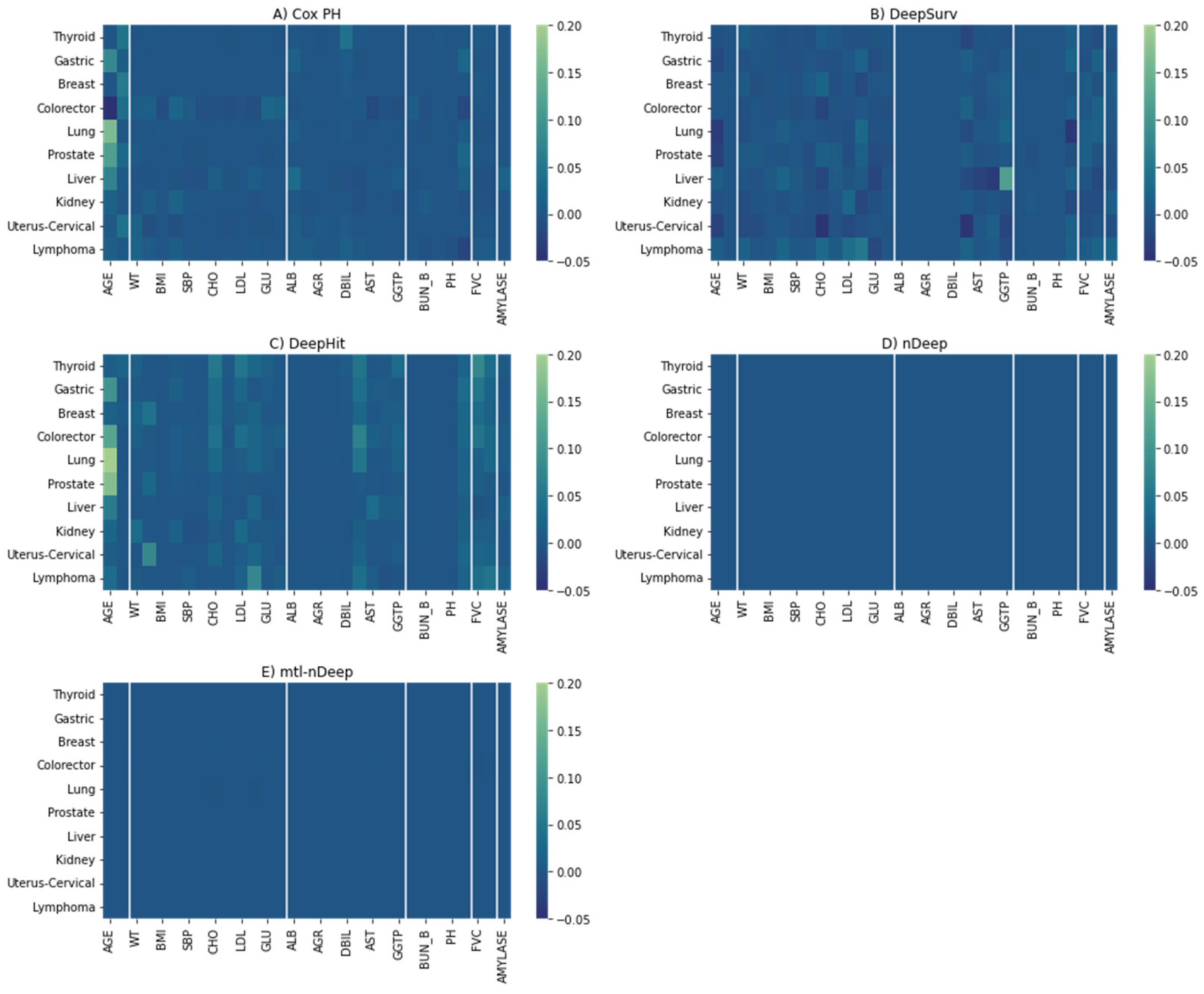
3.2. Feature Importance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization—The Top 10 Causes of Death. Available online: https://www.who.int/news-room/fact-sheets/detail/the-top-10-causes-of-death (accessed on 2 December 2022).
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: {GLOBOCAN} estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA A Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M. Introduction to survival analysis in practice. Mach. Learn. Knowl. Extr. 2019, 1, 1013–1038. [Google Scholar] [CrossRef]
- Deepa, P.; Gunavathi, C. A systematic review on machine learning and deep learning techniques in cancer survival prediction. Biophys. Mol. Biol. 2022, 174, 62–71. [Google Scholar]
- Cox, D. Regression models and life-tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B. Random survival forests for R. R News 2007, 7, 25–31. [Google Scholar]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Faraggi, D.; Simon, R. A neural network model for survival data. Stat. Med. 1995, 14, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Zame, W.; Yoon, J.; Van Der Schaar, M. Deephit: A deep learning approach to survival analysis with competing risks. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Kim, S.; Song, H.; Kim, S.; Kim, B.; Lee, J.-G. Revisit Prediction by Deep Survival Analysis. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Chengdu, China, 16–19 May 2022; pp. 514–526. [Google Scholar]
- Wild, C.; Weiderpass, E.; Stewart, B. World Cancer Report: Cancer Research for Cancer Prevention; International Agency for Research on Cancer: Lyon, France, 2020. [Google Scholar]
- Jee, Y.H.; Emberson, J.; Jung, K.J.; Lee, S.J.; Lee, S.; Back, J.H.; Hong, S.; Kimm, H.; Sherliker, P.; Jee, S.H.; et al. Cohort profile: The korean cancer prevention study-II (KCPS-II) Biobank. Int. J. Epidemiol. 2018, 47, 385–386f. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Harrell Jr, F.E.; Lee, K.L.; Califf, R.M.; Pryor, D.B.; Rosati, R.A. Regression modelling strategies for improved prognostic prediction. Stat. Med. 1984, 3, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Maalouf, M.; Trafalis, T.B. Rare events and imbalanced datasets: An overview. Int. J. Data Min. Model. Manag. 2011, 3, 375–388. [Google Scholar] [CrossRef]
- SEER*Explorer SEER Incidence Rates by Age at Diagnosis, 2015–2019. Available online: https://seer.cancer.gov/statistics-network/explorer/application.html?site=1&data_type=1&graph_type=3&compareBy=sex&chk_sex_3=3&chk_sex_2=2&rate_type=2&race=1&advopt_precision=1&advopt_show_ci=on&hdn_view=0#graphArea (accessed on 2 December 2022).
- Tabibzadeh, S. Role of autophagy in aging: The good, the bad, and the ugly. Aging Cell 2022, e13753. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-E.; Paik, H.Y.; Yoon, H.; Lee, J.E.; Kim, N.; Sung, M.-K. Sex-and gender-specific disparities in colorectal cancer risk. World J. Gastroenterol. WJG 2015, 21, 5167. [Google Scholar] [CrossRef]
- Suteau, V.; Munier, M.; Briet, C.; Rodien, P. Sex Bias in Differentiated Thyroid Cancer. Int. J. Mol. Sci. 2021, 22, 12992. [Google Scholar] [CrossRef]
- Shobab, L.; Burman, K.D.; Wartofsky, L. Sex Differences in Differentiated Thyroid Cancer. Thyroid 2022, 32, 224–235. [Google Scholar] [CrossRef]
- Rahbari, R.; Zhang, L.; Kebebew, E. Thyroid cancer gender disparity. Future Oncol. 2010, 6, 1771–1779. [Google Scholar] [CrossRef]
- Morganti, S.; Ceda, G.; Saccani, M.; Milli, B.; Ugolotti, D.; Prampolini, R.; Maggio, M.; Valenti, G.; Ceresini, G. Thyroid disease in the elderly: Sex-related differences in clinical expression. J. Endocrinol. Investig. 2005, 28, 101–104. [Google Scholar]
- Yin, D.-T.; He, H.; Yu, K.; Xie, J.; Lei, M.; Ma, R.; Li, H.; Wang, Y.; Liu, Z. The association between thyroid cancer and insulin resistance, metabolic syndrome and its components: A systematic review and meta-analysis. Int. J. Surg. 2018, 57, 66–75. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Kim, J.H.; Kim, M.K. Association of Metabolic Health and Central Obesity with the Risk of Thyroid Cancer: Data from the Korean Genome and Epidemiology Study. Cancer Epidemiol. Biomark. Prev. 2022, 31, 543–553. [Google Scholar] [CrossRef]
- Osorio-Costa, F.; Rocha, G.Z.; Dias, M.M.; Carvalheira, J.B. Epidemiological and molecular mechanisms aspects linking obesity and cancer. Arq. Bras. Endocrinol. Metabol. 2009, 53, 213–226. [Google Scholar] [PubMed]
- Avgerinos, K.I.; Spyrou, N.; Mantzoros, C.S.; Dalamaga, M. Obesity and cancer risk: Emerging biological mechanisms and perspectives. Metabolism 2019, 92, 121–135. [Google Scholar] [PubMed]
- Gallagher, E.J.; LeRoith, D. Obesity and diabetes: The increased risk of cancer and cancer-related mortality. Physiol. Rev. 2015, 95, 727–748. [Google Scholar] [PubMed]
- Moschos, S.J.; Mantzoros, C.S. The role of the IGF system in cancer: From basic to clinical studies and clinical applications. Oncology 2002, 63, 317–332. [Google Scholar] [CrossRef]
- Crosbie, E.J.; Zwahlen, M.; Kitchener, H.C.; Egger, M.; Renehan, A.G. Body Mass Index, Hormone Replacement Therapy, and Endometrial Cancer Risk: A Meta-Analysis. Cancer Epidemiol. Biomark. Prev. 2010, 19, 3119–3130. [Google Scholar]
- Shaw, E.; Farris, M.; McNeil, J.; Friedenreich, C. Obesity and endometrial cancer. Obes. Cancer 2016, 107–136. [Google Scholar]
- Liu, Z.; Lin, C.; Suo, C.; Zhao, R.; Jin, L.; Zhang, T.; Chen, X. Metabolic dysfunction-associated fatty liver disease and the risk of 24 specific cancers. Metabolism 2022, 127, 154955. [Google Scholar] [CrossRef]
- He, M.-M.; Fang, Z.; Hang, D.; Wang, F.; Polychronidis, G.; Wang, L.; Lo, C.-H.; Wang, K.; Zhong, R.; Knudsen, M.D.; et al. Circulating liver function markers and colorectal cancer risk: A prospective cohort study in the UK Biobank. Int. J. Cancer 2021, 148, 1867–1878. [Google Scholar] [CrossRef]
- Stocker, R.; Yamamoto, Y.; McDonagh, A.F.; Glazer, A.N.; Ames, B.N. Bilirubin is an antioxidant of possible physiological importance. Science 1987, 235, 1043–1046. [Google Scholar] [CrossRef]
- Horsfall, L.J.; Rait, G.; Walters, K.; Swallow, D.M.; Pereira, S.P.; Nazareth, I.; Petersen, I. Serum bilirubin and risk of respiratory disease and death. JAMA 2011, 305, 691–697. [Google Scholar] [CrossRef]
- Sarna, L.; Evangelista, L.; Tashkin, D.; Padilla, G.; Holmes, C.; Brecht, M.L.; Grannis, F. Impact of respiratory symptoms and pulmonary function on quality of life of long-term survivors of non-small cell lung cancer. Chest 2004, 125, 439–445. [Google Scholar] [CrossRef] [PubMed]


| Mean ± SD | Min | Max | Male Mean ± SD | Female Mean ± SD | |
|---|---|---|---|---|---|
| AGE | 41.62 ± 10.53 | 9.00 | 88.00 | 42.04 ± 9.95 | 40.98 ± 11.31 |
| HT | 166.80 ± 8.40 | 130.00 | 198.00 | 171.75 ± 5.95 | 159.31 ± 5.52 |
| WT | 65.79 ± 12.00 | 32.00 | 137.00 | 72.12 ± 9.93 | 56.23 ± 7.78 |
| WC | 80.58 ± 9.45 | 41.00 | 127.00 | 84.80 ± 7.65 | 74.21 ± 8.26 |
| BMI | 23.53 ± 3.17 | 12.91 | 42.36 | 24.42 ± 2.88 | 22.18 ± 3.10 |
| SBP | 117.65 ± 14.11 | 61.00 | 19 9.00 | 121.23 ± 12.87 | 112.25 ± 14.19 |
| DBP | 74.12 ± 10.04 | 30.00 | 134.00 | 76.55 ± 9.56 | 70.45 ± 9.63 |
| CHO | 188.83 ± 33.02 | 3.68 | 382.00 | 192.04 ± 32.86 | 183.99 ± 32.68 |
| HDL | 52.27 ± 10.70 | 2.00 | 118.00 | 48.80 ± 9.01 | 57.50 ± 10.92 |
| TG | 132.82 ± 83.35 | 30.00 | 690.00 | 155.29 ± 90.44 | 98.96 ± 56.51 |
| LDL | 112.13 ± 31.03 | 1.00 | 299.60 | 115.23 ± 31.25 | 107.47 ± 30.11 |
| FVC | 26.93 ± 30.82 | 0.04 | 158.00 | 25.33 ± 30.39 | 29.16 ± 31.33 |
| FEV1 | 28.64 ± 33.96 | 0.42 | 178.00 | 26.58 ± 33.25 | 31.56 ± 34.81 |
| ALB | 4.53 ± 0.25 | 2.20 | 5.90 | 4.58 ± 0.24 | 4.45 ± 0.24 |
| GLOBULIN | 2.76 ± 0.17 | 1.80 | 3.80 | 2.74 ± 0.17 | 2.78 ± 0.16 |
| AGR | 1.64 ± 0.13 | 0.85 | 2.39 | 1.67 ± 0.13 | 1.59 ± 0.11 |
| BIL | 0.87 ± 0.33 | 0.10 | 2.93 | 0.94 ± 0.34 | 0.75 ± 0.28 |
| DBIL | 0.33 ± 0.12 | 0.04 | 1.07 | 0.36 ± 0.12 | 0.28 ± 0.10 |
| ALP | 133.52 ± 50.56 | 10.00 | 445.00 | 142.70 ± 50.77 | 119.69 ± 46.93 |
| AST | 22.69 ± 8.90 | 1.00 | 135.00 | 24.65 ± 9.55 | 19.75 ± 6.85 |
| ALT | 24.43 ± 17.23 | 1.00 | 180.00 | 29.46 ± 18.95 | 16.87 ± 10.68 |
| GGTP | 34.23 ± 32.45 | 1.90 | 390.00 | 44.58 ± 36.75 | 18.67 ± 14.83 |
| GLU | 90.56 ± 15.19 | 10.00 | 208.00 | 92.37 ± 16.18 | 87.83 ± 13.07 |
| AMYLASE | 70.98 ± 19.00 | 3.00 | 195.00 | 69.63 ± 18.65 | 73.04 ± 19.35 |
| CREAT | 0.98 ± 0.18 | 0.38 | 2.40 | 1.09 ± 0.14 | 0.83 ± 0.12 |
| BUN | 13.74 ± 3.25 | 0.45 | 59.00 | 14.50 ± 3.13 | 12.57 ± 3.07 |
| SG | 1.02 ± 0.01 | 1.00 | 1.05 | 1.02 ± 0.01 | 1.02 ± 0.01 |
| PH | 5.68 ± 0.76 | 0.50 | 9.00 | 5.66 ± 0.75 | 5.72 ± 0.77 |
| PP | 43.54 ± 9.64 | 0.00 | 101.00 | 44.69 ± 9.50 | 41.80 ± 9.59 |
| CCR | 92.92 ± 20.02 | 20.14 | 213.37 | 91.66 ± 19.86 | 94.85 ± 20.12 |
| Cancer Site | Number of Cases | Cases/Total Cancer Cases | Cases/Total Sample |
|---|---|---|---|
| Thyroid | 3385 | 0.33120 | 0.02189 |
| Gastric | 1499 | 0.15109 | 0.00969 |
| Breast | 1169 | 0.11783 | 0.00756 |
| Colorectum | 1031 | 0.10392 | 0.00667 |
| Lung | 757 | 0.07630 | 0.00489 |
| Prostate | 697 | 0.07026 | 0.00451 |
| Liver | 439 | 0.04425 | 0.00284 |
| Kidney | 352 | 0.03548 | 0.00228 |
| Uterus-cervical | 306 | 0.03084 | 0.00198 |
| Lymphoma | 286 | 0.02883 | 0.00185 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, C.-Y.; Kim, B.-S.; Jee, S.-H.; Lee, J.-H.; Nguyen, N.-D. A Study on Survival Analysis Methods Using Neural Network to Prevent Cancers. Cancers 2023, 15, 4757. https://doi.org/10.3390/cancers15194757
Bae C-Y, Kim B-S, Jee S-H, Lee J-H, Nguyen N-D. A Study on Survival Analysis Methods Using Neural Network to Prevent Cancers. Cancers. 2023; 15(19):4757. https://doi.org/10.3390/cancers15194757
Chicago/Turabian StyleBae, Chul-Young, Bo-Seon Kim, Sun-Ha Jee, Jong-Hoon Lee, and Ngoc-Dung Nguyen. 2023. "A Study on Survival Analysis Methods Using Neural Network to Prevent Cancers" Cancers 15, no. 19: 4757. https://doi.org/10.3390/cancers15194757
APA StyleBae, C.-Y., Kim, B.-S., Jee, S.-H., Lee, J.-H., & Nguyen, N.-D. (2023). A Study on Survival Analysis Methods Using Neural Network to Prevent Cancers. Cancers, 15(19), 4757. https://doi.org/10.3390/cancers15194757








