Gold Nanoparticles-Mediated Photothermal Therapy of Pancreas Using GATE: A New Simulation Platform
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation
2.1.1. GATE: Geometry and Material Definition
2.1.2. Definition of the Pancreas Model
2.1.3. Laser Source
2.1.4. Temperature Distribution in Pancreas Phantom
Benchmark of the Simulation: Ex Vivo Experiments with Pancreas
2.1.5. GNRs Simulation
2.1.6. Temperature Distribution in GNR-Loaded Pancreas Phantom
Benchmark of the GATE Simulations: Experiment on GNRs Suspension
3. Results
3.1. Validation of the GATE on the Pancreas Model and on the GNRs-Assisted Temperature Increase within the Tumor Phantom
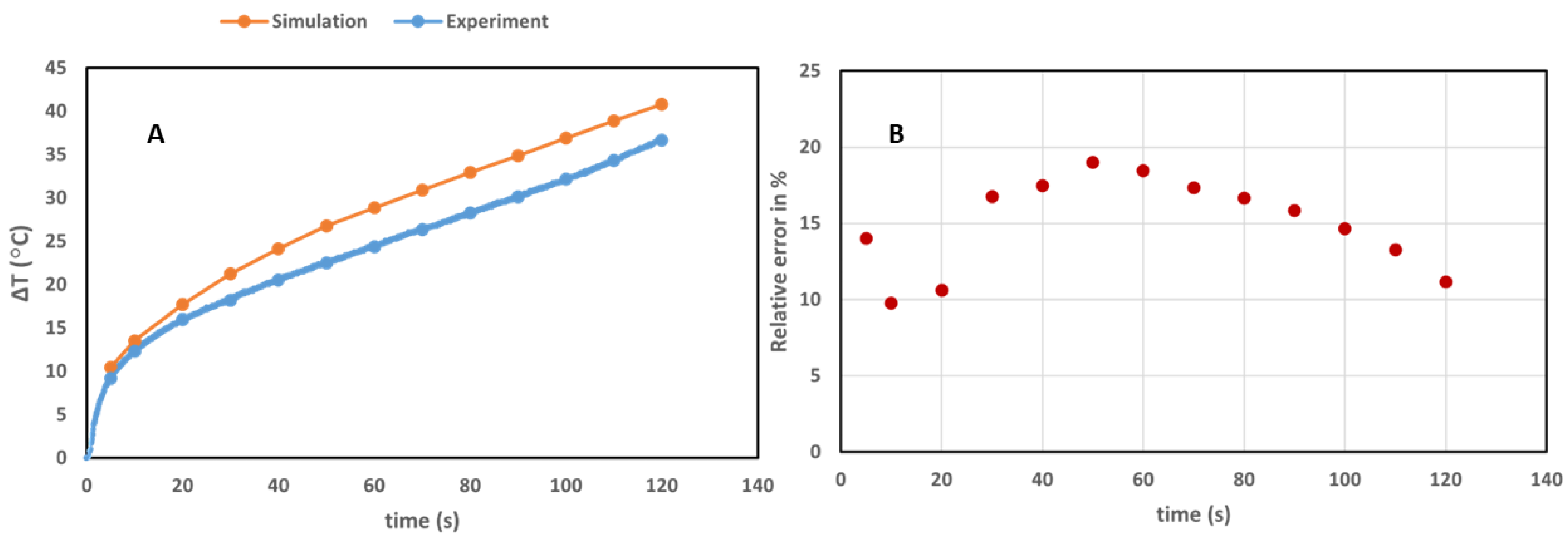
3.1.1. Validation of the Pancreas Model
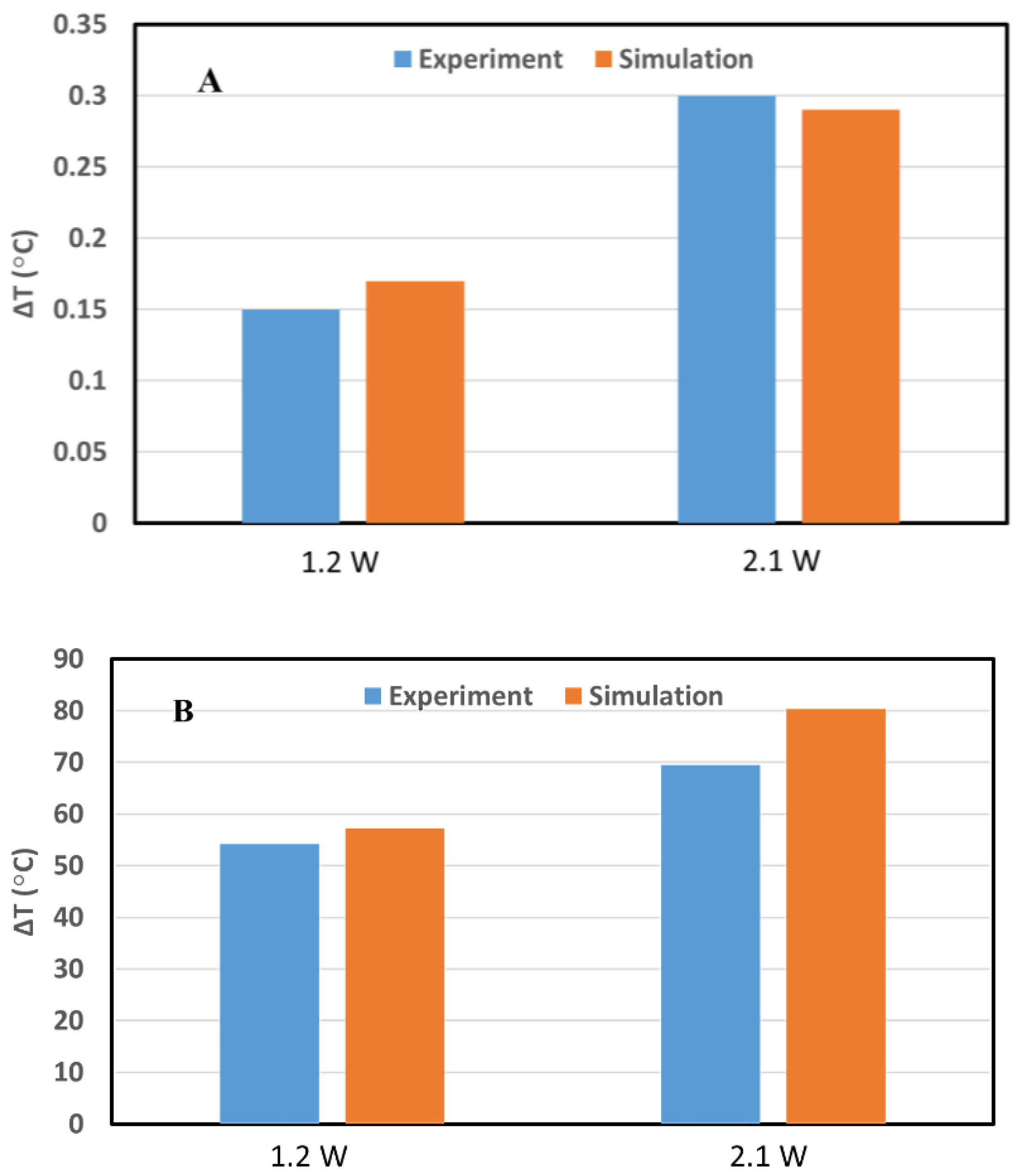
3.1.2. Benchmark of the GATE Simulations for GNRs-Loaded Pancreas Tumor Model
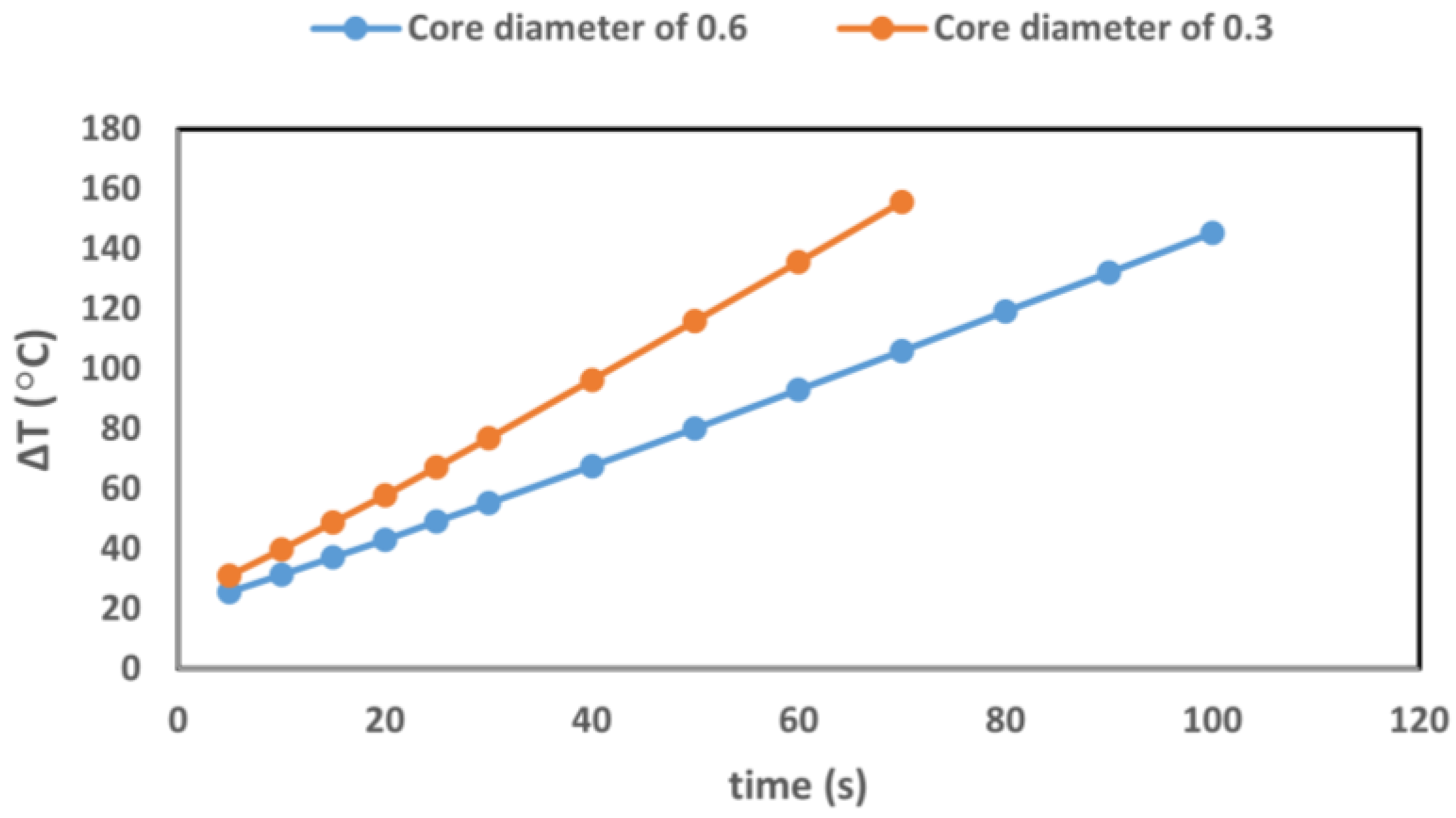
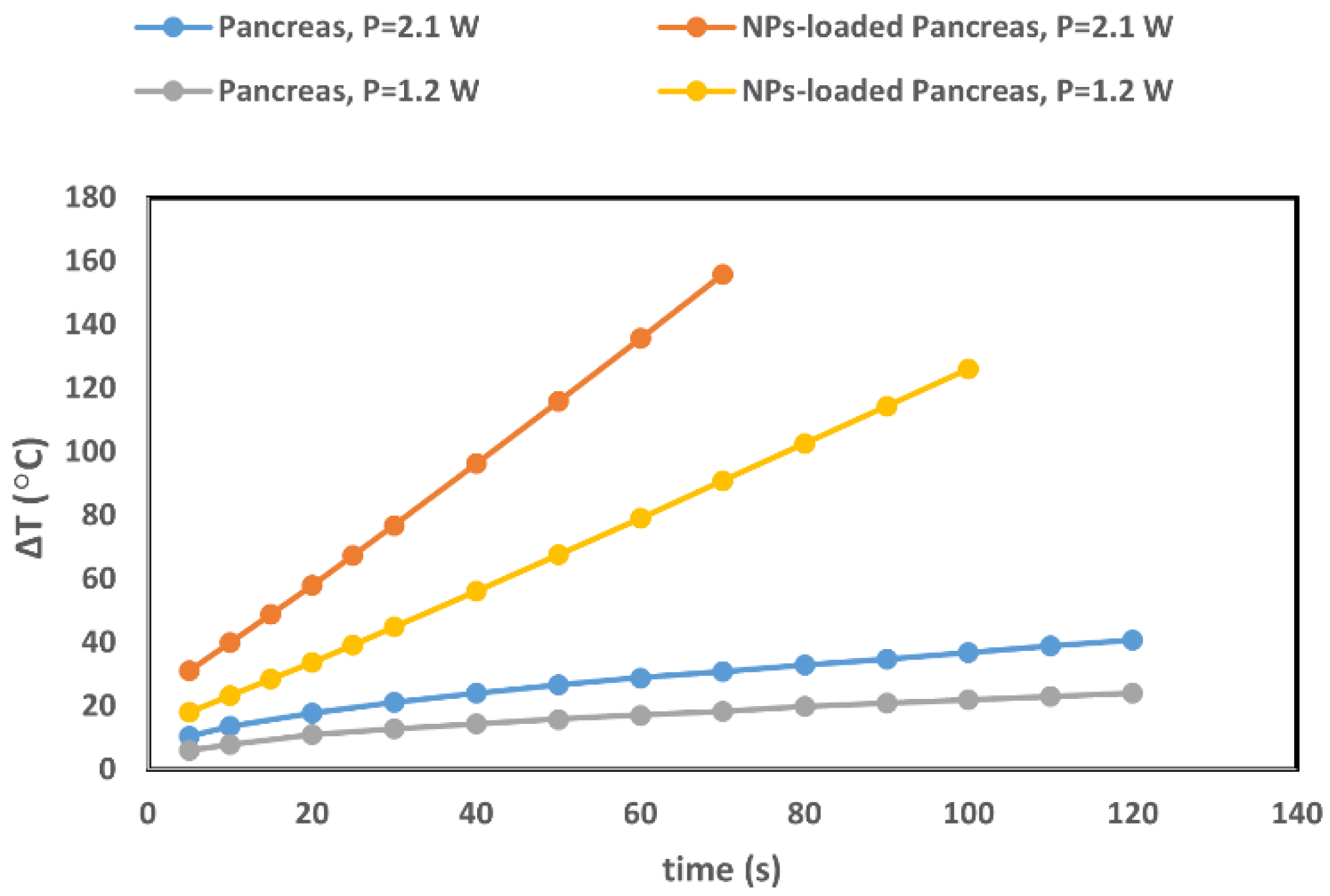
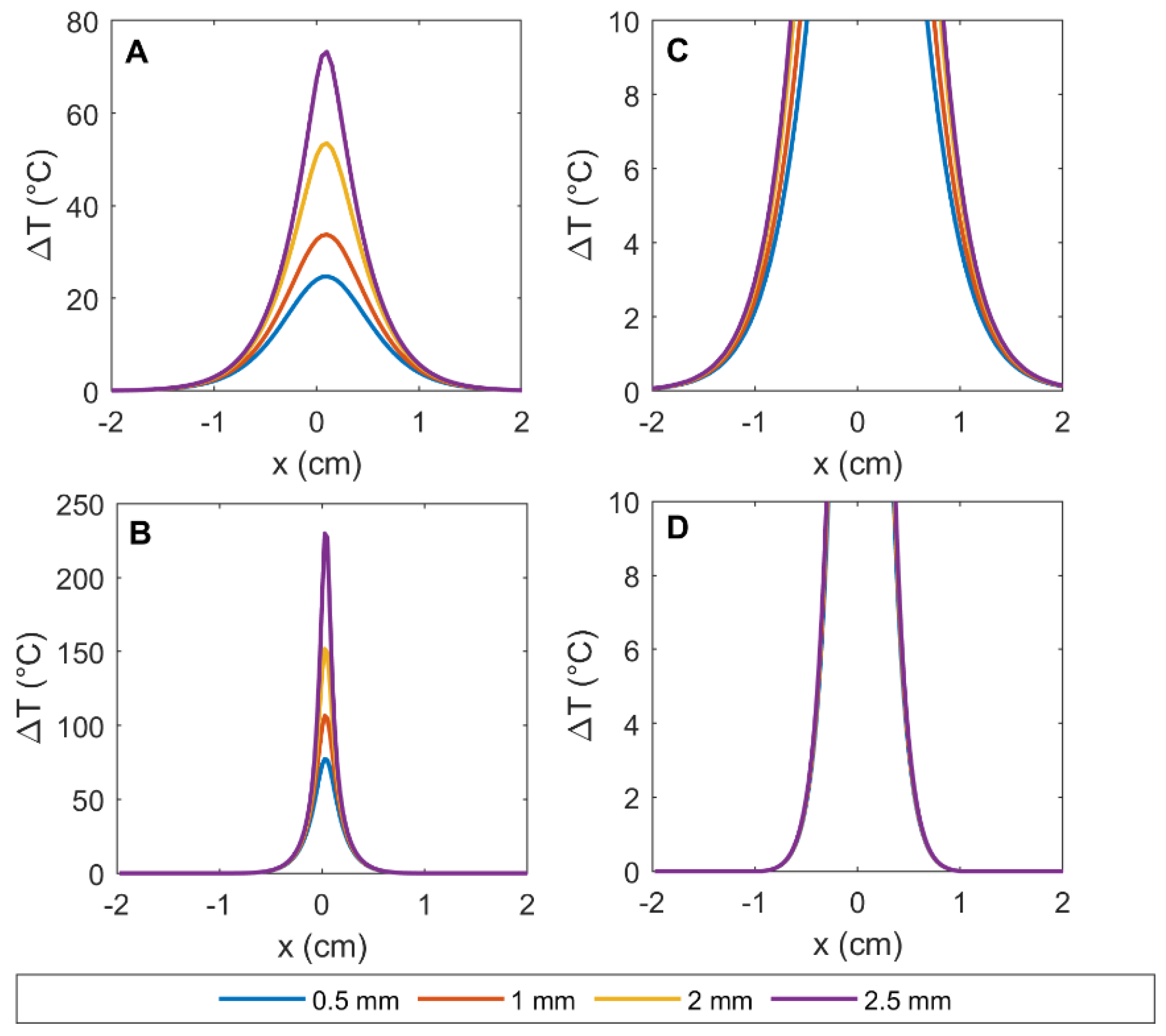
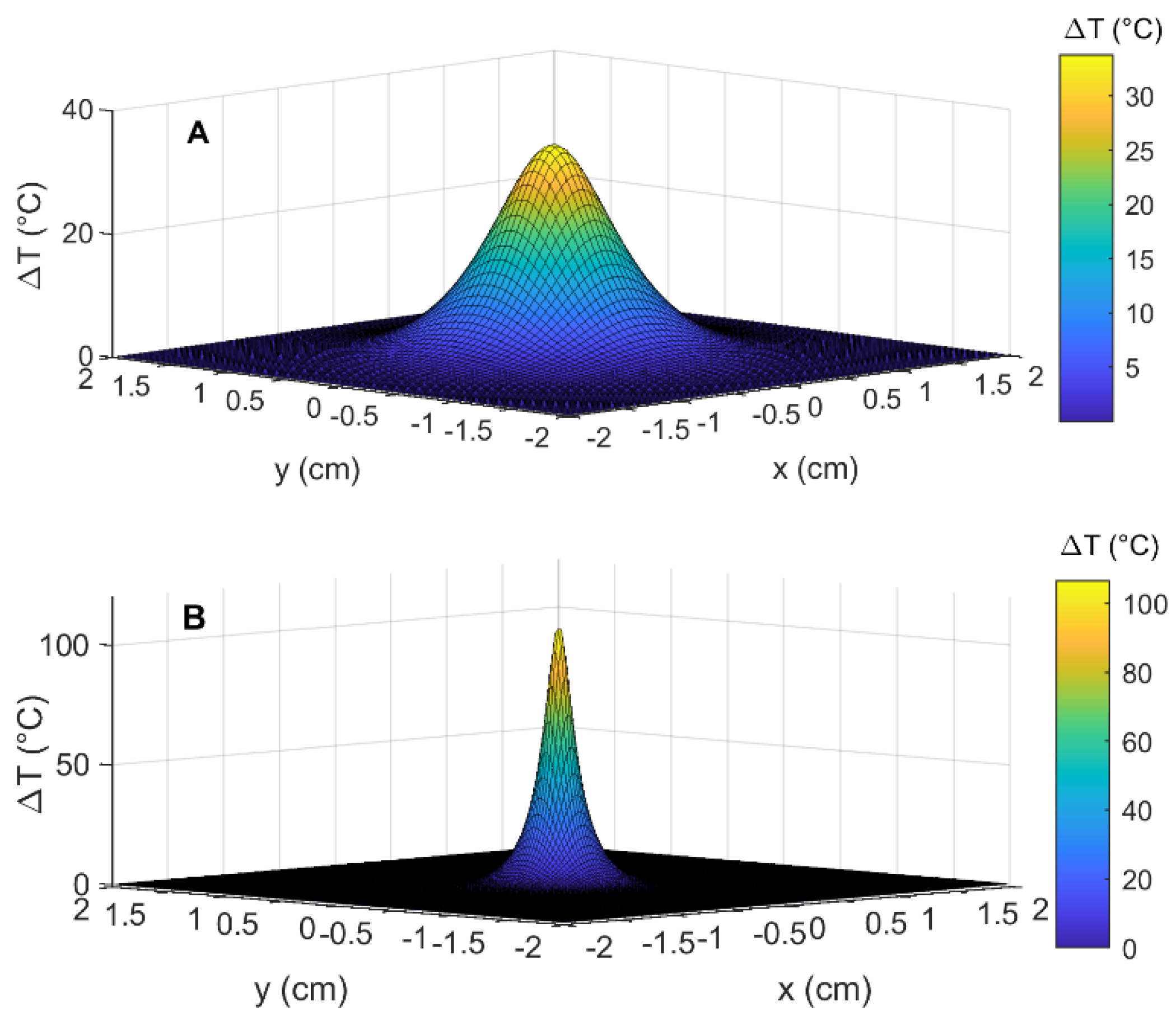
3.2. Simulation Results: Temperature Distribution in the Pancreas, in the Presence and Absence of GNRs
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chu, K.F.; Dupuy, D.E. Thermal ablation of tumours: Biological mechanisms and advances in therapy. Nat. Rev. Cancer 2014, 14, 199–208. [Google Scholar] [CrossRef]
- Habash, R.W.Y.; Bansal, R.; Krewski, D.; Alhafid, H.T. Thermal therapy, part 1: An introduction to thermal therapy. Crit. Rev. Biomed. Eng. 2006, 34, 459–489. [Google Scholar] [CrossRef] [PubMed]
- Jaque, D.; Martínez Maestro, L.; Del Rosal, B.; Haro-Gonzalez, P.; Benayas, A.; Plaza, J.L.; Martín Rodríguez, E.; García Solé, J. Nanoparticles for photothermal therapies. Nanoscale 2014, 23, 9494–9530. [Google Scholar] [CrossRef]
- Stafford, R.J.; Fuentes, D.; Elliott, A.A.; Weinberg, J.S.; Ahrar, K. Laser-induced thermal therapy for tumor ablation. Crit. Rev. Biomed. Eng. 2010, 38, 79–100. [Google Scholar] [CrossRef] [PubMed]
- Asadi, S.; Vaez-zadeh, M.; Masoudi, S.F.; Rahmani, F.; Knaup, C.; Meigooni, A.S. Gold nanoparticle-based brachytherapy enhancement in choroidal melanoma using a full Monte Carlo model of the human eye. J. Appl. Clin. Med. Phys. 2015, 16, 344–357. [Google Scholar] [CrossRef] [PubMed]
- Kuncic, Z.; Lacombe, S. Nanoparticle radio-enhancement: Principles, progress and application to cancer treatment. Phys. Med. Biol. 2018, 63, 02TR01. [Google Scholar] [CrossRef] [PubMed]
- Rasouli, F.S.; Masoudi, S.F.; Asadi, S. On the importance of modeling gold nanoparticles distribution in dose-enhanced radiotherapy. Int. J. Nanomed. 2019, 14, 5865. [Google Scholar] [CrossRef]
- Kanavi, M.R.; Asadi, S.; Balagholi, S.; Alikarami, F.; Nosrati, H.; Ahmadieh, H. Gamma irradiation of ocular melanoma and lymphoma cells in the presence of gold nanoparticles: In vitro study. J. Appl. Clin. Med. Phys. 2018, 19, 268–275. [Google Scholar] [CrossRef]
- Asadi, S.; Vaez-zadeh, M.; Vahidian, M.; Marghchouei, M.; Masoudi, S.F. Ocular brachytherapy dosimetry for and in the presence of gold nanoparticles: A Monte Carlo study. J. Appl. Clin. Med. Phys. 2016, 17, 90–99. [Google Scholar] [CrossRef]
- Kanavi, M.R.; Asadi, S.; Ahmadieh, H. Ex vivo distribution of gold nanoparticles in choroidal melanoma. Int. J. Nanomed. 2017, 12, 8527–8529. [Google Scholar] [CrossRef][Green Version]
- Asadi, S.; Bianchi, L.; De Landro, M.; Korganbayev, S.; Schena, E.; Saccomandi, P. Laser-Induced Optothermal Response of Gold Nanoparticles: From a Physical Viewpoint to Cancer Treatment Application. J. Biophotonics 2020, 14, e202000161. [Google Scholar] [CrossRef] [PubMed]
- Maor, I.; Asadi, S.; Korganbayev, S.; Dahis, D.; Shamay, Y.; Schena, E.; Azhari, H.; Saccomandi, P.; Weitz, I.S. Laser-induced thermal response and controlled release of copper oxide nanoparticles from multifunctional polymeric nanocarriers. Sci. Technol. Adv. Mater. 2021, 22, 218–233. [Google Scholar] [CrossRef]
- Liao, S.; Yue, W.; Cai, S.; Tang, Q.; Lu, W.; Huang, L.; Qi, T.; Liao, J. Improvement of gold nanorods in photothermal therapy: Recent progress and perspective. Front. Pharmacol. 2021, 781. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhou, J.; Dong, X.; Cheng, W.-Y.; Duan, H.; Cheung, P.C.K. In vitro and in vivo photothermal cancer therapeutic effects of gold nanorods modified with mushroom β-glucan. J. Agric. Food Chem. 2018, 66, 4091–4098. [Google Scholar] [CrossRef]
- Ali, M.R.K.; Wu, Y.; El-Sayed, M.A. Gold-Nanoparticle-Assisted Plasmonic Photothermal Therapy Advances Toward Clinical Application. J. Phys. Chem. C 2019, 123, 15375–15393. [Google Scholar] [CrossRef]
- Mooney, R.; Schena, E.; Saccomandi, P.; Zhumkhawala, A.; Aboody, K.; Berlin, J.M. Gold nanorod-mediated near-infrared laser ablation: In vivo experiments on mice and theoretical analysis at different settings. Int. J. Hyperth. 2017, 33, 150–159. [Google Scholar] [CrossRef]
- Popp, M.K.; Oubou, I.; Shepherd, C.; Nager, Z.; Anderson, C.; Pagliaro, L. Photothermal therapy using gold nanorods and near-infrared light in a murine melanoma model increases survival and decreases tumor volume. J. Nanomater. 2014, 2014, 126. [Google Scholar] [CrossRef]
- Kang, X.; Guo, X.; An, W.; Niu, X.; Li, S.; Liu, Z.; Yang, Y.; Wang, N.; Jiang, Q.; Yan, C.; et al. Photothermal therapeutic application of gold nanorods-porphyrin-trastuzumab complexes in HER2-positive breast cancer. Sci. Rep. 2017, 7, 42069. [Google Scholar] [CrossRef] [PubMed]
- MacKey, M.A.; Ali, M.R.K.; Austin, L.A.; Near, R.D.; El-Sayed, M.A. The most effective gold nanorod size for plasmonic photothermal therapy: Theory and in vitro experiments. J. Phys. Chem. B 2014, 118, 1319–1326. [Google Scholar] [CrossRef] [PubMed]
- Asadi, S.; Korganbayev, S.; Xu, W.; Mapanao, A.K.; Voliani, V.; Lehto, V.-P.; Saccomandi, P. Experimental Evaluation of Radiation Response and Thermal Properties of NPs-Loaded Tissues-Mimicking Phantoms. Nanomaterials 2022, 12, 945. [Google Scholar] [CrossRef]
- Abadeer, N.S.; Murphy, C.J. Recent Progress in Cancer Thermal Therapy Using Gold Nanoparticles. J. Phys. Chem. C 2016, 120, 4691–4716. [Google Scholar] [CrossRef]
- Rossi, F.; Ratto, F.; Pini, R. Laser Activated Gold Nanorods for the Photothermal Treatment of Cancer. In Excerpt from the Proceedings of the 2012 Comsol Conference in Milan; Chalmers University of Technology: Göteborg, Sweden, 2012. [Google Scholar]
- Li, E.; Liu, G.R.; Tan, V.; He, Z.C. Modeling and simulation of bioheat transfer in the human eye using the 3D alpha finite element method (αFEM). Int. J. Numer. Method Biomed. Eng. 2010, 26, 955–976. [Google Scholar] [CrossRef]
- Yona, G.; Meitav, N.; Kahn, I.; Shoham, S. Realistic numerical and analytical modeling of light scattering in brain tissue for optogenetic applications. eNeuro 2016, 3, ENEURO.0059-15.2015. [Google Scholar] [CrossRef] [PubMed]
- Jan, S.; Santin, G.; Strul, D.; Staelens, S.; Assié, K.; Autret, D.; Avner, S.; Barbier, R.; Bardiès, M.; Bloomfield, P.M.; et al. GATE: A simulation toolkit for PET and SPECT. Phys. Med. Biol. 2004, 49, 4543. [Google Scholar] [CrossRef]
- Sharabiani, M.; Vaez-zadeh, M.; Asadi, S. Size dependence of GNPs dose enhancement effects in cancer treatment—Geant4 and MCNP code. Radiother. Oncol. 2016, 118, S96–S97. [Google Scholar] [CrossRef]
- Qazvini, S.V.; Vahidian, M.; Asadi, S.; Vaez-zadeh, M. GEANT4 versus MCNP5: Monte-Carlo ophthalmic brachytherapy dosimetry in the presence of gold nanoparticles for 125I and 103Pd. Radiother. Oncol. 2016, 1, S105. [Google Scholar] [CrossRef]
- Cuplov, V.; Pain, F.; Jan, S. Simulation of nanoparticle-mediated near-infrared thermal therapy using GATE. Biomed. Opt. Express 2017, 8, 1665–1681. [Google Scholar] [CrossRef] [PubMed]
- Cuplov, V.; Buvat, I.; Pain, F.; Jan, S. Extension of the GATE Monte-Carlo simulation package to model bioluminescence and fluorescence imaging. J. Biomed. Opt. 2014, 19, 26004. [Google Scholar] [CrossRef]
- Rahib, L.; Smith, B.D.; Aizenberg, R.; Rosenzweig, A.B.; Fleshman, J.M.; Matrisian, L.M. Projecting cancer incidence and deaths to 2030: The unexpected burden of thyroid, liver, and pancreas cancers in the United States. Cancer Res. 2014, 74, 2913–2921. [Google Scholar] [CrossRef]
- Han, J.; Chang, K.J. Endoscopic ultrasound-guided direct intervention for solid pancreatic tumors. Clin. Endosc. 2017, 50, 126–137. [Google Scholar] [CrossRef]
- Di Matteo, F.M.; Saccomandi, P.; Martino, M.; Pandolfi, M.; Pizzicannella, M.; Balassone, V.; Schena, E.; Pacella, C.M.; Silvestri, S.; Costamagna, G. Feasibility of EUS-guided Nd: YAG laser ablation of unresectable pancreatic adenocarcinoma. Gastrointest. Endosc. 2018, 88, 168–174. [Google Scholar] [CrossRef]
- Van der Horst, A.; Versteijne, E.; Besselink, M.G.H.; Daams, J.G.; Bulle, E.B.; Bijlsma, M.F.; Wilmink, J.W.; van Delden, O.M.; van Hooft, J.E.; Franken, N.A.P. The clinical benefit of hyperthermia in pancreatic cancer: A systematic review. Int. J. Hyperth. 2018, 34, 969–979. [Google Scholar] [CrossRef] [PubMed]
- Saccomandi, P.; Lapergola, A.; Longo, F.; Schena, E.; Quero, G. Thermal ablation of pancreatic cancer: A systematic literature review of clinical practice and pre-clinical studies. Int. J. Hyperth. 2018, 35, 398–418. [Google Scholar] [CrossRef]
- Baumann, K.W.; Baust, J.M.; Snyder, K.K.; Baust, J.G.; Van Buskirk, R.G. Dual thermal ablation of pancreatic cancer cells as an improved combinatorial treatment strategy. Liver Pancreat. Sci. 2017, 2, 1–10. [Google Scholar] [CrossRef]
- Asadi, S.; Masoudi, S.F.; Shahriari, M. The effects of variations in the density and composition of eye materials on ophthalmic brachytherapy dosimetry. Med. Dosim. 2012, 37, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Dehghannia Rostami, Z.; Masoudi, S.F.; Asadi, S. Dosimetry Comparison of Water Phantom and Complete Eye Definition for 125I and 103Pd Brachytherapy Plaques. Iran. J. Med. Phys. 2011, 8, 19–26. [Google Scholar]
- Bianchi, L.; Cavarzan, F.; Ciampitti, L.; Cremonesi, M.; Grilli, F.; Saccomandi, P. Thermophysical and mechanical properties of biological tissues as a function of temperature: A systematic literature review. Int. J. Hyperth. 2022, 39, 297–340. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y. Insight Segmentation and Registration Toolkit; The National Library of Medicine: Washington, DC, USA, 2001.
- Visvikis, D.; Bardies, M.; Chiavassa, S.; Danford, C.; Kirov, A.; Lamare, F.; Maigne, L.; Staelens, S.; Taschereau, R. Use of the GATE Monte Carlo package for dosimetry applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 569, 335–340. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.-C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Nolf, E. XMedCon: An Open-Source Medical Image Conversion Toolkit. Eur. J. Nucl. Med. Mol. Imaging 2003, 30 (Suppl. 2), S246. Available online: https://xmedcon.sourceforge.io/ (accessed on 23 October 2022).
- Scott, J.A. Photon, Electron, Proton and Neutron Interaction Data for Body Tissues: ICRU Report 46. International Commission on Radiation Units and Measurements, Bethesda, 1992, $40.00 1993. J. Nucl. Med. Jan. 1993, 34, 171. [Google Scholar]
- Huang, X.; Neretina, S.; El-Sayed, M.A. Gold nanorods: From synthesis and properties to biological and biomedical applications. Adv. Mater. 2009, 21, 4880–4910. [Google Scholar] [CrossRef] [PubMed]
- Link, S.; El-Sayed, M.A. Shape and size dependence of radiative, non-radiative and photothermal properties of gold nanocrystals. Int. Rev. Phys. Chem. 2000, 19, 409–453. [Google Scholar] [CrossRef]
- Bohren, C.F. Absorption and Scattering of Light by Small Particles; Wiley: Hoboken, NJ, USA, 1983; ISBN 9783527406647. [Google Scholar]
- Soni, S.; Tyagi, H.; Taylor, R.A.; Kumar, A. Role of optical coefficients and healthy tissue-sparing characteristics in gold nanorod-assisted thermal therapy. Int. J. Hyperth. 2013, 29, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.A.; Phelan, P.E.; Otanicar, T.P.; Adrian, R.; Prasher, R. Nanofluid optical property characterization: Towards efficient direct absorption solar collectors. Nanoscale Res. Lett. 2011, 6, 225. [Google Scholar] [CrossRef]
- Lee, K.S.; El-Sayed, M.A. Dependence of the enhanced optical scattering efficiency relative to that of absorption for gold metal nanorods on aspect ratio, size, end-cap shape, and medium refractive index. J. Phys. Chem. B 2005, 109, 20331–20338. [Google Scholar] [CrossRef]
- Babar, S.; Weaver, J.H. Optical constants of Cu, Ag, and Au revisited. Appl. Opt. 2015, 54, 477–481. [Google Scholar] [CrossRef]
- Wilson, R.H.; Chandra, M.; Scheiman, J.; Simeone, D.; McKenna, B.; Purdy, J.; Mycek, M.-A. Optical spectroscopy detects histological hallmarks of pancreatic cancer. Opt. Express 2009, 17, 17502–17516. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lloyd, W.R.; Chandra, M.; Wilson, R.H.; McKenna, B.; Simeone, D.; Scheiman, J.; Mycek, M.-A. Characterizing human pancreatic cancer precursor using quantitative tissue optical spectroscopy. Biomed. Opt. Express 2013, 4, 2828–2834. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, A.; Bianchi, L.; Asadi, S.; Saccomandi, P. Measurement of ex vivo liver, brain and pancreas thermal properties as function of temperature. Sensors 2021, 21, 4236. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Qin, Z.; Bischof, J.C. Thermophysical and biological responses of gold nanoparticle laser heating. Chem. Soc. Rev. 2012, 41, 1191–1217. [Google Scholar] [CrossRef]
- Morra, F.; De Landro, M.; Korganbayev, S.; Wolf, A.; Dostovalov, A.; Cigada, A.; Saccomandi, P. Spatially resolved thermometry during laser ablation in tissues: Distributed and quasi-distributed fiber optic-based sensing. Opt. Fiber Technol. 2020, 58, 102295. [Google Scholar] [CrossRef]
- Mohammadi, A.; Bianchi, L.; Korganbayev, S.; De Landro, M.; Saccomandi, P. Thermomechanical modeling of laser ablation therapy of tumors: Sensitivity analysis and optimization of influential variables. IEEE Trans. Biomed. Eng. 2021, 69, 302–313. [Google Scholar] [CrossRef]
- Korganbayev, S.; Orrico, A.; Bianchi, L.; Paloschi, D.; Wolf, A.; Dostovalov, A.; Saccomandi, P. PID controlling approach based on FBG array measurements for laser ablation of pancreatic tissues. IEEE Trans. Instrum. Meas. 2021, 70, 7006409. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Wolf, A.A.; Parygin, A.V.; Zyubin, V.E.; Babin, S.A. Femtosecond point-by-point inscription of Bragg gratings by drawing a coated fiber through ferrule. Opt. Express 2016, 24, 16232. [Google Scholar] [CrossRef]
- Bianchi, L.; Mooney, R.; Cornejo, Y.; Hyde, C.; Schena, E.; Berlin, J.M.; Aboody, K.; Saccomandi, P. Fiber Bragg grating sensors-based thermometry of gold nanorod-enhanced photothermal therapy in tumor model. IEEE Sens. J. 2021, 22, 11297–11306. [Google Scholar] [CrossRef]
- Alekseeva, A.V.; Bogatyrev, V.A.; Khlebtsov, B.N.; Mel’Nikov, A.G.; Dykman, L.A.; Khlebtsov, N.G. Gold nanorods: Synthesis and optical properties. Colloid J. 2006, 68, 661–678. [Google Scholar] [CrossRef]
- Scaffardi, L.B.; Tocho, J.O. Size dependence of refractive index of gold nanoparticles. Nanotechnology 2006, 17, 1309. [Google Scholar] [CrossRef]
- Papavassiliou, G.C. Optical properties of small inorganic and organic metal particles. Prog. Solid State Chem. 1979, 12, 185–271. [Google Scholar] [CrossRef]
- Derkachova, A.; Kolwas, K.; Demchenko, I. Dielectric function for gold in plasmonics applications: Size dependence of plasmon resonance frequencies and damping rates for nanospheres. Plasmonics 2016, 11, 941–951. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: Philadelphia, PA, USA, 1976; p. 404. [Google Scholar]
- Khlebtsov, N.G.; Bogatyrev, V.A.; Dykman, L.A.; Melnikov, A.G. Spectral extinction of colloidal gold and its biospecific conjugates. J. Colloid Interface Sci. 1996, 180, 436–445. [Google Scholar] [CrossRef]
- Granqvist, C.-G.; Hunderi, O. Optical properties of ultrafine gold particles. Phys. Rev. B 1977, 16, 3513. [Google Scholar] [CrossRef]
- Doyle, W.T. Optical properties of a suspension of metal spheres. Phys. Rev. B 1989, 39, 9852. [Google Scholar] [CrossRef]
- Mole Fraction Formula and Calculation. Available online: https://sciencenotes.org/mole-fraction-formula-and-calculation/ (accessed on 19 October 2022).
- Pogue, B.W.; Patterson, M.S. Review of tissue simulating phantoms for optical spectroscopy, imaging and dosimetry. J. Biomed. Opt. 2006, 11, 41102. [Google Scholar] [CrossRef]
- Deng, R.; He, Y.; Qin, Y.; Chen, Q.; Chen, L. Measuring pure water absorption coefficient in the near-infrared spectrum(900–2500 nm). Yaogan Xuebao J. Remote Sens. 2012, 16, 192–206. [Google Scholar]
- Kou, L.; Labrie, D.; Chylek, P. Refractive indices of water and ice in the 0.65-to 2.5-μm spectral range. Appl. Opt. 1993, 32, 3531–3540. [Google Scholar] [CrossRef]
- He, G.S.; Zhu, J.; Yong, K.-T.; Baev, A.; Cai, H.-X.; Hu, R.; Cui, Y.; Zhang, X.-H.; Prasad, P.N. Scattering and absorption cross-section spectral measurements of gold nanorods in water. J. Phys. Chem. C 2010, 114, 2853–2860. [Google Scholar] [CrossRef]
- Fedele, D.; Fusi, F. Thermal effects of NIR laser radiation in biological tissue: A brief survey. Energy Health 2010, 6, 10–15. [Google Scholar]
- Nikfarjam, M.; Muralidharan, V.; Christophi, C. Mechanisms of focal heat destruction of liver tumors. J. Surg. Res. 2005, 127, 208–223. [Google Scholar] [CrossRef] [PubMed]
- Welch, A.J.; van Gemert, M.J.C. Optical-Thermal Response of Laser-Irradiated Tissue; Springer: New York City, NY, USA, 2011; Volume 2. [Google Scholar]
- Rossmanna, C.; Haemmerich, D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Crit. Rev. Biomed. Eng. 2014, 42, 467–492. [Google Scholar] [CrossRef] [PubMed]
- Saccomandi, P.; Schena, E.; Caponero, M.A.; Di Matteo, F.M.; Martino, M.; Pandolfi, M.; Silvestri, S. Theoretical analysis and experimental evaluation of laser-induced interstitial thermotherapy in ex vivo porcine pancreas. IEEE Trans. Biomed. Eng. 2012, 59, 2958–2964. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, L.; Korganbayev, S.; Orrico, A.; De Landro, M.; Saccomandi, P. Quasi-distributed fiber optic sensor-based control system for interstitial laser ablation of tissue: Theoretical and experimental investigations. Biomed. Opt. Express 2021, 12, 2841–2858. [Google Scholar] [CrossRef] [PubMed]




| Parameters | Symbols | Values for Pancreas | Values for GNR-Loaded Tumor |
|---|---|---|---|
| Percent by weight element composition [43] | H | 1.06 | 1.059 |
| C | 1.69 | 1.68 | |
| N | 0.22 | 0.219 | |
| O | 6.94 | 6.939 | |
| Na | 0.02 | 0.019 | |
| P | 0.02 | 0.019 | |
| S | 0.01 | 0.0099 | |
| C | 0.02 | 0.019 | |
| K | 0.02 | 0.019 | |
| Au | / | 0.0012 | |
| Density [43] | (kg/m3) | 1040 | 1,040,012 |
| Thermal diffusivity [20,53] | D (mm2/s) | 0.14 | 0.16 |
| Heat Capacity [20,53] | Cp (mJ/kg∙K) | 3.5546 | 3.6057 |
| Refractive index [52] | RI | 1.394 | 1.3939 |
| Absorption coefficient [51] | µa (1/cm) | 0.0388 | 1.6850 |
| Scattering coefficient [51] | πs (1/cm) | 196.8 | 0.02740 |
| Permittivity [50,54] | 1.767 + 0i | 24.7180 + 3.6581i |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asadi, S.; Bianchi, L.; De Landro, M.; Saccomandi, P. Gold Nanoparticles-Mediated Photothermal Therapy of Pancreas Using GATE: A New Simulation Platform. Cancers 2022, 14, 5686. https://doi.org/10.3390/cancers14225686
Asadi S, Bianchi L, De Landro M, Saccomandi P. Gold Nanoparticles-Mediated Photothermal Therapy of Pancreas Using GATE: A New Simulation Platform. Cancers. 2022; 14(22):5686. https://doi.org/10.3390/cancers14225686
Chicago/Turabian StyleAsadi, Somayeh, Leonardo Bianchi, Martina De Landro, and Paola Saccomandi. 2022. "Gold Nanoparticles-Mediated Photothermal Therapy of Pancreas Using GATE: A New Simulation Platform" Cancers 14, no. 22: 5686. https://doi.org/10.3390/cancers14225686
APA StyleAsadi, S., Bianchi, L., De Landro, M., & Saccomandi, P. (2022). Gold Nanoparticles-Mediated Photothermal Therapy of Pancreas Using GATE: A New Simulation Platform. Cancers, 14(22), 5686. https://doi.org/10.3390/cancers14225686










