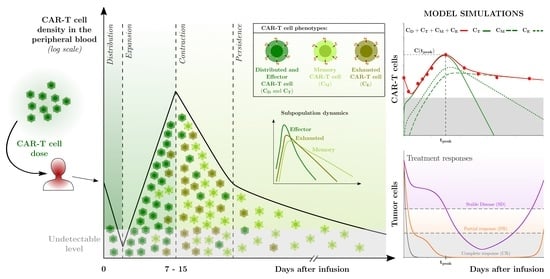
Modeling Patient-Specific CAR-T Cell Dynamics: Multiphasic Kinetics via Phenotypic Differentiation
Abstract
Simple Summary
Abstract
1. Introduction
2. Methods
2.1. Mathematical Model
2.2. Experimental Data
2.3. Mechanisms Underlying the Multiphasic Dynamics of CAR-T Cell Therapy
2.4. Model Settings and Numerical Solution
3. Results
3.1. Description of the Cellular Dynamics of CAR-T Therapy Applied to Different Hematological Cancers
3.2. Description of the Cellular Dynamics of CAR-T Therapy Applied to Patients with Different Outcomes
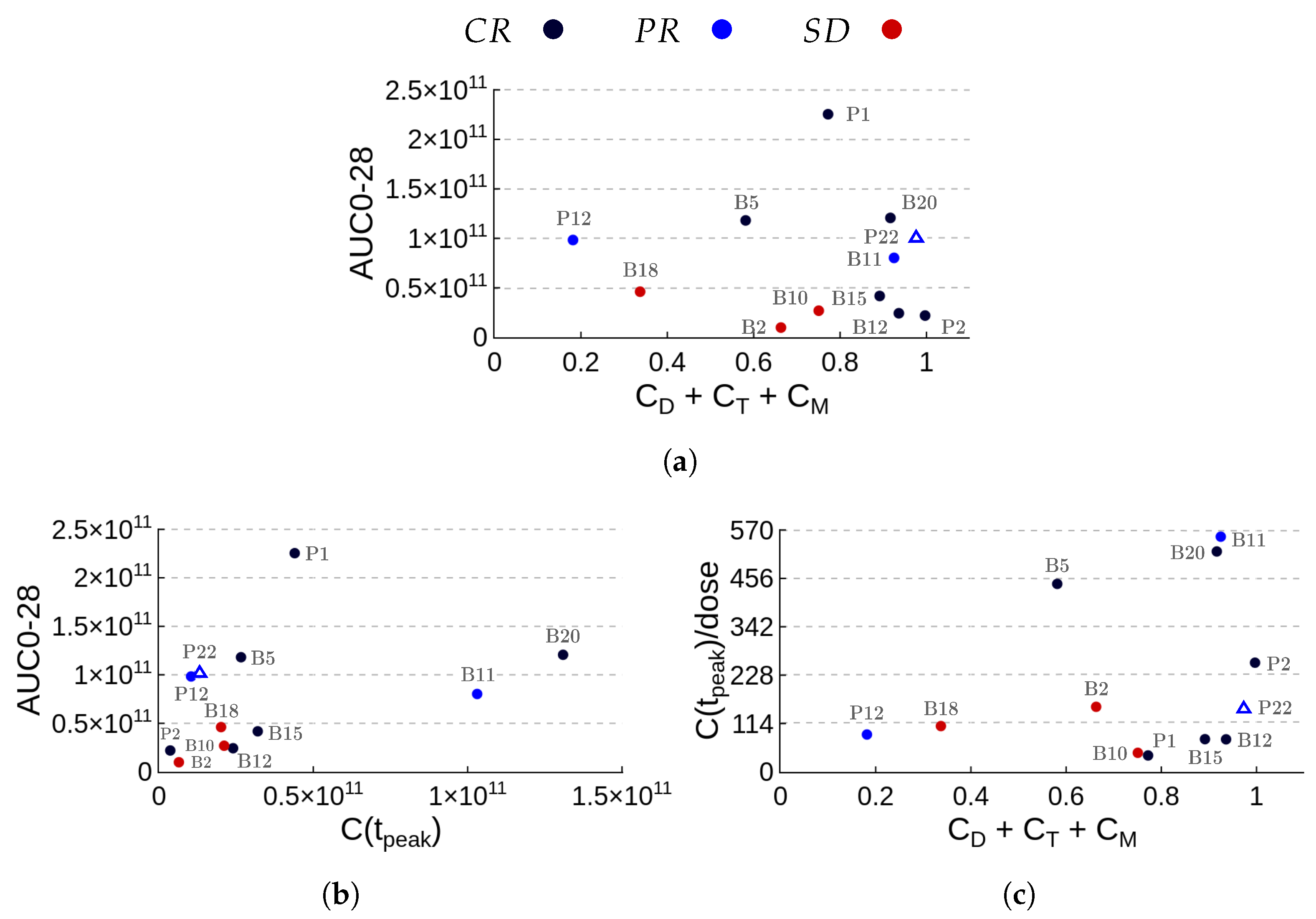
3.3. Assessment of Patient Outcomes through Kinetic Parameters
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAR | Chimeric antigen receptor |
| ALL | Acute lymphoblastic leukemia |
| MCL | Mantle cell lymphoma |
| DLBCL | Diffuse large B cell lymphoma |
| CLL | Chronic lymphocytic leukemia |
| BCMA | B cell maturation antigen |
| HST | Hair stem cell transplantation |
| PB | Peripheral blood |
| BM | Bone marrow |
| ODE | Ordinary differential equation |
| CR | Complete response |
| PR | Partial response |
| SD | Stable disease |
| PD | Progressive disease |
| IDO | Indoleamine 2,3-dioxygenase |
References
- Barros, L.R.C.; Couto, S.C.F.; da Silva Santurio, D.; Paixão, E.A.; Cardoso, F.; da Silva, V.J.; Klinger, P.; Ribeiro, P.d.A.C.; Rós, F.A.; Oliveira, T.G.M.; et al. Systematic Review of Available CAR-T Cell Trials around the World. Cancers 2022, 14, 2667. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Li, J.; Liao, M.Z.; Liu, S.N.; Yu, J.; Jing, J.; Kotani, N.; Kamen, L.; Guelman, S.; Miles, D.R. Clinical Pharmacology Perspectives for Adoptive Cell Therapies in Oncology. Clin. Pharmacol. Ther. 2022, 112, 968–981. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.W.; Kochenderfer, J.N.; Stetler-Stevenson, M.; Cui, Y.K.; Delbrook, C.; Feldman, S.A.; Fry, T.J.; Orentas, R.; Sabatino, M.; Shah, N.N.; et al. T cells expressing CD19 chimeric antigen receptors for acute lymphoblastic leukaemia in children and young adults: A phase 1 dose-escalation trial. Lancet 2015, 385, 517–528. [Google Scholar] [CrossRef]
- Shah, N.N.; Lee, D.W.; Yates, B.; Yuan, C.M.; Shalabi, H.; Martin, S.; Wolters, P.L.; Steinberg, S.M.; Baker, E.H.; Delbrook, C.P.; et al. Long-Term Follow-Up of CD19-CAR T-Cell Therapy in Children and Young Adults With B-ALL. J. Clin. Oncol. 2021, 39, 1650–1659. [Google Scholar] [CrossRef] [PubMed]
- Melenhorst, J.J.; Chen, G.M.; Wang, M.; Porter, D.L.; Chen, C.; Collins, M.A.; Gao, P.; Bandyopadhyay, S.; Sun, H.; Zhao, Z.; et al. Decade-long leukaemia remissions with persistence of CD4+ CAR T cells. Nature 2022, 602, 1476–4687. [Google Scholar] [CrossRef]
- Gardner, R.A.; Finney, O.; Annesley, C.; Brakke, H.; Summers, C.; Leger, K.; Bleakley, M.; Brown, C.; Mgebroff, S.; Kelly-Spratt, K.S.; et al. Intent-to-treat leukemia remission by CD19 CAR T cells of defined formulation and dose in children and young adults. Blood 2017, 129, 3322–3331. [Google Scholar] [CrossRef]
- Poorebrahim, M.; Melief, J.; de Coaña, Y.P.; Wickström, S.L.; Cid-Arregui, A.; Kiessling, R. Counteracting CAR T cell dysfunction. Oncogene 2021, 40, 421–435. [Google Scholar] [CrossRef]
- Shah, N.N.; Fry, T.J. Mechanisms of resistance to CAR T cell therapy. Nat. Rev. Clin. Oncol. 2019, 16, 372–385. [Google Scholar] [CrossRef]
- Larson, R.C.; Maus, M.V. Recent advances and discoveries in the mechanisms and functions of CAR T cells. Nat. Rev. Cancer 2021, 21, 145–161. [Google Scholar] [CrossRef]
- Eyquem, J.; Mansilla-Soto, J.; Giavridis, T.; van der Stegen, S.; Hamieh, M.; Cunanan, K.; Odak, A.; Gönen, M.; Sadelain, M. Targeting a CAR to the TRAC locus with CRISPR/Cas9 enhances tumour rejection. Nature 2017, 543, 113–117. [Google Scholar] [CrossRef]
- Fraietta, J.; Lacey, S.; Orlando, E.; Pruteanu-Malinici, I.; Gohil, M.; Lundh, S.; Boesteanu, A.; Wang, Y.; O’Connor, R.; Hwang, W.T.; et al. Determinants of response and resistance to CD19 chimeric antigen receptor (CAR) T cell therapy of chronic lymphocytic leukemia. Nat. Med. 2018, 24, 563–571. [Google Scholar] [CrossRef] [PubMed]
- Chaudhury, A.; Zhu, X.; Chu, L.; Goliaei, A.; June, C.; Kearns, J.; Stein, A. Chimeric Antigen Receptor T Cell Therapies: A Review of Cellular Kinetic-Pharmacodynamic Modeling Approaches. J. Clin. Pharmacol. 2020, 60, S147–S159. [Google Scholar] [CrossRef] [PubMed]
- Pillai, V.; Muralidharan, K.; Meng, W.; Bagashev, A.; Oldridge, D.A.; Rosenthal, J.; Arnam, J.V.; Melenhorst, J.J.; Mohan, D.; DiNofia, A.M.; et al. CAR T-cell therapy is effective for CD19-dim B-lymphoblastic leukemia but is impacted by prior blinatumomab therapy. Blood Adv. 2019, 3, 3539–3549. [Google Scholar] [CrossRef] [PubMed]
- Ghorashian, S.; Kramer, A.M.; Onuoha, S.; Wright, G.; Bartram, J.; Richardson, R.; Albon, S.J.; Casanovas-Company, J.; Castro, F.; Popova, B.; et al. Enhanced CAR T cell expansion and prolonged persistence in pediatric patients with ALL treated with a low-affinity CD19 CAR. Nat. Med. 2019, 25, 1408–1414. [Google Scholar] [CrossRef]
- Xu, X.; Huang, S.; Xiao, X.; Sun, Q.; Liang, X.; Chen, S.; Zhao, Z.; Huo, Z.; Tu, S.; Li, Y. Challenges and Clinical Strategies of CAR T-Cell Therapy for Acute Lymphoblastic Leukemia: Overview and Developments. Front. Immunol. 2021, 11, 569117. [Google Scholar] [CrossRef] [PubMed]
- Nukala, U.; Messan, M.R.; Yogurtcu, O.N.; Wang, X.; Yang, H. A Systematic Review of the Efforts and Hindrances of Modeling and Simulation of CAR T-cell Therapy. AAPS J. 2021, 23, 52. [Google Scholar] [CrossRef] [PubMed]
- Kast, J.; Nozohouri, S.; Zhou, D.; Yago, M.R.; Chen, P.W.; Ahamadi, M.; Dutta, S.; Upreti, V.V. Recent advances and clinical pharmacology aspects of Chimeric Antigen Receptor (CAR) T-cellular therapy development. Clin. Transl. Sci. 2022, 15, 2057–2074. [Google Scholar] [CrossRef]
- Qi, T.; McGrath, K.; Ranganathan, R.; Dotti, G.; Cao, Y. Cellular kinetics: A clinical and computational review of CAR-T cell pharmacology. Adv. Drug Deliv. Rev. 2022, 188, 114421. [Google Scholar] [CrossRef]
- Arya, V.; Venkatakrishnan, K. Role of Physiologically Based Pharmacokinetic Modeling and Simulation in Enabling Model-Informed Development of Drugs and Biotherapeutics. J. Clin. Pharmacol. 2020, 60, S7–S11. [Google Scholar] [CrossRef]
- Mueller, K.; Maude, S.; Porter, D.; Frey, N.; Wood, P.; Han, X.; Waldron, E.; Chakraborty, A.; Awasthi, R.; Levine, B.; et al. Cellular kinetics of CTL019 in relapsed/refractory B-cell acute lymphoblastic leukemia and chronic lymphocytic leukemia. Blood 2017, 130, 2317–2325. [Google Scholar] [CrossRef]
- Stein, A.M.; Grupp, S.A.; Levine, J.E.; Laetsch, T.W.; Pulsipher, M.A.; Boyer, M.W.; August, K.J.; Levine, B.L.; Tomassian, L.; Shah, S.; et al. Tisagenlecleucel Model-Based Cellular Kinetic Analysis of Chimeric Antigen Receptor–T Cells. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 285–295. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Ayyar, V.S.; Zheng, X.; Chen, W.; Zheng, S.; Mody, H.; Wang, W.; Heald, D.; Singh, A.P.; Cao, Y. Model-Based Cellular Kinetic Analysis of Chimeric Antigen Receptor-T Cells in Humans. Clin. Pharmacol. Ther. 2021, 109, 716–727. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Chen, W.; Zheng, X.; Mody, H.; Carpenter, T.J.; Zong, A.; Heald, D.L. Bench-to-bedside translation of chimeric antigen receptor (CAR) T cells using a multiscale systems pharmacokinetic-pharmacodynamic model: A case study with anti-BCMA CAR-T. CPT Pharmacomet. Syst. Pharmacol. 2021, 10, 362–376. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Zheng, X.; Lin-Schmidt, X.; Chen, W.; Carpenter, T.J.; Zong, A.; Wang, W.; Heald, D.L. Development of a quantitative relationship between CAR-affinity, antigen abundance, tumor cell depletion and CAR-T cell expansion using a multiscale systems PK-PD model. mAbs 2020, 12, 1688616. [Google Scholar] [CrossRef]
- Kimmel, G.J.; Locke, F.L.; Altrock, P.M. The roles of T cell competition and stochastic extinction events in chimeric antigen receptor T cell therapy. Proc. R. Soc. B 2021, 288, 20210229. [Google Scholar] [CrossRef]
- Owens, K.; Bozic, I. Modeling CAR T-Cell Therapy with Patient Preconditioning. Bull. Math. Biol. 2021, 83, 42. [Google Scholar] [CrossRef]
- Hardiansyah, D.; Ng, C.M. Quantitative Systems Pharmacology Model of Chimeric Antigen Receptor T-Cell Therapy. Clin. Transl. Sci. 2019, 12, 343–349. [Google Scholar] [CrossRef]
- Barros, L.R.C.; Paixão, E.A.; Valli, A.M.P.; Naozuka, G.T.; Fassoni, A.C.; Almeida, R.C. CARTmath—A Mathematical Model of CAR-T Immunotherapy in Preclinical Studies of Hematological Cancers. Cancers 2021, 13, 2941. [Google Scholar] [CrossRef]
- Sheih, A.; Voillet, V.; Hanafi, L.A.; DeBerg, H.A.; Yajima, M.; Hawkins, R.; Gersuk, V.; Riddell, S.R.; Maloney, D.G.; Wohlfahrt, M.E.; et al. Clonal kinetics and single-cell transcriptional profiling of CAR-T cells in patients undergoing CD19 CAR-T immunotherapy. Nat. Commun. 2020, 11, 219. [Google Scholar] [CrossRef]
- Fraietta, J.A.; Nobles, C.L.; Sammons, M.A.; Lundh, S.; Carty, S.A.; Reich, T.J.; Cogdill, A.P.; Morrissette, J.J.D.; DeNizio, J.E.; Reddy, S.; et al. Disruption of TET2 promotes the therapeutic efficacy of CD19-targeted T cells. Nature 2018, 558, 307–312. [Google Scholar] [CrossRef]
- Shah, N.; Qin, H.; Yates, B.; Su, L.; Shalabi, H.; Raffeld, M.; Ahlman, M.; Stetler-Stevenson, M.; Yuan, C.; Guo, S.; et al. Clonal expansion of CAR T cells harboring lentivector integration in the CBL gene following anti-CD22 CAR T-cell therapy. Blood Adv. 2019, 3, 2317–2322. [Google Scholar] [CrossRef] [PubMed]
- Kimmel, G.J.; Locke, F.L.; Altrock, P.M. Response to CAR T cell therapy can be explained by ecological cell dynamics and stochastic extinction events. bioRxiv 2020. [Google Scholar] [CrossRef]
- Ninomiya, S.; Narala, N.; Huye, L.; Yagyu, S.; Savoldo, B.; Dotti, G.; Heslop, H.E.; Brenner, M.K.; Rooney, C.M.; Ramos, C.A. Tumor indoleamine 2, 3-dioxygenase (IDO) inhibits CD19-CAR T cells and is downregulated by lymphodepleting drugs. Blood 2015, 125, 3905–3916. [Google Scholar] [CrossRef] [PubMed]
- De Boer, R.J.; Perelson, A.S. Quantifying T lymphocyte turnover. J. Theor. Biol. 2013, 327, 45–87. [Google Scholar] [CrossRef] [PubMed]
- de Pillis, L.G.; Radunskaya, A.E.; Wiseman, C.L. A Validated Mathematical Model of Cell-Mediated Immune Response to Tumor Growth. Cancer Res. 2005, 65, 7950–7958. [Google Scholar] [CrossRef] [PubMed]
- Robertson-Tessi, M.; El-Kareh, A.; Goriely, A. A mathematical model of tumor–immune interactions. J. Theor. Biol. 2012, 294, 56–73. [Google Scholar] [CrossRef]
- Brudno, J.N.; Somerville, R.P.; Shi, V.; Rose, J.J.; Halverson, D.C.; Fowler, D.H.; Gea-Banacloche, J.C.; Pavletic, S.Z.; Hickstein, D.D.; Lu, T.L.; et al. Allogeneic T Cells That Express an Anti-CD19 Chimeric Antigen Receptor Induce Remissions of B-Cell Malignancies That Progress After Allogeneic Hematopoietic Stem-Cell Transplantation Without Causing Graft-Versus-Host Disease. J. Clin. Oncol. 2016, 34, 1112–1121. [Google Scholar] [CrossRef]
- Porter, D.L.; Hwang, W.T.; Frey, N.V.; Lacey, S.F.; Shaw, P.A.; Loren, A.W.; Bagg, A.; Marcucci, K.T.; Shen, A.; Gonzalez, V.; et al. Chimeric antigen receptor T cells persist and induce sustained remissions in relapsed refractory chronic lymphocytic leukemia. Sci. Transl. Med. 2015, 7, 303ra139. [Google Scholar] [CrossRef]
- Rohatgi, A. WebPlotDigitizer, 2020. Version 4.5. Available online: https://apps.automeris.io/wpd/ (accessed on 13 December 2021).
- Cheson, B.; Pfistner, B.; Juweid, M.; Gascoyne, R.; Specht, L.; Horning, S.; Coiffier, B.; Fisher, R.; Hagenbeek, A.; Zucca, E.; et al. International Harmonization Project on Lymphoma: Revised response criteria for malignant lymphoma. J. Clin. Oncol. 2007, 25, 579–586. [Google Scholar] [CrossRef]
- Hallek, M.; Cheson, B.D.; Catovsky, D.; Caligaris-Cappio, F.; Dighiero, G.; Döhner, H.; Hillmen, P.; Keating, M.J.; Montserrat, E.; Rai, K.R.; et al. Guidelines for the diagnosis and treatment of chronic lymphocytic leukemia: A report from the International Workshop on Chronic Lymphocytic Leukemia updating the National Cancer Institute–Working Group 1996 guidelines. Blood 2008, 111, 5446–5456. [Google Scholar] [CrossRef]
- Faires, J.D.; Burden, R.L. Numerical Methods; Cengage Learning: Belmont, CA, USA, 2003. [Google Scholar]
- Ogasawara, K.; Dodds, M.; Mack, T.; Lymp, J.; Dell’Aringa, J.; Smith, J. Population Cellular Kinetics of Lisocabtagene Maraleucel, an Autologous CD19-Directed Chimeric Antigen Receptor T-Cell Product, in Patients with Relapsed/Refractory Large B-Cell Lymphoma. Clin. Pharmacokinet. 2021, 60, 1621–1633. [Google Scholar] [CrossRef] [PubMed]
- Maude, S.L.; Laetsch, T.W.; Buechner, J.; Rives, S.; Boyer, M.; Bittencourt, H.; Bader, P.; Verneris, M.R.; Stefanski, H.E.; Myers, G.D.; et al. Tisagenlecleucel in Children and Young Adults with B-Cell Lymphoblastic Leukemia. N. Engl. J. Med. 2018, 378, 439–448. [Google Scholar] [CrossRef] [PubMed]
- Beider, K.; Itzhaki, O.; Schachter, J.; Grushchenko-Polaq, A.; Voevoda-Dimenshtein, V.; Rosenberg, E.; Ostrovsky, O.; Devillers, O.; Frommer, R.; Zeltzer, L.; et al. Molecular and Functional Signatures Associated with CAR T Cell Exhaustion and Impaired Clinical Response in Patients with B Cell Malignancies. Cells 2022, 11, 1140. [Google Scholar] [CrossRef] [PubMed]
- Lynn, R.C.; Weber, E.W.; Sotillo, E.; Gennert, D.; Xu, P.; Good, Z.; Anbunathan, H.; Lattin, J.; Jones, R.; Tieu, V.; et al. c-Jun overexpression in CAR T cells induces exhaustion resistance. Nature 2019, 576, 293–300. [Google Scholar] [CrossRef] [PubMed]
- Maus, M.V. A decade of CAR T cell evolution. Nat. Cancer 2022, 3, 270–271. [Google Scholar] [CrossRef]
- Chong, E.A.; Ruella, M.; Schuster, S.J. Five-Year Outcomes for Refractory B-Cell Lymphomas with CAR T-Cell Therapy. N. Engl. J. Med. 2021, 384, 673–674. [Google Scholar] [CrossRef]

 ) of CAR-T cell kinetics from a representative patient profile were split among the four phases of CAR-T cell dynamics to which lines in the logplot of the CAR-T cell population along time were fitted. The corresponding (growth or decline) rates are denoted by , and , associated with the distribution, expansion, contraction, and persistence phases, respectively. These rates are used as first approximations to the parameters of the leading mechanism(s) of each phase. Specifically, the distribution phase is mainly driven by the reduction rate of the injected CAR-T cells so that ; the expansion phase is driven by the combined effect between the expansion () and mortality (), leading to ; the contraction and persistence phases are mainly driven by the mortality of exhausted and memory CAR-T cells, respectively, which yield and . (b) The per capita rate of the total CAR-T cell population () is displayed over time after infusion together with the calibrated values of , , , and .
) of CAR-T cell kinetics from a representative patient profile were split among the four phases of CAR-T cell dynamics to which lines in the logplot of the CAR-T cell population along time were fitted. The corresponding (growth or decline) rates are denoted by , and , associated with the distribution, expansion, contraction, and persistence phases, respectively. These rates are used as first approximations to the parameters of the leading mechanism(s) of each phase. Specifically, the distribution phase is mainly driven by the reduction rate of the injected CAR-T cells so that ; the expansion phase is driven by the combined effect between the expansion () and mortality (), leading to ; the contraction and persistence phases are mainly driven by the mortality of exhausted and memory CAR-T cells, respectively, which yield and . (b) The per capita rate of the total CAR-T cell population () is displayed over time after infusion together with the calibrated values of , , , and .
 ) of CAR-T cell kinetics from a representative patient profile were split among the four phases of CAR-T cell dynamics to which lines in the logplot of the CAR-T cell population along time were fitted. The corresponding (growth or decline) rates are denoted by , and , associated with the distribution, expansion, contraction, and persistence phases, respectively. These rates are used as first approximations to the parameters of the leading mechanism(s) of each phase. Specifically, the distribution phase is mainly driven by the reduction rate of the injected CAR-T cells so that ; the expansion phase is driven by the combined effect between the expansion () and mortality (), leading to ; the contraction and persistence phases are mainly driven by the mortality of exhausted and memory CAR-T cells, respectively, which yield and . (b) The per capita rate of the total CAR-T cell population () is displayed over time after infusion together with the calibrated values of , , , and .
) of CAR-T cell kinetics from a representative patient profile were split among the four phases of CAR-T cell dynamics to which lines in the logplot of the CAR-T cell population along time were fitted. The corresponding (growth or decline) rates are denoted by , and , associated with the distribution, expansion, contraction, and persistence phases, respectively. These rates are used as first approximations to the parameters of the leading mechanism(s) of each phase. Specifically, the distribution phase is mainly driven by the reduction rate of the injected CAR-T cells so that ; the expansion phase is driven by the combined effect between the expansion () and mortality (), leading to ; the contraction and persistence phases are mainly driven by the mortality of exhausted and memory CAR-T cells, respectively, which yield and . (b) The per capita rate of the total CAR-T cell population () is displayed over time after infusion together with the calibrated values of , , , and .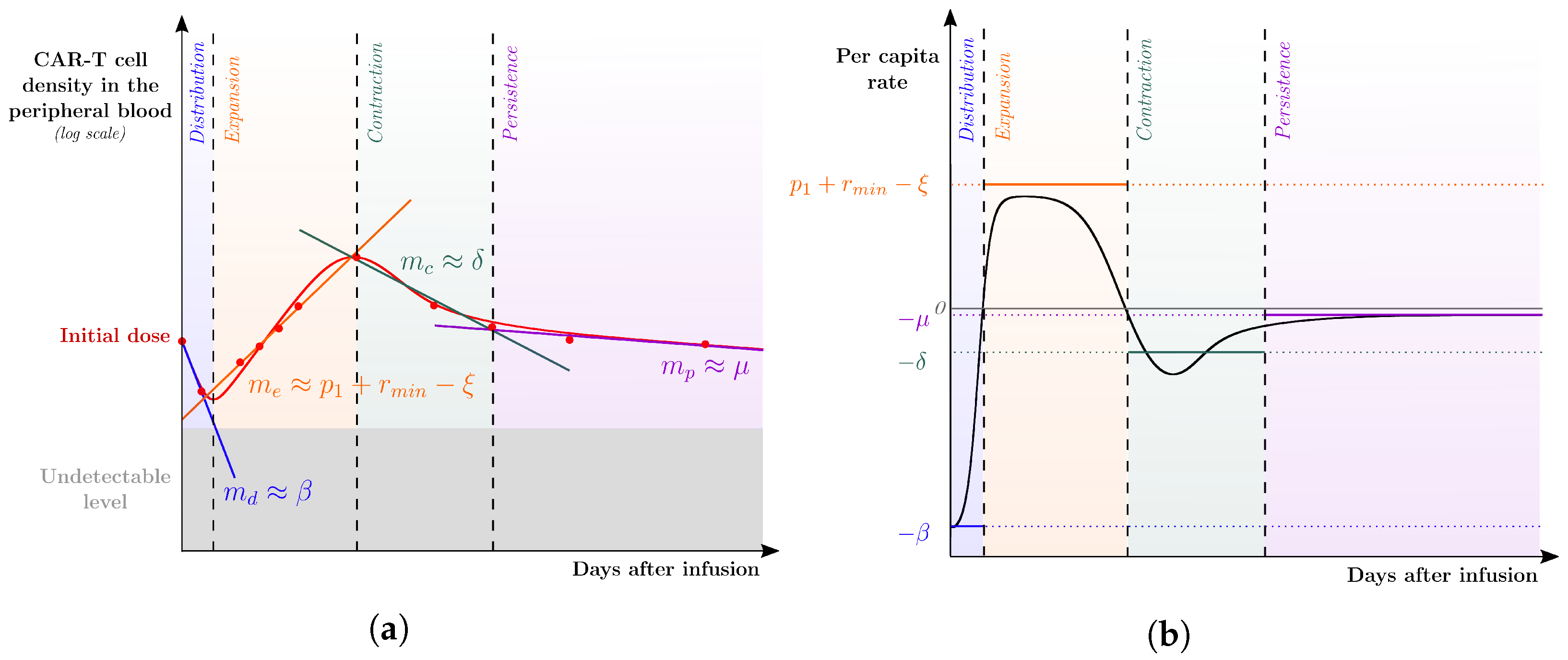
 ) from [22]. Each column corresponds to the dynamics of the total CAR-T cell population (
) from [22]. Each column corresponds to the dynamics of the total CAR-T cell population ( ) for different diseases (DLBCL, pediatric and adult ALL, and CLL) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The mean dose value of cells (
) for different diseases (DLBCL, pediatric and adult ALL, and CLL) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The mean dose value of cells ( ) presented in [21] is used as a surrogate for the actual doses when not reported for patients with ALL. The gray region represents the undetectable levels (below the threshold of cells to DLBCL and pediatric ALL, cells to adult ALL, and cells to CLL [22]). Data points in this region (
) presented in [21] is used as a surrogate for the actual doses when not reported for patients with ALL. The gray region represents the undetectable levels (below the threshold of cells to DLBCL and pediatric ALL, cells to adult ALL, and cells to CLL [22]). Data points in this region ( ) were not used for calibration and error calculation due to their high uncertainties. The bottom row presents the time-dependent expansion rate function () for each patient.
) were not used for calibration and error calculation due to their high uncertainties. The bottom row presents the time-dependent expansion rate function () for each patient.
 ) from [22]. Each column corresponds to the dynamics of the total CAR-T cell population (
) from [22]. Each column corresponds to the dynamics of the total CAR-T cell population ( ) for different diseases (DLBCL, pediatric and adult ALL, and CLL) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The mean dose value of cells (
) for different diseases (DLBCL, pediatric and adult ALL, and CLL) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The mean dose value of cells ( ) presented in [21] is used as a surrogate for the actual doses when not reported for patients with ALL. The gray region represents the undetectable levels (below the threshold of cells to DLBCL and pediatric ALL, cells to adult ALL, and cells to CLL [22]). Data points in this region (
) presented in [21] is used as a surrogate for the actual doses when not reported for patients with ALL. The gray region represents the undetectable levels (below the threshold of cells to DLBCL and pediatric ALL, cells to adult ALL, and cells to CLL [22]). Data points in this region ( ) were not used for calibration and error calculation due to their high uncertainties. The bottom row presents the time-dependent expansion rate function () for each patient.
) were not used for calibration and error calculation due to their high uncertainties. The bottom row presents the time-dependent expansion rate function () for each patient.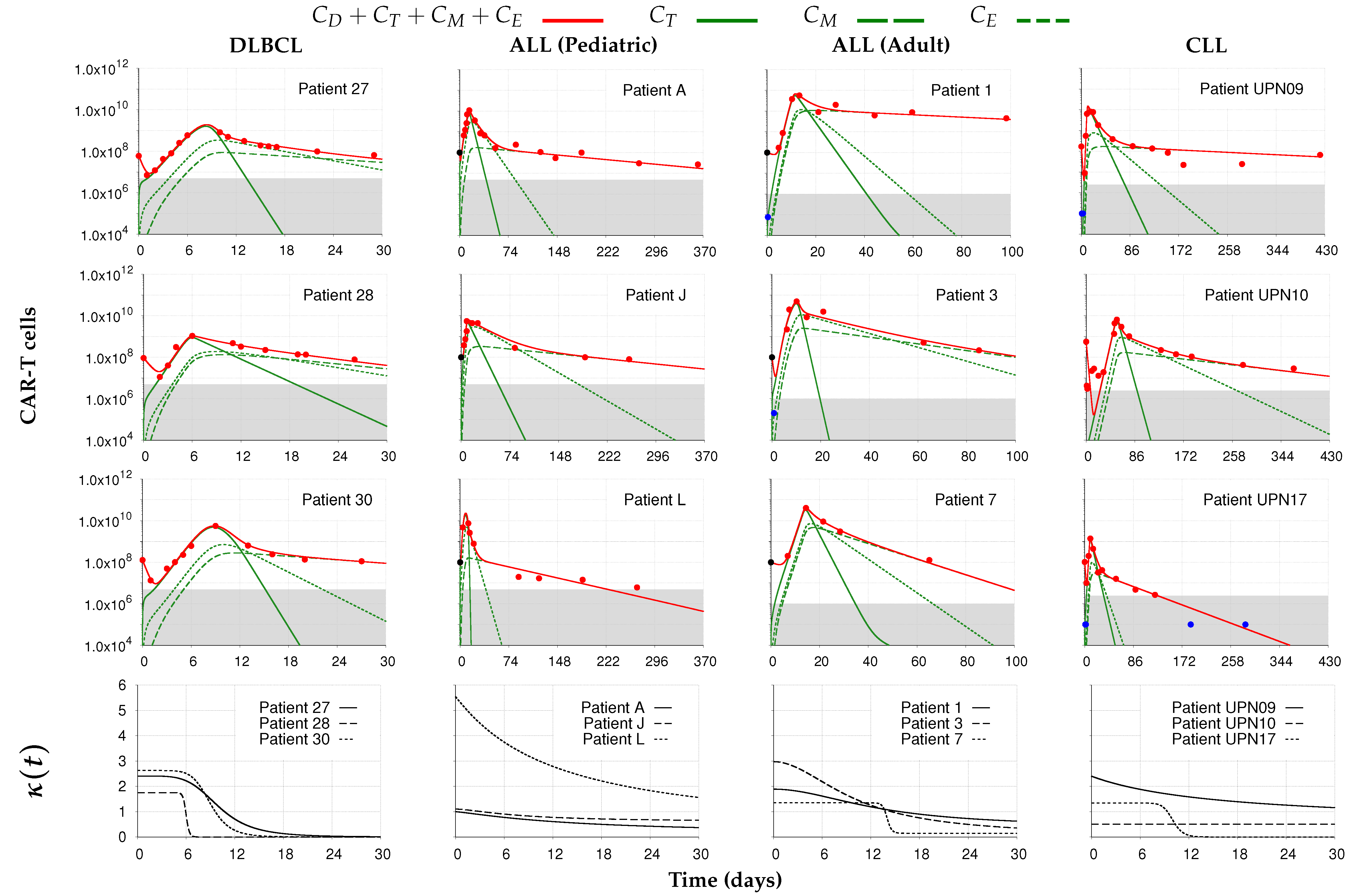
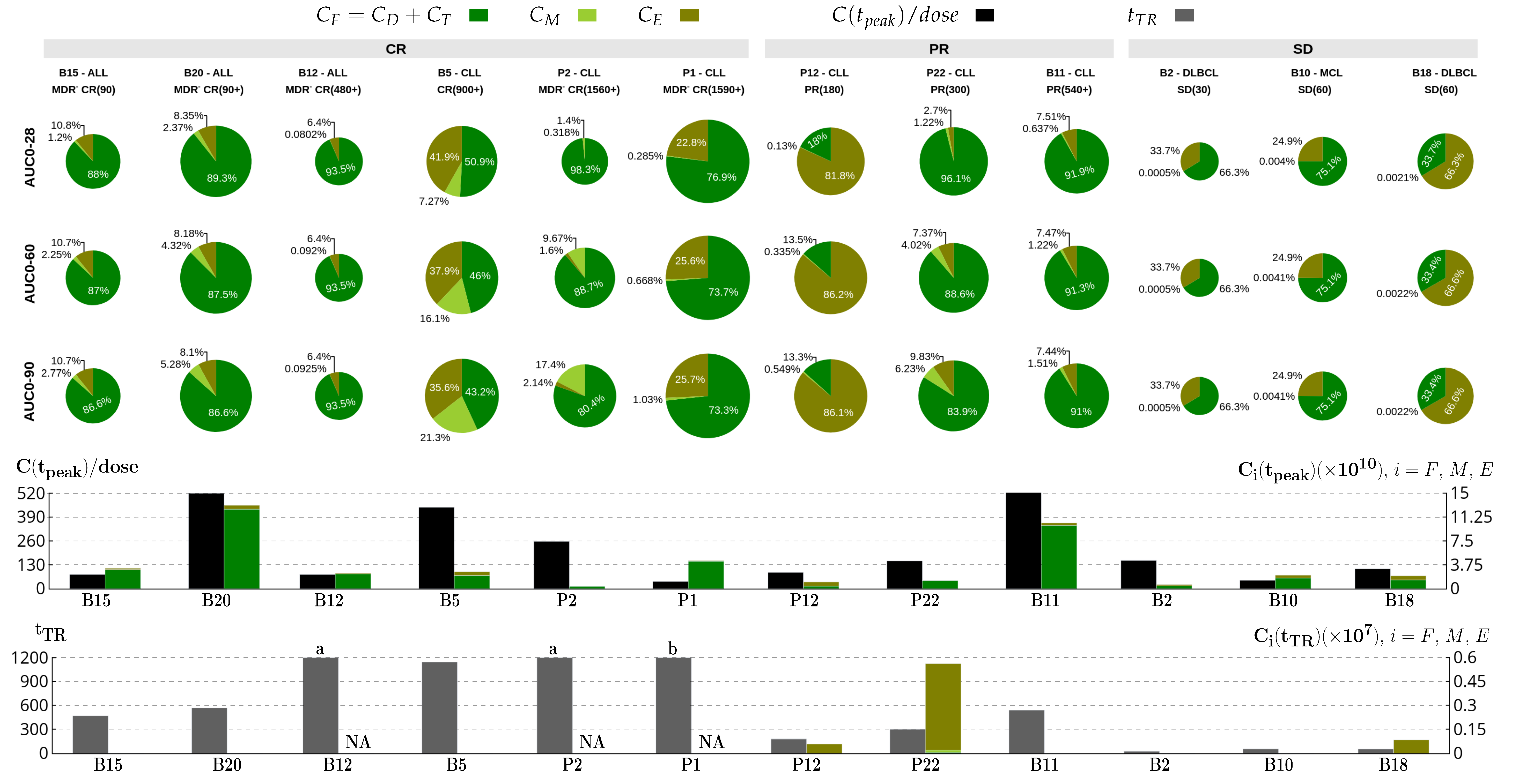
 ) from [37,38]. Each column corresponds to the dynamics of the total CAR-T cell population (
) from [37,38]. Each column corresponds to the dynamics of the total CAR-T cell population ( ) for different therapy responses at the last follow-up (interval from infusion to the last follow-up in days) (CR—complete response, PR—partial response, and SD—stable disease) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The gray region represents the undetectable level. Data points (
) for different therapy responses at the last follow-up (interval from infusion to the last follow-up in days) (CR—complete response, PR—partial response, and SD—stable disease) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The gray region represents the undetectable level. Data points ( ) may assume any value in this region, but some (
) may assume any value in this region, but some ( ) were not used for calibration and error calculation of the model due to their greater uncertainty. The bottom row presents the time-dependent expansion rate function () for each patient.
) were not used for calibration and error calculation of the model due to their greater uncertainty. The bottom row presents the time-dependent expansion rate function () for each patient.
 ) from [37,38]. Each column corresponds to the dynamics of the total CAR-T cell population (
) from [37,38]. Each column corresponds to the dynamics of the total CAR-T cell population ( ) for different therapy responses at the last follow-up (interval from infusion to the last follow-up in days) (CR—complete response, PR—partial response, and SD—stable disease) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The gray region represents the undetectable level. Data points (
) for different therapy responses at the last follow-up (interval from infusion to the last follow-up in days) (CR—complete response, PR—partial response, and SD—stable disease) and different patients. The total CAR-T cell population is divided into effector (), memory (), and exhausted () phenotypes, shown in continuous, dashed, and dotted green, respectively. The gray region represents the undetectable level. Data points ( ) may assume any value in this region, but some (
) may assume any value in this region, but some ( ) were not used for calibration and error calculation of the model due to their greater uncertainty. The bottom row presents the time-dependent expansion rate function () for each patient.
) were not used for calibration and error calculation of the model due to their greater uncertainty. The bottom row presents the time-dependent expansion rate function () for each patient.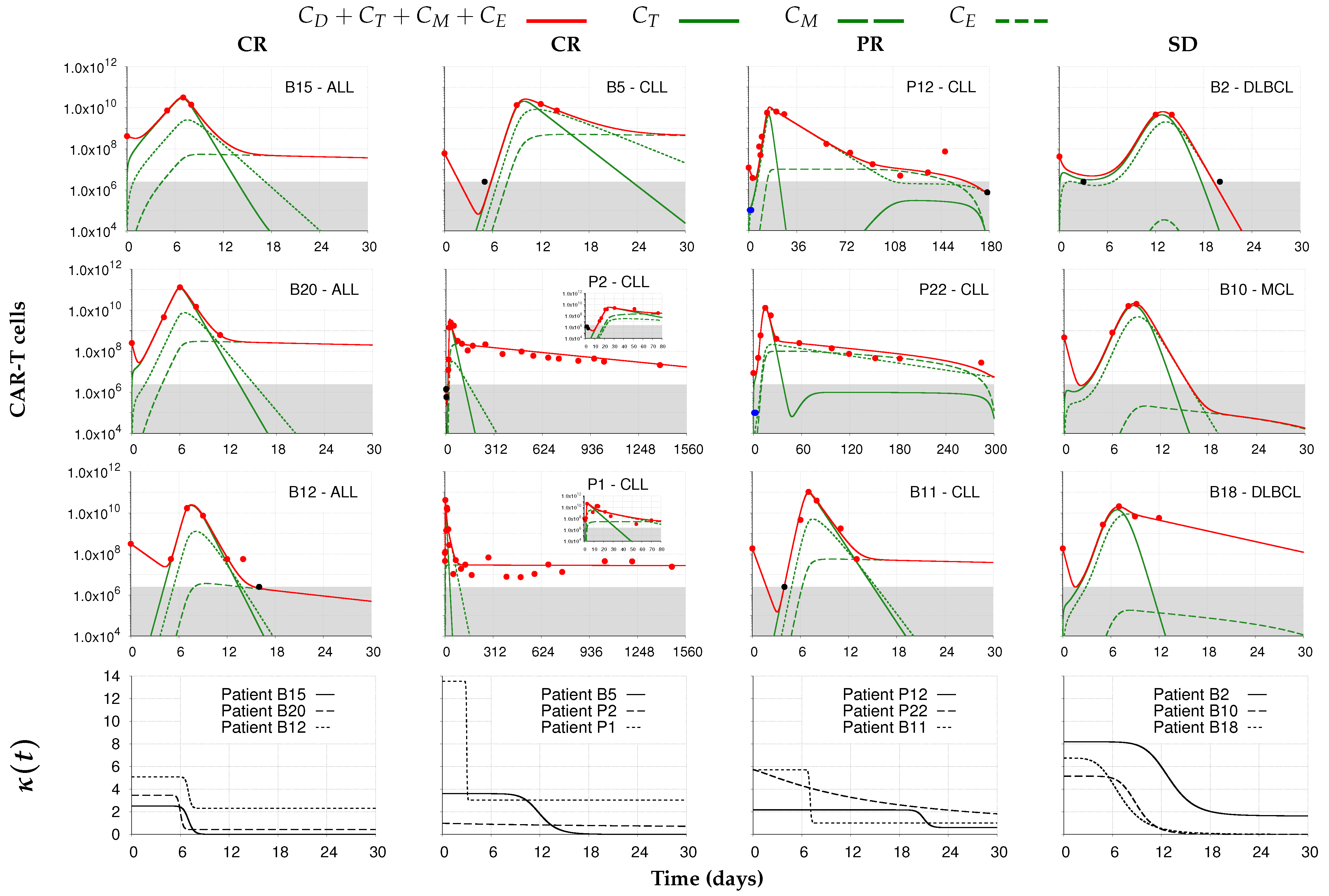
| Parameter | Unit | Biological Meaning |
|---|---|---|
| day | Reduction rate of infused cells due to natural death during their distribution in the patient’s body | |
| day | Engraftment rate of injected cells to blood and tumor niche | |
| day | Minimum expansion rate of effector CAR-T cells | |
| day | Initial expansion rate of effector CAR-T cells | |
| day | Rate that regulates the duration of maximum expansion period of effector CAR-T cells | |
| - | Expansion coefficient that regulates the decay of maximum expansion period of effector CAR-T cells | |
| A, a | cell | Half-saturation constants of functions and |
| day | Death rate of effector CAR-T cells | |
| day | Conversion rate of effector CAR-T cells into memory CAR-T cells | |
| day | Exhaustion rate of effector CAR-T cells | |
| (cell.day) | Conversion coefficient of memory CAR-T cells into effector CAR-T cells due to interaction with tumor cells | |
| (cell.day) | Inhibition coefficient of effector CAR-T cells due to interaction with tumor cells | |
| day | Death rate of memory CAR-T cells | |
| day | Death rate of exhausted CAR-T cells | |
| r | day | Maximum growth rate of tumor cells |
| b | cell | Inverse of the carrying capacity of tumor cells |
| day | Cytotoxic rate of the functional CAR-T cells on tumor cells | |
| - | Half-saturation constant of the cytotoxic effect on tumor cells |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paixão, E.A.; Barros, L.R.C.; Fassoni, A.C.; Almeida, R.C. Modeling Patient-Specific CAR-T Cell Dynamics: Multiphasic Kinetics via Phenotypic Differentiation. Cancers 2022, 14, 5576. https://doi.org/10.3390/cancers14225576
Paixão EA, Barros LRC, Fassoni AC, Almeida RC. Modeling Patient-Specific CAR-T Cell Dynamics: Multiphasic Kinetics via Phenotypic Differentiation. Cancers. 2022; 14(22):5576. https://doi.org/10.3390/cancers14225576
Chicago/Turabian StylePaixão, Emanuelle A., Luciana R. C. Barros, Artur C. Fassoni, and Regina C. Almeida. 2022. "Modeling Patient-Specific CAR-T Cell Dynamics: Multiphasic Kinetics via Phenotypic Differentiation" Cancers 14, no. 22: 5576. https://doi.org/10.3390/cancers14225576
APA StylePaixão, E. A., Barros, L. R. C., Fassoni, A. C., & Almeida, R. C. (2022). Modeling Patient-Specific CAR-T Cell Dynamics: Multiphasic Kinetics via Phenotypic Differentiation. Cancers, 14(22), 5576. https://doi.org/10.3390/cancers14225576