Convection-Enhanced Delivery of Antiangiogenic Drugs and Liposomal Cytotoxic Drugs to Heterogeneous Brain Tumor for Combination Therapy
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
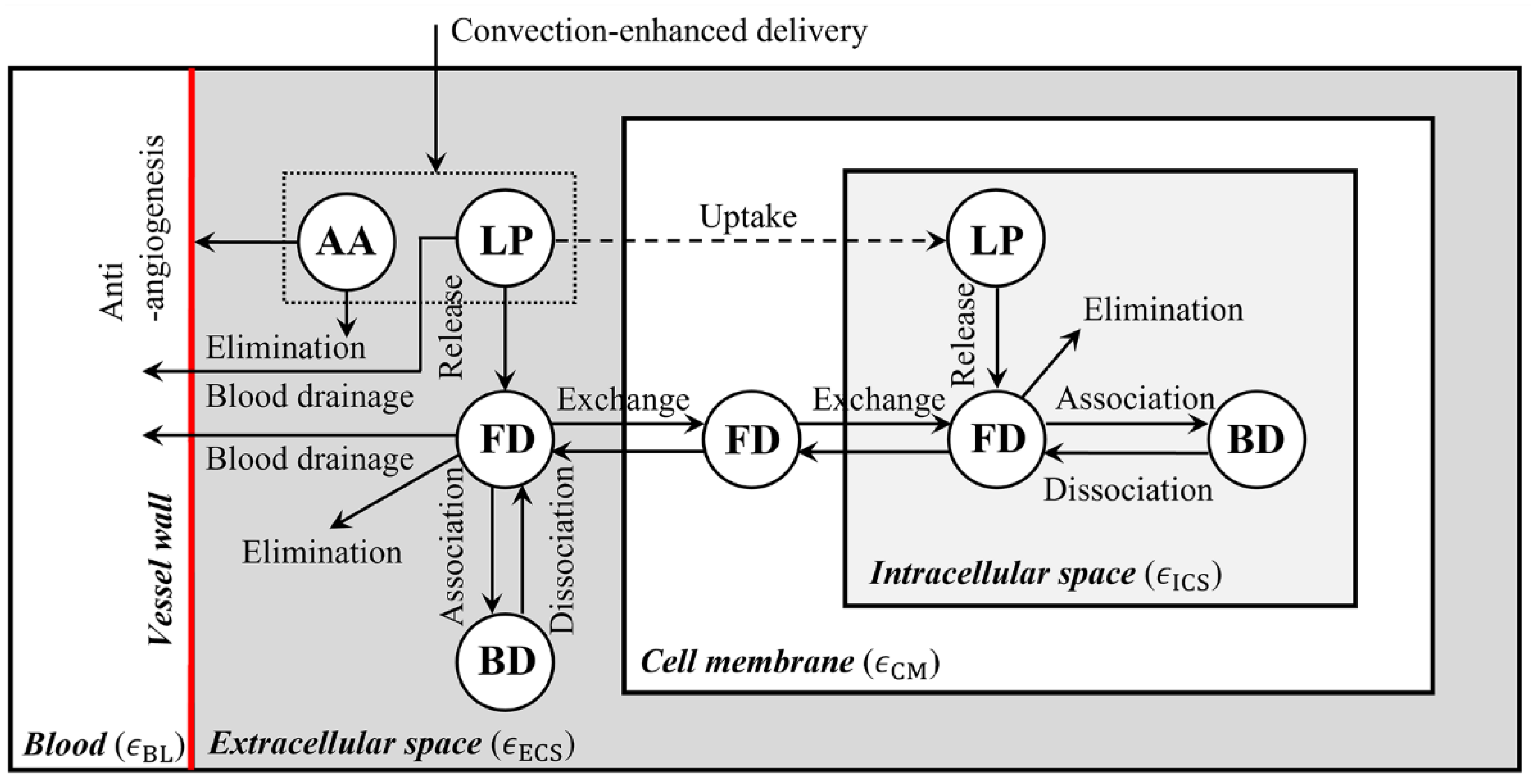
2.1. Mathematical Model
2.2. MR Imaging and Processing Protocol
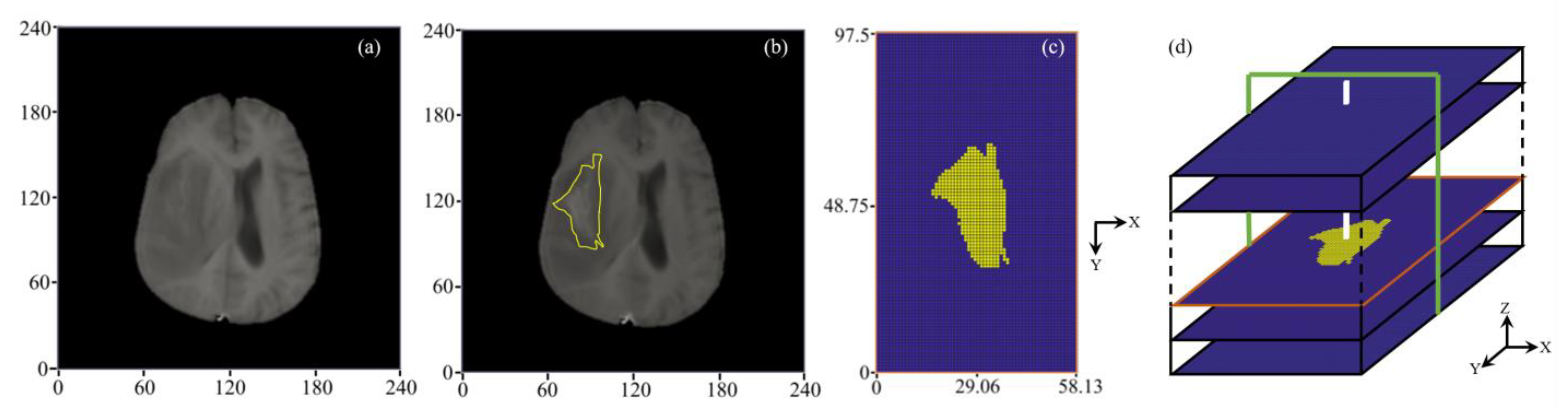
2.2.1. 3D Reconstruction of Brain Tumor
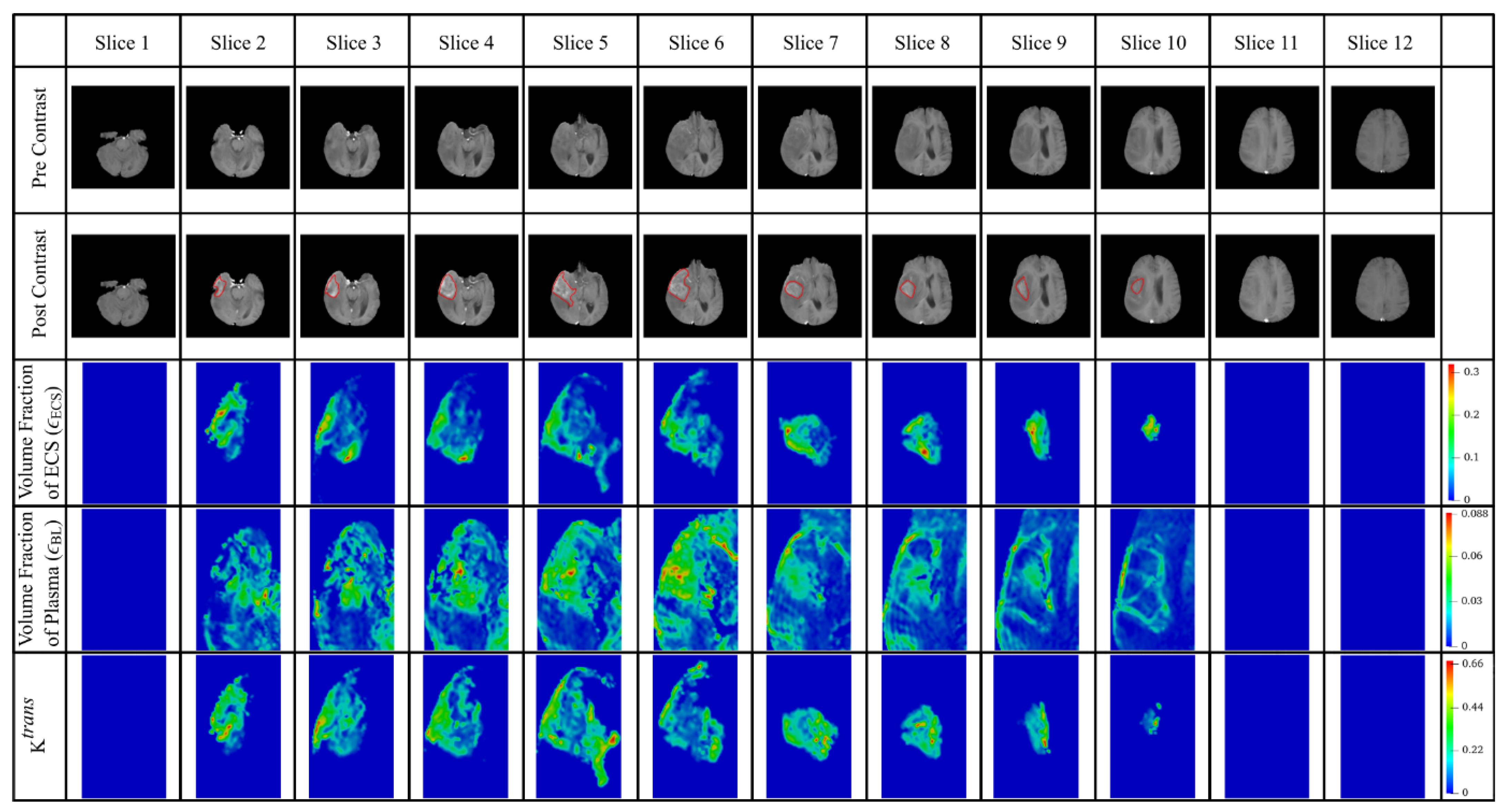
2.2.2. Extraction of Tumor Heterogenous Properties
2.3. Model Parameters
2.3.1. Volume Fraction ()
2.3.2. Microvasculature Surface Area per Unit Tissue Volume ()
2.3.3. Infusion Settings
2.4. Numerical Methods
2.5. Boundary Conditions
2.6. Qualification of Delivery Outcomes
2.6.1. Spatial-Averaged Concentration
2.6.2. Location of Distance Course
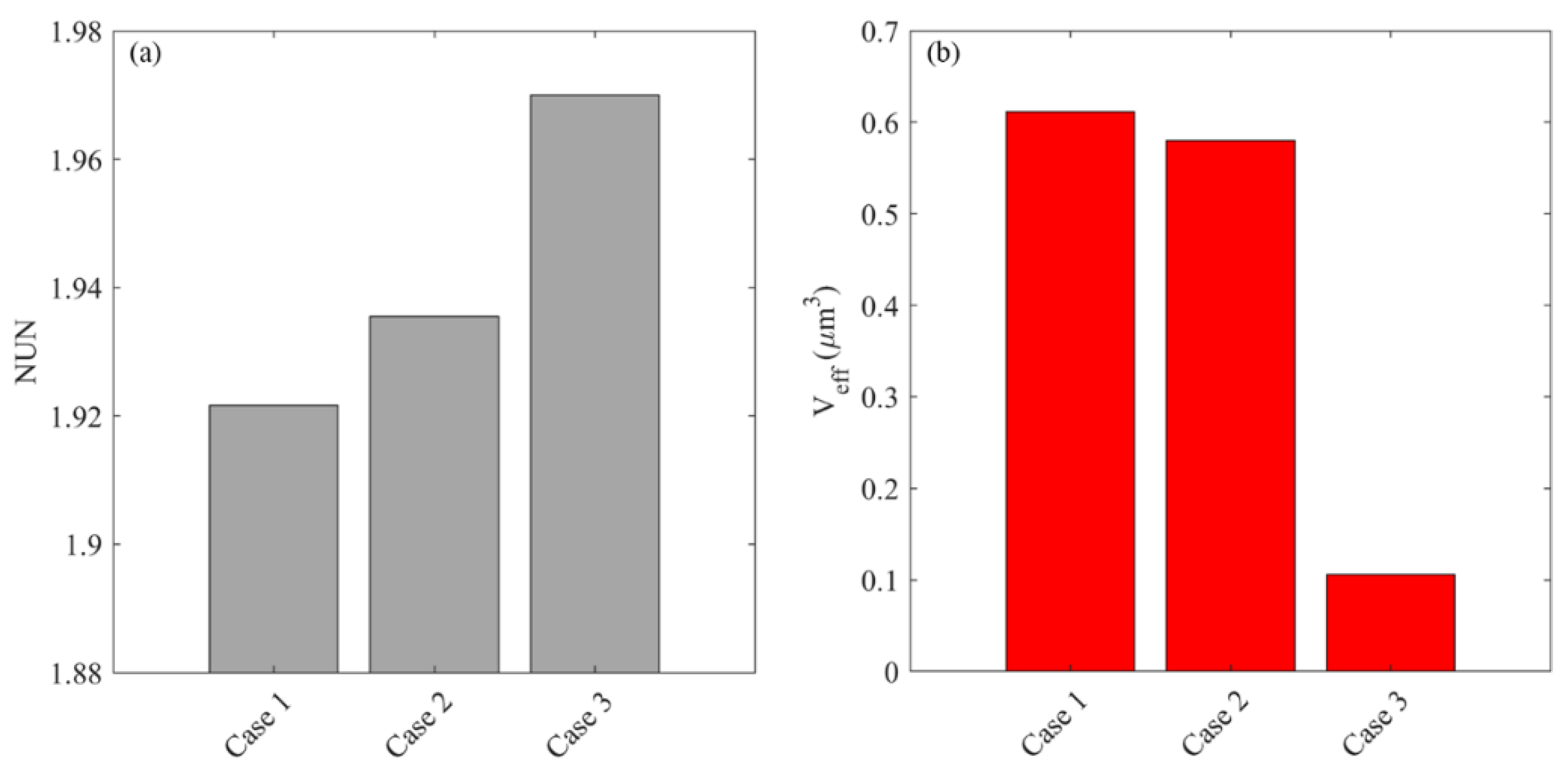
2.6.3. Distribution Non-Uniformity
2.6.4. Effective Distribution Volume
3. Results
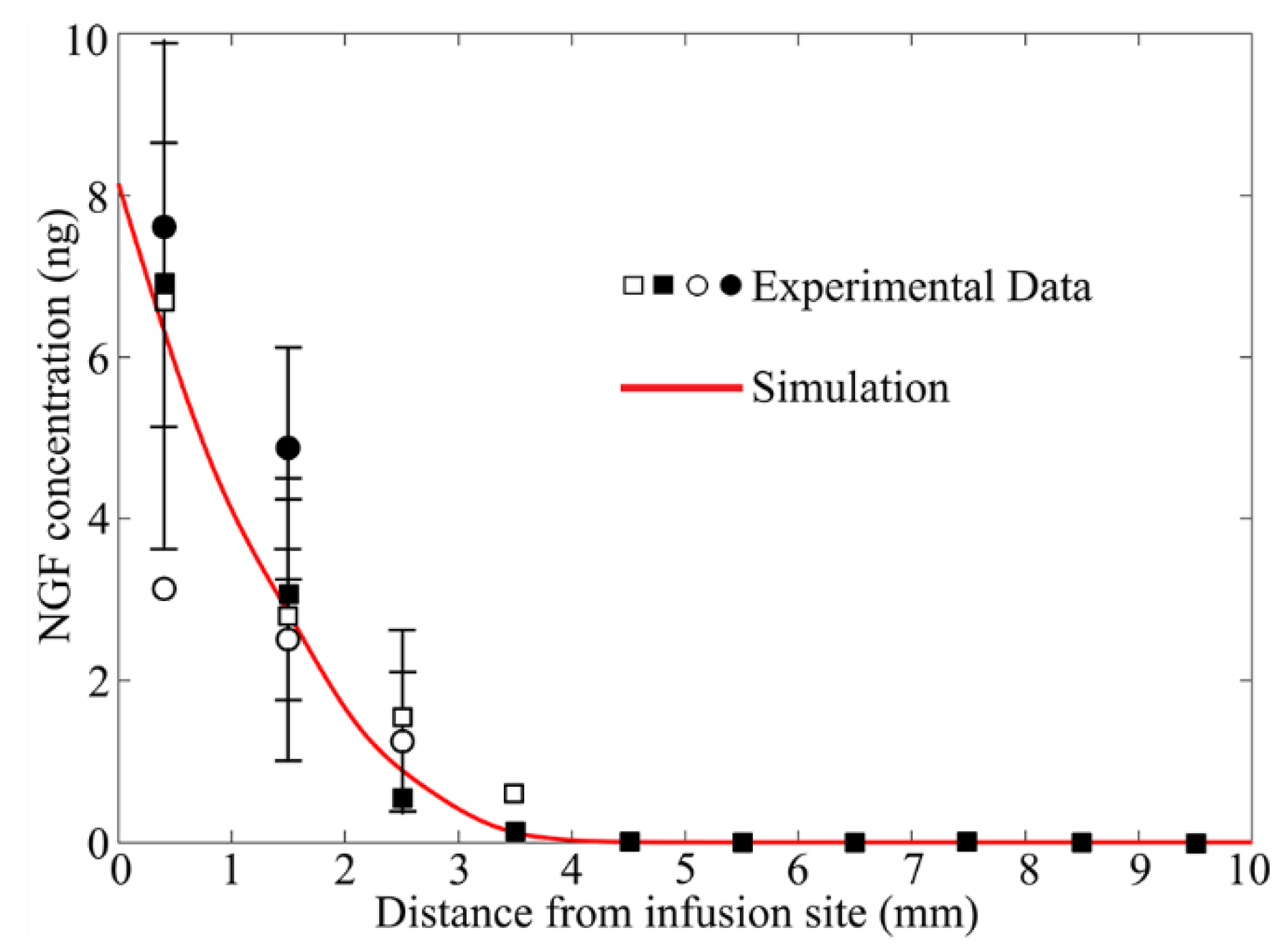
3.1. Model Validation
3.2. Baseline Study
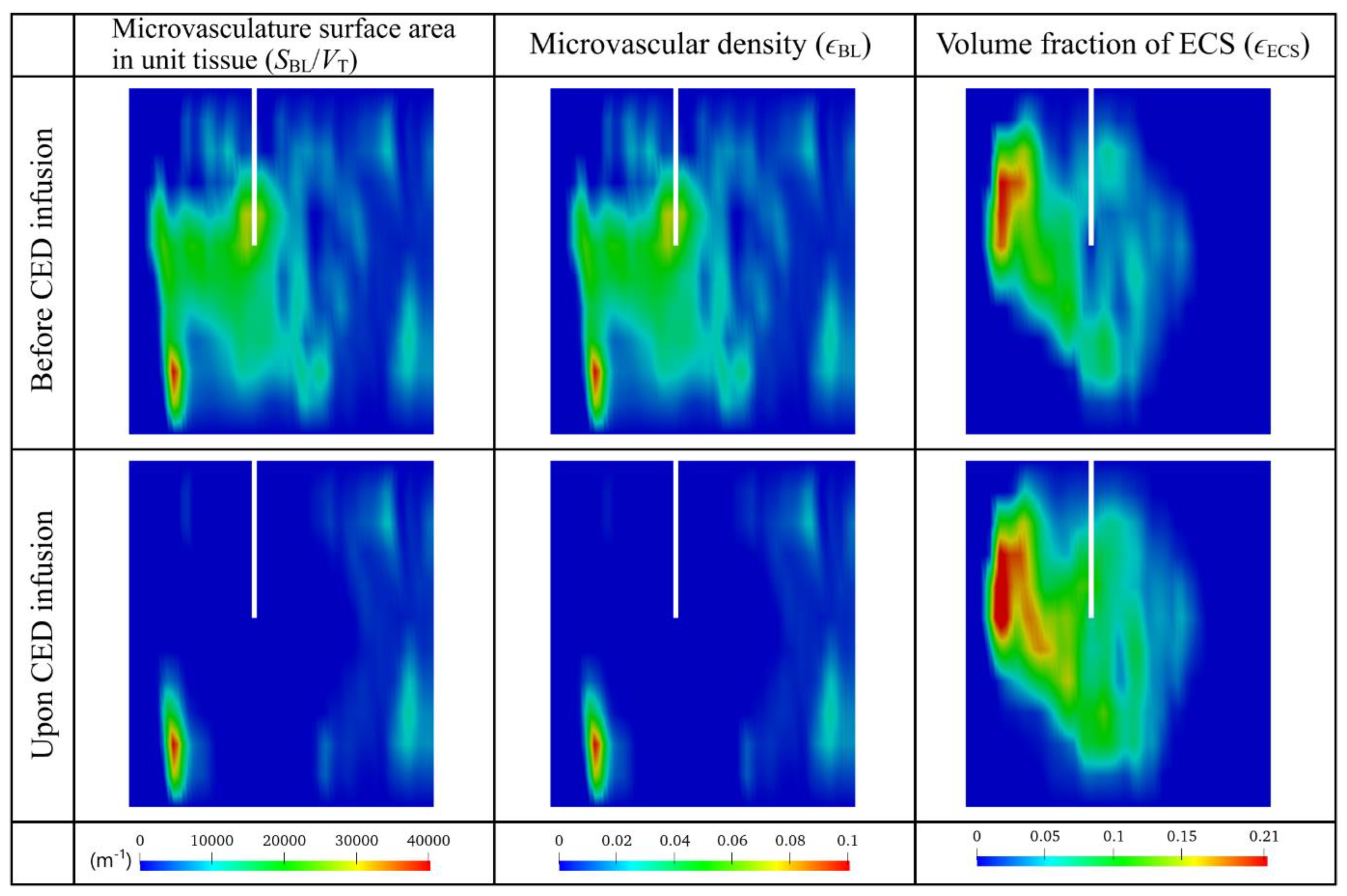
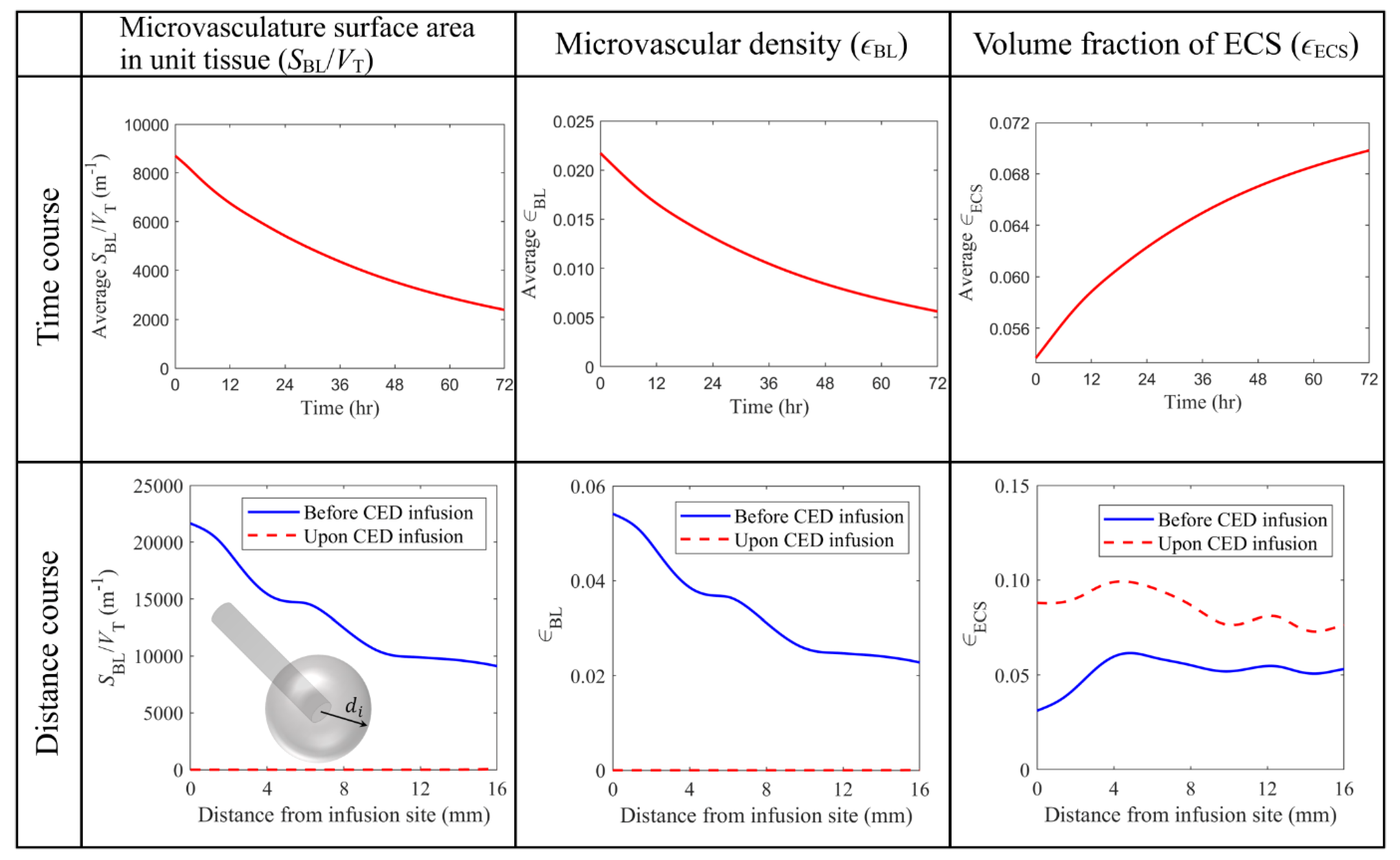
3.2.1. Antiangiogenic Effect
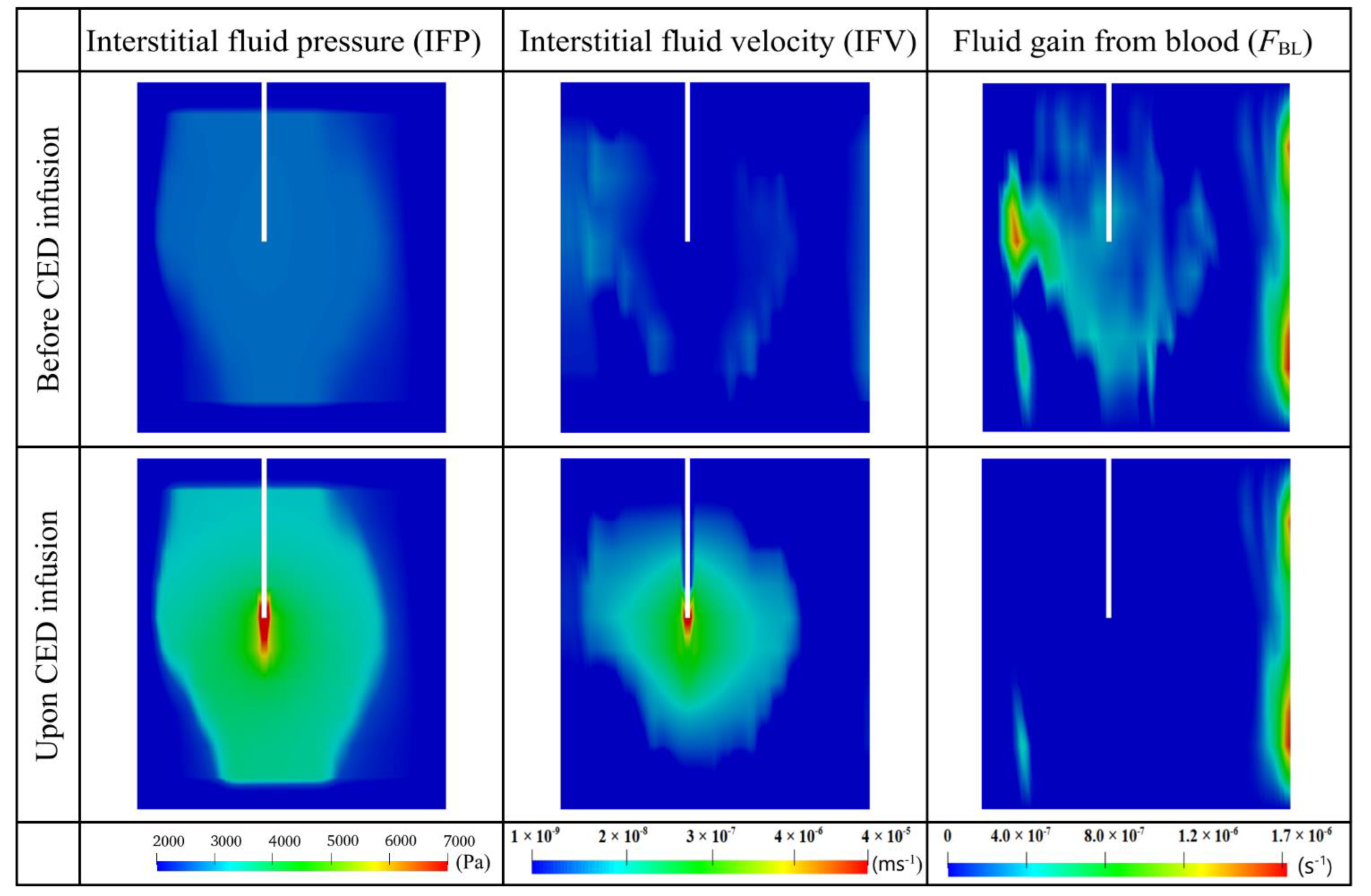
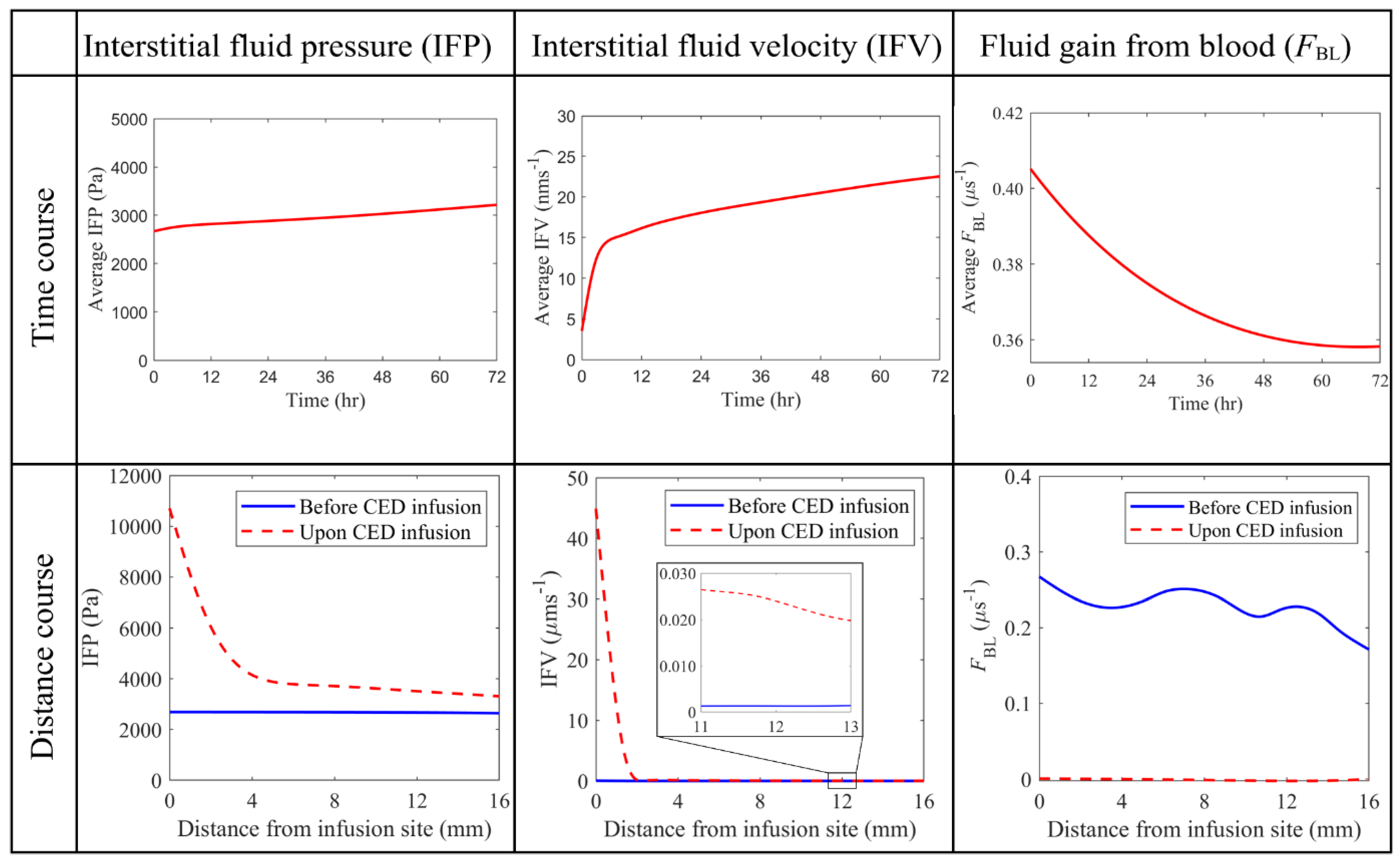
3.2.2. Interstitial Fluid Flow
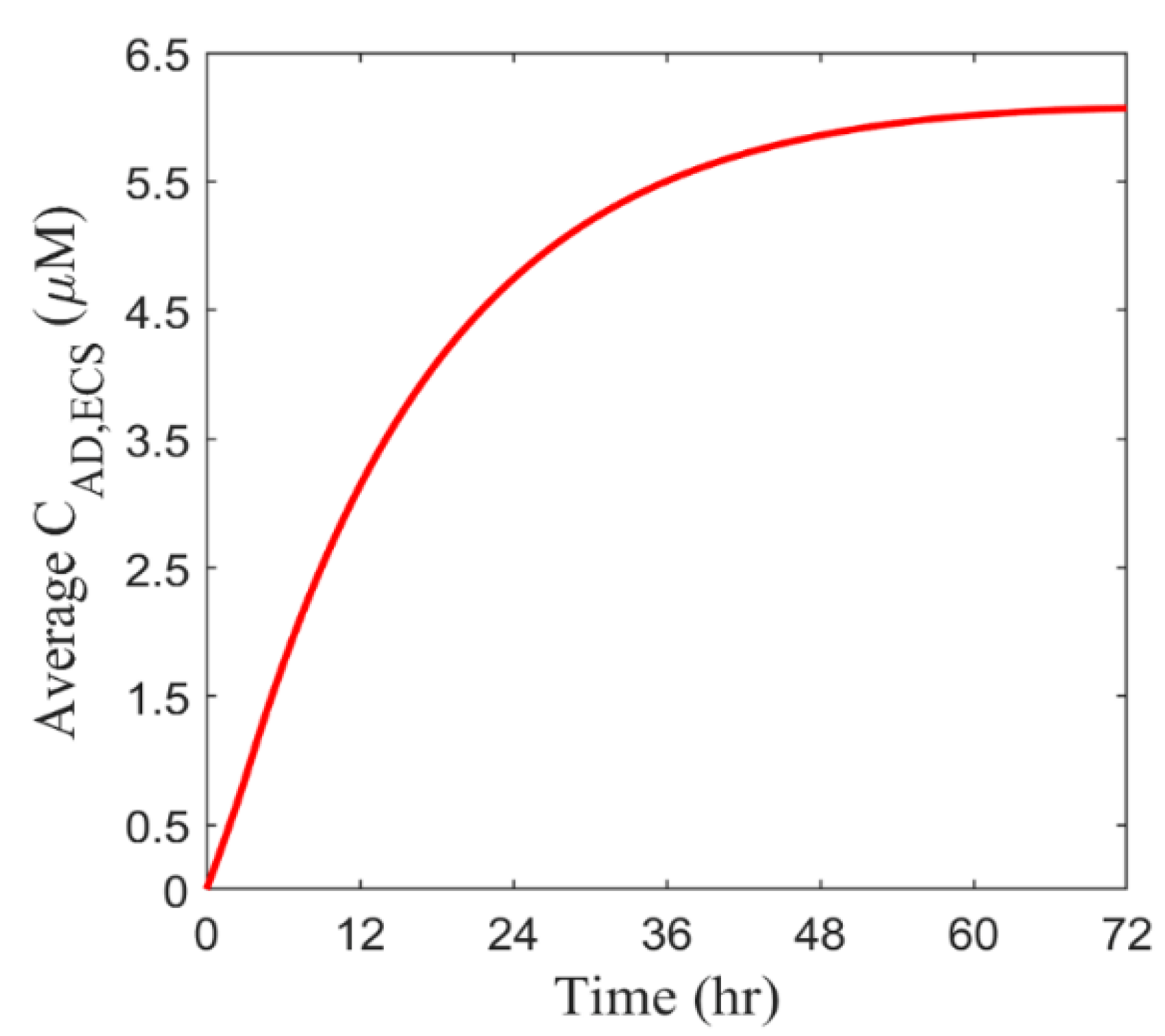
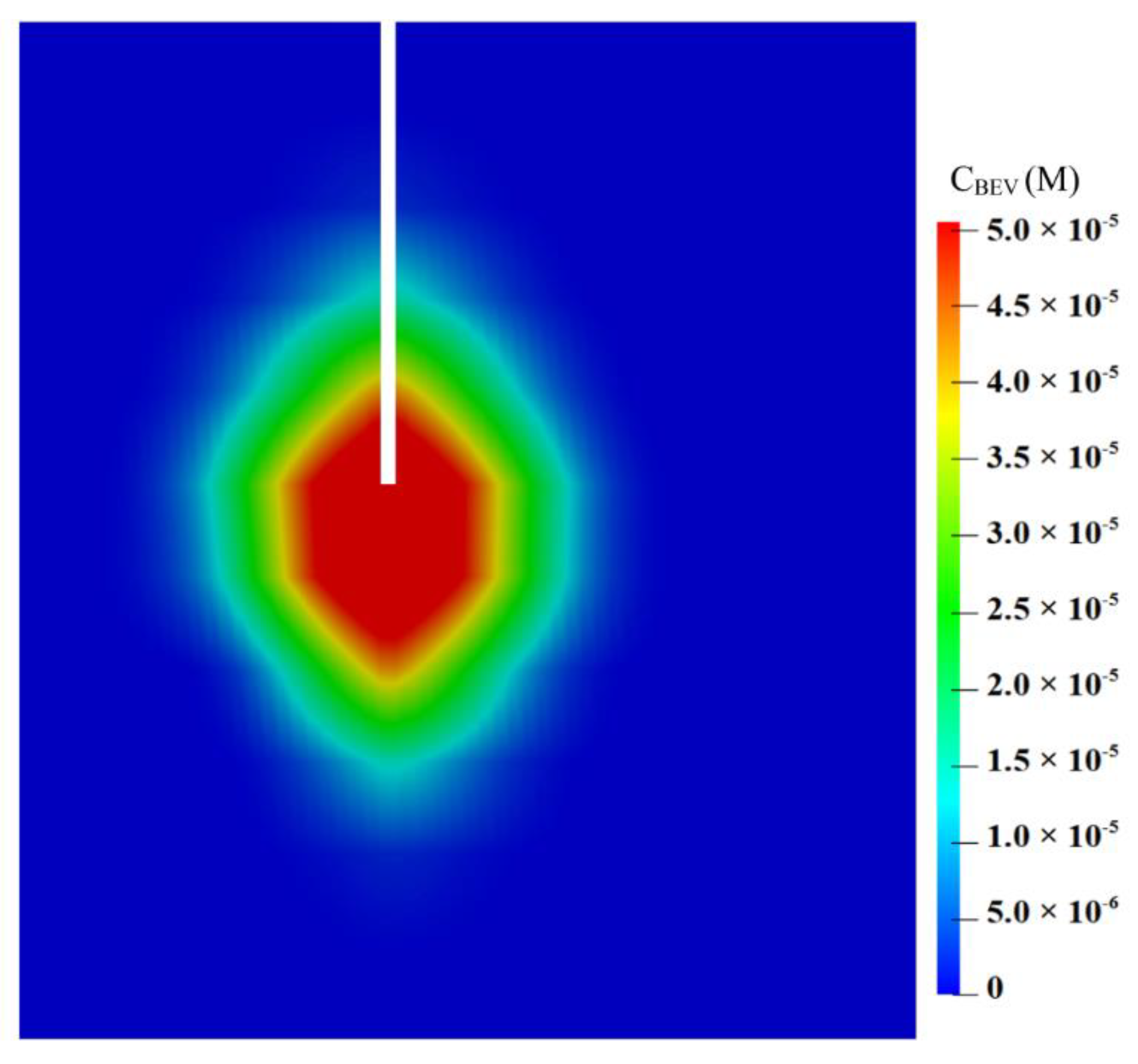
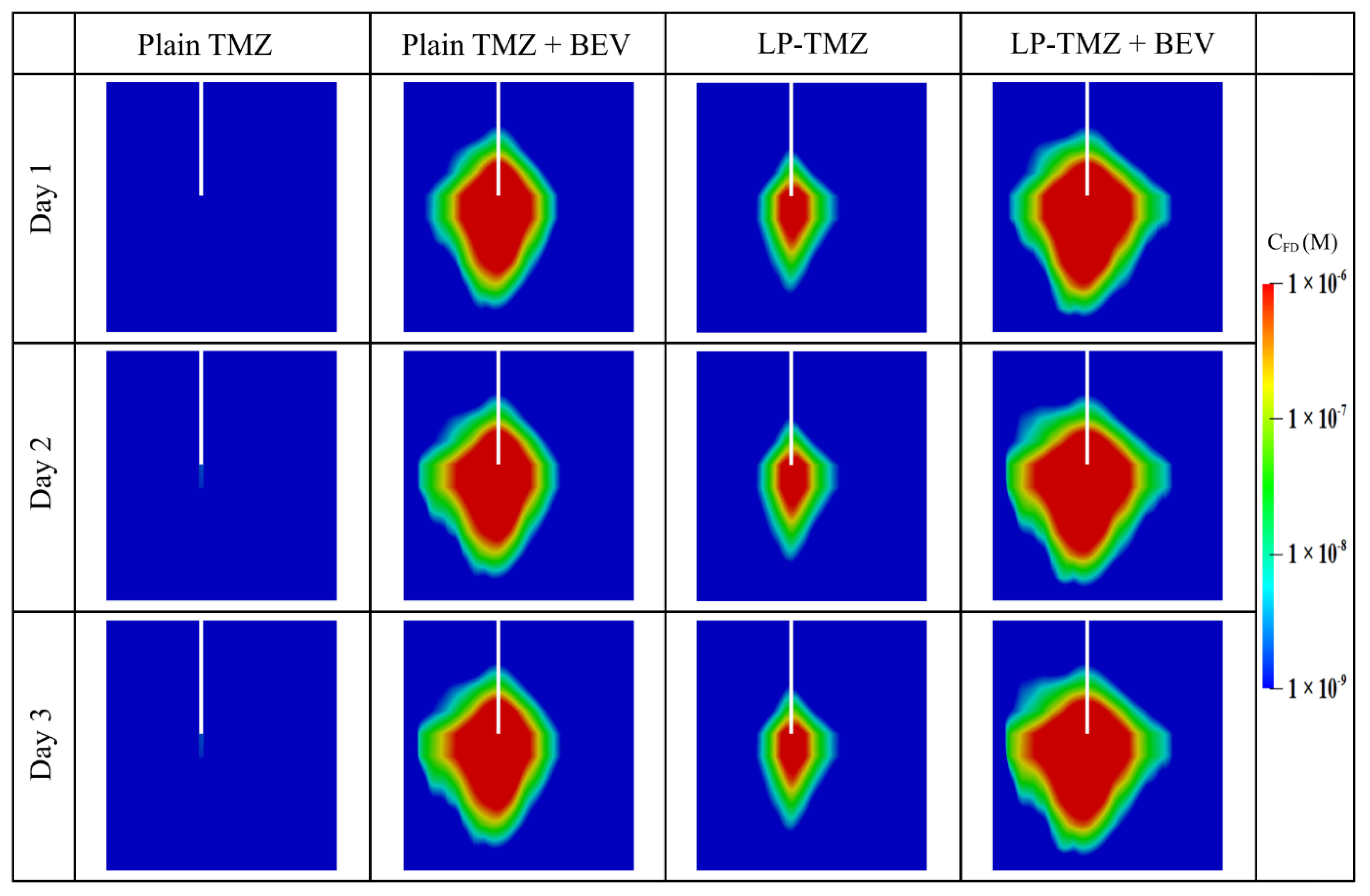
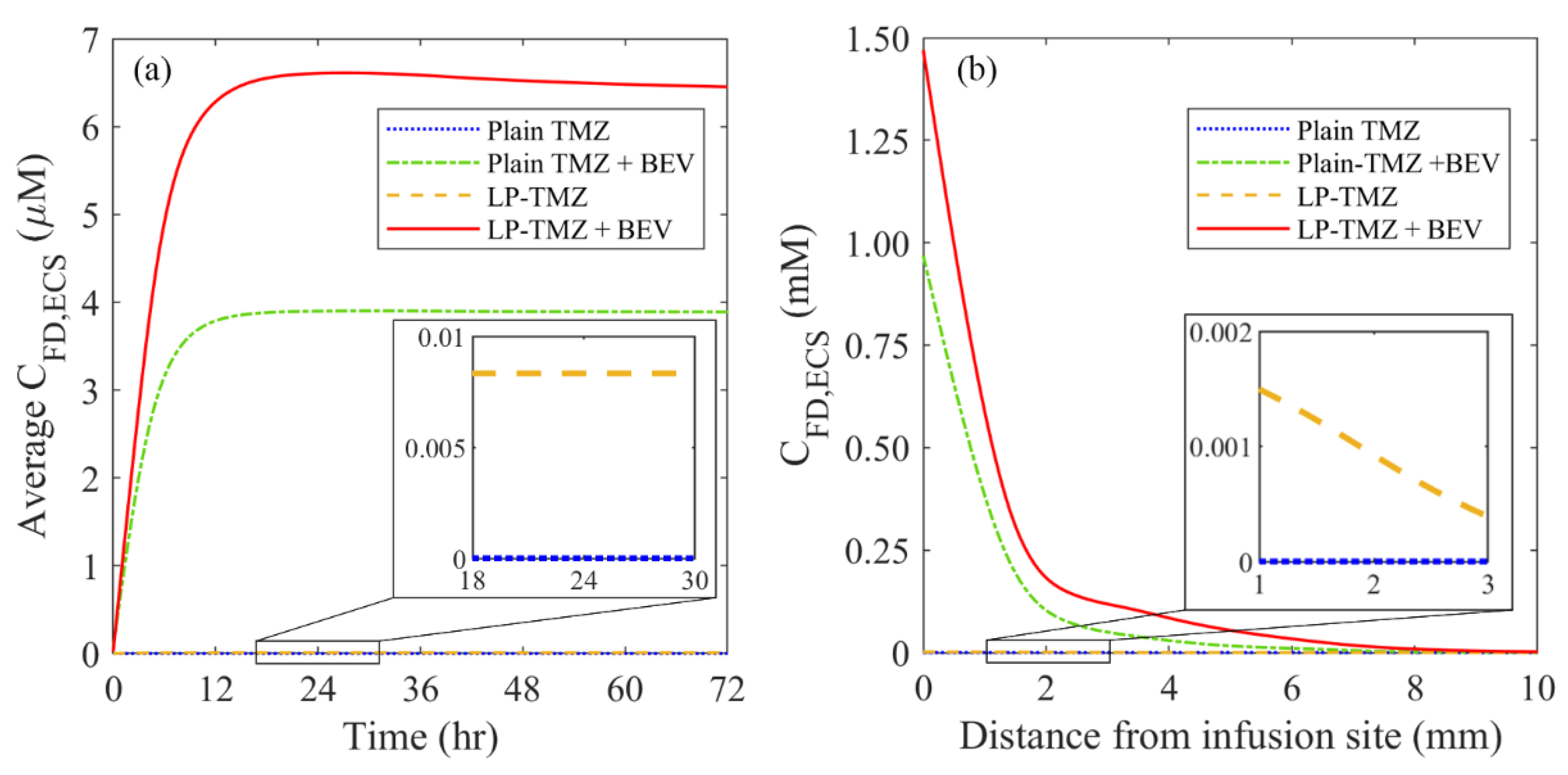
3.2.3. Drug Concentration
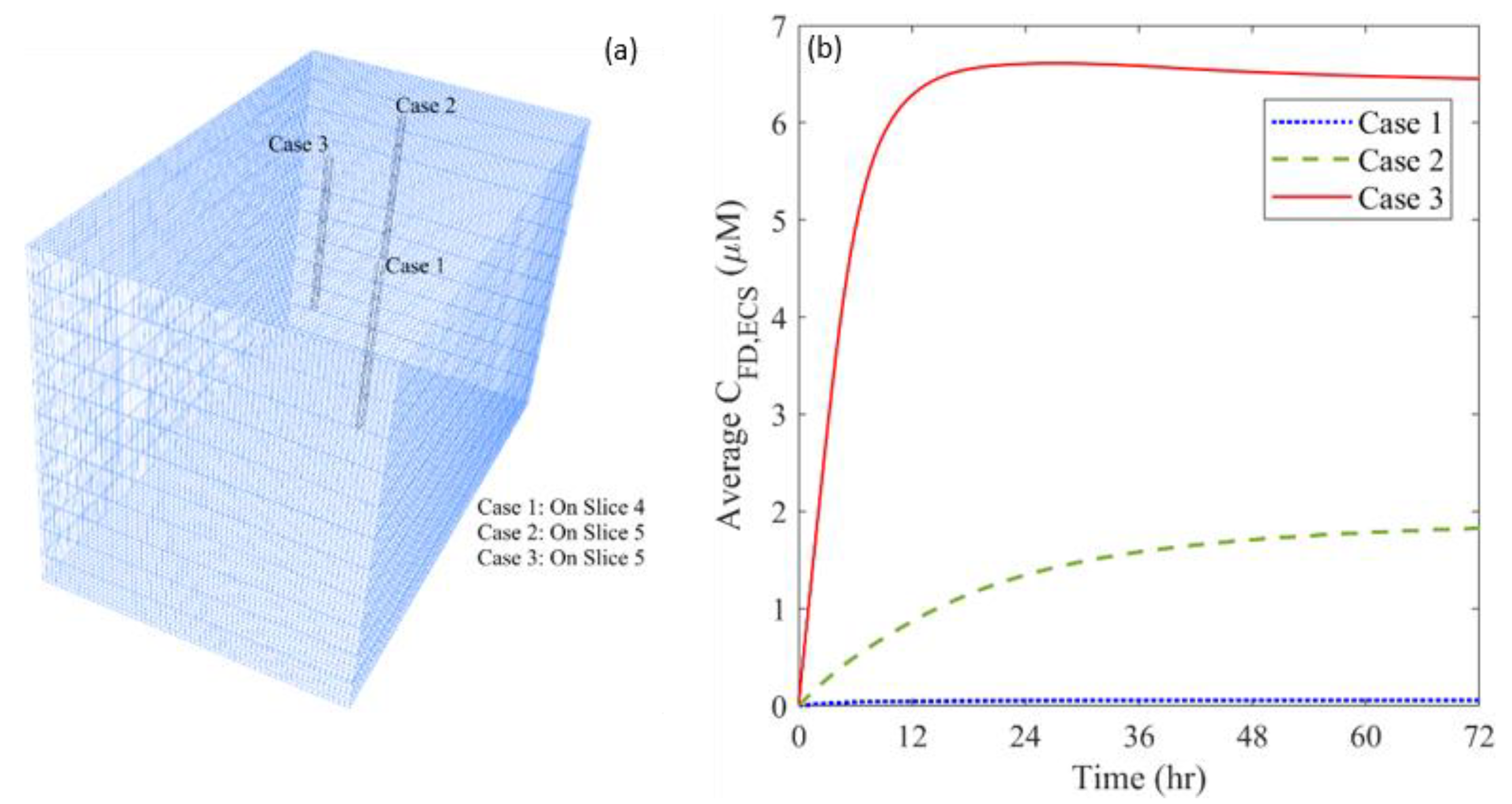
3.3. Effect of Heterogeneous Microvasculature
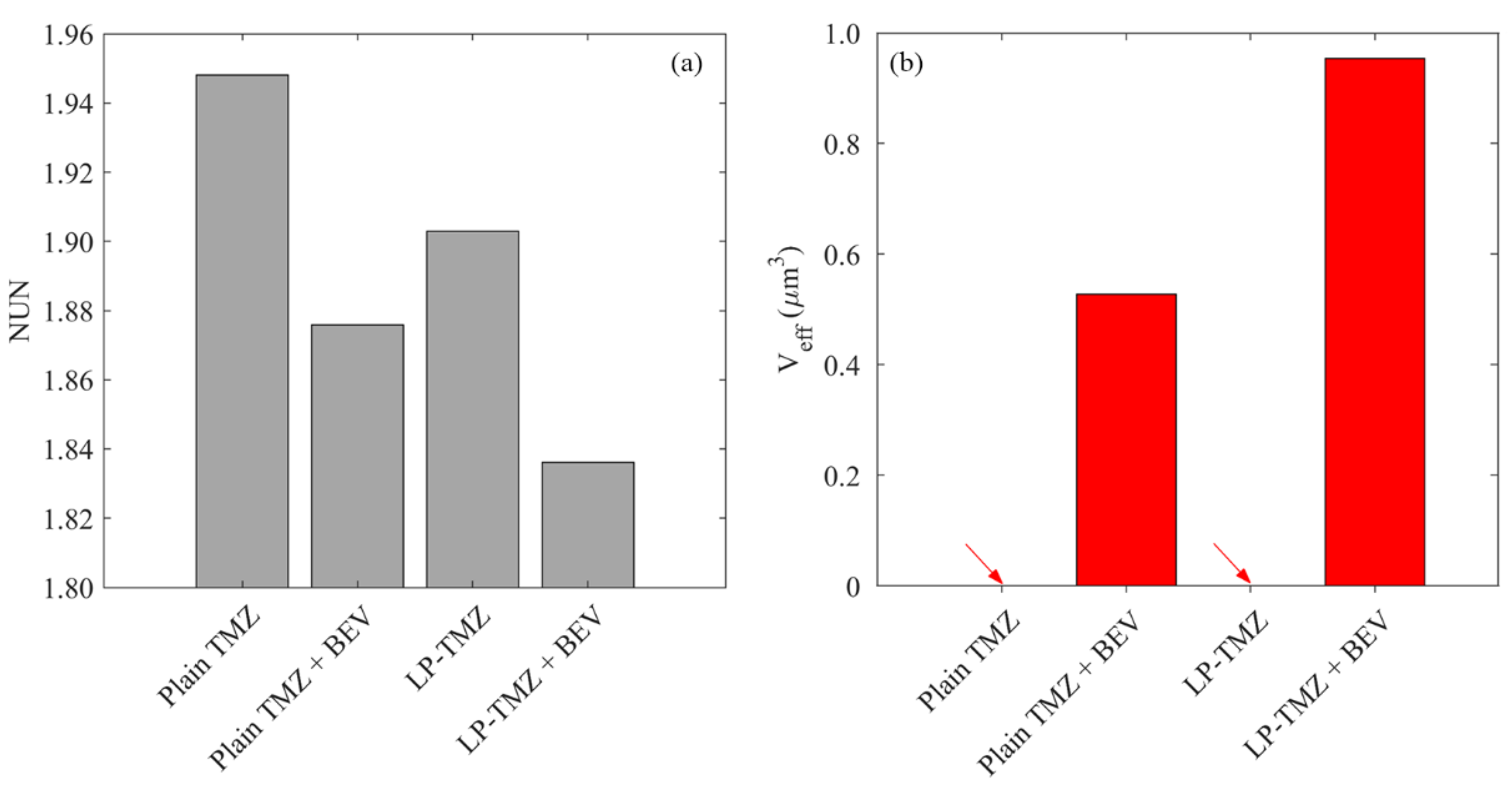
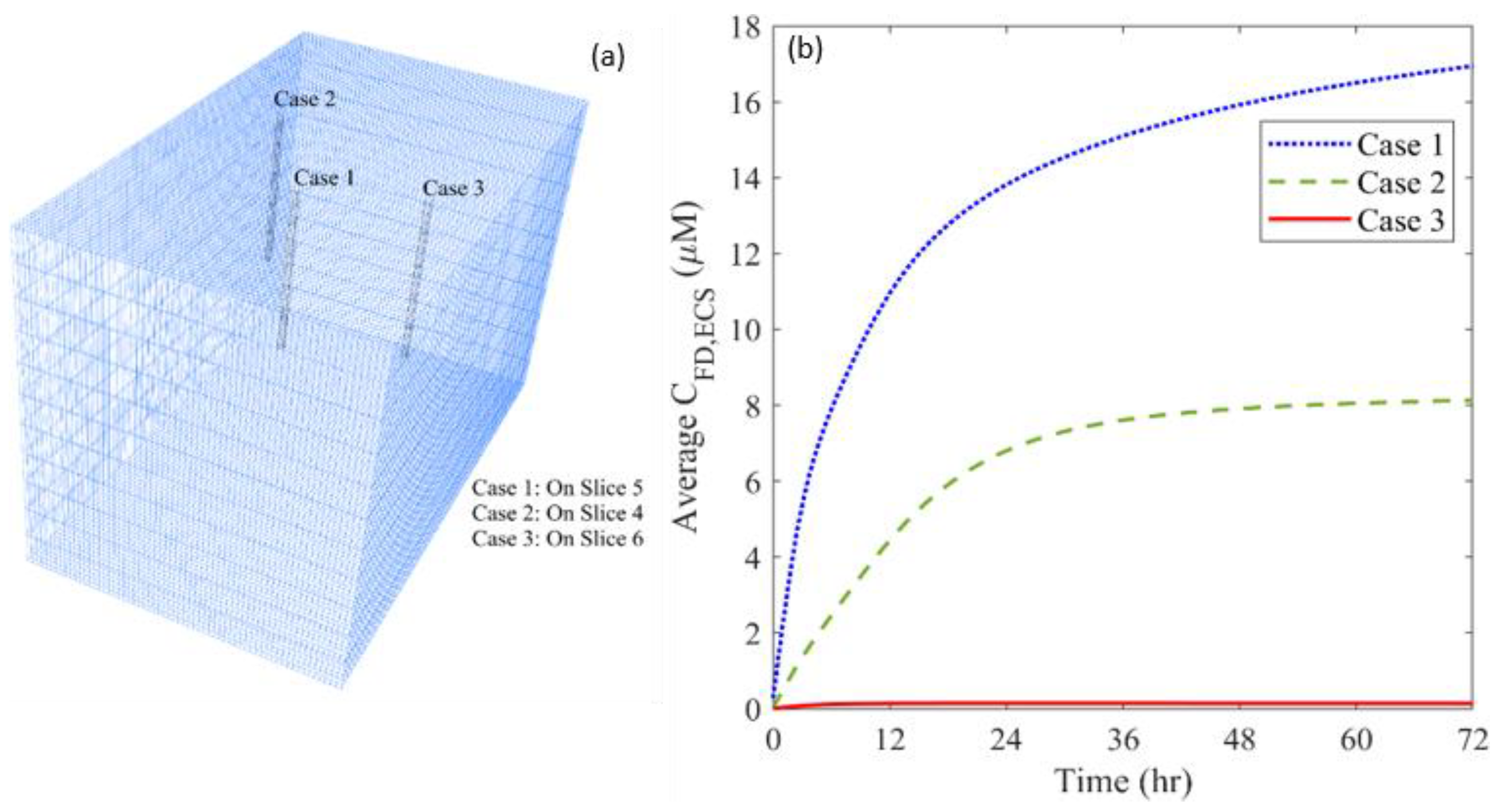
3.4. Effect of Heterogeneous Cell Density
4. Discussion
- (a)
- The insertion of a catheter into the brain tissue has the potential to result in trauma and oedema. The fluid generated from damaged cells and the enhanced leakage from damaged blood vessels [86] can alter the interstitial fluid flow and cause swelling of brain tissue. However, there is a lack of accurate models to describe such a physiochemical process. Moreover, since oedema eventually disappears and the tissue properties can get back to normal levels [87,88], the effect of oedema is not considered. The mathematical model needs to be developed with support from in vivo experiments to describe this process.
- (b)
- The antiangiogenic effect is reflected by the reduction of blood vessel diameter. Although blood vessels shirk significantly in response to the antiangiogenic drugs [66], both the vessel diameter and length can change [67]. Disappointingly, there is no such model to define the relationship between the changes in morphological characteristics of microvasculature and the antiangiogenic drug concentration. For improvement, results from microscale studies on the dynamic changes of blood vessels in antiangiogenic treatment will be needed for model development. In addition, modelling on the capillary level can be applied to predict the dynamic response of the microvascular network to the antiangiogenic drugs [89,90], which would shed light on the development of the combination therapy.
- (c)
- Drug diffusivity can also be location-dependent in a brain tumor, subject to the local in vivo environment. This variation of drug property can also affect drug transport and accumulation. However, the diffusivity of each drug is assumed to be uniform in the brain tumor in this study due to the lack of relevant information that can be extracted from the applied medical images. This assumption can be relaxed by using diffusion-weighted MR images [91], where the signal intensity is related to the diffusivity of water molecules.
- (d)
- Liposome cell uptake is ignored in this study owing to its complex nature. This process is controlled by several factors including particle size [92], ligands [93] and/or energy consumption [94,95]. A bespoken model needs to be developed to describe this process when focusing on a specific type of liposome.
- (e)
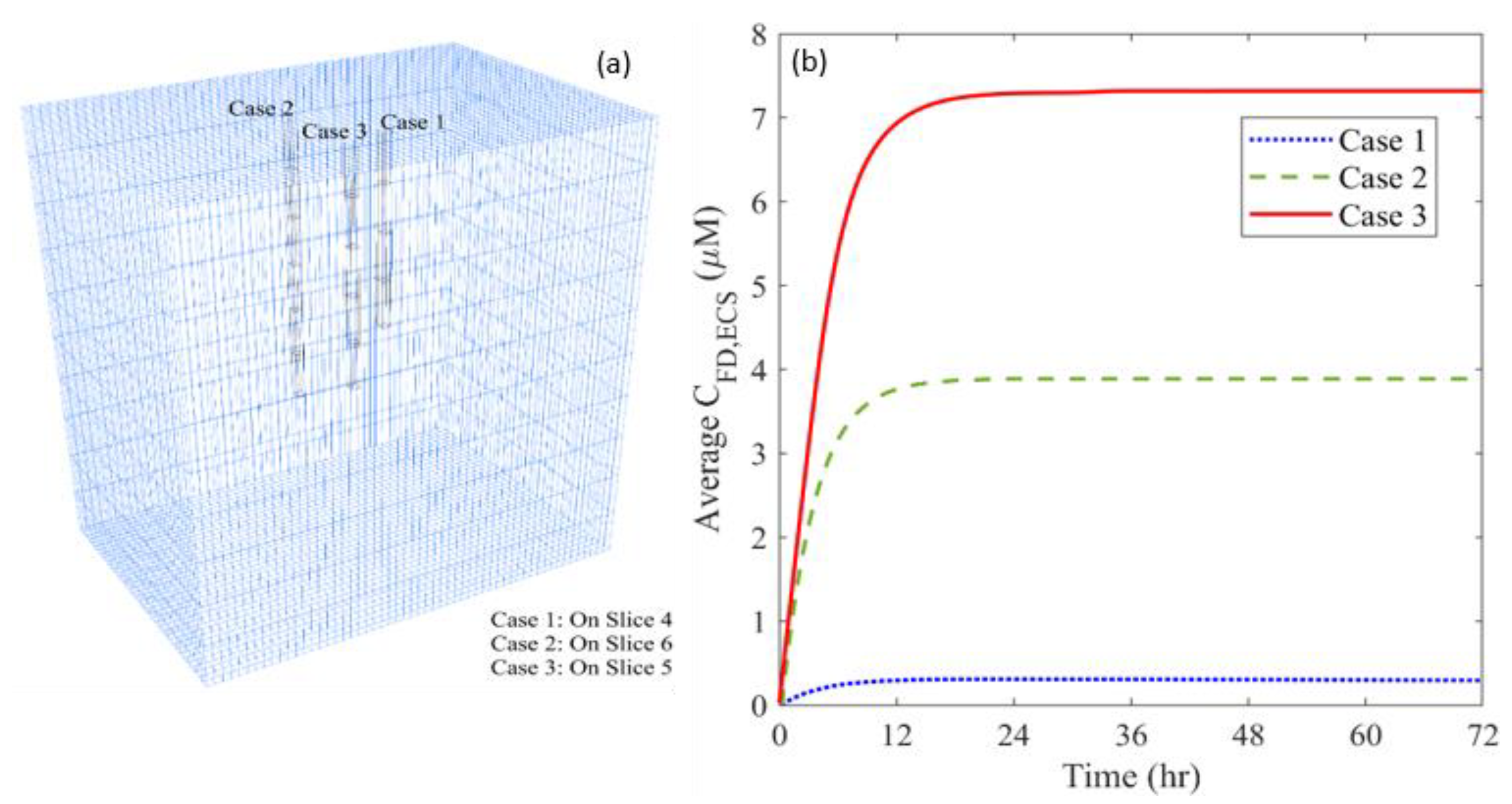
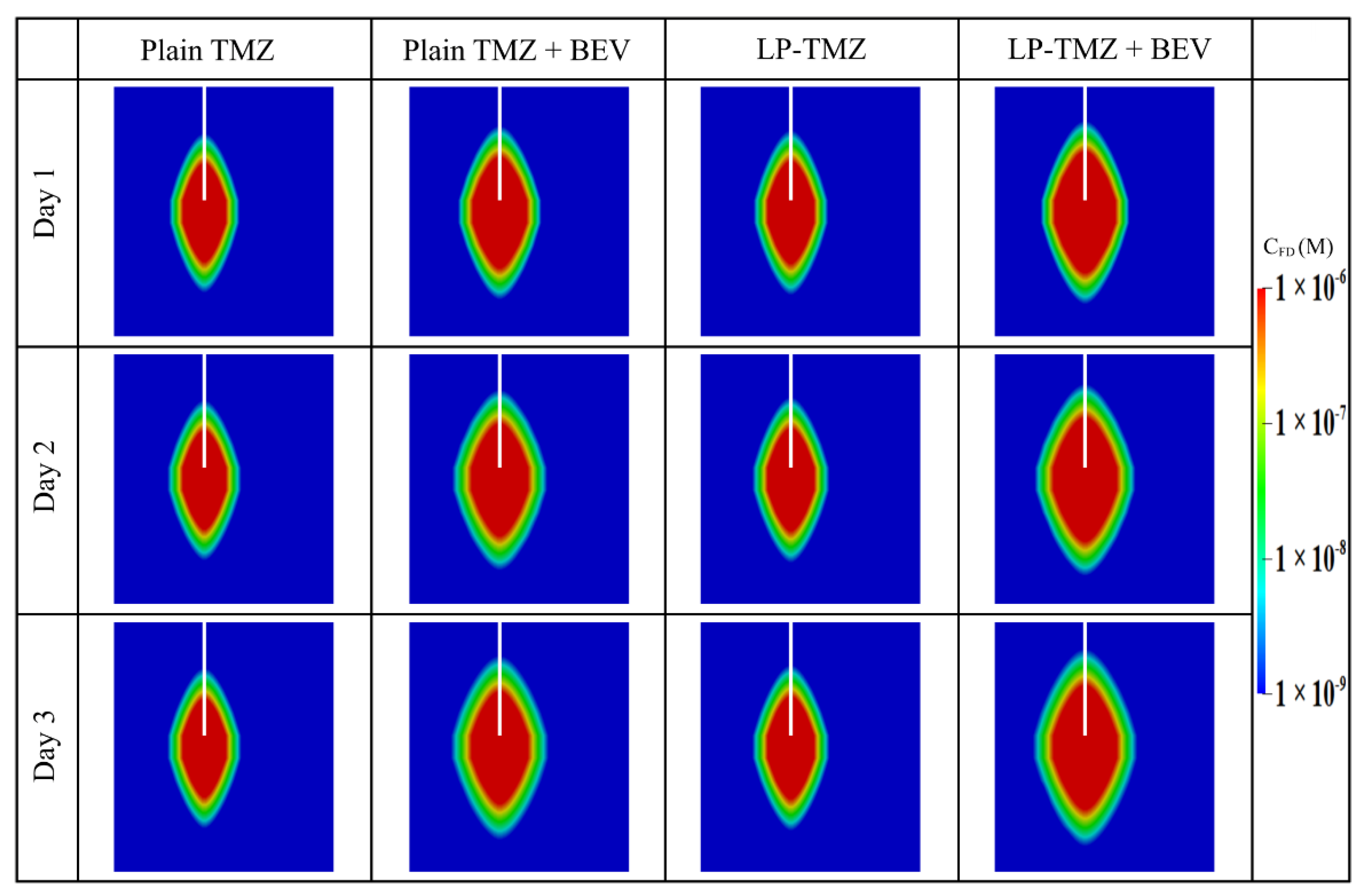
- Only one catheter is placed in this study to examine the effectiveness of combination therapy in treating heterogeneous brain tumors. However, it is important to note that the cytotoxic drugs can penetrate a short distance from the infusion site; it is approximately 8 mm, as shown in Figure 12. This limited penetration depth results in highly localized cell killing, which is less effective for treating large tumors. In practice, it becomes more common to use multiple catheters [96] or a catheter with multiple injection-ports [97] simultaneously to enlarge the coverage of the drug to the tumor for better treatment outcomes. In this regard, the arrangement of catheters, the infusion directions and locations will be the key and worthy of in-depth study in the future.
- (f)
- The infusate administrated into the brain tumor is able to push the soft tissue back to form backflow. Drugs in the backflow would transport along the track of the infusion catheter to the normal tissue, reducing the treatment effectiveness. The formation of backflow depends on the infusion rate, tumor location and more importantly, the local tissue properties. Given the difficulty to obtain the heterogeneous tissue mechanical properties from the applied medical images, this phenomenon is not simulated in this study. This limitation can be overcome by incorporating the tissue mechanics model, solid-fluid interaction and corresponding tissue properties [27,98].
- (g)
- In the current study, the anti-angiogenetic and cytotoxic drugs were infused simultaneously inside the brain tumor due to the lack of clinical information regarding their infusion timings. Future studies in this direction should attempt to optimize the infusion schedule between antiangiogenetic and cytotoxic treatment to maximize the therapeutic output.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Modelling Using Patient 2′s Data
Appendix A.1. Tumor Geometry and Tissue Properties
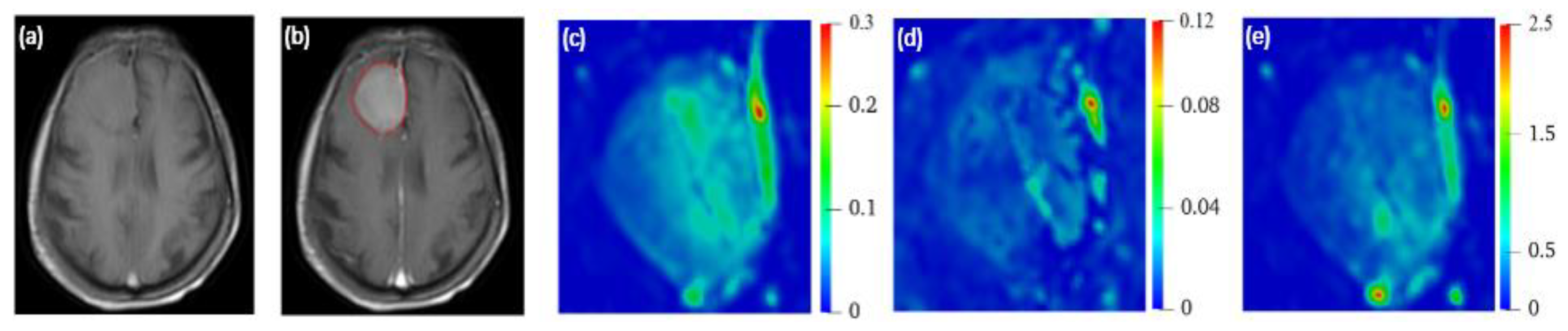
Appendix A.2. Baseline Study
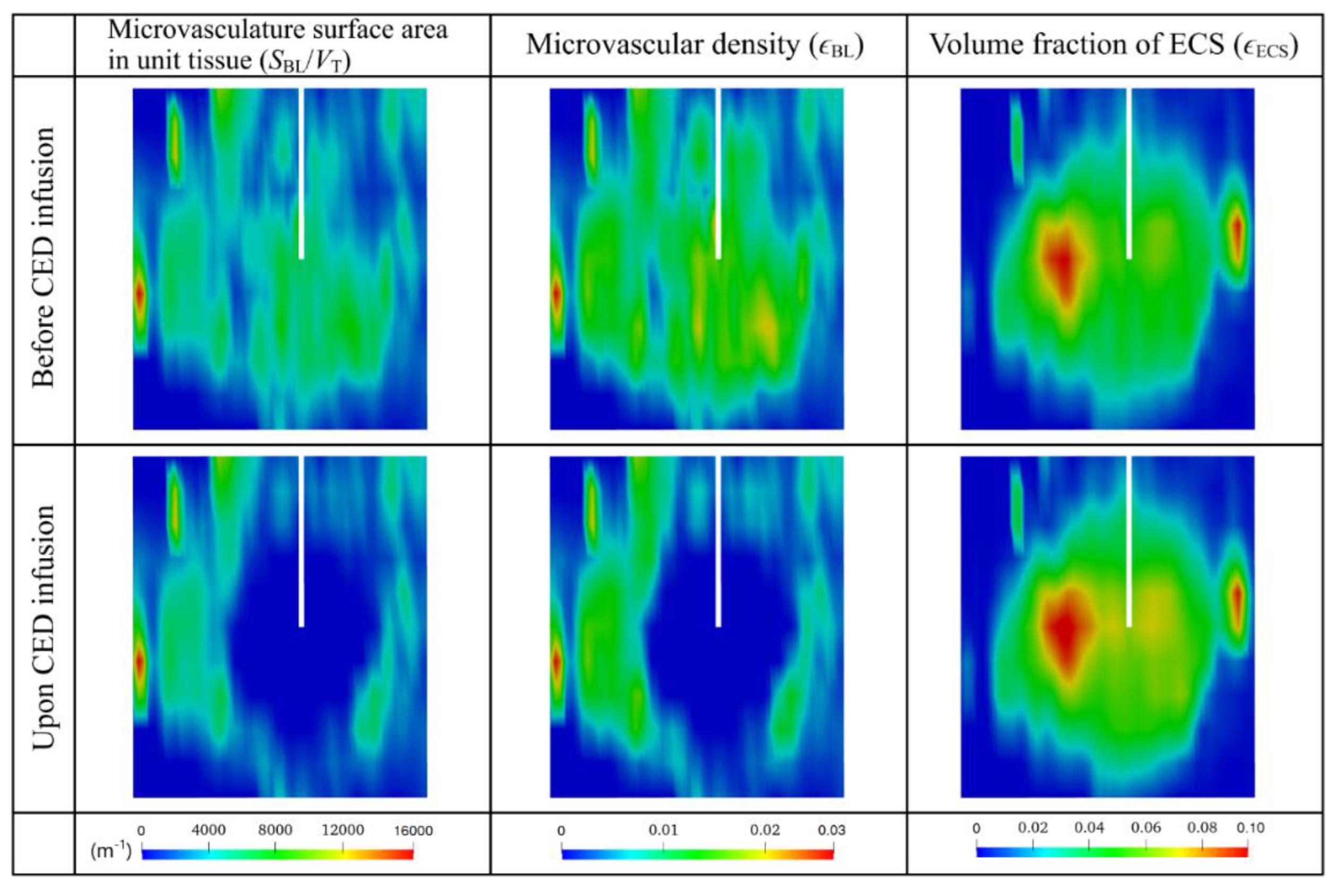


Appendix A.3. Effect of Microvascular Density
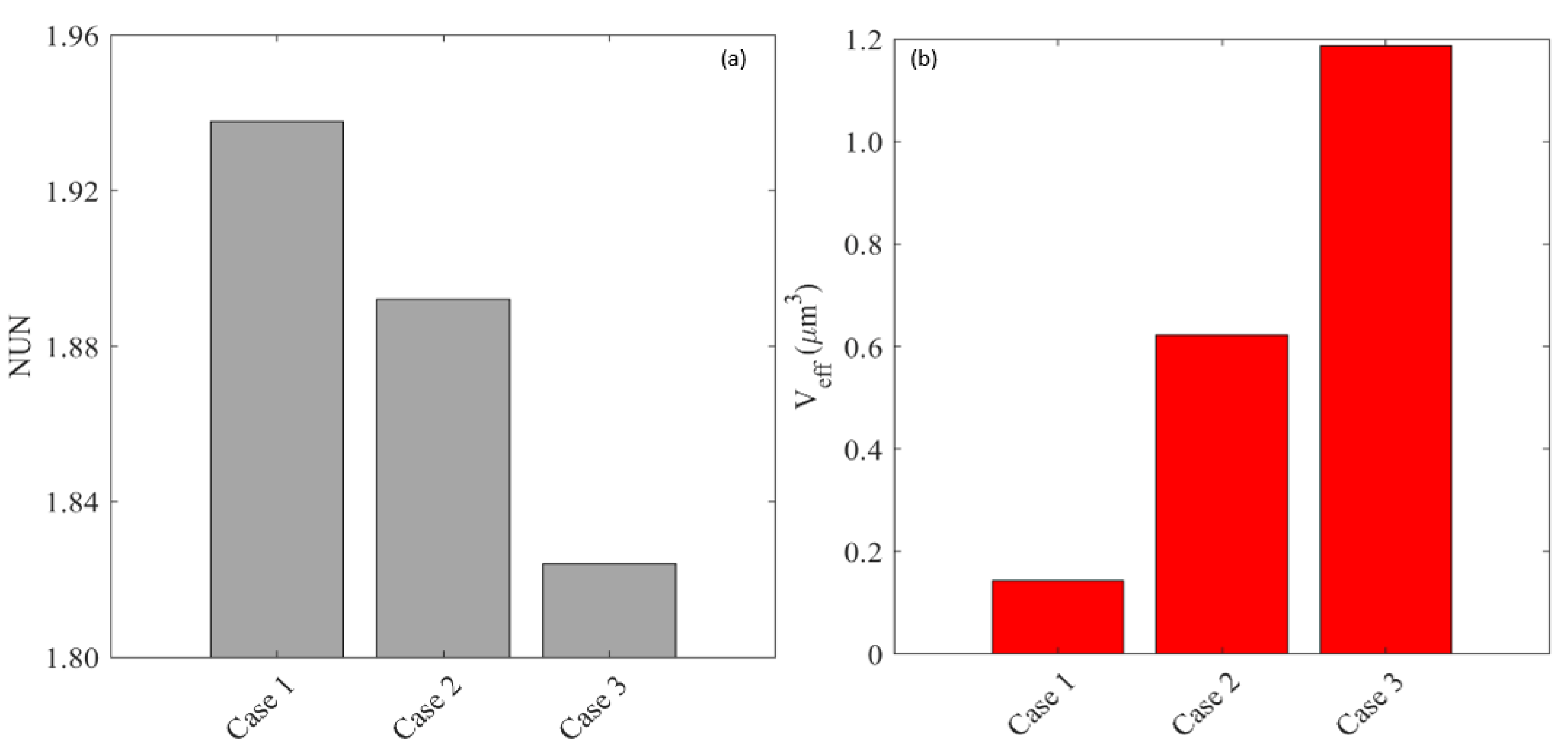
Appendix A.4. Effect of Cell Density

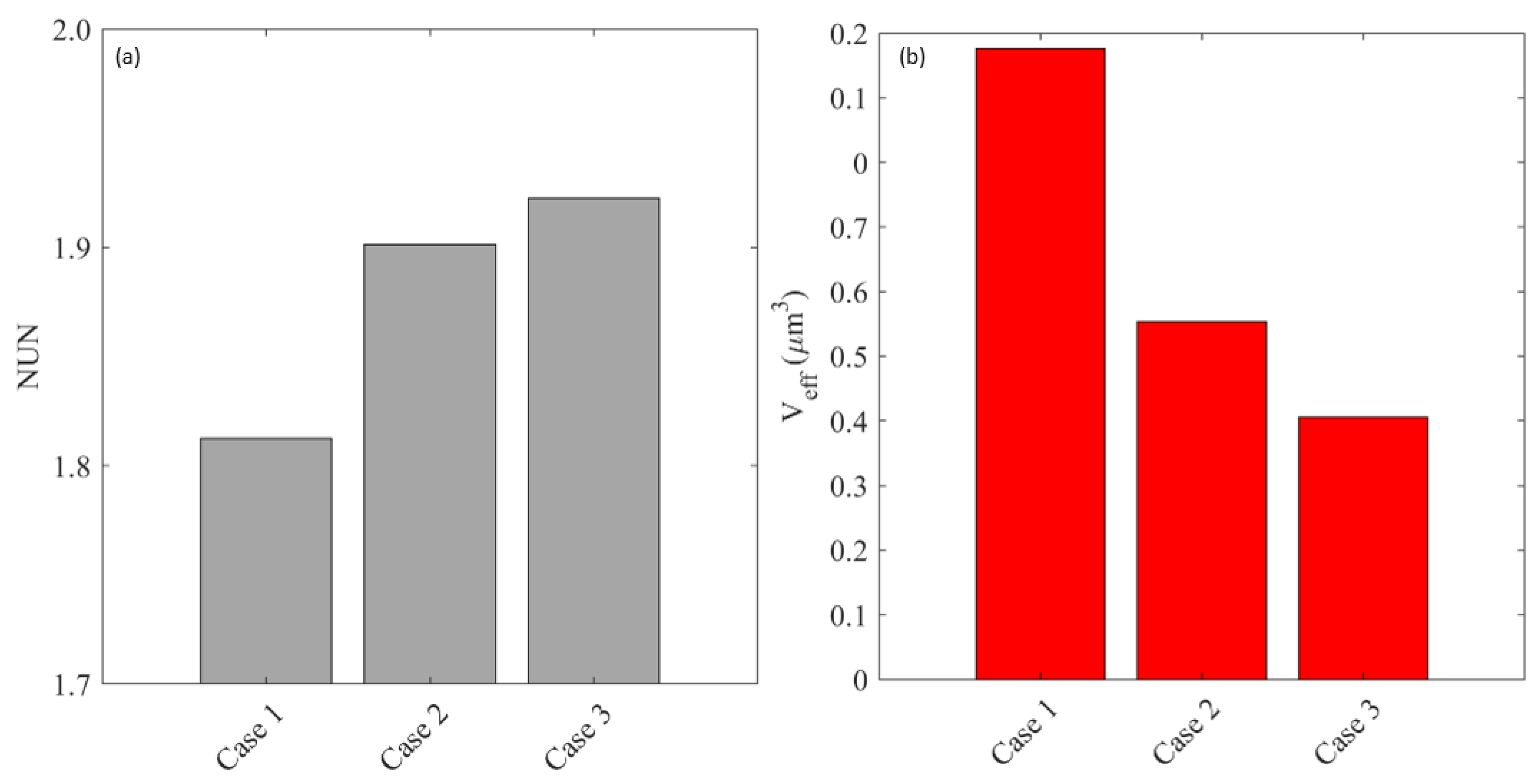
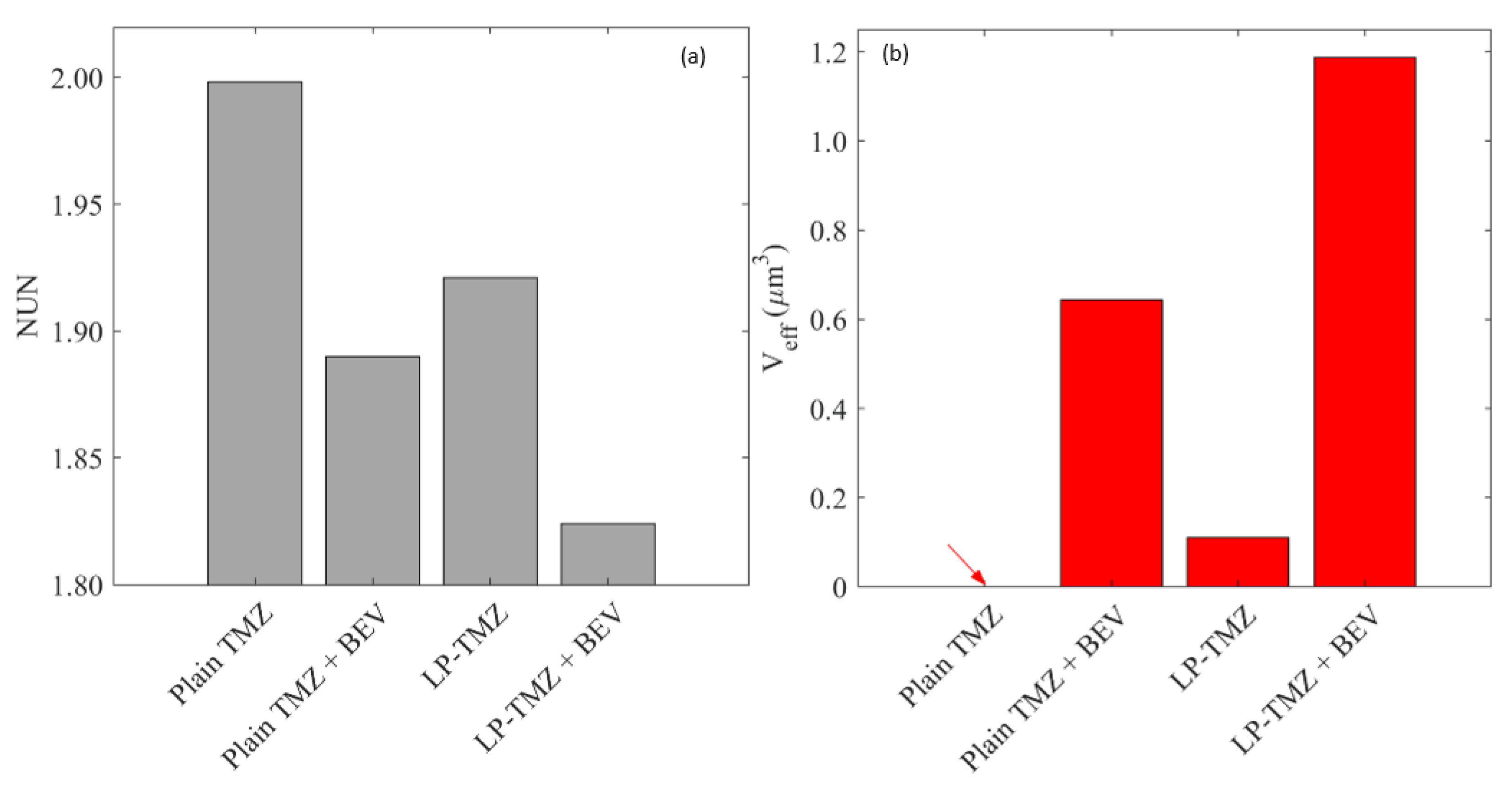
Appendix B. Impact of the Assumption of Homogeneous Tissue Properties
References
- Wild, C.P.; Stewart, B.W.; Wild, C. World Cancer Report 2014; World Health Organization: Geneva, Switzerland, 2014. [Google Scholar]
- Louis, D.N.; Perry, A.; Reifenberger, G.; Von Deimling, A.; Figarella-Branger, D.; Cavenee, W.K.; Ohgaki, H.; Wiestler, O.D.; Kleihues, P.; Ellison, D.W. The 2016 World Health Organization classification of tumors of the central nervous system: A summary. Acta Neuropathol. 2016, 131, 803–820. [Google Scholar] [CrossRef] [PubMed]
- Ostrom, Q.T.; McCulloh, C.; Chen, Y.; Devine, K.; Wolinsky, Y.; Davitkov, P.; Robbins, S.; Cherukuri, R.; Patel, A.; Gupta, R. Family history of cancer in benign brain tumor subtypes versus gliomas. Front. Oncol. 2012, 2, 19. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.I.; Beg, S.; Samad, A.; Baboota, S.; Kohli, K.; Ali, J.; Ahuja, A.; Akbar, M. Strategy for effective brain drug delivery. Eur. J. Pharm. Sci. 2010, 40, 385–403. [Google Scholar] [CrossRef] [PubMed]
- Lonser, R.R.; Sarntinoranont, M.; Morrison, P.F.; Oldfield, E.H. Convection-enhanced delivery to the central nervous system. J. Neurosurg. 2015, 122, 697–706. [Google Scholar] [CrossRef]
- Groothuis, D.R. The blood-brain and blood-tumor barriers: A review of strategies for increasing drug delivery. Neuro-Oncol. 2000, 2, 45–59. [Google Scholar] [CrossRef]
- Raghavan, R.; Brady, M.L.; Rodríguez-Ponce, M.I.; Hartlep, A.; Pedain, C.; Sampson, J.H. Convection-enhanced delivery of therapeutics for brain disease, and its optimization. Neurosurg. Focus 2006, 20, E12. [Google Scholar] [CrossRef]
- Jain, R.K. Transport of molecules in the tumor interstitium: A review. Cancer Res. 1987, 47, 3039–3051. [Google Scholar]
- Wei, X.; Meel, M.H.; Breur, M.; Bugiani, M.; Hulleman, E.; Phoenix, T.N. Defining tumor-associated vascular heterogeneity in pediatric high-grade and diffuse midline gliomas. Acta Neuropathol. Commun. 2021, 9, 1–18. [Google Scholar] [CrossRef]
- Jain, R.K.; Di Tomaso, E.; Duda, D.G.; Loeffler, J.S.; Sorensen, A.G.; Batchelor, T.T. Angiogenesis in brain tumours. Nat. Rev. Neurosci. 2007, 8, 610–622. [Google Scholar] [CrossRef]
- Saito, R.; Bringas, J.R.; McKnight, T.R.; Wendland, M.F.; Mamot, C.; Drummond, D.C.; Kirpotin, D.B.; Park, J.W.; Berger, M.S.; Bankiewicz, K.S. Distribution of liposomes into brain and rat brain tumor models by convection-enhanced delivery monitored with magnetic resonance imaging. Cancer Res. 2004, 64, 2572–2579. [Google Scholar] [CrossRef]
- Jain, R.K. Normalizing tumor vasculature with anti-angiogenic therapy: A new paradigm for combination therapy. Nat. Med. 2001, 7, 987–989. [Google Scholar] [CrossRef] [PubMed]
- Krauze, M.T.; Saito, R.; Noble, C.; Bringas, J.; Forsayeth, J.; Mcknight, T.R.; Park, J.; Bankiewicz, K.S. Effects of the perivascular space on convection-enhanced delivery of liposomes in primate putamen. Exp. Neurol. 2005, 196, 104–111. [Google Scholar] [CrossRef] [PubMed]
- Zhan, W.; Alamer, M.; Xu, X.Y. Computational modelling of drug delivery to solid tumour: Understanding the interplay between chemotherapeutics and biological system for optimised delivery system. Adv. Drug Deliv. Rev. 2018, 132, 81–103. [Google Scholar] [CrossRef]
- Harashima, H.; Tsuchihashi, M.; Iida, S.; Doi, H.; Kiwada, H. Pharmacokinetic/pharmacodynamic modeling of antitumor agents encapsulated into liposomes. Adv. Drug Deliv. Rev. 1999, 40, 39–61. [Google Scholar] [CrossRef]
- Akalın, A.A.; Dedekargınoğlu, B.; Choi, S.R.; Han, B.; Ozcelikkale, A. Predictive Design and Analysis of Drug Transport by MultiScale Computational Models Under Uncertainty. Pharm. Res. 2022, 39, 1–23. [Google Scholar] [CrossRef]
- Baxter, L.T.; Jain, R.K. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvasc. Res. 1989, 37, 77–104. [Google Scholar] [CrossRef]
- Baxter, L.T.; Jain, R.K. Transport of fluid and macromolecules in tumors. II. Role of heterogeneous perfusion and lymphatics. Microvasc. Res. 1990, 40, 246–263. [Google Scholar] [CrossRef]
- Baxter, L.T.; Jain, R.K. Transport of fluid and macromolecules in tumors: III. Role of binding and metabolism. Microvasc. Res. 1991, 41, 5–23. [Google Scholar] [CrossRef]
- Sefidgar, M.; Soltani, M.; Raahemifar, K.; Bazmara, H.; Nayinian, S.M.M.; Bazargan, M. Effect of tumor shape, size, and tissue transport properties on drug delivery to solid tumors. J. Biol. Eng. 2014, 8, 12–24. [Google Scholar] [CrossRef]
- Zhan, W.; Gedroyc, W.; Xu, X.Y. Towards a multiphysics modelling framework for thermosensitive liposomal drug delivery to solid tumour combined with focused ultrasound hyperthermia. Biophys. Rep. 2019, 5, 43–59. [Google Scholar] [CrossRef]
- Arifin, D.Y.; Lee, K.Y.T.; Wang, C.-H. Chemotherapeutic drug transport to brain tumor. J. Control. Release 2009, 137, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Arifin, D.Y.; Lee, K.Y.T.; Wang, C.-H.; Smith, K.A. Role of convective flow in carmustine delivery to a brain tumor. Pharm. Res. 2009, 26, 2289–2302. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, R.; Brady, M. Predictive models for pressure-driven fluid infusions into brain parenchyma. Phys. Med. Biol. 2011, 56, 6179–6205. [Google Scholar] [CrossRef] [PubMed]
- Zhan, W.; Wang, C.-H. Convection enhanced delivery of liposome encapsulated doxorubicin for brain tumour therapy. J. Control. Release 2018, 285, 212–229. [Google Scholar] [CrossRef]
- Karolak, A.; Markov, D.A.; McCawley, L.J.; Rejniak, K.A. Towards personalized computational oncology: From spatial models of tumour spheroids, to organoids, to tissues. J. R. Soc. Interface 2018, 15, 20170703. [Google Scholar] [CrossRef]
- Orozco, G.A.; Smith, J.H.; García, J.J. Three-dimensional nonlinear finite element model to estimate backflow during flow-controlled infusions into the brain. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2020, 234, 1018–1028. [Google Scholar] [CrossRef]
- Rosenbluth, K.H.; Eschermann, J.F.; Mittermeyer, G.; Thomson, R.; Mittermeyer, S.; Bankiewicz, K.S. Analysis of a simulation algorithm for direct brain drug delivery. Neuroimage 2012, 59, 2423–2429. [Google Scholar] [CrossRef]
- Woodall, R.T.; Hormuth, D.A., II; Wu, C.; Abdelmalik, M.R.; Phillips, W.T.; Bao, A.; Hughes, T.J.; Brenner, A.J.; Yankeelov, T.E. Patient specific, imaging-informed modeling of rhenium-186 nanoliposome delivery via convection-enhanced delivery in glioblastoma multiforme. Biomed. Phys. Eng. Express 2021, 7, 045012. [Google Scholar] [CrossRef]
- Zhao, J.; Salmon, H.; Sarntinoranont, M. Effect of heterogeneous vasculature on interstitial transport within a solid tumor. Microvasc. Res. 2007, 73, 224–236. [Google Scholar] [CrossRef]
- Zhan, W.; Gedroyc, W.; Xu, X.Y. Effect of heterogeneous microvasculature distribution on drug delivery to solid tumour. J. Phys. D Appl. Phys. 2014, 47, 475401. [Google Scholar] [CrossRef]
- Bhandari, A.; Bansal, A.; Singh, A.; Gupta, R.K.; Sinha, N. Comparison of transport of chemotherapeutic drugs in voxelized heterogeneous model of human brain tumor. Microvasc. Res. 2019, 124, 76–90. [Google Scholar] [CrossRef] [PubMed]
- Su, D.; Ma, R.; Salloum, M.; Zhu, L. Multi-scale study of nanoparticle transport and deposition in tissues during an injection process. Med. Biol. Eng. Comput. 2010, 48, 853–863. [Google Scholar] [CrossRef] [PubMed]
- Zhan, W. Convection enhanced delivery of anti-angiogenic and cytotoxic agents in combination therapy against brain tumour. Eur. J. Pharm. Sci. 2020, 141, 105094. [Google Scholar] [CrossRef] [PubMed]
- Linninger, A.A.; Somayaji, M.R.; Mekarski, M.; Zhang, L. Prediction of convection-enhanced drug delivery to the human brain. J. Theor. Biol. 2008, 250, 125–138. [Google Scholar] [CrossRef]
- Less, J.R.; Skalak, T.C.; Sevick, E.M.; Jain, R.K. Microvascular architecture in a mammary carcinoma: Branching patterns and vessel dimensions. Cancer Res. 1991, 51, 265–273. [Google Scholar]
- Huang, Y.; Gu, B.; Liu, C.; Stebbing, J.; Gedroyc, W.; Thanou, M.; Xu, X.Y. Thermosensitive Liposome-Mediated Drug Delivery in Chemotherapy: Mathematical Modelling for Spatio–temporal Drug Distribution and Model-Based Optimisation. Pharmaceutics 2019, 11, 637. [Google Scholar] [CrossRef]
- Eikenberry, S. A tumor cord model for doxorubicin delivery and dose optimization in solid tumors. Theor. Biol. Med. Model. 2009, 6, 16–35. [Google Scholar] [CrossRef]
- Saltzman, W.M.; Radomsky, M.L. Drugs released from polymers: Diffusion and elimination in brain tissue. Chem. Eng. Sci. 1991, 46, 2429–2444. [Google Scholar] [CrossRef]
- Zhan, W.; Arifin, D.Y.; Lee, T.K.; Wang, C.-H. Mathematical Modelling of Convection Enhanced Delivery of Carmustine and Paclitaxel for Brain Tumour Therapy. Pharm. Res. 2017, 34, 860–873. [Google Scholar] [CrossRef]
- Magdoom, K.N.; Pishko, G.L.; Rice, L.; Pampo, C.; Siemann, D.W.; Sarntinoranont, M. MRI-based computational model of heterogeneous tracer transport following local infusion into a mouse hind limb tumor. PLoS ONE 2014, 9, e89594. [Google Scholar]
- Bhandari, A.; Bansal, A.; Singh, A.; Sinha, N. Numerical study of transport of anticancer drugs in heterogeneous vasculature of human brain tumors using dynamic contrast enhanced-magnetic resonance imaging. J. Biomech. Eng. 2018, 140, 051010. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Haris, M.; Rathore, D.; Purwar, A.; Sarma, M.; Bayu, G.; Husain, N.; Rathore, R.K.S.; Gupta, R.K. Quantification of physiological and hemodynamic indices using T1 dynamic contrast-enhanced MRI in intracranial mass lesions. J. Magn. Reson. Imaging Off. J. Int. Soc. Magn. Reson. Med. 2007, 26, 871–880. [Google Scholar]
- Sahoo, P.; Rathore, R.K.; Awasthi, R.; Roy, B.; Verma, S.; Rathore, D.; Behari, S.; Husain, M.; Husain, N.; Pandey, C.M. Subcompartmentalization of extracellular extravascular space (EES) into permeability and leaky space with local arterial input function (AIF) results in improved discrimination between high-and low-grade glioma using dynamic contrast-enhanced (DCE) MRI. J. Magn. Reson. Imaging 2013, 38, 677–688. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, A.; Bansal, A.; Jain, R.; Singh, A.; Sinha, N. Effect of tumor volume on drug delivery in heterogeneous vasculature of human brain tumors. J. Eng. Sci. Med. Diagn. Ther. 2019, 2, 021004. [Google Scholar] [CrossRef]
- Bhandari, A.; Bansal, A.; Singh, A.; Sinha, N. Study of perfusion kinetics in human brain tumor using leaky tracer kinetic model of DCE-MRI data and CFD. In Advanced Computational Methods in Life System Modeling and Simulation; Springer: Berlin, Germany, 2017; pp. 63–73. [Google Scholar]
- Singh, A.; Rathore, R.K.S.; Haris, M.; Verma, S.K.; Husain, N.; Gupta, R.K. Improved bolus arrival time and arterial input function estimation for tracer kinetic analysis in DCE-MRI. J. Magn. Reson. Imaging Off. J. Int. Soc. Magn. Reson. Med. 2009, 29, 166–176. [Google Scholar] [CrossRef]
- Magdoom, K.; Pishko, G.L.; Hwan Kim, J.; Sarntinoranont, M. Evaluation of a voxelized model based on DCE-MRI for tracer transport in tumor. J. Biomech. Eng. 2012, 134, 091004. [Google Scholar] [CrossRef] [PubMed]
- Kimelberg, H. Water homeostasis in the brain: Basic concepts. Neuroscience 2004, 129, 851–860. [Google Scholar] [CrossRef]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook/edición Don W. Green Y Robert H. Perry 1973, 100, 628–660. [Google Scholar]
- Kohandel, M.; Haselwandter, C.A.; Kardar, M.; Sengupta, S.; Sivaloganathan, S. Quantitative model for efficient temporal targeting of tumor cells and neovasculature. Comput. Math. Methods Med. 2011, 2011, 790721. [Google Scholar] [CrossRef]
- Sniegowski, M.; Mandava, N.; Kahook, M.Y. Sustained intraocular pressure elevation after intravitreal injection of bevacizumab and ranibizumab associated with trabeculitis. Open Ophthalmol. J. 2010, 4, 28–29. [Google Scholar] [CrossRef]
- Tian, X.-H.; Lin, X.-N.; Wei, F.; Feng, W.; Huang, Z.-C.; Wang, P.; Ren, L.; Diao, Y. Enhanced brain targeting of temozolomide in polysorbate-80 coated polybutylcyanoacrylate nanoparticles. Int. J. Nanomed. 2011, 6, 445. [Google Scholar]
- Gao, J.; Wang, Z.; Liu, H.; Wang, L.; Huang, G. Liposome encapsulated of temozolomide for the treatment of glioma tumor: Preparation, characterization and evaluation. Drug Discov. Ther. 2015, 9, 205–212. [Google Scholar] [CrossRef]
- Zhan, W. Delivery of liposome encapsulated temozolomide to brain tumour: Understanding the drug transport for optimisation. Int. J. Pharm. 2019, 557, 280–292. [Google Scholar] [CrossRef] [PubMed]
- Rosso, L.; Brock, C.S.; Gallo, J.M.; Saleem, A.; Price, P.M.; Turkheimer, F.E.; Aboagye, E.O. A new model for prediction of drug distribution in tumor and normal tissues: Pharmacokinetics of temozolomide in glioma patients. Cancer Res. 2009, 69, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.; Mi, X.; Xu, L.X. Study of Thermally Targeted Nano-Particle Drug Delivery for Tumor Therapy. In Proceedings of the ASME 2008 First International Conference on Micro/Nanoscale Heat Transfer, Tainan, Taiwan, 6–9 June 2008; pp. 1399–1406. [Google Scholar]
- Ziemys, A.; Klemm, S.; Milosevic, M.; Yokoi, K.; Ferrari, M.; Kojic, M. Computational analysis of drug transport in tumor microenvironment as a critical compartment for nanotherapeutic pharmacokinetics. Drug Deliv. 2016, 23, 2524–2531. [Google Scholar] [CrossRef]
- Swabb, E.A.; Wei, J.; Gullino, P.M. Diffusion and convection in normal and neoplastic tissues. Cancer Res. 1974, 34, 2814–2822. [Google Scholar]
- Friedman, H.S.; Kerby, T.; Calvert, H. Temozolomide and treatment of malignant glioma. Clin. Cancer Res. 2000, 6, 2585–2597. [Google Scholar]
- Yang, B.; Li, X.; He, L.; Zhu, Y. Computer-aided design of temozolomide derivatives based on alkylglycerone phosphate synthase structure with isothiocyanate and their pharmacokinetic/toxicity prediction and anti-tumor activity in vitro. Biomed. Rep. 2018, 8, 235–240. [Google Scholar] [CrossRef] [Green Version]
- Fung, L.K.; Shin, M.; Tyler, B.; Brem, H.; Saltzman, W.M. Chemotherapeutic drugs released from polymers: Distribution of 1, 3-bis (2-chloroethyl)-l-nitrosourea in the rat brain. Pharm. Res. 1996, 13, 671–682. [Google Scholar] [CrossRef]
- Tolaney, S.M.; Boucher, Y.; Duda, D.G.; Martin, J.D.; Seano, G.; Ancukiewicz, M.; Barry, W.T.; Goel, S.; Lahdenrata, J.; Isakoff, S.J. Role of vascular density and normalization in response to neoadjuvant bevacizumab and chemotherapy in breast cancer patients. Proc. Natl. Acad. Sci. USA 2015, 112, 14325–14330. [Google Scholar] [CrossRef]
- Mirzoeva, O.K.; Kawaguchi, T.; Pieper, R.O. The Mre11/Rad50/Nbs1 complex interacts with the mismatch repair system and contributes to temozolomide-induced G2 arrest and cytotoxicity. Mol. Cancer Ther. 2006, 5, 2757–2766. [Google Scholar] [CrossRef] [PubMed]
- Saucier-Sawyer, J.K.; Seo, Y.-E.; Gaudin, A.; Quijano, E.; Song, E.; Sawyer, A.J.; Deng, Y.; Huttner, A.; Saltzman, W.M. Distribution of polymer nanoparticles by convection-enhanced delivery to brain tumors. J. Control. Release 2016, 232, 103–112. [Google Scholar] [CrossRef]
- Fukumura, D.; Jain, R.K. Imaging angiogenesis and the microenvironment. Apmis 2008, 116, 695–715. [Google Scholar] [CrossRef] [PubMed]
- Seki, T.; Yanaihara, N.; Shapiro, J.S.; Saito, M.; Tabata, J.; Yokomizo, R.; Noguchi, D.; Kuroda, T.; Kawabata, A.; Suzuki, J. Interleukin-6 as an enhancer of anti-angiogenic therapy for ovarian clear cell carcinoma. Sci. Rep. 2021, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, A.; Bansal, A.; Singh, A.; Sinha, N. Perfusion kinetics in human brain tumor with DCE-MRI derived model and CFD analysis. J. Biomech. 2017, 59, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Mardor, Y.; Roth, Y.; Lidar, Z.; Jonas, T.; Pfeffer, R.; Maier, S.E.; Faibel, M.; Nass, D.; Hadani, M.; Orenstein, A. Monitoring response to convection-enhanced taxol delivery in brain tumor patients using diffusion-weighted magnetic resonance imaging. Cancer Res. 2001, 61, 4971–4973. [Google Scholar]
- Barua, N.U.; Hopkins, K.; Woolley, M.; O’Sullivan, S.; Harrison, R.; Edwards, R.J.; Bienemann, A.S.; Wyatt, M.J.; Arshad, A.; Gill, S.S. A novel implantable catheter system with transcutaneous port for intermittent convection-enhanced delivery of carboplatin for recurrent glioblastoma. Drug Deliv. 2016, 23, 167–173. [Google Scholar] [CrossRef]
- Wang, W.; Sivakumar, W.; Torres, S.; Jhaveri, N.; Vaikari, V.P.; Gong, A.; Howard, A.; Golden, E.B.; Louie, S.G.; Schönthal, A.H. Effects of convection-enhanced delivery of bevacizumab on survival of glioma-bearing animals. Neurosurg. Focus 2015, 38, E8. [Google Scholar] [CrossRef]
- Nordling-David, M.M.; Yaffe, R.; Guez, D.; Meirow, H.; Last, D.; Grad, E.; Salomon, S.; Sharabi, S.; Levi-Kalisman, Y.; Golomb, G. Liposomal temozolomide drug delivery using convection enhanced delivery. J. Control. Release 2017, 261, 138–146. [Google Scholar] [CrossRef]
- Linninger, A.A.; Somayaji, M.R.; Zhang, L.; Hariharan, M.S.; Penn, R.D. Rigorous mathematical modeling techniques for optimal delivery of macromolecules to the brain. IEEE Trans. Biomed. Eng. 2008, 55, 2303–2313. [Google Scholar] [CrossRef]
- Krewson, C.E.; Klarman, M.L.; Saltzman, W.M. Distribution of nerve growth factor following direct delivery to brain interstitium. Brain Res. 1995, 680, 196–206. [Google Scholar] [CrossRef]
- Heldin, C.-H.; Rubin, K.; Pietras, K.; Östman, A. High interstitial fluid pressure—an obstacle in cancer therapy. Nat. Rev. Cancer 2004, 4, 806–813. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, T.; Afzal, J.; Lamborn, K.R.; Bollen, A.W.; Bauer, W.F.; Koo, M.-S.; Kahl, S.B.; Deen, D.F. Toxicity, biodistribution, and convection-enhanced delivery of the boronated porphyrin BOPP in the 9L intracerebral rat glioma model. Int. J. Radiat. Oncol.* Biol.* Phys. 2005, 63, 247–252. [Google Scholar] [CrossRef]
- Bobo, R.H.; Laske, D.W.; Akbasak, A.; Morrison, P.F.; Dedrick, R.L.; Oldfield, E.H. Convection-enhanced delivery of macromolecules in the brain. Proc. Natl. Acad. Sci. USA 1994, 91, 2076–2080. [Google Scholar] [CrossRef]
- Brady, M.; Raghavan, R.; Chen, Z.-J.; Broaddus, W.C. Quantifying fluid infusions and tissue expansion in brain. IEEE Trans. Biomed. Eng. 2011, 58, 2228–2237. [Google Scholar] [CrossRef] [PubMed]
- Mehta, J.N.; Rausch, M.K.; Rylander, C.G. Convection-Enhanced Delivery with Controlled Catheter Movement: A Parametric Finite Element Analysis. Int. J. Numer. Methods Biomed. Eng. 2022, e3635. [Google Scholar] [CrossRef]
- Forte, A.E.; Gentleman, S.M.; Dini, D. On the characterization of the heterogeneous mechanical response of human brain tissue. Biomech. Model. Mechanobiol. 2017, 16, 907–920. [Google Scholar] [CrossRef]
- Boucher, Y.; Jain, R.K. Microvascular pressure is the principal driving force for interstitial hypertension in solid tumors: Implications for vascular collapse. Cancer Res. 1992, 52, 5110–5114. [Google Scholar]
- Raghunathan, S.; Evans, D.; Sparks, J.L. Poroviscoelastic modeling of liver biomechanical response in unconfined compression. Ann. Biomed. Eng. 2010, 38, 1789–1800. [Google Scholar] [CrossRef]
- Fleming, A.B.; Saltzman, W.M. Pharmacokinetics of the carmustine implant. Clin. Pharmacokinet. 2002, 41, 403–419. [Google Scholar] [CrossRef]
- Neeves, K.; Lo, C.; Foley, C.; Saltzman, W.; Olbricht, W. Fabrication and characterization of microfluidic probes for convection enhanced drug delivery. J. Control. Release 2006, 111, 252–262. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, K.; Atay, N.; Abler, D.; Bhargava, S.; Sahoo, P.; Rockne, R.C.; Munson, J.M. Utilizing Dynamic Contrast-Enhanced Magnetic Resonance Imaging (DCE-MRI) to Analyze Interstitial Fluid Flow and Transport in Glioblastoma and the Surrounding Parenchyma in Human Patients. Pharmaceutics 2021, 13, 212. [Google Scholar] [CrossRef] [PubMed]
- Unterberg, A.; Stover, J.; Kress, B.; Kiening, K. Edema and brain trauma. Neuroscience 2004, 129, 1019–1027. [Google Scholar] [CrossRef] [PubMed]
- Teo, C.S.; Tan, W.H.K.; Lee, T.; Wang, C.-H. Transient interstitial fluid flow in brain tumors: Effect on drug delivery. Chem. Eng. Sci. 2005, 60, 4803–4821. [Google Scholar] [CrossRef]
- Yu, J.; Guo, Y.; Zhao, S.; Xu, K. Brainstem edema caused by traumatic carotid-cavernous fistula: A case report and review of the literature. Exp. Ther. Med. 2015, 10, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Kashkooli, F.M.; Soltani, M.; Hamedi, M.-H. Drug delivery to solid tumors with heterogeneous microvascular networks: Novel insights from image-based numerical modeling. Eur. J. Pharm. Sci. 2020, 151, 105399. [Google Scholar] [CrossRef]
- Mousavi, M.; Manshadi, M.D.; Soltani, M.; Kashkooli, F.M.; Rahmim, A.; Mosavi, A.; Kvasnica, M.; Atkinson, P.M.; Kovács, L.; Koltay, A. Modeling the efficacy of different anti-angiogenic drugs on treatment of solid tumors using 3D computational modeling and machine learning. Comput. Biol. Med. 2022, 146, 105511. [Google Scholar] [CrossRef]
- Saini, J.; Gupta, P.K.; Awasthi, A.; Pandey, C.; Singh, A.; Patir, R.; Ahlawat, S.; Sadashiva, N.; Mahadevan, A.; Gupta, R.K. Multiparametric imaging-based differentiation of lymphoma and glioblastoma: Using T1-perfusion, diffusion, and susceptibility-weighted MRI. Clin. Radiol. 2018, 73, 986.e7–986.e15. [Google Scholar] [CrossRef]
- Hatakeyama, H.; Akita, H.; Maruyama, K.; Suhara, T.; Harashima, H. Factors governing the in vivo tissue uptake of transferrin-coupled polyethylene glycol liposomes in vivo. Int. J. Pharm. 2004, 281, 25–33. [Google Scholar] [CrossRef]
- Noble, G.T.; Stefanick, J.F.; Ashley, J.D.; Kiziltepe, T.; Bilgicer, B. Ligand-targeted liposome design: Challenges and fundamental considerations. Trends Biotechnol. 2014, 32, 32–45. [Google Scholar] [CrossRef]
- Milligan, L.; Summers, M. The biological basis of maintenance and its relevance to assessing responses to nutrients. Proc. Nutr. Soc. 1986, 45, 185–193. [Google Scholar] [CrossRef]
- Wrobel, I.; Collins, D. Fusion of cationic liposomes with mammalian cells occurs after endocytosis. Biochim. Et Biophys. Acta (BBA)-Biomembr. 1995, 1235, 296–304. [Google Scholar] [CrossRef]
- Barua, N.U.; Gill, S.S.; Love, S. Convection-enhanced drug delivery to the brain: Therapeutic potential and neuropathological considerations. Brain Pathol. 2014, 24, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Prezelski, K.; Keiser, M.; Stein, J.M.; Lucas, T.H.; Davidson, B.; Gonzalez-Alegre, P.; Vitale, F. Design and validation of a multi-point injection technology for MR-guided convection enhanced delivery in the brain. Front. Med. Technol. 2021, 3, 725844. [Google Scholar] [CrossRef]
- GarcÃa, J.J.; Molano, A.B.; Smith, J.H. Description and validation of a finite element model of backflow during infusion into a brain tissue phantom. J. Comput. Nonlinear Dyn. 2013, 8, 011017. [Google Scholar] [CrossRef]

| Parameter | Unit | Value |
|---|---|---|
| Repetition time () | ||
| Echo time () | ||
| Flip angle () | ||
| Field of view | ||
| Slice thickness | ||
| Reconstruction matrix | ||
| Time of acquisition | min | 2.15 |
| Temporal resolution | sec | 3.8 |
| Demographic Characteristics | Patient 1 | Patient 2 |
|---|---|---|
| Age (Years) | 67 | 72 |
| Gender | M | F |
| Tumor type | Glioblastoma | Meningioma |
| Newly diagnosed or recurrent tumor | Newly diagnosed | Newly diagnosed |
| Tumor grade | IV | I |
| Symbol | Parameter | Unit | Brain Tumor | Normal Tissue |
|---|---|---|---|---|
| Hydraulic conductivity of microvasculature wall | [23] | [23] | ||
| Baseline of blood vessel surface area per unit tissue volume | [17] | [17] | ||
| Blood pressure | [49] | [49] | ||
| Osmotic reflection coefficient for proteins in blood | [17] | [17] | ||
| Osmotic pressure of blood | [49] | [49] | ||
| Osmotic pressure of interstitial fluid | [49] | [49] | ||
| Interstitial fluid density | [50] | [50] | ||
| Interstitial fluid viscosity | [50] | [50] | ||
| Tissue hydraulic conductivity | [23] | [23] | ||
| Angiogenesis parameter | [51] | [51] | ||
| Angiogenesis parameter | [51] | [51] | ||
| Angiogenesis parameter | [51] | [51] |
| Symbol | Parameter | Unit | Bevacizumab | Liposome | Temozolomide |
|---|---|---|---|---|---|
| MW | Molecular weight | [52] | [53] | ||
| Transvascular permeability | (T) [54] (N) [55] | (T) [56] (N) [56] | |||
| Diffusivity in tissue ECS | (T) ‡ [8] (N) ‡ [8] | (T) [57] (N) [58] | (T) [31] (N) [59] | ||
| Binding constant of free drugs with proteins | [60] | ||||
| CM/ECS partition coefficient | [61] | ||||
| ICS/ECS partition coefficient | [62] | ||||
| Antiangiogenic rate | ‡ [63] | ||||
| Elimination rate due to reactions | [51] | [60] | |||
| Drug release rate | [54] | ||||
| Drug dose that kills 90% of tumor cells | [64] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhandari, A.; Jaiswal, K.; Singh, A.; Zhan, W. Convection-Enhanced Delivery of Antiangiogenic Drugs and Liposomal Cytotoxic Drugs to Heterogeneous Brain Tumor for Combination Therapy. Cancers 2022, 14, 4177. https://doi.org/10.3390/cancers14174177
Bhandari A, Jaiswal K, Singh A, Zhan W. Convection-Enhanced Delivery of Antiangiogenic Drugs and Liposomal Cytotoxic Drugs to Heterogeneous Brain Tumor for Combination Therapy. Cancers. 2022; 14(17):4177. https://doi.org/10.3390/cancers14174177
Chicago/Turabian StyleBhandari, Ajay, Kartikey Jaiswal, Anup Singh, and Wenbo Zhan. 2022. "Convection-Enhanced Delivery of Antiangiogenic Drugs and Liposomal Cytotoxic Drugs to Heterogeneous Brain Tumor for Combination Therapy" Cancers 14, no. 17: 4177. https://doi.org/10.3390/cancers14174177
APA StyleBhandari, A., Jaiswal, K., Singh, A., & Zhan, W. (2022). Convection-Enhanced Delivery of Antiangiogenic Drugs and Liposomal Cytotoxic Drugs to Heterogeneous Brain Tumor for Combination Therapy. Cancers, 14(17), 4177. https://doi.org/10.3390/cancers14174177





