GraphChrom: A Novel Graph-Based Framework for Cancer Classification Using Chromosomal Rearrangement Endpoints
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
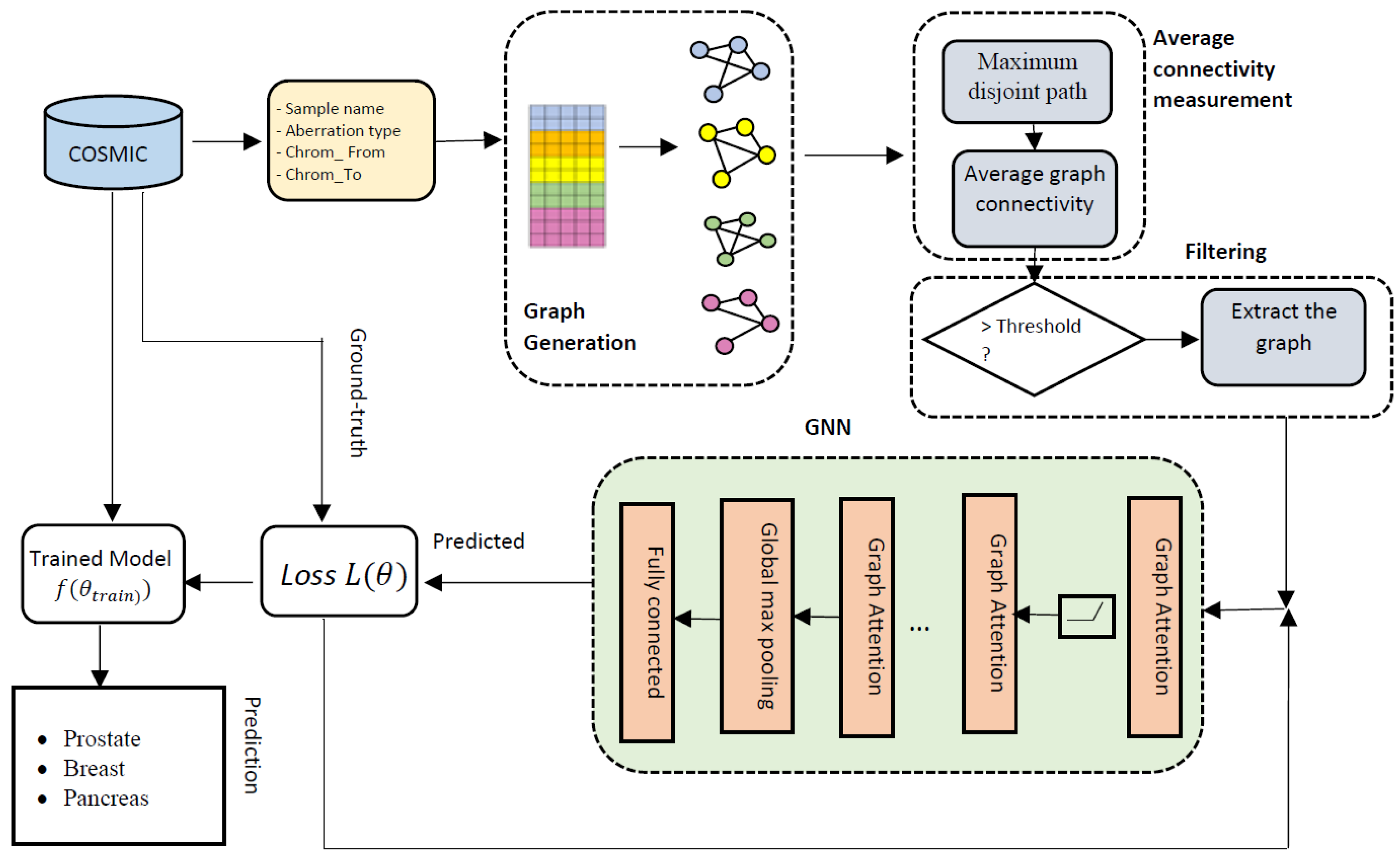
2.1. Catalogue of Somatic Mutations in Cancer (COSMIC)
2.2. Overall Architecture of GraphChrom
2.2.1. CRE Graph Generation
2.2.2. Maximum Disjoint Path between Two Chromosomes
2.2.3. Average Connectivity of CA Graphs
2.2.4. Filtering
2.2.5. Graph Neural Network (GNN)
2.3. Baseline Models
3. Results and Discussion
3.1. GraphChrom Predicts Cancer with High Accuracy
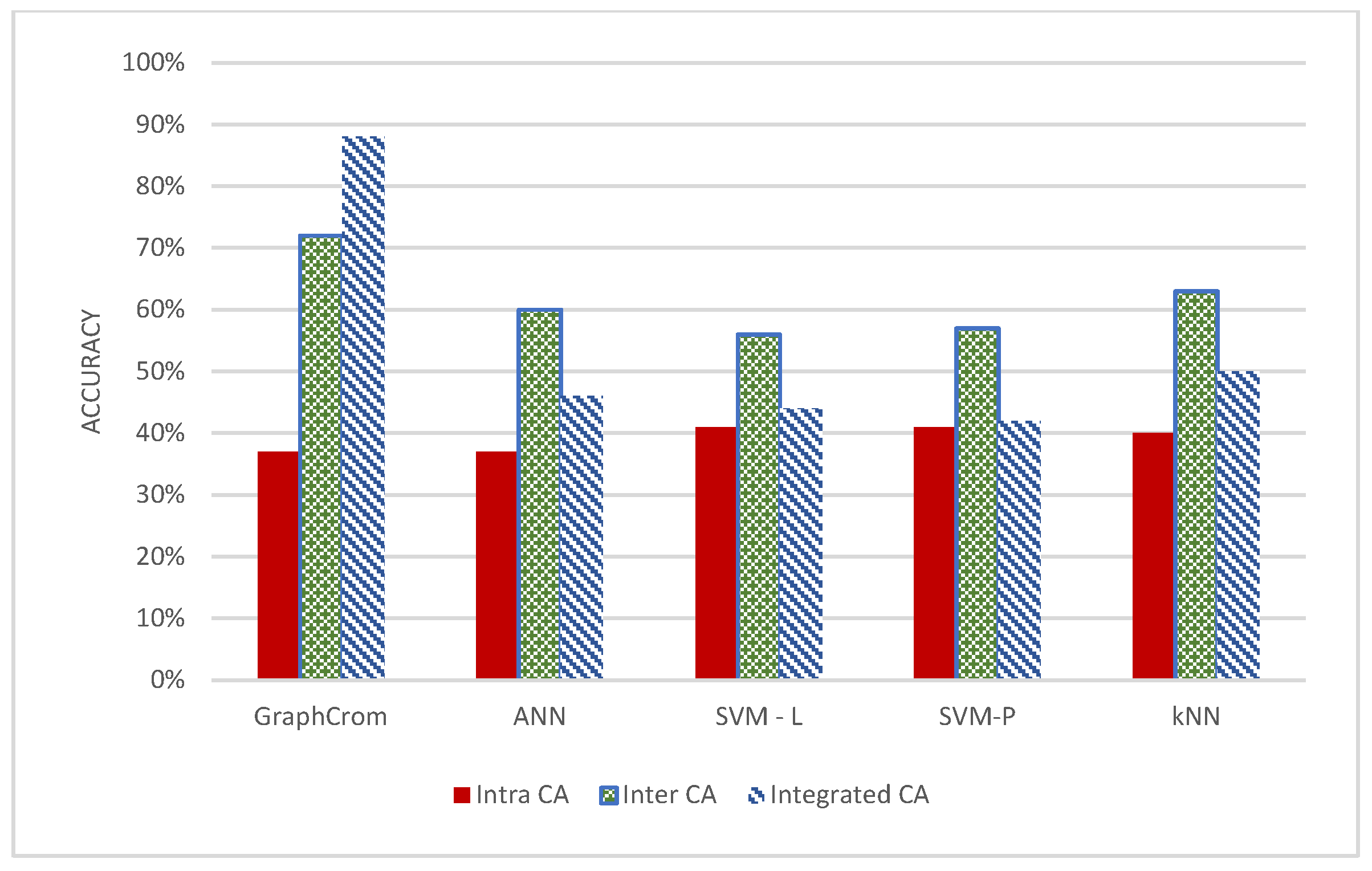
3.2. Effect of Inter- and Intrachromosomal Aberrations in Prediction
3.3. GraphChrom Outperforms Baseline Models
3.4. Local Chromosomal Aberrations Affect Prediction
3.5. Metrics for Classification
4. Conclusions
Supplementary Materials
Funding
Institutional review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; PCAWG Structural Variation Working Group; Roberts, N.; Wala, J.A.; Shapira, O.; Schumacher, S.E.; Kumar, K.; Khurana, E.; Waszak, S.; Korbel, J.O.; et al. Patterns of somatic structural variation in human cancer genomes. Nature 2020, 578, 112–121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ying, R.; Leskovec, J. Representation Learning on Graphs: Methods and Applications. arXiv 2017, arXiv:1709.05584. [Google Scholar]
- Duesberg, P.; Li, R.; Fabarius, A.; Hehlmann, R. The Chromosomal Basis of Cancer. Anal. Cell. Pathol. 2005, 27, 293–318. [Google Scholar] [CrossRef] [PubMed]
- Koschny, R.; Holland, H.; Koschny, T.; Vitzthum, H.E. Comparative genomic hybridization pattern of non-anaplastic and anaplastic oligodendrogliomas—A meta-analysis. Pathol. Res. Pract. 2006, 202, 23–30. [Google Scholar] [CrossRef]
- Heng, H.H. Genome Chaos: Rethinking Genetics, Evolution, and Molecular Medicine; Academic Press, Elsevier: London, UK, 2019; p. 535. ISBN 978-0128136355. [Google Scholar]
- Mirzaei, G.; Petreaca, R.C. Distribution of copy number variations and rearrangement endpoints in human cancers with a review of literature. Mutat. Res. Mol. Mech. Mutagen. 2021, 824, 111773. [Google Scholar] [CrossRef]
- Jiao, W.; Atwal, G.; Polak, P.; Karlic, R.; Cuppen, E.; Danyi, A.; de Ridder, J.; van Herpen, C.; Lolkema, M.P.; Steeghs, N.; et al. A deep learning system accurately classifies primary and metastatic cancers using passenger mutation patterns. Nat. Commun. 2020, 11, 728. [Google Scholar] [CrossRef]
- Kim, B.-H.; Yu, K.; Lee, P.C.W. Cancer classification of single-cell gene expression data by neural network. BMC Bioinform. 2019, 36, 1360–1366. [Google Scholar] [CrossRef]
- Maulik, U.; Chakraborty, D. Fuzzy Preference Based Feature Selection and Semisupervised SVM for Cancer Classification. IEEE Trans. NanoBioscience 2014, 13, 152–160. [Google Scholar] [CrossRef]
- Abdel-Zaher, A.M.; Eldeib, A.M. Eldeib, Breast cancer classification using deep belief networks. Expert Syst. Appl. 2016, 46, 139–144. [Google Scholar] [CrossRef]
- Lingyun, G.; Mingquan, Y.; Xiaojie, L.; Daobin, H.; Hybrid, M. Based on Information Gain and Support Vector Machine for Gene Selection in Cancer Classification. Genom. Proteom. Bioinform. 2017, 15, 389–395. [Google Scholar] [CrossRef]
- Khan, J.; Wei, J.S.; Ringnér, M.; Saal, L.H.; Ladanyi, M.; Westermann, F.; Berthold, F.; Schwab, M.; Antonescu, C.R.; Peterson, C.; et al. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001, 7, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Mitra, P.; Mitra, S.; Pal, S.K. Evolutionary Modular MLP with Rough Sets and ID3 Algorithm for Staging of Cervical Cancer. Neural Comput. Appl. 2001, 10, 67–76. [Google Scholar] [CrossRef]
- Mohammed, M.; Mwambi, H.; Mboya, I.B.; Elbashir, M.K.; Omolo, B. A stacking ensemble deep learning approach to cancer type classification based on TCGA data. Sci. Rep. 2021, 11, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chen, P.; McGough, M.; Xing, F.; Wang, C.; Bui, M.; Xie, Y.; Sapkota, M.; Cui, L.; Dhillon, J.; et al. Pathologist-level interpretable whole-slide cancer diagnosis with deep learning. Nat. Mach. Intell. 2019, 1, 236–245. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, H.-O.; Lee, S.; Jeong, W.-K. CPEM: Accurate cancer type classification based on somatic alterations using an ensemble of a random forest and a deep neural network. Sci. Rep. 2019, 9, 16927. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, A.; Cherniavsky, Y. Generalization of the Menger’s theorem to simplicial complexes and certain invariants of the underlying topological spaces, Geometric Topology. arXiv 2012, arXiv:1208.5439v3. [Google Scholar]
- Li, Y.; Kang, K.; Krahn, J.M.; Croutwater, N.; Lee, K.; Umbach, D.M.; Li, L. A comprehensive genomic pan-cancer classification using The Cancer Genome Atlas gene expression data. BMC Genom. 2017, 18, 1–13. [Google Scholar] [CrossRef]
- Prado-Vázquez, G.; Gamez-Pozo, A.; Trilla-Fuertes, L.; Arevalillo, J.M.; Zapater-Moros, A.; Ferrer-Gómez, M.; Díaz-Almirón, M.; López-Vacas, R.; Navarro, H.; Maín, P.; et al. A novel approach to triple-negative breast cancer molecular classification reveals a luminal immune-positive subgroup with good prognoses. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Wang, C.; Long, Y.; Li, W.; Dai, W.; Xie, S.; Liu, Y.; Zhang, Y.; Liu, M.; Tian, Y.; Li, Q.; et al. Exploratory study on classification of lung cancer subtypes through a combined K-nearest neighbor classifier in breathomics. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Mahfouz, M.A.; Shoukry, A.; Mohamed, A. EKNN: Ensemble classifier incorporating connectivity and density into kNN with application to cancer diagnosis. Artif. Intell. Med. 2020, 111, 101985. [Google Scholar] [CrossRef]
- Khan, S.; Islam, N.; Jan, Z.; Din, I.U.; Rodrigues, J.J.P.C. A novel deep learning based framework for the detection and classification of breast cancer using transfer learning. Pattern Recognit. Lett. 2019, 125, 1–6. [Google Scholar] [CrossRef]
- Liu, S.; Xu, C.; Zhang, Y.; Liu, J.; Liu, X.; Dehmer, M. Feature selection of gene expression data for Cancer classification using double RBF-kernels. BMC Bioinform. 2018, 19, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Shi, Y.; Li, C.; Kim, J.; Cai, W.; Han, Z. DeepGene: An advanced cancer type classifier based on deep learning and somatic point mutations. BMC Bioinform. 2016, 17, 243–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tolkach, Y.; Dohmgörgen, T.; Toma, M.; Kristiansen, G. High-accuracy prostate cancer pathology using deep learning. Nat. Mach. Intell. 2020, 2, 1–8. [Google Scholar] [CrossRef]
- Gao, F.; Wang, W.; Tan, M.; Zhu, L.; Zhang, Y.; Fessler, E.; Vermeulen, L.; Wang, X. DeepCC: A novel deep learning-based framework for cancer molecular subtype classification. Oncogenesis 2019, 8, 1–12. [Google Scholar] [CrossRef]
- Tandel, G.S.; Biswas, M.; Kakde, O.G.; Tiwari, A.; Suri, H.S.; Turk, M.; Laird, J.R.; Asare, C.K.; Ankrah, A.A.; Khanna, N.N.; et al. A Review on a Deep Learning Perspective in Brain Cancer Classification. Cancers 2019, 11, 111. [Google Scholar] [CrossRef] [Green Version]
- Mendiratta, G.; Ke, E.; Aziz, M.; Liarakos, D.; Tong, M.; Stites, E.C. Cancer gene mutation frequencies for the U.S. population. Nat. Commun. 2021, 12, 5961. [Google Scholar] [CrossRef]
- Martínez-Jiménez, F.; Muiños, F.; Sentís, I.; Deu-Pons, J.; Reyes-Salazar, I.; Arnedo-Pac, C.; Mularoni, L.; Pich, O.; Bonet, J.; Kranas, H.; et al. A compendium of mutational cancer driver genes. Nat. Cancer 2020, 20, 555–572. [Google Scholar] [CrossRef]
- Bamford, S.; Dawson, E.; Forbes, S.; Clements, J.; Pettett, R.; Dogan, A.; Flanagan, A.; Teague, J.; Futreal, P.A.; Stratton, M.R.; et al. The COSMIC (Catalogue of Somatic Mutations in Cancer) database and website. Br. J. Cancer 2004, 91, 355–358. [Google Scholar] [CrossRef]
- Mitelman, F.; Johansson, B.; Mertens, F.E. Mitelman Database of Chromosome Aberrations and Gene Fusions in Cancer, Cancer Genome Anatomy Project. 2014. Available online: https://mitelmandatabase.isb-cgc.org/ (accessed on 1 June 2022).
- Korla, P.K.; Cheng, J.; Huang, C.H.; Tsai, J.J.P.; Liu, Y.H.; Kurubanjerdjit, N.; Hsieh, W.T.; Chen, H.Y.; Ng, K.-L. FARE-CAFE: A database of functional and regulatory elements of cancer-associated fusion events. Database 2015, 2015, bav086. [Google Scholar] [CrossRef] [Green Version]
- Yoshihara, K.; Wang, Q.; Torres-Garcia, W.; Zheng, S.; Vegesna, R.; Kim, H.; Verhaak, R.G.W. The landscape and therapeutic relevance of cancer-associated transcript fusions. Oncogene 2014, 34, 4845–4854. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Wu, N.; Liu, J.; Wu, Z.; Dong, D. FusionCancer: A database of cancer fusion genes derived from RNA-seq data. Diagn. Pathol. 2015, 10, 1–4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frenkel-Morgenstern, M.; Gorohovski, A.; Lacroix, V.; Rogers, M.; Ibanez, K.; Boullosa, C.; Andres Leon, E.; Ben-Hur, A.; Valencia, A. ChiTaRS: A database of human, mouse and fruit fly chimeric transcripts and RNA-sequencing data. Nucleic Acids Res. 2012, 41, D142–D151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kong, F.; Zhu, J.; Wu, J.; Peng, J.; Wang, Y.; Wang, Q.; Fu, S.; Yuan, L.-L.; Li, T. dbCRID: A database of chromosomal rearrangements in human diseases. Nucleic Acids Res. 2010, 39, D895–D900. [Google Scholar] [CrossRef] [PubMed]
- Prakash, T.; Sharma, V.; Adati, N.; Ozawa, R.; Kumar, N.; Nishida, Y.; Fujikake, T.; Takeda, T.; Taylor, T.D. Expression of Conjoined Genes: Another Mechanism for Gene Regulation in Eukaryotes. PLoS ONE 2010, 5, e13284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, D.-S.; Huh, J.-W.; Kim, H.-S. HYBRIDdb: A database of hybrid genes in the human genome. BMC Genom. 2007, 8, 128. [Google Scholar] [CrossRef] [Green Version]
- Novo, F.J.; De Mendíbil, I.O.; Vizmanos, J.L. TICdb: A collection of gene-mapped translocation breakpoints in cancer. BMC Genom. 2007, 8, 33. [Google Scholar] [CrossRef] [Green Version]
- Kim, P.; Yoon, S.; Kim, N.; Lee, S.; Ko, M.; Lee, H.; Kang, H.; Kim, J.; Lee, S. ChimerDB 2.0—a knowledgebase for fusion genes updated. Nucleic Acids Res. 2009, 38, D81–D85. [Google Scholar] [CrossRef] [Green Version]
- Huret, J.-L.; Ahmad, M.; Arsaban, M.; Bernheim, A.; Cigna, J.; Desangles, F.; Guignard, J.-C.; Jacquemot-Perbal, M.-C.; Labarussias, M.; Leberre, V.; et al. Atlas of Genetics and Cytogenetics in Oncology and Haematology in 2013. Nucleic Acids Res. 2012, 41, D920–D924. [Google Scholar] [CrossRef]
- Latysheva, N.S.; Babu, M.M. Discovering and understanding oncogenic gene fusions through data intensive computational approaches. Nucleic Acids Res. 2016, 44, 4487–4503. [Google Scholar] [CrossRef] [Green Version]
- Beineke, L.W.; Oellermann, O.R.; Pippert, R.E. The average connectivity of a graph. Discret. Math. 2002, 252, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Hamilton, W.L. Graph Representation Learning. Synth. Lect. Artif. Intell. Mach. Learn. 2020, 14, 1–159. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Y.-C.; Wang, B.; Kuo, C.-C.J. Graph representation learning: A survey. APSIPA Trans. Signal Inf. Process. 2020, 9, E15. [Google Scholar] [CrossRef]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention Networks, “It is a co,”. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017; pp. 1–12. [Google Scholar]
- Siri, S.O.; Martino, J.; Gottifredi, V. Structural Chromosome Instability: Types, Origins, Consequences, and Therapeutic Opportunities. Cancers 2021, 13, 3056. [Google Scholar] [CrossRef]
- Nowell, P.C.; Hungerford, D.A. Chromosome Studies on Normal and Leukemic Human Leukocytes. J. Natl. Cancer Inst. 1960, 25, 85–109. [Google Scholar] [CrossRef]





| Cancer Type | No. of Aberrations | No. of Graphs |
|---|---|---|
| Breast | 86,485 | 598 |
| Pancreatic | 51,623 | 513 |
| Prostate | 91,854 | 478 |
| Cancer Type | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| Breast | 0.89 | 0.96 | 0.92 | 30640 |
| Pancreatic | 0.86 | 0.8 | 0.83 | 26459 |
| Prostate | 0.91 | 0.89 | 0.9 | 32849 |
| Accuracy | 0.89 | |||
| Macro average | 0.88 | 0.88 | 0.88 | 89948 |
| Weighted average | 0.89 | 0.89 | 0.89 | 89948 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirzaei, G. GraphChrom: A Novel Graph-Based Framework for Cancer Classification Using Chromosomal Rearrangement Endpoints. Cancers 2022, 14, 3060. https://doi.org/10.3390/cancers14133060
Mirzaei G. GraphChrom: A Novel Graph-Based Framework for Cancer Classification Using Chromosomal Rearrangement Endpoints. Cancers. 2022; 14(13):3060. https://doi.org/10.3390/cancers14133060
Chicago/Turabian StyleMirzaei, Golrokh. 2022. "GraphChrom: A Novel Graph-Based Framework for Cancer Classification Using Chromosomal Rearrangement Endpoints" Cancers 14, no. 13: 3060. https://doi.org/10.3390/cancers14133060
APA StyleMirzaei, G. (2022). GraphChrom: A Novel Graph-Based Framework for Cancer Classification Using Chromosomal Rearrangement Endpoints. Cancers, 14(13), 3060. https://doi.org/10.3390/cancers14133060





