Dual-Intended Deep Learning Model for Breast Cancer Diagnosis in Ultrasound Imaging
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
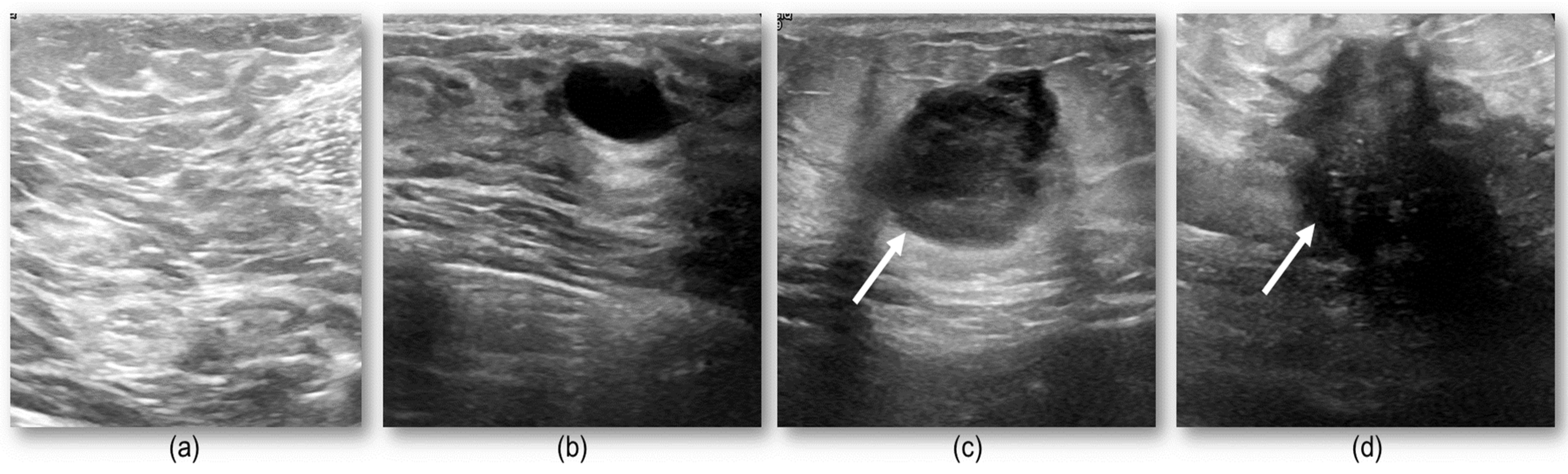
2.1. Study Data
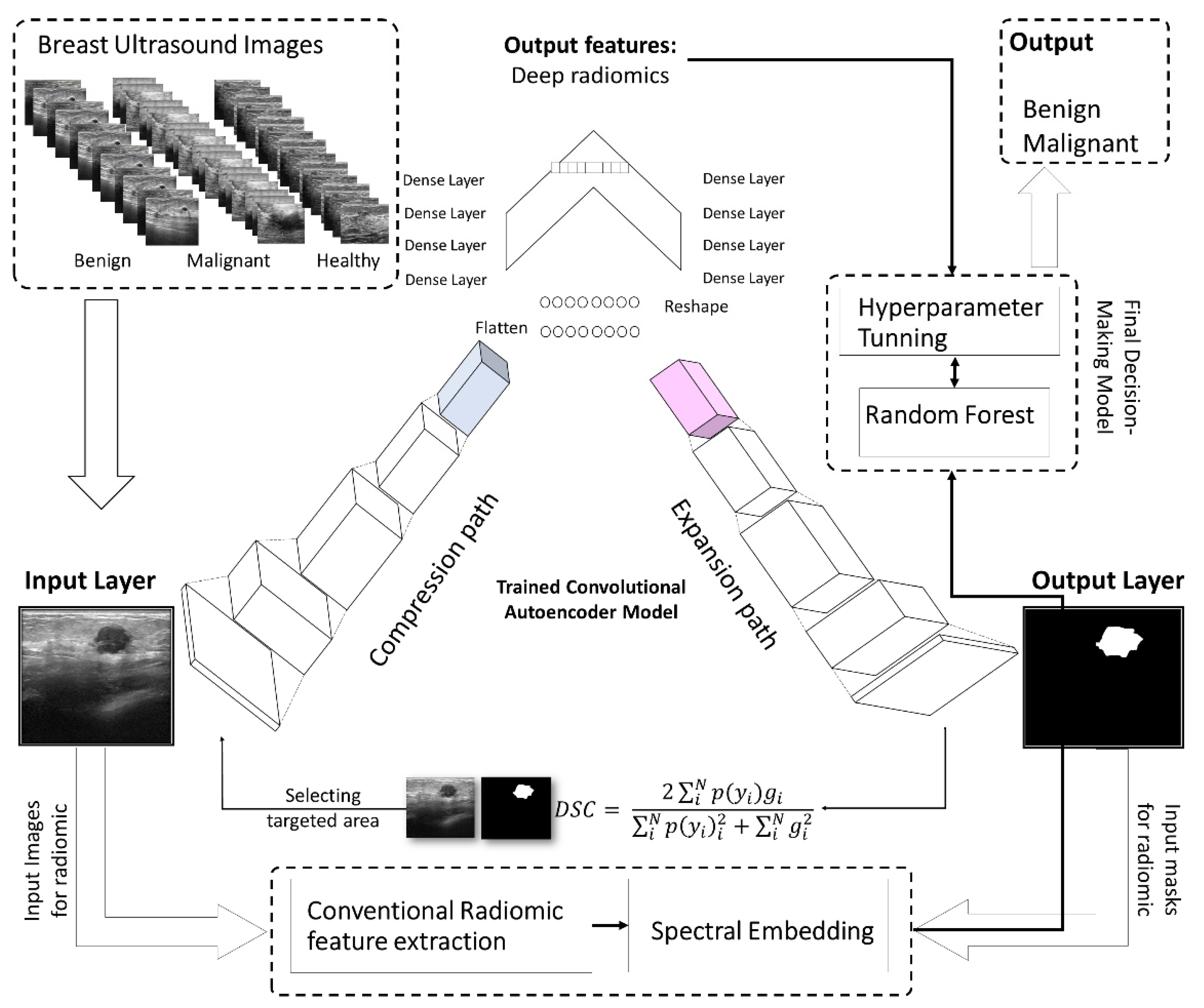
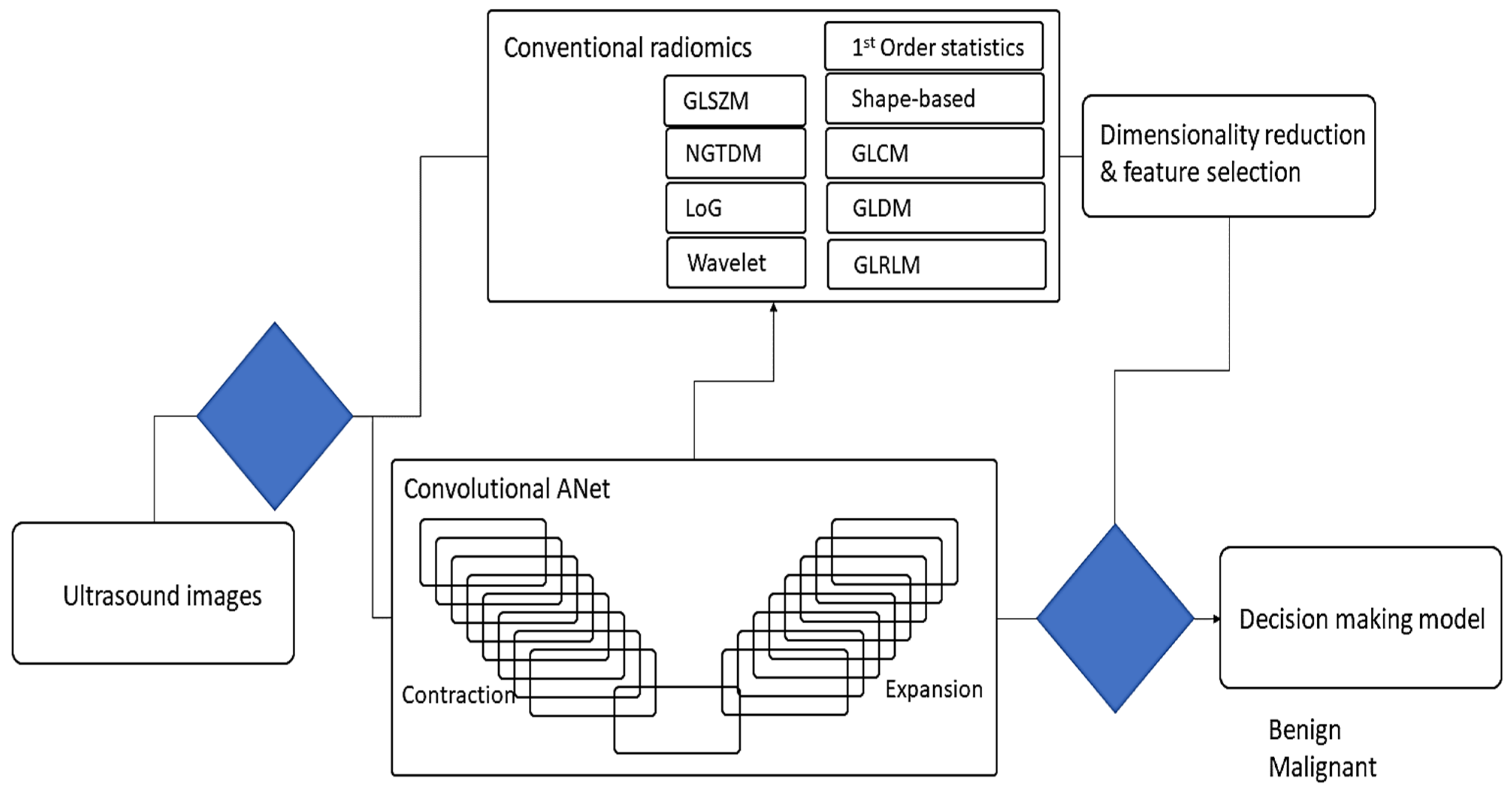
2.2. The Proposed Deep Learning Model
2.3. Conventional Radiomics in Breast US Imaging
2.4. Dimensionality Reduction
2.5. Metrics for Breast Lesions Finding
2.6. Breast Lesions Detection
2.7. Evaluation of Classifying Lesions
3. Results
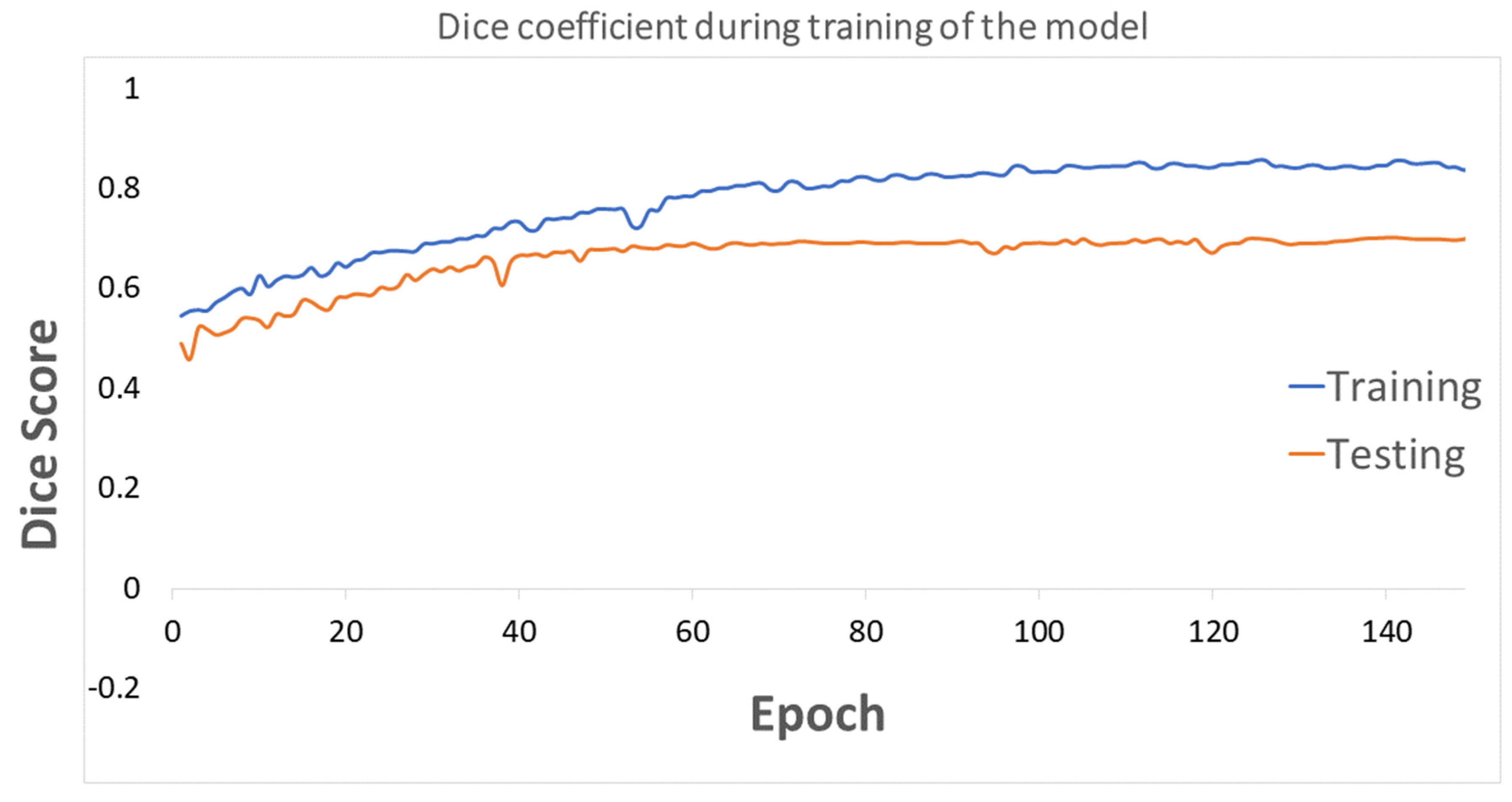
3.1. Segmentation of the Breast Lesions
3.2. Conventional and Deep Latent Space Radiomics
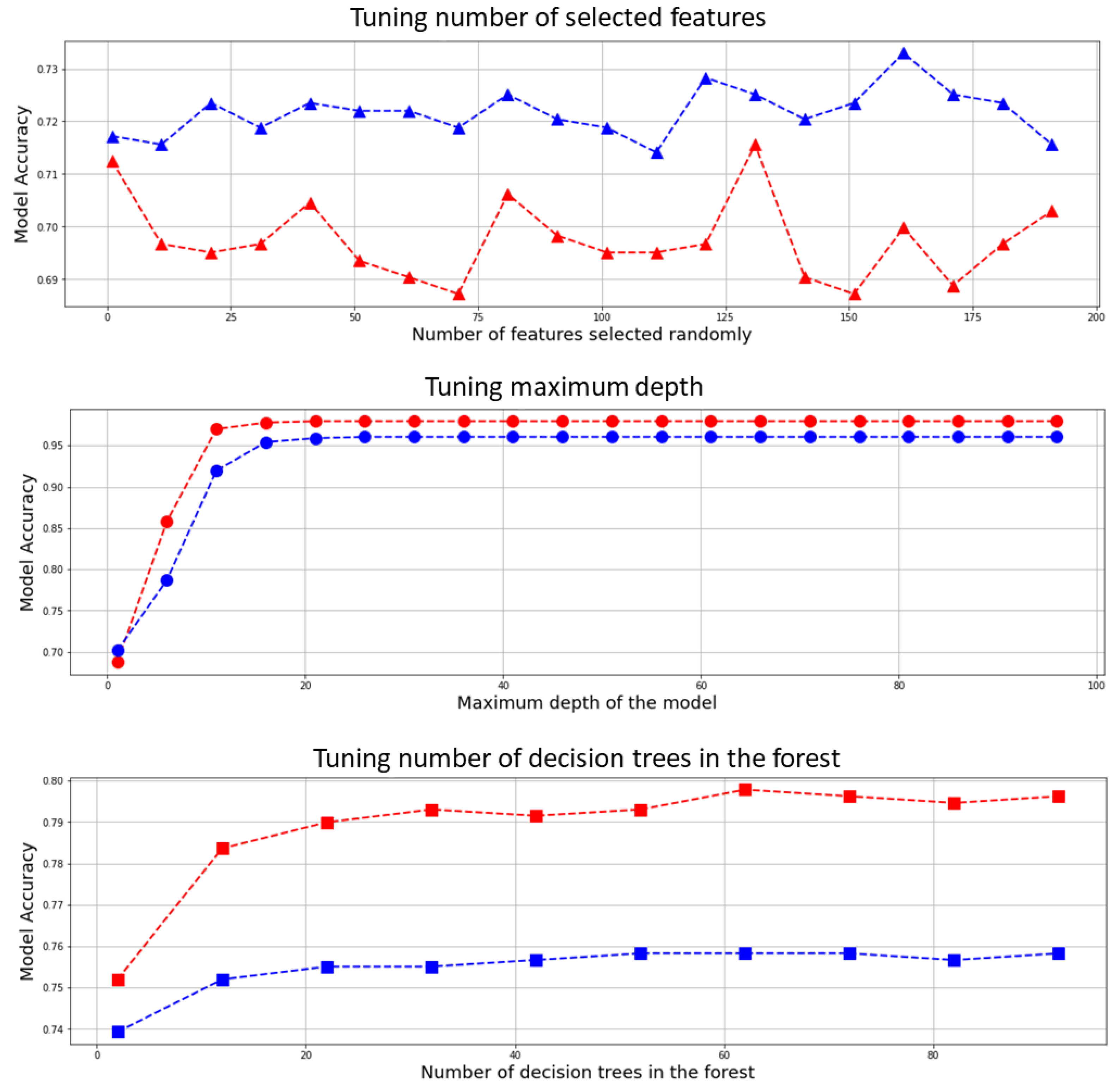
3.3. Optimizing the Classifier’s Hyperparameters
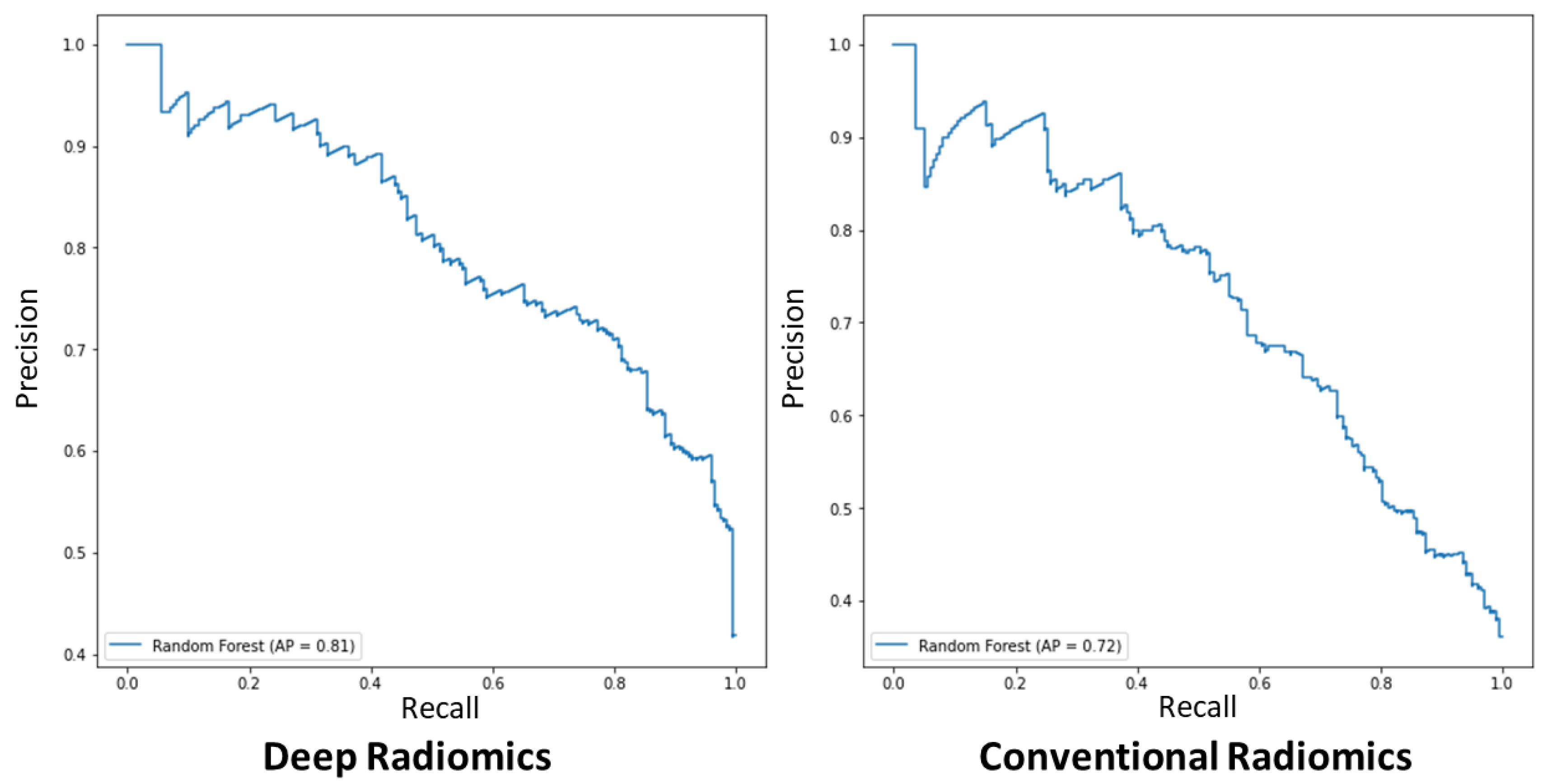
3.4. Classification Performance of the Proposed Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Computational Complexity of the Proposed Model
References
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E.; Jemal, A. Cancer statistics. A Cancer J. Clin. 2021, 71, 7–33. [Google Scholar] [CrossRef] [PubMed]
- World Health Organisation. Cancer—Key Facts. 2018. Available online: http://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 26 November 2018).
- Jalalian, A.; Mashohor, S.; Mahmud, R.; Karasfi, B.; Saripan, M.I.; Ramli, A.R.B. Foundation and methodologies in computer-aided diagnosis systems for breast cancer detection. EXCLI J. 2017, 16, 113–137. [Google Scholar] [CrossRef] [PubMed]
- Scott, A.M.; Lashley, M.G.; Drury, N.B.; Dale, P.S. Comparison of Call-Back Rates between Digital Mammography and Digital Breast Tomosynthesis. Am. Surg. 2019, 85, 855–857. [Google Scholar] [CrossRef] [PubMed]
- Pisano, E.D.; Gatsonis, C.; Hendrick, E.; Yaffe, M.; Baum, J.K.; Acharyya, S.; Conant, E.F.; Fajardo, L.L.; Bassett, L.; D’Orsi, C.; et al. Diagnostic Performance of Digital versus Film Mammography for Breast-Cancer Screening. N. Engl. J. Med. 2005, 353, 1773–1783. [Google Scholar] [CrossRef]
- Mario, J.; Venkataraman, S.; Dialani, V.; Slanetz, P.J. Benign breast lesions that mimic cancer: Determining radiologic-pathologic concordance. Appl. Radiol. 2015, 24–32. [Google Scholar] [CrossRef]
- Morrell, S.; Barratt, A.; Irwig, L.; Howard, K.; Biesheuvel, C.; Armstrong, B. Estimates of overdiagnosis of invasive breast cancer associated with screening mammography. Cancer Causes Control 2009, 21, 275–282. [Google Scholar] [CrossRef]
- Puliti, D.; Paci, E. The other side of technology: Risk of overdiagnosis of breast cancer with mammography screening. Futur. Oncol. 2009, 5, 481–491. [Google Scholar] [CrossRef]
- Alagoz, O.; Chhatwal, J.; Burnside, E.S. Optimal Policies for Reducing Unnecessary Follow-up Mammography Exams in Breast Cancer Diagnosis. Decis. Anal. 2013, 10, 200–224. [Google Scholar] [CrossRef] [Green Version]
- Berg, W.A. Reducing Unnecessary Biopsy and Follow-up of Benign Cystic Breast Lesions. Radiology 2020, 295, 52–53. [Google Scholar] [CrossRef]
- Cho, K.R.; Seo, B.K.; Woo, O.H.; Song, S.E.; Choi, J.; Whang, S.Y.; Park, E.K.; Park, A.Y.; Shin, H.; Chung, H.H. Breast Cancer Detection in a Screening Population: Comparison of Digital Mammography, Computer-Aided Detection Applied to Digital Mammography and Breast Ultrasound. J. Breast Cancer 2016, 19. [Google Scholar] [CrossRef]
- Theek, B.; Magnuska, Z.; Gremse, F.; Hahn, H.; Schulz, V.; Kiessling, F. Automation of data analysis in molecular cancer imaging and its potential impact on future clinical practice. Methods 2020, 188, 30–36. [Google Scholar] [CrossRef] [PubMed]
- Le, E.P.V.; Wang, Y.; Huang, Y.; Hickman, S.; Gilbert, F.J. Artificial intelligence in breast imaging. Clin. Radiol. 2019, 74, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Chabi, M.-L.; Borget, I.; Ardiles, R.; Aboud, G.; Boussouar, S.; Vilar, V.; Dromain, C.; Balleyguier, C. Evaluation of the Accuracy of a Computer-aided Diagnosis (CAD) System in Breast Ultrasound according to the Radiologist’s Experience. Acad. Radiol. 2012, 19, 311–319. [Google Scholar] [CrossRef] [PubMed]
- Burt, J.R.; Torosdagli, N.; Khosravan, N.; Raviprakash, H.; Mortazi, A.; Tissavirasingham, F.; Hussein, S.; Bagci, U. Deep learning beyond cats and dogs: Recent advances in diagnosing breast cancer with deep neural networks. Br. J. Radiol. 2018, 91, 20170545. [Google Scholar] [CrossRef]
- Shen, W.-C.; Chang, R.-F.; Moon, W.K.; Chou, Y.-H.; Huang, C.-S. Breast Ultrasound Computer-Aided Diagnosis Using BI-RADS Features. Acad. Radiol. 2007, 14, 928–939. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Choi, Y.; Kim, E.-K.; Han, B.-K.; Yoon, J.H.; Choi, J.S.; Chang, J.M. Deep learning-based computer-aided diagnosis in screening breast ultrasound to reduce false-positive diagnoses. Sci. Rep. 2021, 11, 395. [Google Scholar] [CrossRef]
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef] [Green Version]
- Lambin, P.; Rios-Velazquez, E.; Leijenaar, R.; Carvalho, S.; van Stiphout, R.G.P.M.; Granton, P.; Zegers, C.M.L.; Gillies, R.; Boellard, R.; Dekker, A.; et al. Radiomics: Extracting more information from medical images using advanced feature analysis. Eur. J. Cancer 2012, 48, 441–446. [Google Scholar] [CrossRef] [Green Version]
- Aerts, H.; Velazquez, E.R.; Leijenaar, R.T.H.; Parmar, C.; Grossmann, P.; Carvalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; Rietveld, D.; et al. Data from: Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nat. Commun. 2014, 5, 1–9. [Google Scholar] [CrossRef]
- Lambin, P.; Leijenaar, R.T.H.; Deist, T.M.; Peerlings, J.; de Jong, E.E.C.; van Timmeren, J.; Sanduleanu, S.; Larue, R.T.H.M.; Even, A.J.G.; Jochems, A.; et al. Radiomics: The bridge between medical imaging and personalized medicine. Nat. Rev. Clin. Oncol. 2017, 14, 749–762. [Google Scholar] [CrossRef]
- Wei, M.; Du, Y.; Wu, X.; Su, Q.; Zhu, J.; Zheng, L.; Lv, G.; Zhuang, J. A Benign and Malignant Breast Tumor Classification Method via Efficiently Combining Texture and Morphological Features on Ultrasound Images. Comput. Math. Methods Med. 2020, 2020, 5894010. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, B.; Sharifipour, H.M.; Maldague, X.P.V. A Diagnostic Biomarker for Breast Cancer Screening via Hilbert Embedded Deep Low-Rank Matrix Approximation. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Sun, Q.; Lin, X.; Zhao, Y.; Li, L.; Yan, K.; Liang, D.; Sun, D.; Li, Z.-C. Deep Learning vs. Radiomics for Predicting Axillary Lymph Node Metastasis of Breast Cancer Using Ultrasound Images: Don’t Forget the Peritumoral Region. Front. Oncol. 2020, 10, 53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pang, T.; Wong, J.H.D.; Ng, W.L.; Chan, C.S. Deep learning radiomics in breast cancer with different modalities: Overview and future. Expert Syst. Appl. 2020, 158, 113501. [Google Scholar] [CrossRef]
- Fei, X.; Zhou, S.; Han, X.; Wang, J.; Ying, S.; Chang, C.; Zhou, W.; Shi, J. Doubly supervised parameter transfer classifier for diagnosis of breast cancer with imbalanced ultrasound imaging modalities. Pattern Recognit. 2021, 120, 108139. [Google Scholar] [CrossRef]
- Yap, M.H.; Edirisinghe, E.; Bez, H. Processed images in human perception: A case study in ultrasound breast imaging. Eur. J. Radiol. 2010, 73, 682–687. [Google Scholar] [CrossRef]
- Pan, P.; Chen, H.; Li, Y.; Cai, N.; Cheng, L.; Wang, S. Tumor segmentation in automated whole breast ultrasound using bidirectional LSTM neural network and attention mechanism. Ultrasonics 2020, 110, 106271. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, H.; Li, Y.; Liu, Q.; Xu, X.; Wang, S.; Yap, P.-T.; Shen, D. Multi-task learning for segmentation and classification of tumors in 3D automated breast ultrasound images. Med. Image Anal. 2020, 70, 101918. [Google Scholar] [CrossRef]
- Al-Dhabyani, W.; Gomaa, M.; Khaled, H.; Fahmy, A. Dataset of breast ultrasound images. Data Brief 2019, 28, 104863. [Google Scholar] [CrossRef]
- Suk, H.I.; Shen, D. Deep learning-based feature representation for AD/MCI classification. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Nagoya, Japan, 22–26 September 2013; pp. 583–590. [Google Scholar]
- Virmani, J.; Agarwal, R. Deep feature extraction and classification of breast ultrasound images. Multimed. Tools Appl. 2020, 79, 27257–27292. [Google Scholar] [CrossRef]
- Antropova, N.; Huynh, B.Q.; Giger, M.L. A deep feature fusion methodology for breast cancer diagnosis demonstrated on three imaging modality datasets. Med. Phys. 2017, 44, 5162–5171. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, B.; Kawakita, S.; Amini, A.; Akbari, H.; Advani, S.; Akhloufi, M.; Maldague, X.; Ahadian, S. Impartially Validated Multiple Deep-Chain Models to Detect COVID-19 in Chest X-ray Using Latent Space Radiomics. J. Clin. Med. 2021, 10, 3100. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, B.; LaRiviere, M.J.; Cohen, E.A.; Buckingham, T.H.; Yee, S.S.; Black, T.A.; Chien, A.L.; Noël, P.; Hwang, W.-T.; Katz, S.I.; et al. Combining radiomic phenotypes of non-small cell lung cancer with liquid biopsy data may improve prediction of response to EGFR inhibitors. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, B.; Akbari, H.; Maldague, X. Detecting Vasodilation as Potential Diagnostic Biomarker in Breast Cancer Using Deep Learning-Driven Thermomics. Biosensors 2020, 10, 164. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, B.; Jahani, N.; Lariviere, M.J.; Cohen, E.; Hsieh, M.-K.; Luna, J.; Chitalia, R.D.; Thompson, J.C.; Carpenter, E.L.; Katz, S.I.; et al. Correlative hierarchical clustering-based low-rank dimensionality reduction of radiomics-driven phenotype in non-small cell lung cancer. In Medical Imaging 2019: Imaging Informatics for Healthcare, Research, and Applications; SPIE Medical Imaging: San Diego, CA, USA, 2019; Volume 10954, pp. 278–285. [Google Scholar] [CrossRef]
- Ha, S.; Choi, H.; Paeng, J.C.; Cheon, G.J. Radiomics in Oncological PET/CT: A Methodological Overview. Nucl. Med. Mol. Imaging 2019, 53, 14–29. [Google Scholar] [CrossRef] [PubMed]
- Bouveyron, C. High-Dimensional Statistical Learning and Its Application to Oncological Diagnosis by Radiomics. In Healthcare and Artificial Intelligence; Springer International Publishing: Cham, Switzerland, 2020; pp. 121–128. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Yousefi, B.; Akbari, H.; Hershman, M.; Kawakita, S.; Fernandes, H.; Ibarra-Castanedo, C.; Ahadian, S.; Maldague, X. SPAER: Sparse Deep Convolutional Autoencoder Model to Extract Low Dimensional Imaging Biomarkers for Early Detection of Breast Cancer Using Dynamic Thermography. Appl. Sci. 2021, 11, 3248. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Lei, Y.; Wang, T.; Curran, W.J.; Liu, T.; Yang, X. A review of deep learning based methods for medical image multi-organ segmentation. Phys. Med. 2021, 85, 107–122. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–11. [Google Scholar]
- Sorensen, T. A method of establishing groups of equal amplitude in plant sociology based on similarity of species and its application to analyses of the vegetation on Danish commons. Biol. Skar. 1948, 5, 1–34. [Google Scholar]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Google. Python 3 Google Compute Engine Backend, T4, and P100 GPU and 27.4 Gb RAM; Google: Mountain View, CA, USA, 2020. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Zheng, X. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Khan, A.I.; Shah, J.L.; Bhat, M.M. CoroNet: A deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Methods Programs Biomed. 2020, 196, 105581. [Google Scholar] [CrossRef] [PubMed]
- Zhai, D.; Hu, B.; Gong, X.; Zou, H.; Luo, J. ASS-GAN: Asymmetric semi-supervised GAN for breast ultrasound image segmentation. Neurocomputing 2022, 493, 204–216. [Google Scholar] [CrossRef]
- Gare, G.R.; Li, J.; Joshi, R.; Magar, R.; Vaze, M.P.; Yousefpour, M.; Rodriguez, R.L.; Galeotti, J.M. W-Net: Dense and diagnostic semantic segmentation of subcutaneous and breast tissue in ultrasound images by incorporating ultrasound RF waveform data. Med. Image Anal. 2021, 76, 102326. [Google Scholar] [CrossRef] [PubMed]
- Maghsoudi, O.H.; Christopher, S.; Gastounioti, A.; Pantalone, L.; Wu, F.-F.; Cohen, E.A.; Stacey, W.; Conant, E.F.; Vachon, C.; Kontos, D. Abstract 2600: Deep-LIBRA: An artificial intelligence approach for fully-automated assessment of breast density in digital mammography. Cancer Res. 2021, 81, 2600. [Google Scholar] [CrossRef]
- Maghsoudi, O.H.; Gastounioti, A.; Scott, C.; Pantalone, L.; Wu, F.-F.; Cohen, E.A.; Winham, S.; Conant, E.F.; Vachon, C.; Kontos, D. Deep-LIBRA: An artificial-intelligence method for robust quantification of breast density with independent validation in breast cancer risk assessment. Med. Image Anal. 2021, 73, 102138. [Google Scholar] [CrossRef]
- He, K.; Sun, J. Convolutional neural networks at constrained time cost. In Proceedings of the IEEE conference on computer vision and pattern recognition, Boston, MA, USA, 7–12 June 2015; pp. 5353–5360. [Google Scholar]
- Chen, T.; Lin, L.; Zuo, W.; Luo, X.; Zhang, L. Learning a wavelet-like auto-encoder to accelerate deep neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22 February–1 March 2022. [Google Scholar]

| Type of Texture Analysis | Categories |
|---|---|
| Conventional Radiomics | First-Order Statistics (FO) |
| Shape-Based Expression (SB) | |
| Gray Level Co-Occurrence Matrix (GLCM) | |
| Gray Level Dependence Matrix (GLDM) | |
| Gray Level Run Length Matrix (GLRLM) | |
| Gray Level Size Zone Matrix (GLSZM) | |
| Neighboring Gray Tone Difference Matrix (NGTDM) | |
| Laplacian Of Gaussian (LOG) | |
| Wavelet | |
| Deep Learning model-made Radiomics | Deep Convolutional Autoencoders |
| Accuracy of Different Multivariate Models for Breast Cancer Diagnosis in Ultrasound Images | |||||
|---|---|---|---|---|---|
| Methods | Hyperparameter | Radiomics | Classification Accuracy 1 (%) | Kappa Coefficient (κ) | t-Test 2 t-Statistic, Two-Tailed p-Value |
| Random Forest | No. est. = 10 | Conv | 69.03 (52.9–74.3) | 57.4 (±18.5) | – |
| Max depth = 2 | Deep | 67.7 (45.5–72.7) | 59.8 (±17.2) | 10.2, <0.0005 | |
| Rand. state = 10 | Conv + Deep | 71.7 (52.9–74.3) | 60.1 (±17.1) | 6.01, <0.0005 | |
| No. est. = 25 | Conv | 73.1 (59.8– 78.8) | 65.1 (±14.6) | – | |
| Max depth = 3 | Deep | 73.3 (59.9–76.9) | 64.7 (±14.7) | 10.1, <0.0005 | |
| Rand. state = 30 | Conv + Deep | 73.2 (59.8–76.7) | 64.9 (±14.8) | 7.9, <0.0005 | |
| No. est. = 15 | Conv | 75.6 (62.4–82.05) | 69.1 (±13.6) | – | |
| Max depth = 4 | Deep | 75.2 (62.4–81.2) | 69.8 (±13.5) | 16.9, <0.0005 | |
| Rand. state = 65 | Conv + Deep | 75.2 (62.4–80.4) | 69.7 (±13.2) | 19.7, <0.0005 | |
| No. est. = 22 | Conv | 78.8 (64.7–85.5) | 73.7 (±12.5) | – | |
| Max depth = 5 | Deep | 78.5 (64.5–83.9) | 73.9 (±12.2) | 21.6, <0.0005 | |
| Rand. state = 80 | Conv + Deep | 78.5 (65.1–84.1) | 74.0 (±12.0) | 29.8, <0.0005 | |
| No. est. = 22 | Conv | 83.9 (67.9–90.2) | 79.2 (±12.8) | – | |
| Max depth = 6 | Deep | 84.9 (66.6–90.9) | 78.4 (±12.1) | 30.7, <0.0005 | |
| Rand. state = 80 | Conv + Deep | 84.6 (66.8–89.9) | 79.6 (±12.2) | 37.8, <0.0005 | |
| No. est. = 22 | Conv | 85.1 (65.9–89.9) | 77.9 (±13.3) | – | |
| Max depth = 6 | Deep | 83.7 (65.1–89.8) | 78.1 (±12.5) | 33.2, <0.0005 | |
| Rand. state = 90 | Conv + Deep | 85.3 (65.3–89.1) | 78.8 (±12.7) | 39.1, <0.0005 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vigil, N.; Barry, M.; Amini, A.; Akhloufi, M.; Maldague, X.P.V.; Ma, L.; Ren, L.; Yousefi, B. Dual-Intended Deep Learning Model for Breast Cancer Diagnosis in Ultrasound Imaging. Cancers 2022, 14, 2663. https://doi.org/10.3390/cancers14112663
Vigil N, Barry M, Amini A, Akhloufi M, Maldague XPV, Ma L, Ren L, Yousefi B. Dual-Intended Deep Learning Model for Breast Cancer Diagnosis in Ultrasound Imaging. Cancers. 2022; 14(11):2663. https://doi.org/10.3390/cancers14112663
Chicago/Turabian StyleVigil, Nicolle, Madeline Barry, Arya Amini, Moulay Akhloufi, Xavier P. V. Maldague, Lan Ma, Lei Ren, and Bardia Yousefi. 2022. "Dual-Intended Deep Learning Model for Breast Cancer Diagnosis in Ultrasound Imaging" Cancers 14, no. 11: 2663. https://doi.org/10.3390/cancers14112663
APA StyleVigil, N., Barry, M., Amini, A., Akhloufi, M., Maldague, X. P. V., Ma, L., Ren, L., & Yousefi, B. (2022). Dual-Intended Deep Learning Model for Breast Cancer Diagnosis in Ultrasound Imaging. Cancers, 14(11), 2663. https://doi.org/10.3390/cancers14112663







