Performance Comparison of Deep Learning Autoencoders for Cancer Subtype Detection Using Multi-Omics Data
Abstract
Simple Summary
Abstract
1. Introduction
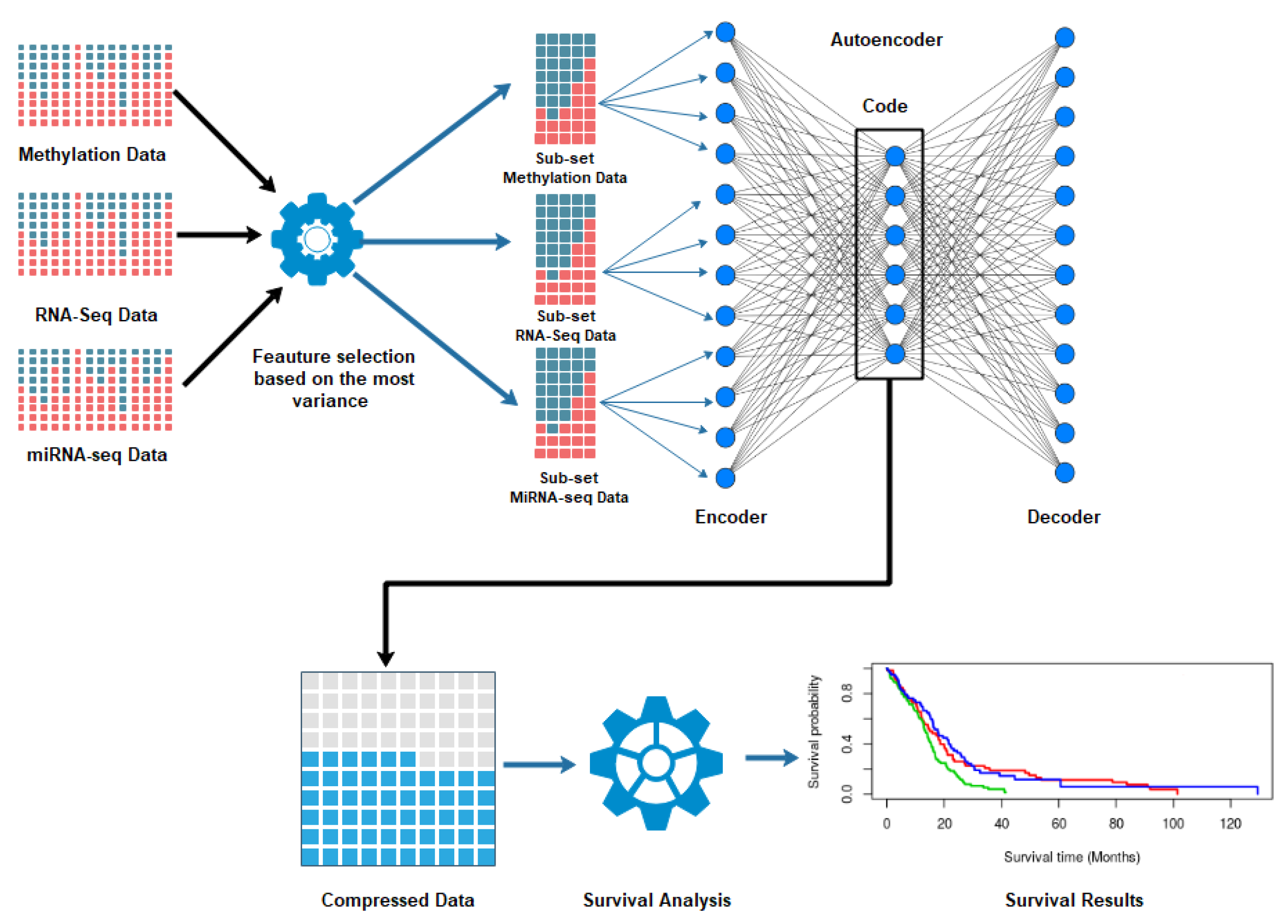
2. Materials and Methods
2.1. Dataset and Prepossessing
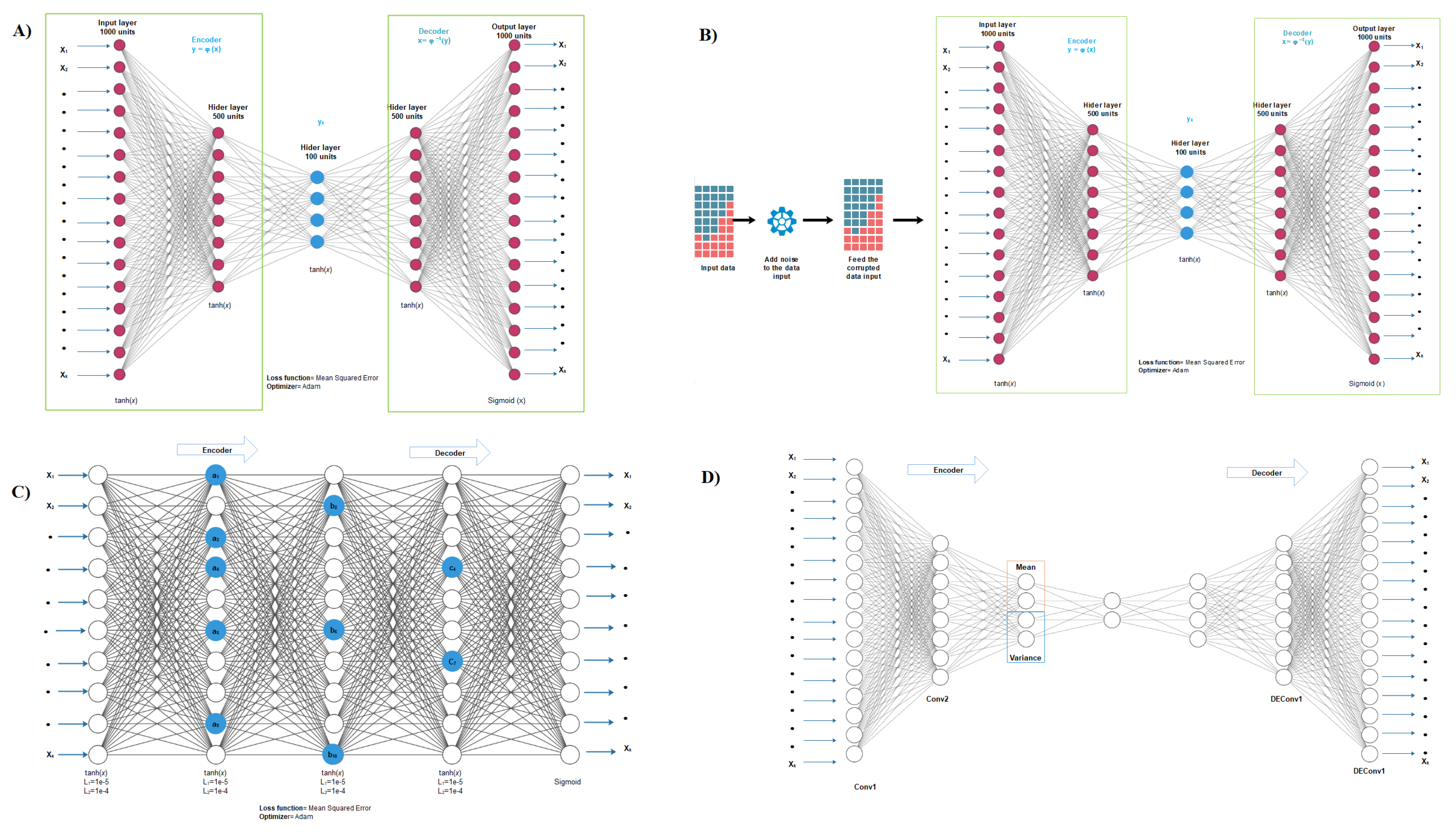
2.2. Autoencoder Construction
2.3. Autoencoder Implementation
2.4. Clustering and Subtyping
2.5. Evaluation Metrics for Subtyping
2.6. COX Model for Feature Selection
2.7. Comparison with Other Data Integration Methods
2.8. Differential Expression and Enrichment Analysis on Detected Subtypes
3. Results and Discussion
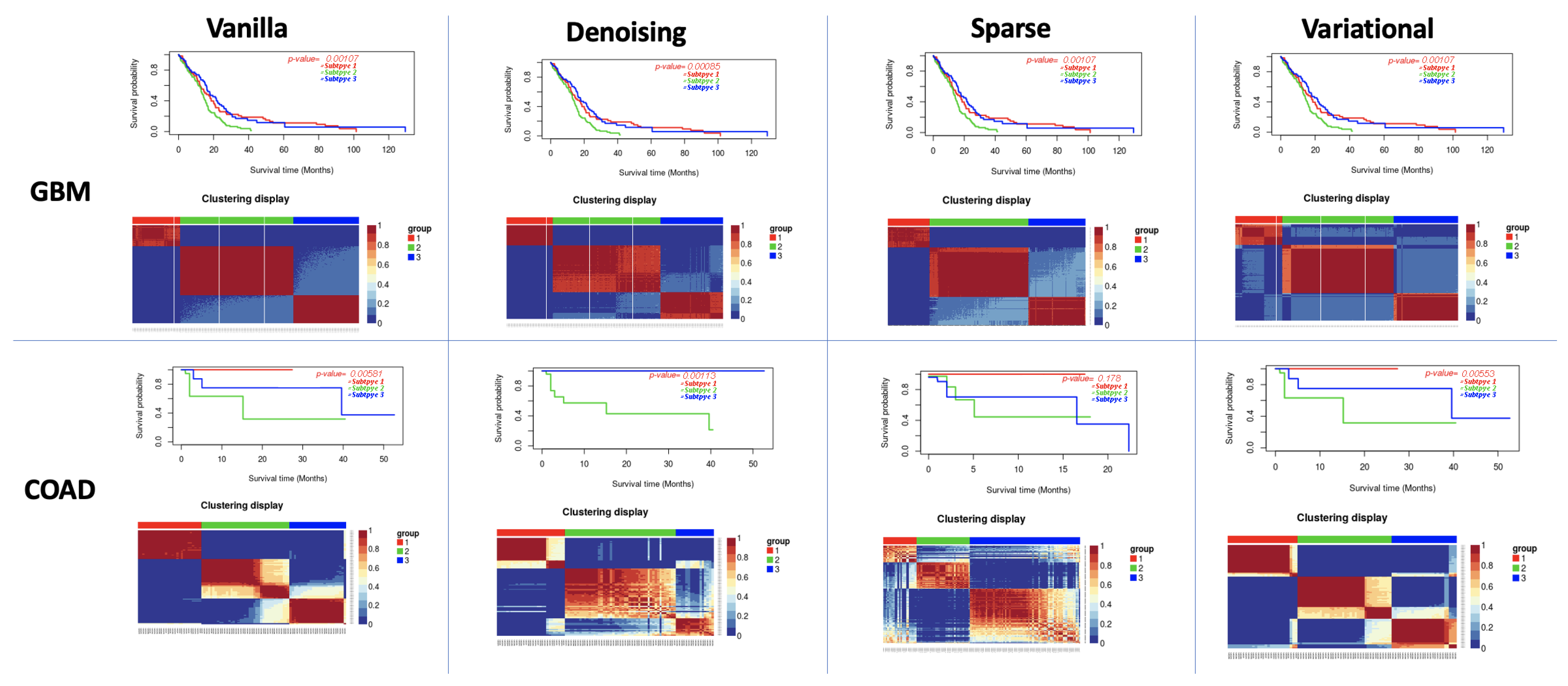
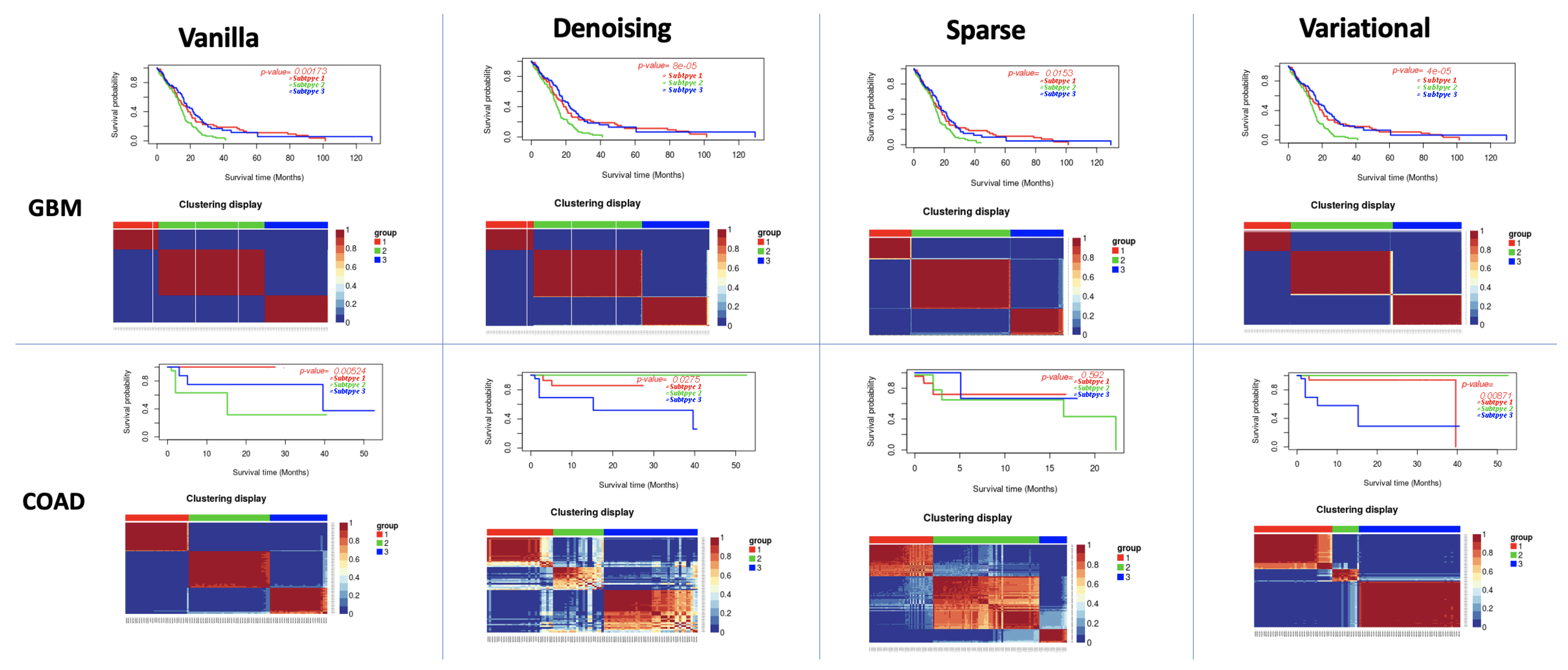
3.1. Performance of Different Autoencoders
3.2. Performance of Different Autoencoders for Gbm
3.3. Performance of Different Autoencoders for Coad
3.4. Effect of Different Similarity Measures
3.5. Effect of Supervised Feature Selection
3.6. Comparison with Other Subtype Detection Methods
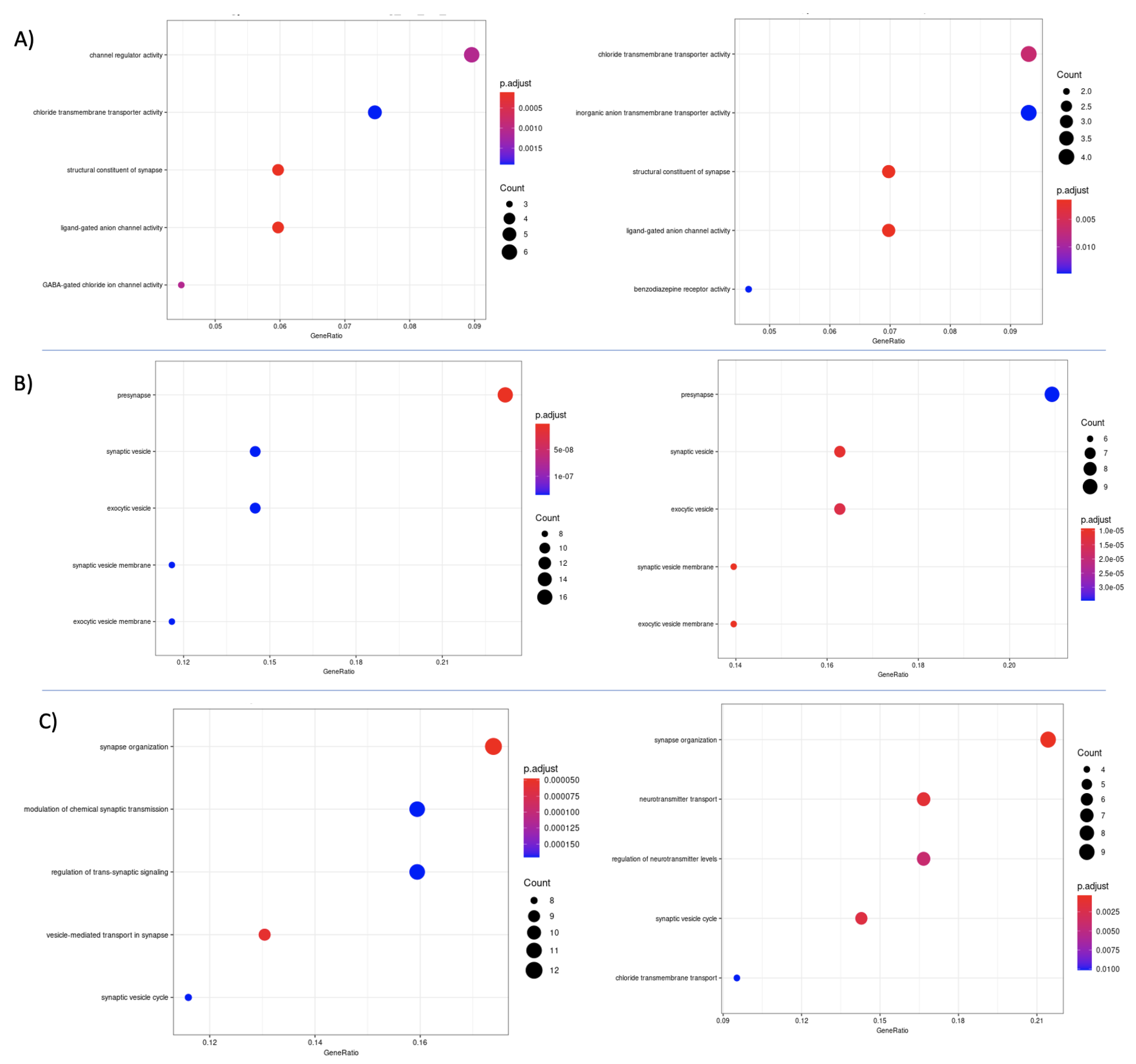
3.7. Differential Expression and Enrichment Analysis on Detected Subtypes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TCGA | The Cancer Genome Atlas |
| SNF | Similarity network fusion |
| DL | Deep learning |
| GBM | Glioblastoma multiforme |
| COAD | Colon Adenocarcinoma |
| KRCC | Kidney renal clear cell carcinoma |
| BIC | Breast invasive carcinoma |
| VAR | Maximum variance |
| PCA | Principal Component Analysis |
| PAM | Partitioning around medoids |
| DE | Differential expression |
| GO | Gene Ontology |
| CL1 | Cluster 1 |
| GEO | Gene Expression Omnibus |
| TME | surrounding tumor microenvironmen |
References
- Rana, P.; Berry, C.; Ghosh, P.; Fong, S.S. Recent advances on constraint-based models by integrating machine learning. Curr. Opin. Biotechnol. 2020, 64, 85–91. [Google Scholar] [CrossRef]
- Martini, P.; Chiogna, M.; Calura, E.; Romualdi, C. MOSClip: Multi-omic and survival pathway analysis for the identification of survival associated gene and modules. Nucleic Acids Res. 2019, 47, e80. [Google Scholar] [CrossRef]
- Ramazzotti, D.; Lal, A.; Wang, B.; Batzoglou, S.; Sidow, A. Multi-omic tumor data reveal diversity of molecular mechanisms that correlate with survival. Nat. Commun. 2018, 9, 1–14. [Google Scholar] [CrossRef]
- Ritchie, M.D.; Holzinger, E.R.; Li, R.; Pendergrass, S.A.; Kim, D. Methods of integrating data to uncover genotype–phenotype interactions. Nat. Rev. Genet. 2015, 16, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Chung, R.H.; Kang, C.Y. A multi-omics data simulator for complex disease studies and its application to evaluate multi-omics data analysis methods for disease classification. GigaScience 2019, 8, giz045. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Chaudhary, K.; Garmire, L.X. More is better: Recent progress in multi-omics data integration methods. Front. Genet. 2017, 8, 84. [Google Scholar] [CrossRef] [PubMed]
- Ebrahim, A.; Brunk, E.; Tan, J.; O’brien, E.J.; Kim, D.; Szubin, R.; Lerman, J.A.; Lechner, A.; Sastry, A.; Bordbar, A.; et al. Multi-omic data integration enables discovery of hidden biological regularities. Nat. Commun. 2016, 7, 13091. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333. [Google Scholar] [CrossRef] [PubMed]
- Chiu, Y.C.; Chen, H.I.H.; Zhang, T.; Zhang, S.; Gorthi, A.; Wang, L.J.; Huang, Y.; Chen, Y. Predicting drug response of tumors from integrated genomic profiles by deep neural networks. BMC Med. Genom. 2019, 12, 18. [Google Scholar]
- Luck, M.; Sylvain, T.; Cardinal, H.; Lodi, A.; Bengio, Y. Deep learning for patient-specific kidney graft survival analysis. arXiv 2017, arXiv:1705.10245. [Google Scholar]
- Ng, A.; Ngiam, J.; Foo, C.Y.; Mai, Y.; Suen, C.; Coates, A.; Maas, A.; Hannun, A.; Huval, B.; Wang, T.; et al. Stanford Deep Learning Tutorial; Stanford University: Stanford, CA, USA, 2015; Available online: http://ufldl.stanford.edu/tutorial/unsupervised/Autoencoders/ (accessed on 1 December 2020).
- Marivate, V.N.; Nelwamodo, F.V.; Marwala, T. Autoencoder, principal component analysis and support vector regression for data imputation. arXiv 2007, arXiv:0709.2506. [Google Scholar]
- Mirza, B.; Wang, W.; Wang, J.; Choi, H.; Chung, N.C.; Ping, P. Machine learning and integrative analysis of biomedical big data. Genes 2019, 10, 87. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhao, Y.; Liao, X.; Shi, W.; Li, K.; Zou, Q.; Peng, S. Deep learning in omics: A survey and guideline. Briefings Funct. Genom. 2018, 18, 41–57. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Ding, Z.; Fu, Y. Feature selection guided auto-encoder. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Chaudhary, K.; Poirion, O.B.; Lu, L.; Garmire, L.X. Deep learning–based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res. 2018, 24, 1248–1259. [Google Scholar] [CrossRef]
- Tan, J.; Ung, M.; Cheng, C.; Greene, C.S. Unsupervised feature construction and knowledge extraction from genome-wide assays of breast cancer with denoising autoencoders. In Proceedings of the Pacific Symposium on Biocomputing Co-Chairs, Kohala Coast, HI, USA, 4–8 January 2015; World Scientific: Singapore, 2014; pp. 132–143. [Google Scholar]
- Ronen, J.; Hayat, S.; Akalin, A. Evaluation of colorectal cancer subtypes and cell lines using deep learning. Life Sci. Alliance 2019, 2. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Sun, K.; Yang, X.; Dai, C.; Guo, Y. Integrated multi-omics analysis using variational autoencoders: Application to pan-cancer classification. In Proceedings of the 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), IEEE, San Diego, CA, USA, 18–21 November 2019; pp. 765–769. [Google Scholar]
- Simidjievski, N.; Bodnar, C.; Tariq, I.; Scherer, P.; Andres Terre, H.; Shams, Z.; Jamnik, M.; Liò, P. Variational autoencoders for cancer data integration: Design principles and computational practice. Front. Genet. 2019, 10, 1205. [Google Scholar] [CrossRef] [PubMed]
- Sheet, S.; Ghosh, A.; Ghosh, R.; Chakrabarti, A. Identification of Cancer Mediating Biomarkers using Stacked Denoising Autoencoder Model-An Application on Human Lung Data. Procedia Comput. Sci. 2020, 167, 686–695. [Google Scholar] [CrossRef]
- Makki, J. Diversity of breast carcinoma: Histological subtypes and clinical relevance. Clin. Med. Insights Pathol. 2015, 8, CPath.S31563. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2016. CA Cancer J. Clin. 2016, 66, 7–30. [Google Scholar] [CrossRef]
- Society, A.C. Colorectal Cancer Facts & Figures 2014–2016; American Cancer Society: Atlanta, GA, USA, 2014. [Google Scholar]
- Acs, A. Cancer Facts and Figures 2010; American Cancer Society, National Home Office: Atlanta, GA, USA, 2010; pp. 1–44. [Google Scholar]
- Chow, W.H.; Dong, L.M.; Devesa, S.S. Epidemiology and risk factors for kidney cancer. Nat. Rev. Urol. 2010, 7, 245. [Google Scholar] [CrossRef] [PubMed]
- Colaprico, A.; Silva, T.C.; Olsen, C.; Garofano, L.; Cava, C.; Garolini, D.; Sabedot, T.S.; Malta, T.M.; Pagnotta, S.M.; Castiglioni, I.; et al. TCGAbiolinks: An R/Bioconductor package for integrative analysis of TCGA data. Nucleic Acids Res. 2016, 44, e71. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Le, T.D.; Liu, L.; Su, N.; Wang, R.; Sun, B.; Colaprico, A.; Bontempi, G.; Li, J. CancerSubtypes: An R/Bioconductor package for molecular cancer subtype identification, validation and visualization. Bioinformatics 2017, 33, 3131–3133. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Ma, S. A selective review of robust variable selection with applications in bioinformatics. Briefings Bioinform. 2015, 16, 873–883. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Doersch, C. Tutorial on variational autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 1 August 2020).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/tutorials/generative/autoencoder (accessed on 1 November 2020).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1965; Volume 1, pp. 281–297. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Partitioning around medoids (program pam). In Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990; Volume 344, pp. 68–125. [Google Scholar]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. Methodol. 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, F.; Ren, J.; Li, X.; Jiang, Y.; Ma, S. A selective review of multi-level omics data integration using variable selection. High-Throughput 2019, 8, 4. [Google Scholar] [CrossRef]
- Smyth, G.K. Limma: Linear models for microarray data. In Bioinformatics and Computational Biology Solutions Using R and Bioconductor; Springer: Berlin/Heidelberg, Germany, 2005; pp. 397–420. [Google Scholar]
- Yu, G.; Wang, L.G.; Han, Y.; He, Q.Y. clusterProfiler: An R package for comparing biological themes among gene clusters. Omics J. Integr. Biol. 2012, 16, 284–287. [Google Scholar] [CrossRef]
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler, H.; Cherry, J.M.; Davis, A.P.; Dolinski, K.; Dwight, S.S.; Eppig, J.T.; et al. Gene ontology: Tool for the unification of biology. Nat. Genet. 2000, 25, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Verhaak, R.G.; Hoadley, K.A.; Purdom, E.; Wang, V.; Qi, Y.; Wilkerson, M.D.; Miller, C.R.; Ding, L.; Golub, T.; Mesirov, J.P.; et al. Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell 2010, 17, 98–110. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zheng, H.; Wang, J.; Wang, C.; Wu, F.X. Integrating omics data with a multiplex network-based approach for the identification of cancer subtypes. IEEE Trans. Nanobiosci. 2016, 15, 335–342. [Google Scholar] [CrossRef] [PubMed]
- Ji’an Yang, L.W.; Xu, Z.; Wu, L.; Liu, B.; Wang, J.; Tian, D.; Xiong, X.; Chen, Q. Integrated analysis to evaluate the prognostic value of signature mRNAs in glioblastoma multiforme. Front. Genet. 2020, 11, 253. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Lv, X.; Jiang, Y.; Li, G.; Qiao, Q. Identification of aberrantly methylated differentially expressed genes in glioblastoma multiforme and their association with patient survival. Exp. Ther. Med. 2019, 18, 2140–2152. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Cannons, J.L.; Dutta, M.; Griffiths, G.M.; Schwartzberg, P.L. Positive and negative signaling through SLAM receptors regulate synapse organization and thresholds of cytolysis. Immunity 2012, 36, 1003–1016. [Google Scholar] [CrossRef] [PubMed]
- Xiong, D.D.; Xu, W.Q.; He, R.Q.; Dang, Y.W.; Chen, G.; Luo, D.Z. In silico analysis identified miRNA-based therapeutic agents against glioblastoma multiforme. Oncol. Rep. 2019, 41, 2194–2208. [Google Scholar] [CrossRef]
- Südhof, T.C. Towards an understanding of synapse formation. Neuron 2018, 100, 276–293. [Google Scholar] [CrossRef]
- Dabrowski, A.; Terauchi, A.; Strong, C.; Umemori, H. Distinct sets of FGF receptors sculpt excitatory and inhibitory synaptogenesis. Development 2015, 142, 1818–1830. [Google Scholar] [CrossRef] [PubMed]
- Yool, A.J.; Ramesh, S.A. Molecular targets for combined therapeutic strategies to limit glioblastoma cell migration and invasion. Front. Pharmacol. 2020, 11, 358. [Google Scholar] [CrossRef]
- Corsi, L.; Mescola, A.; Alessandrini, A. Glutamate receptors and glioblastoma multiforme: An old “Route” for new perspectives. Int. J. Mol. Sci. 2019, 20, 1796. [Google Scholar] [CrossRef] [PubMed]
- Graner, M.W. Roles of extracellular vesicles in high-grade gliomas: Tiny particles with outsized influence. Annu. Rev. Genom. Hum. Genet. 2019, 20, 331–357. [Google Scholar] [CrossRef] [PubMed]
- Van der Pol, E.; Böing, A.N.; Harrison, P.; Sturk, A.; Nieuwland, R. Classification, functions, and clinical relevance of extracellular vesicles. Pharmacol. Rev. 2012, 64, 676–705. [Google Scholar] [CrossRef] [PubMed]
- Yáñez-Mó, M.; Siljander, P.R.M.; Andreu, Z.; Bedina Zavec, A.; Borràs, F.E.; Buzas, E.I.; Buzas, K.; Casal, E.; Cappello, F.; Carvalho, J.; et al. Biological properties of extracellular vesicles and their physiological functions. J. Extracell. Vesicles 2015, 4, 27066. [Google Scholar] [CrossRef]
- Simon, T.; Jackson, E.; Giamas, G. Breaking through the glioblastoma micro-environment via extracellular vesicles. Oncogene 2020, 39, 4477–4490. [Google Scholar] [CrossRef]
| Dataset | Number of Cluster | Autoencoder Vanilla | Autoencoder Denoising | Autoencoder Sparse | Autoencoder Variational | ||||
|---|---|---|---|---|---|---|---|---|---|
| PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | ||
| GBM | 3 | 0.002 | 0.001 | 9 × 10 | 9 × 10 | 0.015 | 0.001 | 5 × 10 | 0.001 |
| 4 | 0.002 | 2 × 10 | 0.06 | 2 × 10 | 0.109 | 6 × 10 | 0.006 | 6 × 10 | |
| 5 | 2 × 10 | 1 × 10 | 0.001 | 1 × 10 | 0.015 | 7 × 10 | 5 × 10 | 3 × 10 | |
| 6 | 3 × 10 | 2 × 10 | 0.003 | 4 × 10 | 0.018 | 1 × 10 | 1 × 10 | 2 × 10 | |
| BIC | 3 | 0.0667 | 0.664 | 0.193 | 0.508 | 0.089 | 0.078 | 0.271 | 0.443 |
| 4 | 0.0049 | 0.183 | 0.145 | 0.0275 | 0.016 | 0.304 | 0.0659 | 0.194 | |
| 5 | 0.322 | 0.0273 | 0.0481 | 0.0476 | 0.003 | 0.37 | 0.103 | 0.219 | |
| 6 | 0.212 | 0.621 | 0.0306 | 0.0457 | 0.007 | 0.0012 | 0.367 | 0.441 | |
| COAD | 3 | 0.00524 | 0.00581 | 0.0275 | 0.00011 | 0.592 | 0.178 | 0.00871 | 0.0053 |
| 4 | 0.0144 | 0.0135 | 0.044 | 0.0007 | 0.007 | 0.221 | 0.054 | 0.0181 | |
| 5 | 0.0309 | 0.031 | 0.0159 | 0.0041 | 0.0094 | 0.292 | 0.0951 | 0.0006 | |
| 6 | 0.0241 | 0.0336 | 0.0341 | 0.00547 | 0.97 | 0.212 | 0.0802 | 0.014 | |
| KRCC | 3 | 0.288 | 0.392 | 0.165 | 0.135 | 0.346 | 0.229 | 0.00608 | 0.0266 |
| 4 | 0.471 | 0.6144 | 0.437 | 0.47 | 0.614 | 0.174 | 0.0353 | 0.0393 | |
| 5 | 0.665 | 0.347 | 0.691 | 0.036 | 0.508 | 0.321 | 0.131 | 0.0141 | |
| 6 | 0.369 | 0.527 | 0.268 | 0.068 | 0.541 | 0.349 | 0.0669 | 0.0324 | |
| Dataset | Number of Cluster | Autoencoder Vanilla | Autoencoder Denoising | Autoencoder Sparse | Autoencoder Variational | ||||
|---|---|---|---|---|---|---|---|---|---|
| PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | ||
| GBM | 3 | 1 | 0.91 | 0.98 | 0.91 | 0.97 | 0.83 | 0.98 | 0.87 |
| 4 | 0.84 | 0.58 | 0.77 | 0.6 | 0.66 | 0.59 | 0.95 | 0.6 | |
| 5 | 0.8 | 0.62 | 0.82 | 0.73 | 0.71 | 0.64 | 0.88 | 0.51 | |
| 6 | 0.73 | 0.57 | 0.77 | 0.73 | 0.75 | 0.61 | 0.85 | 0.64 | |
| BIC | 3 | 0.96 | 0.86 | 0.53 | 0.65 | 0.77 | 0.82 | 0.95 | 0.81 |
| 4 | 0.91 | 0.87 | 0.67 | 0.81 | 0.84 | 0.79 | 0.85 | 0.78 | |
| 5 | 0.69 | 0.63 | 0.63 | 0.67 | 0.69 | 0.67 | 0.65 | 0.74 | |
| 6 | 0.67 | 0.74 | 0.61 | 0.6 | 0.66 | 0.55 | 0.59 | 0.74 | |
| COAD | 3 | 0.97 | 0.82 | 0.7 | 0.67 | 0.75 | 0.58 | 0.83 | 0.82 |
| 4 | 0.65 | 0.7 | 0.74 | 0.57 | 0.69 | 0.53 | 0.6 | 0.67 | |
| 5 | 0.8 | 0.68 | 0.72 | 0.59 | 0.56 | 0.45 | 0.96 | 0.73 | |
| 6 | 0.89 | 0.69 | 0.59 | 0.527 | 0.43 | 0.41 | 0.69 | 0.65 | |
| KRCC | 3 | 0.83 | 0.77 | 0.58 | 0.48 | 0.65 | 0.64 | 0.95 | 0.63 |
| 4 | 0.78 | 0.8 | 0.65 | 0.56 | 0.81 | 0.68 | 0.95 | 0.49 | |
| 5 | 0.55 | 0.67 | 0.59 | 0.46 | 0.79 | 0.64 | 0.78 | 0.58 | |
| 6 | 0.7 | 0.59 | 0.65 | 0.53 | 0.75 | 0.62 | 0.67 | 0.68 | |
| Dataset | Number of Cluster | Autoencoder Vanilla | Autoencoder Denoising | Autoencoder Sparse | Autoencoder Variational | ||||
|---|---|---|---|---|---|---|---|---|---|
| PAM/Spearman | k-Means/ Euclidean | PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | PAM/Spearman | k-Means/Euclidean | ||
| COAD | 3 | 0.0002 | 0.0027 | 0.0025 | 0.0025 | 0.005 | 0.005 | 0.0024 | 0.0027 |
| 4 | 0.0081 | 0.0067 | 0.0076 | 0.0076 | 0.162 | 0.0072 | 9 × 10 | 0.012 | |
| 5 | 0.016 | 0.016 | 0.0097 | 0.0097 | 0.0253 | 0.0017 | 0.0032 | 0.026 | |
| 6 | 0.0323 | 0.0217 | 0.0205 | 0.015 | 0.0007 | 0.0082 | 0.0082 | 0.051 | |
| KRCC | 3 | 4 × 10 | 7 × 10 | 1 × 10 | 8 × 10 | 0.1 | 1 × 10 | 0.006 | 0.026 |
| 4 | 5 × 10 | 3 × 10 | 9 × 10 | 1 × 10 | 0.1 | 5 × 10 | 0.035 | 0.039 | |
| 5 | 9 × 10 | 3 × 10 | 1 × 10 | 2 × 10 | 0.5 | 2 × 10 | 0.1 | 0.014 | |
| 6 | 3 × 10 | 9 × 10 | 1 × 10 | 6 × 10 | 0.4 | 3 × 10 | 0.67 | 0.032 | |
| Silhoutte Index Result | |||||||||
| COAD | 3 | 0.99 | 0.91 | 1 | 0.85 | 1 | 0.9 | 0.88 | 0.96 |
| 4 | 0.95 | 0.76 | 0.98 | 0.76 | 0.98 | 0.76 | 0.85 | 0.78 | |
| 5 | 0.98 | 0.67 | 0.83 | 0.68 | 0.82 | 0.65 | 0.93 | 0.78 | |
| 6 | 0.87 | 0.63 | 0.87 | 0.6 | 0.77 | 0.63 | 0.81 | 0.6 | |
| KRCC | 3 | 0.74 | 0.82 | 0.77 | 0.83 | 0.28 | 0.1 | 0.95 | 0.63 |
| 4 | 0.68 | 0.74 | 0.69 | 0.8 | 0.38 | 0.1 | 0.95 | 0.49 | |
| 5 | 0.64 | 0.71 | 0.66 | 0.64 | 0.48 | 0.22 | 0.78 | 0.58 | |
| 6 | 0.54 | 0.62 | 0.75 | 0.6 | 0.55 | 0.26 | 0.66 | 0.68 | |
| Principal Component Analysis Results | |||||||
|---|---|---|---|---|---|---|---|
| Dataset | Number of Cluster | PCA | Kernel PCA | Sparse PCA | |||
| p-Value | Silhoutte Index | p-Value | Silhoutte Index | p-Value | Silhoutte Index | ||
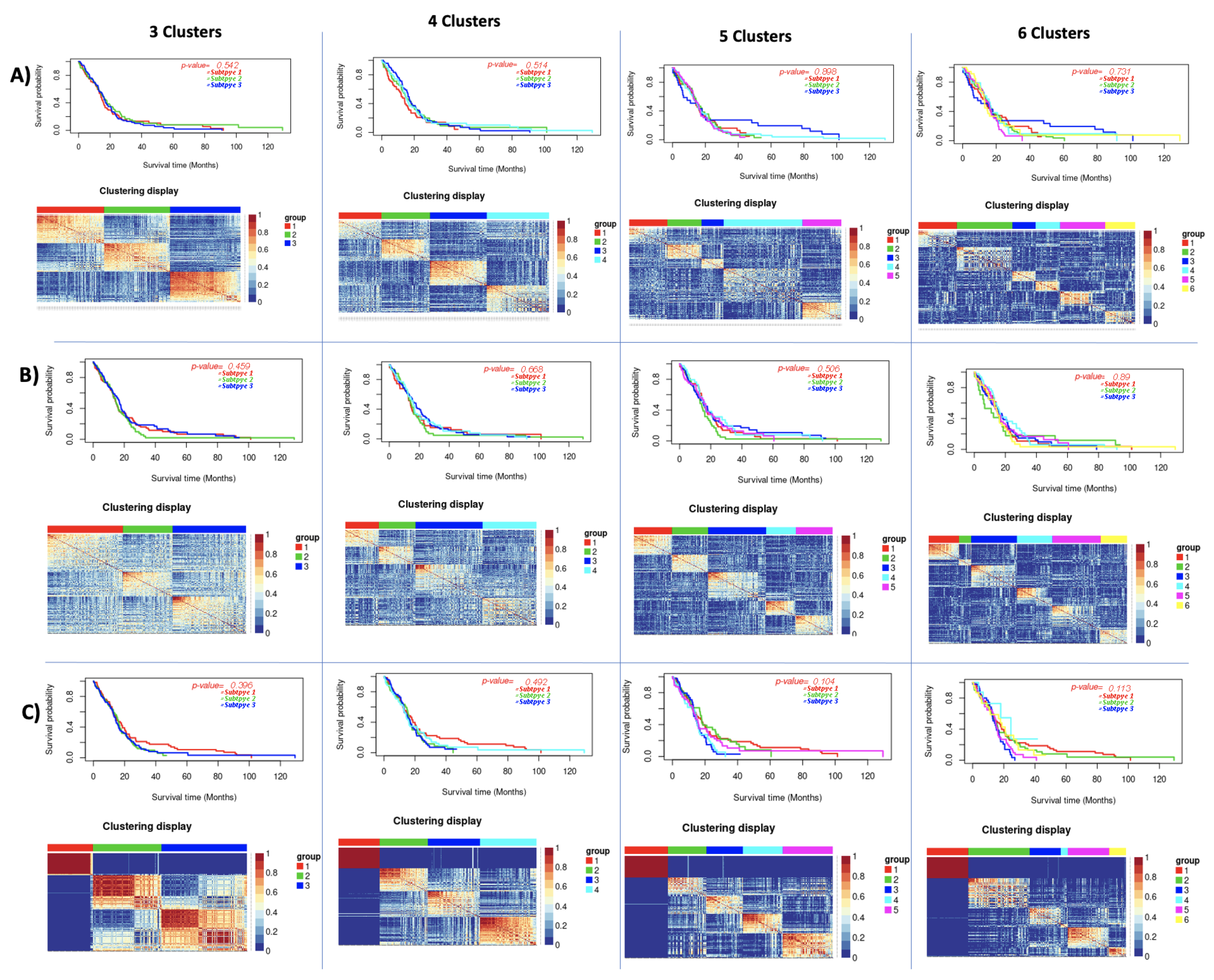
| GBM | 3 | 0.542 | 0.56 | 0.459 | 0.23 | 0.396 | 0.65 |
| 4 | 0.514 | 0.42 | 0.668 | 0.31 | 0.492 | 0.61 | |
| 5 | 0.989 | 0.35 | 0.506 | 0.5 | 0.104 | 0.61 | |
| 6 | 0.731 | 0.38 | 0.89 | 0.5 | 0.113 | 0.58 | |
| Similarity Network Fusion Results | |||||||
| Dataset | Number of Cluster | p-Value | Silhoutte Index | ||||
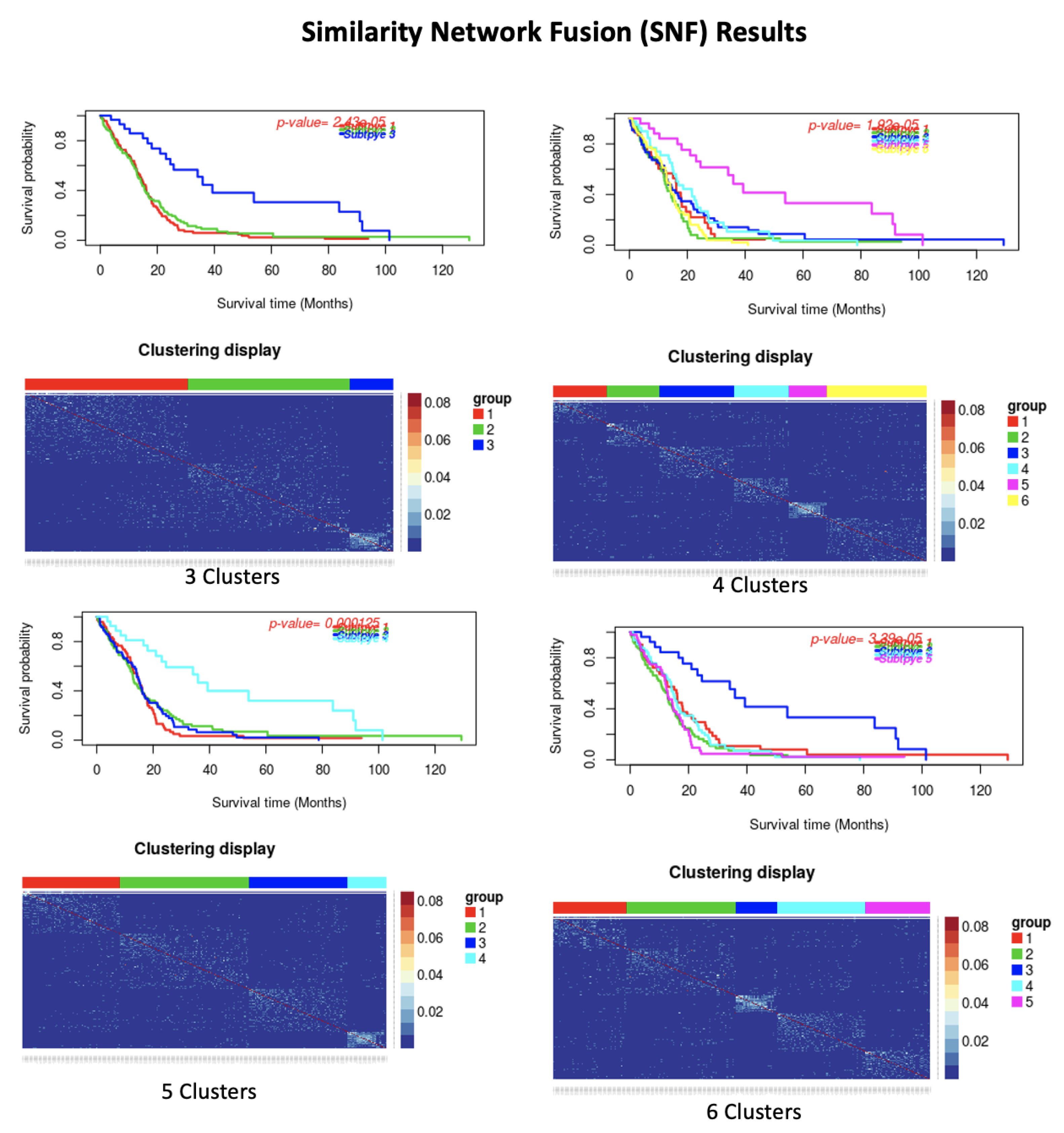
| GBM | 3 | 2.43 × 10 | 0.46 | ||||
| 4 | 0.001 | 0.47 | |||||
| 5 | 3.39 × 10 | 0.47 | |||||
| 6 | 1.92 × 10 | 0.46 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franco, E.F.; Rana, P.; Cruz, A.; Calderón, V.V.; Azevedo, V.; Ramos, R.T.J.; Ghosh, P. Performance Comparison of Deep Learning Autoencoders for Cancer Subtype Detection Using Multi-Omics Data. Cancers 2021, 13, 2013. https://doi.org/10.3390/cancers13092013
Franco EF, Rana P, Cruz A, Calderón VV, Azevedo V, Ramos RTJ, Ghosh P. Performance Comparison of Deep Learning Autoencoders for Cancer Subtype Detection Using Multi-Omics Data. Cancers. 2021; 13(9):2013. https://doi.org/10.3390/cancers13092013
Chicago/Turabian StyleFranco, Edian F., Pratip Rana, Aline Cruz, Víctor V. Calderón, Vasco Azevedo, Rommel T. J. Ramos, and Preetam Ghosh. 2021. "Performance Comparison of Deep Learning Autoencoders for Cancer Subtype Detection Using Multi-Omics Data" Cancers 13, no. 9: 2013. https://doi.org/10.3390/cancers13092013
APA StyleFranco, E. F., Rana, P., Cruz, A., Calderón, V. V., Azevedo, V., Ramos, R. T. J., & Ghosh, P. (2021). Performance Comparison of Deep Learning Autoencoders for Cancer Subtype Detection Using Multi-Omics Data. Cancers, 13(9), 2013. https://doi.org/10.3390/cancers13092013








