Is There One Key Step in the Metastatic Cascade?
Abstract
:Simple Summary
Abstract
1. Introduction
2. Material and Methods
2.1. The Drake Equation
2.2. The Metastatic Drake Equation
2.3. Parameters Estimation from the Literature
2.4. Numerical Simulations
2.4.1. Twenty-Four-Hour Time Scale
2.4.2. Six-Month Time Scale
3. Results
3.1. 24-Hour Time Scale
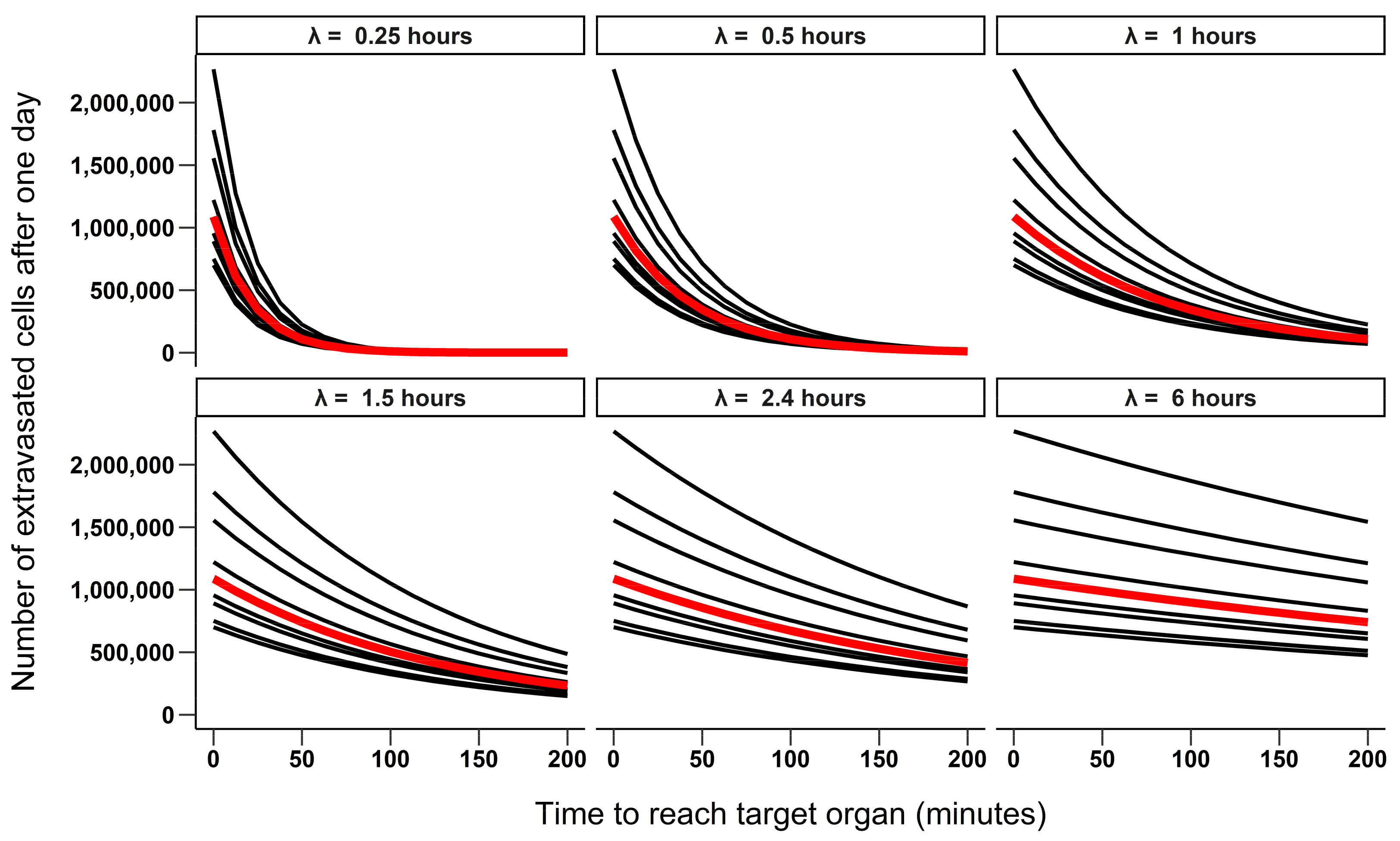
3.1.1. Simulating the Number of Extravasated Cells as Function of Half-Life and Time to Reach the Target Organ
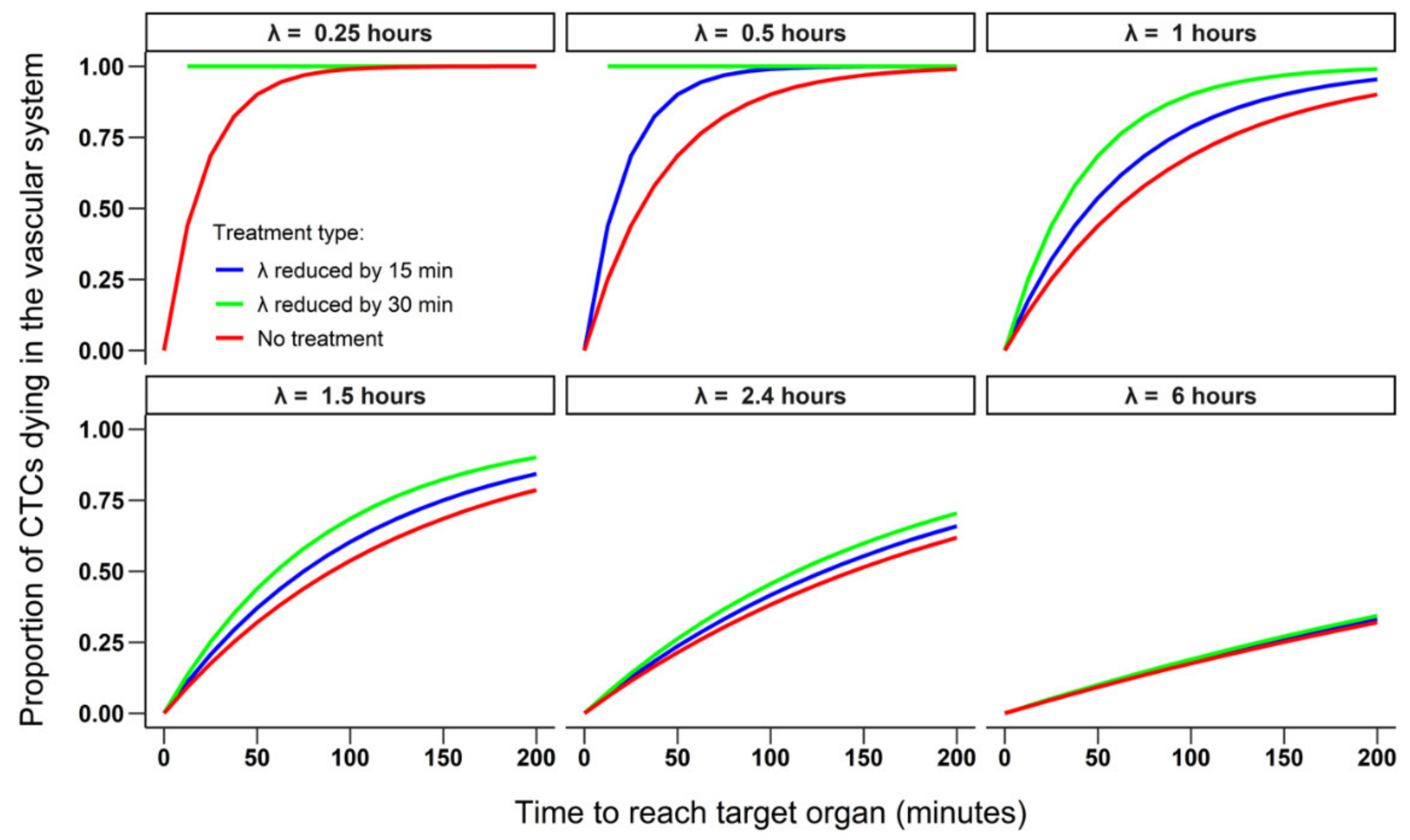
3.1.2. Simulating the Effect of a Treatment on the Survival and Extravasation of CTCs
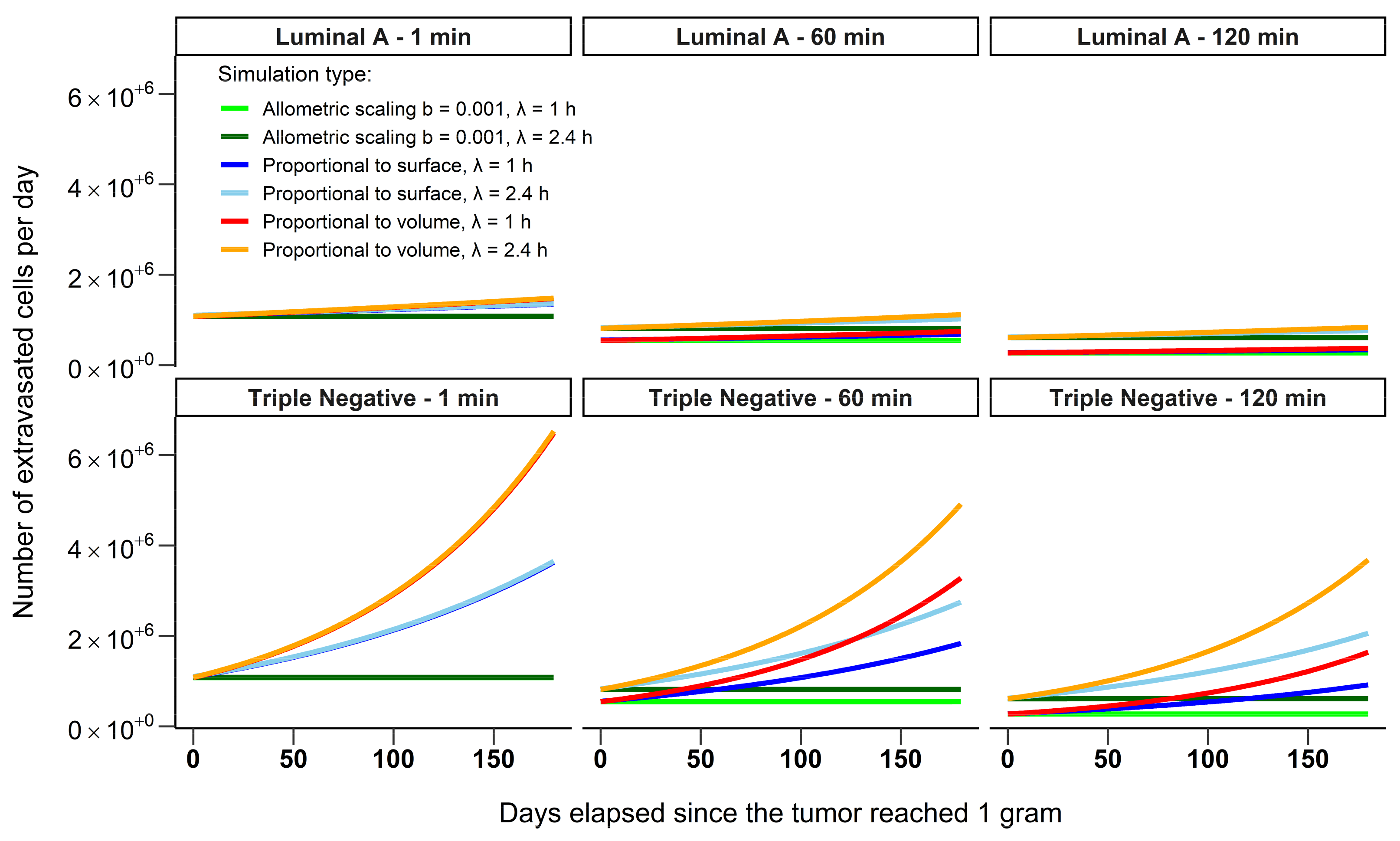
3.2. Six-Month Time Scale
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dillekås, H.; Rogers, M.S.; Straume, O. Are 90% of deaths from cancer caused by metastases? Cancer Med. 2019, 8, 5574–5576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bohl, C.R.; Harihar, S.; Denning, W.L.; Sharma, R.; Welch, D.R. Metastasis suppressors in breast cancers: Mechanistic insights and clinical potential. J. Mol. Med. 2014, 92, 13–30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, I.; Steeg, P.S. Metastasis suppressors: Functional pathways. Lab. Investig. 2018, 98, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Stoletov, K.; Beatty, P.H.; Lewis, J.D. Novel therapeutic targets for cancer metastasis. Expert Rev. Anticancer Ther. 2020, 20, 97–109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lambert, A.W.; Pattabiraman, D.R.; Weinberg, R.A. Emerging biological principles of metastasis. Cell 2017, 168, 670–691. [Google Scholar] [CrossRef] [Green Version]
- Eslami, S.Z.; Majidzadeh, A.K.; Halvaei, S.; Babapirali, F.; Esmaeili, R. Microbiome and breast cancer: New role for an ancient population. Front. Oncol. 2020, 10, 120. [Google Scholar] [CrossRef] [Green Version]
- Franssen, L.C.; Lorenzi, T.; Burgess, A.E.F.; Chaplain, M.A.J. A mathematical framework for modelling the metastatic spread of cancer. Bull. Math. Biol. 2019, 81, 1965–2010. [Google Scholar] [CrossRef] [Green Version]
- Ganesh, K.; Massagué, J. Targeting metastatic cancer. Nat. Med. 2021, 27, 34–44. [Google Scholar] [CrossRef]
- Chambers, A.F.; Groom, A.C.; MacDonald, I.C. Dissemination and growth of cancer cells in metastatic sites. Nat. Rev. Cancer 2002, 2, 563–572. [Google Scholar] [CrossRef]
- Mehlen, P.; Puisieux, A. Metastasis: A question of life or death. Nat. Rev. Cancer 2006, 6, 449–458. [Google Scholar] [CrossRef]
- Arnal, A.; Ujvari, B.; Crespi, B.; Gatenby, R.A.; Tissot, T.; Vittecoq, M.; Ewald, P.W.; Casali, A.; Ducasse, H.; Jacqueline, C.; et al. Evolutionary perspective of cancer: Myth, metaphors, and reality. Evol. Appl. 2015, 8, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Valastyan, S.; Weinberg, R.A. Tumor metastasis: Molecular insights and evolving paradigms. Cell 2011, 147, 275–292. [Google Scholar] [CrossRef] [Green Version]
- Dujon, A.M.; Aktipis, A.; Alix-Panabières, C.; Amend, S.R.; Boddy, A.M.; Brown, J.S.; Capp, J.; DeGregori, J.; Ewald, P.; Gatenby, R.; et al. Identifying key questions in the ecology and evolution of cancer. Evol. Appl. 2021, 14, 877–892. [Google Scholar] [CrossRef] [PubMed]
- Luzzi, K.J.; MacDonald, I.C.; Schmidt, E.E.; Kerkvliet, N.; Morris, V.L.; Chambers, A.F.; Groom, A.C. Multistep nature of metastatic inefficiency: Dormancy of solitary cells after successful extravasation and limited survival of early micrometastases. Am. J. Pathol. 1998, 153, 865–873. [Google Scholar] [CrossRef]
- Warner, H.V.; Sivakumar, N.; Peirce, S.M.; Lazzara, M.J. Multiscale computational models of cancer. Curr. Opin. Biomed. Eng. 2019, 11, 137–144. [Google Scholar] [CrossRef]
- Drake, F.D. Discussion at space science board, national academy of sciences. In Proceedings of the Conference on Extraterrestrial Intelligent Life, Green Bank, WV, USA, 1–2 November 1961. [Google Scholar]
- Sandberg, A.; Drexler, E.; Ord, T. Dissolving the Fermi Paradox. arXiv 2018, arXiv:1806.02404. [Google Scholar]
- Hunter, K.W.; Crawford, N.P.; Alsarraj, J. Mechanisms of metastasis. Breast Cancer Res. 2008, 10, S2. [Google Scholar] [CrossRef] [Green Version]
- Dujon, A.M.; Bramwell, G.; Roche, B.; Thomas, F.; Ujvari, B. Transmissible cancers in mammals and bivalves: How many examples are there? BioEssays 2020, 43, 2000222. [Google Scholar] [CrossRef]
- Naxerova, K.; Jain, R.K. Using tumour phylogenetics to identify the roots of metastasis in humans. Nat. Rev. Clin. Oncol. 2015, 12, 258–272. [Google Scholar] [CrossRef]
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef] [Green Version]
- Butler, T.P.; Gullino, P.M. Quantitation of cell shedding into efferent blood of mammary adenocarcinoma. Cancer Res. 1975, 35, 512–516. [Google Scholar] [PubMed]
- Meng, S.; Tripathy, D.; Frenkel, E.P.; Shete, S.; Naftalis, E.Z.; Huth, J.F.; Beitsch, P.D.; Leitch, M.; Hoover, S.; Euhus, D.; et al. Circulating tumor cells in patients with breast cancer dormancy. Clin. Cancer Res. 2004, 10, 8152–8162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, M.C.; Whisler, J.A.; Jeon, J.S.; Kamm, R.D. Mechanisms of tumor cell extravasation in an in vitro microvascular network platform. Integr. Biol. 2013, 5, 1262–1271. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.S.; Bersini, S.; Gilardi, M.; Dubini, G.; Charest, J.L.; Moretti, M.; Kamm, R.D. Human 3D vascularized organotypic microfluidic assays to study breast cancer cell extravasation. Proc. Natl. Acad. Sci. USA 2015, 112, E818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martin, M.D.; Kremers, G.-J.; Short, K.W.; Rocheleau, J.V.; Xu, L.; Piston, D.W.; Matrisian, L.M.; Gorden, D.L. Rapid extravasation and establishment of breast cancer micrometastases in the liver microenvironment. Mol. Cancer Res. 2010, 8, 1319–1327. [Google Scholar] [CrossRef] [Green Version]
- Esteva-Font, C.; Jin, B.J.; Verkman, A.S. Aquaporin-1 gene deletion reduces breast tumor growth and lung metastasis in tumor-producing MMTV-PyVT mice. FASEB J. 2014, 28, 1446–1453. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H.; Kim, Y.S.; Han, W.; Ryu, H.S.; Chang, J.M.; Cho, N.; Moon, W.K. Tumor growth rate of invasive breast cancers during wait times for surgery assessed by ultrasonography. Medicine 2016, 95, e4874. [Google Scholar] [CrossRef]
- Lloyd, M.C.; Gatenby, R.A.; Brown, J.S. Ecology of the Metastatic Process. In Ecology and Evolution of Cancer; Academic Press: Cambridge, MA, USA, 2017; pp. 153–165. ISBN 9780128043806. [Google Scholar]
- Nguyen, D.X.; Bos, P.D.; Massagué, J. Metastasis: From dissemination to organ-specific colonization. Nat. Rev. Cancer 2009, 9, 274–284. [Google Scholar] [CrossRef]
- Yu, M.; Stott, S.; Toner, M.; Maheswaran, S.; Haber, D.A. Circulating tumor cells: Approaches to isolation and characterization. J. Cell Biol. 2011, 192, 373–382. [Google Scholar] [CrossRef]
- Alix-Panabières, C.; Pantel, K. Liquid biopsy: From discovery to clinical application. Cancer Discov. 2021, 11, 858–873. [Google Scholar] [CrossRef]
- Rack, B.; Schindlbeck, C.; Jückstock, J.; Andergassen, U.; Hepp, P.; Zwingers, T.; Friedl, T.W.P.; Lorenz, R.; Tesch, H.; Fasching, P.A.; et al. Circulating tumor cells predict survival in early average-to-high risk breast cancer patients. JNCI J. Natl. Cancer Inst. 2014, 106. [Google Scholar] [CrossRef] [PubMed]
- Pantel, K.; Alix-Panabières, C. Liquid biopsy and minimal residual disease—Latest advances and implications for cure. Nat. Rev. Clin. Oncol. 2019, 16, 409–424. [Google Scholar] [CrossRef]
- Pantel, K.; Speicher, M.R. The biology of circulating tumor cells. Oncogene 2016, 35, 1216–1224. [Google Scholar] [CrossRef] [PubMed]
- Pantel, K.; Alix-Panabières, C. Tumour microenvironment: Informing on minimal residual disease in solid tumours. Nat. Rev. Clin. Oncol. 2017, 14, 325–326. [Google Scholar] [CrossRef]
- Hanin, L.; Bunimovich-Mendrazitsky, S. Reconstruction of the natural history of metastatic cancer and assessment of the effects of surgery: Gompertzian growth of the primary tumor. Math. Biosci. 2014, 247, 47–58. [Google Scholar] [CrossRef]
- Hanin, L.; Korosteleva, O. Does extirpation of the primary breast tumor give boost to growth of metastases? Evidence revealed by mathematical modeling. Math. Biosci. 2010, 223, 133–141. [Google Scholar] [CrossRef]
- Kumar, S.; Weaver, V.M. Mechanics, malignancy, and metastasis: The force journey of a tumor cell. Cancer Metastasis Rev. 2009, 28, 113–127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aceto, N.; Bardia, A.; Miyamoto, D.T.; Donaldson, M.C.; Wittner, B.S.; Spencer, J.A.; Yu, M.; Pely, A.; Engstrom, A.; Zhu, H.; et al. Circulating tumor cell clusters are oligoclonal precursors of breast cancer metastasis. Cell 2014, 158, 1110–1122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castro-Giner, F.; Aceto, N. Tracking cancer progression: From circulating tumor cells to metastasis. Genome Med. 2020, 12, 31. [Google Scholar] [CrossRef] [Green Version]
- Celià-Terrassa, T.; Kang, Y. Metastatic niche functions and therapeutic opportunities. Nat. Cell Biol. 2018, 20, 868–877. [Google Scholar] [CrossRef] [Green Version]
- Pienta, K.J.; Hammarlund, E.U.; Brown, J.S.; Amend, S.R.; Axelrod, R.M. Cancer recurrence and lethality are enabled by enhanced survival and reversible cell cycle arrest of polyaneuploid cells. Proc. Natl. Acad. Sci. USA 2021, 118, e2020838118. [Google Scholar] [CrossRef]
- Pienta, K.J.; Hammarlund, E.U.; Axelrod, R.; Brown, J.S.; Amend, S.R. Poly-aneuploid cancer cells promote evolvability, generating lethal cancer. Evol. Appl. 2020, 13, 1626–1634. [Google Scholar] [CrossRef]
- Mallin, M.M.; Pienta, K.J.; Amend, S.R. Cancer cell foraging to explain bone-specific metastatic progression. Bone 2020, 115788. [Google Scholar] [CrossRef]
- Ibrahim-Hashim, A.; Robertson-Tessi, M.; Enriquez-Navas, P.M.; Damaghi, M.; Balagurunathan, Y.; Wojtkowiak, J.W.; Russell, S.; Yoonseok, K.; Lloyd, M.C.; Bui, M.M.; et al. Defining cancer subpopulations by adaptive strategies rather than molecular properties provides novel insights into intratumoral evolution. Cancer Res. 2017, 77, 2242–2254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robey, I.F.; Baggett, B.K.; Kirkpatrick, N.D.; Roe, D.J.; Dosescu, J.; Sloane, B.F.; Hashim, A.I.; Morse, D.L.; Raghunand, N.; Gatenby, R.A.; et al. Bicarbonate increases tumor pH and inhibits spontaneous metastases. Cancer Res. 2009, 69, 2260–2268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiang, S.P.H.; Cabrera, R.M.; Segall, J.E. Tumor cell intravasation. Am. J. Physiol. Cell Physiol. 2016, 311, C1–C14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdul Pari, A.A.; Singhal, M.; Augustin, H.G. Emerging paradigms in metastasis research. J. Exp. Med. 2021, 218. [Google Scholar] [CrossRef]
- Yang, H.; Kuo, Y.; Smith, Z.I.; Spangler, J. Targeting cancer metastasis with antibody therapeutics. WIREs Nanomed. Nanobiotechnol. 2021, 13, e1698. [Google Scholar] [CrossRef]
- Jacot, W.; Mazel, M.; Mollevi, C.; Pouderoux, S.; D’Hondt, V.; Cayrefourcq, L.; Bourgier, C.; Boissiere-Michot, F.; Berrabah, F.; Lopez-Crapez, E.; et al. Clinical correlations of programmed cell death ligand 1 status in liquid and standard biopsies in breast cancer. Clin. Chem. 2020, 66, 1093–1101. [Google Scholar] [CrossRef]
- Artzy-Randrup, Y.; Epstein, T.; Brown, J.S.; Costa, R.L.; Czerniecki, B.J.; Gatenby, R.A. Novel evolutionary dynamics of small populations in breast cancer adjuvant and neoadjuvant therapy. NPJ Breast Cancer 2021, 7, 26. [Google Scholar] [CrossRef]
- Cunningham, J.J.; Brown, J.S.; Vincent, T.L.; Gatenby, R.A. Divergent and convergent evolution in metastases suggest treatment strategies based on specific metastatic sites. Evol. Med. Public Health 2015, 2015, 76–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dujon, A.M.; Capp, J.-P.; Brown, J.S.; Pujol, P.; Gatenby, R.A.; Ujvari, B.; Alix-Panabières, C.; Thomas, F. Is There One Key Step in the Metastatic Cascade? Cancers 2021, 13, 3693. https://doi.org/10.3390/cancers13153693
Dujon AM, Capp J-P, Brown JS, Pujol P, Gatenby RA, Ujvari B, Alix-Panabières C, Thomas F. Is There One Key Step in the Metastatic Cascade? Cancers. 2021; 13(15):3693. https://doi.org/10.3390/cancers13153693
Chicago/Turabian StyleDujon, Antoine M., Jean-Pascal Capp, Joel S. Brown, Pascal Pujol, Robert A. Gatenby, Beata Ujvari, Catherine Alix-Panabières, and Frédéric Thomas. 2021. "Is There One Key Step in the Metastatic Cascade?" Cancers 13, no. 15: 3693. https://doi.org/10.3390/cancers13153693
APA StyleDujon, A. M., Capp, J.-P., Brown, J. S., Pujol, P., Gatenby, R. A., Ujvari, B., Alix-Panabières, C., & Thomas, F. (2021). Is There One Key Step in the Metastatic Cascade? Cancers, 13(15), 3693. https://doi.org/10.3390/cancers13153693








