Spin Readout Techniques of the Nitrogen-Vacancy Center in Diamond
Abstract
“The only thing you can do easily is be wrong, and that’s hardly worth the effort.”—Norton Juster, The Phantom Tollbooth
1. Introduction
2. Quantifying Readout Performance
2.1. Photon Summation
2.2. Thresholding
2.3. Spin-Readout Noise
2.4. Averaging
2.5. Sensitivity
2.6. Summary
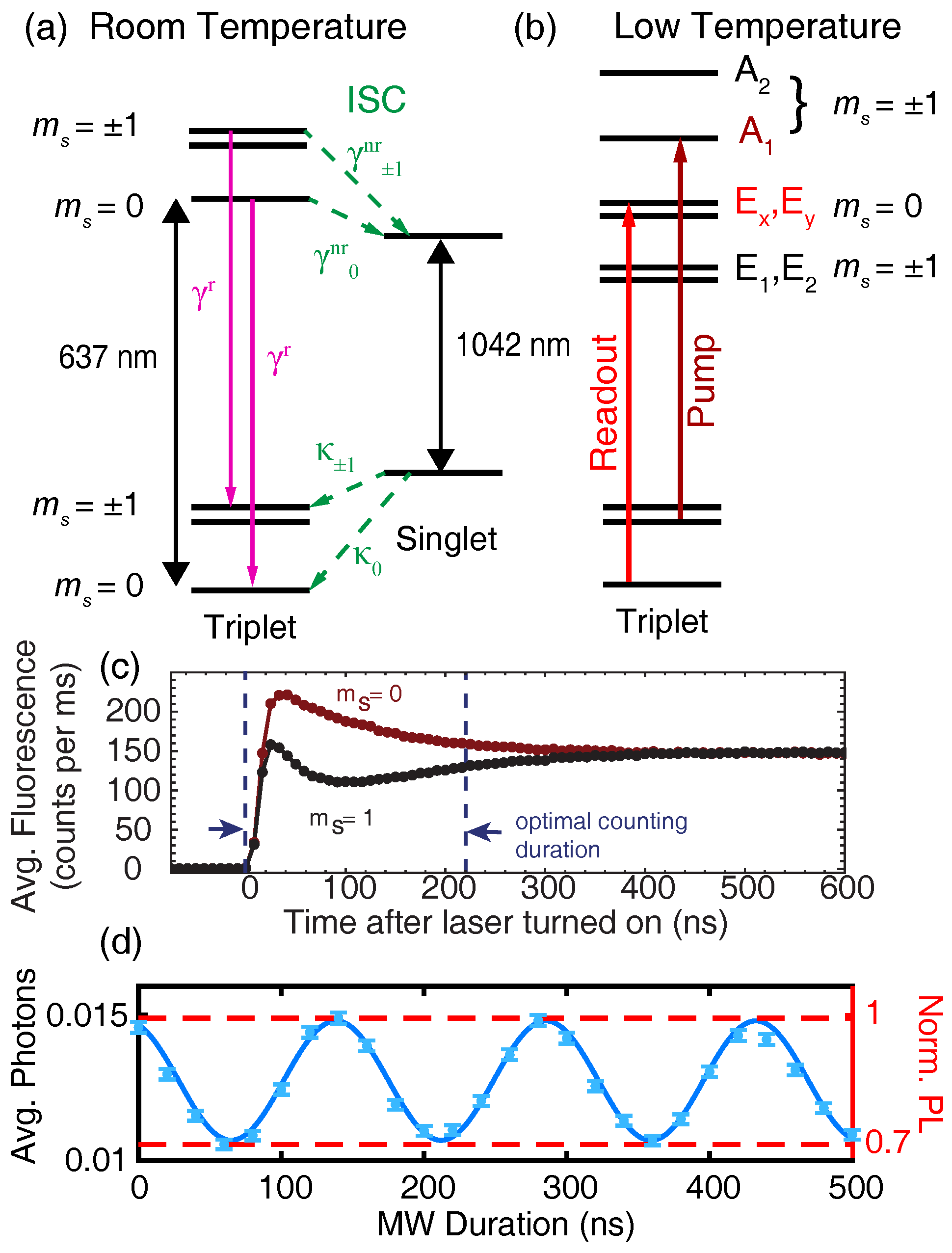
3. Traditional Spin Readout
4. Maximizing Photon Collection Efficiency
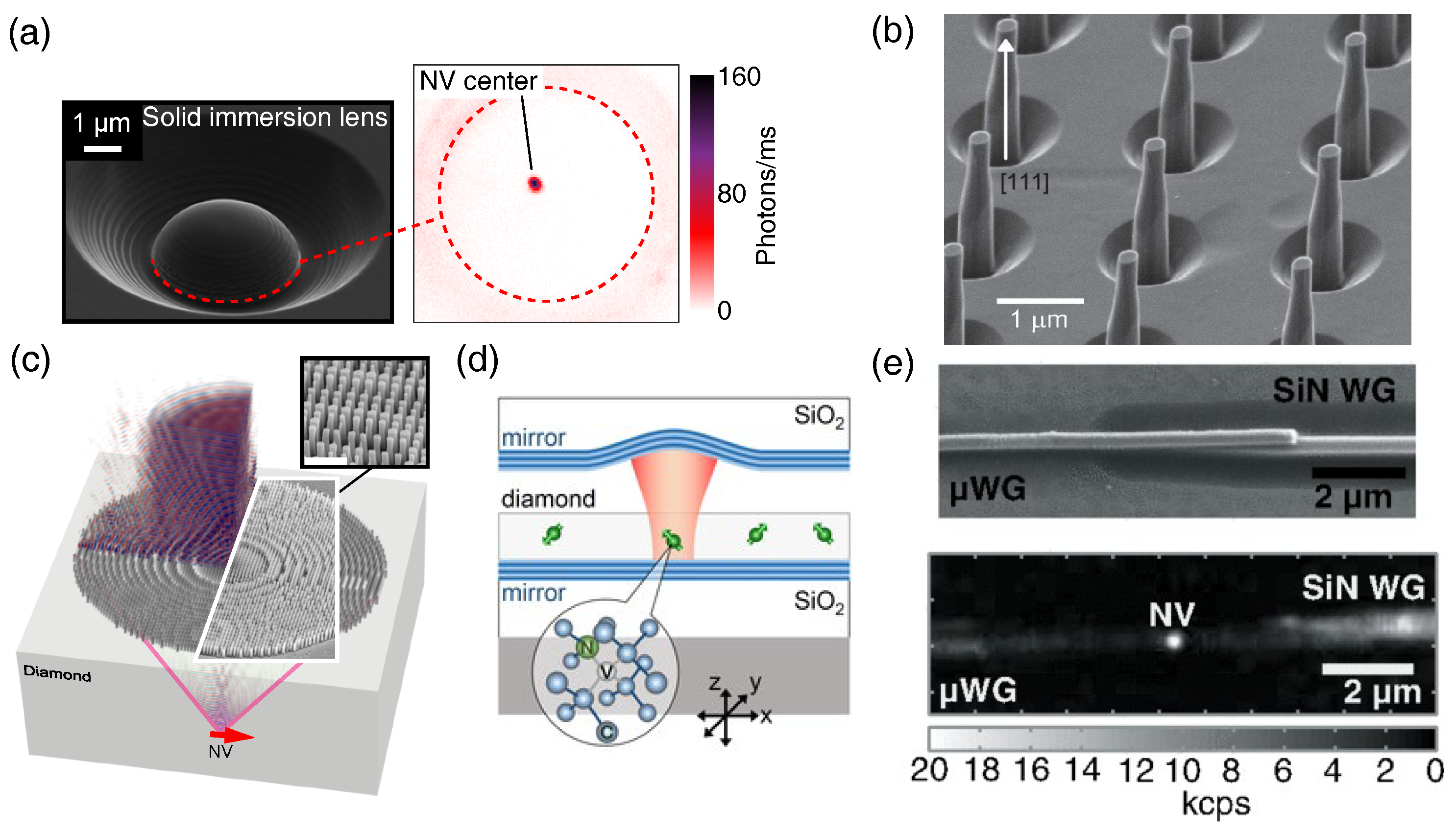
4.1. Crystal Alignment
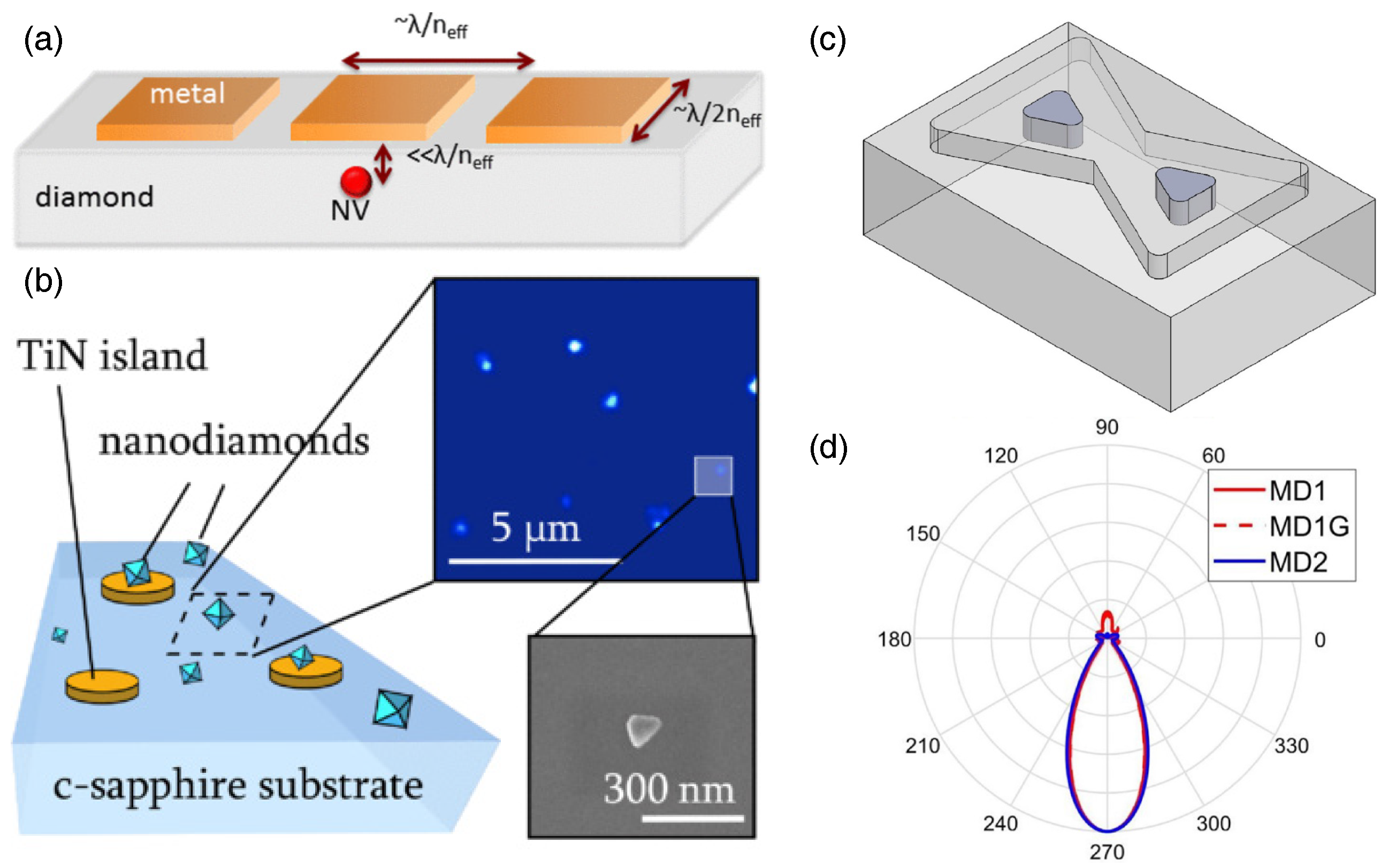
4.2. Photonic Structures
4.3. Waveguides and Cavities
4.4. Summary
5. Radiative Lifetime Engineering
6. Low-Temperature Resonant Readout
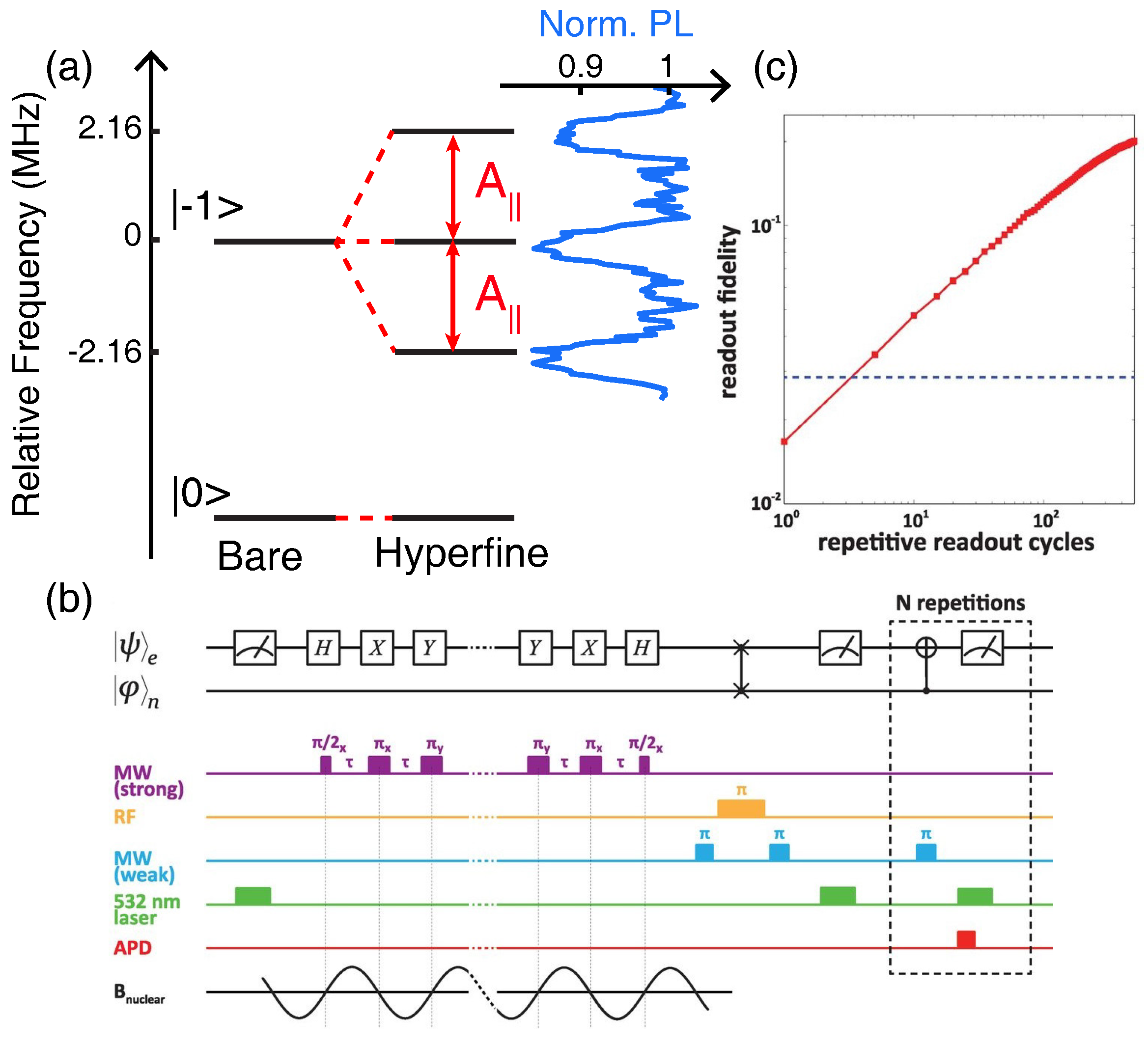
7. Nuclear-Assisted Readout
8. Spin-to-Charge Conversion
9. Photocurrent Readout
10. Accounting for Measurement Overhead
11. Real-Time Signal Processing Techniques
12. Discussion
13. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| NV | Nitrogen-Vacancy |
| PL | Photoluminescence |
| SNR | Signal-to-noise ratio |
| SCC | Spin-to-charge conversion |
| ISC | Intersystem crossing |
| LAC | Level anti-crossing |
| SQL | Standard quantum limit |
| ZPL | Zero-phonon line |
Appendix A. Spin-Readout Noise Calculations
Appendix A.1. Photon Summation
Appendix A.2. Thresholding
References
- Gambetta, J.M.; Chow, J.M.; Steffen, M. Building logical qubits in a superconducting quantum computing system. NPJ Quantum Inf. 2017, 3, 2. [Google Scholar] [CrossRef]
- Brown, K.R.; Kim, J.; Monroe, C. Co-designing a scalable quantum computer with trapped atomic ions. NPJ Quantum Inf. 2016, 2, 16034. [Google Scholar] [CrossRef]
- Silverstone, J.W.; Bonneau, D.; O’Brien, J.L.; Thompson, M.G. Silicon Quantum Photonics. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 390–402. [Google Scholar] [CrossRef]
- Awschalom, D.D.; Bassett, L.C.; Dzurak, A.S.; Hu, E.L.; Petta, J.R. Quantum Spintronics: Engineering and Manipulating Atom-Like Spins in Semiconductors. Science 2013, 339, 1174–1179. [Google Scholar] [CrossRef] [PubMed]
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Fortschr. Phys. 2000, 48, 771–783. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Clerk, A.A.; Devoret, M.H.; Girvin, S.M.; Marquardt, F.; Schoelkopf, R.J. Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 2010, 82, 1155–1208. [Google Scholar] [CrossRef]
- Heremans, F.J.; Yale, C.G.; Awschalom, D.D. Control of Spin Defects in Wide-Bandgap Semiconductors for Quantum Technologies. Proc. IEEE 2016, 104, 2009–2023. [Google Scholar] [CrossRef]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C.L. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Dutt, M.V.G.; Childress, L.; Jiang, L.; Togan, E.; Maze, J.; Jelezko, F.; Zibrov, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond. Science 2007, 316, 1312–1316. [Google Scholar] [CrossRef] [PubMed]
- Maurer, P.C.; Kucsko, G.; Latta, C.; Jiang, L.; Yao, N.Y.; Bennett, S.D.; Pastawski, F.; Hunger, D.; Chisholm, N.; Markham, M.; et al. Room-Temperature Quantum Bit Memory Exceeding One Second. Science 2012, 336, 1283. [Google Scholar] [CrossRef] [PubMed]
- Pfender, M.; Aslam, N.; Simon, P.; Antonov, D.; Thiering, G.; Burk, S.; Fávaro de Oliveira, F.; Denisenko, A.; Fedder, H.; Meijer, J.; et al. Protecting a Diamond Quantum Memory by Charge State Control. Nano Lett. 2017, 17, 5931–5937. [Google Scholar] [CrossRef] [PubMed]
- Childress, L.; Gurudev Dutt, M.V.; Taylor, J.M.; Zibrov, A.S.; Jelezko, F.; Wrachtrup, J.; Hemmer, P.R.; Lukin, M.D. Coherent Dynamics of Coupled Electron and Nuclear Spin Qubits in Diamond. Science 2006, 314, 281–285. [Google Scholar] [CrossRef] [PubMed]
- Neumann, P.; Beck, J.; Steiner, M.; Rempp, F.; Fedder, H.; Hemmer, P.R.; Wrachtrup, J.; Jelezko, F. Single-Shot Readout of a Single Nuclear Spin. Science 2010, 329, 542–544. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.Q.; Xing, J.; Ma, W.L.; Wang, P.; Li, C.H.; Po, H.C.; Zhang, Y.R.; Fan, H.; Liu, R.B.; Pan, X.Y. Single-Shot Readout of a Nuclear Spin Weakly Coupled to a Nitrogen-Vacancy Center at Room Temperature. Phys. Rev. Lett. 2017, 118, 150504. [Google Scholar] [CrossRef] [PubMed]
- Casola, F.; van der Sar, T.; Yacoby, A. Probing condensed matter physics with magnetometry based on nitrogen-vacancy centres in diamond. Nat. Rev. Mater. 2018, 3, 17088. [Google Scholar] [CrossRef]
- Lovchinsky, I.; Sushkov, A.O.; Urbach, E.; de Leon, N.P.; Choi, S.; De Greve, K.; Evans, R.; Gertner, R.; Bersin, E.; Müller, C.; et al. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science 2016, 351, 836–841. [Google Scholar] [CrossRef] [PubMed]
- Aslam, N.; Pfender, M.; Neumann, P.; Reuter, R.; Zappe, A.; Fávaro de Oliveira, F.; Denisenko, A.; Sumiya, H.; Onoda, S.; Isoya, J.; et al. Nanoscale nuclear magnetic resonance with chemical resolution. Science 2017, 357, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Arcizet, O.; Jacques, V.; Siria, A.; Poncharal, P.; Vincent, P.; Seidelin, S. A single nitrogen-vacancy defect coupled to a nanomechanical oscillator. Nat. Phys. 2011, 7, 879–883. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682. [Google Scholar] [CrossRef] [PubMed]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 35002. [Google Scholar] [CrossRef]
- Rondin, L.; Tetienne, J.P.; Hingant, T.; Roch, J.F.; Maletinsky, P.; Jacques, V. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 2014, 77, 56503. [Google Scholar] [CrossRef] [PubMed]
- Schirhagl, R.; Chang, K.; Loretz, M.; Degen, C.L. Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 2014, 65, 83–105. [Google Scholar] [CrossRef] [PubMed]
- Schröder, T.; Mouradian, S.L.; Zheng, J.; Trusheim, M.E.; Walsh, M.; Chen, E.H.; Li, L.; Bayn, I.; Englund, D. Quantum nanophotonics in diamond. J. Opt. Soc. Am. B 2016, 33, B65–B83. [Google Scholar] [CrossRef]
- McDonough, R.N.; Whalen, A.D. Detection of Signals in Noise; Academic Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Vijay, R.; Slichter, D.H.; Siddiqi, I. Observation of Quantum Jumps in a Superconducting Artificial Atom. Phys. Rev. Lett. 2011, 106, 110502. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R.; Yacoby, A.; Walsworth, R.; Lukin, M.D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. [Google Scholar] [CrossRef]
- D’Anjou, B.; Coish, W.A. Optimal post-processing for a generic single-shot qubit readout. Phys. Rev. A 2014, 89, 12313. [Google Scholar] [CrossRef]
- D’Anjou, B.; Kuret, L.; Childress, L.; Coish, W.A. Maximal Adaptive-Decision Speedups in Quantum-State Readout. Phys. Rev. X 2016, 6, 011017. [Google Scholar] [CrossRef]
- Robledo, L.; Childress, L.; Bernien, H.; Hensen, B.; Alkemade, P.F.A.; Hanson, R. High-fidelity projective read-out of a solid-state spin quantum register. Nature 2011, 477, 574–578. [Google Scholar] [CrossRef] [PubMed]
- Magesan, E.; Gambetta, J.M.; Córcoles, A.; Chow, J.M. Machine Learning for Discriminating Quantum Measurement Trajectories and Improving Readout. Phys. Rev. Lett. 2015, 114, 200501. [Google Scholar] [CrossRef] [PubMed]
- Harty, T.; Allcock, D.; Ballance, C.; Guidoni, L.; Janacek, H.; Linke, N.; Stacey, D.; Lucas, D. High-Fidelity Preparation, Gates, Memory, and Readout of a Trapped-Ion Quantum Bit. Phys. Rev. Lett. 2014, 113, 220501. [Google Scholar] [CrossRef] [PubMed]
- Shields, B.J.; Unterreithmeier, Q.P.; de Leon, N.P.; Park, H.; Lukin, M.D. Efficient readout of a single spin state in diamond via spin-to-charge conversion. Phys. Rev. Lett. 2015, 114, 136402. [Google Scholar] [CrossRef] [PubMed]
- Gruber, A.; Dräbenstedt, A.; Tietz, C.; Fleury, L.; Wrachtrup, J.; von Borczyskowski, C. Scanning Confocal Optical Microscopy and Magnetic Resonance on Single Defect Centers. Science 1997, 276, 2012–2014. [Google Scholar] [CrossRef]
- Jelezko, F.; Gaebel, T.; Popa, I.; Gruber, A.; Wrachtrup, J. Observation of Coherent Oscillations in a Single Electron Spin. Phys. Rev. Lett. 2004, 92, 76401. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, G.; Neumann, P.; Twitchen, D.; Markham, M.; Kolesov, R.; Mizuochi, N.; Isoya, J.; Achard, J.; Beck, J.; Tissler, J.; et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 2009, 8, 383. [Google Scholar] [CrossRef] [PubMed]
- Dolde, F.; Jakobi, I.; Naydenov, B.; Zhao, N.; Pezzagna, S.; Trautmann, C.; Meijer, J.; Neumann, P.; Jelezko, F.; Wrachtrup, J. Room-temperature entanglement between single defect spins in diamond. Nat. Phys. 2013, 9, 139–143. [Google Scholar] [CrossRef]
- Neumann, P.; Mizuochi, N.; Rempp, F.; Hemmer, P.; Watanabe, H.; Yamasaki, S.; Jacques, V.; Gaebel, T.; Jelezko, F.; Wrachtrup, J. Multipartite Entanglement Among Single Spins in Diamond. Science 2008, 320, 1326–1329. [Google Scholar] [CrossRef] [PubMed]
- Taminiau, T.H.; Cramer, J.; van der Sar, T.; Dobrovitski, V.V.; Hanson, R. Universal control and error correction in multi-qubit spin registers in diamond. Nat. Nanotechnol. 2014, 9, 171. [Google Scholar] [CrossRef] [PubMed]
- Van Oort, E.; Manson, N.B.; Glasbeek, M. Optically detected spin coherence of the diamond N-V centre in its triplet ground state. J. Phys. C Solid State Phys. 1988, 21, 4385. [Google Scholar] [CrossRef]
- Goldman, M.L.; Doherty, M.W.; Sipahigil, A.; Yao, N.Y.; Bennett, S.D.; Manson, N.B.; Kubanek, A.; Lukin, M.D. State-selective intersystem crossing in nitrogen-vacancy centers. Phys. Rev. B 2015, 91, 165201. [Google Scholar] [CrossRef]
- Gupta, A.; Hacquebard, L.; Childress, L. Efficient signal processing for time-resolved fluorescence detection of nitrogen-vacancy spins in diamond. J. Opt. Soc. Am. B 2016, 33, B28. [Google Scholar] [CrossRef]
- Hopper, D.A.; Grote, R.R.; Exarhos, A.L.; Bassett, L.C. Near-infrared-assisted charge control and spin readout of the nitrogen-vacancy center in diamond. Phys. Rev. B 2016, 94, 241201. [Google Scholar] [CrossRef]
- Acosta, V.M.; Jarmola, A.; Bauch, E.; Budker, D. Optical properties of the nitrogen-vacancy singlet levels in diamond. Phys. Rev. B 2010, 82, 201202. [Google Scholar] [CrossRef]
- Waldherr, G.; Beck, J.; Steiner, M.; Neumann, P.; Gali, A.; Frauenheim, T.; Jelezko, F.; Wrachtrup, J. Dark States of Single Nitrogen-Vacancy Centers in Diamond Unraveled by Single Shot NMR. Phys. Rev. Lett. 2011, 106, 157601. [Google Scholar] [CrossRef] [PubMed]
- Robledo, L.; Bernien, H.; Van Der Sar, T.; Hanson, R. Spin dynamics in the optical cycle of single nitrogen-vacancy centres in diamond. New J. Phys. 2011, 13, 025013. [Google Scholar] [CrossRef]
- Plakhotnik, T.; Moerner, W.; Palm, V.; Wild, U.P. Single molecule spectroscopy: maximum emission rate and saturation intensity. Opt. Commun. 1995, 114, 83–88. [Google Scholar] [CrossRef]
- Jamali, M.; Gerhardt, I.; Rezai, M.; Frenner, K.; Fedder, H.; Wrachtrup, J.J. Microscopic diamond solid-immersion-lenses fabricated around single defect centers by focused ion beam milling. Rev. Sci. Instrum. 2014, 85, 123703. [Google Scholar] [CrossRef] [PubMed]
- Parks, S.M.; Grote, R.R.; Hopper, D.A.; Bassett, L.C. Fabrication of (111)-faced single-crystal diamond plates by laser nucleated cleaving. Diam. Rel. Mater. 2018, 84, 20–25. [Google Scholar] [CrossRef]
- Miyazaki, T.; Miyamoto, Y.; Makino, T.; Kato, H.; Yamasaki, S.; Fukui, T.; Doi, Y.; Tokuda, N.; Hatano, M.; Mizuochi, N. Atomistic mechanism of perfect alignment of nitrogen-vacancy centers in diamond. Appl. Phys. Lett. 2014, 105, 261601. [Google Scholar] [CrossRef]
- Lesik, M.; Tetienne, J.P.; Tallaire, A.; Achard, J.; Mille, V.; Gicquel, A.; Roch, J.F.; Jacques, V. Perfect preferential orientation of nitrogen-vacancy defects in a synthetic diamond sample. Appl. Phys. Lett. 2014, 104, 113107. [Google Scholar] [CrossRef]
- Michl, J.; Teraji, T.; Zaiser, S.; Jakobi, I.; Waldherr, G.; Dolde, F.; Neumann, P.; Doherty, M.W.; Manson, N.B.; Isoya, J.; et al. Perfect alignment and preferential orientation of nitrogen-vacancy centers during chemical vapor deposition diamond growth on (111) surfaces. Appl. Phys. Lett. 2014, 104, 102407. [Google Scholar] [CrossRef]
- Fukui, T.; Doi, Y.; Miyazaki, T.; Miyamoto, Y.; Kato, H.; Matsumoto, T.; Makino, T.; Yamasaki, S.; Morimoto, R.; Tokuda, N.; et al. Perfect selective alignment of nitrogen-vacancy centers in diamond. Appl. Phys. Express 2014, 7, 55201. [Google Scholar] [CrossRef]
- Ozawa, H.; Tahara, K.; Ishiwata, H.; Hatano, M.; Iwasaki, T. Formation of perfectly aligned nitrogen-vacancy- center ensembles in chemical-vapor-deposition-grown diamond (111). Appl. Phys. Express 2017, 10, 45501. [Google Scholar] [CrossRef]
- Hadden, J.P.; Harrison, J.P.; Stanley-Clarke, A.C.; Marseglia, L.; Ho, Y.L.D.; Patton, B.R.; O’Brien, J.L.; Rarity, J.G. Strongly enhanced photon collection from diamond defect centers under microfabricated integrated solid immersion lenses. Appl. Phys. Lett. 2010, 97, 241901. [Google Scholar] [CrossRef]
- Marseglia, L.; Hadden, J.P.; Stanley-Clarke, A.C.; Harrison, J.P.; Patton, B.; Ho, Y.L.D.; Naydenov, B.; Jelezko, F.; Meijer, J.; Dolan, P.R.; et al. Nanofabricated solid immersion lenses registered to single emitters in diamond. Appl. Phys. Lett. 2011, 98, 14–17. [Google Scholar] [CrossRef]
- Grote, R.R.; Huang, T.Y.; Mann, S.A.; Hopper, D.A.; Exarhos, A.L.; Lopez, G.G.; Garnett, E.C.; Bassett, L.C. Imaging a Nitrogen-Vacancy Center with a Diamond Immersion Metalens. arXiv, 2017; arXiv:1711.00901. [Google Scholar]
- Neu, E.; Appel, P.; Ganzhorn, M.; Miguel-Sánchez, J.; Lesik, M.; Mille, V.; Jacques, V.; Tallaire, A.; Achard, J.; Maletinsky, P. Photonic nano-structures on (111)-oriented diamond. Appl. Phys. Lett. 2014, 104, 153108. [Google Scholar] [CrossRef]
- Riedel, D.; Söllner, I.; Shields, B.J.; Starosielec, S.; Appel, P.; Neu, E.; Maletinsky, P.; Warburton, R.J. Deterministic Enhancement of Coherent Photon Generation from a Nitrogen-Vacancy Center in Ultrapure Diamond. Phys. Rev. X 2017, 7, 031040. [Google Scholar]
- Mouradian, S.L.; Schröder, T.; Poitras, C.B.; Li, L.; Goldstein, J.; Chen, E.H.; Walsh, M.; Cardenas, J.; Markham, M.L.; Twitchen, D.J.; et al. Scalable Integration of Long-Lived Quantum Memories into a Photonic Circuit. Phys. Rev. X 2015, 5, 31009. [Google Scholar] [CrossRef]
- Babinec, T.M.; Hausmann, B.J.M.; Khan, M.; Zhang, Y.; Maze, J.R.; Hemmer, P.R.; Lončar, M. A diamond nanowire single-photon source. Nat. Nanotechnol. 2010, 5, 195. [Google Scholar] [CrossRef] [PubMed]
- Momenzadeh, S.A.; Stöhr, R.J.; de Oliveira, F.F.; Brunner, A.; Denisenko, A.; Yang, S.; Reinhard, F.; Wrachtrup, J. Nanoengineered Diamond Waveguide as a Robust Bright Platform for Nanomagnetometry Using Shallow Nitrogen Vacancy Centers. Nano Lett. 2015, 15, 165–169. [Google Scholar] [CrossRef] [PubMed]
- Maletinsky, P.; Hong, S.; Grinolds, M.S.; Hausmann, B.; Lukin, M.D.; Walsworth, R.L.; Loncar, M.; Yacoby, A. A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres. Nat. Nanotechnol. 2012, 7, 320–324. [Google Scholar] [CrossRef] [PubMed]
- Appel, P.; Neu, E.; Ganzhorn, M.; Barfuss, A.; Batzer, M.; Gratz, M.; Tschöpe, A.; Maletinsky, P. Fabrication of all diamond scanning probes for nanoscale magnetometry. Rev. Sci. Instrum. 2016, 87, 063703. [Google Scholar] [CrossRef] [PubMed]
- Hausmann, B.J.M.; Shields, B.; Quan, Q.; Maletinsky, P.; McCutcheon, M.; Choy, J.T.; Babinec, T.M.; Kubanek, A.; Yacoby, A.; Lukin, M.D.; et al. Integrated Diamond Networks for Quantum Nanophotonics. Nano Lett. 2012, 12, 1578–1582. [Google Scholar] [CrossRef] [PubMed]
- Gould, M.; Chakravarthi, S.; Christen, I.R.; Thomas, N.; Dadgostar, S.; Song, Y.; Lee, M.L.; Hatami, F.; Fu, K.M.C. Large-scale GaP-on-diamond integrated photonics platform for NV center-based quantum information. J. Opt. Soc. Am. B 2016, 33, B35–B42. [Google Scholar] [CrossRef]
- Faraon, A.; Barclay, P.E.; Santori, C.; Fu, K.M.C.; Beausoleil, R.G. Resonant enhancement of the zero-phonon emission from a colour centre in a diamond cavity. Nat. Photonics 2011, 5, 301. [Google Scholar] [CrossRef]
- Hausmann, B.J.M.; Shields, B.J.; Quan, Q.; Chu, Y.; de Leon, N.P.; Evans, R.; Burek, M.J.; Zibrov, A.S.; Markham, M.; Twitchen, D.J.; et al. Coupling of NV Centers to Photonic Crystal Nanobeams in Diamond. Nano Lett. 2013, 13, 5791–5796. [Google Scholar] [CrossRef] [PubMed]
- Faraon, A.; Santori, C.; Huang, Z.; Acosta, V.M.; Beausoleil, R.G. Coupling of Nitrogen-Vacancy Centers to Photonic Crystal Cavities in Monocrystalline Diamond. Phys. Rev. Lett. 2012, 109, 33604. [Google Scholar] [CrossRef] [PubMed]
- Grote, R.R.; Bassett, L.C. Single-mode optical waveguides on native high-refractive-index substrates. APL Photonics 2016, 1, 71302. [Google Scholar] [CrossRef]
- Mouradian, S.L.; Englund, D. A tunable waveguide-coupled cavity design for scalable interfaces to solid-state quantum emitters. APL Photonics 2017, 2, 046103. [Google Scholar] [CrossRef]
- Johnson, S.; Dolan, P.R.; Grange, T.; Trichet, A.A.P.; Hornecker, G.; Chen, Y.C.; Weng, L.; Hughes, G.M.; Watt, A.A.R.; Auffèves, A.; et al. Tunable cavity coupling of the zero phonon line of a nitrogen-vacancy defect in diamond. New J. Phys. 2015, 17, 122003. [Google Scholar] [CrossRef]
- Bogdanović, S.; Liddy, M.S.Z.; van Dam, S.B.; Coenen, L.C.; Fink, T.; Lončar, M.; Hanson, R. Robust nano-fabrication of an integrated platform for spin control in a tunable microcavity. APL Photonics 2017, 2, 126101. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.A.; Rosenberg, I.; Rapaport, R.; Bar-Gill, N. Purcell-enhanced optical spin readout of nitrogen-vacancy centers in diamond. Phys. Rev. B 2015, 92, 235410. [Google Scholar] [CrossRef]
- Wang, C.F.; Hanson, R.; Awschalom, D.D.; Hu, E.L.; Feygelson, T.; Yang, J.; Butler, J.E. Fabrication and characterization of two-dimensional photonic crystal microcavities in nanocrystalline diamond. Appl. Phys. Lett. 2007, 91, 201112. [Google Scholar] [CrossRef]
- Wolters, J.; Schell, A.W.; Kewes, G.; Nüsse, N.; Schoengen, M.; Döscher, H.; Hannappel, T.; Löchel, B.; Barth, M.; Benson, O. Enhancement of the zero phonon line emission from a single nitrogen vacancy center in a nanodiamond via coupling to a photonic crystal cavity. Appl. Phys. Lett. 2010, 97, 141108. [Google Scholar] [CrossRef]
- Barclay, P.E.; Santori, C.; Fu, K.M.; Beausoleil, R.G.; Painter, O. Coherent interference effects in a nano-assembled diamond NV center cavity-QED system. Opt. Express 2009, 17, 8081–8197. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.C.; Bracher, D.O.; Cui, S.; Ohno, K.; McLellan, C.A.; Zhang, X.; Andrich, P.; Alemán, B.; Russell, K.J.; Magyar, A.P.; et al. Deterministic coupling of delta-doped nitrogen vacancy centers to a nanobeam photonic crystal cavity. Appl. Phys. Lett. 2014, 105, 261101. [Google Scholar] [CrossRef]
- Englund, D.; Shields, B.; Rivoire, K.; Hatami, F.; Vučković, J.; Park, H.; Lukin, M.D. Deterministic Coupling of a Single Nitrogen Vacancy Center to a Photonic Crystal Cavity. Nano Lett. 2010, 10, 3922–3926. [Google Scholar] [CrossRef] [PubMed]
- Kühn, S.; Håkanson, U.; Rogobete, L.; Sandoghdar, V. Enhancement of Single-Molecule Fluorescence Using a Gold Nanoparticle as an Optical Nanoantenna. Phys. Rev. Lett. 2006, 97, 17402. [Google Scholar] [CrossRef] [PubMed]
- Akimov, A.V.; Mukherjee, A.; Yu, C.L.; Chang, D.E.; Zibrov, A.S.; Hemmer, P.R.; Park, H.; Lukin, M.D. Generation of single optical plasmons in metallic nanowires coupled to quantum dots. Nature 2007, 450, 402. [Google Scholar] [CrossRef] [PubMed]
- Schietinger, S.; Barth, M.; Aichele, T.; Benson, O. Plasmon-Enhanced Single Photon Emission from a Nanoassembled Metal-Diamond Hybrid Structure at Room Temperature. Nano Lett. 2009, 9, 1694–1698. [Google Scholar] [CrossRef] [PubMed]
- Akselrod, G.M.; Argyropoulos, C.; Hoang, T.B.; Ciracì, C.; Fang, C.; Huang, J.; Smith, D.R.; Mikkelsen, M.H. Probing the mechanisms of large Purcell enhancement in plasmonic nanoantennas. Nat. Photonics 2014, 8, 835. [Google Scholar] [CrossRef]
- Hoang, T.B.; Akselrod, G.M.; Mikkelsen, M.H. Ultrafast room-temperature single photon emission from quantum dots coupled to plasmonic nanocavities. Nano Lett. 2015, 16, 270–275. [Google Scholar] [CrossRef] [PubMed]
- Anger, P.; Bharadwaj, P.; Novotny, L. Enhancement and Quenching of Single-Molecule Fluorescence. Phys. Rev. Lett. 2006, 96, 113002. [Google Scholar] [CrossRef] [PubMed]
- Shalaginov, M.Y.; Ishii, S.; Liu, J.; Liu, J.; Irudayaraj, J.; Lagutchev, A.; Kildishev, A.V.; Shalaev, V.M. Broadband enhancement of spontaneous emission from nitrogen-vacancy centers in nanodiamonds by hyperbolic metamaterials. Appl. Phys. Lett. 2013, 102, 173114. [Google Scholar] [CrossRef]
- Bulu, I.; Babinec, T.; Hausmann, B.; Choy, J.T.; Loncar, M. Plasmonic resonators for enhanced diamond NV- center single photon sources. Opt. Express 2011, 19, 5268–5276. [Google Scholar] [CrossRef] [PubMed]
- Riedel, D.; Rohner, D.; Ganzhorn, M.; Kaldewey, T.; Appel, P.; Neu, E.; Warburton, R.; Maletinsky, P. Low-Loss Broadband Antenna for Efficient Photon Collection from a Coherent Spin in Diamond. Phys. Rev. Appl. 2014, 2, 64011. [Google Scholar] [CrossRef]
- Karamlou, A.; Trusheim, M.E.; Englund, D. Metal-dielectric antennas for efficient photon collection from diamond color centers. Opt. Express 2018, 26, 3341–3352. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, S.; Shalaginov, M.Y.; Akimov, A.; Lagutchev, A.S.; Kapitanova, P.; Liu, J.; Woods, D.; Ferrera, M.; Belov, P.; Irudayaraj, J.; et al. Electron spin contrast of Purcell-enhanced nitrogen-vacancy ensembles in nanodiamonds. Phys. Rev. B 2017, 96, 035146. [Google Scholar] [CrossRef]
- Babinec, T.M.; Fedder, H.; Choy, J.; Bulu, I.; Doherty, M.; Hemmer, P.; Wrachtrup, J.; Loncar, M. Design of Diamond Photonic Devices for Spintronics. In Proceedings of the 2012 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 6–11 May 2012; p. JW1I.6. [Google Scholar]
- Hopper, D.A.; Grote, R.R.; Parks, S.M.; Bassett, L.C. Amplified Sensitivity of Nitrogen-Vacancy Spins in Nanodiamonds Using All-Optical Charge Readout. ACS Nano 2018, 12, 4678–4686. [Google Scholar] [CrossRef] [PubMed]
- Tamarat, P.; Manson, N.B.; Harrison, J.P.; McMurtrie, R.L.; Nizovtsev, A.; Santori, C.; Neumann, P.; Beausoleil, R.G.; Gaebel, T.; Jelezko, F.; et al. Spin-flip and spin-conserving optical transitions of the nitrogen-vacancy centre in diamond. New J. Phys. 2008, 10, 45004. [Google Scholar] [CrossRef]
- Batalov, A.; Jacques, V.; Kaiser, F.; Siyushev, P.; Neumann, P.; Rogers, L.; McMurtrie, R.; Manson, N.; Jelezko, F.; Wrachtrup, J. Low temperature studies of the excited-state structure of negatively charged nitrogen-vacancy color centers in diamond. Phys. Rev. Lett. 2009, 102, 195506. [Google Scholar] [CrossRef] [PubMed]
- Fu, K.M.C.; Santori, C.; Barclay, P.E.; Rogers, L.J.; Manson, N.B.; Beausoleil, R.G. Observation of the dynamic Jahn-Teller effect in the excited states of nitrogen-vacancy centers in diamond. Phys. Rev. Lett. 2009, 103, 256404. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, G.; Dobrovitski, V.; Toyli, D.; Heremans, F.; Weis, C.; Schenkel, T.; Awschalom, D. Excited-state spin coherence of a single nitrogen–vacancy centre in diamond. Nat. Phys. 2010, 6, 668. [Google Scholar] [CrossRef]
- Buckley, B.B.; Fuchs, G.D.; Bassett, L.C.; Awschalom, D.D. Spin-Light Coherence for Single-Spin Measurement and Control in Diamond. Science 2010, 330, 1212–1215. [Google Scholar] [CrossRef] [PubMed]
- Togan, E.; Chu, Y.; Trifonov, A.; Jiang, L.; Maze, J.; Childress, L.; Dutt, M.G.; Sørensen, A.S.; Hemmer, P.; Zibrov, A.S.; et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 2010, 466, 730. [Google Scholar] [CrossRef] [PubMed]
- Yale, C.G.; Buckley, B.B.; Christle, D.J.; Burkard, G.; Heremans, F.J.; Bassett, L.C.; Awschalom, D.D. All-optical control of a solid-state spin using coherent dark states. Proc. Natl. Acad. Sci. USA 2013, 110, 7595–7600. [Google Scholar] [CrossRef] [PubMed]
- Bassett, L.C.; Heremans, F.J.; Christle, D.J.; Yale, C.G.; Burkard, G.; Buckley, B.B.; Awschalom, D.D. Ultrafast optical control of orbital and spin dynamics in a solid-state defect. Science 2014, 345, 1333–1337. [Google Scholar] [CrossRef] [PubMed]
- Olmschenk, S.; Younge, K.C.; Moehring, D.L.; Matsukevich, D.N.; Maunz, P.; Monroe, C. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 2007, 76, 52314. [Google Scholar] [CrossRef]
- Vamivakas, A.N.; Lu, C.Y.; Matthiesen, C.; Zhao, Y.; Fält, S.; Badolato, A.; Atatüre, M. Observation of spin-dependent quantum jumps via quantum dot resonance fluorescence. Nature 2010, 467, 297. [Google Scholar] [CrossRef] [PubMed]
- Bassett, L.C.; Heremans, F.J.; Yale, C.; Buckley, B.; Awschalom, D.D. Electrical tuning of single nitrogen-vacancy center optical transitions enhanced by photoinduced fields. Phys. Rev. Lett. 2011, 107, 266403. [Google Scholar] [CrossRef] [PubMed]
- Blok, M.S.; Bonato, C.; Markham, M.L.; Twitchen, D.J.; Dobrovitski, V.V.; Hanson, R. Manipulating a qubit through the backaction of sequential partial measurements and real-time feedback. Nat. Phys. 2014, 10, 189. [Google Scholar] [CrossRef]
- Bernien, H.; Hensen, B.; Pfaff, W.; Koolstra, G.; Blok, M.S.; Robledo, L.; Taminiau, T.H.; Markham, M.; Twitchen, D.J.; Childress, L.; et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 2013, 497, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Cramer, J.; Kalb, N.; Rol, M.A.; Hensen, B.; Blok, M.S.; Markham, M.; Twitchen, D.J.; Hanson, R.; Taminiau, T.H. Repeated quantum error correction on a continuously encoded qubit by real-time feedback. Nat. Commun. 2016, 7, 11526. [Google Scholar] [CrossRef] [PubMed]
- Terblanche, C.J.; Reynhardt, E.C.; van Wyk, J.A. 13C Spin–Lattice Relaxation in Natural Diamond: Zeeman Relaxation at 4.7 T and 300 K Due to Fixed Paramagnetic Nitrogen Defects. Solid State Nucl. Magn. Reson. 2001, 20, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Reiserer, A.; Kalb, N.; Blok, M.S.; van Bemmelen, K.J.; Taminiau, T.H.; Hanson, R.; Twitchen, D.J.; Markham, M. Robust quantum-network memory using decoherence-protected subspaces of nuclear spins. Phys. Rev. X 2016, 6, 021040. [Google Scholar] [CrossRef]
- Kalb, N.; Reiserer, A.A.; Humphreys, P.C.; Bakermans, J.J.; Kamerling, S.J.; Nickerson, N.H.; Benjamin, S.C.; Twitchen, D.J.; Markham, M.; Hanson, R. Entanglement distillation between solid-state quantum network nodes. Science 2017, 356, 928–932. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Hodges, J.S.; Maze, J.R.; Maurer, P.; Taylor, J.M.; Cory, D.G.; Hemmer, P.R.; Walsworth, R.L.; Yacoby, A.; Zibrov, A.S.; et al. Repetitive Readout of a Single Electronic Spin via Quantum Logic with Nuclear Spin Ancillae. Science 2009, 326, 267–272. [Google Scholar] [CrossRef] [PubMed]
- Steiner, M.; Neumann, P.; Beck, J.; Jelezko, F.; Wrachtrup, J. Universal enhancement of the optical readout fidelity of single electron spins at nitrogen-vacancy centers in diamond. Phys. Rev. B 2010, 81, 35205. [Google Scholar] [CrossRef]
- Neumann, P.; Kolesov, R.; Jacques, V.; Beck, J.; Tisler, J.; Batalov, A.; Rogers, L.; Manson, N.B.; Balasubramanian, G.; Jelezko, F.; et al. Excited-state spectroscopy of single NV defects in diamond using optically detected magnetic resonance. New J. Phys. 2009, 11, 13017. [Google Scholar] [CrossRef]
- D’Anjou, B.; Coish, W.A. Enhancing qubit readout through dissipative sub-Poissonian dynamics. Phys. Rev. A 2017, 96, 52321. [Google Scholar] [CrossRef]
- Häberle, T.; Oeckinghaus, T.; Schmid-Lorch, D.; Pfender, M.; de Oliveira, F.F.; Momenzadeh, S.A.; Finkler, A.; Wrachtrup, J. Nuclear quantum-assisted magnetometer. Rev. Sci. Instrum. 2017, 88, 13702. [Google Scholar] [CrossRef] [PubMed]
- Waldherr, G.; Beck, J.; Neumann, P.; Said, R.S.; Nitsche, M.; Markham, M.L.; Twitchen, D.J.; Twamley, J.; Jelezko, F.; Wrachtrup, J. High-dynamic-range magnetometry with a single nuclear spin in diamond. Nat. Nanotechnol. 2012, 7, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Zaiser, S.; Rendler, T.; Jakobi, I.; Wolf, T.; Lee, S.y.; Wagner, S.; Neumann, P.; Bergholm, V.; Schulte-Herbrüggen, T.; Neumann, P.; et al. Enhancing quantum sensing sensitivity by a quantum memory. Nat. Commun. 2016, 7, 12279. [Google Scholar] [CrossRef] [PubMed]
- Pfender, M.; Aslam, N.; Sumiya, H.; Onoda, S.; Neumann, P.; Isoya, J.; Meriles, C.A.; Wrachtrup, J. Nonvolatile nuclear spin memory enables sensor-unlimited nanoscale spectroscopy of small spin clusters. Nat. Commun. 2017, 8, 834. [Google Scholar] [CrossRef] [PubMed]
- Dréau, A.; Spinicelli, P.; Maze, J.R.; Roch, J.F.; Jacques, V. Single-Shot Readout of Multiple Nuclear Spin Qubits in Diamond under Ambient Conditions. Phys. Rev. Lett. 2013, 110, 60502. [Google Scholar] [CrossRef] [PubMed]
- Elzerman, J.M.; Hanson, R.; Willems van Beveren, L.H.; Witkamp, B.; Vandersypen, L.M.K.; Kouwenhoven, L.P. Single-shot read-out of an individual electron spin in a quantum dot. Nature 2004, 430, 431–435. [Google Scholar] [CrossRef] [PubMed]
- Morello, A.; Pla, J.J.; Zwanenburg, F.A.; Chan, K.W.; Tan, K.Y.; Huebl, H.; Mottonen, M.; Nugroho, C.D.; Yang, C.; van Donkelaar, J.A.; et al. Single-shot readout of an electron spin in silicon. Nature 2010, 467, 687–691. [Google Scholar] [CrossRef] [PubMed]
- Waldherr, G.; Neumann, P.; Huelga, S.F.; Jelezko, F.; Wrachtrup, J. Violation of a Temporal Bell Inequality for Single Spins in a Diamond Defect Center. Phys. Rev. Lett. 2011, 107, 090401. [Google Scholar] [CrossRef] [PubMed]
- Jayakumar, H.; Henshaw, J.; Dhomkar, S.; Pagliero, D.; Laraoui, A.; Manson, N.B.; Albu, R.; Doherty, M.W.; Meriles, C.A. Optical patterning of trapped charge in nitrogen-doped diamond. Nat. Commun. 2016, 7, 12660. [Google Scholar] [CrossRef] [PubMed]
- Dhomkar, S.; Henshaw, J.; Jayakumar, H.; Meriles, C. Long-term data storage in diamond. Sci. Adv. 2016, 2, e1600911. [Google Scholar] [CrossRef] [PubMed]
- Aslam, N.; Waldherr, G.; Neumann, P.; Jelezko, F.; Wrachtrup, J. Photo-induced ionization dynamics of the nitrogen vacancy defect in diamond investigated by single-shot charge state detection. New J. Phys. 2013, 15, 013064. [Google Scholar] [CrossRef]
- Jaskula, J.; Shields, B.J.; Bauch, E.; Lukin, M.D.; Trifonov, A.S. Improved quantum sensing with a single solid- state spin via spin-to-charge conversion. arXiv, 2017; arXiv:1711.02023. [Google Scholar]
- Ariyaratne, A.; Bluvstein, D.; Myers, B.A.; Jayich, A.C.B. Nanoscale electrical conductivity imaging using a nitrogen-vacancy center in diamond. Nat. Commun. 2018, 9, 2406. [Google Scholar] [CrossRef] [PubMed]
- Bourgeois, E.; Jarmola, A.; Siyushev, P.; Gulka, M.; Hruby, J.; Jelezko, F.; Budker, D.; Nesladek, M. Photoelectric detection of electron spin resonance of nitrogen-vacancy centres in diamond. Nat. Commun. 2015, 6, 8577. [Google Scholar] [CrossRef] [PubMed]
- Brenneis, A.; Gaudreau, L.; Seifert, M.; Karl, H.; Brandt, M.S.; Huebl, H.; Garrido, J.A.; Koppens, F.H.; Holleitner, A.W. Ultrafast electronic readout of diamond nitrogen-vacancy centres coupled to graphene. Nat. Nanotechnol. 2015, 10, 135–139. [Google Scholar] [CrossRef] [PubMed]
- Bourgeois, E.; Londero, E.; Buczak, K.; Hruby, J.; Gulka, M.; Balasubramaniam, Y.; Wachter, G.; Stursa, J.; Dobes, K.; Aumayr, F.; et al. Enhanced photoelectric detection of NV magnetic resonances in diamond under dual-beam excitation. Phys. Rev. B 2017, 95, 41402. [Google Scholar] [CrossRef]
- Hrubesch, F.M.; Braunbeck, G.; Stutzmann, M.; Reinhard, F.; Brandt, M.S. Efficient Electrical Spin Readout of NV- Centers in Diamond. Phys. Rev. Lett. 2017, 118, 037601. [Google Scholar] [CrossRef] [PubMed]
- Gulka, M.; Bourgeois, E.; Hruby, J.; Siyushev, P.; Wachter, G.; Aumayr, F.; Hemmer, P.R.; Gali, A.; Jelezko, F.; Trupke, M.; Nesladek, M. Pulsed Photoelectric Coherent Manipulation and Detection of NV- Center Spins in Diamond. Phys. Rev. Appl. 2017, 7, 044032. [Google Scholar] [CrossRef]
- Heremans, F.J.; Fuchs, G.D.; Wang, C.F.; Hanson, R.; Awschalom, D.D. Generation and transport of photoexcited electrons in single-crystal diamond. Appl. Phys. Lett. 2009, 94, 7–10. [Google Scholar] [CrossRef]
- Bourdeauducq, S.; Jördens, R.; Zotov, P.; Britton, J.; Slichter, D.; Leibrandt, D.; Allcock, D.; Hankin, A.; Kermarrec, F.; Sionneau, Y.; et al. m-labs/artiq: 3.6. Available online: https://zenodo.org/record/51303 (accessed on 30 August 2018).
- Binder, J.M.; Stark, A.; Tomek, N.; Scheuer, J.; Frank, F.; Jahnke, K.D.; Müller, C.; Schmitt, S.; Metsch, M.H.; Unden, T.; et al. Qudi: A modular python suite for experiment control and data processing. SoftwareX 2017, 6, 85–90. [Google Scholar] [CrossRef]
- Lim, S.H.; Mar, W.; Matheu, P.; Derkacs, D.; Yu, E.T. Photocurrent spectroscopy of optical absorption enhancement in silicon photodiodes via scattering from surface plasmon polaritons in gold nanoparticles. J. Appl. Phys. 2007, 101, 104309. [Google Scholar] [CrossRef]
- Wee, T.-L.; Tzeng, Y.K.; Han, C.C.; Chang, H.C.; Fann, W.; Hsu, J.H.; Chen, K.M.; Yu, Y.C. Two-photon Excited Fluorescence of Nitrogen-Vacancy Centers in Proton-Irradiated Type lb Diamond. J. Phys. Chem. A 2007, 111, 9379–9386. [Google Scholar]
- Bogdanov, S.I.; Shalaginov, M.Y.; Lagutchev, A.S.; Chiang, C.C.; Shah, D.; Baburin, A.S.; Ryzhikov, I.A.; Rodionov, I.A.; Kildishev, A.V.; Boltasseva, A.; et al. Ultrabright Room-Temperature Sub-Nanosecond Emission from Single Nitrogen-Vacancy Centers Coupled to Nanopatch Antennas. Nano Lett. 2018, 18, 4837–4844. [Google Scholar] [CrossRef] [PubMed]
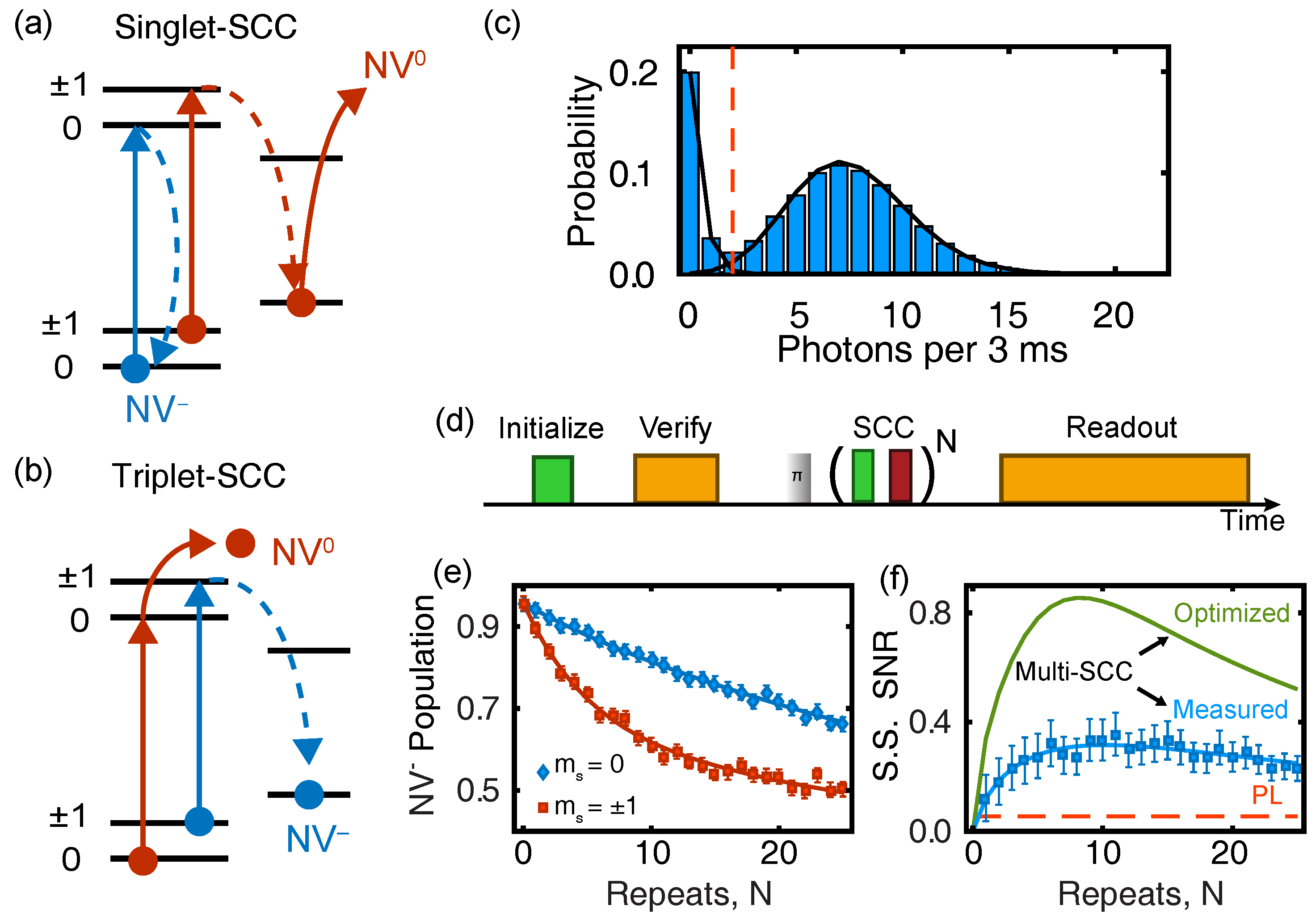
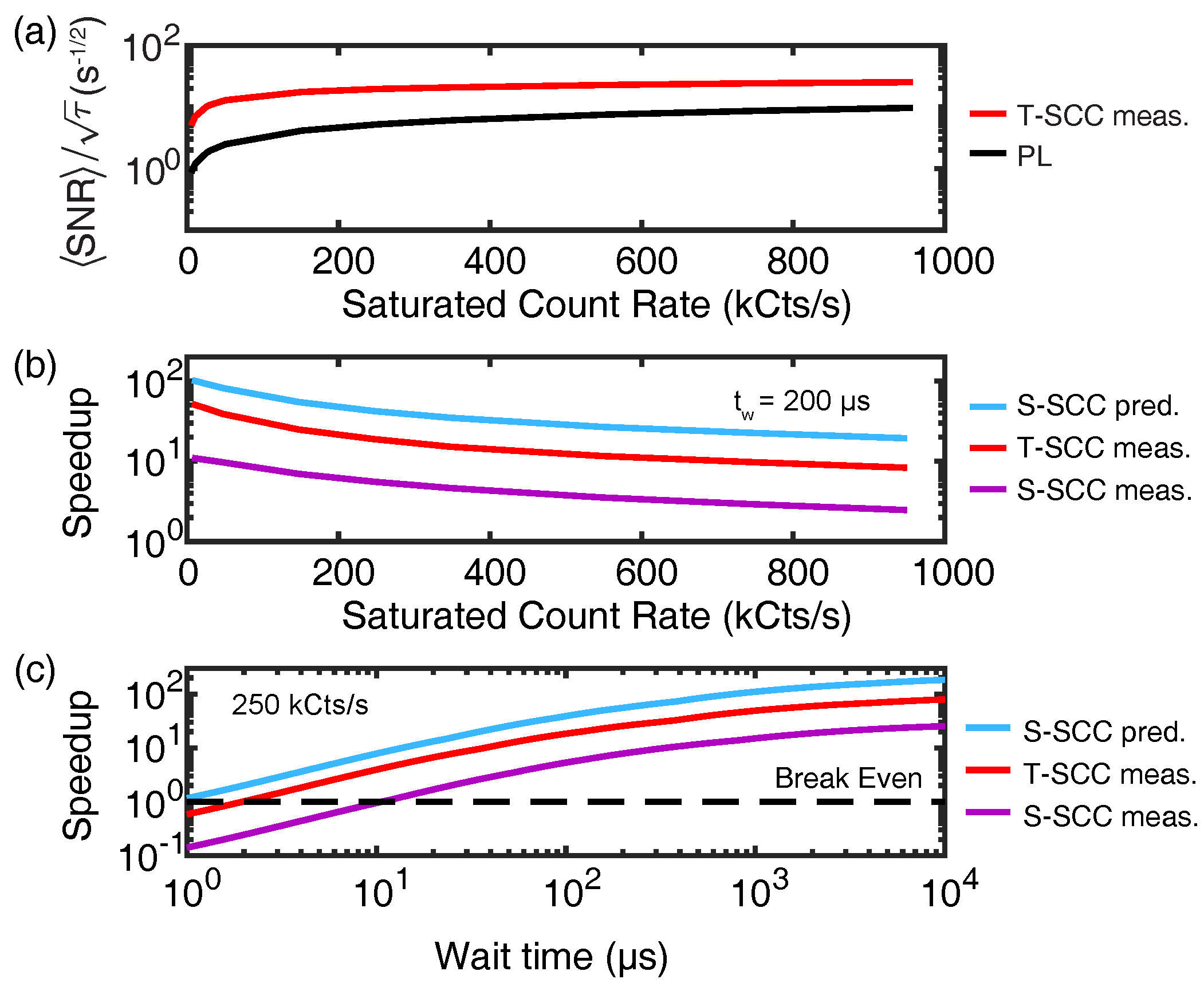

| Metric | Relation to SNR | Use Case |
|---|---|---|
| Contrast, C, & Count rate, | traditional PL readout | |
| Spin-readout noise, | magnetometry | |
| Fidelity, | quantum algorithms, large signals | |
| Repeats for | magnetometry, general experiments |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hopper, D.A.; Shulevitz, H.J.; Bassett, L.C. Spin Readout Techniques of the Nitrogen-Vacancy Center in Diamond. Micromachines 2018, 9, 437. https://doi.org/10.3390/mi9090437
Hopper DA, Shulevitz HJ, Bassett LC. Spin Readout Techniques of the Nitrogen-Vacancy Center in Diamond. Micromachines. 2018; 9(9):437. https://doi.org/10.3390/mi9090437
Chicago/Turabian StyleHopper, David A., Henry J. Shulevitz, and Lee C. Bassett. 2018. "Spin Readout Techniques of the Nitrogen-Vacancy Center in Diamond" Micromachines 9, no. 9: 437. https://doi.org/10.3390/mi9090437
APA StyleHopper, D. A., Shulevitz, H. J., & Bassett, L. C. (2018). Spin Readout Techniques of the Nitrogen-Vacancy Center in Diamond. Micromachines, 9(9), 437. https://doi.org/10.3390/mi9090437





