Roughness Evolution and Charging in Plasma-Based Surface Engineering of Polymeric Substrates: The Effects of Ion Reflection and Secondary Electron Emission
Abstract
1. Introduction
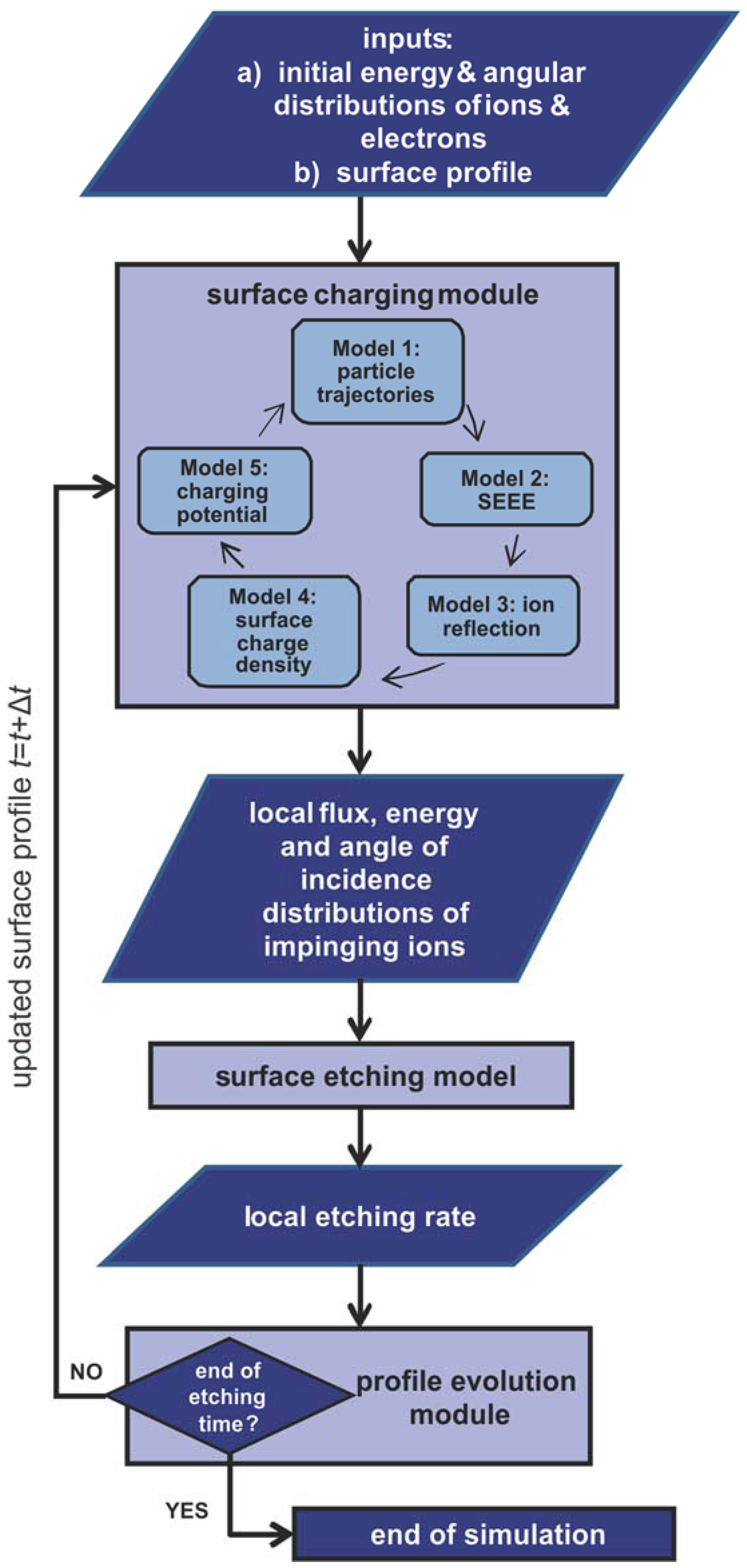
2. The Modeling Framework
2.1. The Surface Charging Module
2.1.1. Particle Trajectory Model
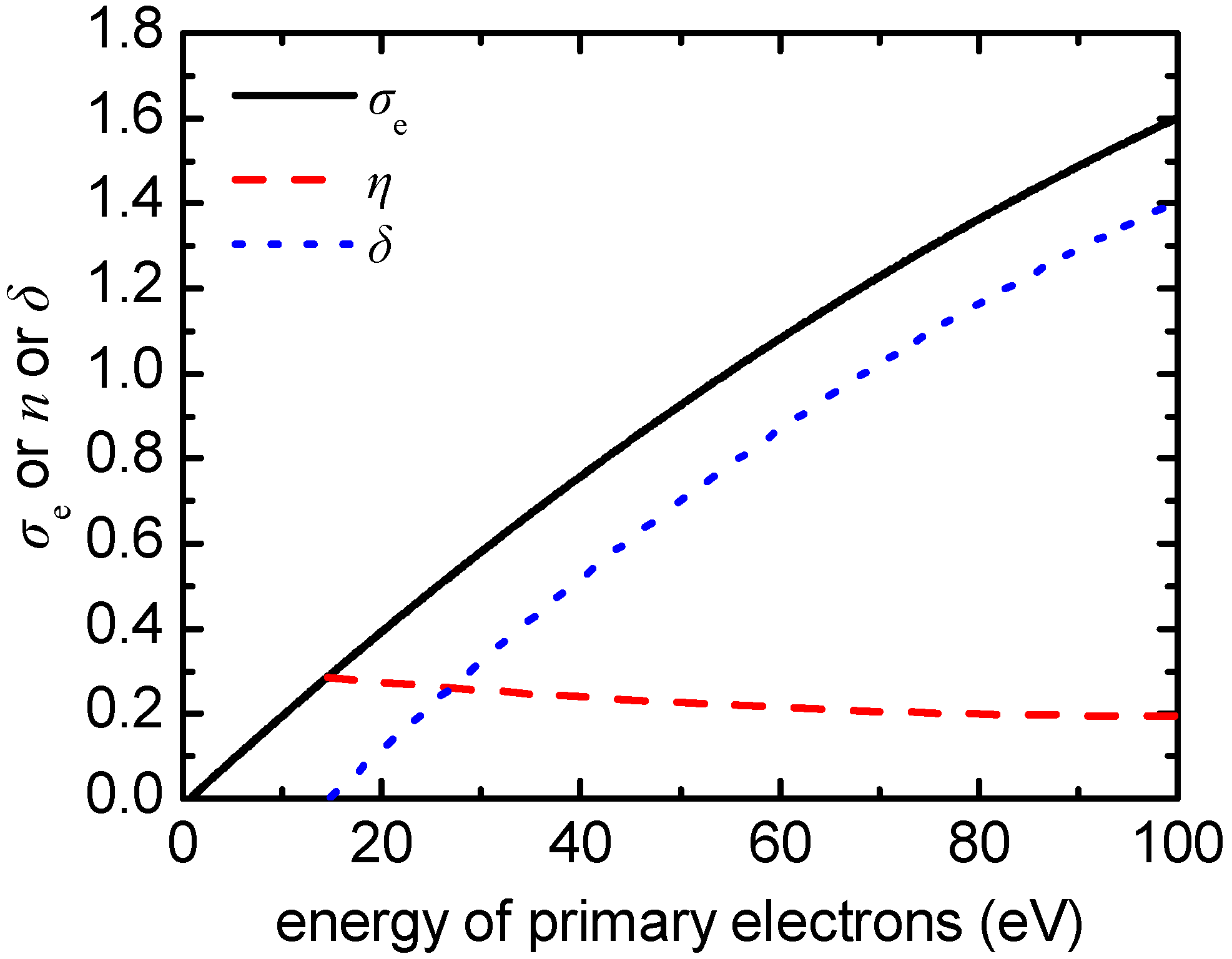
2.1.2. Secondary Electron-Electron Emission Model
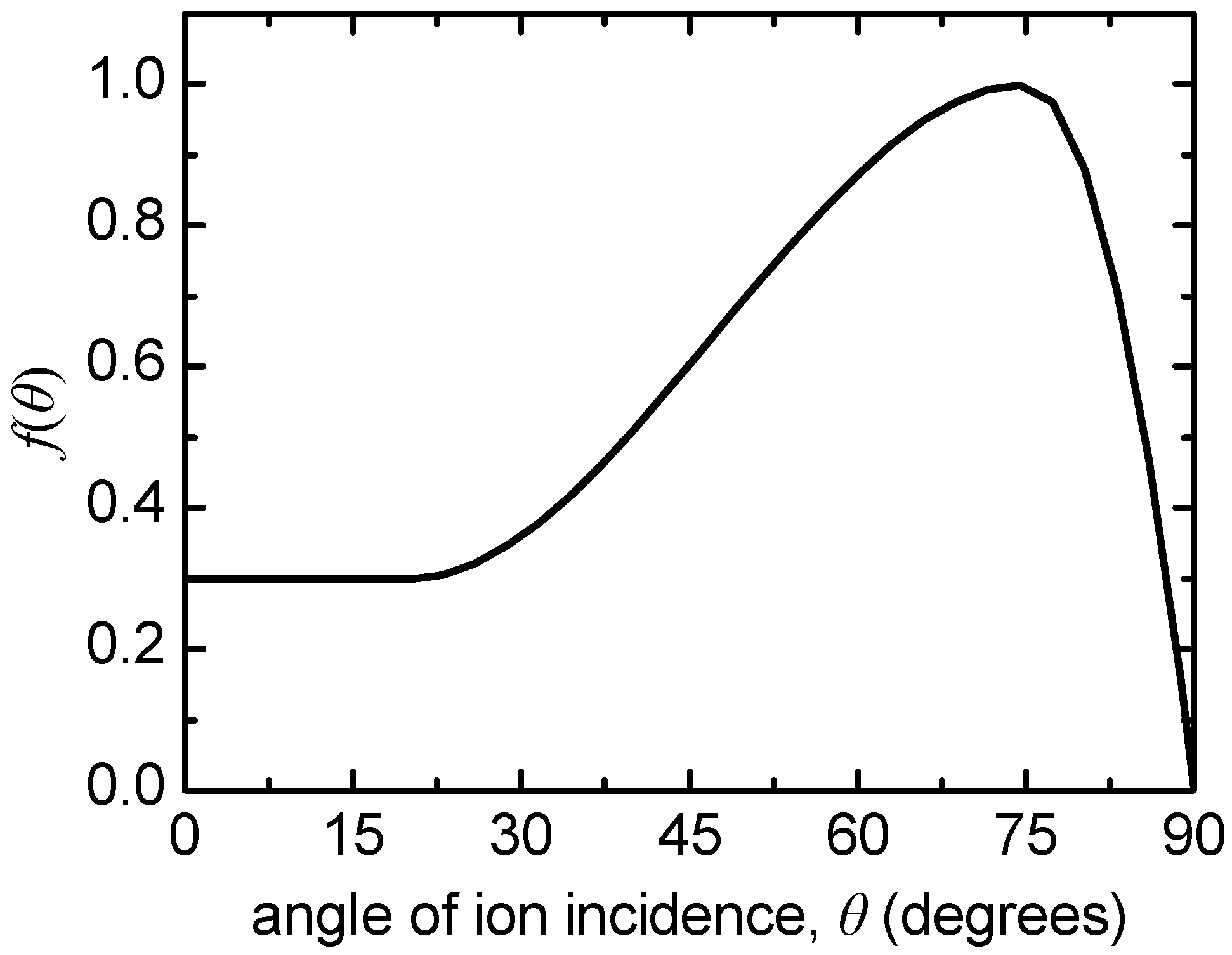
2.1.3. Ion Reflection Model
2.1.4. Surface Charge Density Model
2.1.5. Charging Potential Model
2.2. Surface Etching Model
2.3. Profile Evolution Module
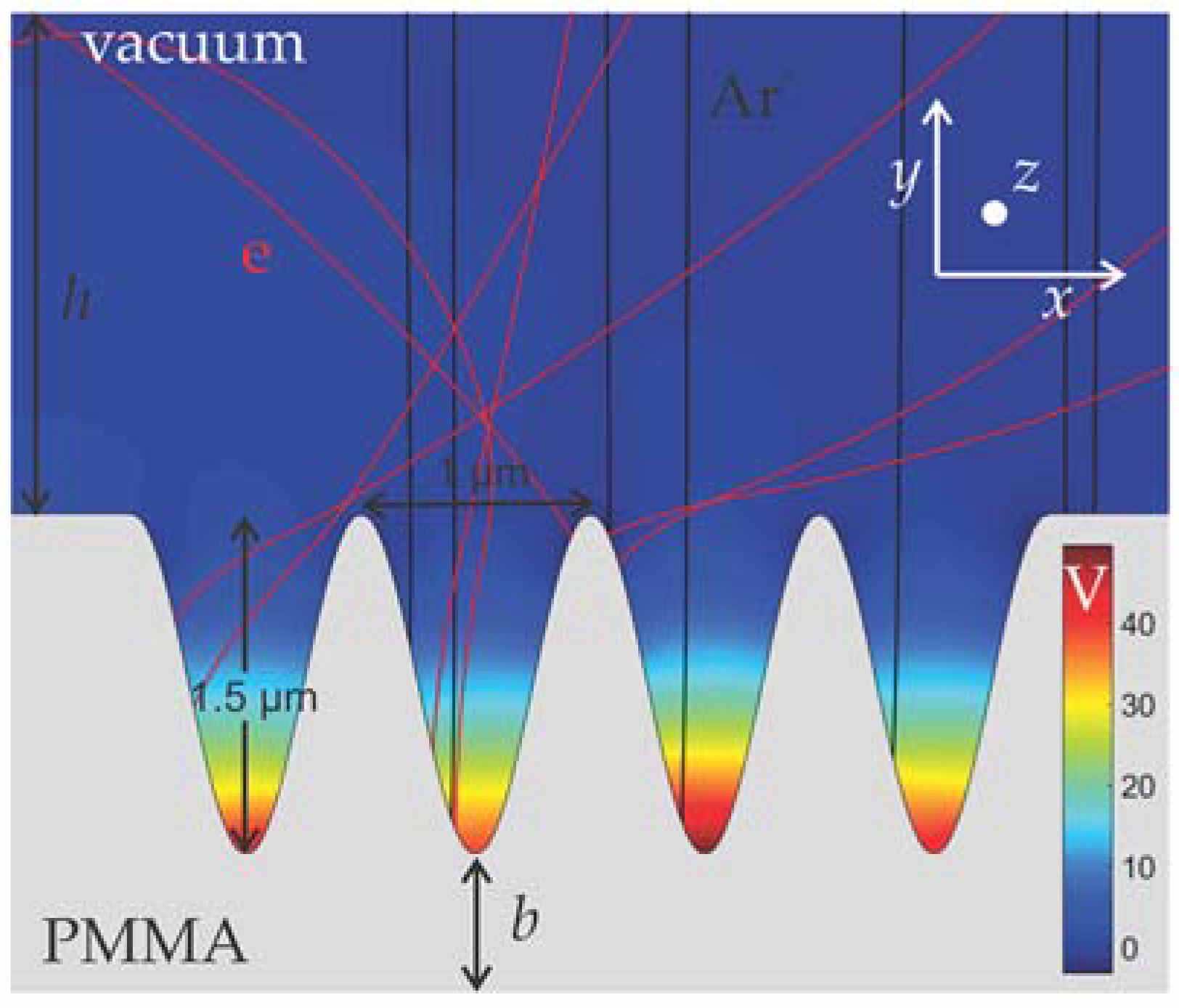
3. Case Study
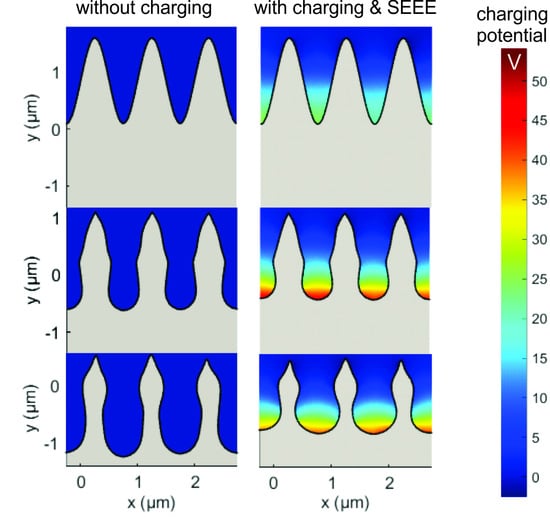
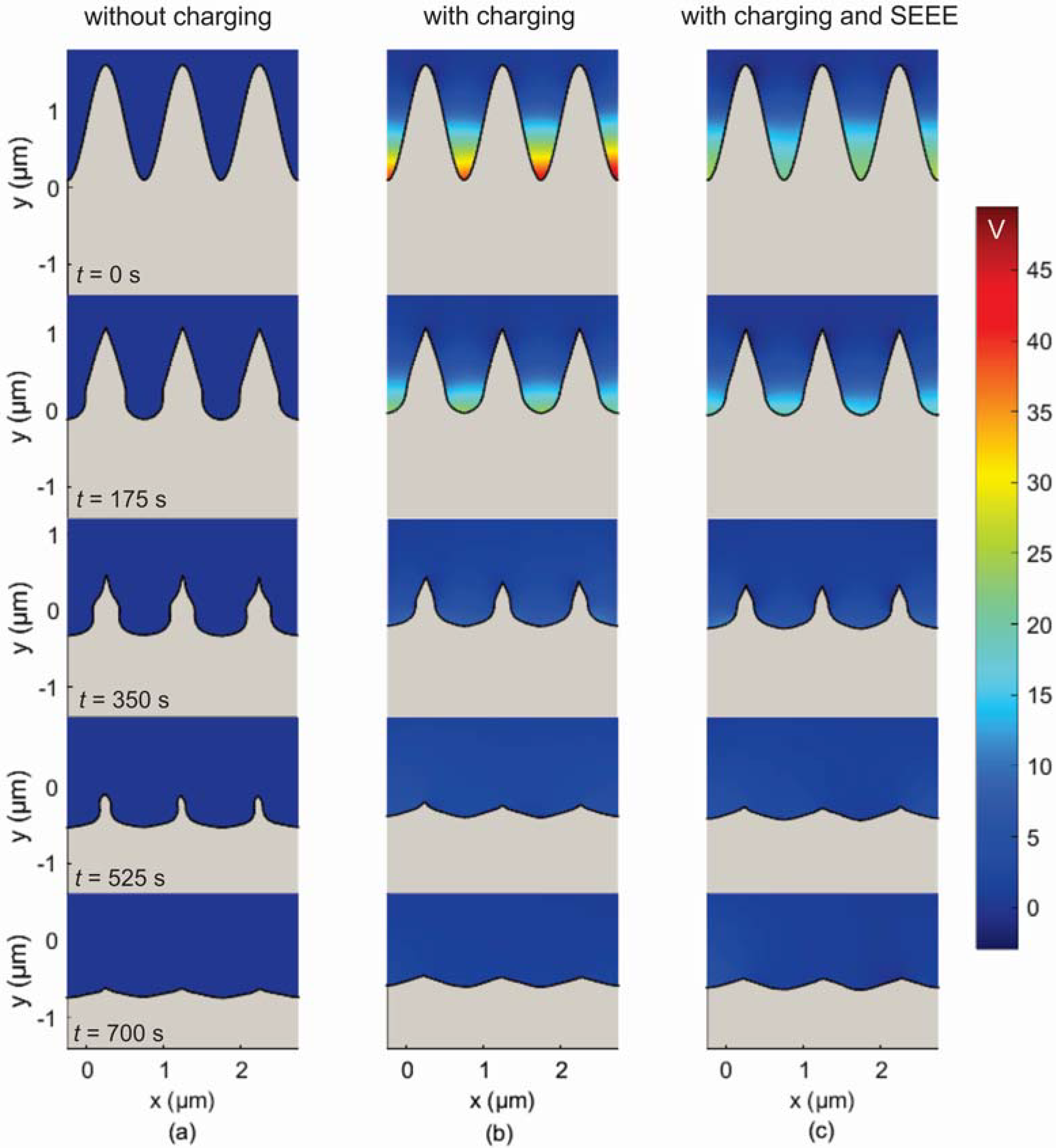
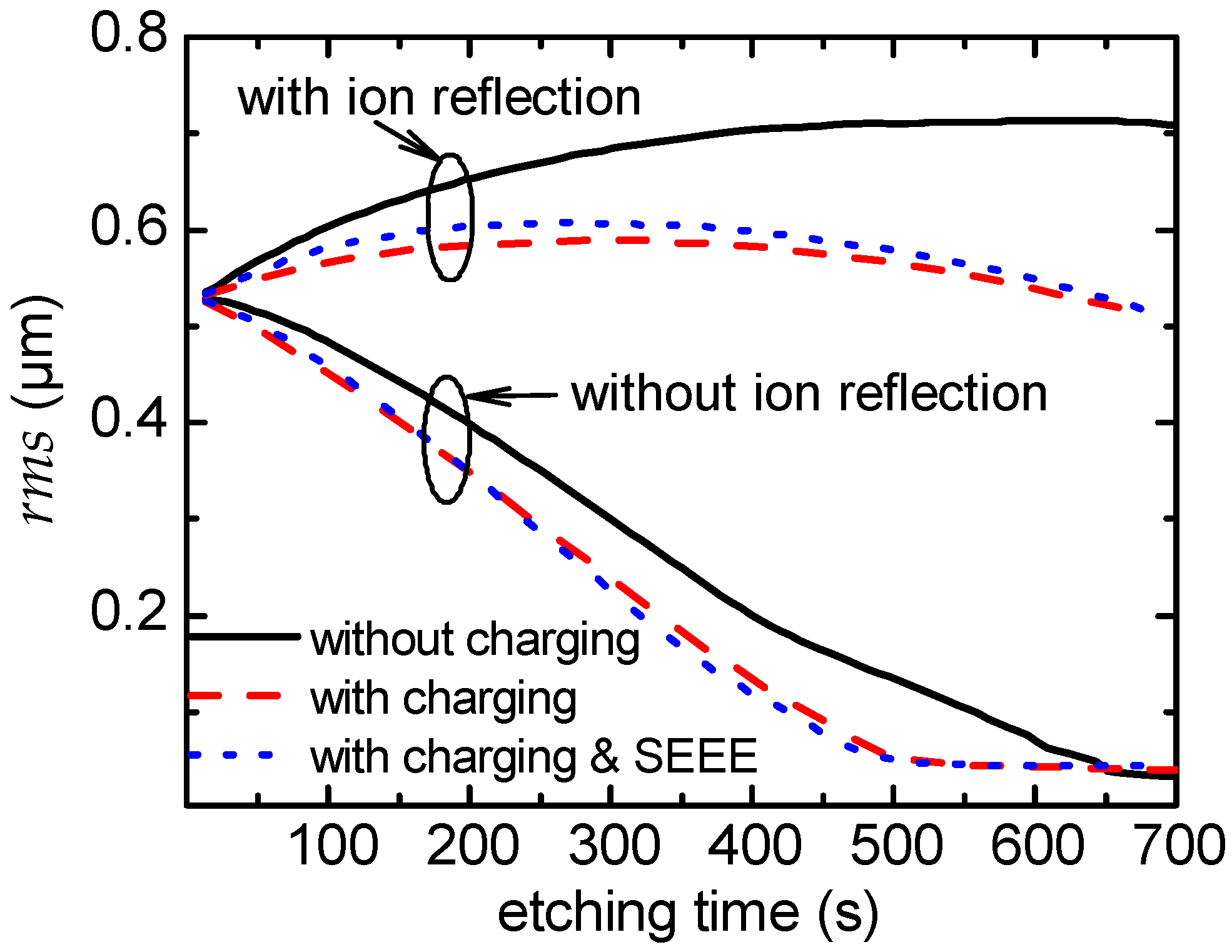
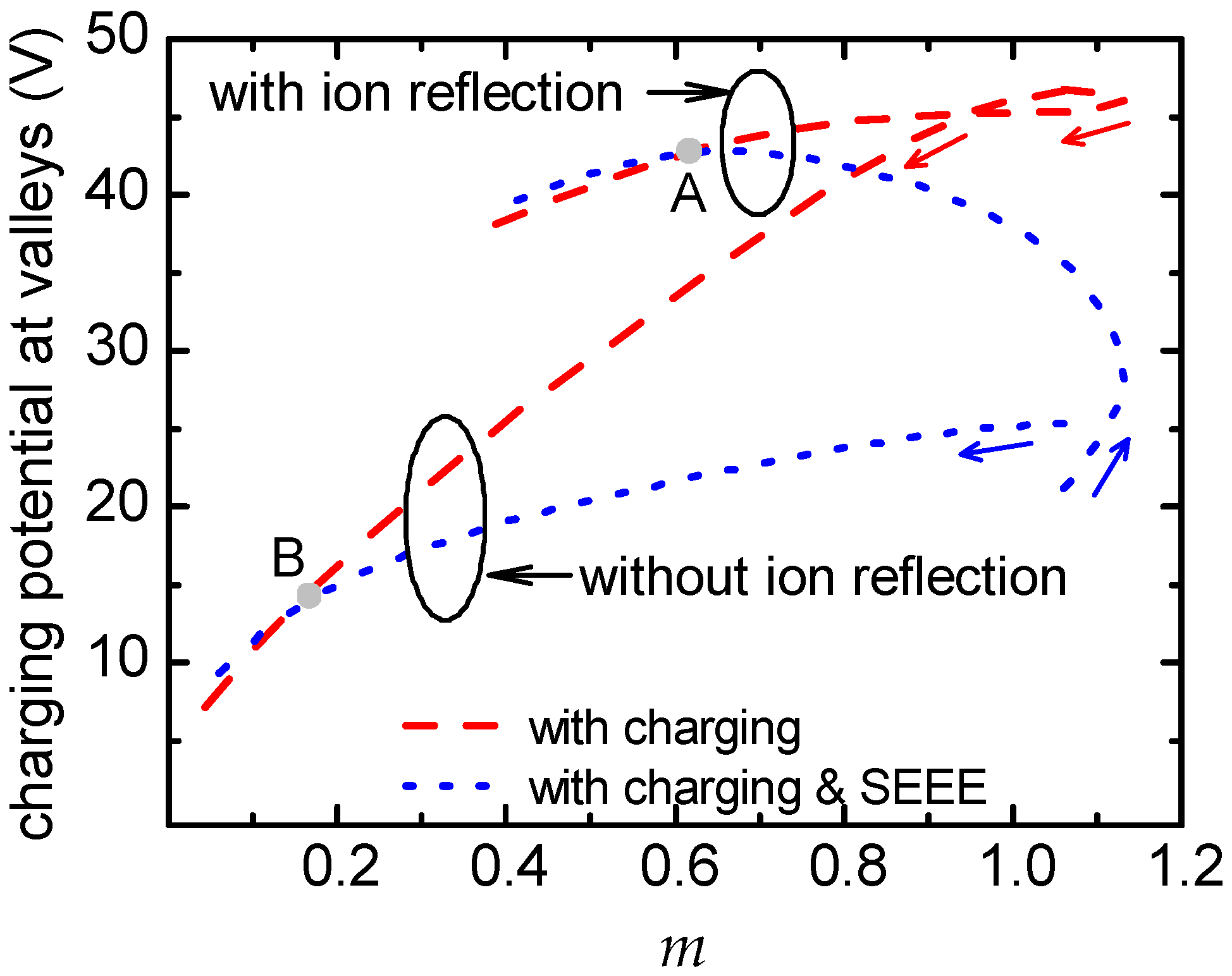
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gogolides, E.; Ellinas, K.; Tserepi, A. Hierarchical micro and nano structured, hydrophilic, superhydrophobic and superoleophobic surfaces incorporated in microfluidics, microarrays and lab on chip microsystems. Microelectron. Eng. 2015, 132, 135–155. [Google Scholar] [CrossRef]
- Ellinas, K.; Pujari, S.P.; Dragatogiannis, D.A.; Charitidis, C.A.; Tserepi, A.; Zuilhof, H.; Gogolides, E. Plasma micro-nanotextured, scratch, water and hexadecane resistant, superhydrophobic, and superamphiphobic polymeric surfaces with perfluorinated monolayers. ACS Appl. Mater. Interfaces 2014, 6, 6510–6524. [Google Scholar] [CrossRef] [PubMed]
- Vourdas, N.; Tserepi, A.; Gogolides, E. Nanotextured super-hydrophobic transparent poly(methyl methacrylate) surfaces using high-density plasma processing. Nanotechnology 2007, 18, 125304. [Google Scholar] [CrossRef]
- Murphy, W.L.; McDevitt, T.C.; Engler, A.J. Materials as stem cell regulators. Nat. Mater. 2014, 13, 547–557. [Google Scholar] [CrossRef] [PubMed]
- Metavarayuth, K.; Sitasuwan, P.; Zhao, X.; Lin, Y.; Wang, Q. Influence of surface topographical cues on the differentiation of mesenchymal stem cells in vitro. ACS Biomater. Sci. Eng. 2016, 2, 142–151. [Google Scholar] [CrossRef]
- Borghi, F.F.; Rider, A.E.; Kumar, S.; Han, Z.J.; Haylock, D.; Ostrikov, K. Emerging stem cell controls: Nanomaterials and plasma effects. J. Nanomater. 2013, 2013, 329139. [Google Scholar] [CrossRef]
- Tserepi, A.; Gogolides, E.; Bourkoula, A.; Kanioura, A.; Kokkoris, G.; Petrou, P.S.; Kakabakos, S.E. Plasma nanotextured polymeric surfaces for controlling cell attachment and proliferation: A short review. Plasma Chem. Plasma Process. 2016, 36, 107–120. [Google Scholar] [CrossRef]
- Bourkoula, A.; Constantoudis, V.; Kontziampasis, D.; Petrou, P.S.; Kakabakos, S.E.; Tserepi, A.; Gogolides, E. Roughness threshold for cell attachment and proliferation on plasma micro-nanotextured polymeric surfaces: The case of primary human skin fibroblasts and mouse immortalized 3t3 fibroblasts. J. Phys. D Appl. Phys. 2016, 49, 304002. [Google Scholar] [CrossRef]
- Di Mundo, R.; Nardulli, M.; Milella, A.; Favia, P.; Dagostino, R.; Gristina, R. Cell adhesion on nanotextured slippery superhydrophobic substrates. Langmuir 2011, 27, 4914–4921. [Google Scholar] [CrossRef] [PubMed]
- Gristina, R.; D’Aloia, E.; Senesi, G.S.; Milella, A.; Nardulli, M.; Sardella, E.; Favia, P.; D’Agostino, R. Increasing cell adhesion on plasma deposited fluorocarbon coatings by changing the surface topography. J. Biomed. Mater. Res. Part B 2009, 88, 139–149. [Google Scholar] [CrossRef] [PubMed]
- Ting, Y.-H.; Park, S.-M.; Liu, C.-C.; Liu, X.; Himpsel, F.J.; Nealey, P.F.; Wendt, A.E. Plasma etch removal of poly(methyl methacrylate) in block copolymer lithography. J. Vac. Sci. Technol. B 2008, 26, 1684–1689. [Google Scholar] [CrossRef]
- Vlachopoulou, M.-E.; Kokkoris, G.; Cardinaud, C.; Gogolides, E.; Tserepi, A. Plasma etching of poly(dimethylsiloxane): Roughness formation, mechanism, control, and application in the fabrication of microfluidic structures. Plasma Processes Polym. 2013, 10, 29–40. [Google Scholar] [CrossRef]
- Nest, D.; Chung, T.-Y.; Graves, D.B.; Engelmann, S.; Bruce, R.L.; Weilnboeck, F.; Oehrlein, G.S.; Wang, D.; Andes, C.; Hudson, E.A. Understanding the roughening and degradation of 193 nm photoresist during plasma processing: Synergistic roles of vacuum ultraviolet radiation and ion bombardment. Plasma Process. Polym. 2009, 6, 649–657. [Google Scholar] [CrossRef]
- Bruce, R.L.; Weilnboeck, F.; Lin, T.; Phaneuf, R.J.; Oehrlein, G.S.; Long, B.K.; Willson, C.G.; Vegh, J.J.; Nest, D.; Graves, D.B. Relationship between nanoscale roughness and ion-damaged layer in argon plasma exposed polystyrene films. J. Appl. Phys. 2010, 107, 084310. [Google Scholar] [CrossRef]
- Bruce, R.L.; Engelmann, S.; Lin, T.; Kwon, T.; Phaneuf, R.J.; Oehrlein, G.S.; Long, B.K.; Willson, C.G.; Végh, J.J.; Nest, D.; et al. Study of ion and vacuum ultraviolet-induced effects on styrene- and ester-based polymers exposed to argon plasma. J. Vac. Sci. Technol. B 2009, 27, 1142–1155. [Google Scholar] [CrossRef]
- Ko, T.-J.; Jo, W.; Lee, H.J.; Oh, K.H.; Moon, M.-W. Nanostructures formed on carbon-based materials with different levels of crystallinity using oxygen plasma treatment. Thin Solid Films 2015, 590, 324–329. [Google Scholar] [CrossRef]
- Vourdas, N.; Kontziampasis, D.; Kokkoris, G.; Constantoudis, V.; Goodyear, A.; Tserepi, A.; Cooke, M.; Gogolides, E. Plasma directed assembly and organization: Bottom-up nanopatterning using top-down technology. Nanotechnology 2010, 21, 085302. [Google Scholar] [CrossRef] [PubMed]
- Kokkoris, G.; Vourdas, N.; Gogolides, E. Plasma etching and roughening of thin polymeric films: A fast, accurate, in situ method of surface roughness measurement. Plasma Process. Polym. 2008, 5, 825–833. [Google Scholar] [CrossRef]
- Gogolides, E.; Constantoudis, V.; Kokkoris, G.; Kontziampasis, D.; Tsougeni, K.; Boulousis, G.; Vlachopoulou, M.; Tserepi, A. Controlling roughness: From etching to nanotexturing and plasma-directed organization on organic and inorganic materials. J. Phys. D Appl. Phys. 2011, 44, 174021. [Google Scholar] [CrossRef]
- Kontziampasis, D.; Trantidou, T.; Regoutz, A.; Humphrey, E.J.; Carta, D.; Terracciano, C.M.; Prodromakis, T. Effects of ar and O2 plasma etching on parylene c: Topography versus surface chemistry and the impact on cell viability. Plasma Process. Polym. 2016, 13, 324–333. [Google Scholar] [CrossRef]
- Giapis, K.P.; Hwang, G.S. Pattern-dependent charging and the role of electron tunneling. Jpn. J. Appl. Phys. 1998, 37 Pt 1, 2281–2290. [Google Scholar] [CrossRef]
- Kunstler, W.; Frubing, P.; Gerhard-Multhaupt, R.; Cerny, J.; Klemberg-Sapieha, J.; Martinu, L.; Wertheimer, M.R.; Hollander, A.; Behnisch, J. Surface-charging behavior of plasma-treated polymer films. In Proceedings of the 1998 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (Cat. No.98CH36257), Atlanta, GA, USA, 25–28 Octobor 1998; IEEE: Piscataway, NJ, USA; pp. 609–612. [Google Scholar]
- Bormashenko, E.; Whyman, G.; Multanen, V.; Shulzinger, E.; Chaniel, G. Physical mechanisms of interaction of cold plasma with polymer surfaces. J. Colloid Interface Sci. 2015, 448, 175–179. [Google Scholar] [CrossRef] [PubMed]
- Memos, G.; Lidorikis, E.; Kokkoris, G. The interplay between surface charging and microscale roughness during plasma etching of polymeric substrates. J. Appl. Phys. 2018, 123, 073303. [Google Scholar] [CrossRef]
- Memos, G.; Kokkoris, G. Modeling of charging on unconventional surface morphologies of pmma substrates during ar plasma etching. Plasma Process. Polym. 2016, 13, 565–578. [Google Scholar] [CrossRef]
- Mouchtouris, S.; Kokkoris, G. Multiscale modeling of low pressure plasma etching processes: Linking the operating parameters of the plasma reactor with surface roughness evolution. Plasma Process. Polym. 2017, 14, 1600147. [Google Scholar] [CrossRef]
- Kokkoris, G.; Tserepi, A.; Boudouvis, A.G.; Gogolides, E. Simulation of SiO2 and si feature etching for microelectronics and microelectromechanical systems fabrication: A combined simulator coupling modules of surface etching, local flux calculation, and profile evolution. J. Vac. Sci. Technol. A 2004, 22, 1896–1902. [Google Scholar] [CrossRef]
- Ono, K.; Nakazaki, N.; Tsuda, H.; Takao, Y.; Eriguchi, K. Surface morphology evolution during plasma etching of silicon: Roughening, smoothing and ripple formation. J. Phys. D Appl. Phys. 2017, 50, 414001. [Google Scholar] [CrossRef]
- Palov, A.P.; Yu, A.M.; Rakhimova, T.V.; Shamiryan, D. Charging and the secondary electron–electron emission on a trench surface: Broadening and shift of ion energy spectrum at plasma trench etching. J. Phys. D Appl. Phys. 2010, 43, 075203. [Google Scholar] [CrossRef]
- Palov, A.P.; Mankelevich, Y.A.; Rakhimova, T.V.; Shamiryan, D. Charging of submicron structures during silicon dioxide etching in one- and two-frequency gas discharges. Plasma Phys. Rep. 2010, 36, 891–901. [Google Scholar] [CrossRef]
- Matlab. Available online: http://www.mathworks.com/products/matlab/ (accessed on 17 August 2018).
- Sethian, J.A. Fast marching methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
- Song, Z.G.; Ong, C.K.; Gong, H. Secondary and backscattered electron yields of polymer surface under electron beam irradiation. Appl. Surf. Sci. 1997, 119, 169–175. [Google Scholar] [CrossRef]
- Rau, É.I.; Evstaf’eva, E.N.; Andrianov, M.V. Mechanisms of charging of insulators under irradiation with medium-energy electron beams. Phys. Solid State 2008, 50, 621–630. [Google Scholar] [CrossRef]
- Boubaya, M.; Blaise, G. Charging regime of pmma studied by secondary electron emission. Eur. Phys. J. Appl. Phys. 2007, 37, 79–86. [Google Scholar] [CrossRef]
- Masaaki, Y.; Kosuke, M.; Yasuaki, K.; Hiroaki, K.; Yoshihiko, H. Analysis of charging phenomena of polymer films on silicon substrates under electron beam irradiation. Jpn. Appl. Phys. 2008, 47, 4890–4892. [Google Scholar]
- Lin, Y.; Joy, D.C. A new examination of secondary electron yield data. Surf. Interface Anal. 2005, 37, 895–900. [Google Scholar] [CrossRef]
- Yu, K.K.; Zhang, G.J.; Zheng, N.; Raitses, Y.; Fisch, N.J. Monte carlo simulation of surface-charging phenomena on insulators prior to flashover in vacuum. IEEE Trans. Plasma Sci. 2009, 37, 698–704. [Google Scholar]
- Burke, E.A. Secondary emission from polymers. IEEE Trans. Nucl. Sci. 1980, 27, 1759–1764. [Google Scholar] [CrossRef]
- Dapor, M.; Ciappa, M.; Fichtner, W. Monte carlo modeling in the low-energy domain of the secondary electron emission of polymethylmethacrylate for critical-dimension scanning electron microscopy. J. Micro/Nanolithogr. MEMS MOEMS 2010, 9, 023001. [Google Scholar]
- Dapor, M. Spectra of electrons emerging from pmma. Imaging Microsc. 2016, 18, 38–39. [Google Scholar]
- Palov, A.; Haruhisa, F.; Sanju, H. Monte carlo simulation of 1 ev–35 kev electron scattering in teflon. Jpn. J. Appl. Phys. 1998, 37, 6170. [Google Scholar] [CrossRef]
- Dekker, A.J. Solid State Physics; Prentice-Hall: Upper Saddle River, NJ, USA, 1962. [Google Scholar]
- Seiler, H. Secondary electron emission in the scanning electron microscope. J. Appl. Phys. 1983, 54, R1–R18. [Google Scholar] [CrossRef]
- Masaaki, Y.; Takahiro, N.; Hiroaki, K. A monte carlo calculation of secondary electron emission from organic compounds. Jpn. J. Appl. Phys. 2004, 43, 4004–4008. [Google Scholar]
- Seggern, H.V. Charging dynamics of dielectrics irradiated by low energy electrons. IEEE Trans. Nucl. Sci. 1985, 32, 1503–1511. [Google Scholar] [CrossRef]
- Hwang, G.S.; Giapis, K.P. On the origin of the notching effect during etching in uniform high density plasmas. J. Vac. Sci. Technol. B 1997, 15, 70–87. [Google Scholar] [CrossRef]
- Giapis, K.P.; Hwang, G.S. Plasma interactions with high aspect ratio patterned surfaces: Ion transport, scattering, and the role of charging. Thin Solid Films 2000, 374, 175–180. [Google Scholar] [CrossRef]
- Zhao, Z.; Dai, Z.; Wang, Y. Feature profile evolution during etching of SiO2 in radio-frequency or direct-current plasmas. Plasma Sci. Technol. 2012, 14, 64–70. [Google Scholar] [CrossRef]
- Radmilović-Radjenović, M.; Radjenović, B.; Savić, M. The surface charging effects in three-dimensional simulation of the profiles of plasma-etched nanostructures. Int. J. Numer. Model. Electron. Netw. Devices Fields 2011, 24, 535–544. [Google Scholar] [CrossRef]
- Dai, Z.L.; Zhang, S.Q.; Wang, Y.N. Study on feature profile evolution for chlorine etching of silicon in an rf biased sheath. Vacuum 2013, 89, 197–202. [Google Scholar] [CrossRef]
- Dai, Z.L.; Yue, G.; Wang, Y.N. Study on mechanism of etching in low pressure radio-frequency plasmas. Curr. Appl. Phys. 2011, 11, S121–S125. [Google Scholar] [CrossRef]
- Wang, M.; Kushner, M.J. High energy electron fluxes in dc-augmented capacitively coupled plasmas. Ii. Effects on twisting in high aspect ratio etching of dielectrics. J. Appl. Phys. 2010, 107, 023309. [Google Scholar] [CrossRef]
- Comsol. Available online: http://www.comsol.com/ (accessed on 17 August 2018).
- Guo, W.; Sawin, H.H. Modeling of the angular dependence of plasma etching. J. Vac. Sci. Technol. A 2009, 27, 1326–1336. [Google Scholar] [CrossRef]
- Yin, Y.P.; Sawin, H.H. Angular etching yields of polysilicon and dielectric materials in cl-2/ar and fluorocarbon plasmas. J. Vac. Sci. Technol. A 2008, 26, 161–173. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods. Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Osher, S.; Fedkiw, R.P. Level Set Methods and Dynamic Implicit Surfaces, Applied Mathematical Sciences; Springer: New York, NY, USA, 2003; Volume 153. [Google Scholar]
- φetch. Available online: www.phietch.org (accessed on 17 August 2018).
- Hwang, G.S.; Giapis, K.P. Aspect ratio independent etching of dielectrics. Appl. Phys. Lett. 1997, 71, 458–460. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, G.C.; Lu, T.M. Characterization of Amorphous and Crystalline Rough Surface—Principles and Applications; Academic Press: Cambridge, MA, USA, 2001; Volume 37. [Google Scholar]
- Kokkoris, G.; Gogolides, E. The potential of ion-driven etching with simultaneous deposition of impurities for inducing periodic dots on surfaces. J. Phys. D Appl. Phys. 2012, 45, 165204. [Google Scholar] [CrossRef]
- Sánchez-García, J.A.; Vázquez, L.; Gago, R.; Redondo-Cubero, A.; Albella, J.M.; Czigány, Z. Tuning the surface morphology in self-organized ion beam nanopatterning of si(001) via metal incorporation: From holes to dots. Nanotechnology 2008, 19, 355306. [Google Scholar] [CrossRef] [PubMed]
- Ohmori, T.; Goto, T.; Makabe, T. Negative charge injection to a wafer in a pulsed two-frequency capacitively coupled plasma for oxide etching; diagnostics by emission-selected computerized tomography. J. Phys. D Appl. Phys. 2004, 37, 2223–2231. [Google Scholar] [CrossRef]
- Ohmori, T.; Makabe, T. In situ measurement of plasma charging on SiO2 hole bottoms and reduction by negative charge injection during etching. Appl. Surf. Sci. 2008, 254, 3696–3709. [Google Scholar] [CrossRef]
- Wang, M.; Kushner, M.J. High energy electron fluxes in dc-augmented capacitively coupled plasmas i. Fundamental characteristics. J. Appl. Phys. 2010, 107, 023308. [Google Scholar] [CrossRef]
- Economou, D.J. Fast (tens to hundreds of ev) neutral beams for materials processing. J. Phys. D Appl. Phys. 2008, 41, 024001. [Google Scholar] [CrossRef]
- Economou, D.J. Modeling and simulation of fast neutral beam sources for materials processing. Plasma Process. Polym. 2009, 6, 308–319. [Google Scholar] [CrossRef]
- Kokkoris, G.; Tserepi, A.; Gogolides, E. The potential of neutral beams for deep silicon nanostructure etching. J. Phys. D Appl. Phys. 2008, 41, 024004. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memos, G.; Lidorikis, E.; Kokkoris, G. Roughness Evolution and Charging in Plasma-Based Surface Engineering of Polymeric Substrates: The Effects of Ion Reflection and Secondary Electron Emission. Micromachines 2018, 9, 415. https://doi.org/10.3390/mi9080415
Memos G, Lidorikis E, Kokkoris G. Roughness Evolution and Charging in Plasma-Based Surface Engineering of Polymeric Substrates: The Effects of Ion Reflection and Secondary Electron Emission. Micromachines. 2018; 9(8):415. https://doi.org/10.3390/mi9080415
Chicago/Turabian StyleMemos, George, Elefterios Lidorikis, and George Kokkoris. 2018. "Roughness Evolution and Charging in Plasma-Based Surface Engineering of Polymeric Substrates: The Effects of Ion Reflection and Secondary Electron Emission" Micromachines 9, no. 8: 415. https://doi.org/10.3390/mi9080415
APA StyleMemos, G., Lidorikis, E., & Kokkoris, G. (2018). Roughness Evolution and Charging in Plasma-Based Surface Engineering of Polymeric Substrates: The Effects of Ion Reflection and Secondary Electron Emission. Micromachines, 9(8), 415. https://doi.org/10.3390/mi9080415