Asymmetrical Induced Charge Electroosmotic Flow on a Herringbone Floating Electrode and Its Application in a Micromixer
Abstract
1. Introduction
2. Theory and Methods
2.1. Micromixer Design
2.2. Mathematical Model
2.3. Numerical Simulation
2.4. Evaluation of the Mixing Efficiency
3. Results and Discussion
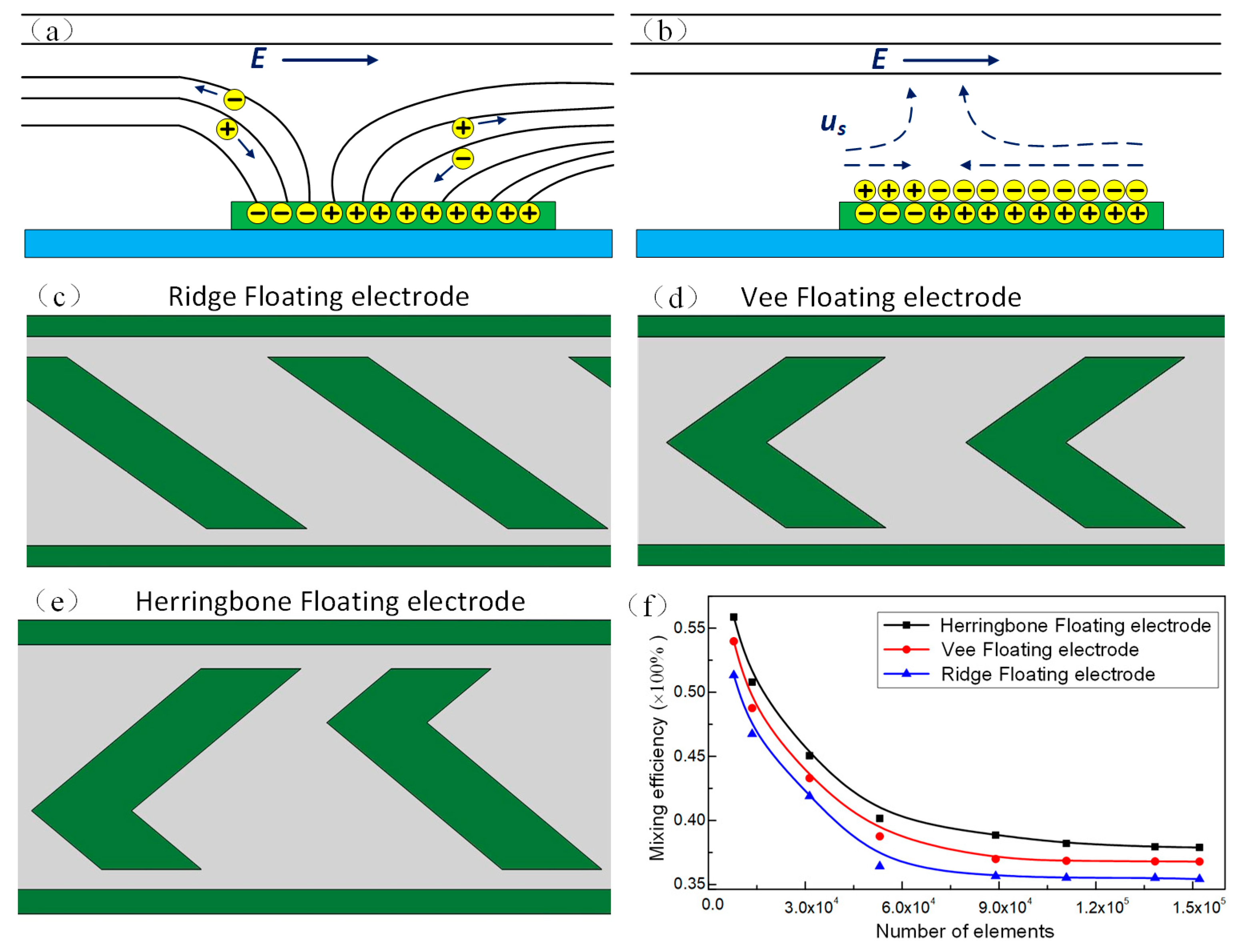
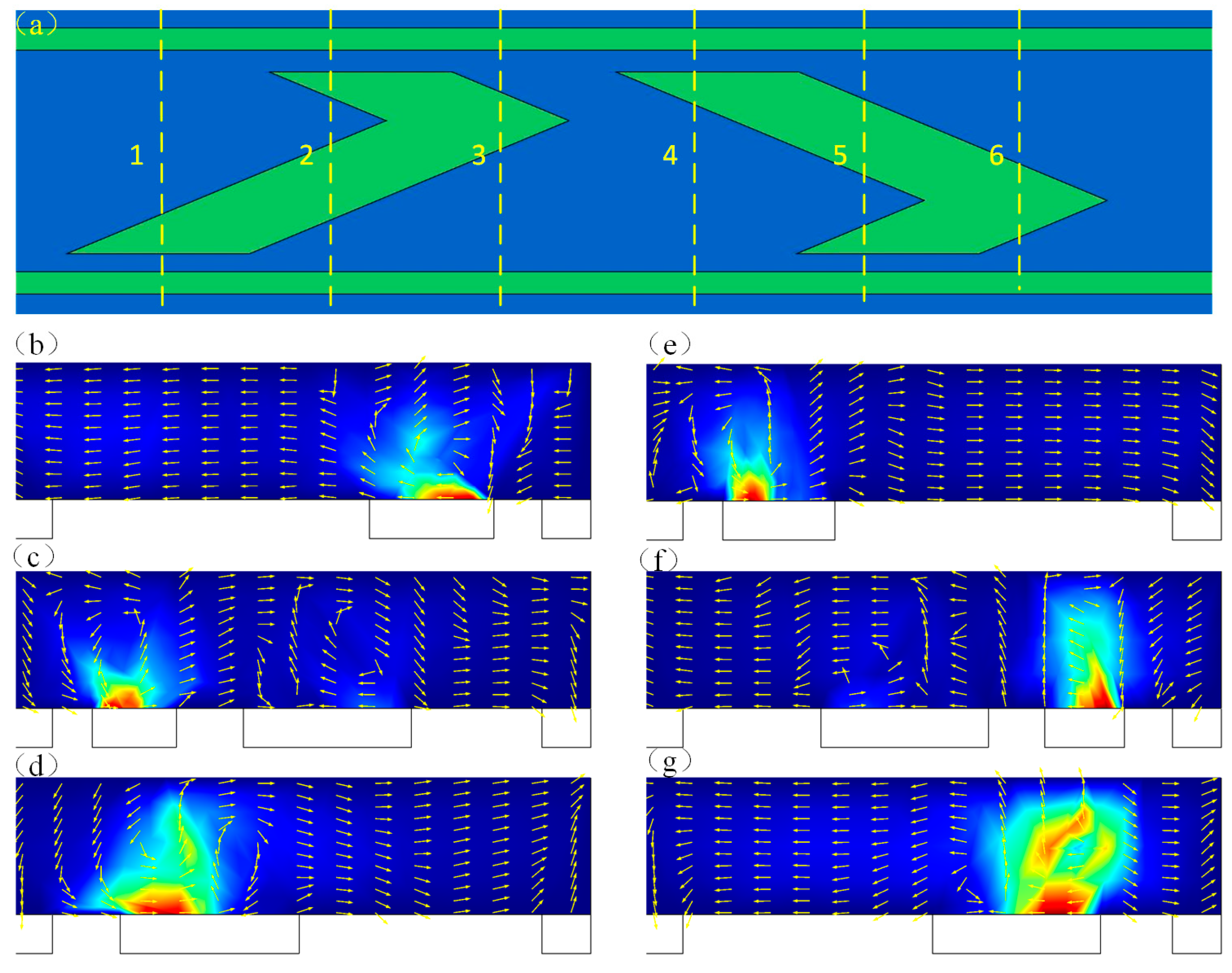
3.1. The Microstream Driven by Induced Charge Electroosmotics (ICEO) in the Channel
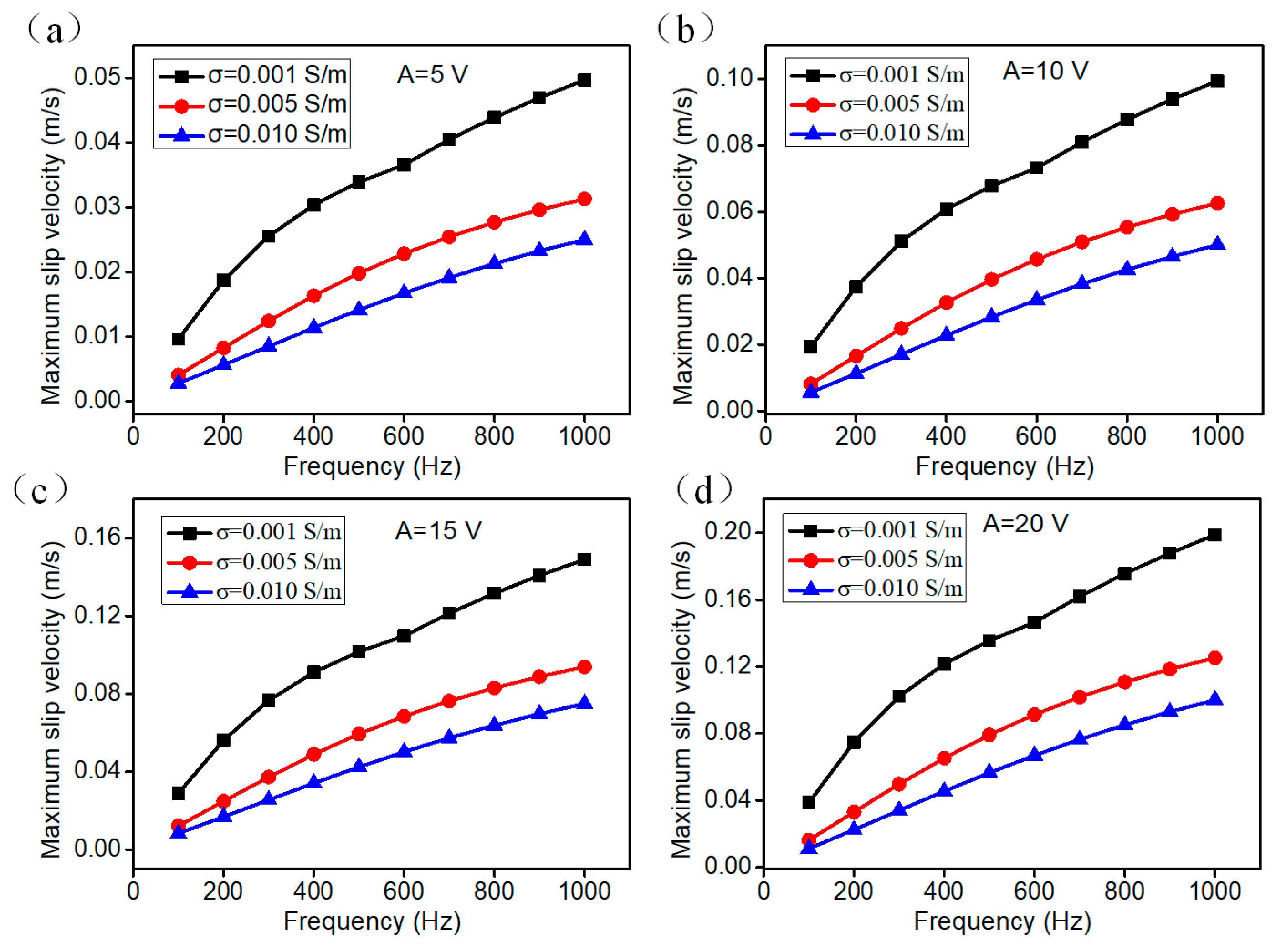
3.2. The Electroosmotic Flow Velocity near the Floating Electrode
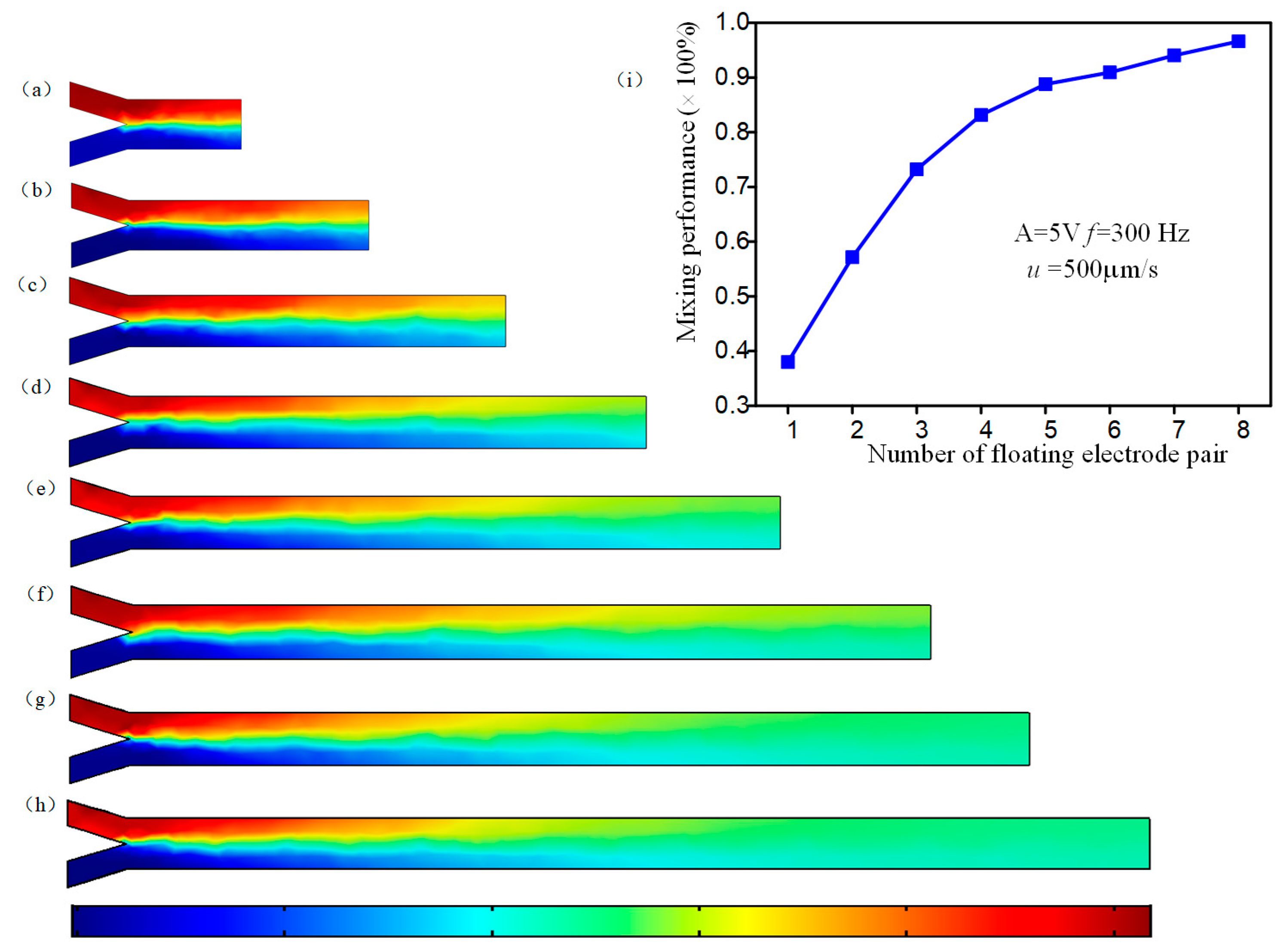
3.3. Mixing Performance of the Device with Different Number of Herringbone Floating Electrode Pairs
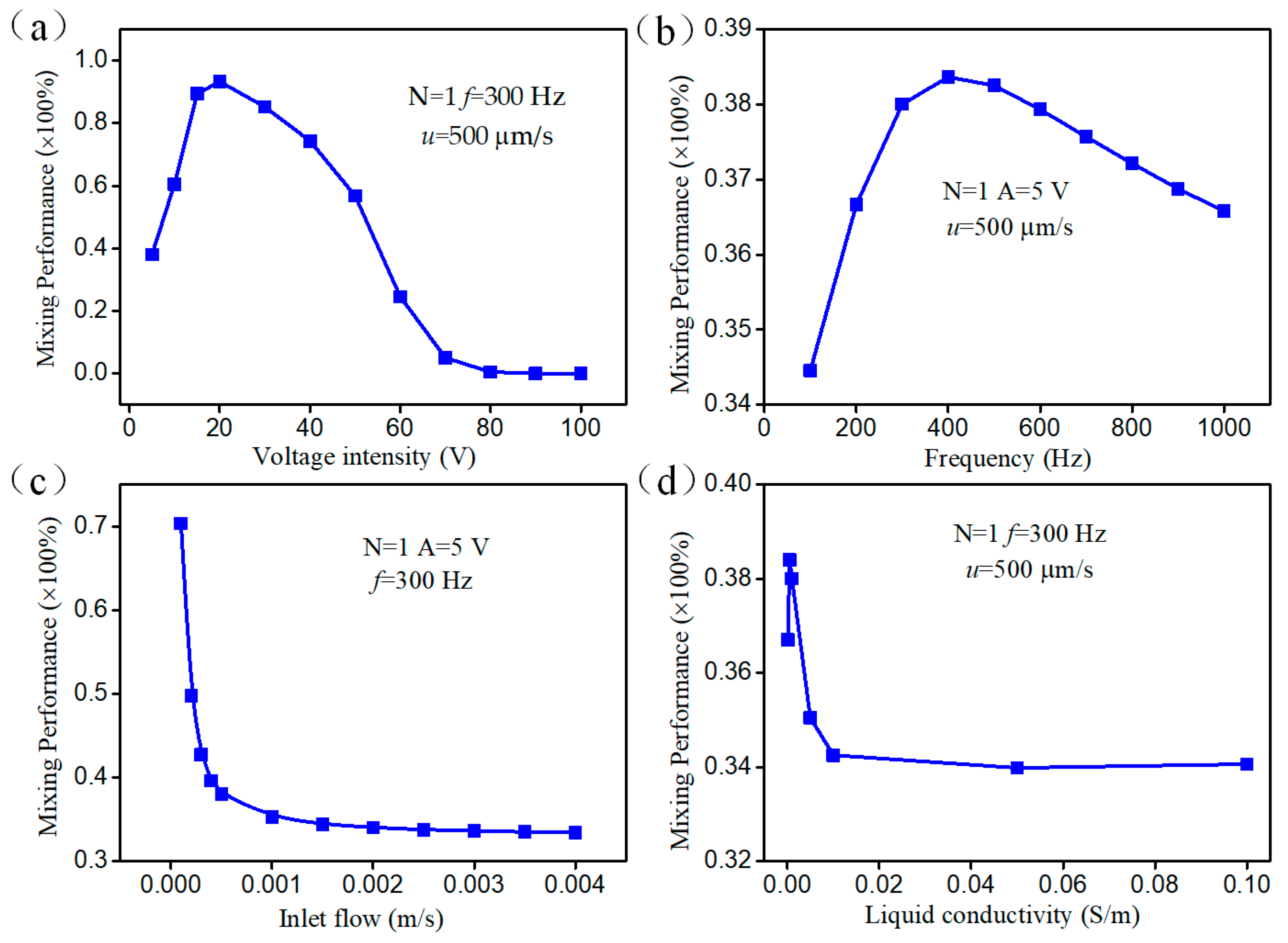
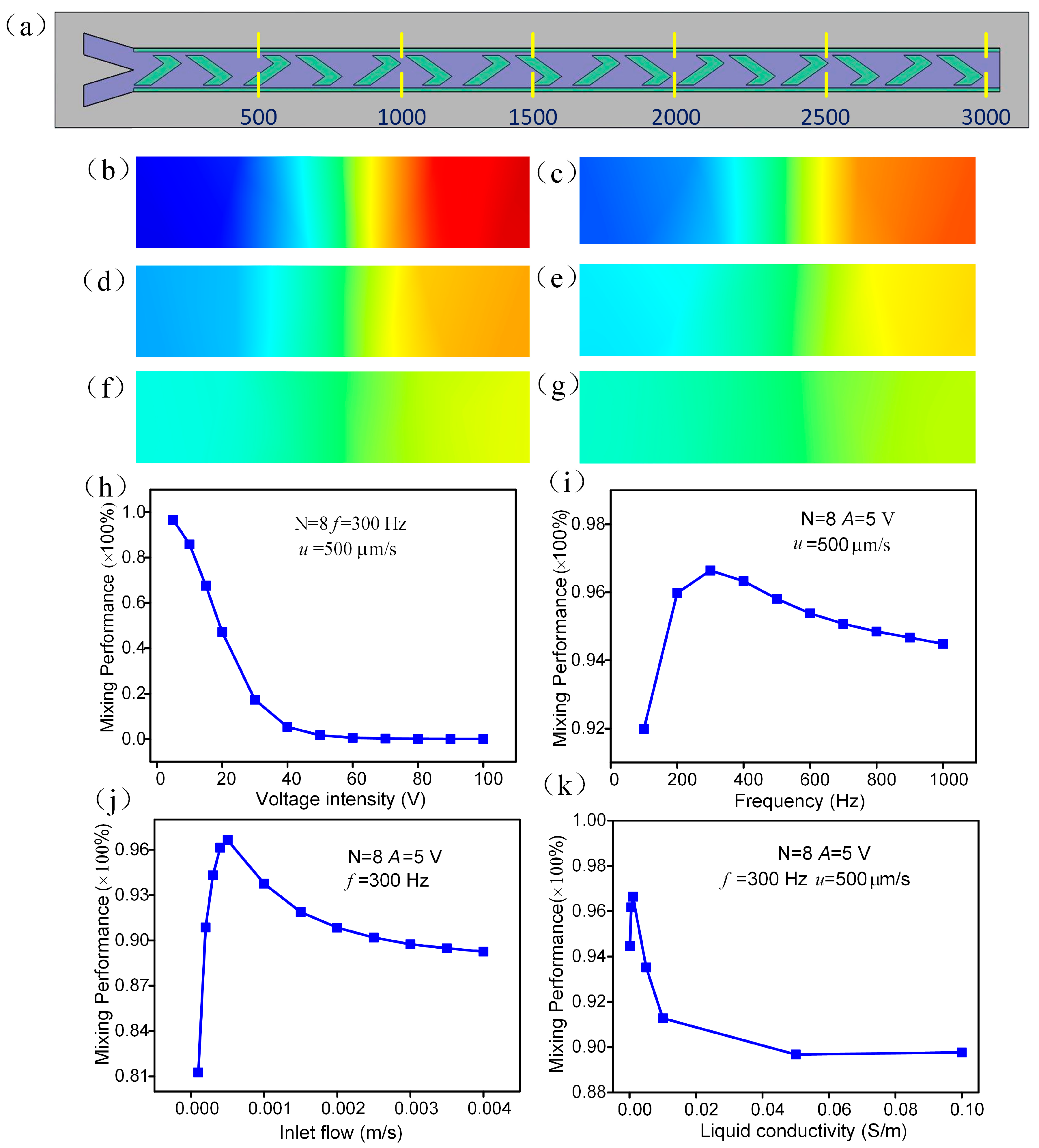
3.4. Parametric Effect on Mixing Performance
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kockmann, N.; Kiefer, T.; Engler, M.; Woias, P. Convective mixing and chemical reactions in microchannels with high flow rates. Sens. Actuators B 2006, 117, 495–508. [Google Scholar] [CrossRef]
- Mariotti, A.; Galletti, C.; Mauri, R.; Salvetti, M.V.; Brunazzi, E. Steady and unsteady regimes in a t-shaped micro-mixer: Synergic experimental and numerical investigation. Chem. Eng. J. 2018, 341, 414–431. [Google Scholar] [CrossRef]
- Kim, J.; Jang, Y.; Byun, D.; Kim, D.H.; Kim, M.J. Mixing enhancement by biologically inspired convection in a micro-chamber using alternating current galvanotactic control of the tetrahymena pyriformis. Appl. Phys. Lett. 2013, 103, 103703. [Google Scholar] [CrossRef]
- Pham, N.; Radajewski, D.; Round, A.; Brennich, M.; Pernot, P.; Biscans, B.; Bonnete, F.; Teychene, S. Coupling high throughput microfluidics and small-angle x-ray scattering to study protein crystallization from solution. Anal. Chem. 2017, 89, 2282–2287. [Google Scholar] [CrossRef] [PubMed]
- Jeong, G.S.; Chung, S.; Kim, C.B.; Lee, S.H. Applications of micromixing technology. Analyst 2010, 135, 460–473. [Google Scholar] [CrossRef] [PubMed]
- Hansen, C.L.; Classen, S.; Berger, J.M.; Quake, S.R. A microfluidic device for kinetic optimization of protein crystallization and in situ structure determination. J. Am. Chem. Soc. 2006, 128, 3142–3143. [Google Scholar] [CrossRef] [PubMed]
- Duncombe, T.A.; Tentori, A.M.; Herr, A.E. Microfluidics: Reframing biological enquiry. Nat. Rev. Mol. Cell Biol. 2015, 16, 554–567. [Google Scholar] [CrossRef] [PubMed]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Ren, Y.; Liu, W.; Tao, Y.; Jiang, H. Simulation analysis of improving microfluidic heterogeneous immunoassay using induced charge electroosmosis on a floating gate. Micromachines 2017, 8, 212. [Google Scholar] [CrossRef]
- Sharma, S.; Zapatero-Rodríguez, J.; Estrela, P.; O’Kennedy, R. Point-of-care diagnostics in low resource settings: Present status and future role of microfluidics. Biosensors 2015, 5, 577–601. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.-H.; Fan, S.-K.; Kim, C.-J.; Yao, D.-J. Ewod microfluidic systems for biomedical applications. Microfluid. Nanofluid. 2014, 16, 965–987. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Y.; Zeng, Y.; He, M. A microfluidic exosearch chip for multiplexed exosome detection towards blood-based ovarian cancer diagnosis. Lab Chip 2016, 16, 489–496. [Google Scholar] [CrossRef] [PubMed]
- Hessel, V.; Löwe, H.; Schönfeld, F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005, 60, 2479–2501. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Chang, C.-L.; Wang, Y.-N.; Fu, L.-M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [PubMed]
- Cai, G.; Xue, L.; Zhang, H.; Lin, J. A review on micromixers. Micromachines 2017, 8, 274. [Google Scholar] [CrossRef]
- Hong, C.C.; Choi, J.W.; Ahn, C.H. A novel in-plane passive microfluidic mixer with modified tesla structures. Lab Chip 2004, 4, 109–113. [Google Scholar] [CrossRef] [PubMed]
- Hossain, S.; Ansari, M.A.; Husain, A.; Kim, K.-Y. Analysis and optimization of a micromixer with a modified tesla structure. Chem. Eng. J. 2010, 158, 305–314. [Google Scholar] [CrossRef]
- Lin, Y.; Gerfen, G.J.; Rousseau, D.L.; Yeh, S.-R. Ultrafast microfluidic mixer and freeze-quenching device. Anal. Chem. 2003, 75, 5381–5386. [Google Scholar] [CrossRef] [PubMed]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezić, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Marschewski, J.; Jung, S.; Ruch, P.; Prasad, N.; Mazzotti, S.; Michel, B.; Poulikakos, D. Mixing with herringbone-inspired microstructures: Overcoming the diffusion limit in co-laminar microfluidic devices. Lab Chip 2015, 15, 1923–1933. [Google Scholar] [CrossRef] [PubMed]
- Leung, A.K.; Tam, Y.Y.; Chen, S.; Hafez, I.M.; Cullis, P.R. Microfluidic mixing: A general method for encapsulating macromolecules in lipid nanoparticle systems. J. Phys. Chem. B 2015, 119, 8698–8706. [Google Scholar] [CrossRef] [PubMed]
- Ansari, M.A.; Kim, K.-Y. Parametric study on mixing of two fluids in a three-dimensional serpentine microchannel. Chem. Eng. J. 2009, 146, 439–448. [Google Scholar] [CrossRef]
- Liu, R.H.; Stremler, M.A.; Sharp, K.V.; Olsen, M.G.; Santiago, J.G.; Adrian, R.J.; Aref, H.; Beebe, D.J. Passive mixing in a three-dimensional serpentine microchannel. J. Microelectromech. Syst. 2000, 9, 190–197. [Google Scholar] [CrossRef]
- Feng, X.; Ren, Y.; Jiang, H. Effect of the crossing-structure sequence on mixing performance within three-dimensional micromixers. Biomicrofluidics 2014, 8, 034106. [Google Scholar] [CrossRef] [PubMed]
- Cannon, D.M.; Kuo, T.-C.; Bohn, P.W.; Sweedler, J.V. Nanocapillary array interconnects for gated analyte injections and electrophoretic separations in multilayer microfluidic architectures. Anal. Chem. 2003, 75, 2224–2230. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhe, J.; Chung, B.T.F.; Dutta, P. A rapid magnetic particle driven micromixer. Microfluid. Nanofluid. 2008, 4, 375–389. [Google Scholar] [CrossRef]
- Lee, S.H.; van Noort, D.; Lee, J.Y.; Zhang, B.T.; Park, T.H. Effective mixing in a microfluidic chip using magnetic particles. Lab Chip 2009, 9, 479–482. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.S.; Jiao, Z.J.; Huang, X.Y.; Yang, C.; Nguyen, N.T. Acoustically induced bubbles in a microfluidic channel for mixing enhancement. Microfluid. Nanofluid. 2009, 6, 847–852. [Google Scholar] [CrossRef]
- Ahmed, D.; Mao, X.; Juluri, B.K.; Huang, T.J. A fast microfluidic mixer based on acoustically driven sidewall-trapped microbubbles. Microfluid. Nanofluid. 2009, 7, 727. [Google Scholar] [CrossRef]
- Chen, H.; Gao, Y.; Petkovic, K.; Yan, S.; Best, M.; Du, Y.; Zhu, Y. Reproducible bubble-induced acoustic microstreaming for bead disaggregation and immunoassay in microfluidics. Microfluid. Nanofluid. 2017, 21, 30. [Google Scholar] [CrossRef]
- Huang, C.; Tsou, C. The implementation of a thermal bubble actuated microfluidic chip with microvalve, micropump and micromixer. Sens. Actuators A 2014, 210, 147–156. [Google Scholar] [CrossRef]
- Jian, Y. Transient mhd heat transfer and entropy generation in a microparallel channel combined with pressure and electroosmotic effects. Int. J. Heat. Mass Transfer 2015, 89, 193–205. [Google Scholar] [CrossRef]
- Li, S.-X.; Jian, Y.-J.; Xie, Z.-Y.; Liu, Q.-S.; Li, F.-Q. Rotating electro-osmotic flow of third grade fluids between two microparallel plates. Colloids Surf. A 2015, 470, 240–247. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Continuous-flow trapping and localized enrichment of micro- and nano-particles using induced-charge electrokinetics. Soft Matter 2018, 14, 1056–1066. [Google Scholar] [CrossRef] [PubMed]
- Prabhakaran, R.A.; Zhou, Y.; Zhao, C.; Hu, G.; Song, Y.; Wang, J.; Yang, C.; Xuan, X. Induced charge effects on electrokinetic entry flow. Phys. Fluids 2017, 29, 062001. [Google Scholar] [CrossRef]
- Hu, Q.; Ren, Y.; Liu, W.; Chen, X.; Tao, Y.; Jiang, H. Fluid flow and mixing induced by ac continuous electrowetting of liquid metal droplet. Micromachines 2017, 8, 119. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Q.; Ren, Y.; Cui, P.; Yao, B.; Li, Y.; Hui, M.; Jiang, T.; Bai, L. On the bipolar dc flow field-effect-transistor for multifunctional sample handing in microfluidics: A theoretical analysis under the debye–huckel limit. Micromachines 2018, 9, 82. [Google Scholar] [CrossRef]
- Sasaki, N.; Kitamori, T.; Kim, H.-B. Ac electroosmotic micromixer for chemical processing in a microchannel. Lab Chip 2006, 6, 550–554. [Google Scholar] [CrossRef] [PubMed]
- Melvin, E.M.; Moore, B.R.; Gilchrist, K.H.; Grego, S.; Velev, O.D. On-chip collection of particles and cells by ac electroosmotic pumping and dielectrophoresis using asymmetric microelectrodes. Biomicrofluidics 2011, 5, 034113. [Google Scholar] [CrossRef] [PubMed]
- Mirzajani, H.; Cheng, C.; Wu, J.; Ivanoff, C.S.; Najafi Aghdam, E.; Badri Ghavifekr, H. Design and characterization of a passive, disposable wireless ac-electroosmotic lab-on-a-film for particle and fluid manipulation. Sens. Actuators B 2016, 235, 330–342. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, H.; Shi, L.; Liu, Z.; Joo, S. An enhanced electroosmotic micromixer with an efficient asymmetric lateral structure. Micromachines 2016, 7, 218. [Google Scholar] [CrossRef]
- Hughes, M.P. Fifty years of dielectrophoretic cell separation technology. Biomicrofluidics 2016, 10, 032801. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Rosano, J.M.; Wang, Y.; Garson, C.J.; Prabhakarpandian, B.; Pant, K.; Klarmann, G.J.; Perantoni, A.; Alvarez, L.M.; Lai, E. Continuous-flow sorting of stem cells and differentiation products based on dielectrophoresis. Lab Chip 2015, 15, 1320–1328. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Ren, Y.; Tao, Y.; Chen, X.; Wu, Q. Electrode cooling effect on out-of-phase electrothermal streaming in rotating electric fields. Micromachines 2017, 8, 327. [Google Scholar] [CrossRef]
- Salari, A.; Navi, M.; Dalton, C. A novel alternating current multiple array electrothermal micropump for lab-on-a-chip applications. Biomicrofluidics 2015, 9, 014113. [Google Scholar] [CrossRef] [PubMed]
- Sigurdson, M.; Wang, D.; Meinhart, C.D. Electrothermal stirring for heterogeneous immunoassays. Lab Chip 2005, 5, 1366–1373. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Ren, Y.; Liu, W.; Wu, Y.; Jia, Y.; Lang, Q.; Jiang, H. Enhanced particle trapping performance of induced charge electroosmosis. Electrophoresis 2016, 37, 1326–1336. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Liu, J.; Liu, W.; Lang, Q.; Tao, Y.; Hu, Q.; Hou, L.; Jiang, H. Scaled particle focusing in a microfluidic device with asymmetric electrodes utilizing induced-charge electroosmosis. Lab Chip 2016, 16, 2803–2812. [Google Scholar] [CrossRef] [PubMed]
- Yalcin, S.E.; Sharma, A.; Qian, S.; Joo, S.W.; Baysal, O. Manipulating particles in microfluidics by floating electrodes. Electrophoresis 2010, 31, 3711–3718. [Google Scholar] [CrossRef] [PubMed]
- Paustian, J.S.; Pascall, A.J.; Wilson, N.M.; Squires, T.M. Induced charge electroosmosis micropumps using arrays of janus micropillars. Lab Chip 2014, 14, 3300–3312. [Google Scholar] [CrossRef] [PubMed]
- Hossan, M.R.; Diganta, D.; Nazmul, I.; Prashanta, D. Review: Electric field driven pumping in microfluidic device. Electrophoresis 2018, 39, 702–731. [Google Scholar]
- Wu, Y.; Ren, Y.; Tao, Y.; Hou, L.; Jiang, H. Large-scale single particle and cell trapping based on rotating electric field induced-charge electroosmosis. Anal. Chem. 2016, 88, 11791–11798. [Google Scholar] [CrossRef] [PubMed]
- Zehavi, M.; Yossifon, G. Particle dynamics and rapid trapping in electro-osmotic flow around a sharp microchannel corner. Phys. Fluids 2014, 26, 082002. [Google Scholar] [CrossRef]
- Harrison, H.; Lu, X.; Patel, S.; Thomas, C.; Todd, A.; Johnson, M.; Raval, Y.; Tzeng, T.-R.; Song, Y.; Wang, J.; et al. Electrokinetic preconcentration of particles and cells in microfluidic reservoirs. Analyst 2015, 140, 2869–2875. [Google Scholar] [CrossRef] [PubMed]
- SQUIRES, T.M.; BAZANT, M.Z. Induced-charge electro-osmosis. J. Fluid Mech. 2004, 509, 217–252. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, W.; Jia, Y.; Tao, Y.; Shao, J.; Ding, Y.; Jiang, H. Induced-charge electroosmotic trapping of particles. Lab Chip 2015, 15, 2181–2191. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Ren, Y.; Tao, Y.; Hou, L.; Hu, Q.; Jiang, H. A novel micromixer based on the alternating current-flow field effect transistor. Lab Chip 2017, 17, 186–197. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Liu, W.; Tao, Y.; Hui, M.; Wu, Q. On ac-field-induced nonlinear electroosmosis next to the sharp corner-field-singularity of leaky dielectric blocks and its application in on-chip micro-mixing. Micromachines 2018, 9, 102. [Google Scholar] [CrossRef]
- Chen, X.; Ren, Y.; Liu, W.; Feng, X.; Jia, Y.; Tao, Y.; Jiang, H. A simplified microfluidic device for particle separation with two consecutive steps: Induced charge electro-osmotic prefocusing and dielectrophoretic separation. Anal. Chem. 2017, 89, 9583–9592. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena. Curr. Opin. Colloid Interface Sci. 2010, 15, 203–213. [Google Scholar] [CrossRef]
- Lin, Y.; Yu, X.; Wang, Z.; Tu, S.-T.; Wang, Z. Design and evaluation of an easily fabricated micromixer with three-dimensional periodic perturbation. Chem. Eng. J. 2011, 171, 291–300. [Google Scholar] [CrossRef]
- Xuan, X.; Li, D. Electroosmotic flow in microchannels with arbitrary geometry and arbitrary distribution of wall charge. J. Colloid Interface Sci. 2005, 289, 291–303. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface 2009, 152, 48–88. [Google Scholar] [CrossRef] [PubMed]
- Xuan, X.; Xu, B.; Sinton, D.; Li, D. Electroosmotic flow with joule heating effects. Lab Chip 2004, 4, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Li, D. Multiscale phenomena in microfluidics and nanofluidics. Chem. Eng. Sci. 2007, 62, 3443–3454. [Google Scholar] [CrossRef]
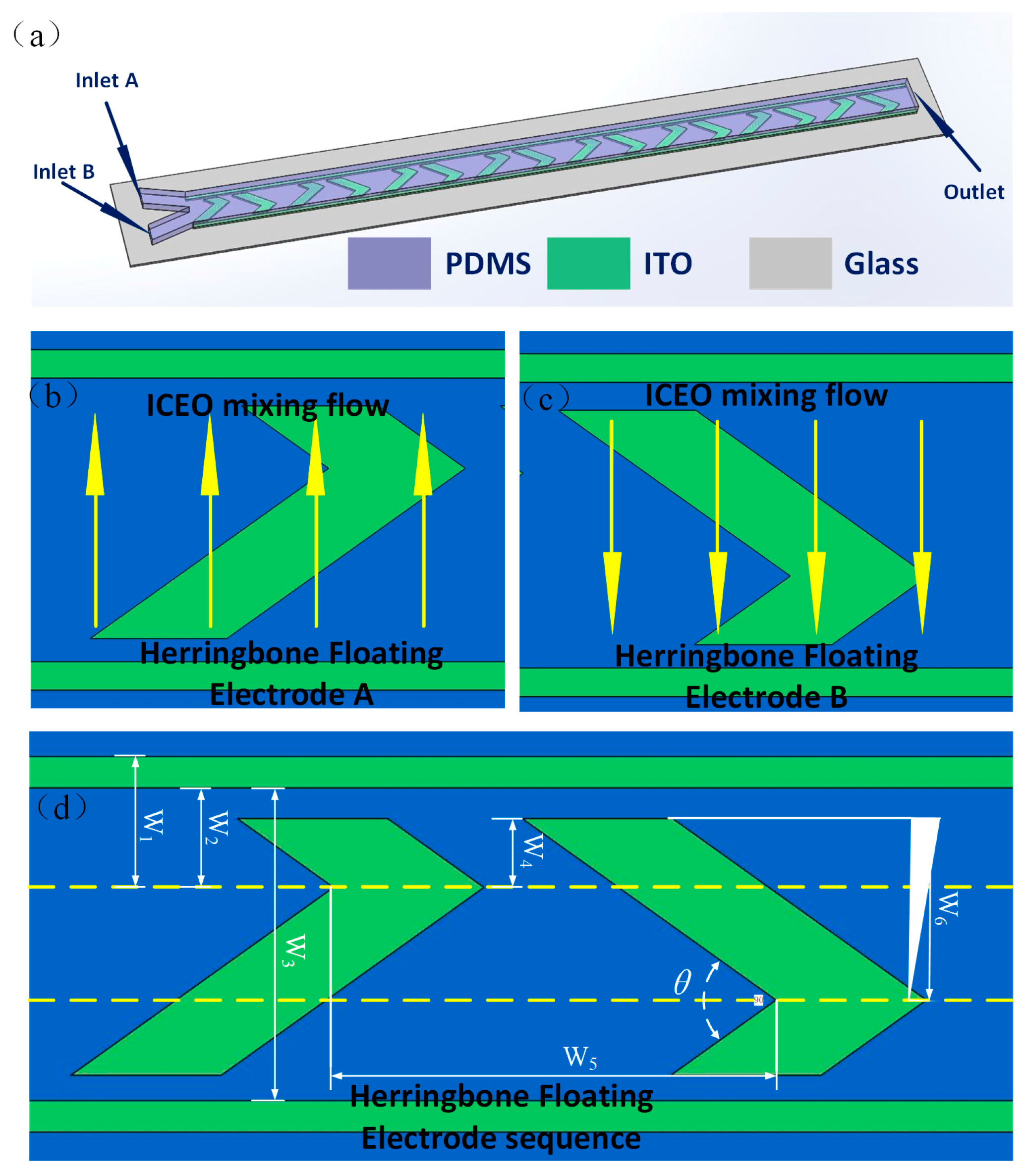
| Parameter | W1 | W2 | W3 | W4 | W5 | W6 | θ |
|---|---|---|---|---|---|---|---|
| Value (μm) | 50 | 40 | 150 | 30 | 200 | 100 | 90o |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Guo, J.; Cao, Z.; Jiang, H. Asymmetrical Induced Charge Electroosmotic Flow on a Herringbone Floating Electrode and Its Application in a Micromixer. Micromachines 2018, 9, 391. https://doi.org/10.3390/mi9080391
Hu Q, Guo J, Cao Z, Jiang H. Asymmetrical Induced Charge Electroosmotic Flow on a Herringbone Floating Electrode and Its Application in a Micromixer. Micromachines. 2018; 9(8):391. https://doi.org/10.3390/mi9080391
Chicago/Turabian StyleHu, Qingming, Jianhua Guo, Zhongliang Cao, and Hongyuan Jiang. 2018. "Asymmetrical Induced Charge Electroosmotic Flow on a Herringbone Floating Electrode and Its Application in a Micromixer" Micromachines 9, no. 8: 391. https://doi.org/10.3390/mi9080391
APA StyleHu, Q., Guo, J., Cao, Z., & Jiang, H. (2018). Asymmetrical Induced Charge Electroosmotic Flow on a Herringbone Floating Electrode and Its Application in a Micromixer. Micromachines, 9(8), 391. https://doi.org/10.3390/mi9080391




