Novel High-Capacitance-Ratio MEMS Switch: Design, Analysis and Performance Verification
Abstract
1. Introduction
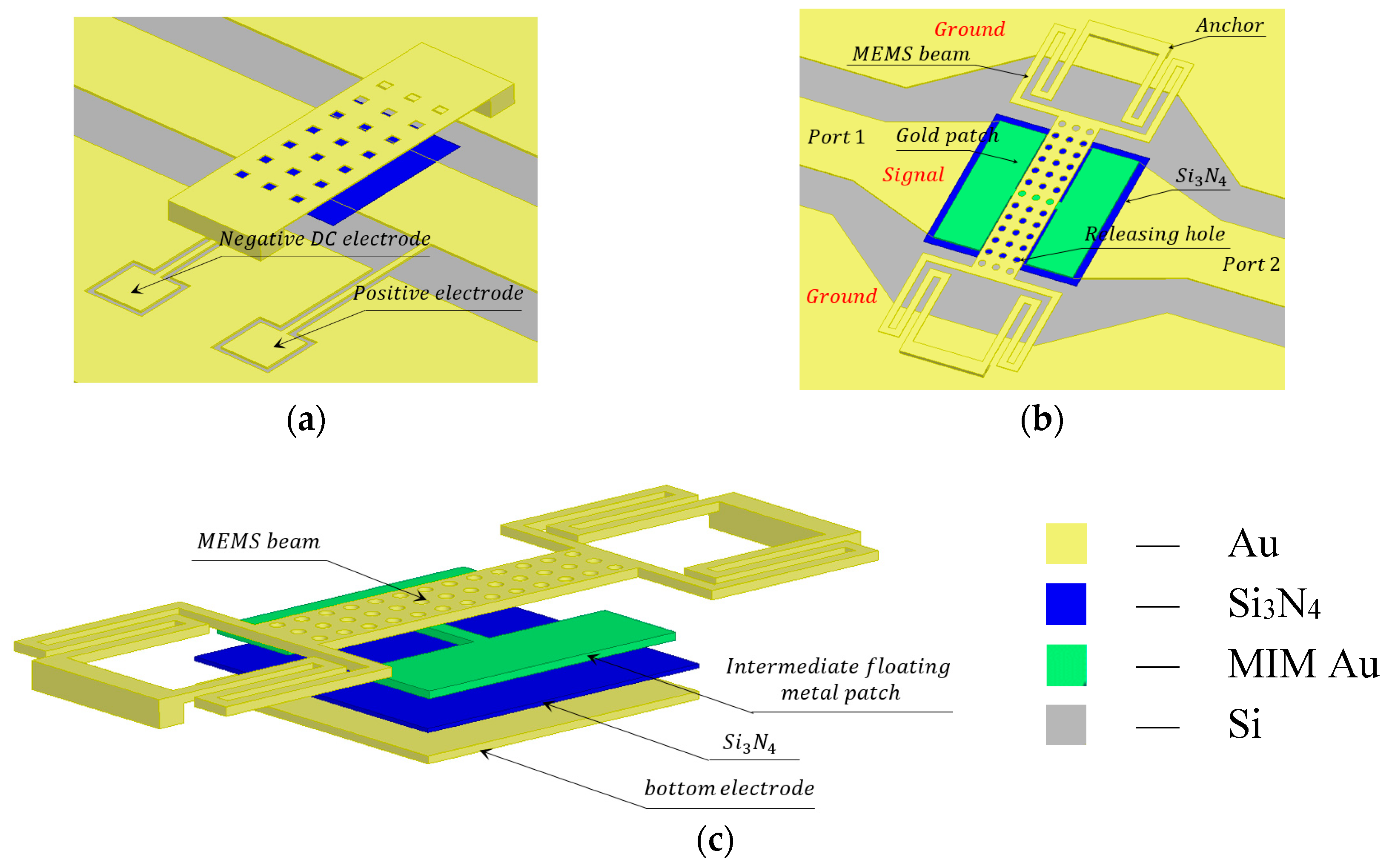
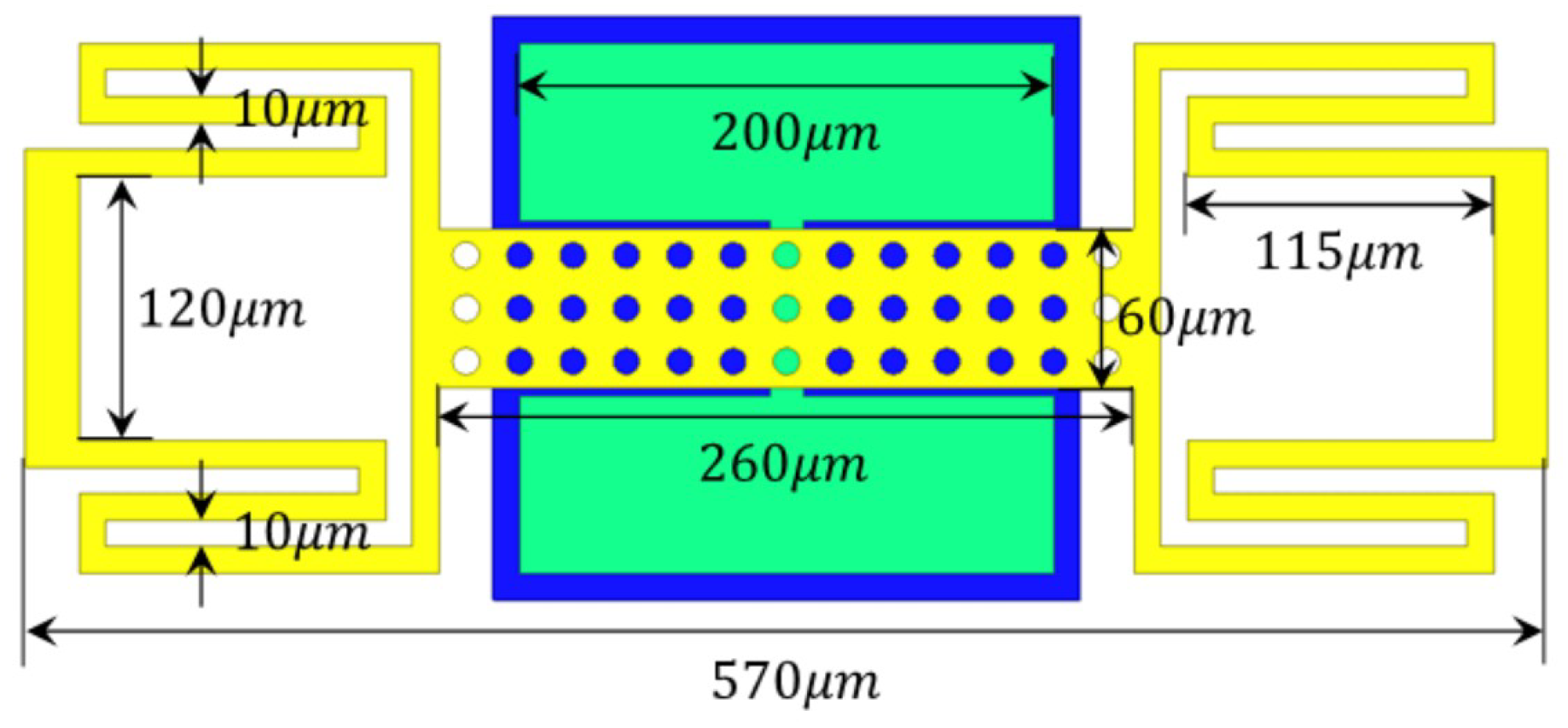
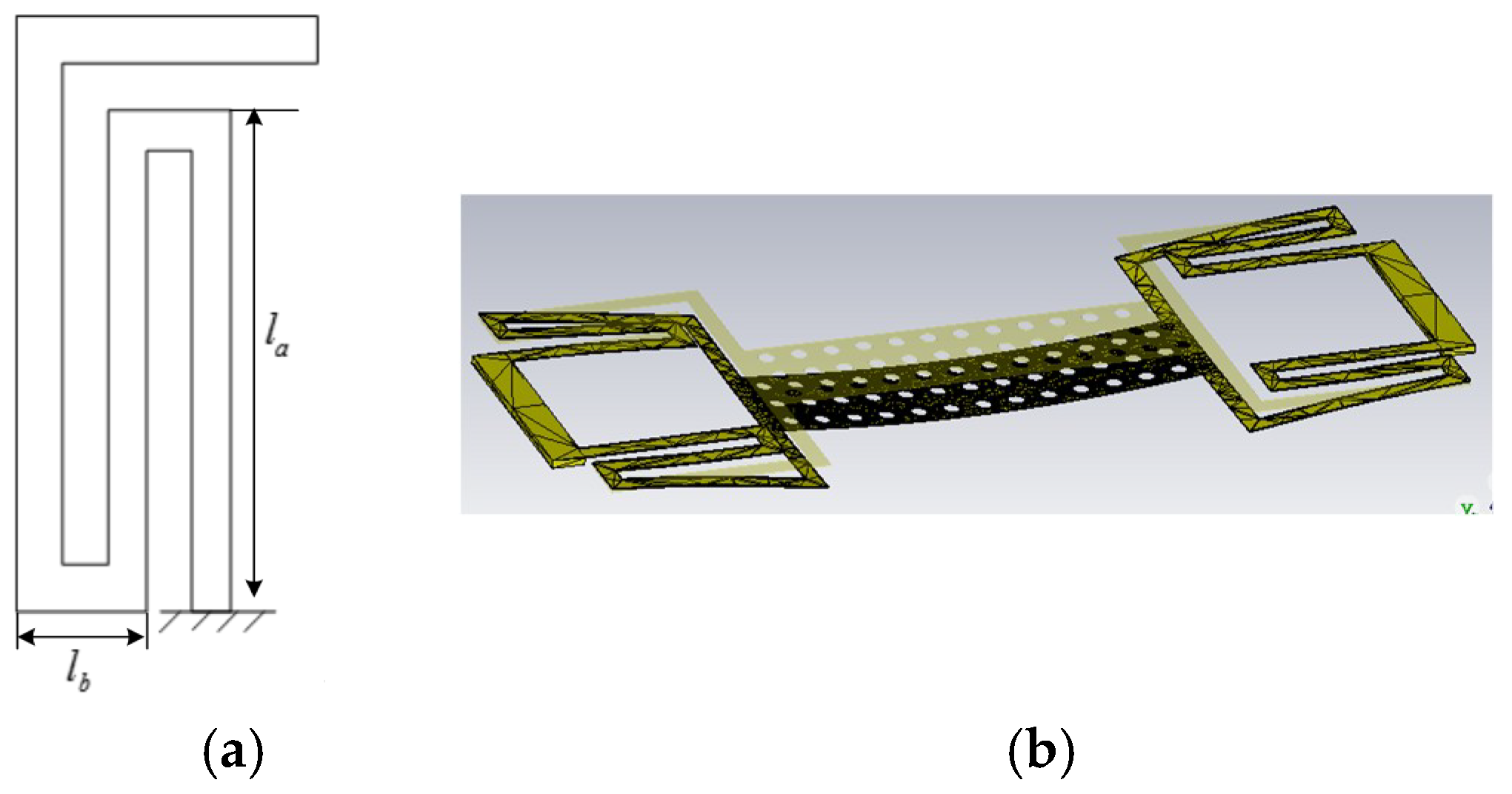
2. Design of the High OFF/ON Capacitance Ratio RF MEMS Switch
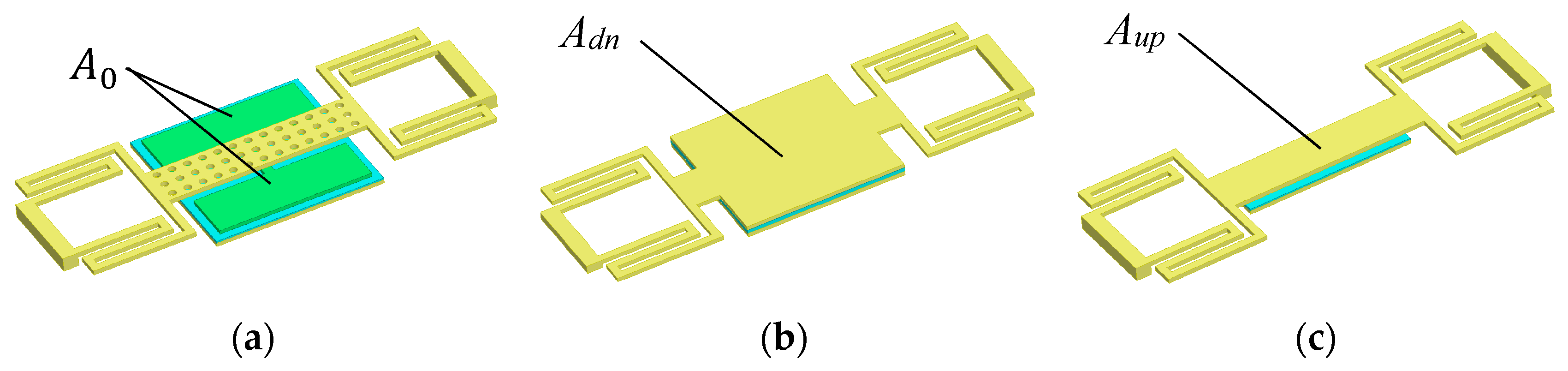
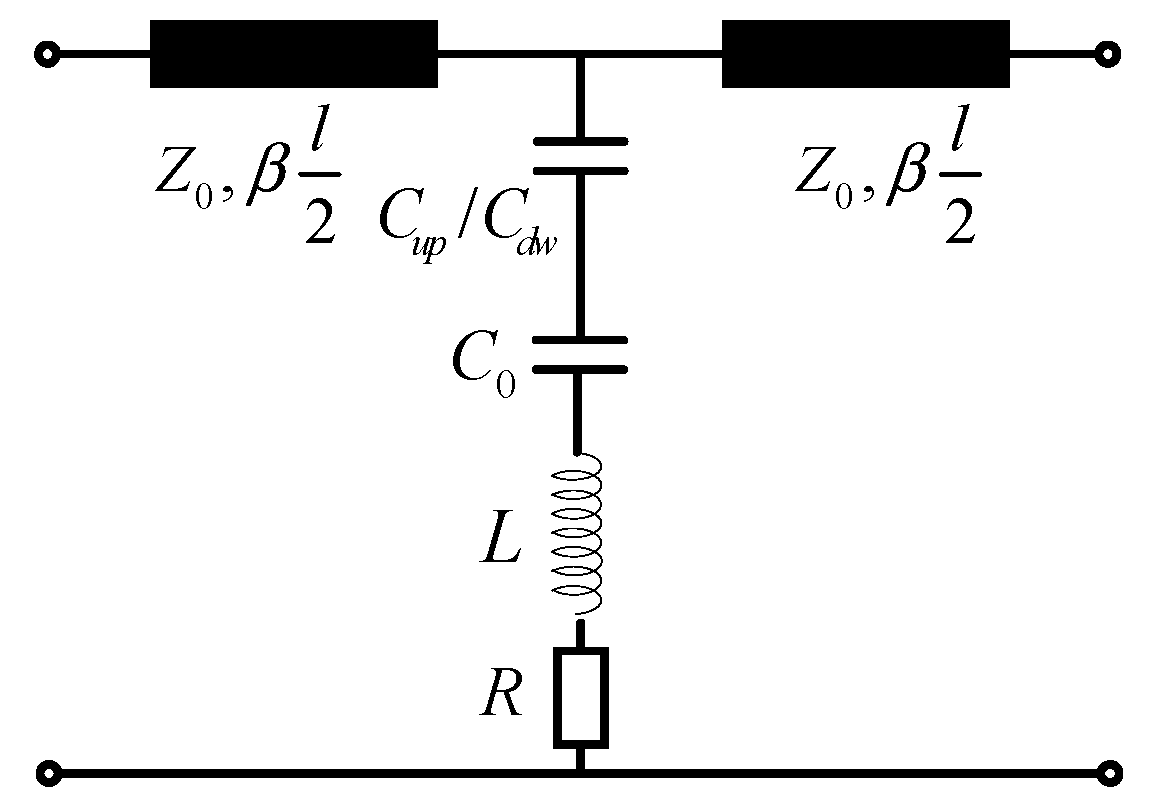
3. Analysis of High OFF/ON Capacitance Ratio RF MEMS Switch
3.1 Restriction Factors of the Conventional RF MEMS Off-to-On Capacitance Ratio
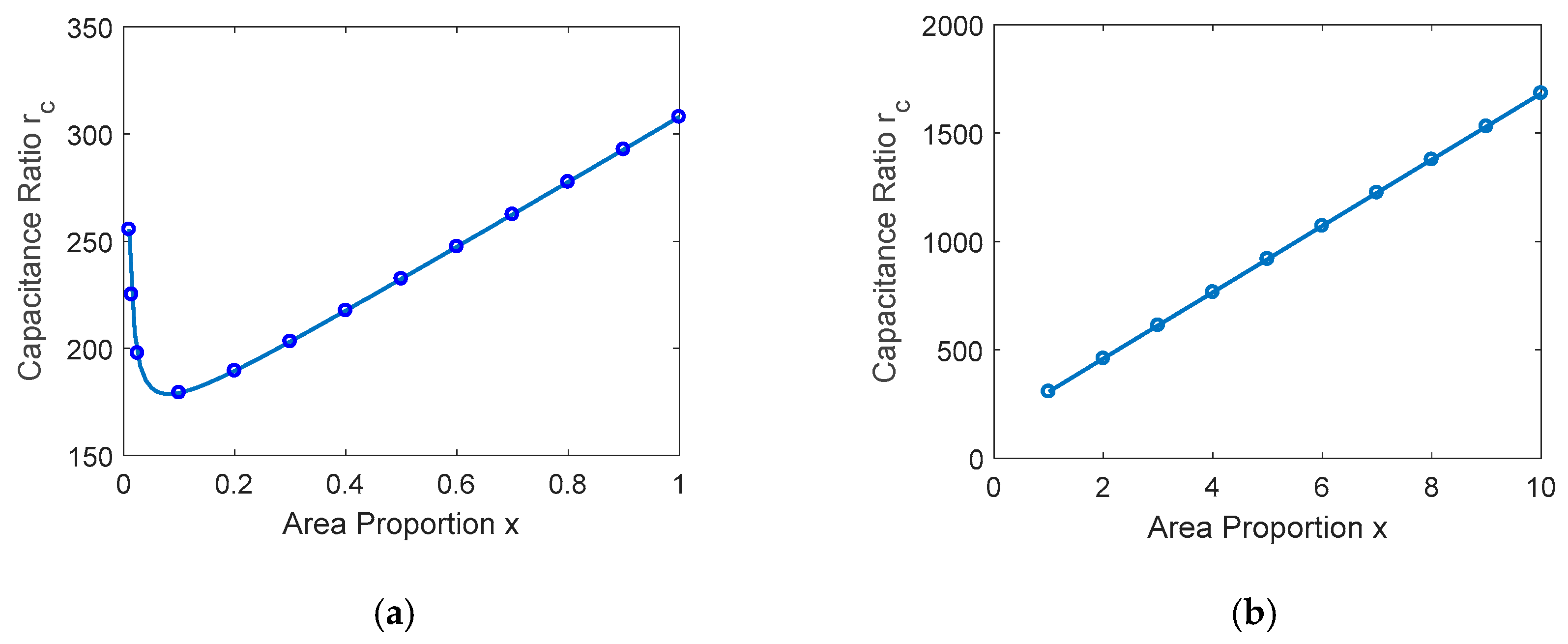
3.2 The High OFF/ON Capacitance Ratio of the Proposed RF MEMS Switch
4. Fabrication, Measurements and Discussions
4.1. Fabrication
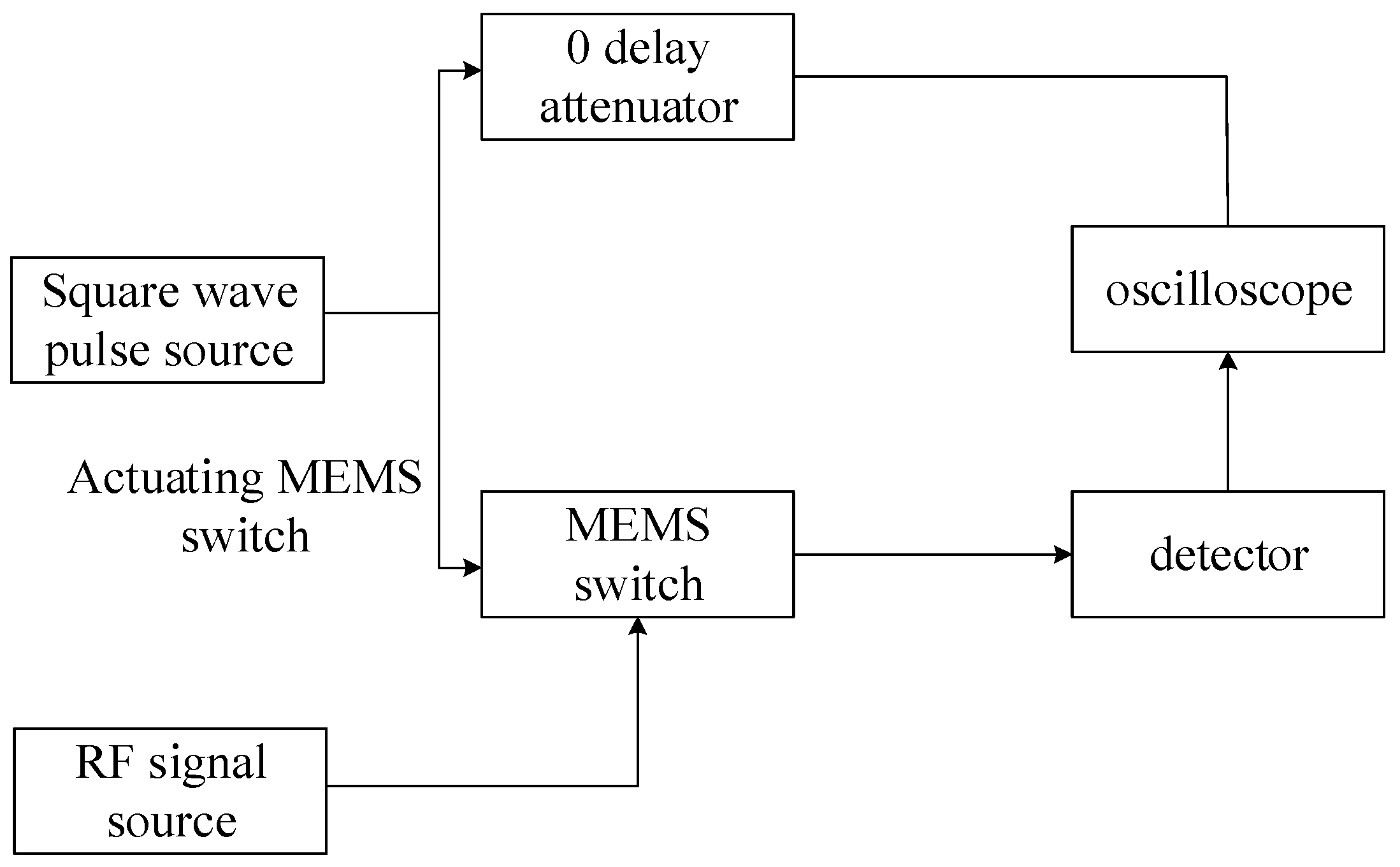
4.2. Measurement and Results
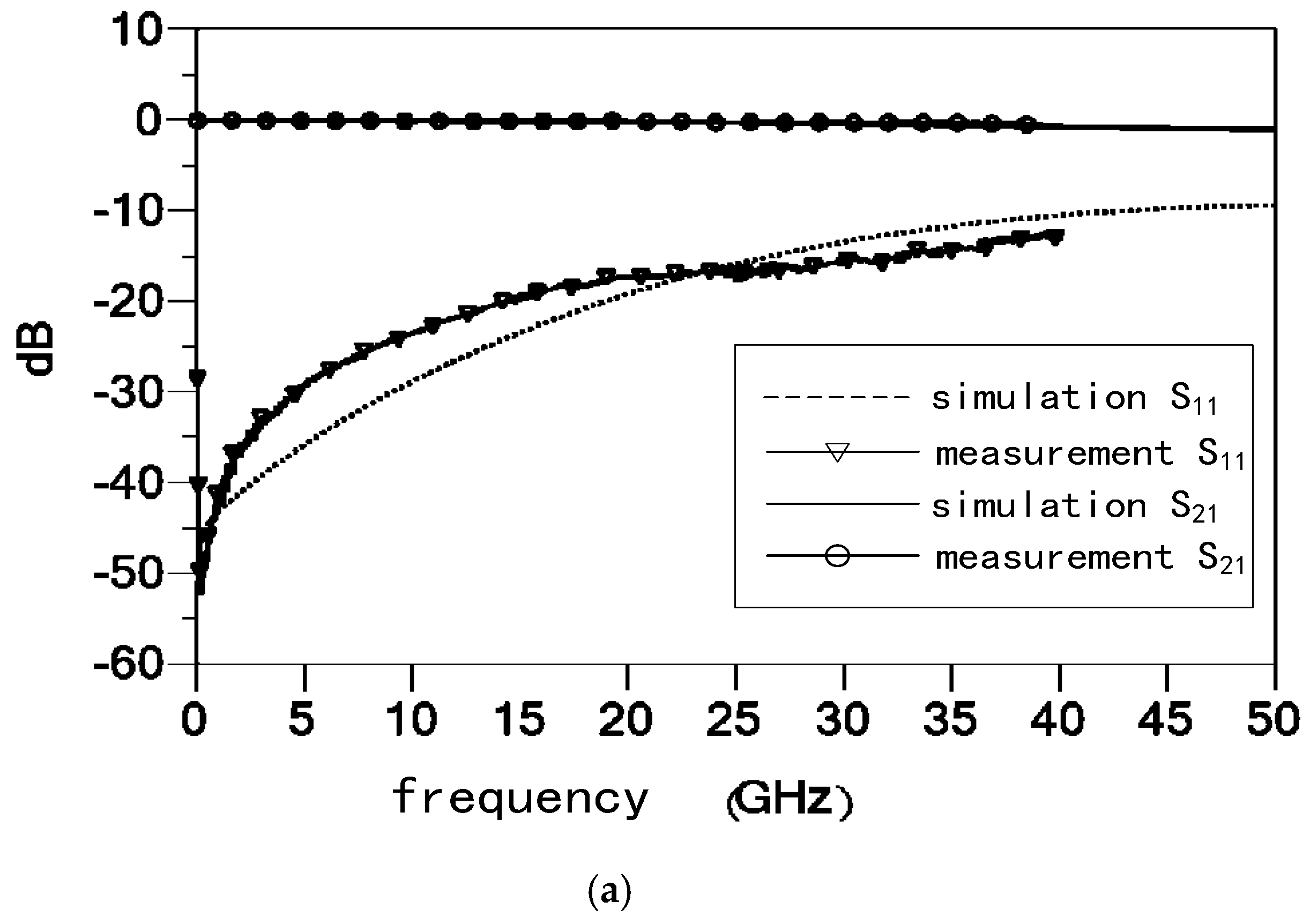
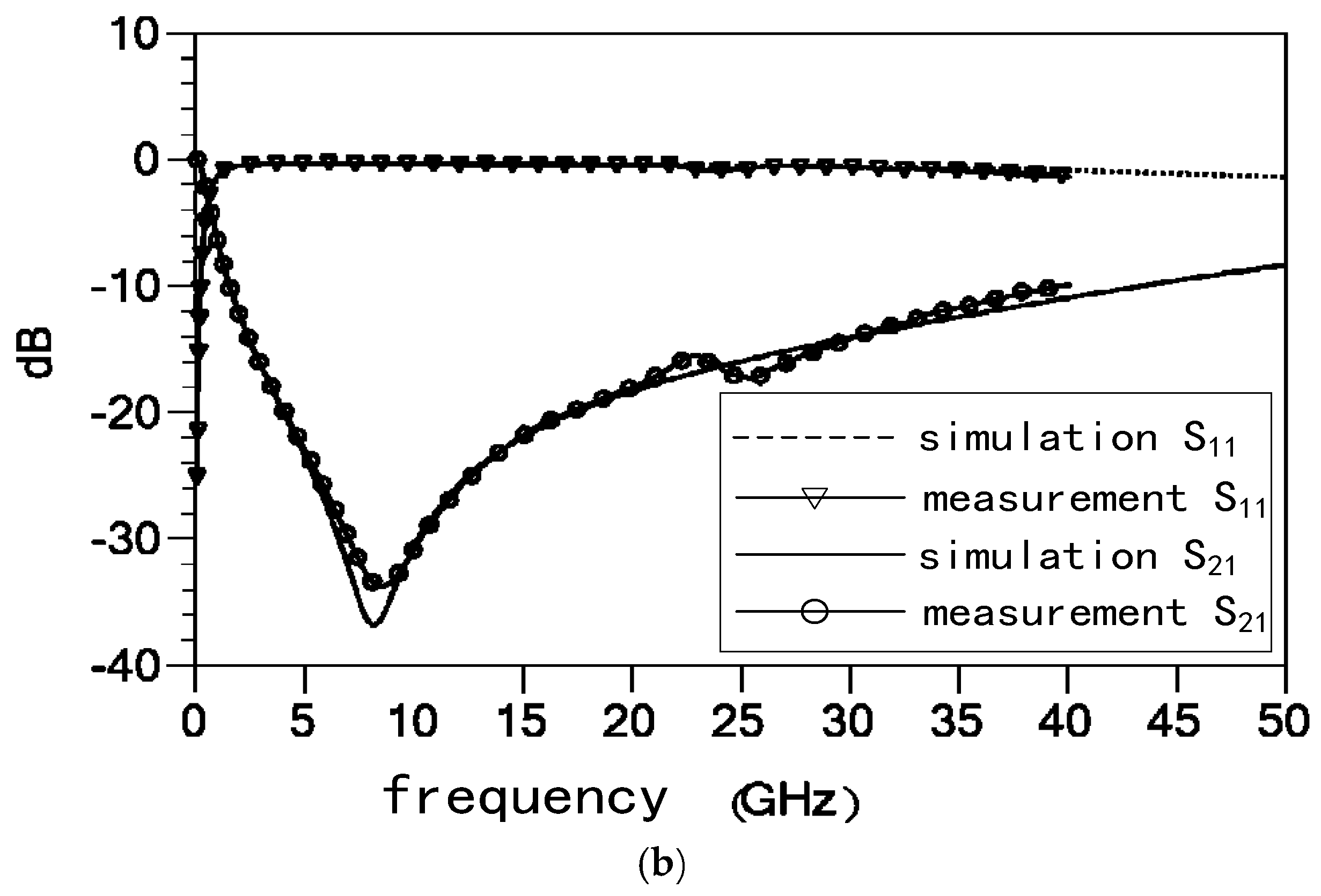
4.2.1. Insertion Loss and Isolation
4.2.2. Capacitance Ratio
4.2.3. Actuation Voltage
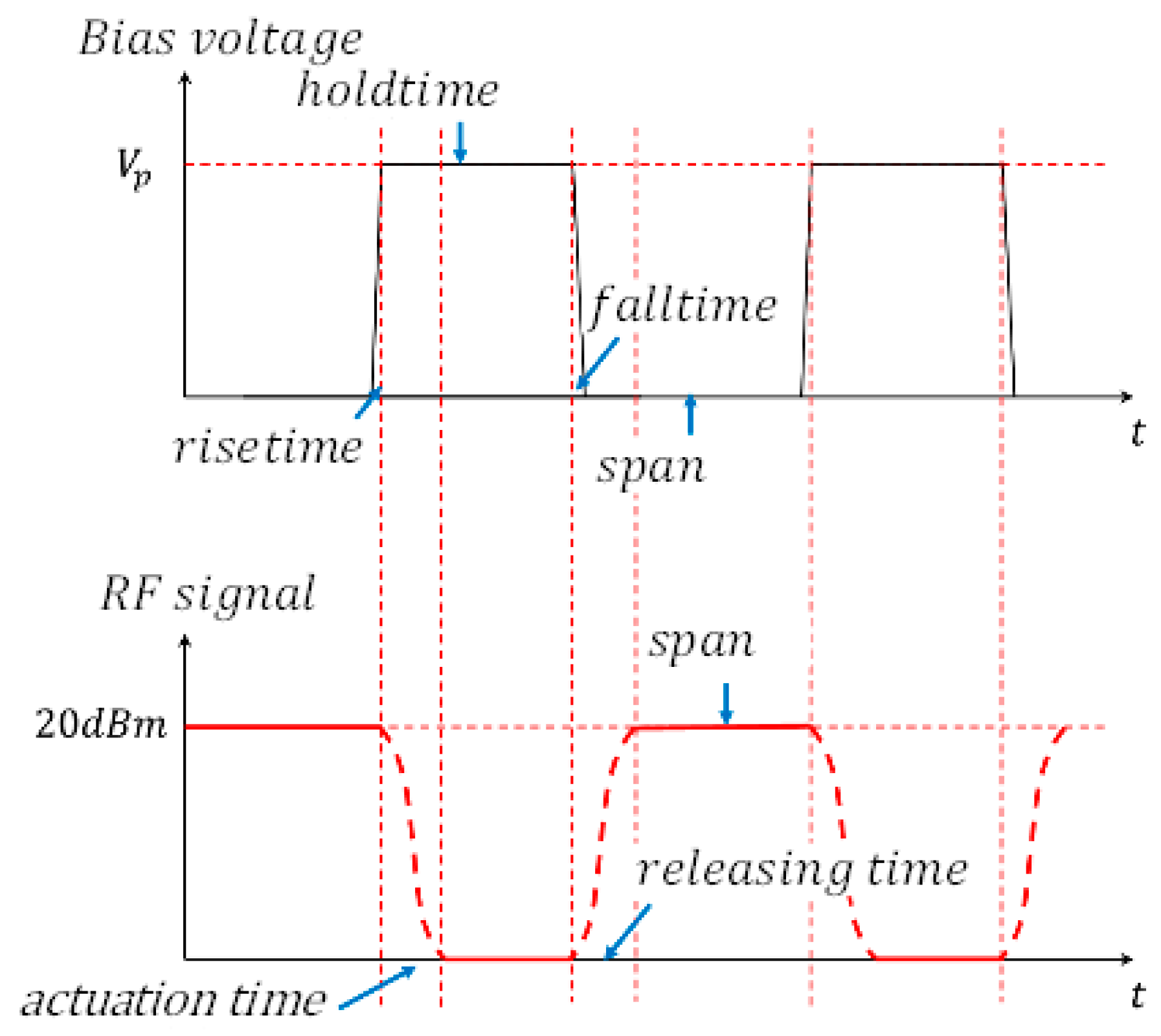
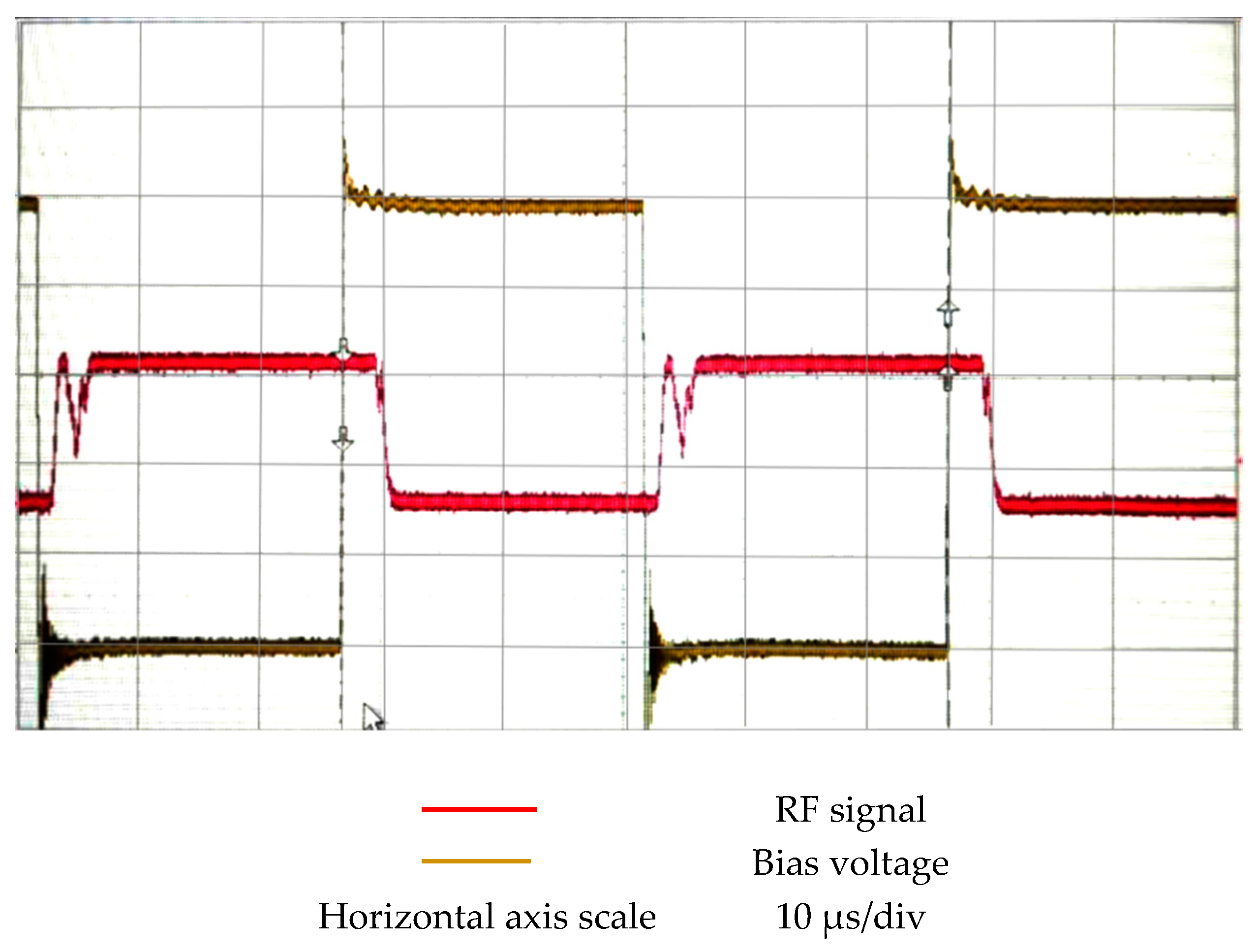
4.2.4. Actuation and Releasing Time
4.3. Advancements
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kale, N.S. Tutorial T4: MEMS: Design, Fabrication, and their applications as chemical and biosensors. In Proceedings of the 28th International Conference on VLSI Design, Bangalore, India, 3–7 January 2015. [Google Scholar]
- Mansour, R.R. RF MEMS-CMOS device integration: An overview of the potential for RF researchers. IEEE Microw. Mag. 2013, 14, 39–56. [Google Scholar] [CrossRef]
- Fall, M.; Fouladi, S.; Domingue, F.; Dieppedale, C.; Reig, B.; Mansour, R.R. High capacitance ratio RF MEMS dielectric-less switched capacitor. In Proceedings of the European Microwave Conference (EuMC), Nuremberg, Germany, 6–10 October 2013; pp. 1327–1330. [Google Scholar]
- Park, J.Y.; Kim, G.H.; Chung, K.W.; Bu, J.U. Fully integrated micromachined capacitive switches for RF applications. IEEE MTT-S Int. Microw. Symp. 2000, 1, 283–286. [Google Scholar]
- Al-Dahleh, R.; Mansour, R.R. High-capacitance-ratio warped-beam capacitive MEMS switch designs. J. Microelectromech. Syst. 2010, 19, 538–547. [Google Scholar] [CrossRef]
- Chang, C.; Chang, P. Innovative micromachined microwave switch with very low insertion loss. Sens. Actuators A Phys. 2010, 79, 71–75. [Google Scholar] [CrossRef]
- Bozler, C.; Drangmeister, R.; Duffy, S.; Gouker, M.; Knecht, J.; Kushner, L.; Parr, R.; Rabe, S.; Travis, L. MEMs microswitch arrays for reconfigurable distributed microwave components. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Salt Lake City, UT, USA, 1–21 July 2000; pp. 587–591. [Google Scholar]
- Entesari, K.; Rebeiz, G.M. A differential 4-bit 6.5-10-GHz RF MEMS tunable filter. IEEE Trans. Microw. Theory Tech. 2005, 53, 1103–1110. [Google Scholar] [CrossRef]
- Rebeiz, G.M. RF MEMS: Theory, Design, and Technology; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Demirel, K.; Yazgan, E.; Demir, Ş.; Akın, T. A new temperature-tolerant RF MEMS switch structure design and fabrication for Ka-Band applications. J. Microelectromech. Syst. 2016, 25, 60–68. [Google Scholar] [CrossRef]
- Fernandez-Bolanos, M.; Tsamados, D.; Dainesi, P.; Ionescu, A.M. Reliability of RF MEMS capacitive switches and distributed MEMS phase shifters using AlN dielectric. In Proceedings of the IEEE 22nd International Conference on Micro Electro Mechanical Systems, Sorrento, Italy, 25–29 January 2009; pp. 638–641. [Google Scholar]
- Goldsmith, C.L.; Yao, Z.; Eshelman, S.; Denniston, D. Performance of low-loss RF MEMS capacitive switches. IEEE Microw. Guided Wave Lett. 1998, 8, 269–271. [Google Scholar] [CrossRef]
- Blondy, P.; Crunteanu, A.; Champeaux, C.; Catherinot, A.; Tristant, P.; Vendier, O. Dielectric less capacitive MEMS switches. In Proceedings of the 2004 IEEE MTT-S International Microwave Symposium Digest, Fort Worth, TX, USA, 8 October 2004; pp. 573–576. [Google Scholar]

| Reference | Insertion Loss (dB) | Insulation (dB) | Up Capacitance (fF) | Down Capacitance (pF) | Actuating Voltage (V) | Air Gap (μm) | Response Time (μs) | Capacitance Ratio |
|---|---|---|---|---|---|---|---|---|
| [4] | 0.08 | 42 | 83 | 50 | 8 | 2.5–3.5 | - | 600 |
| [7] | 0.15 | 40 | 4–6 | 1–1.5 | 80 | ~15 | 1–20 | 250 |
| [10] | 0.35 | 37 | 51 | 6 | 117.6 | 2 | - | 22 |
| [11] | 0.2 | 38.5 | 24 | 1.55 | 12 | ~2 | 10–15 | 64.6 |
| [12] | 0.7 | 35 | 35 | 3 | 30 | 3~5 | 7 | 85.7 |
| [13] | 1.5 | 20 | 22 | 2.2 | 30 | 3.2 | - | 100 |
| This paper | 0.5 | 34 | 54.2 | 20.8 | 21 | 2 | <10 | 383.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, K.; Guo, X.; Smith, S.; Deng, Z.; Li, W. Novel High-Capacitance-Ratio MEMS Switch: Design, Analysis and Performance Verification. Micromachines 2018, 9, 390. https://doi.org/10.3390/mi9080390
Han K, Guo X, Smith S, Deng Z, Li W. Novel High-Capacitance-Ratio MEMS Switch: Design, Analysis and Performance Verification. Micromachines. 2018; 9(8):390. https://doi.org/10.3390/mi9080390
Chicago/Turabian StyleHan, Ke, Xubing Guo, Stewart Smith, Zhongliang Deng, and Wuyu Li. 2018. "Novel High-Capacitance-Ratio MEMS Switch: Design, Analysis and Performance Verification" Micromachines 9, no. 8: 390. https://doi.org/10.3390/mi9080390
APA StyleHan, K., Guo, X., Smith, S., Deng, Z., & Li, W. (2018). Novel High-Capacitance-Ratio MEMS Switch: Design, Analysis and Performance Verification. Micromachines, 9(8), 390. https://doi.org/10.3390/mi9080390





