Analysis of Shape Geometry and Roughness of Ti6Al4V Parts Fabricated by Nanosecond Laser Ablation
Abstract
:1. Introduction
2. Materials and Methods
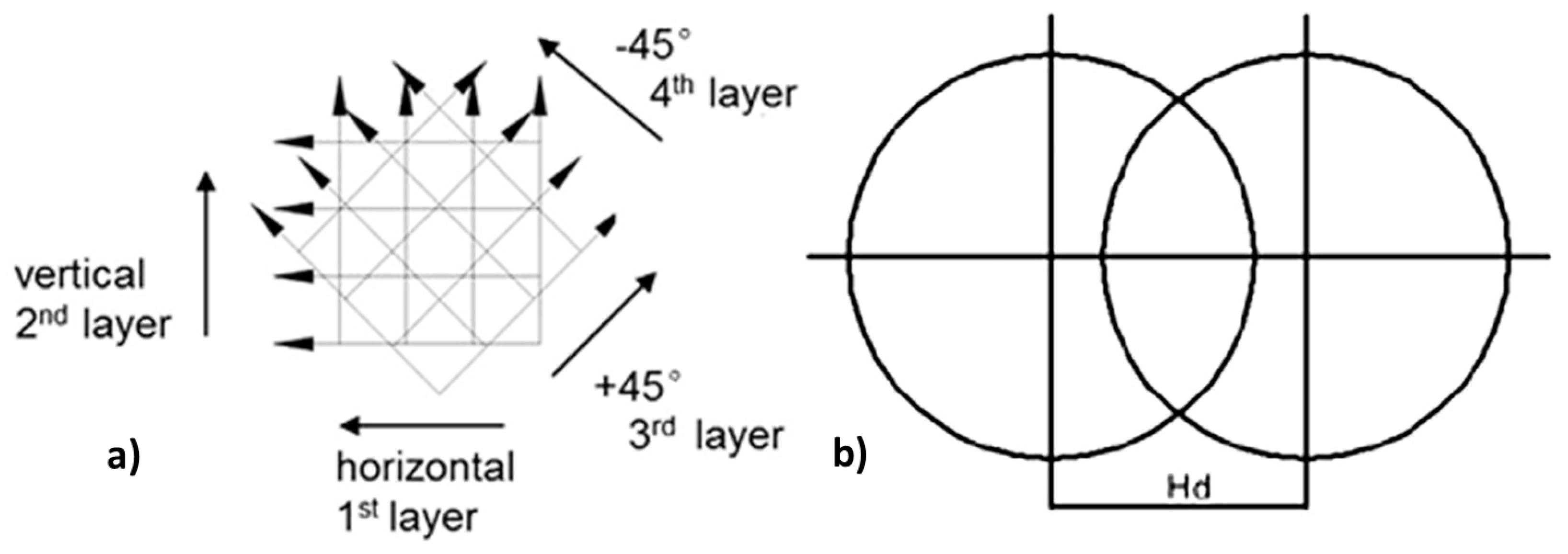
2.1. Laser Machine Setup and Materials
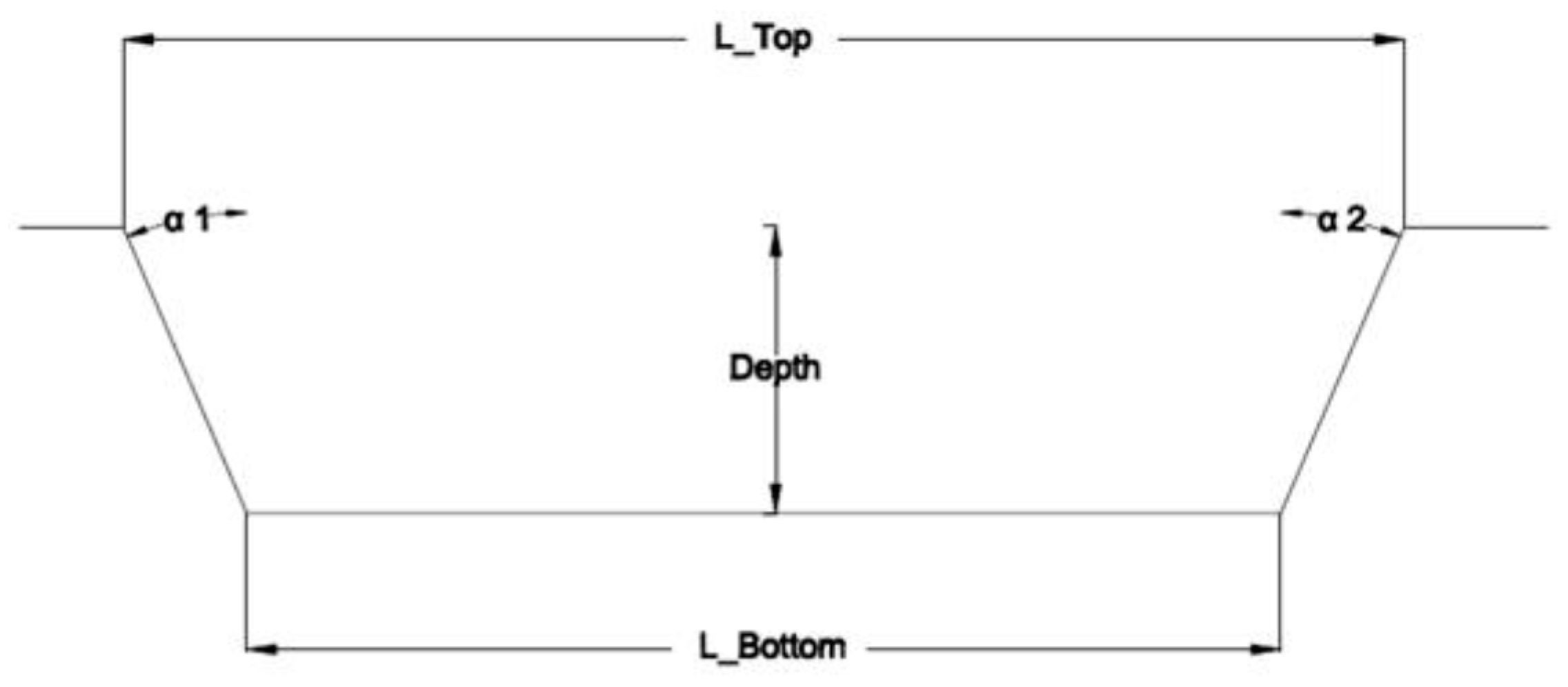
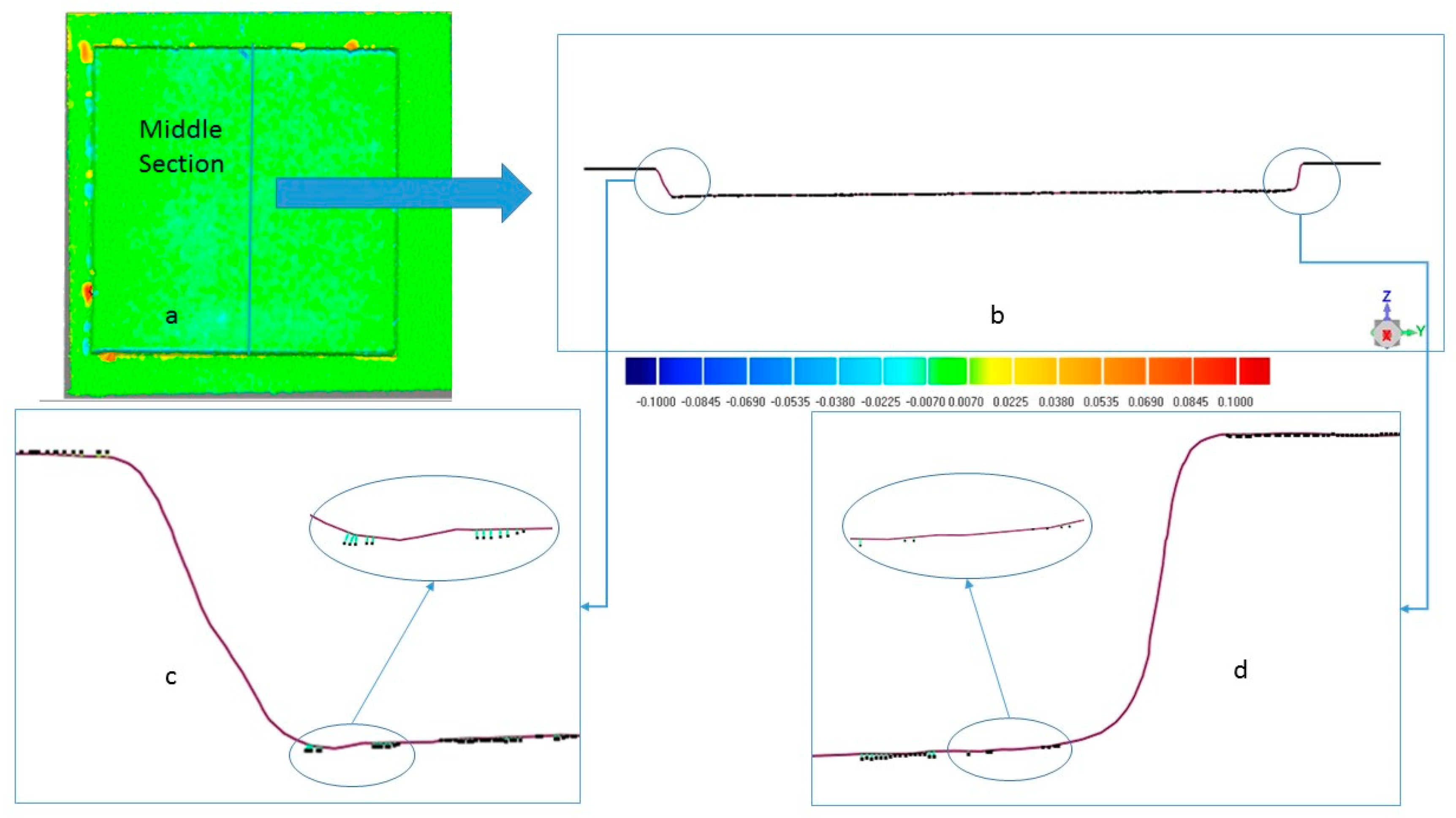
2.2. Dimensional Measurements
3. Results
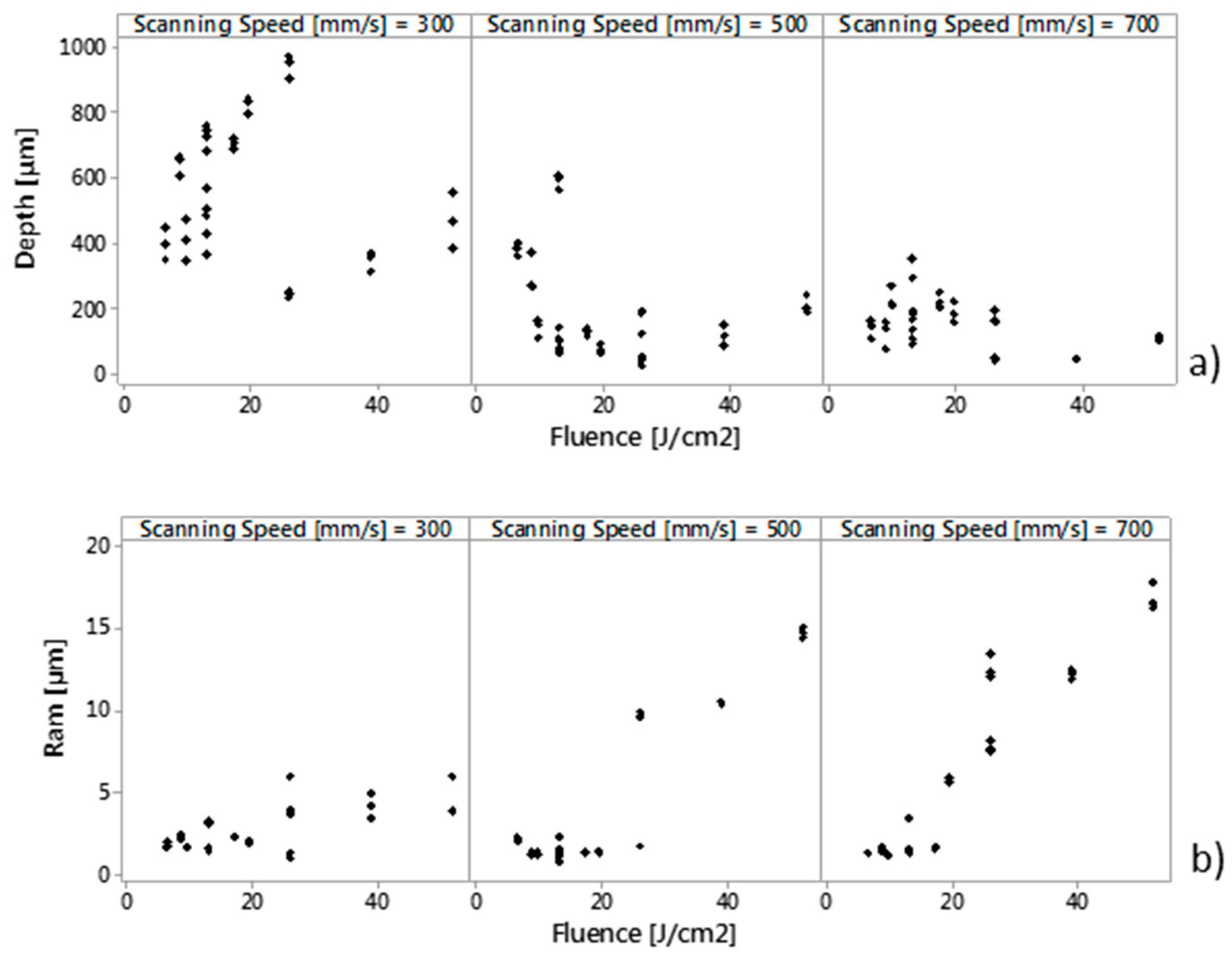
3.1. Measurement Results
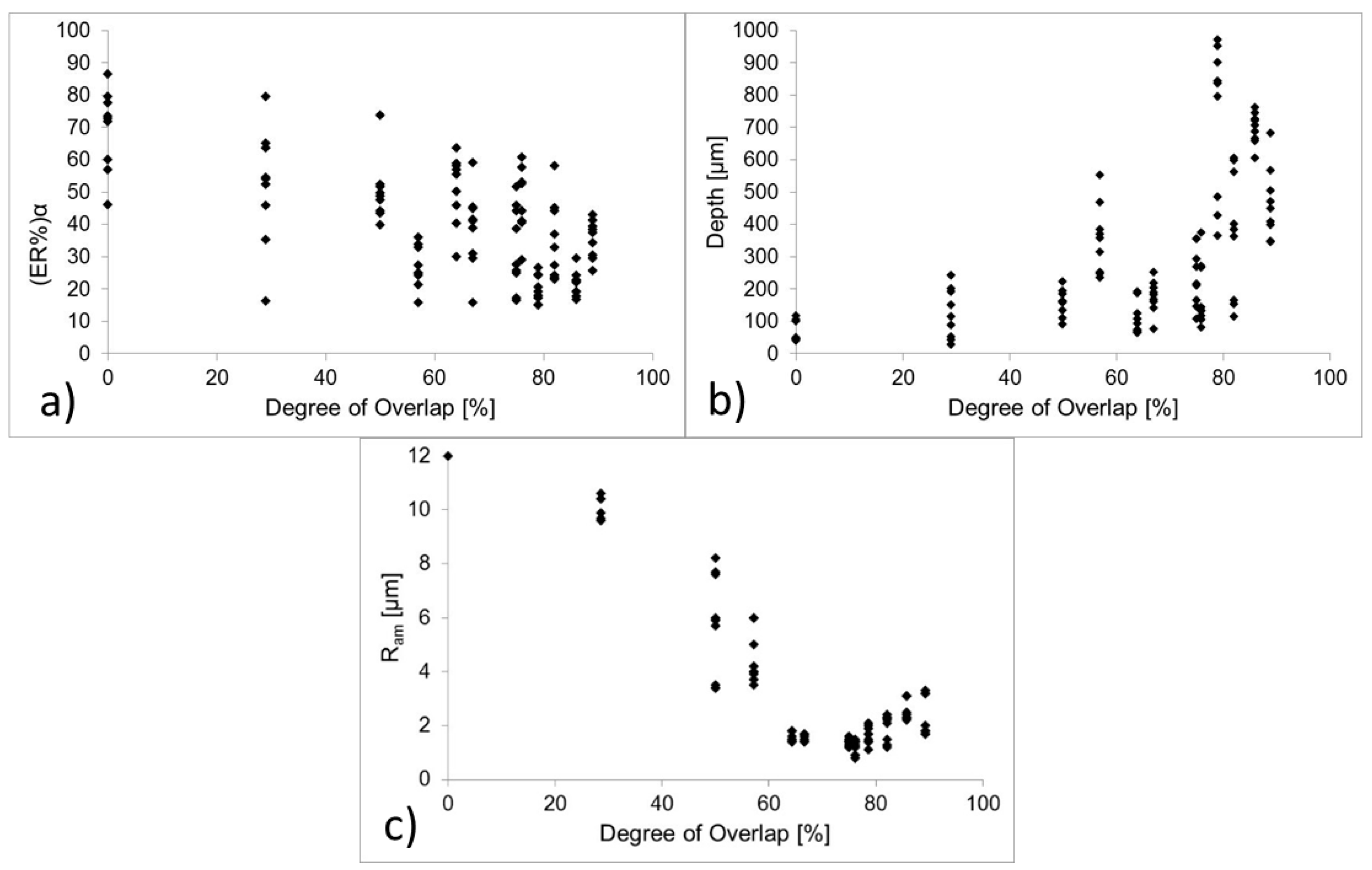
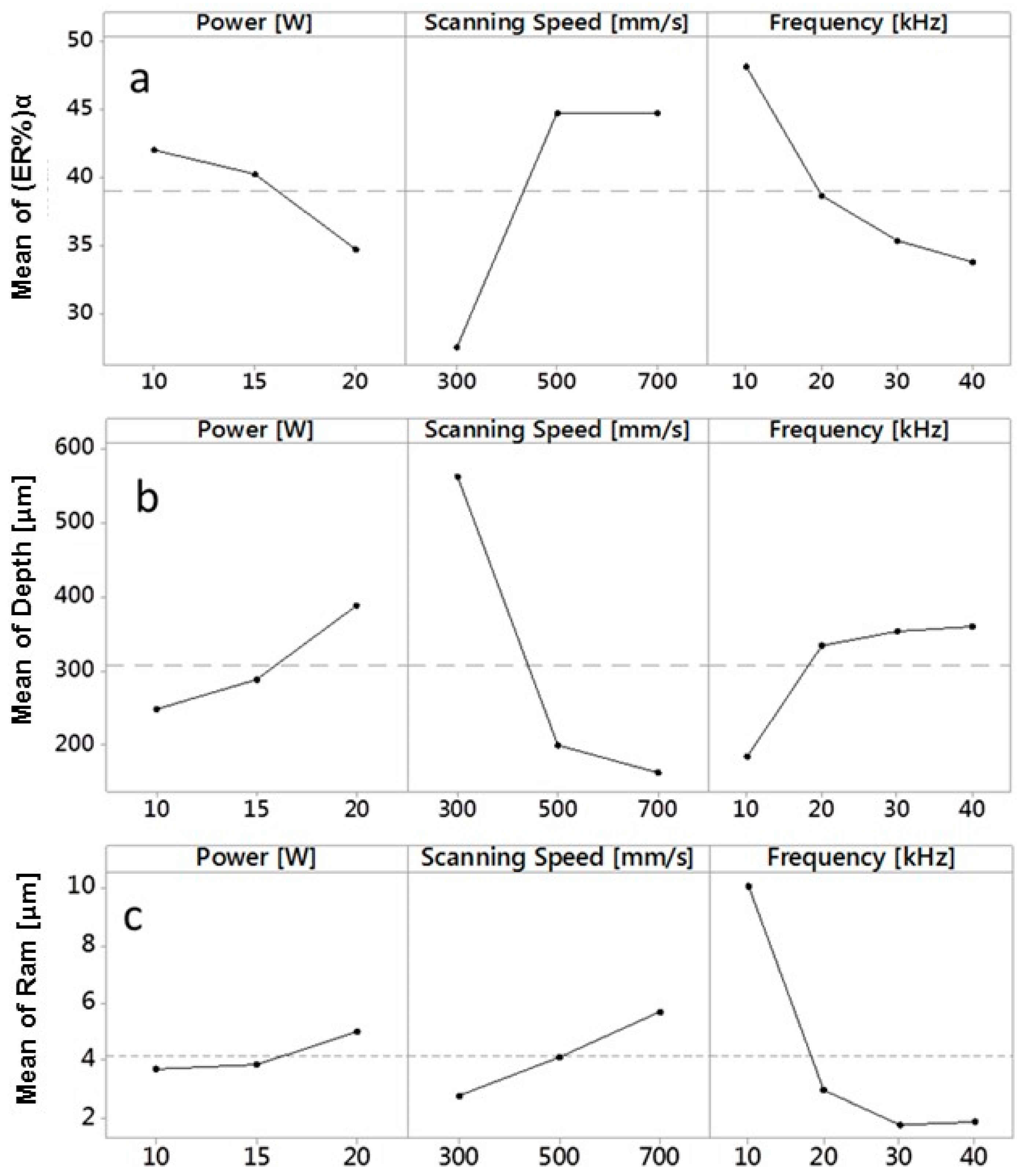
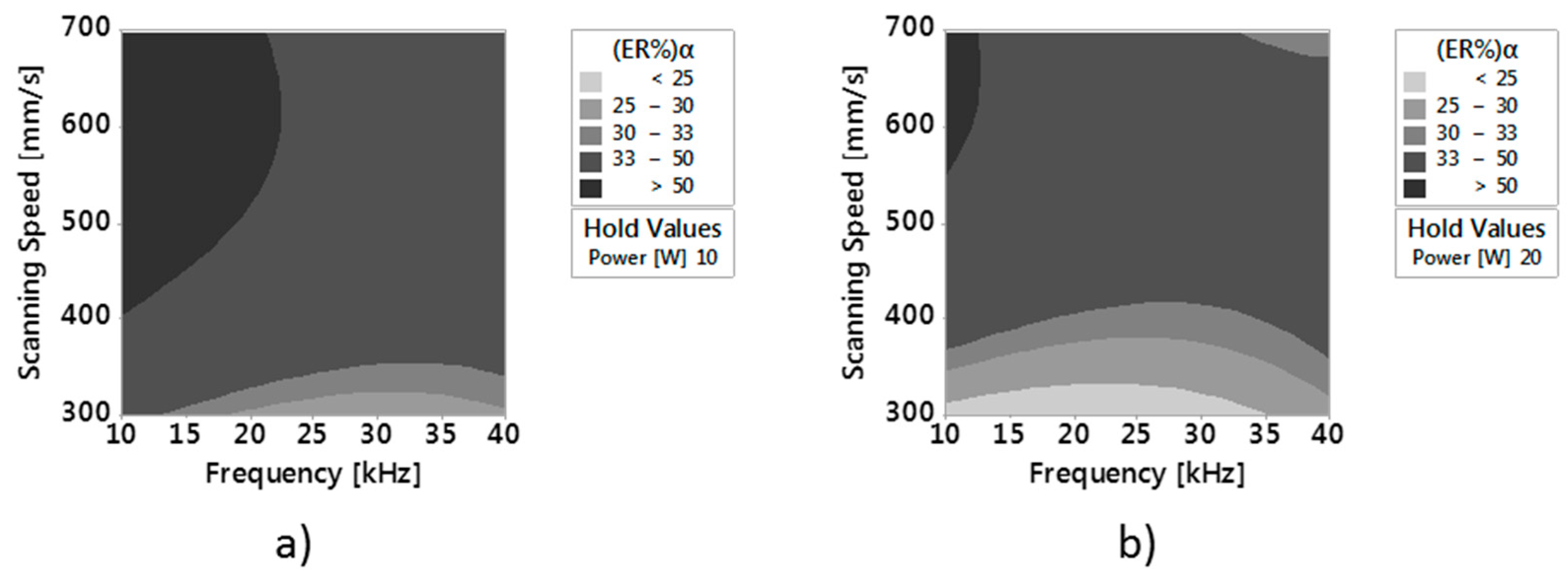
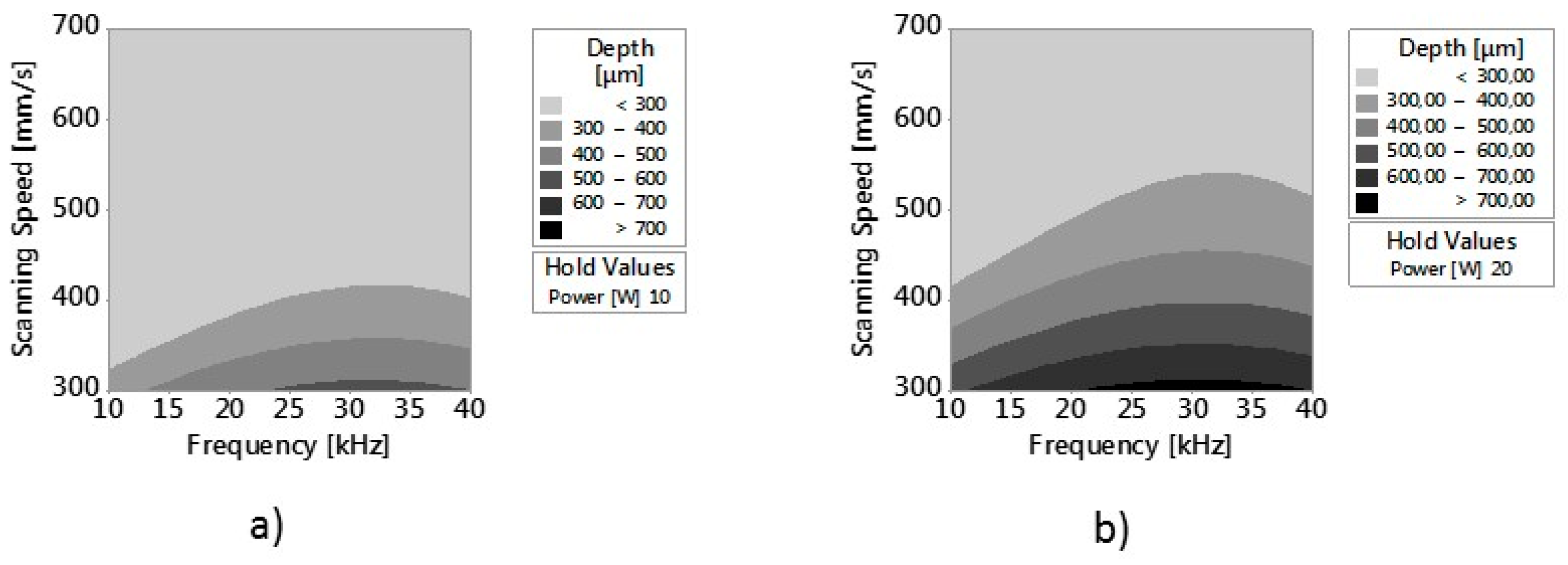
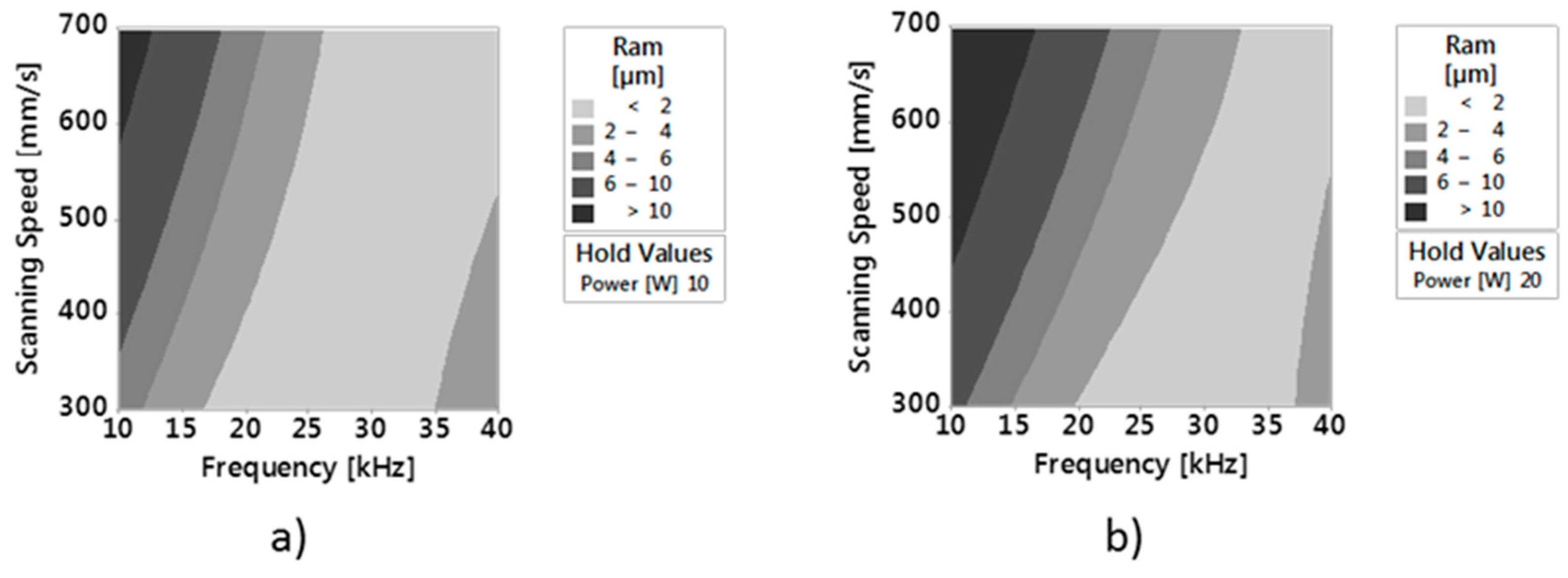
3.2. Effect of Degree of Overlap on (ER%)α, Depth and Ram
4. Discussion
- The slope of the curves confirms results of ANOVA on significance of input process parameters on analyzed results;
- The lowest value of (ER%)α can be obtained setting P = 20 W, v = 300 mm/min, Fp = 40 kHz.
- The lowest value of Ram can be obtained for P = 10 W, v = 300 mm/min and Fp = 30 kHz;
- A peak of Depth is present for P = 20 W, v = 300 mm/min, Fp = 40 kHz.
5. Conclusions
- Wall shape angles can be controlled setting appropriate values of process parameters.
- Values of roughness lower than 2 µm can be obtained setting proper values of power, frequency and scanning speed
- Values of roughness lower than 2 µm and of (ER%)α lower than 25% can be obtained with an average power of 20 W, Frequency between 20 kHz and 35 kHz and scanning speeds equal to or slightly higher than 300 mm/min.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| P | average laser power |
| Fp | frequency |
| v | scanning speed |
| Hd | hatch distance |
| O | degree of overlap |
| D | laser spot diameter |
| ER | error index |
| Xm | single measured dimension |
| XCAD | single CAD dimension |
| Ram | arithmetic average roughness |
| α | probability error |
| L_Top | channel top Width, |
| L_Bottom | channel bottom width |
| α1, α2 | channel side angles |
References
- Heyl, P.; Olschewski, T.; Wijnaendts, R.W. Manufacturing of 3D structures for micro-tools using laser ablation. Microelectron. Eng. 2001, 57, 775–780. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Petkov, P.V.; Petkov, S.P. Laser milling. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2002, 216, 657–667. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Ji, C.; Petkov, P.V.; Dobrev, T. Laser milling as a rapid micromanufacturing process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 1–7. [Google Scholar] [CrossRef]
- Campanelli, S.L.; Casalino, G.; Contuzzi, N. Multi-objective optimization of laser milling of 5754 aluminium alloy. Opt. Laser Technol. 2013, 52, 48–56. [Google Scholar] [CrossRef]
- Teixidor, D.; Ferrer, I.; Ciurana, J.; Özel, T. Optimization of process parameters for pulsed laser milling of micro-channels on AISI H13 tool steel. Robot. Comput. Integr. Manuf. 2013, 29, 209–218. [Google Scholar] [CrossRef]
- Darwish, S.; Ahmed, N.; Alahmari, A.M.; Mufti, N.A. A comparison of laser beam machining of micro-channels under dry and wet mediums. Int. J. Adv. Manuf. Technol. 2016, 83, 1539–1555. [Google Scholar] [CrossRef]
- Chen, H.C.; Chang, L.B.; Jeng, M.J.; Lai, C.S. Characterization of laser carved micro channel polycrystalline silicon solar cell. Solid State Electron. 2011, 61, 23–28. [Google Scholar] [CrossRef]
- Karazi, S.M.; Issa, A.; Brabazon, D. Comparison of ANN and DoE for the prediction of laser-machined micro-channel dimensions. Opt. Lasers Eng. 2009, 47, 956–964. [Google Scholar] [CrossRef] [Green Version]
- Schille, J.; Schneider, L.; Loeschner, U.; Ebert, R.; Scully, P.; Goddard, N.; Steiger, B.; Exner, H. Micro processing of metals using a high repetition rate femtosecond laser: From laser process parameter study to machining examples. In Proceedings of the 30th International Congress on Applications of Lasers and Electro-Optics ICALEO, Orlando, FL, USA, 23–27 October 2011; pp. 773–782. [Google Scholar]
- Bulushev, E.; Bessmeltsev, V.; Dostovalov, A.; Goloshevsky, N.; Wolf, A. High-speed and crack-free direct-writing of microchannels on glass by an IR femtosecond laser. Opt. Lasers Eng. 2016, 79, 39–47. [Google Scholar] [CrossRef]
- Rysava, Z.; Bruschi, S. Comparison between EBM and DMLS Ti6Al4V Machinability Characteristics under Dry Micro-Milling Conditions. Mater. Sci. Forum 2016, 836–837, 177–184. [Google Scholar] [CrossRef]
- Álvarez, I.; Enguita, J.M.; Frade, M.; Marina, J.; Ojea, G. On-Line Metrology with Conoscopic Holography: Beyond Triangulation. Sensors 2009, 9, 7021–7037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sirat, G.; Psaltis, D. Conoscopic Holography. Opt. Lett. 1985, 10, 4–6. [Google Scholar] [CrossRef] [PubMed]
- Rotella, G.; Orazi, L.; Alfano, M.; Candamano, S. CIRP Journal of Manufacturing Science and Technology Innovative high-speed femtosecond laser nano-patterning for improved adhesive bonding of Ti6Al4V titanium alloy. CIRP J. Manuf. Sci. Technol. 2017, 18, 101–106. [Google Scholar] [CrossRef]
- Dai, F.Z.; Geng, J.; Tan, W.S.; Ren, X.D.; Lu, J.Z.; Huang, S. Friction and wear on laser textured Ti6Al4V surface subjected to laser shock peening with contacting foil. Opt. Laser Technol. 2018, 103, 142–150. [Google Scholar] [CrossRef]
- Almeida, I.; Division, P. Surface Modification of Ti6Al4V Alloy by Pulsed Lasers: Microstructure and Hydrophobic 2 fR. Mater. Res. 2017, 20, 8–14. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]



| Sample | Average Laser Power (W) | Scanning Speed (mm/s) | Frequency (kHz) | Degree of Overlap (%) |
|---|---|---|---|---|
| 1 | 10 | 500 | 40 | 82 |
| 2 | 20 | 500 | 10 | 29 |
| 3 | 10 | 500 | 30 | 76 |
| 4 | 15 | 300 | 40 | 89 |
| 5 | 10 | 500 | 10 | 29 |
| 6 | 15 | 500 | 10 | 29 |
| 7 | 20 | 300 | 20 | 79 |
| 8 | 15 | 700 | 20 | 50 |
| 9 | 10 | 700 | 20 | 50 |
| 10 | 10 | 300 | 20 | 79 |
| 11 | 10 | 700 | 10 | 0 |
| 12 | 20 | 300 | 30 | 86 |
| 13 | 20 | 700 | 10 | 0 |
| 14 | 20 | 700 | 40 | 75 |
| 15 | 20 | 300 | 10 | 57 |
| 16 | 20 | 500 | 30 | 76 |
| 17 | 10 | 500 | 20 | 64 |
| 18 | 10 | 700 | 30 | 67 |
| 19 | 15 | 500 | 20 | 64 |
| 20 | 15 | 500 | 30 | 76 |
| 21 | 15 | 700 | 40 | 75 |
| 22 | 20 | 700 | 30 | 67 |
| 23 | 20 | 700 | 20 | 50 |
| 24 | 15 | 300 | 30 | 86 |
| 25 | 10 | 300 | 30 | 86 |
| 26 | 15 | 700 | 10 | 0 |
| 27 | 20 | 300 | 40 | 89 |
| 28 | 15 | 300 | 20 | 79 |
| 29 | 15 | 700 | 30 | 67 |
| 30 | 10 | 700 | 40 | 75 |
| 31 | 15 | 300 | 10 | 57 |
| 32 | 10 | 300 | 10 | 57 |
| 33 | 20 | 500 | 40 | 82 |
| 34 | 10 | 300 | 40 | 89 |
| 35 | 15 | 500 | 40 | 82 |
| 36 | 20 | 500 | 20 | 64 |
| Geometrical Entities | Average Laser Power (W) | Scanning Speed (mm/s) | Frequency (kHz) |
|---|---|---|---|
| ER L Top (ER% L_Top) | NS | NS | S |
| ER L Bottom (ER% L_bottom) | NS | S | S |
| (ER%)α | S | S | S |
| Depth | S | S | S |
| Ram | S | S | S |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campanelli, S.L.; Lavecchia, F.; Contuzzi, N.; Percoco, G. Analysis of Shape Geometry and Roughness of Ti6Al4V Parts Fabricated by Nanosecond Laser Ablation. Micromachines 2018, 9, 324. https://doi.org/10.3390/mi9070324
Campanelli SL, Lavecchia F, Contuzzi N, Percoco G. Analysis of Shape Geometry and Roughness of Ti6Al4V Parts Fabricated by Nanosecond Laser Ablation. Micromachines. 2018; 9(7):324. https://doi.org/10.3390/mi9070324
Chicago/Turabian StyleCampanelli, Sabina Luisa, Fulvio Lavecchia, Nicola Contuzzi, and Gianluca Percoco. 2018. "Analysis of Shape Geometry and Roughness of Ti6Al4V Parts Fabricated by Nanosecond Laser Ablation" Micromachines 9, no. 7: 324. https://doi.org/10.3390/mi9070324
APA StyleCampanelli, S. L., Lavecchia, F., Contuzzi, N., & Percoco, G. (2018). Analysis of Shape Geometry and Roughness of Ti6Al4V Parts Fabricated by Nanosecond Laser Ablation. Micromachines, 9(7), 324. https://doi.org/10.3390/mi9070324






