Topology Optimization of Spatially Compliant Mechanisms with an Isomorphic Matrix of a 3-UPC Type Parallel Prototype Manipulator
Abstract
:1. Introduction
2. Isomorphic Mapping Matrix of the 3-UPC Type Parallel Prototype Manipulator
3. Topology Optimization Model of the Three-DOF Spatially Compliant Mechanism
3.1. Model of the Solid Isotropic Material with Penalization (SIMP)
3.2. Sensitivity Analysis
3.3. Solution of the Topology Optimization Model
4. Topology Structure of the Three-DOF Spatially Compliant Mechanism
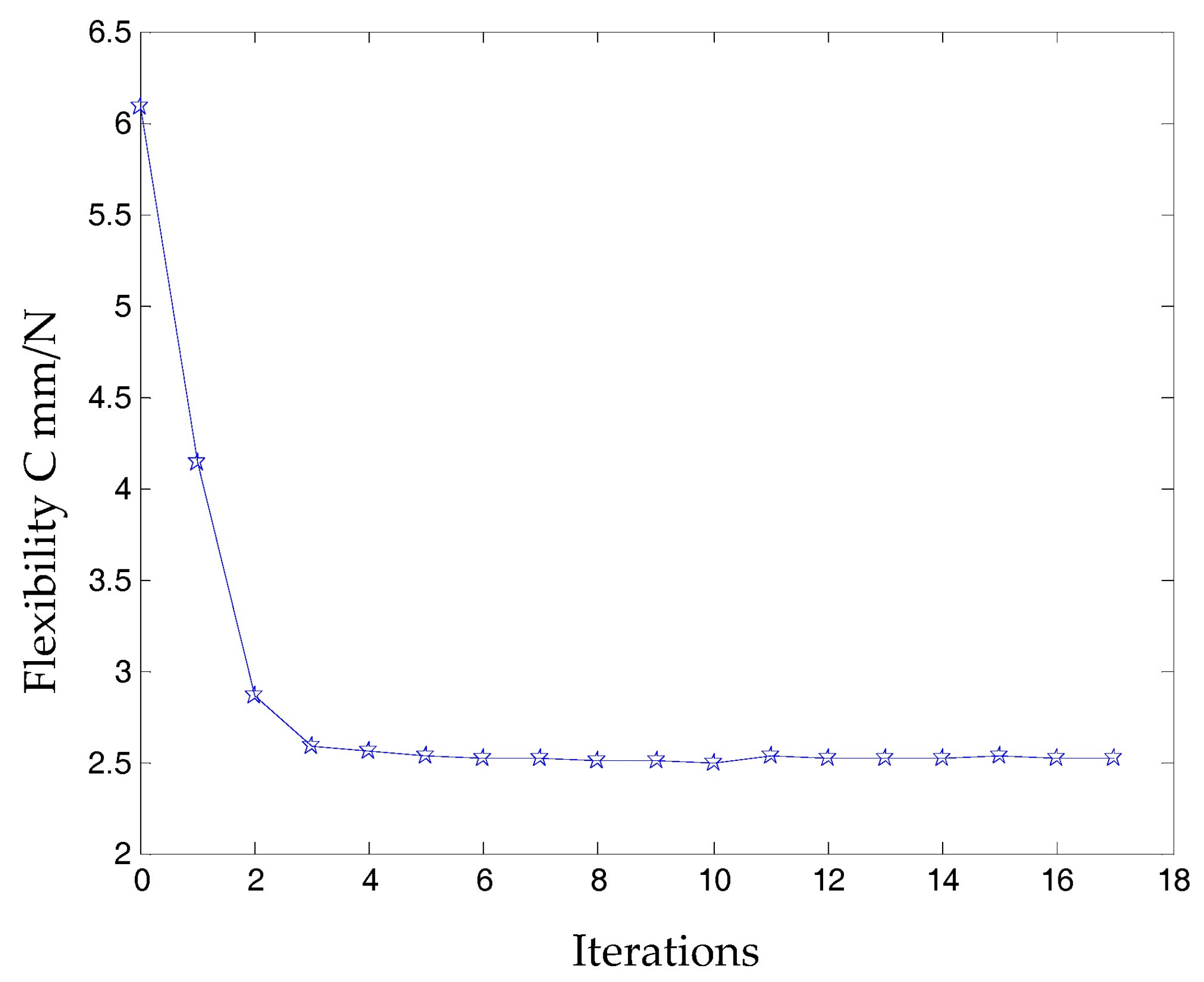
4.1. Design Domain and Iterative Algorithm
4.2. The Topology Optimization Structure of the Three-DOF Spatially Compliant Mechanism
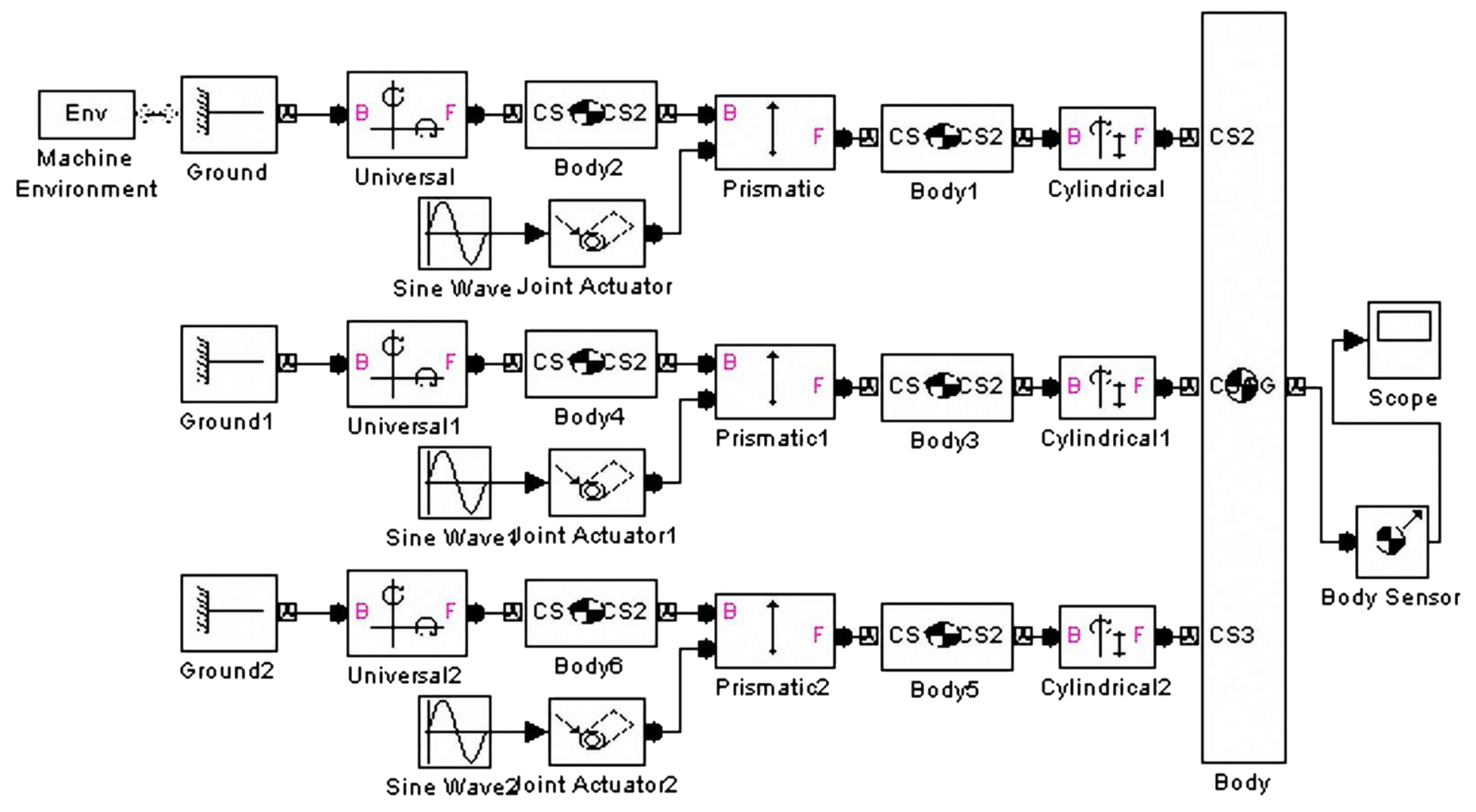
5. Numerical Implementation
5.1. Analysis of Differential Kinematic Characteristics
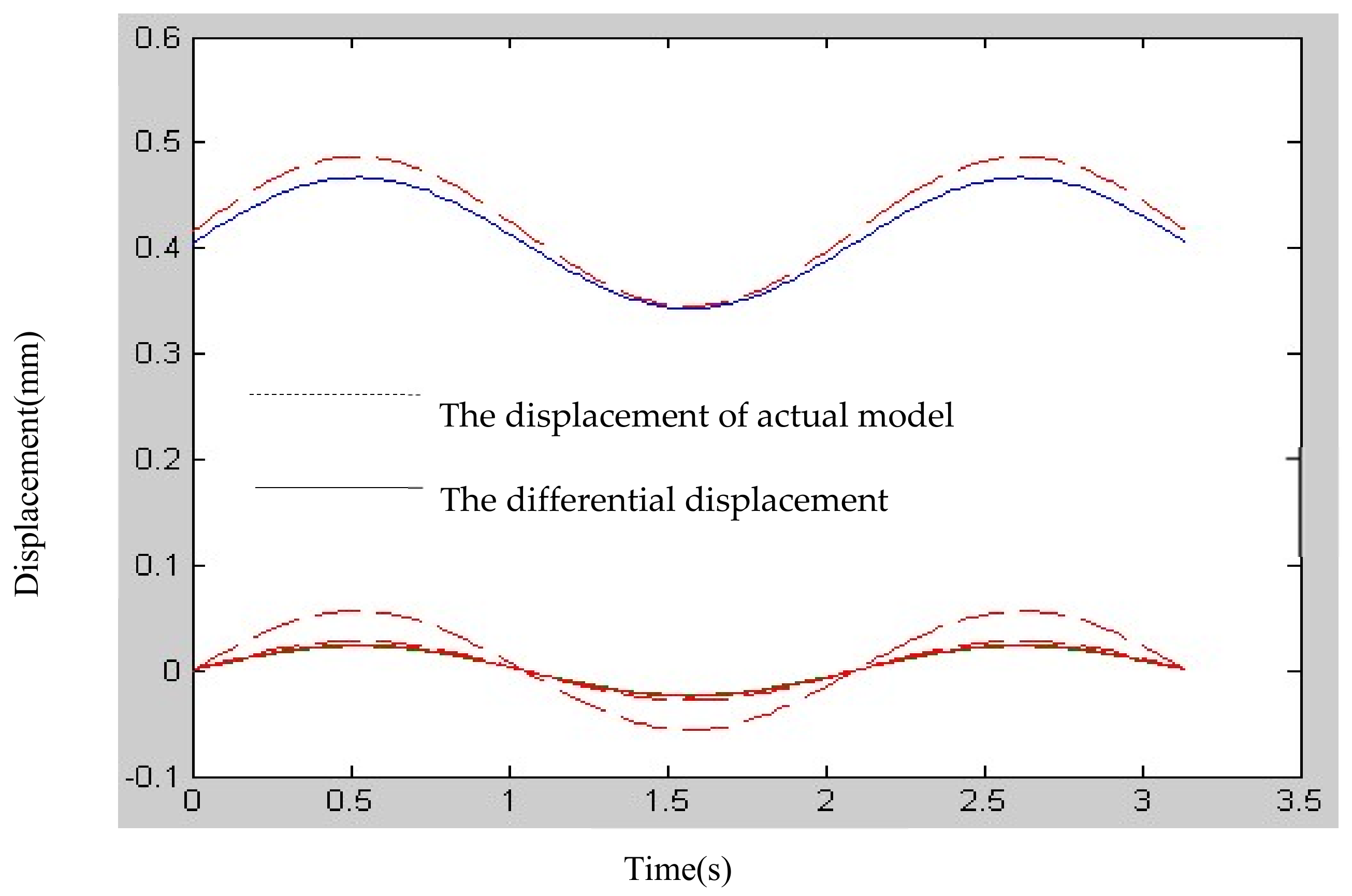
5.2. Differential Kinematic Characteristics of the Topology Optimization Structure
5.3. Experimental Study
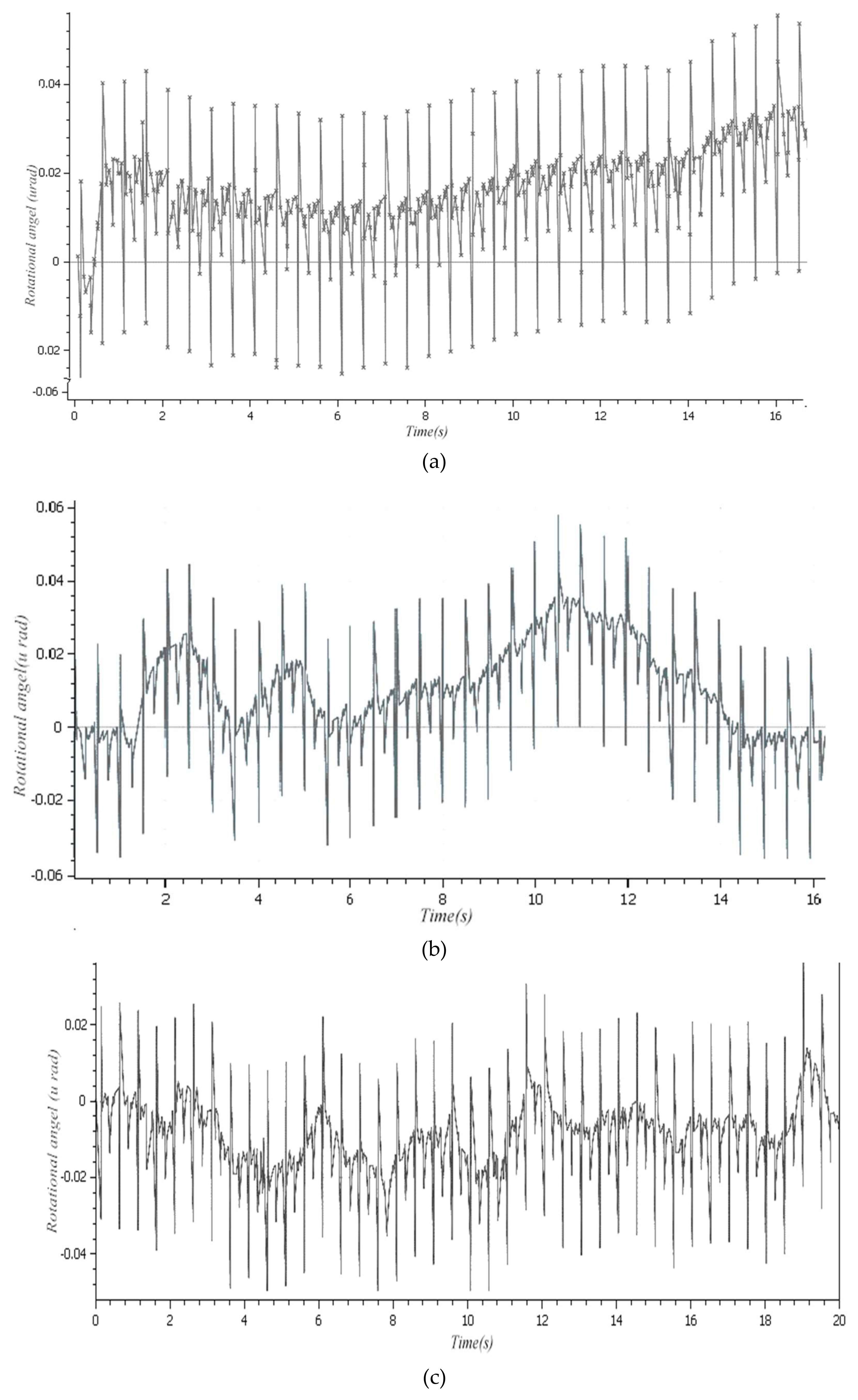
5.4. Experimental Results and Analysis
5.5. Modal Analysis of the First Three Orders
6. Conclusions
- (1)
- In order to build accurate modeling after the structural topology optimization, the SIMP topology optimization method combined with the isomorphic mapping matrix of 3-UPC type parallel prototype manipulator was used for the structural synthesis for the spatially compliant mechanism with three rotational DOFs.
- (2)
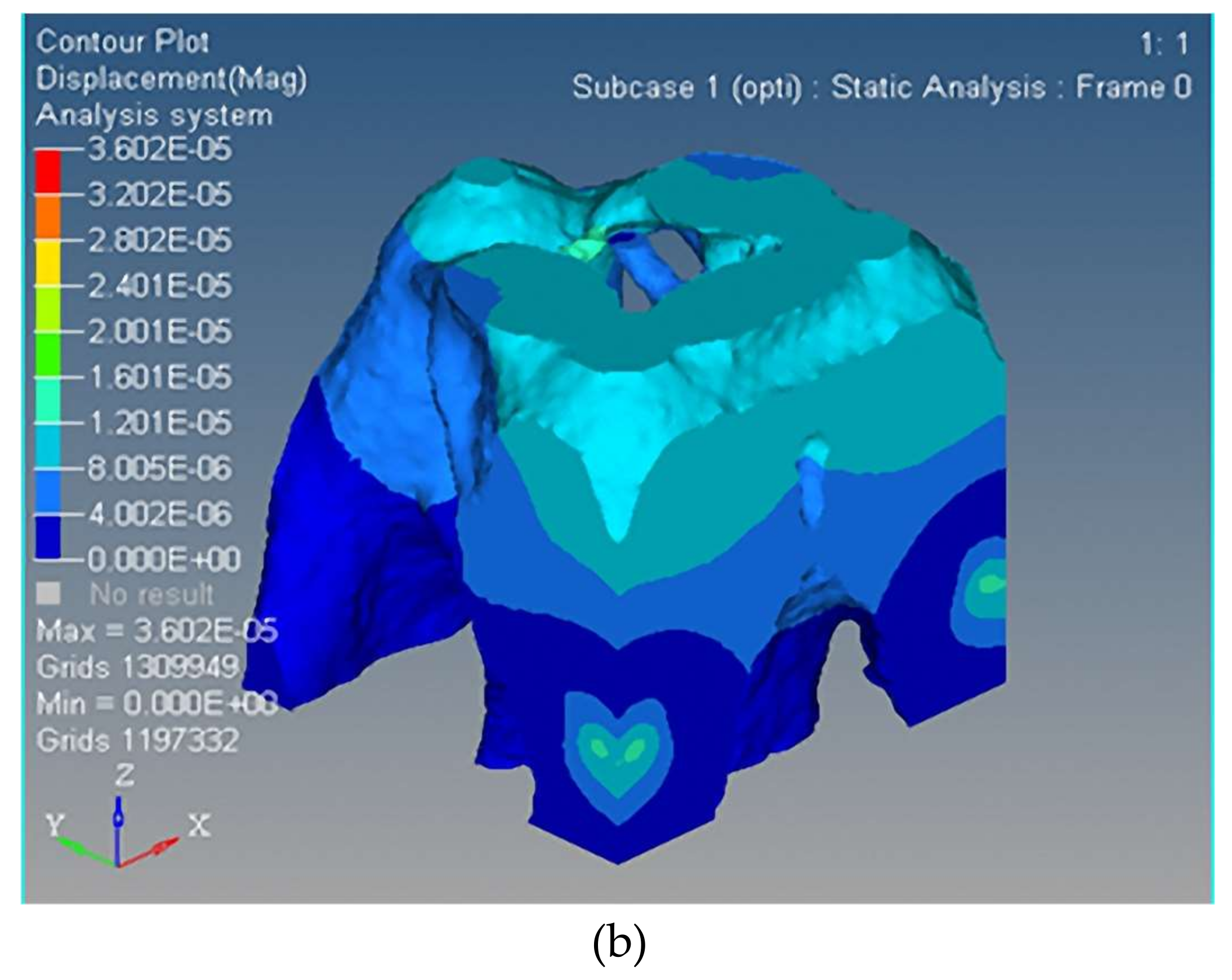
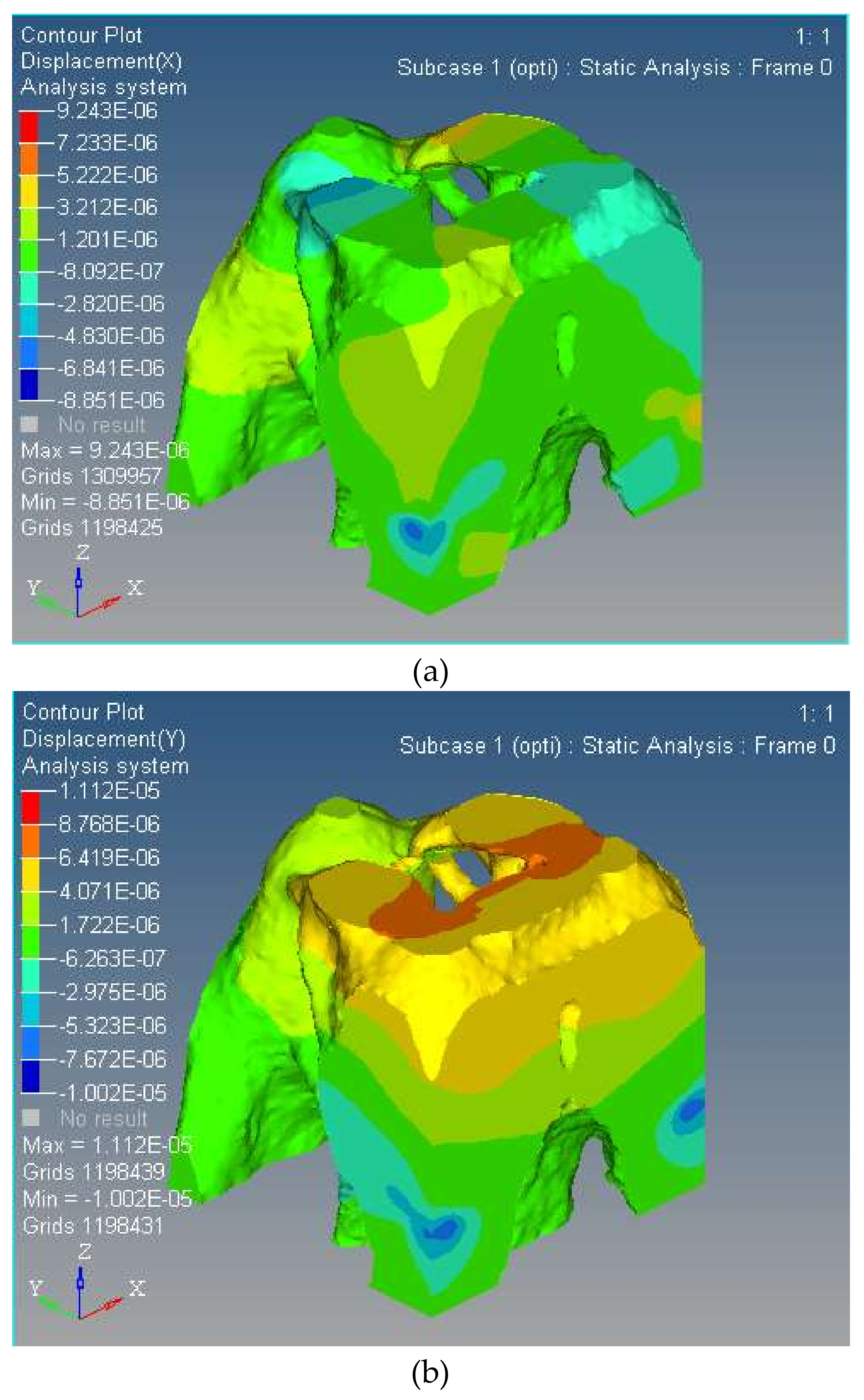
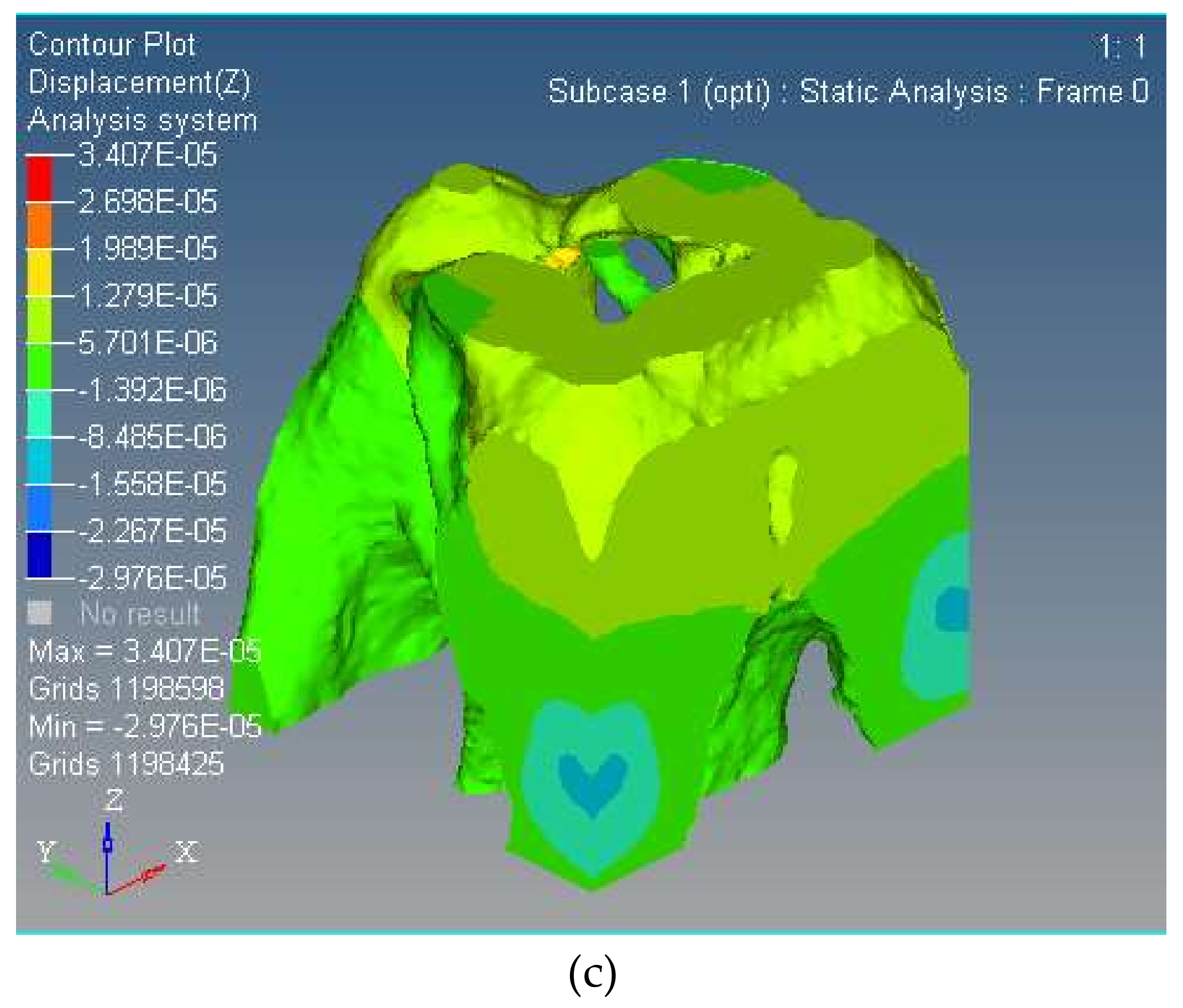
- The optimized three-DOF spatially compliant mechanism with the isomorphic mapping matrix was imported to Hyperworks for finite element static analysis. The maximum and minimum rotational angles of 0.47 × 10−4 rad and −0.21 × 10−4 rad in x direction, 0.51 × 10−4 rad and −0.46 × 10−4 rad in y direction, and 0.12 × 10−4 rad and −0.48 × 10−5 rad in z direction were obtained by simulation, while the corresponding experimental rotational angles of the maximum and minimum were 0.36 × 10−4 rad and −0.18 × 10−4 rad in x direction, 0.39 × 10−4 rad and −0.12 × 10−4 rad in y direction, and 0.18 × 10−4 rad and −0.32 × 10−4 rad in z direction, respectively.
- (3)
- The comparative simulation studies, the stress distribution and the first/second order modal of the proposed spatially compliant mechanism, show that the proposed method can ensure the integral isomorphism characteristics between the proposed spatially compliant mechanism and the conventional parallel prototype manipulator with uniform stiffness and vibration suppression.
- (4)
- The compliant mechanism obtained through the topology optimization had a very irregular shape, which is related to the configuration of the topological optimization conditions. By using a topological optimization method combining a Jacobian matrix with the SIMP method of isomorphism mapping, regardless of the initial optimization conditions, the resulting topologies all had the same differential motion characteristics as the parallel prototype mechanism, i.e., isomorphism. The piezoelectric actuator is in an enclosed space and its spatial configuration is determined based on the parallel prototype mechanism actuator configuration. The approach adopted consisted of interrupting the printing process during 3D printing and resuming it once the piezoelectric actuator is implanted. Therefore, there is no better way to implement the driver than the 3D printing technology.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Howell, L.L. Compliant Mechanisms; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Xu, Q. New flexure parallel-kinematic micro-positioning system with large workspace. IEEE Trans. Robot. 2012, 28, 478–491. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestri, E. Second-order approximation pseudo-rigid model of leaf flexure hinge. Mech. Mach. Theory 2017, 116, 352–359. [Google Scholar] [CrossRef]
- Pucheta, M.A.; Cardona, A. Design of bi stable compliant mechanisms using precision-position and rigid-body replacement methods. Mech. Mach. Theory 2010, 45, 304–326. [Google Scholar] [CrossRef]
- Naves, M.; Brouwer, D.M.; Aarts, R.G. Building block-based spatial topology synthesis method for large-stroke flexure hinges. ASME Trans. J. Mech. Robot. 2017, 9, 041006. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Fatikow, S. Design and analysis of a multi-notched flexure hinge for compliant mechanisms. Precis. Eng. 2017, 48, 292–304. [Google Scholar] [CrossRef]
- Rad, F.P.; Berselli, G.; Vertechy, R.; Parenti-Castelli, V. Design and stiffness analysis of a compliant spherical chain with three degrees of freedom. Precis. Eng. 2017, 47, 1–9. [Google Scholar]
- Zhao, S.S.; Bi, S.S.; Zong, G.H.; Yu, J. New large-deflection flexure pivot based on curved flexure element. Chin. J. Mech. Eng. 2009, 45, 8–12. [Google Scholar] [CrossRef]
- Xu, Q. Design, testing and precision control of a novel long-stroke flexure micropositioning system. Mech. Mach. Theory 2013, 70, 209–224. [Google Scholar] [CrossRef]
- Trease, B.P.; Moon, Y.M.; Kota, S. Design of large displacement compliant joints. J. Mech. Des. 2004, 127, 788–798. [Google Scholar] [CrossRef]
- Choi, Y.J.; Sreenivasan, S.V.; Choi, B.J. Kinematic design of large displacement precision XY positioning stage by using cross strip flexure joints and over-constrained mechanism. Mech. Mach. Theory 2008, 43, 724–737. [Google Scholar] [CrossRef]
- Tan, K.; Zong, G.H.; Bi, S.S.; Yu, Z. Multi-leaf configuration of expanded-motion-range flexure hinges. Dual Use Technol. Prod. 2007, 3, 38–39. [Google Scholar]
- Hao, G.; Kong, X. A normalization-based approach to the mobility analysis of spatial compliant multi-beam modules. Mech. Mach. Theory 2013, 59, 1–19. [Google Scholar] [CrossRef]
- Howell, L.L.; Midah, A. A method for the design of compliant mechanisms with small-length flexural pivots. J. Eng. Des. 1994, 116, 280–289. [Google Scholar] [CrossRef]
- Howell, L.L.; Midah, A. A loop-closure theory for the analysis and synthesis of compliant mechanisms. J. Mech. Des. 1996, 118, 121–125. [Google Scholar] [CrossRef]
- Lum, G.Z.; Teo, T.J.; Yang, G.; Yeo, S.H.; Sitti, M. Integrating mechanism synthesis and topological optimization technique for stiffness-oriented design of a three degrees-of-freedom flexure-based parallel mechanism. Precis. Eng. 2015, 39, 125–133. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. A comprehensive survey on modern microgrippers design: Mechanical structure. J. Mech. Des. 2017, 139, 060801. [Google Scholar] [CrossRef]
- Hudgens, J.; Tesar, D. A fully-parallel six degree-of-freedom micromanipulator: Kinematic analysis and dynamic model. In Proceedings of the 20th Biennial ASME Mechanisms Conference, Kissimmee, FL, USA, 25–28 September 1988; pp. 29–37. [Google Scholar]
- Mclnroy, J.E.; Hamann, J.C. Design and control of flexure jointed hexapods. IEEE Trans. Robot. Autom. 2000, 16, 372–381. [Google Scholar] [CrossRef]
- Yi, B.J.; Chung, G.B.; Na, H.Y.; Kim, W.K.; Suh, I.H. Design and experiment of 3-dof parallel micromechanism utilizing flexure hinges. IEEE Trans. Robot. Autom. 2003, 19, 604–612. [Google Scholar]
- Hao, G.; Li, H. Conceptual design of multi-DOF compliant parallel manipulators composed of wire-beam based compliant mechanisms. Proc. Inst. Mech. Eng. Part C 2015, 229, 538–555. [Google Scholar] [CrossRef]
- Sigmund, O. On the design of compliant mechanisms using topology optimization. Mech. Struct. Mach. 1997, 25, 493–524. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization-Part I: One-material structures. Comput. Methods Appl. Mech. Eng. 2001, 190, 6577–6604. [Google Scholar] [CrossRef]
- Sigmund, O. Design of multiphysics actuators using topology optimization-Part II: Two-material structures. Comput. Methods Appl. Mech. Eng. 2001, 190, 6605–6627. [Google Scholar] [CrossRef]
- Nishiwaki, S.; Frecker, M.I.; Min, S.; Kikuchi, N. Topology optimization of compliant mechanisms using the homogenization method. Int. J. Num. Methods Eng. 1998, 42, 535–559. [Google Scholar] [CrossRef]
- Saxena, A.; Ananthasuresh, G.K. On an optimal property of compliant topologies. Struct. Multidiscip. Optim. 2000, 19, 36–49. [Google Scholar] [CrossRef]
- Wang, M.Y.; Steven, G.P. A simple evolution procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar]
- Saxena, A. Topology design of a large displacement compliant mechanisms with multiple materials and multiple output ports. Struct. Multidiscip. Optim. 2005, 30, 477–490. [Google Scholar] [CrossRef]
- Lu, K.; Kota, S. Topology and dimensional synthesis of compliant mechanisms using discrete optimization. J. Mech. Des. 2006, 128, 1080–1091. [Google Scholar] [CrossRef]
- Ansola, R.; Veguera, E.; Maturana, A.; Canales, J. 3D compliant mechanisms synthesis by a finite element addition procedure. Finite Elem. Anal. Des. 2010, 46, 760–769. [Google Scholar] [CrossRef]
- Ni, Z.; Zhang, D.; Wu, Y.; Tian, Y.; Hu, M. Analysis of parasitic motion in parallelogram compliant mechanism. Precis. Eng. 2010, 34, 133–138. [Google Scholar] [CrossRef]
- Verotti, M. Effect of initial curvature in uniform flexures on position accuracy. Mech. Mach. Theory 2018, 119, 106–118. [Google Scholar] [CrossRef]
- Pei, X.; Yu, J.; Zong, G.; Bi, S.; Yu, Z. Analysis of rotational precision for an isosceles-trapezoidal flexural pivot. J. Mech. Des. 2008, 130, 680–682. [Google Scholar]
- Jin, M.; Zhang, X. A new topology optimization method for planar compliant parallel mechanisms. Mech. Mach. Theory 2016, 95, 42–58. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, X.; Zhu, B. A numerical method for static analysis of pseudo-rigid-body model of compliant mechanisms. Proc. Inst. Mech. Eng. C 2014, 228, 3170–3177. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C. Type Synthesis of Parallel Mechanisms; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fang, Y.; Tsai, L.W. Structure synthesis of a class of 3-DOF rotational parallel manipulators. IEEE Trans. Robot. Autom. 2004, 20, 117–121. [Google Scholar] [CrossRef]
- Hao, G.; Kong, X. A structure design method for compliant parallel manipulators with actuation isolation. Mech. Sci. 2016, 7, 247–253. [Google Scholar] [CrossRef]
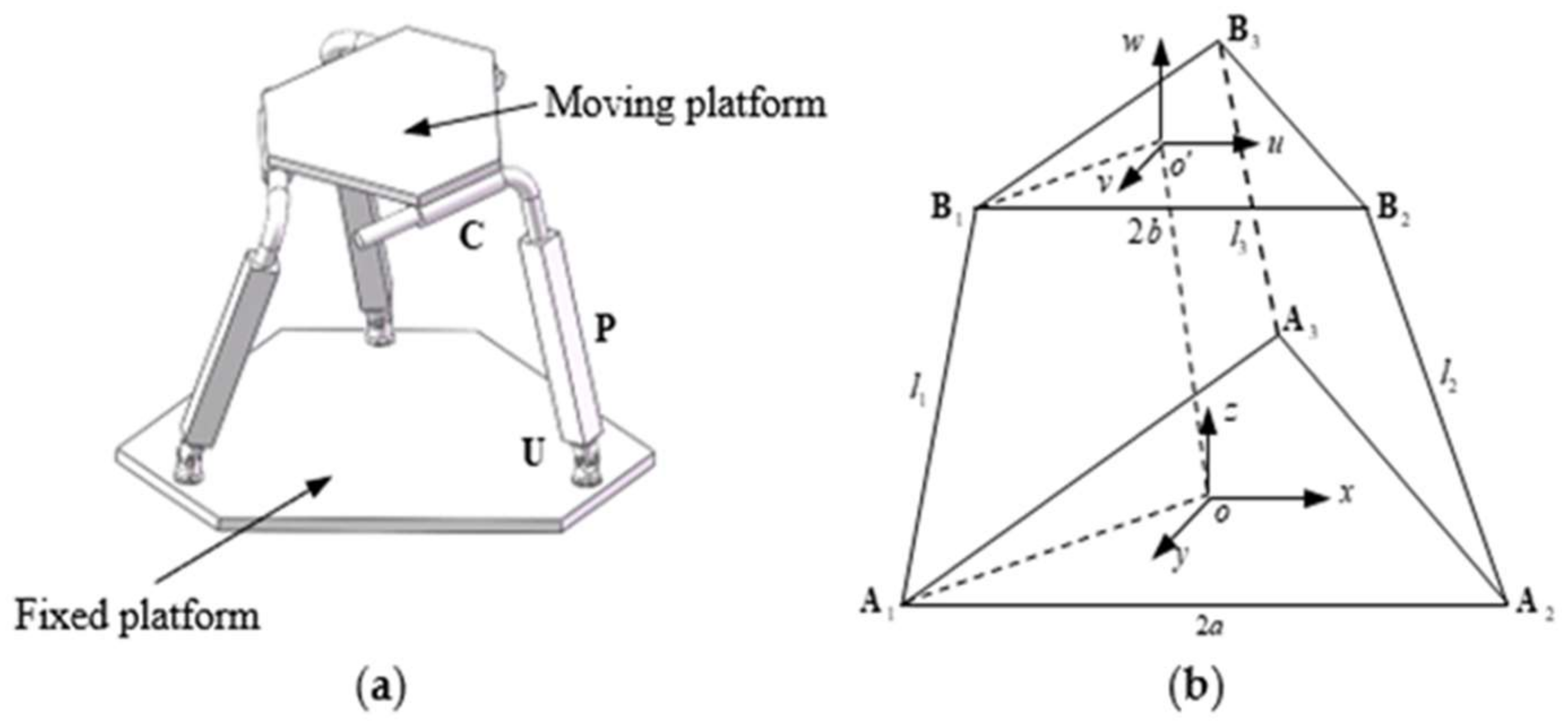
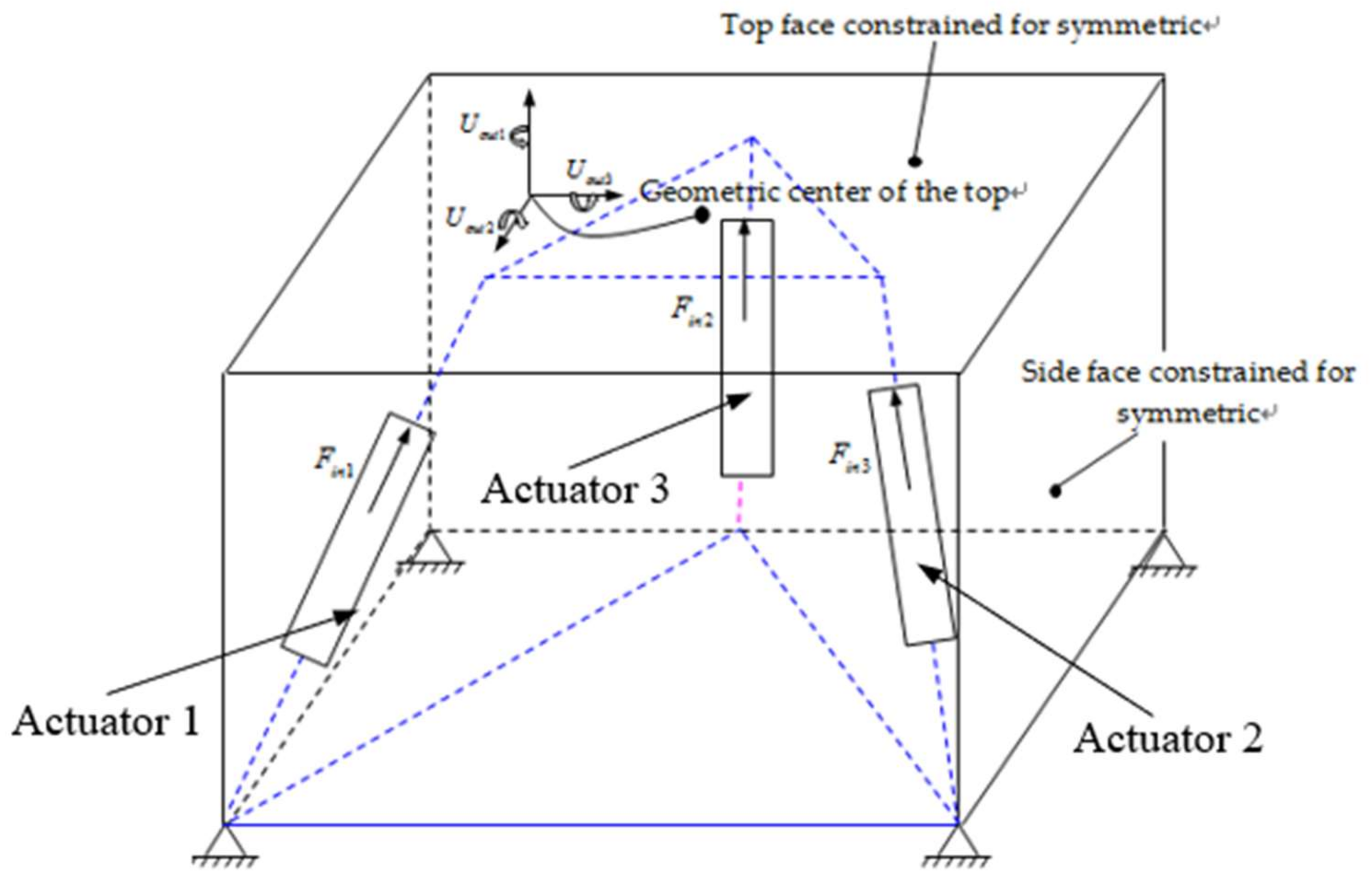
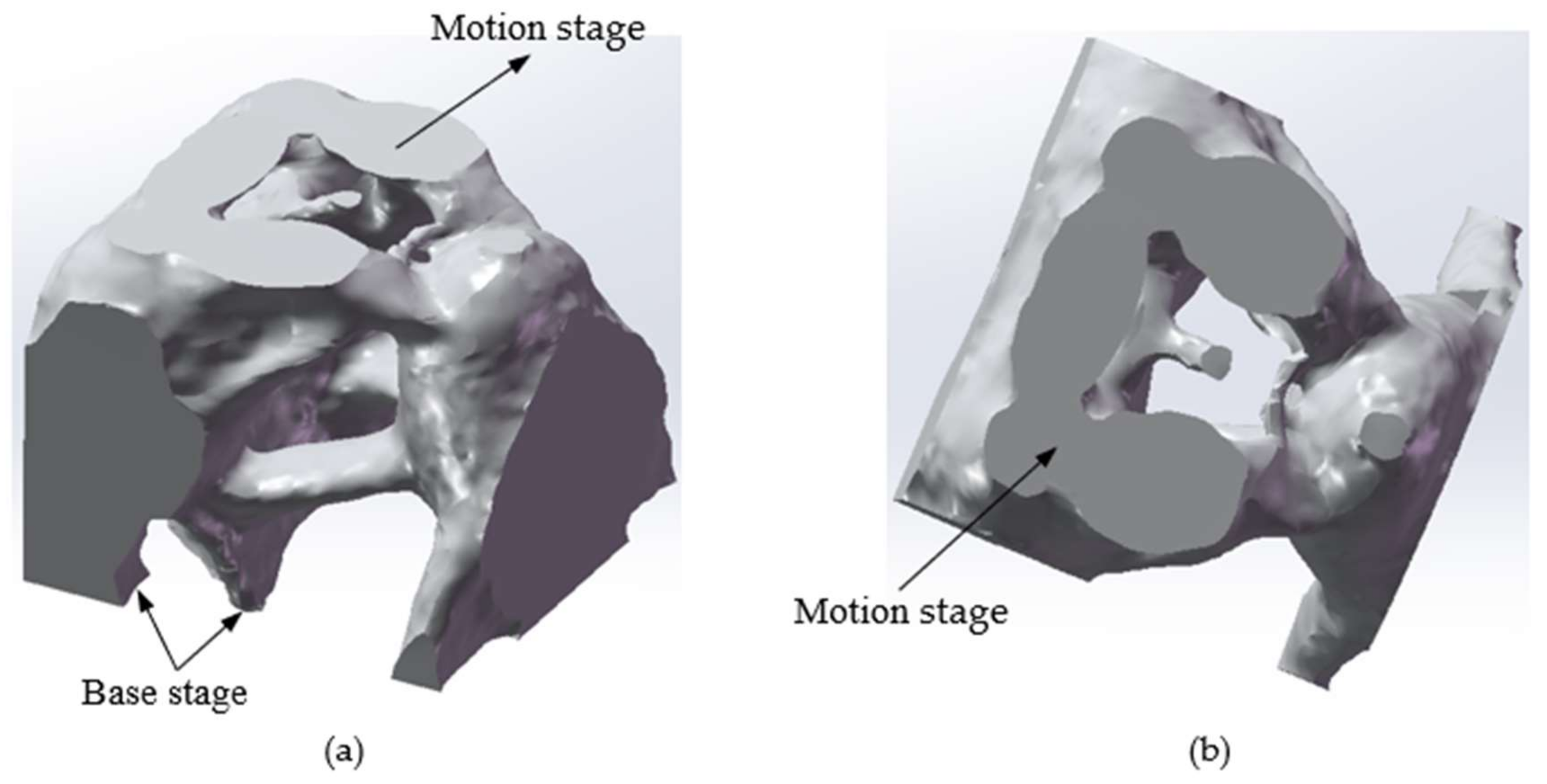





| Structural Parameters | Values | Output | Values |
|---|---|---|---|
| Length of moving platform | Actuator 1 | ||
| Length of fixed platform | Actuator 2 | ||
| Height | Actuator 3 |
| Max | Min | |
|---|---|---|
| Before | 8.769 × 10−2 MPa | 2.152 × 10−6 MPa |
| After | 8.752 × 10−2 MPa | 2.983 × 10−13 Mpa |
| Terms | Values |
|---|---|
| Model of PZT | PSt150 VS10 |
| Nominal stroke (μm) | 9 ± 10% |
| Stiffness (N/μm) | 50 ± 20% |
| Nominal pull/thrust (N) | 550/100 |
| Electrostatic capacity (μF) | 0.35 ± 20% |
| Resonant frequency (kHz) | 40 |
| Length (mm) | 19 ± 0.3 |
| Driving voltage (V) | 0–120 |
| Direction | Simulation (maximum) | Experiment (maximum) | Simulation (minimum) | Experiment (minimum) |
|---|---|---|---|---|
| Rotation around -axis | 0.47 × 10−4 rad | 0.36 × 10−4 rad | −0.21 × 10−4 rad | −0.18 × 10−4 rad |
| Rotation around -axis | 0.51 × 10−4 rad | 0.39 × 10−4 rad | −0.46 × 10−4 rad | −0.12 × 10−4 rad |
| Rotation around -axis | 0.12 × 10−4 rad | 0.18 × 10−4 rad | −0.48 × 10−5 rad | −0.32 × 10−4 rad |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Zhan, W.; Wu, F.; Simeone, A. Topology Optimization of Spatially Compliant Mechanisms with an Isomorphic Matrix of a 3-UPC Type Parallel Prototype Manipulator. Micromachines 2018, 9, 184. https://doi.org/10.3390/mi9040184
Zhu D, Zhan W, Wu F, Simeone A. Topology Optimization of Spatially Compliant Mechanisms with an Isomorphic Matrix of a 3-UPC Type Parallel Prototype Manipulator. Micromachines. 2018; 9(4):184. https://doi.org/10.3390/mi9040184
Chicago/Turabian StyleZhu, Dachang, Wanghu Zhan, Fupei Wu, and Alessandro Simeone. 2018. "Topology Optimization of Spatially Compliant Mechanisms with an Isomorphic Matrix of a 3-UPC Type Parallel Prototype Manipulator" Micromachines 9, no. 4: 184. https://doi.org/10.3390/mi9040184
APA StyleZhu, D., Zhan, W., Wu, F., & Simeone, A. (2018). Topology Optimization of Spatially Compliant Mechanisms with an Isomorphic Matrix of a 3-UPC Type Parallel Prototype Manipulator. Micromachines, 9(4), 184. https://doi.org/10.3390/mi9040184







