Prediction of Necrotic Core and Hypoxic Zone of Multicellular Spheroids in a Microbioreactor with a U-Shaped Barrier
Abstract
:1. Introduction
2. Material and Methods
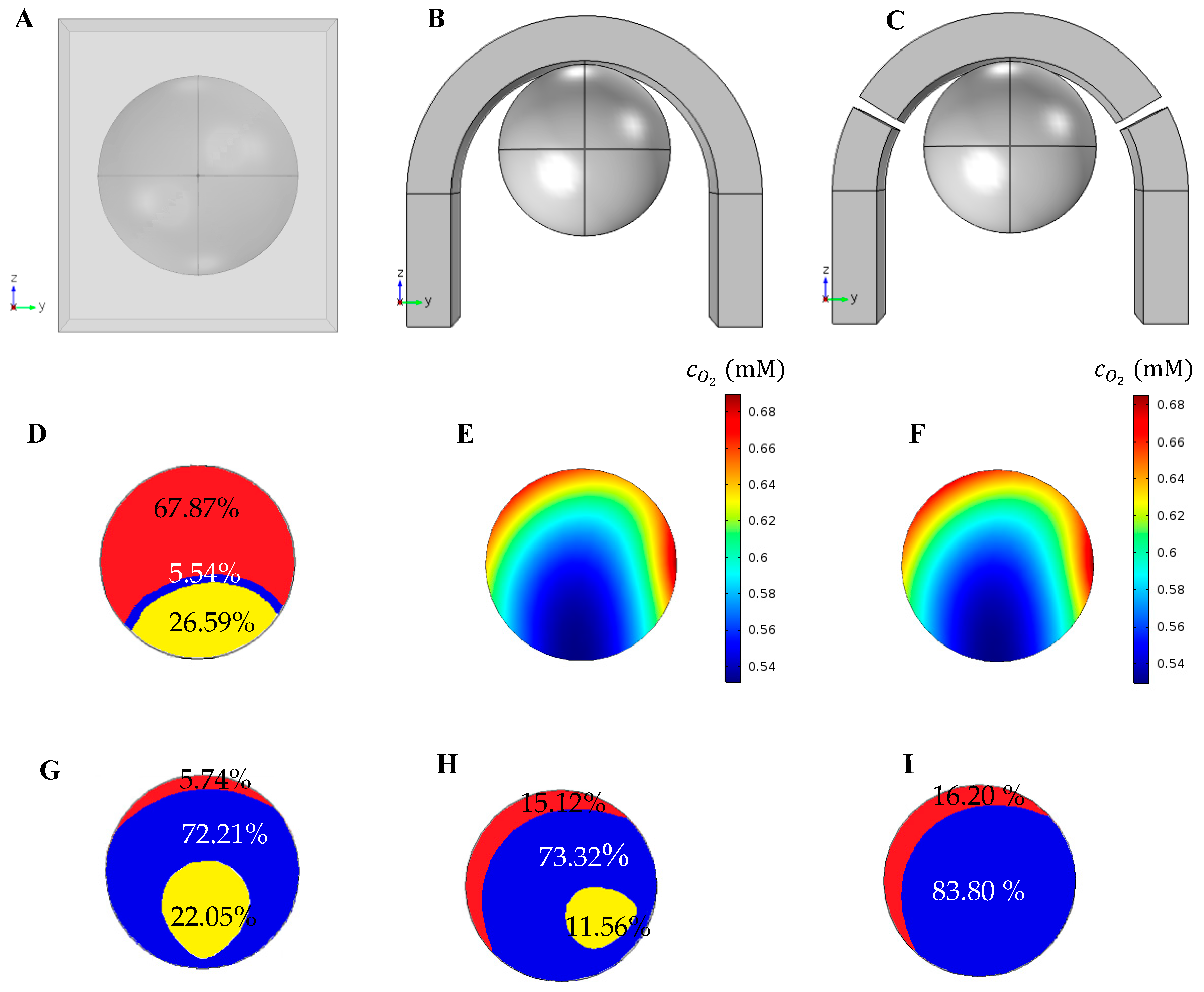
2.1. Geometry
2.2. Governing Equations and Boundary Conditions
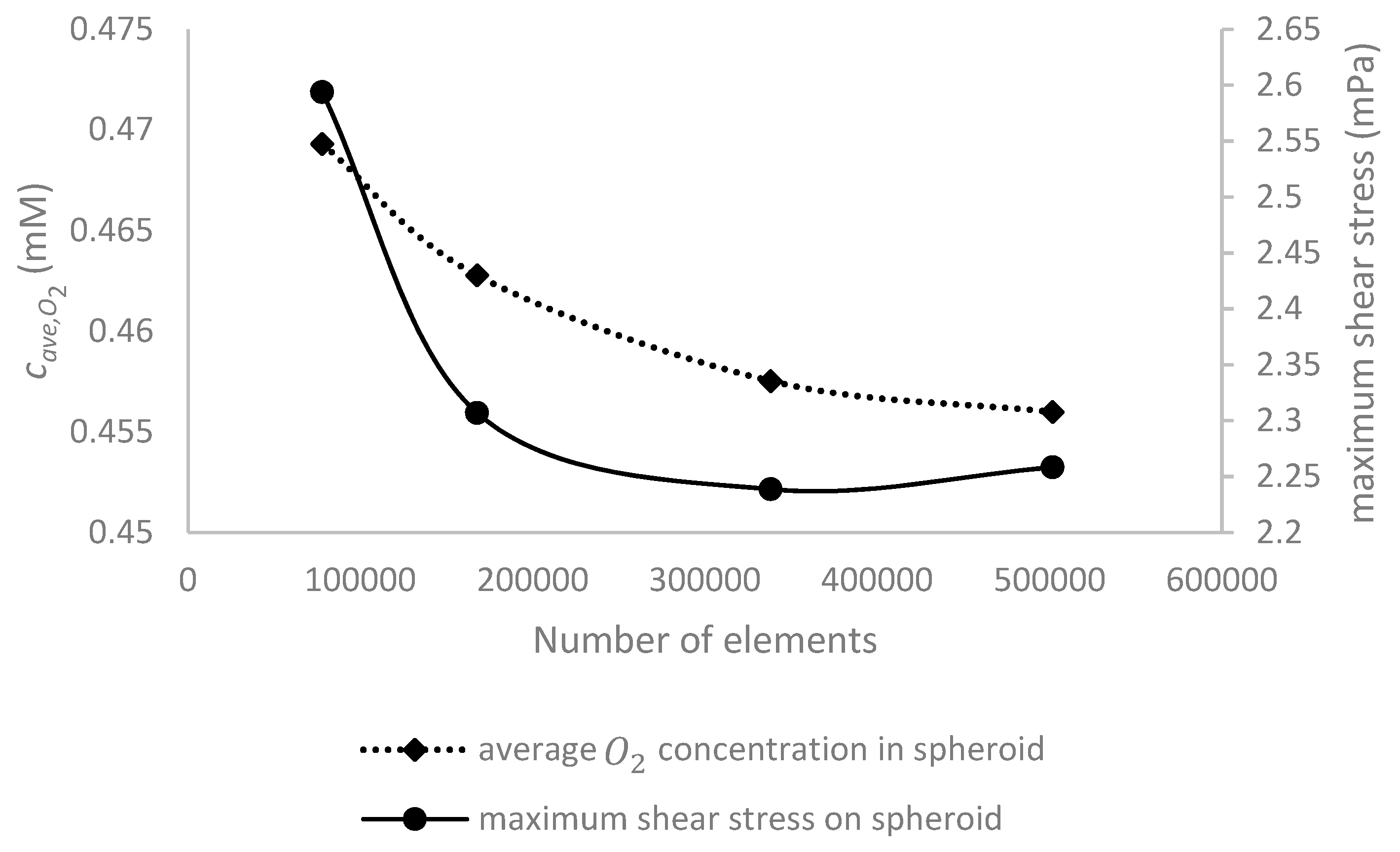
3. Convergence and Grid Independence Study
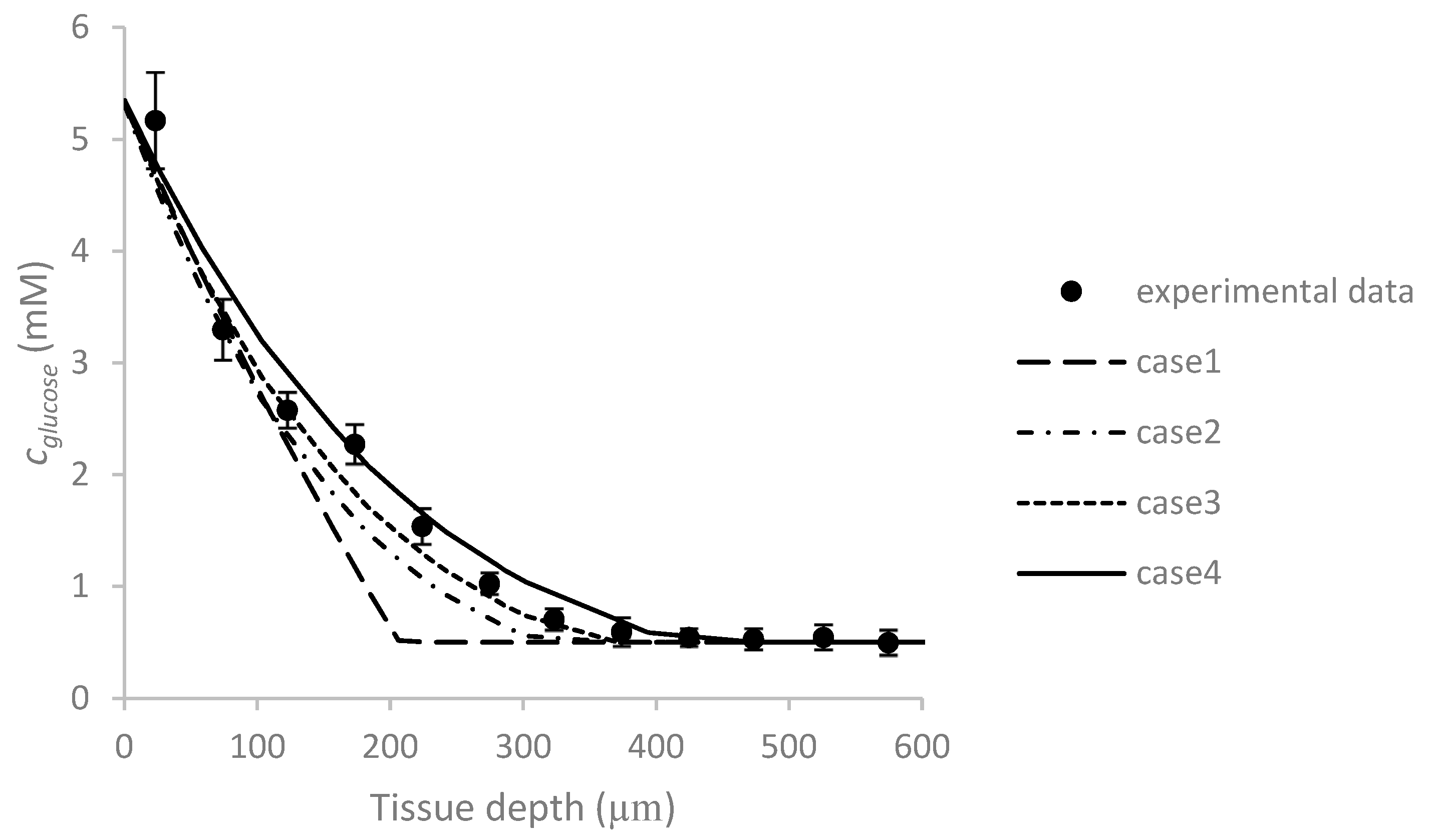
4. Validation
5. Results and Discussion
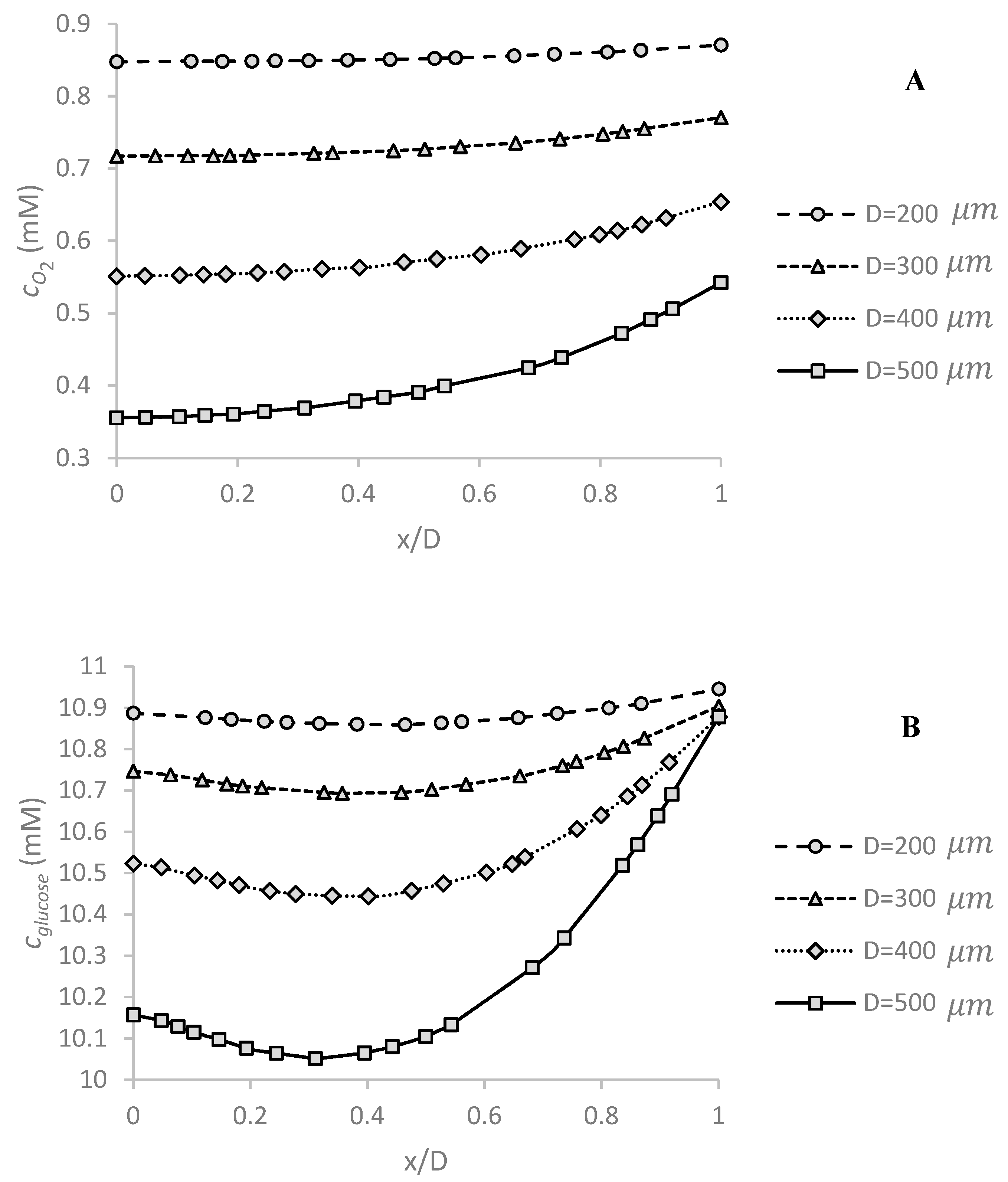
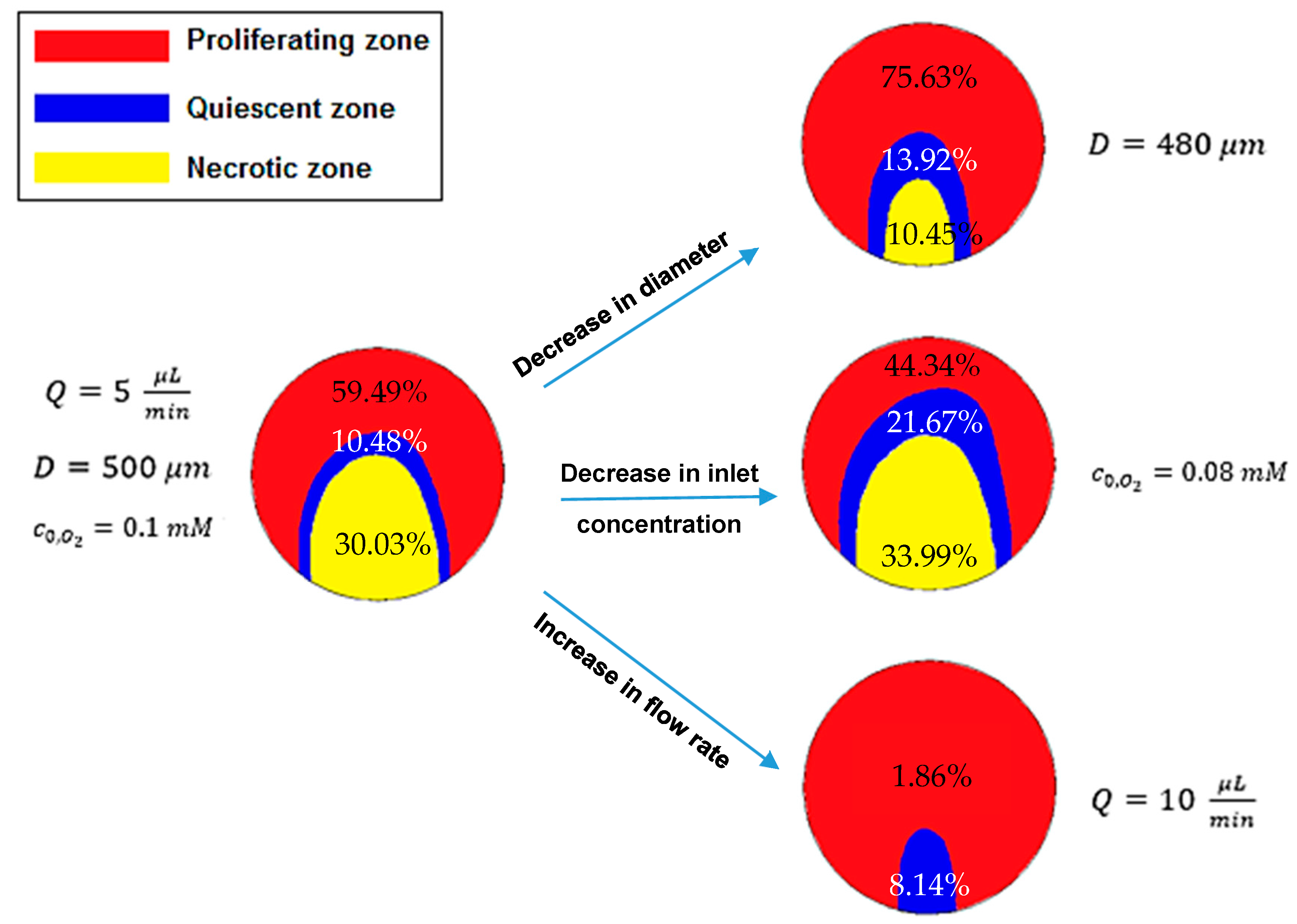
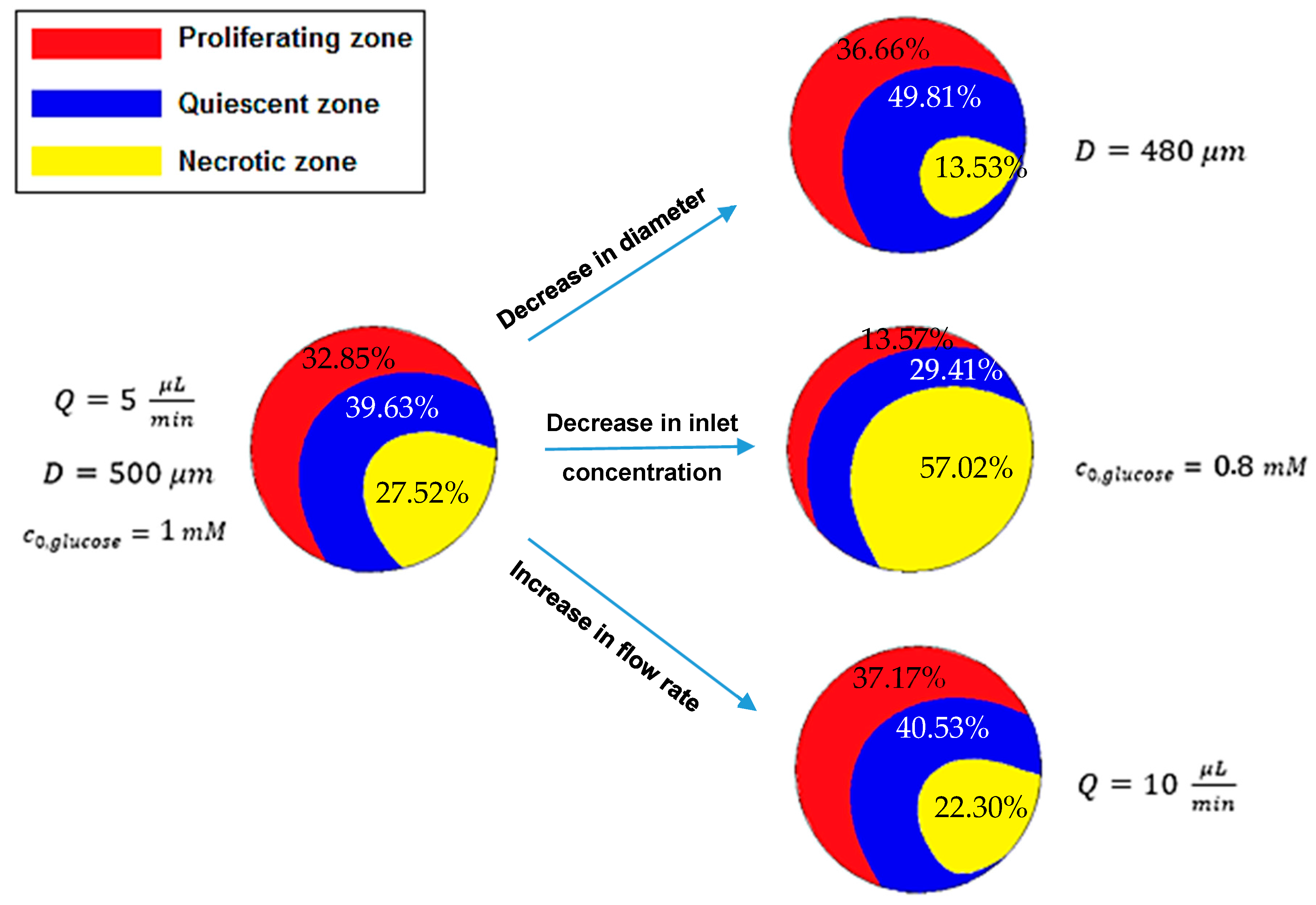
5.1. Effect of Spheroid Diameter on Oxygen and Glucose Concentration Distribution
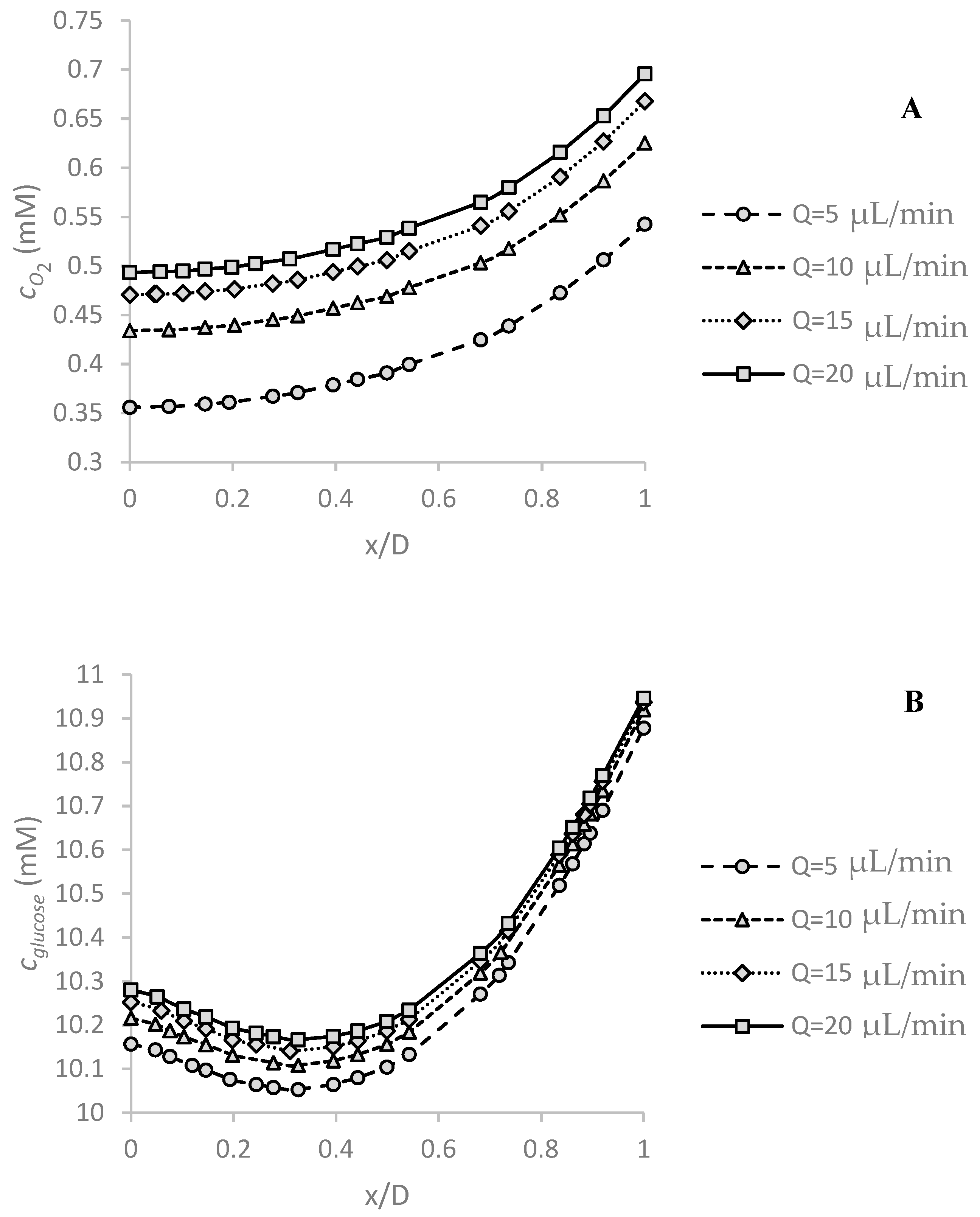
5.2. Effect of Volume Flow Rate of Medium on Oxygen and Glucose Concentration Profile
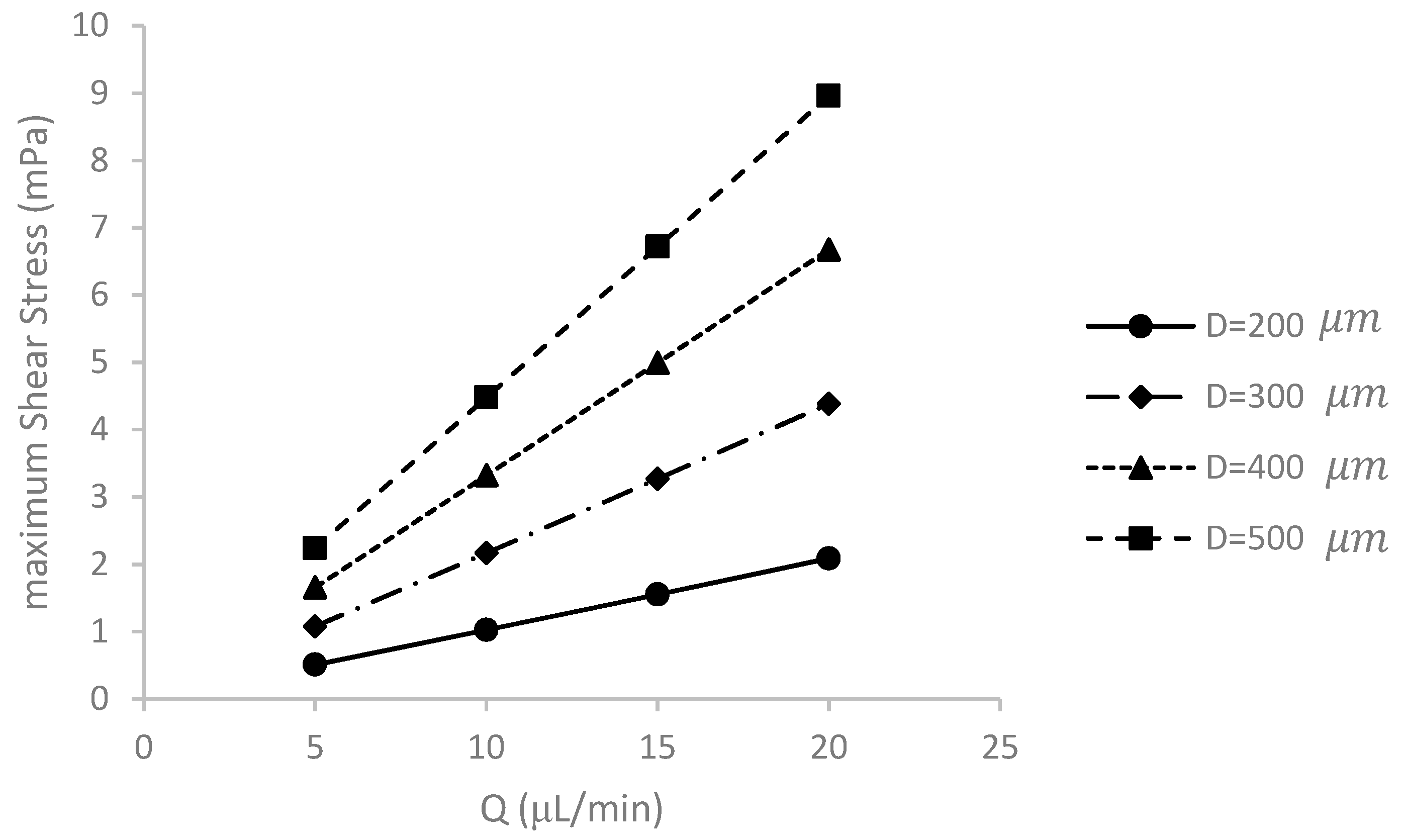
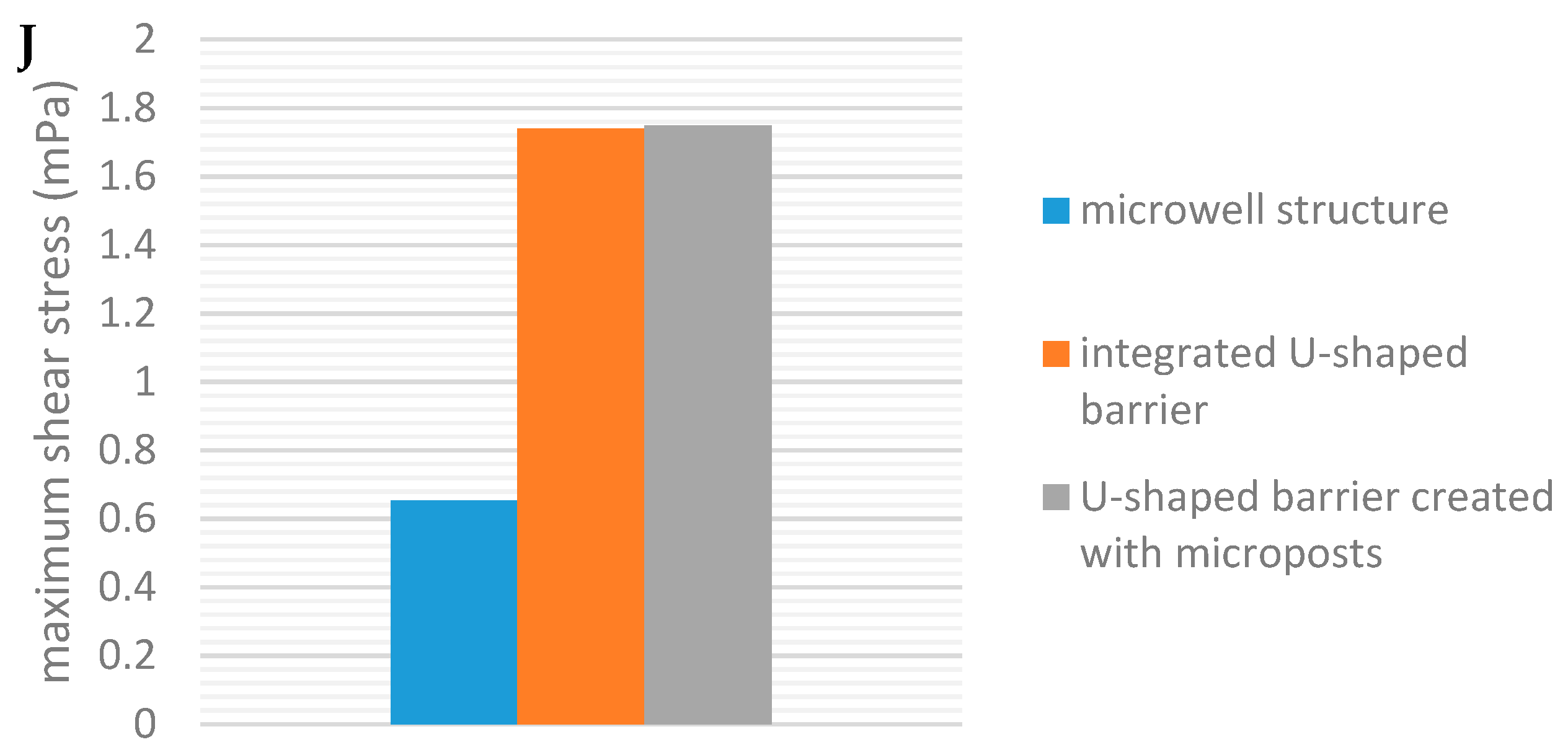
5.3. Effect of Medium Flow Rate and Spheroid Diameter on Maximum Shear Stress Applied to the Spheroid Surface
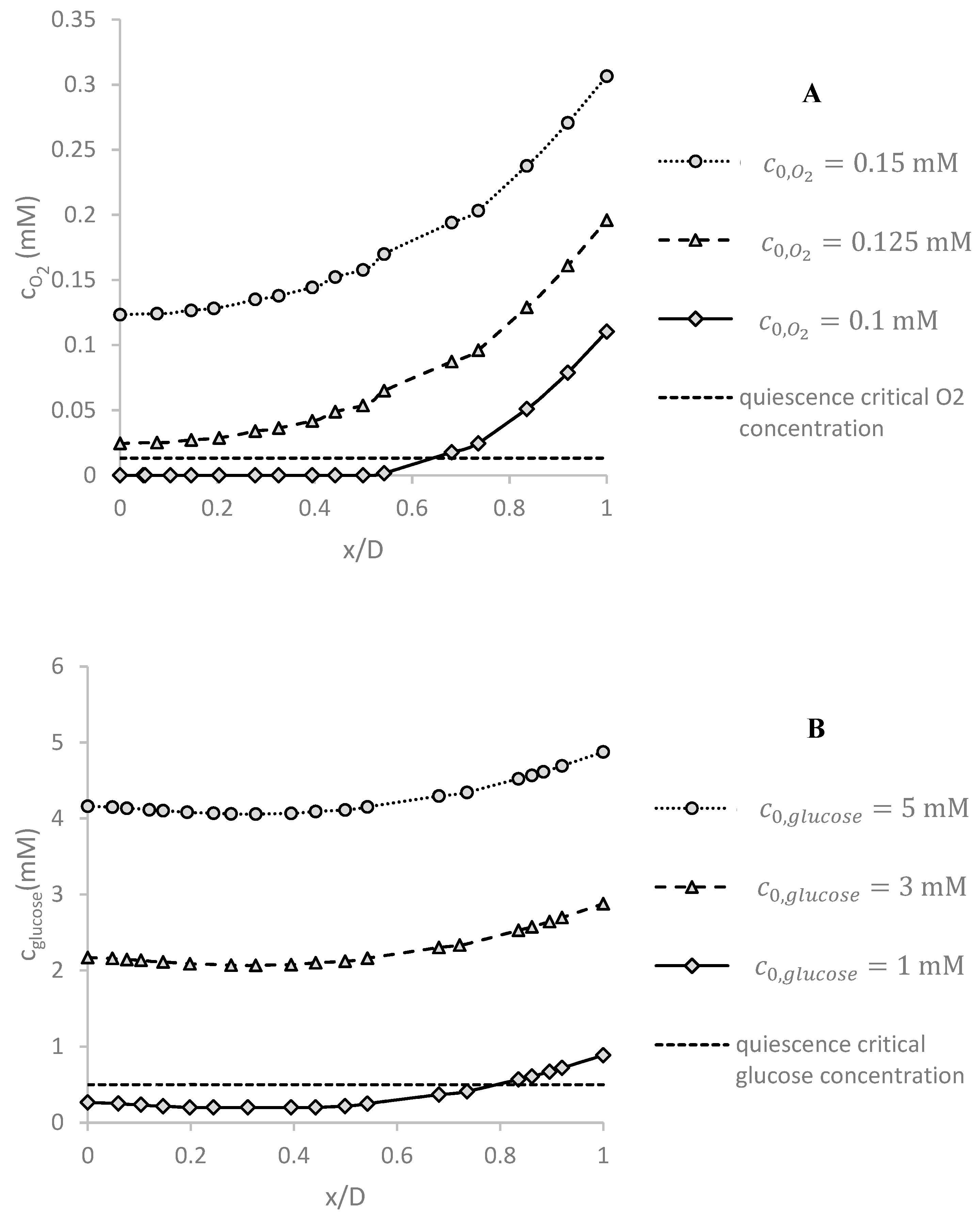
5.4. Effect of the Inlet Concentration on Oxygen and Glucose Concentration Distributions
5.5. Quiescent and Necrotic Zones Based on Oxygen Concentration
5.6. Quiescent and Necrotic Zones Based on Glucose Concentration
5.7. Comparison of the Different Trap Types
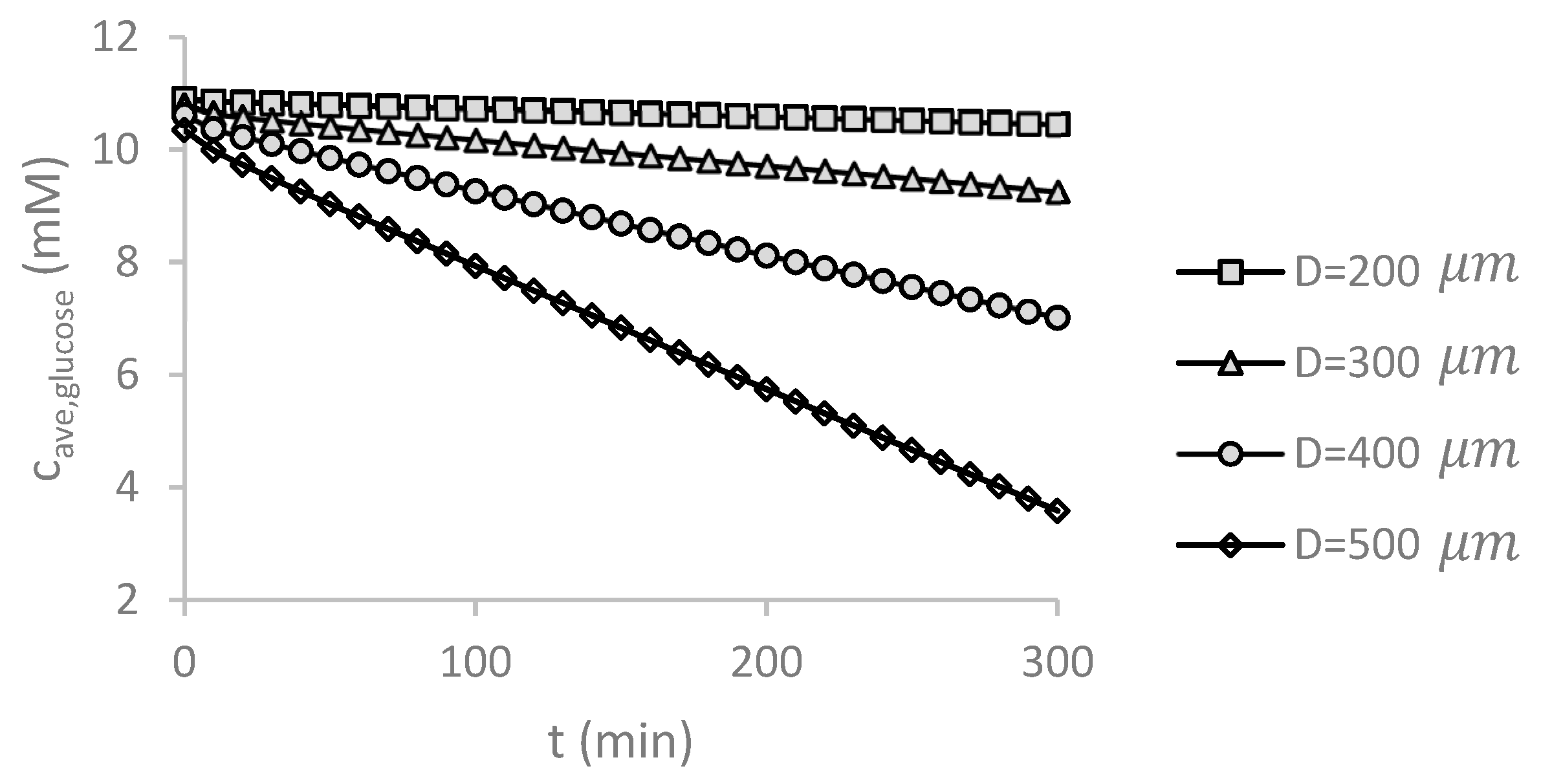
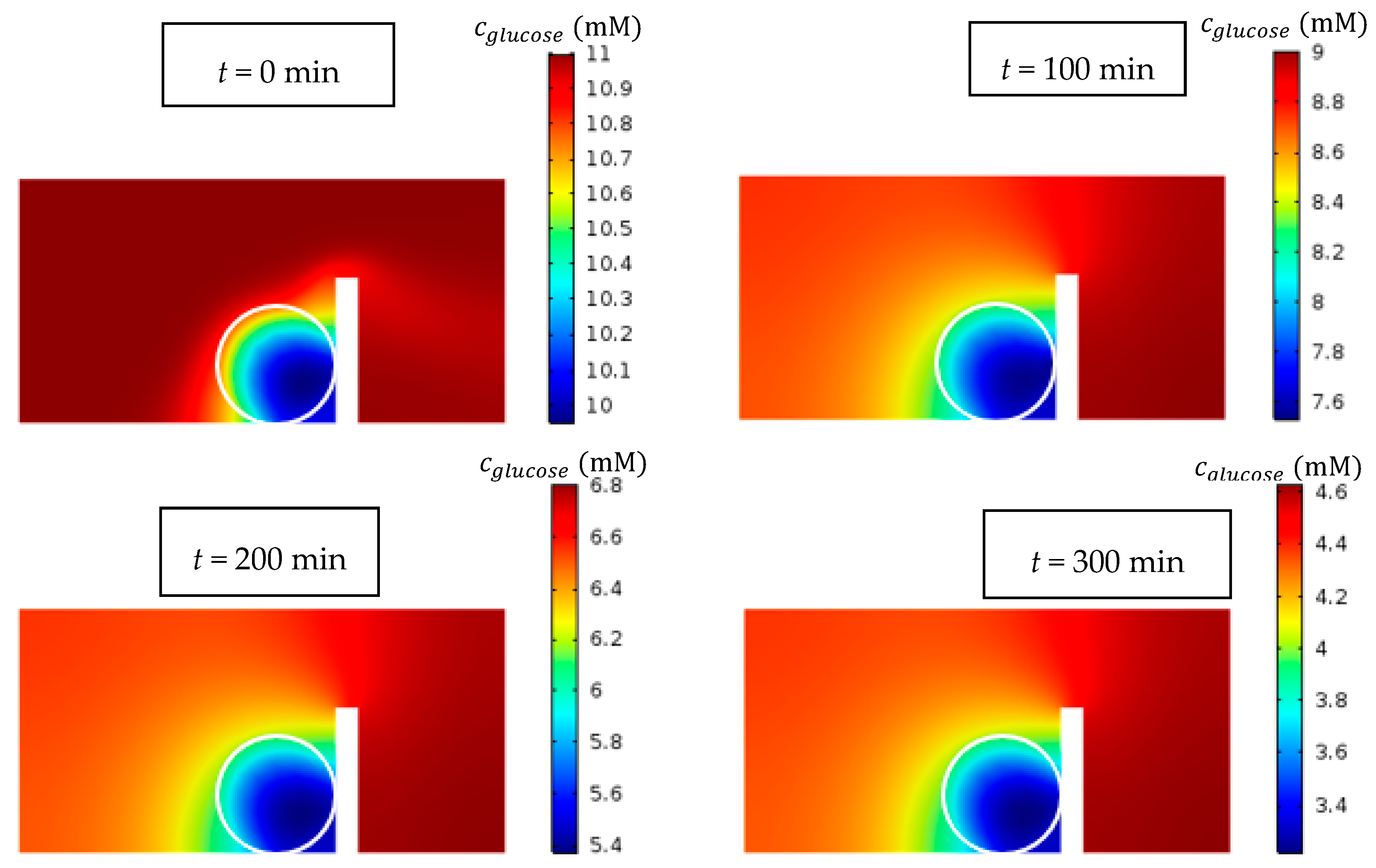
5.8. Temporal Changes in Glucose Concentration without Supplying Medium
6. Limitations of the Simulation
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Nguyen, N.-T.; Hejazian, M.; Ooi, C.H.; Kashaninejad, N. Recent Advances and Future Perspectives on Microfluidic Liquid Handling. Micromachines 2017, 8, 186. [Google Scholar] [CrossRef]
- Kashaninejad, N.; Shiddiky, M.J.A.; Nguyen, N.-T. Advances in microfluidics-based assisted reproductive technology: From sperm sorter to reproductive system-on-a-chip. Adv. Biosyst. 2018, 2, 1700197. [Google Scholar] [CrossRef]
- Portillo-Lara, R.; Annabi, N. Microengineered cancer-on-a-chip platforms to study the metastatic microenvironment. Lab Chip 2016, 16, 4063–4081. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, J.; Sun, Y. Microfluidic approaches for cancer cell detection, characterization, and separation. Lab Chip 2012, 12, 1753–1767. [Google Scholar] [CrossRef] [PubMed]
- Moghadas, H.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.-T. Challenge in particle delivery to cells in a microfluidic device. Drug Deliv. Transl. Res. 2017. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-T.; Shaegh, S.A.M.; Kashaninejad, N.; Phan, D.-T. Design, fabrication and characterization of drug delivery systems based on lab-on-a-chip technology. Adv. Drug Deliv. Rev. 2013, 65, 1403–1419. [Google Scholar] [CrossRef] [PubMed]
- Kashaninejad, N.; Nikmaneshi, M.R.; Moghadas, H.; Kiyoumarsi Oskouei, A.; Rismanian, M.; Barisam, M.; Saidi, M.S.; Firoozabadi, B. Organ-Tumor-on-a-Chip for Chemosensitivity Assay: A Critical Review. Micromachines 2016, 7, 130. [Google Scholar] [CrossRef]
- Asghar, W.; El Assal, R.; Shafiee, H.; Pitteri, S.; Paulmurugan, R.; Demirci, U. Engineering cancer microenvironments for in vitro 3-D tumor models. Mater. Today 2015, 18, 539–553. [Google Scholar] [CrossRef] [PubMed]
- Grimes, D.R.; Kelly, C.; Bloch, K.; Partridge, M. A method for estimating the oxygen consumption rate in multicellular tumour spheroids. J. R. Soc. Interface 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Moghadas, H.; Saidi, M.S.; Kashaninejad, N.; Kiyoumarsioskouei, A.; Nguyen, N.-T. Fabrication and characterization of low-cost, bead-free, durable and hydrophobic electrospun membrane for 3D cell culture. Biomed. Microdevices 2017, 19, 74. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Hartanto, Y.; Zhang, H. Advances in multicellular spheroids formation. J. R. Soc. Interface 2017, 14, 20160877. [Google Scholar] [CrossRef] [PubMed]
- Bhise, N.S.; Ribas, J.; Manoharan, V.; Zhang, Y.S.; Polini, A.; Massa, S.; Dokmeci, M.R.; Khademhosseini, A. Organ-on-a-chip platforms for studying drug delivery systems. J. Control. Release 2014, 190, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Moshksayan, K.; Kashaninejad, N.; Warkiani Ebrahimi, M.; Lock, G.J.; Moghadas, H.; Firoozabadi, B.; Saidi, M.S.; Nguyen, N.-T. Spheroids-on-a-chip: Recent advances and design considerations in microfluidic platforms for spheroid formation and culture. Sens. Actuators B Chem. 2018, 263, 151–176. [Google Scholar] [CrossRef]
- Liu, W.; Xu, J.; Li, T.; Zhao, L.; Ma, C.; Shen, S.; Wang, J. Monitoring tumor response to anticancer drugs using stable three-dimensional culture in a recyclable microfluidic platform. Anal. Chem. 2015, 87, 9752–9760. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.Y.; Di Carlo, D.; Lee, L.P. Microfluidic self-assembly of tumor spheroids for anticancer drug discovery. Biomed. Microdevices 2008, 10, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.-Y.; Tseng, S.-Y.; Yang, S.-M.; Hsu, L.; Liu, C.-H.; Chang, H.-Y. A microfluidic chip with a U-shaped microstructure array for multicellular spheroid formation, culturing and analysis. Biofabrication 2014, 6, 015009. [Google Scholar] [CrossRef] [PubMed]
- Sutherland, R.; Carlsson, J.; Durand, R.; Yuhas, J. Spheroids in cancer research. Cancer Res. 1981, 41, 2980–2984. [Google Scholar]
- Xu, J.; Vilanova, G.; Gomez, H. A mathematical model coupling tumor growth and angiogenesis. PLoS ONE 2016, 11, e0149422. [Google Scholar] [CrossRef] [PubMed]
- Harris, A.L. Hypoxia—A key regulatory factor in tumour growth. Nat. Rev. Cancer 2002, 2, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Vaupel, P.; Thews, O.; Hoeckel, M. Treatment resistance of solid tumors. Med. Oncol. 2001, 18, 243–259. [Google Scholar] [CrossRef]
- Curcio, E.; Salerno, S.; Barbieri, G.; De Bartolo, L.; Drioli, E.; Bader, A. Mass transfer and metabolic reactions in hepatocyte spheroids cultured in rotating wall gas-permeable membrane system. Biomaterials 2007, 28, 5487–5497. [Google Scholar] [CrossRef] [PubMed]
- Däster, S.; Amatruda, N.; Calabrese, D.; Ivanek, R.; Turrini, E.; Droeser, R.A.; Zajac, P.; Fimognari, C.; Spagnoli, G.C.; Iezzi, G. Induction of hypoxia and necrosis in multicellular tumor spheroids is associated with resistance to chemotherapy treatment. Oncotarget 2017, 8, 1725. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Li, D. Three-dimensional modeling of transport of nutrients for multicellular tumor spheroid culture in a microchannel. Biomed. Microdevices 2007, 9, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Anada, T.; Fukuda, J.; Sai, Y.; Suzuki, O. An oxygen-permeable spheroid culture system for the prevention of central hypoxia and necrosis of spheroids. Biomaterials 2012, 33, 8430–8441. [Google Scholar] [CrossRef] [PubMed]
- Astolfi, M.; Péant, B.; Lateef, M.; Rousset, N.; Kendall-Dupont, J.; Carmona, E.; Monet, F.; Saad, F.; Provencher, D.; Mes-Masson, A.-M. Micro-dissected tumor tissues on chip: An ex vivo method for drug testing and personalized therapy. Lab Chip 2016, 16, 312–325. [Google Scholar] [CrossRef] [PubMed]
- Grist, S.M.; Schmok, J.C.; Gaxiola, A.D.; Cheung, K.C. Microfluidic platform with integrated thin-film optical oxygen sensors for transient hypoxia. In Proceedings of the 14th IEEE International New Circuits and Systems Conference (NEWCAS), Vancouver, BC, Canada, 26–29 June 2016; pp. 1–4. [Google Scholar]
- Barisam, M.; Saidi, M.; Kashaninejad, N.; Vadivelu, R.; Nguyen, N.-T. Numerical Simulation of the Behavior of Toroidal and Spheroidal Multicellular Aggregates in Microfluidic Devices with Microwell and U-Shaped Barrier. Micromachines 2017, 8, 358. [Google Scholar] [CrossRef]
- Kashaninejad, N.; Chan, W.K.; Nguyen, N.-T. Fluid mechanics of flow through rectangular hydrophobic microchannels. In Proceedings of the ASME 9th International Conference on Nanochannels, Microchannels, and Minichannels, Edmonton, AL, Canada, 19–22 June 2011; pp. 647–655. [Google Scholar] [CrossRef]
- Lin, S. Oxygen diffusion in a spherical cell with nonlinear oxygen uptake kinetics. J. Theor. Biol. 1976, 60, 449–457. [Google Scholar] [CrossRef]
- Buchwald, P. FEM-based oxygen consumption and cell viability models for avascular pancreatic islets. Theor. Biol. Med. Model. 2009, 6, 5. [Google Scholar] [CrossRef] [PubMed]
- Panteli, J.T.; Forbes, N.S. Engineered bacteria detect spatial profiles in glucose concentration within solid tumor cell masses. Biotechnol. Bioeng. 2016, 113, 2474–2484. [Google Scholar] [CrossRef] [PubMed]
- Rivenzon-Segal, D.; Rushkin, E.; Polak-Charcon, S.; Degani, H. Glucose transporters and transport kinetics in retinoic acid-differentiated T47D human breast cancer cells. Am. J. Physiol.-Endocrinol. Metab. 2000, 279, E508–E519. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Qu, H.; Hu, G.; Zhang, Q.; Song, K.; Guan, H.; Liu, T.; Qin, J. A microfluidic-based multi-shear device for investigating the effects of low fluid-induced stresses on osteoblasts. PLoS ONE 2014, 9, e89966. [Google Scholar] [CrossRef] [PubMed]
- Shemesh, J.; Jalilian, I.; Shi, A.; Yeoh, G.H.; Tate, M.L.K.; Warkiani, M.E. Flow-induced stress on adherent cells in microfluidic devices. Lab Chip 2015, 15, 4114–4127. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-W.; Stantz, K.M. Development of a mathematical model to estimate intra-tumor oxygen concentrations through multi-parametric imaging. Biomed. Eng. Online 2016, 15, 114. [Google Scholar] [CrossRef] [PubMed]
- Hirschhaeuser, F.; Menne, H.; Dittfeld, C.; West, J.; Mueller-Klieser, W.; Kunz-Schughart, L.A. Multicellular tumor spheroids: An underestimated tool is catching up again. J. Biotechnol. 2010, 148, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Jackson, A.R.; Huang, C.-Y.C.; Brown, M.D.; Gu, W.Y. 3D finite element analysis of nutrient distributions and cell viability in the intervertebral disc: Effects of deformation and degeneration. J. Biomech. Eng. 2011, 133, 091006. [Google Scholar] [CrossRef] [PubMed]
- Ong, L.J.Y.; Islam, A.B.; DasGupta, R.; Iyer, N.G.; Leo, H.L.; Toh, Y.C. A 3D printed microfluidic perfusion device for multicellular spheroid cultures. Biofabrication 2017, 9, 045005. [Google Scholar] [CrossRef] [PubMed]
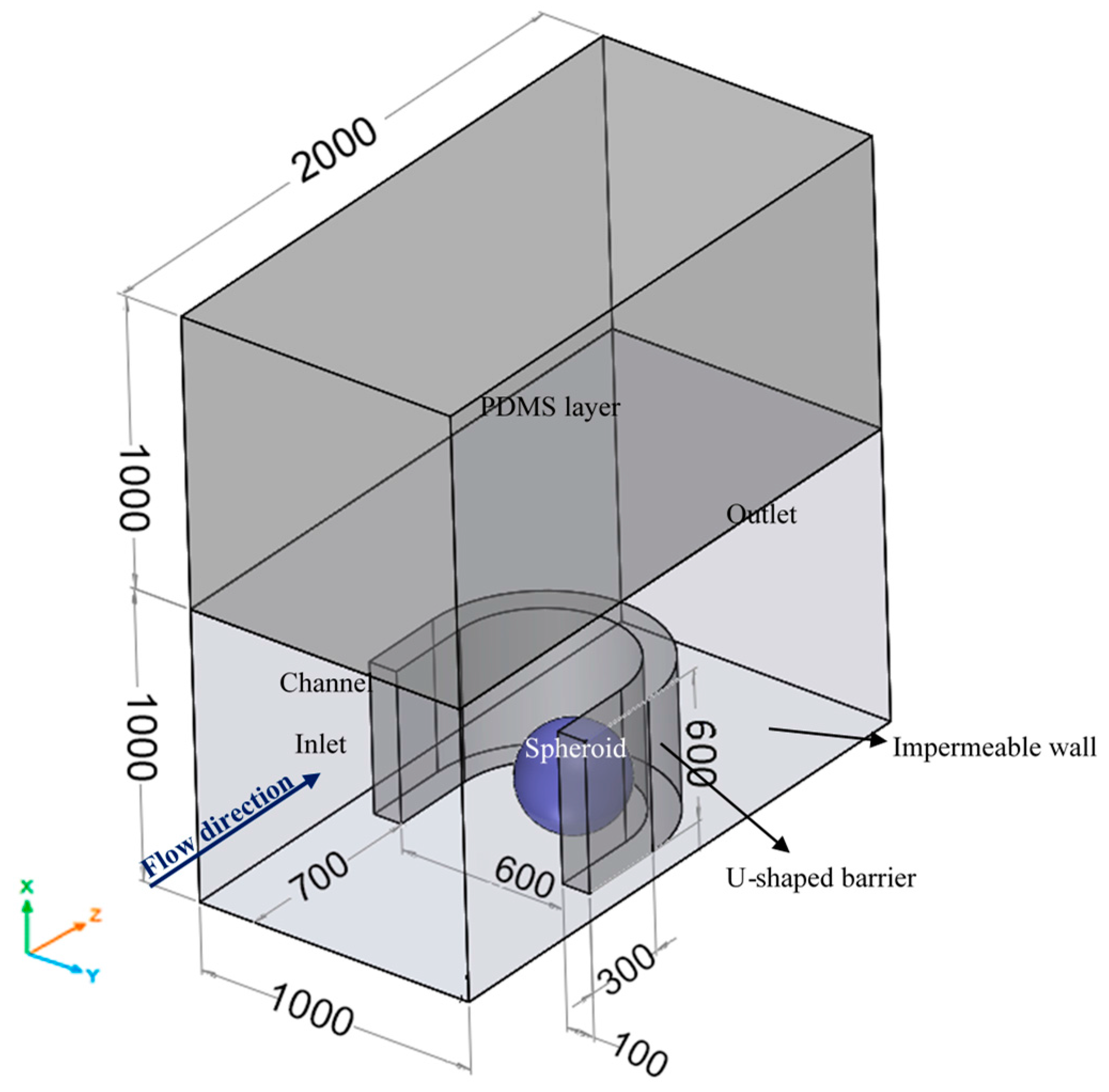
| Parameters | Values (μm) | Parameters | Values (μm) |
|---|---|---|---|
| Width of the channel | 1000 | Length of the rectangular cubes in barrier | 300 |
| Height of the channel | 1000 | Position of the barrier (center of cylinder) | (0,500,1000) |
| Length of the channel | 2000 | Spheroid diameter (D) | 200, 300, 400, 500 |
| Inner radius of the barrier (half of a cylinder and two rectangular cubes) | 300 | Position of spheroid (center) | (D/2,500,1300 − D/2) |
| Thickness of the barrier | 100 | Thickness of the top PDMS layer | 1000 |
| Height of the barrier | 600 | - | - |
| Parameters | Values | Descriptions |
|---|---|---|
| 993.3 kg/m3 | Density of water at 37 °C | |
| 0.000692 Pa·s | Viscosity of water at 37 °C | |
| 2.6 × 10−9 m2/s | Diffusion coefficient of O2 through H2O | |
| 3.4 × 10−9 m2/s | Diffusion coefficient of O2 through PDMS | |
| 1.83 × 10−9 m2/s | Diffusion coefficient of O2 through cancerous tissue | |
| 9.27 × 10−10 m2/s | Diffusion coefficient of glucose through H2O | |
| 2.7 × 10−10 m2/s | Diffusion coefficient of glucose through cancerous tissue | |
| 6.8 | Solubility of O2 in PDMS vs. H2O | |
| 4.81 | Solubility of O2 in cancerous tissue vs. H2O | |
| 1 | Solubility of glucose in cancerous tissue vs. H2O | |
| 0.0203 mM/s | Maximum reaction rate of O2 | |
| 0.01076 mM/s | Maximum reaction rate of glucose | |
| 0.00463 mM | Michaelis constant of O2 | |
| 0.04 mM | Michaelis constant of glucose |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barisam, M.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.-T. Prediction of Necrotic Core and Hypoxic Zone of Multicellular Spheroids in a Microbioreactor with a U-Shaped Barrier. Micromachines 2018, 9, 94. https://doi.org/10.3390/mi9030094
Barisam M, Saidi MS, Kashaninejad N, Nguyen N-T. Prediction of Necrotic Core and Hypoxic Zone of Multicellular Spheroids in a Microbioreactor with a U-Shaped Barrier. Micromachines. 2018; 9(3):94. https://doi.org/10.3390/mi9030094
Chicago/Turabian StyleBarisam, Maryam, Mohammad Said Saidi, Navid Kashaninejad, and Nam-Trung Nguyen. 2018. "Prediction of Necrotic Core and Hypoxic Zone of Multicellular Spheroids in a Microbioreactor with a U-Shaped Barrier" Micromachines 9, no. 3: 94. https://doi.org/10.3390/mi9030094
APA StyleBarisam, M., Saidi, M. S., Kashaninejad, N., & Nguyen, N.-T. (2018). Prediction of Necrotic Core and Hypoxic Zone of Multicellular Spheroids in a Microbioreactor with a U-Shaped Barrier. Micromachines, 9(3), 94. https://doi.org/10.3390/mi9030094







