Compensation of Hysteresis on Piezoelectric Actuators Based on Tripartite PI Model
Abstract
:1. Introduction
2. Causes of Hysteresis
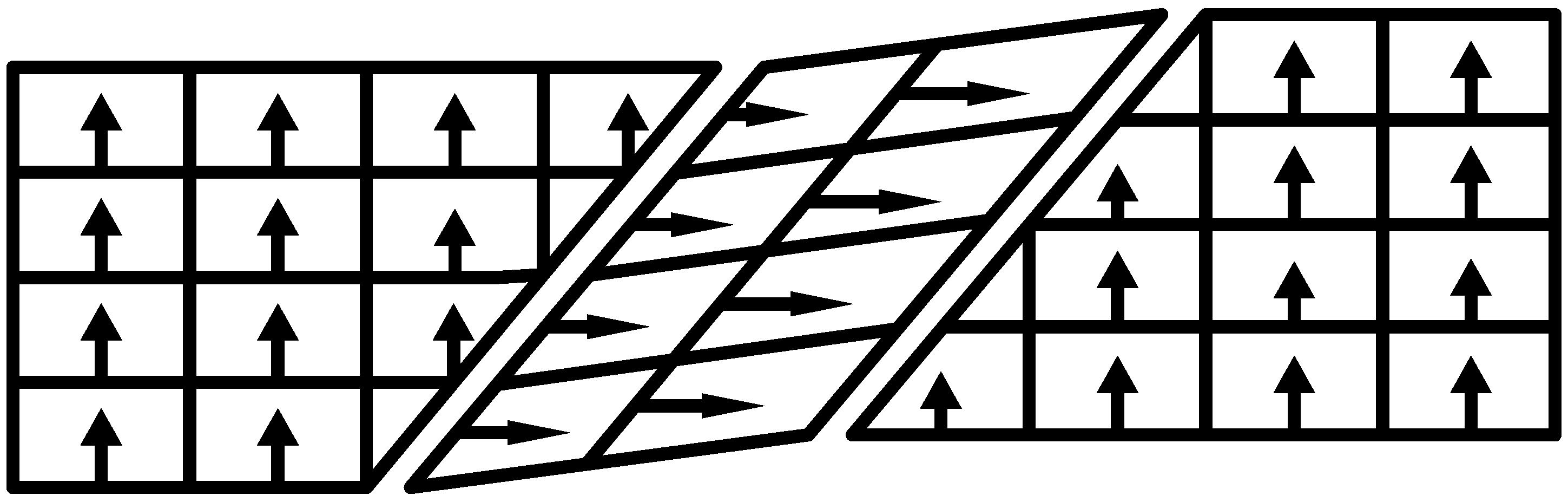
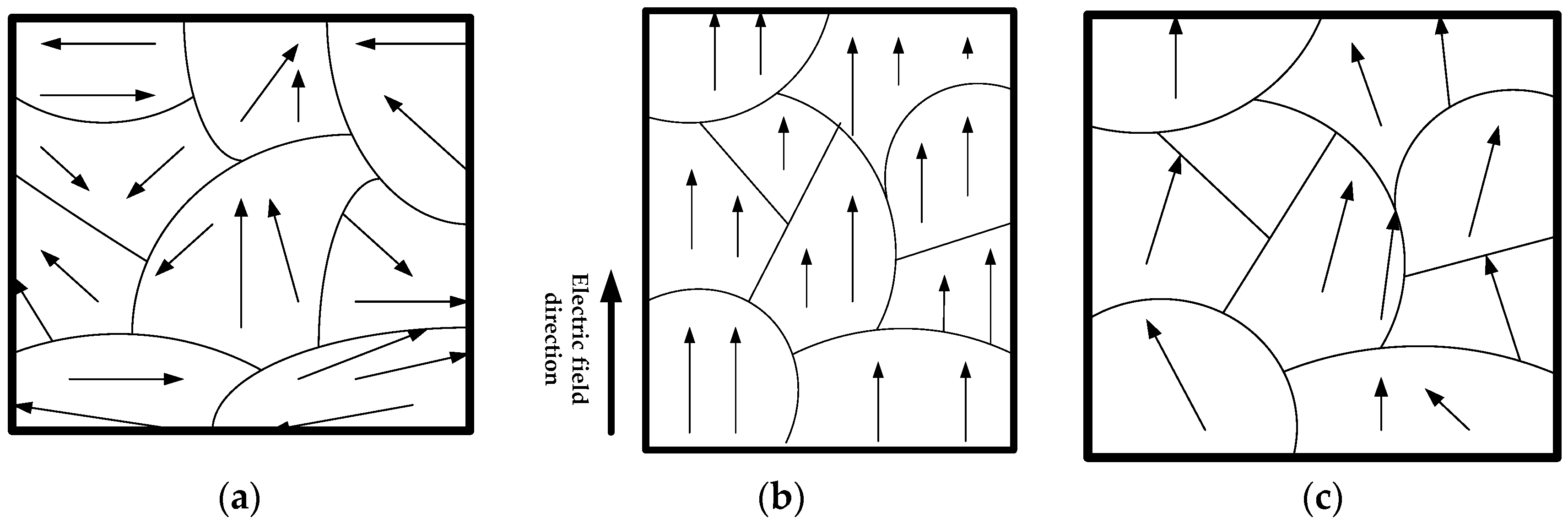
2.1. Micromechanism
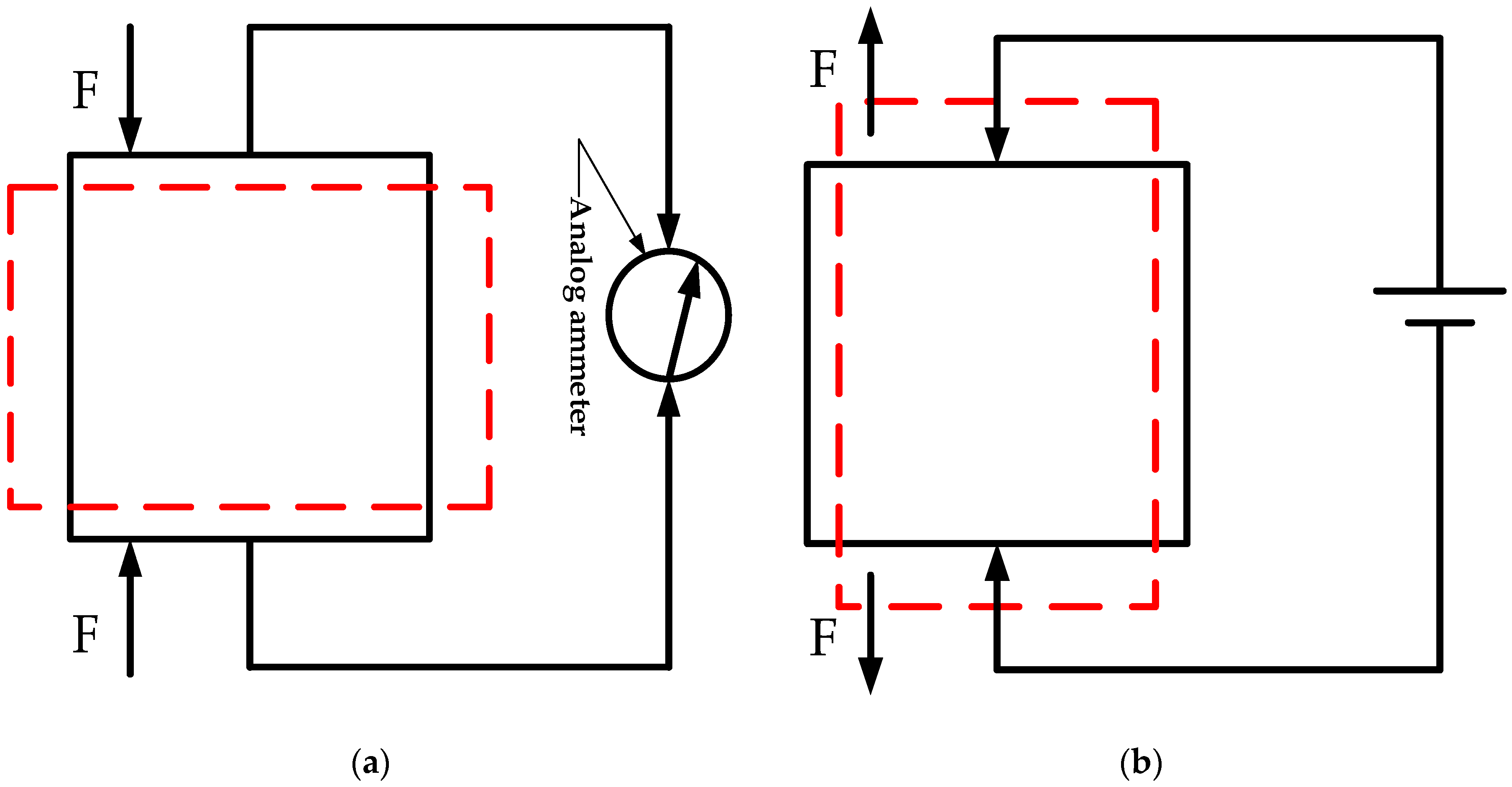
2.2. Analysis of the Causes of Hysteresis
3. Piezoelectric Ceramic Deformation Speed Law
3.1. Derivation of Deformation Speed Law
3.2. Analysis of Deformation Speed Law
4. Hysteresis Modeling
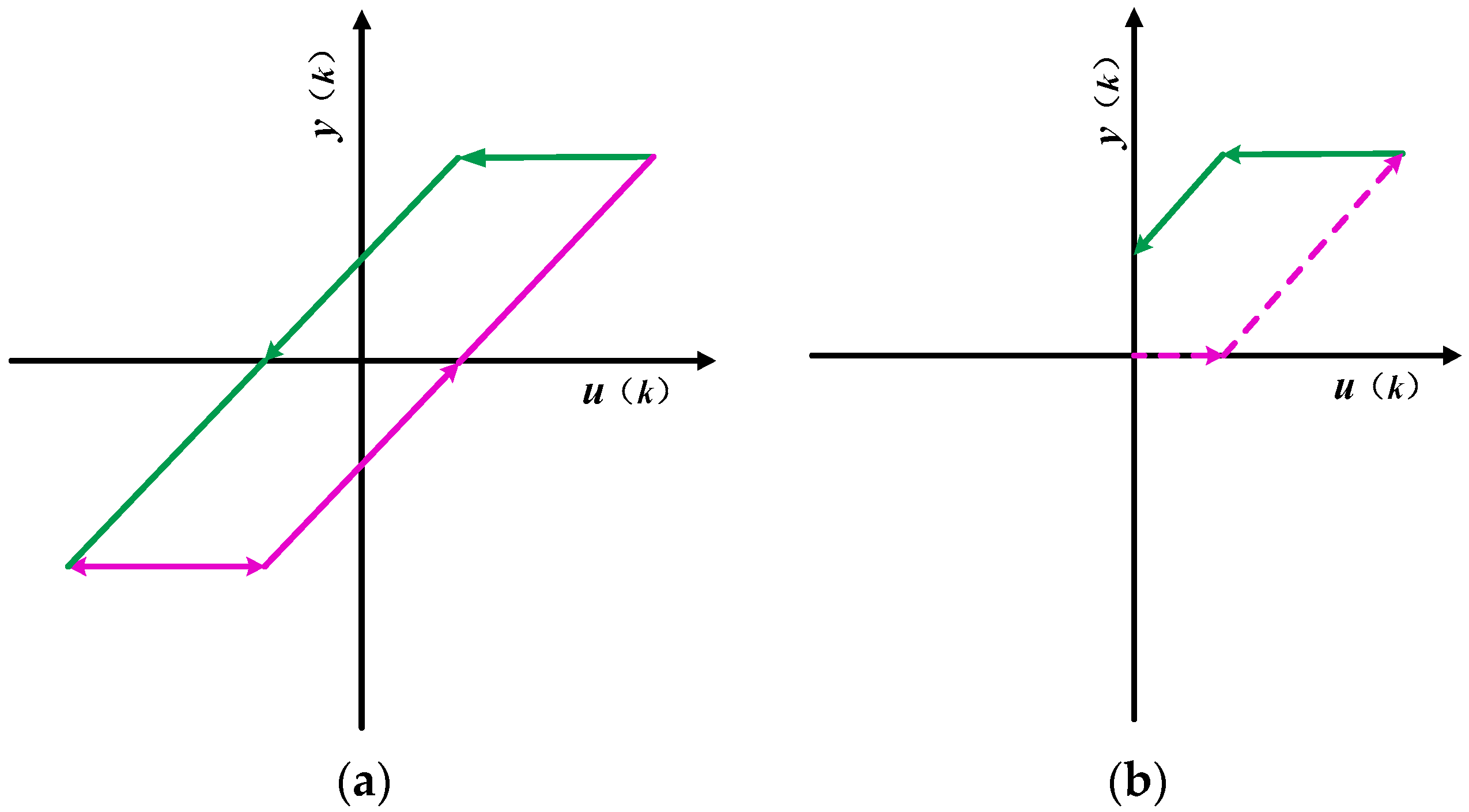
4.1. Play Operator and Prandtle–Ishlinskii Model
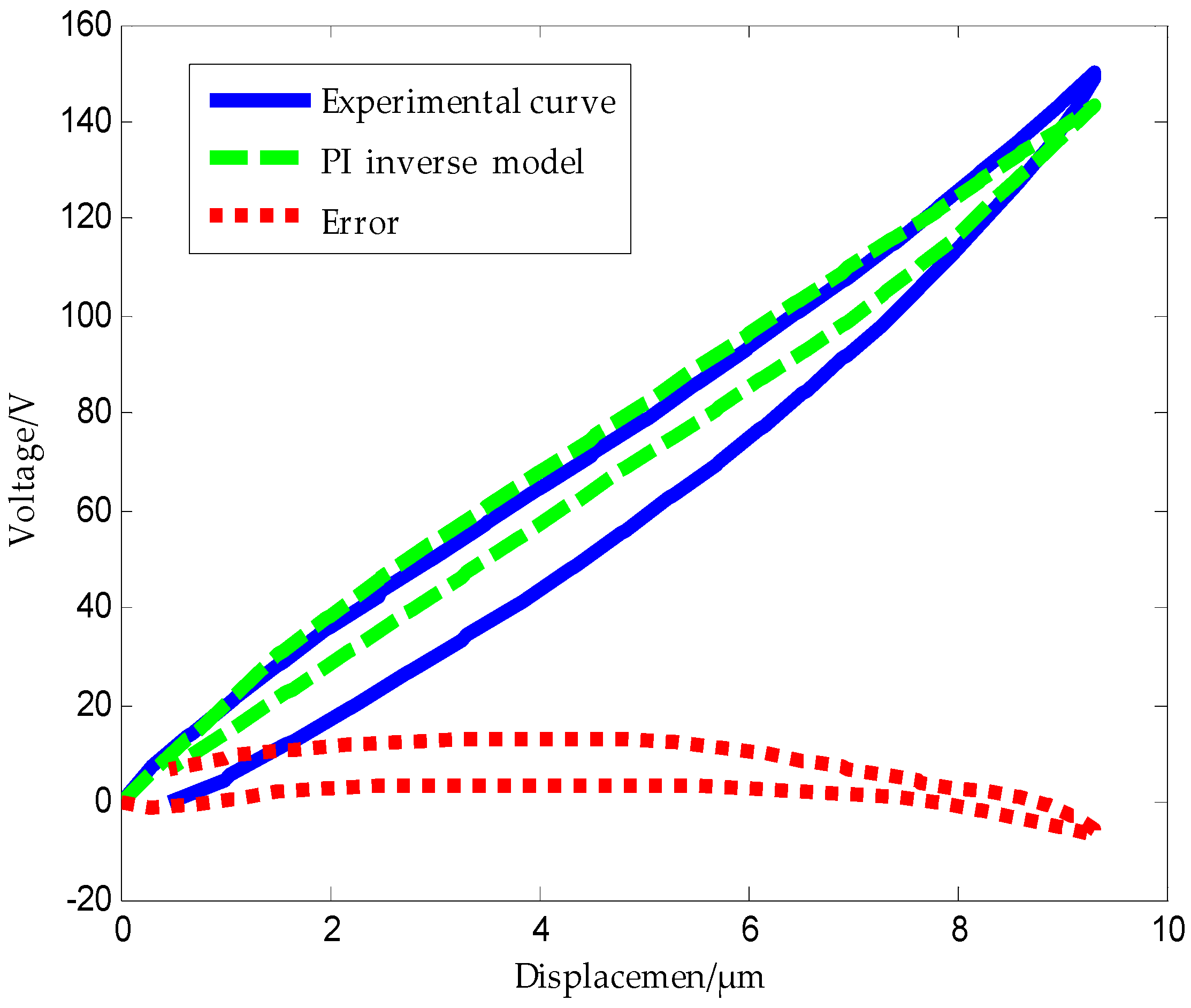
4.2. Traditional PI Modeling and Inverse Model
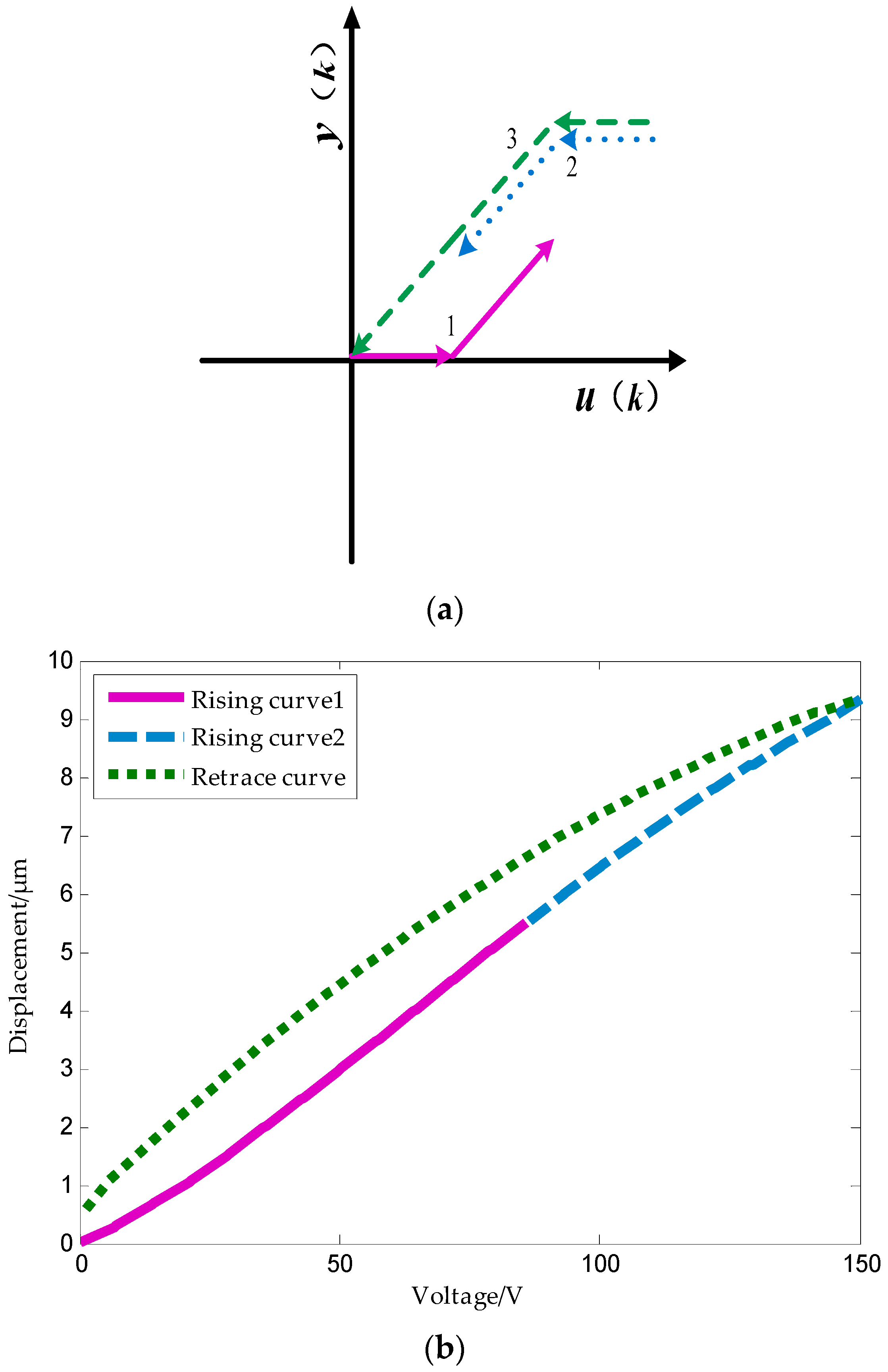
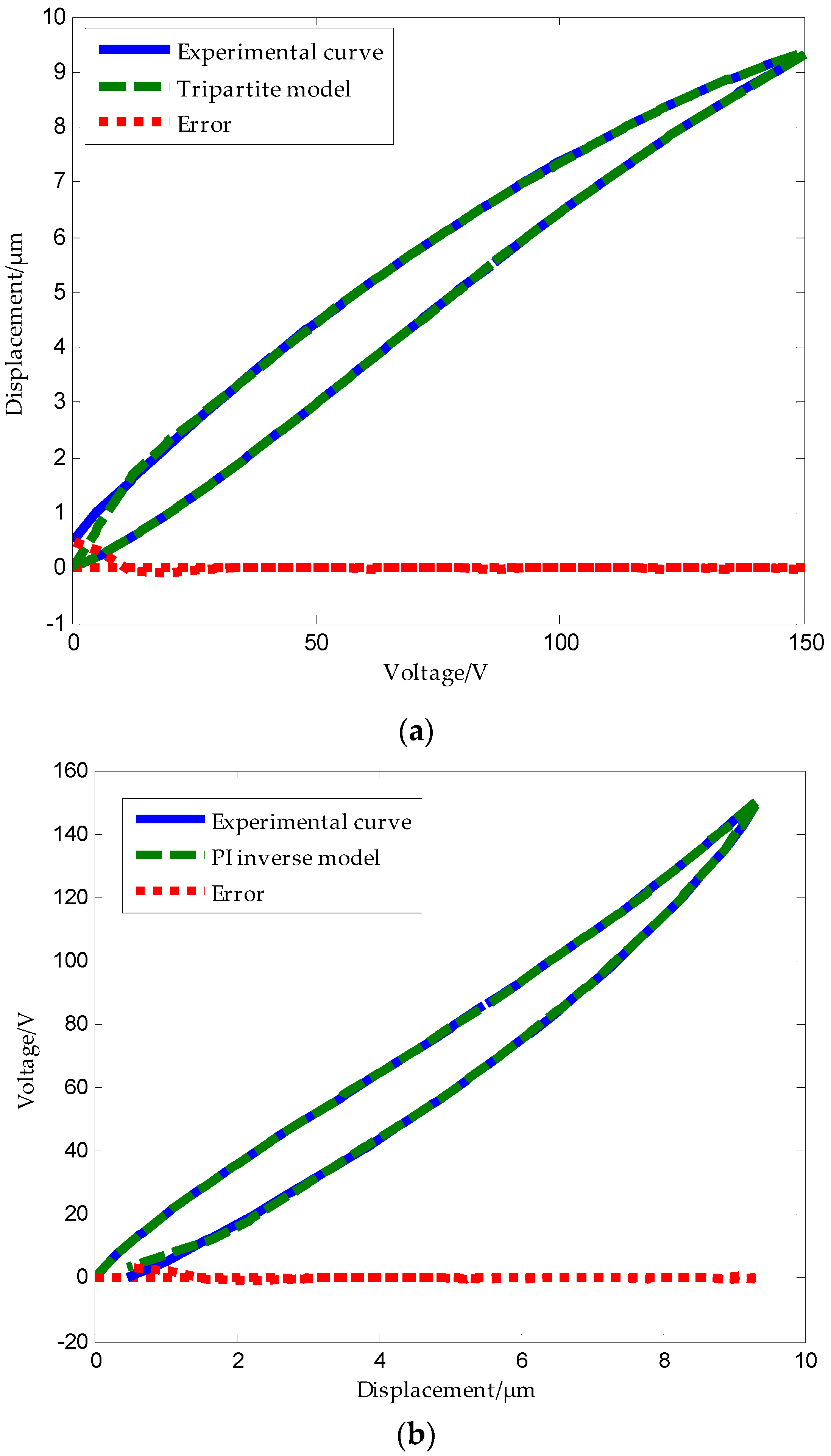
4.3. Tripartite PI Model Based on the Deformation Rate of Piezoelectric Ceramics
- (1)
- The selection of operators is based on the principles of concave-convex consistency, which means that in the hysteresis curve, the concave and convex parts of the curve correspond to the boost part and the depressurization part of the play operator, respectively.
- (2)
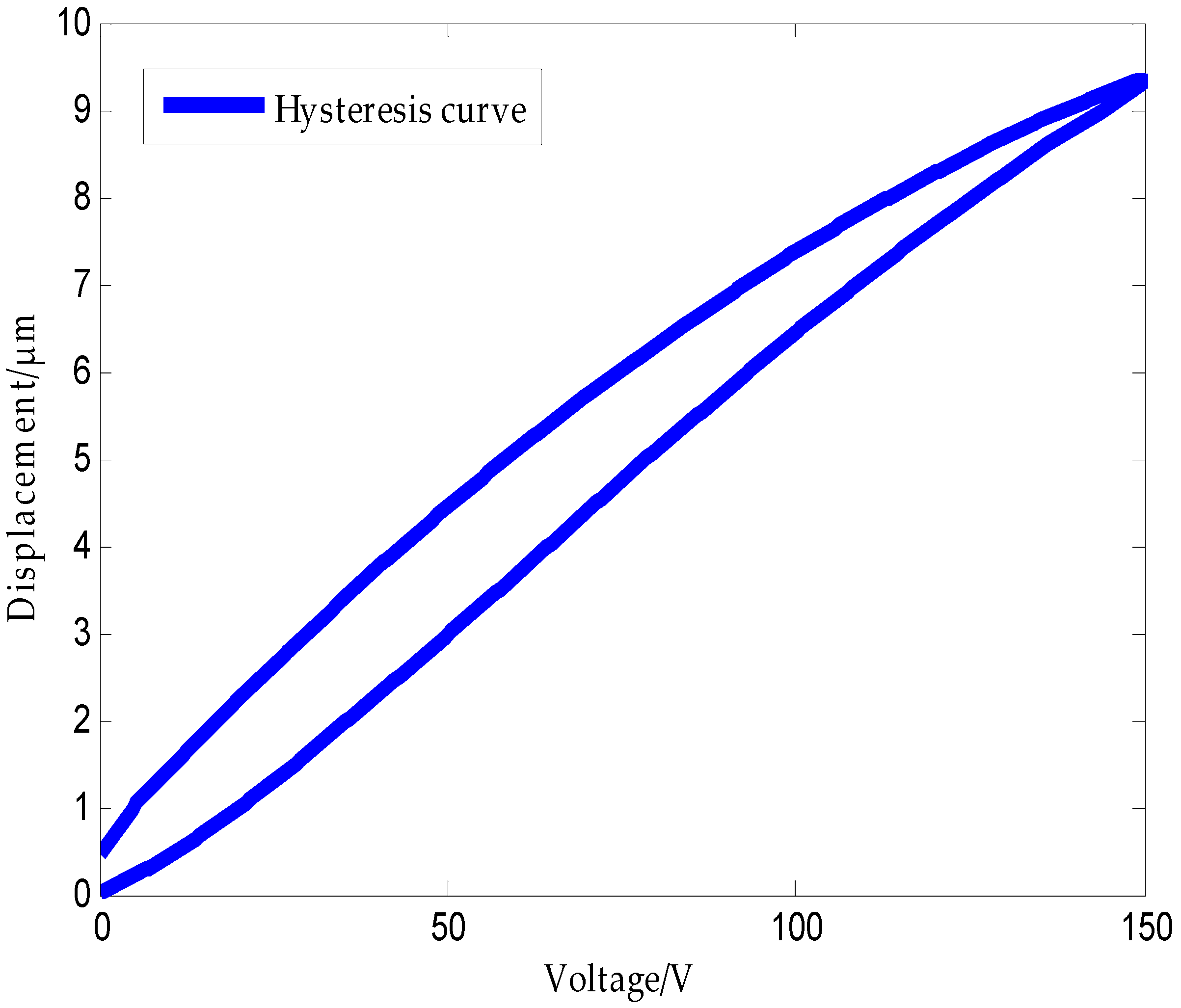
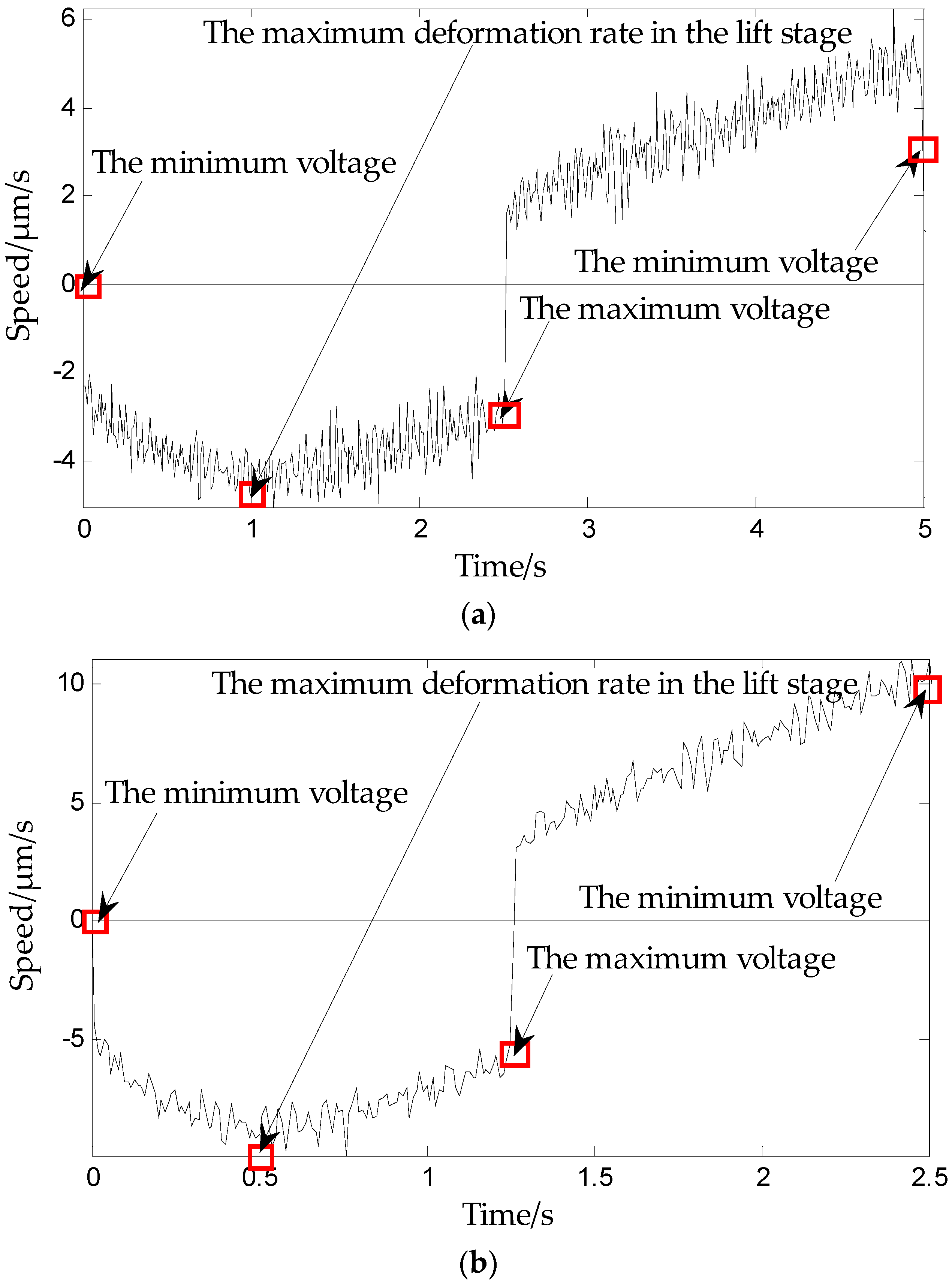
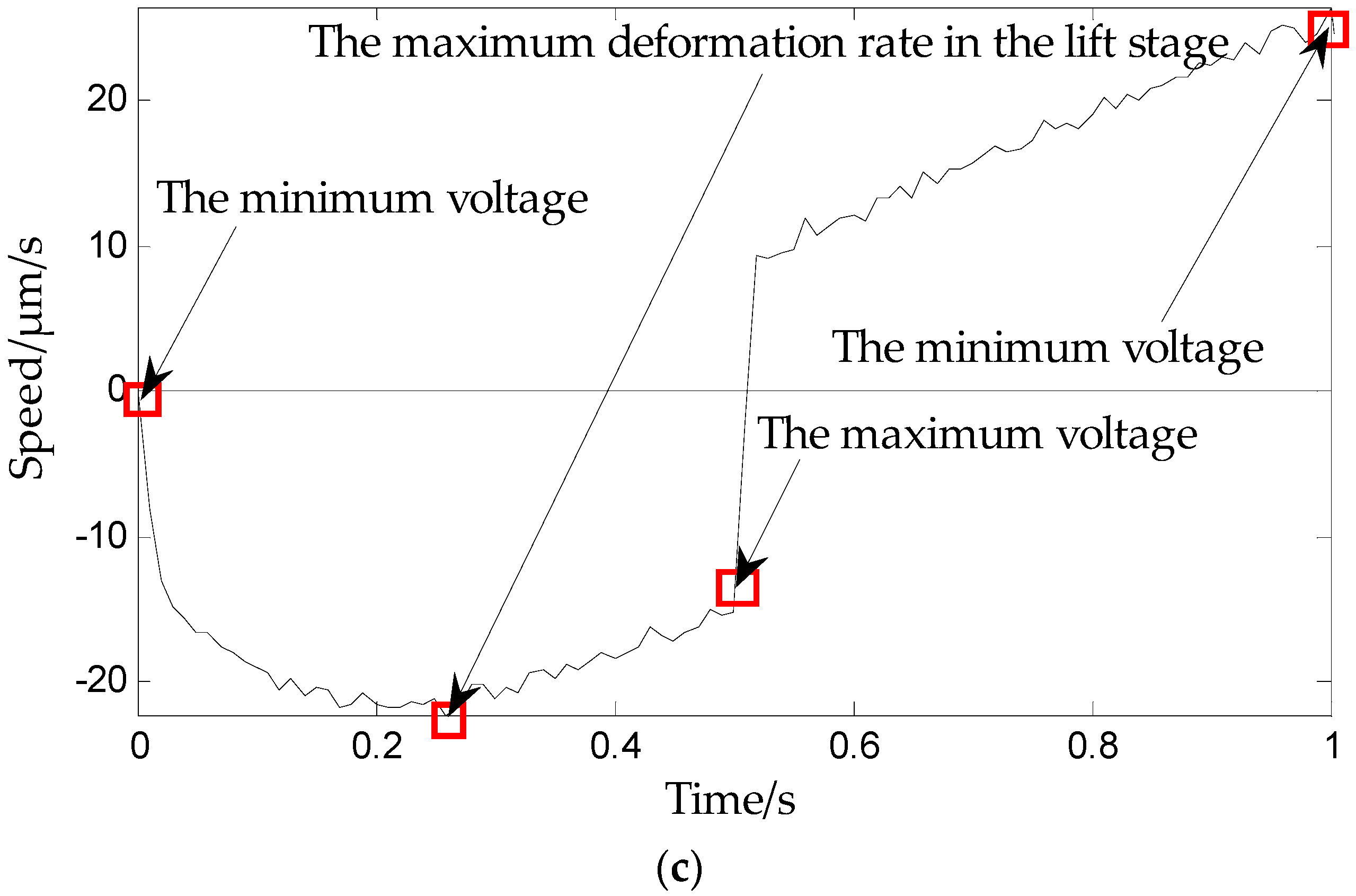
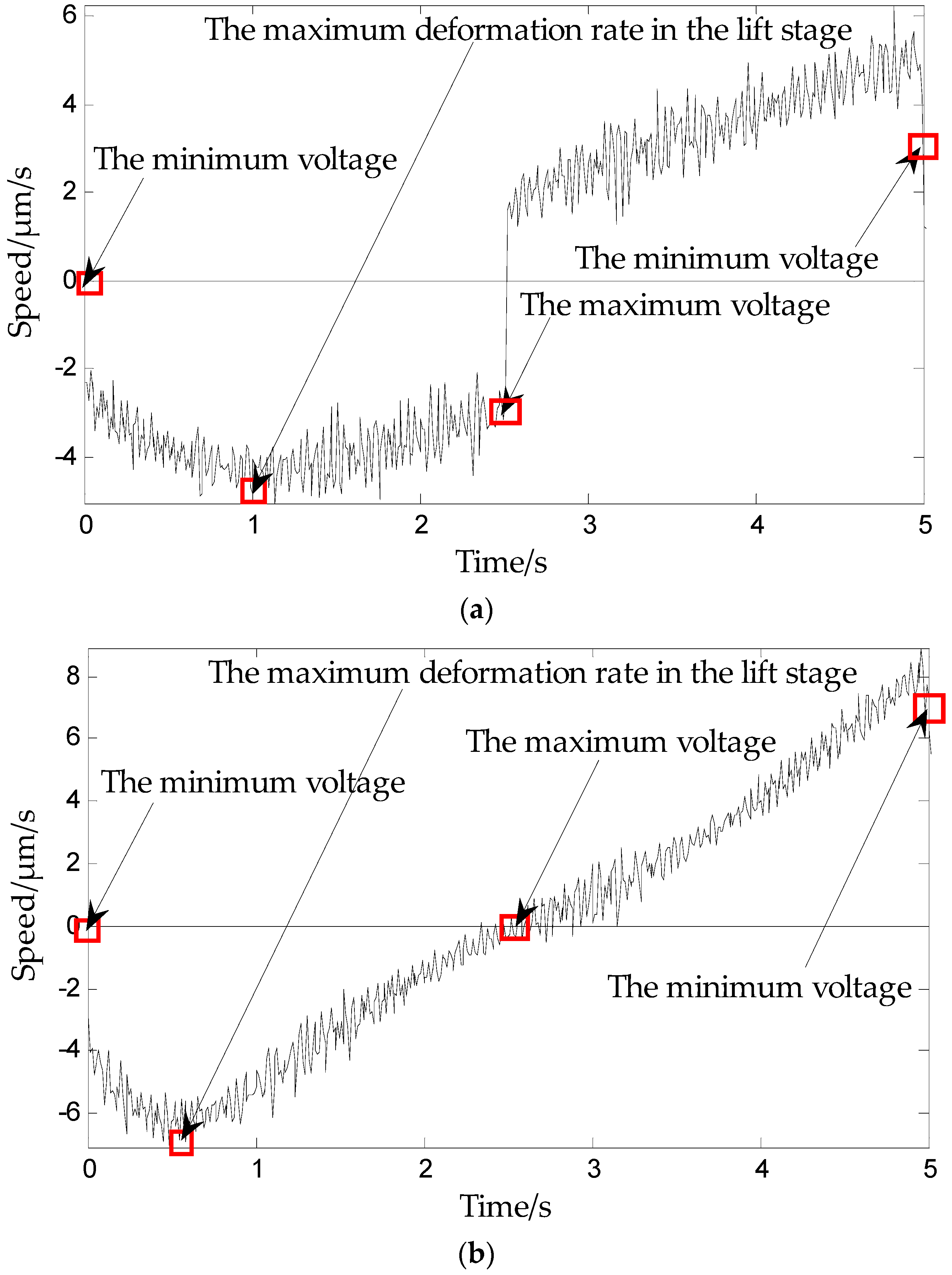
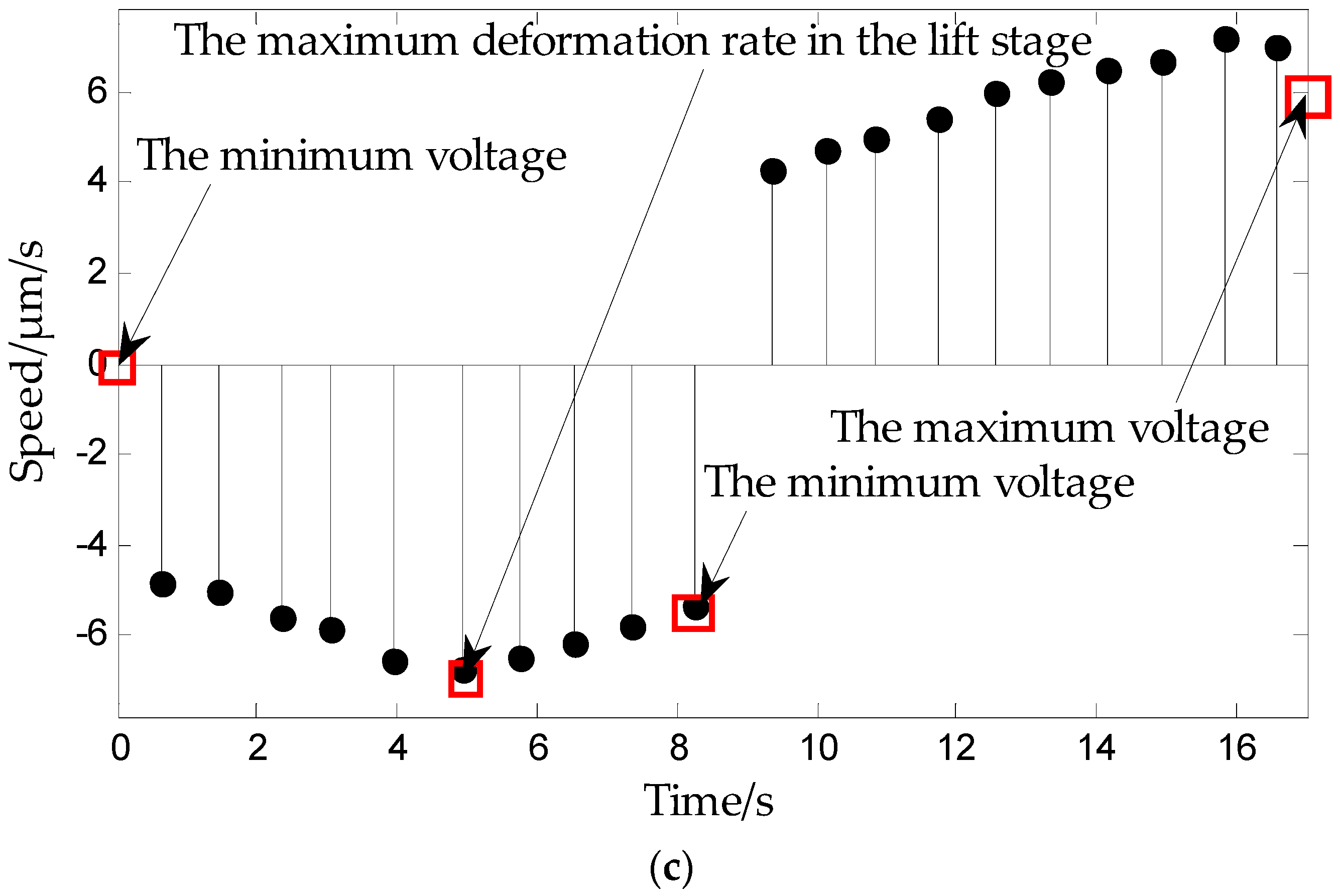
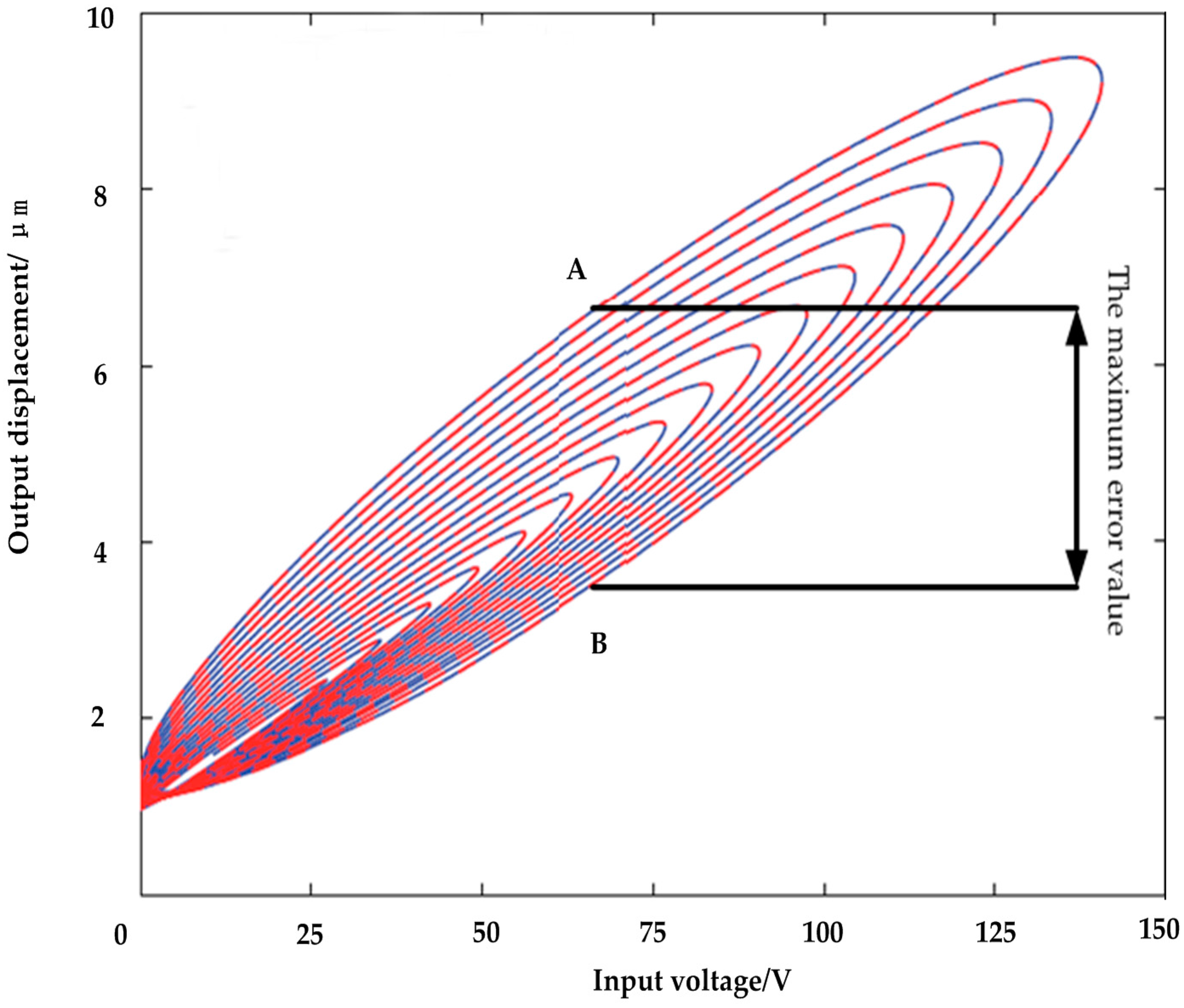
- The rising curve rises from zero voltage to the inflection point voltage uif (uif refers to the voltage indicated by the arrows in Figure 6 and Figure 7), i.e., when the deformation speed rises from 0 to the maximum. The relationship between the voltage and displacement is described by a single lateral play operator as shown in Figure 13 (the dotted portion).
- (3)
- The rising curve rises from the inflection voltage uif to maximum voltage umax (umax refers to the maximum point voltage applied to the piezoelectric ceramic during the whole rising cycle. It is 150 V here). Voltage–position relation in this part is described by a single lateral play operator as shown in Figure 13 (the solid line). One side play operators and hysteresis curves have a counter clock directivity. The reducing portion and rising process in the second part manifest the epirelief characteristic. The reducing portion of play operators point to the origin of coordinates while the second rising hysteresis curve deviates from it. Therefore, we need to model in reverse when we use play operators in the reducing part to describe the second rising process of the hysteresis curve.
- (4)
- The retraced curve’s relation that reduces from the maximum to zero voltage is described by a single lateral play operator as shown in Figure 13 (the solid line).
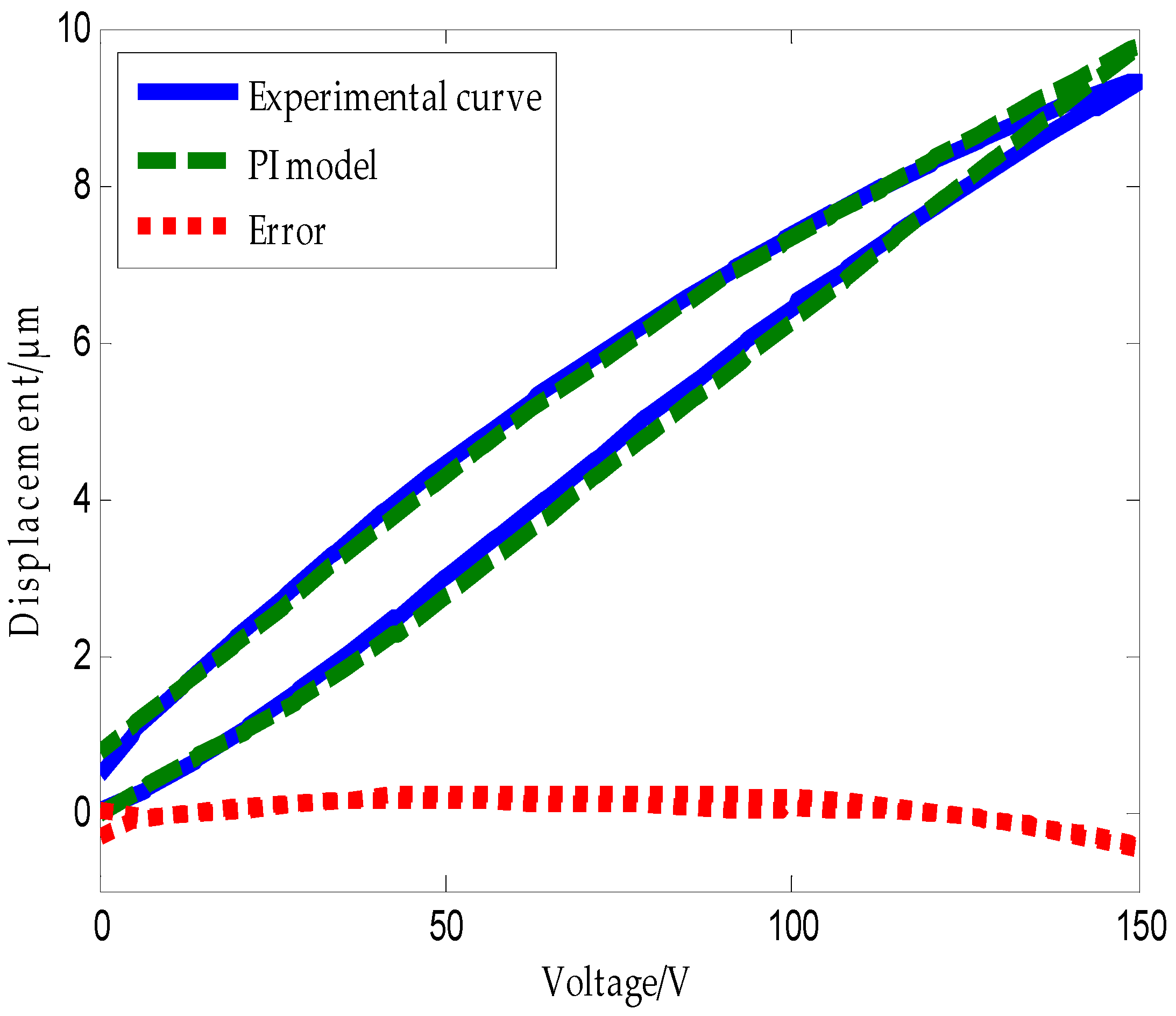
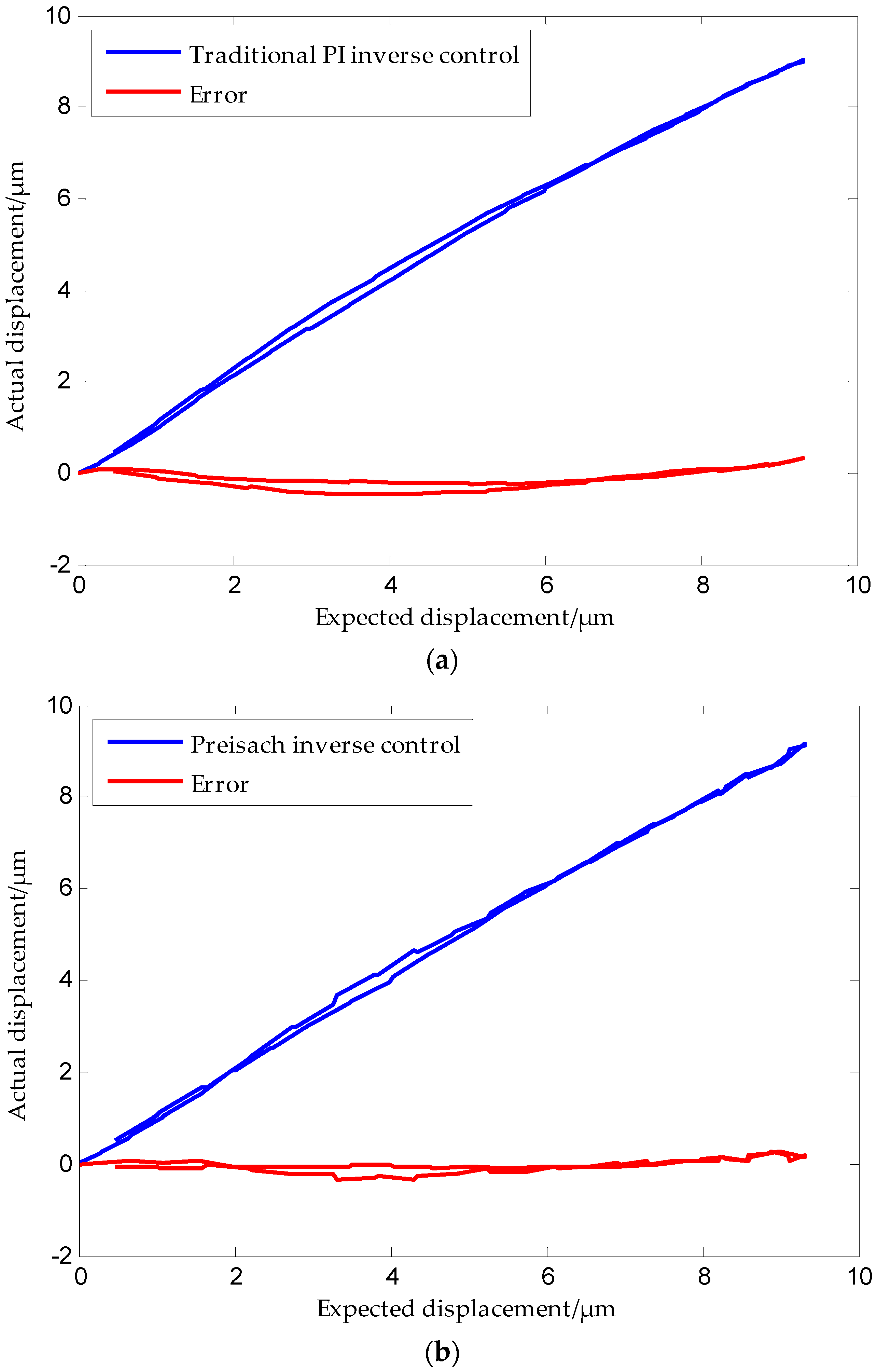
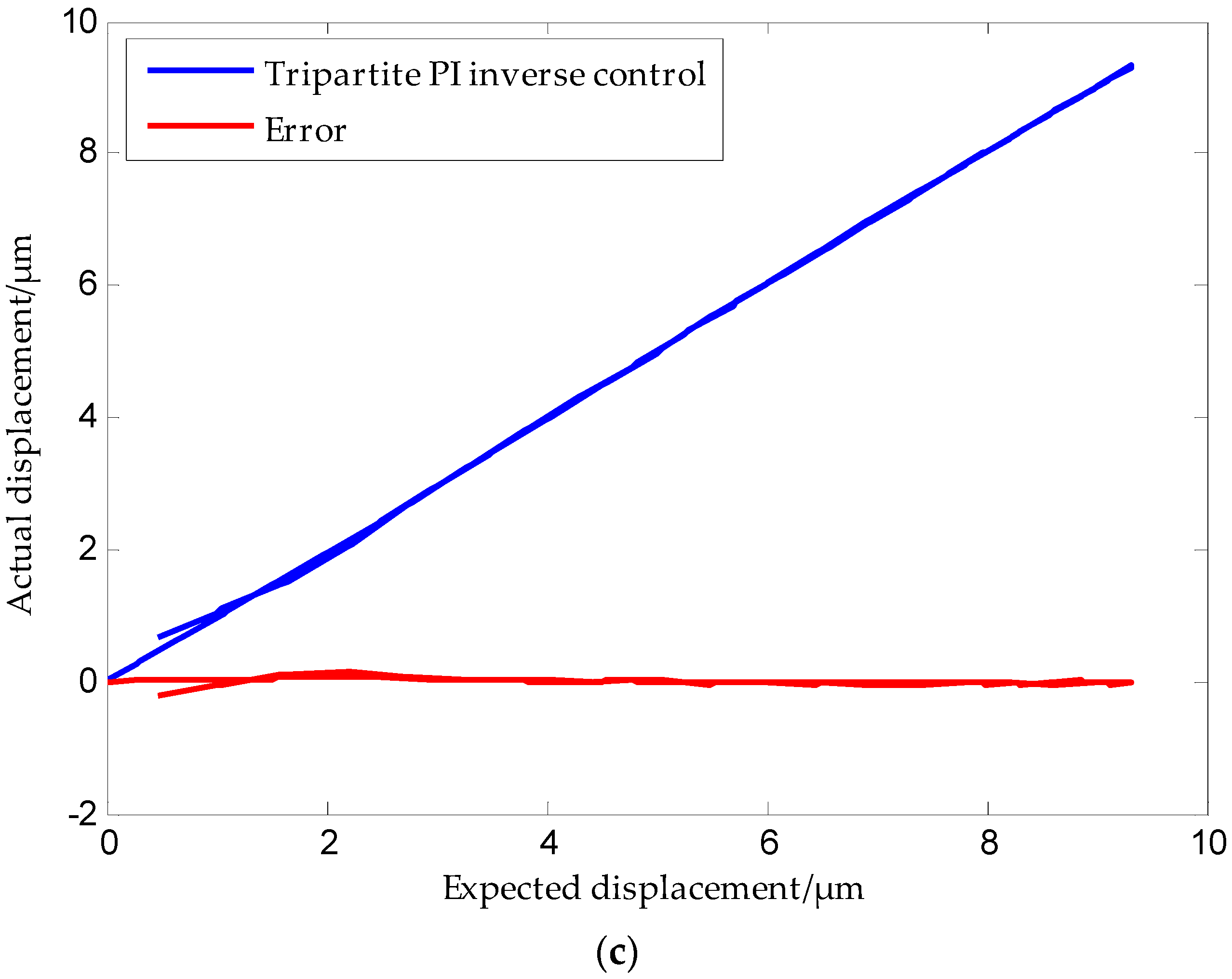
5. Experiment Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tuma, T.; Lygeros, J.; Kartik, V.; Sebastian, A.; Pantazi, A. High-speed multiresolution scanning probe microscopy based on Lissajous scan trajectories. Nanotechnology 2012, 23, 185501. [Google Scholar] [CrossRef] [PubMed]
- Braunsmann, C.; Schäffer, T.E. High-speed atomic force microscopy for large scan sizes using small cantilevers. Nanotechnology 2010, 21, 225705. [Google Scholar] [CrossRef] [PubMed]
- Bhagat, U.; Shirinzadeh, B.; Tian, Y.; Zhang, D. Experimental analysis of laser interferometry-based robust motion tracking control of a flexure-based mechanism. IEEE Trans. Autom. Sci. Eng. 2013, 10, 267–275. [Google Scholar] [CrossRef]
- Hansma, P.K.; Schitter, G.; Fantner, G.E.; Prater, C. High-speed atomic force microscopy. Appl. Phys. 2006, 314, 601–602. [Google Scholar]
- Tuma, T.; Sebastian, A.; Lygeros, J.; Pantazi, A. The four pillars of nanopositioning for scanning probe microscopy: The position sensor, the scanning device, the feedback controller, and the reference trajectory. Control Syst. IEEE 2013, 33, 68–85. [Google Scholar] [CrossRef]
- Clayton, G.M.; Tien, S.; Leang, K.K.; Zou, Q.; Devasia, S. A review of feedforward control approaches in nanopositioning for high-speed SPM. J. Dyn. Syst. Meas. Control 2009, 131, 636–650. [Google Scholar] [CrossRef]
- Park, G.; Bement, M.T.; Hartman, D.A.; Smith, R.E.; Farrar, C.R. The use of active materials for machining processes: A review. Int. J. Mach. Tools. Manuf. 2007, 47, 2189–2206. [Google Scholar] [CrossRef]
- Gozen, B.A.; Ozdoganlar, O.B. Design and evaluation of a mechanical nanomanufacturing system for nanomilling. Precis. Eng. 2012, 36, 19–30. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K.; Tong, H.L. Adaptive sliding-mode control of piezoelectric actuators. IEEE Trans. Ind. Electron. 2009, 56, 3514–3522. [Google Scholar] [CrossRef]
- Zhu, W.; Rui, X. Hysteresis modeling and displacement control of piezoelectric actuators with the frequency-dependent behavior using a generalized Bouc–Wen model. Precis. Eng. 2016, 43, 299–307. [Google Scholar] [CrossRef]
- Janaideh, A.; Farhan, M. Generalized Prandtl-Ishlinskii hysteresis model and its analytical inverse for compensation of hysteresis in smart actuators. Mech. Ind. Eng. 2009, 9, 307–312. [Google Scholar]
- Li, P.; Li, P.; Sui, Y. Adaptive fuzzy hysteresis internal model tracking control of piezoelectric actuators with nanoscale application. IEEE Trans. Fuzzy Syst. 2016, 24, 1246–1254. [Google Scholar] [CrossRef]
- Gu, G.Y.; Li, C.X.; Zhu, L.M.; Su, C.Y. Modeling and identification of piezoelectric-actuated stages cascading hysteresis nonlinearity with linear dynamics. IEEE/ASME Trans. Mechatron. 2016, 21, 1792–1797. [Google Scholar] [CrossRef]
- Mokaberi, B.; Requicha, A.A.G. Compensation of Scanner Creep and Hysteresis for AFM Nanomanipulation. IEEE Trans. Autom. Sci. Eng. 2008, 5, 197–206. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y. Integral resonant damping for high-bandwidth control of piezoceramic stack actuators with asymmetric hysteresis nonlinearity. Mechatronics 2014, 24, 367–375. [Google Scholar] [CrossRef]
- Song, X.; Duggen, L.; Lassen, B.; Mangeot, C. Modeling and identification of hysteresis with modified preisach model in piezoelectric actuator. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics, Munich, Germany, 3–7 July 2017; pp. 1538–1543. [Google Scholar]
- Cao, Y.; Chen, X.B. A survey of modeling and control issues for piezo-electric actuators. J. Dyn. Syst. Meas. Control 2015, 137, 14001. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis (invited). J. Magn. Mag.Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Carrera, Y.; Avila-de La Rosa, G.; Vernon-Carter, E.J.; Alvarez-Ramirez, J. A fractional-order Maxwell model for non-Newtonian fluids. Phys. A Stat. Mech. Its Appl. 2017, 482, 276–285. [Google Scholar] [CrossRef]
- Malczyk, R.; Izydorczyk, J. The frequency-dependent Jiles–Atherton hysteresis model. Phys. B Condens. Matter 2015, 463, 68–75. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Wu, H.; Zou, D. Modelling and compensation of hysteresis in piezoelectric actuators based on Maxwell approach. Electron. Lett. 2015, 52, 188–190. [Google Scholar] [CrossRef]
- Liu, L.; Tan, K.K.; Chen, S.L.; Huang, S.; Lee, T.H. SVD-based Preisach hysteresis identification and composite control of piezo actuators. ISA Trans. 2012, 51, 430–438. [Google Scholar] [CrossRef] [PubMed]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Chen, H.; Tan, Y.; Zhou, X.; Dong, R.; Zhang, Y. Identification of dynamic hysteresis based on duhem model. In Proceedings of the International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 28–29 March 2011; pp. 810–814. [Google Scholar]
- Lin, C.J.; Lin, P.T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Comput. Math. Appl. 2012, 64, 766–787. [Google Scholar] [CrossRef]
- Wang, G.; Chen, G.; Bai, F. Modeling and identification of asymmetric Bouc–Wen hysteresis for piezoelectric actuator via a novel differential evolution algorithm. Sens. Actuators A Phys. 2015, 235, 105–118. [Google Scholar] [CrossRef]
- Huang, X.; Zeng, J.; Ruan, X.; Zheng, L.; Li, G. Structure, electrical and thermal expansion properties of PZnTe-PZT ternary system piezoelectric ceramics. J. Am. Ceram. Soc. 2017, 101, 274–282. [Google Scholar] [CrossRef]
- Zhong, W. Physics of Ferroelectrics; Science Press: Beijing, China, 1996; pp. 294–297, 391–394. [Google Scholar]
- Bridger, K.; Jones, L.; Poppe, F.; Brown, S.A.; Winzer, S.R. High-force cofired multilayer actuators. Proc. SPIE 1996, 2721, 341–352. [Google Scholar]
- Lancée, C.T.; Souquet, J.; Ohigashi, H.; Bom, N. Transducers in medical ultrasound: Part One. Ferro-electric ceramics versus polymer piezoelectric materials. Ultrasonics 1985, 23, 138. [Google Scholar] [CrossRef]
- Rabe, K.M.; Ahn, C.H.; Triscone, J.M. Physics of Ferroelectrics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 203–234. [Google Scholar]
- Merz, W.J. Domain Formation and Domain Wall Motions in Ferroelectric BaTiO3 Single Crystals. Phys. Rev. 1954, 95, 690–698. [Google Scholar] [CrossRef]
- Merz, W.J. Switching Time in Ferroelectric BaTiO3 and Its Dependence on Crystal Thickness. J. Appl. Phys. 1956, 27, 938–943. [Google Scholar] [CrossRef]






| i | ri | wi |
|---|---|---|
| 1 | 0 | 0.0493 |
| 2 | 15 | 0.0298 |
| 3 | 30 | 0.0120 |
| 4 | 45 | 0.0090 |
| 5 | 60 | 0 |
| 6 | 75 | 0 |
| 7 | 90 | 0 |
| 8 | 105 | 0 |
| 9 | 120 | 0 |
| 10 | 135 | 0 |
| i | r1 | w1 | r2 | w2 | r3 | w3 |
|---|---|---|---|---|---|---|
| 1 | 0 | 0.0415 | 0 | 0.0529 | 0 | 0.0322 |
| 2 | 6.42 | 0.0097 | 15 | 0.0027 | 15 | 0.0081 |
| 3 | 12.84 | 0.0082 | 30 | 0.0067 | 30 | 0.0054 |
| 4 | 19.26 | 0.0067 | 45 | 0.0022 | 45 | 0.0044 |
| 5 | 25.68 | 0.0051 | 60 | 0 | 60 | 0.0065 |
| 6 | 32.10 | 0.0043 | 75 | 0 | 75 | 0.0039 |
| 7 | 38.52 | 0.0026 | 90 | 0 | 90 | 0.0087 |
| 8 | 44.94 | 0.0016 | 105 | 0 | 105 | 0.0016 |
| 9 | 51.36 | 0 | 120 | 0 | 120 | 0.0009 |
| 10 | 57.78 | 0 | 135 | 0 | 135 | 0.0008 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, D.; Li, H.; Xu, Y.; Zhang, L. Compensation of Hysteresis on Piezoelectric Actuators Based on Tripartite PI Model. Micromachines 2018, 9, 44. https://doi.org/10.3390/mi9020044
An D, Li H, Xu Y, Zhang L. Compensation of Hysteresis on Piezoelectric Actuators Based on Tripartite PI Model. Micromachines. 2018; 9(2):44. https://doi.org/10.3390/mi9020044
Chicago/Turabian StyleAn, Dong, Haodong Li, Ying Xu, and Lixiu Zhang. 2018. "Compensation of Hysteresis on Piezoelectric Actuators Based on Tripartite PI Model" Micromachines 9, no. 2: 44. https://doi.org/10.3390/mi9020044
APA StyleAn, D., Li, H., Xu, Y., & Zhang, L. (2018). Compensation of Hysteresis on Piezoelectric Actuators Based on Tripartite PI Model. Micromachines, 9(2), 44. https://doi.org/10.3390/mi9020044





