Modular, Discrete Micromixer Elements Fabricated by 3D Printing
Abstract
:1. Introduction
2. Results and Discussion
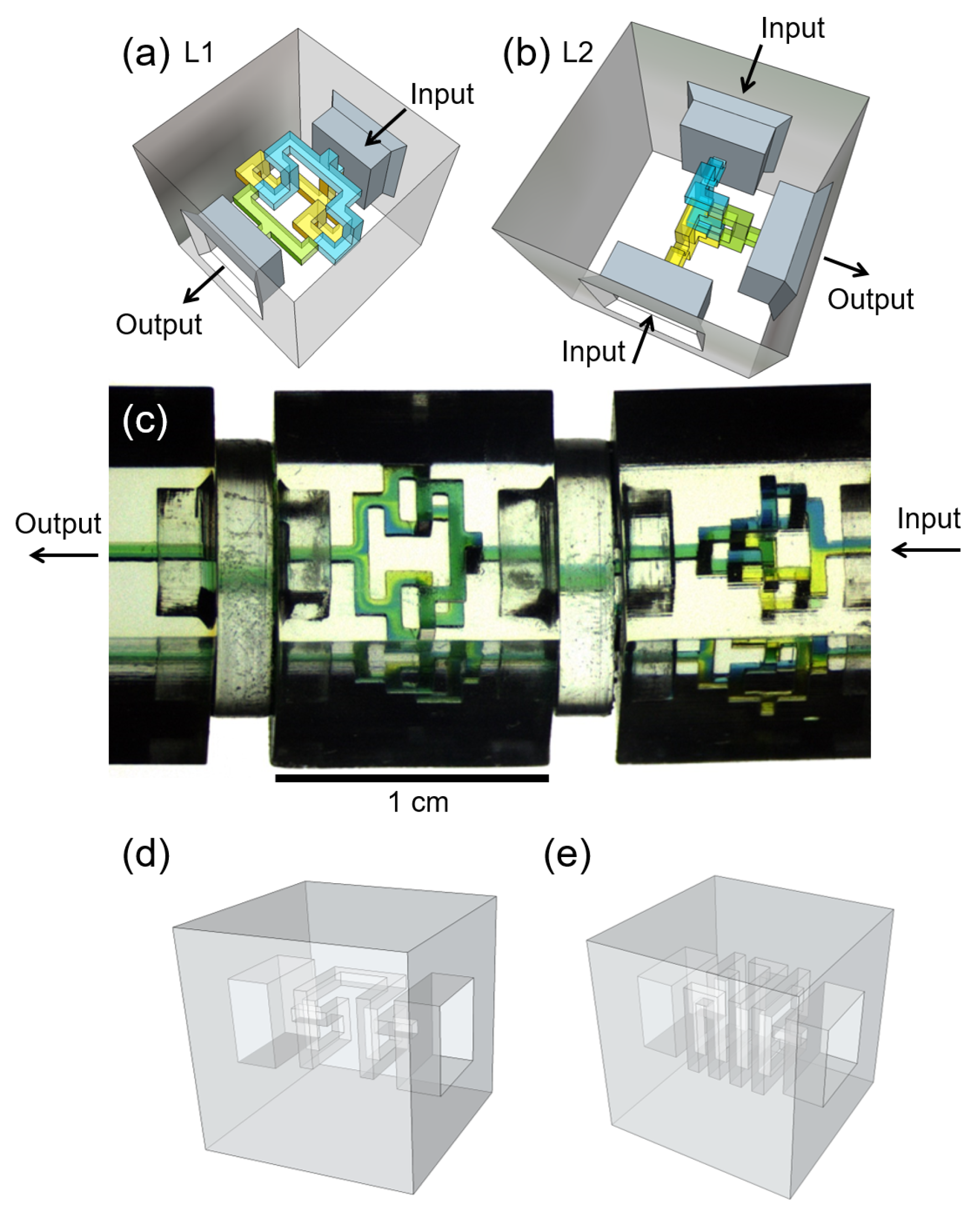
2.1. Design of Laminator Discrete Elements
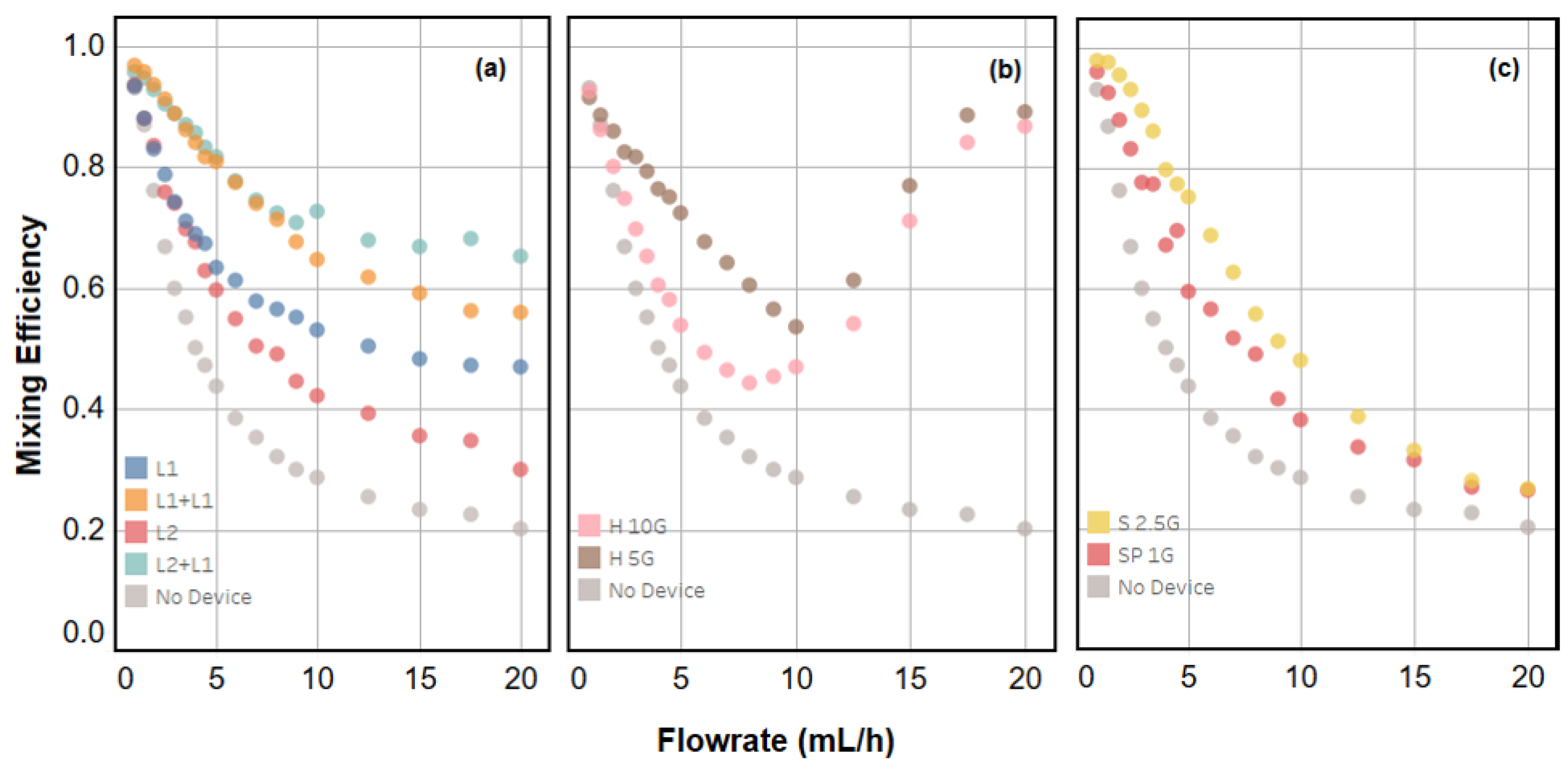
2.2. Quantifying Mixing Efficiency
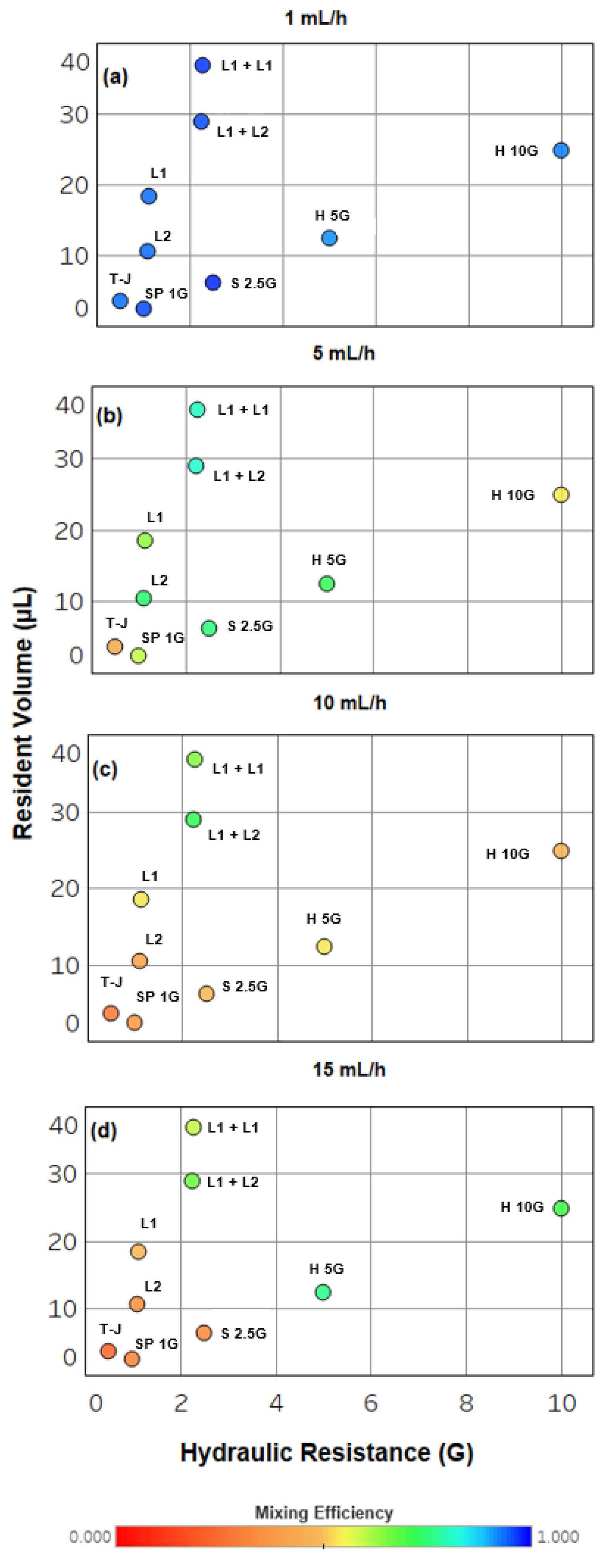
2.3. Device Performance and Engineering Trade-Offs
3. Materials and Methods
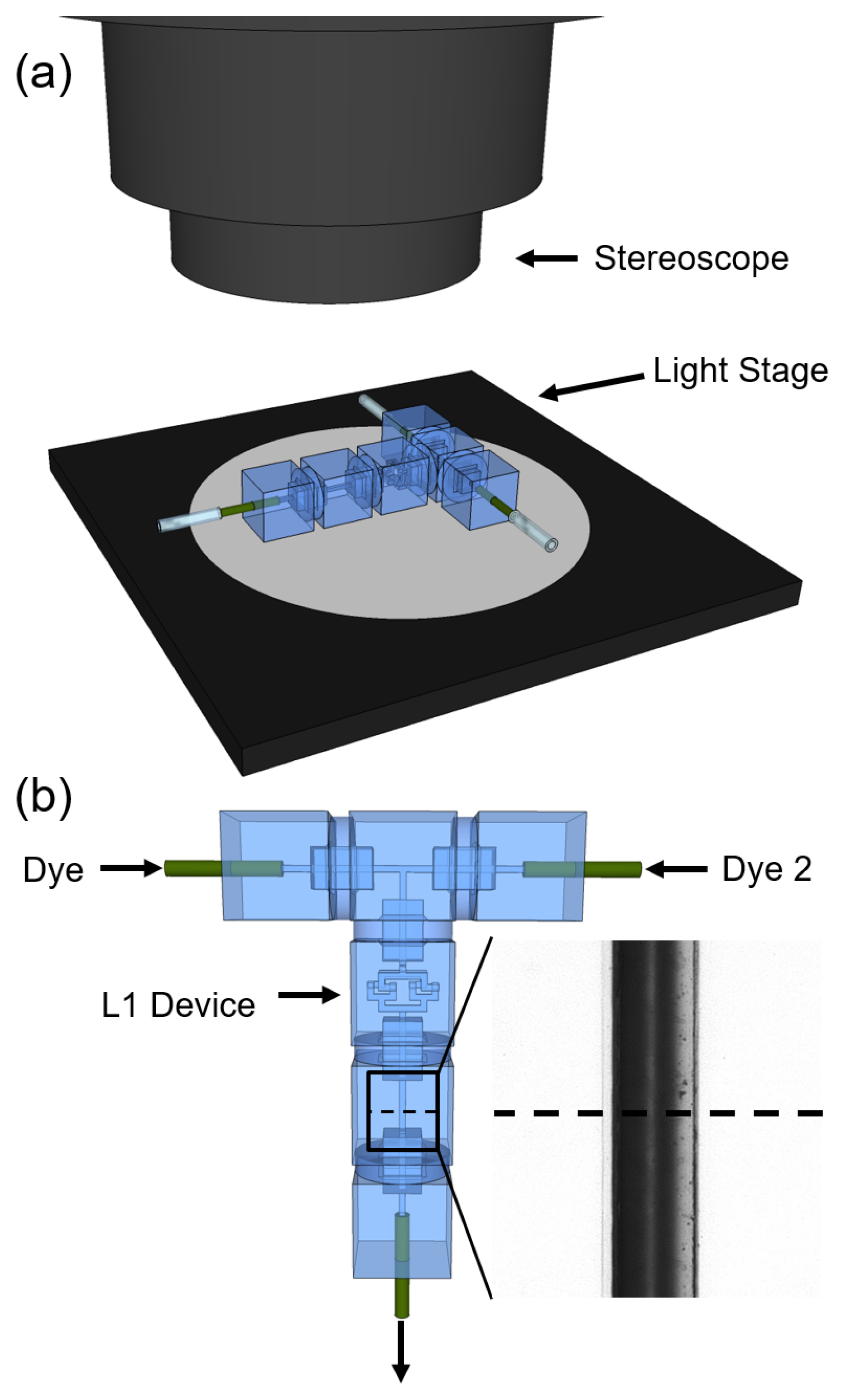
3.1. Microfluidic Experiments
3.2. Data Analysis
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Tice, J.D.; Song, H.; Lyon, A.D.; Ismagilov, R.F. Formation of droplets and mixing in multiphase microfluidics at low values of the Reynolds and the capillary numbers. Langmuir 2003, 19, 9127–9133. [Google Scholar] [CrossRef]
- Teh, S.-Y.; Lin, R.; Hung, L.-H.; Lee, A.P. Droplet microfluidics. Lab Chip 2008, 8, 198–220. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-T.; Wu, Z. Micromixers—A review. J. Micromech. Microeng. 2005, 15, R1–R16. [Google Scholar] [CrossRef]
- Bessoth, F.G.; deMello, A.J.; Manz, A. Microfabricated devices for fluid mixing and their application for chemical synthesis. Anal. Commun. 1999, 36, 213–215. [Google Scholar] [CrossRef]
- Erbacher, C.; Bessoth, F.G.; Busch, M.; Verpoorte, E.; Manz, A. Towards integrated continuous-flow chemical reactors. Microchem. Acta 1999, 131, 19–24. [Google Scholar] [CrossRef]
- Schwesinger, N.; Frank, T.; Wurmus, H. A modular microfluid system with an integrated micromixer. J. Micromech. Microeng. 2006, 6, 99–102. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, D.S.; Lee, S.S.; Kwon, T.H. A split and recombination micromixer fabricated in a PDMS three-dimensional structure. J. Micromech. Microeng. 2006, 16, 1067–1072. [Google Scholar] [CrossRef]
- Liu, R.H.; Stremler, M.A.; Sharp, K.V.; Olsen, M.G.; Santiago, J.G.; Adrian, R.F.; Areh, H.; Beebe, D.J. Passive mixing in a three-dimensional serpentine microchannel. J. Microelectromech. Syst. 2002, 9, 190–197. [Google Scholar] [CrossRef]
- Johnson, T.J.; Ross, D.; Locascio, L.E. Rapid microfluidic mixing. Anal. Chem. 2002, 74, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Howell, P.B.; Mott, D.R.; Fertig, S.; Kaplan, C.R.; Golden, J.P.; Oran, E.S.; Ligler, F.S. A microfluidic mixer with grooves placed on the top and bottom of the channel. Lab Chip 2005, 5, 524–530. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, K.C.; Thompson, B.; Malmstadt, N. Discrete elements for 3D microfluidics. Proc. Natl. Acad. Sci. USA 2014, 111, 15013–15018. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, K.C.; Thompson, B.; Iqbal, D.; Malmstadt, N. Predicting the behavior of microfluidic circuits made from discrete elements. Sci. Rep. 2015, 5, 15609. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, K.C.; Thompson, B.; Tembhekar, A.; Malmstadt, N. Temperature Sensing in Modular Microfluidic Architectures. Micromachines 2016, 7, 11. [Google Scholar] [CrossRef]
- Thompson, B.; Riche, C.T.; Movsesian, N.; Bhargava, K.C.; Gupta, M.; Malmstadt, N. Engineered hydrophobicity of discrete microfluidic elements for double emulsion generation. Microfluid. Nanofluid. 2016, 20, 1–5. [Google Scholar] [CrossRef]
- Bruus, H. Theoritical Microfluidics; Oxford Master Series in Physics; Oxford University Press: Oxford, UK, 2007; Volume 18. [Google Scholar]
- Au, A.K.; Lee, W.; Folch, A. Mail-order microfluidics: evaluation of stereolithography for the production of microfluidic devices. Lab Chip 2014, 14, 1294–1301. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhargava, K.C.; Ermagan, R.; Thompson, B.; Friedman, A.; Malmstadt, N. Modular, Discrete Micromixer Elements Fabricated by 3D Printing. Micromachines 2017, 8, 137. https://doi.org/10.3390/mi8050137
Bhargava KC, Ermagan R, Thompson B, Friedman A, Malmstadt N. Modular, Discrete Micromixer Elements Fabricated by 3D Printing. Micromachines. 2017; 8(5):137. https://doi.org/10.3390/mi8050137
Chicago/Turabian StyleBhargava, Krisna C., Roya Ermagan, Bryant Thompson, Andrew Friedman, and Noah Malmstadt. 2017. "Modular, Discrete Micromixer Elements Fabricated by 3D Printing" Micromachines 8, no. 5: 137. https://doi.org/10.3390/mi8050137
APA StyleBhargava, K. C., Ermagan, R., Thompson, B., Friedman, A., & Malmstadt, N. (2017). Modular, Discrete Micromixer Elements Fabricated by 3D Printing. Micromachines, 8(5), 137. https://doi.org/10.3390/mi8050137




