Field-Dependent Resonant Behavior of Thin Nickel Film-Coated Microcantilever
Abstract
:1. Introduction
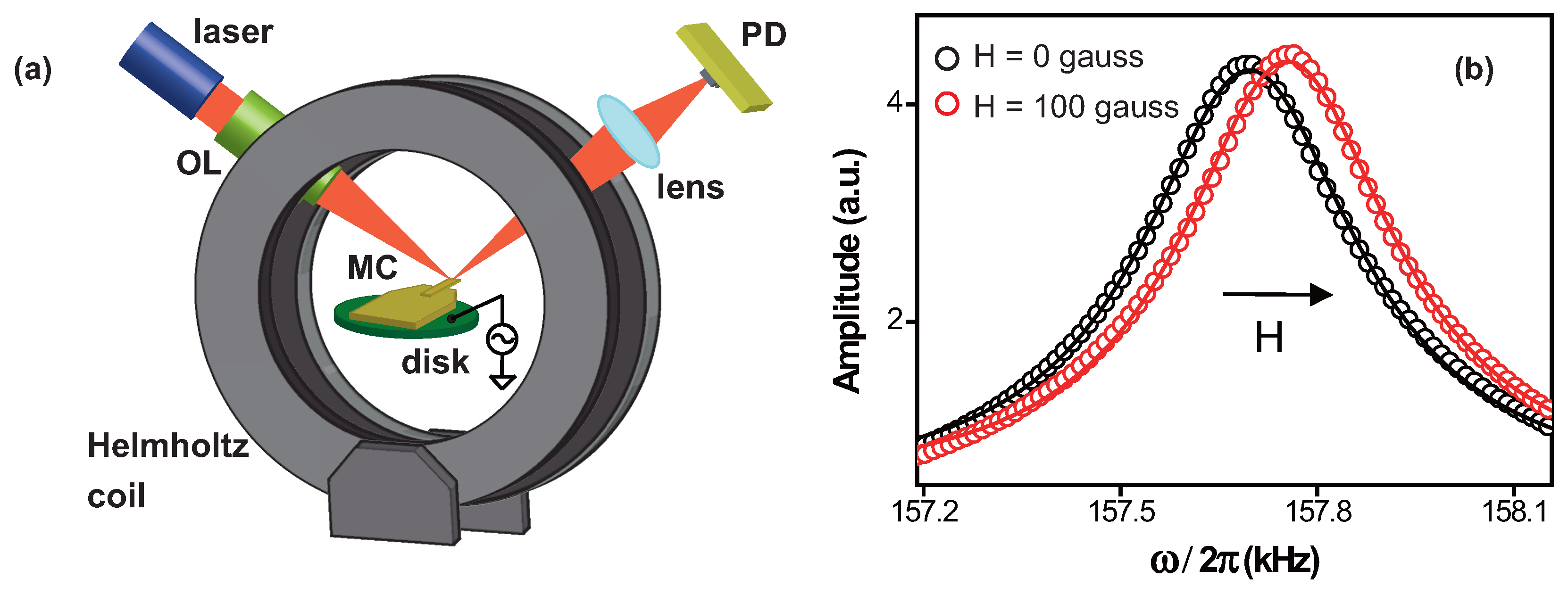
2. Experiment
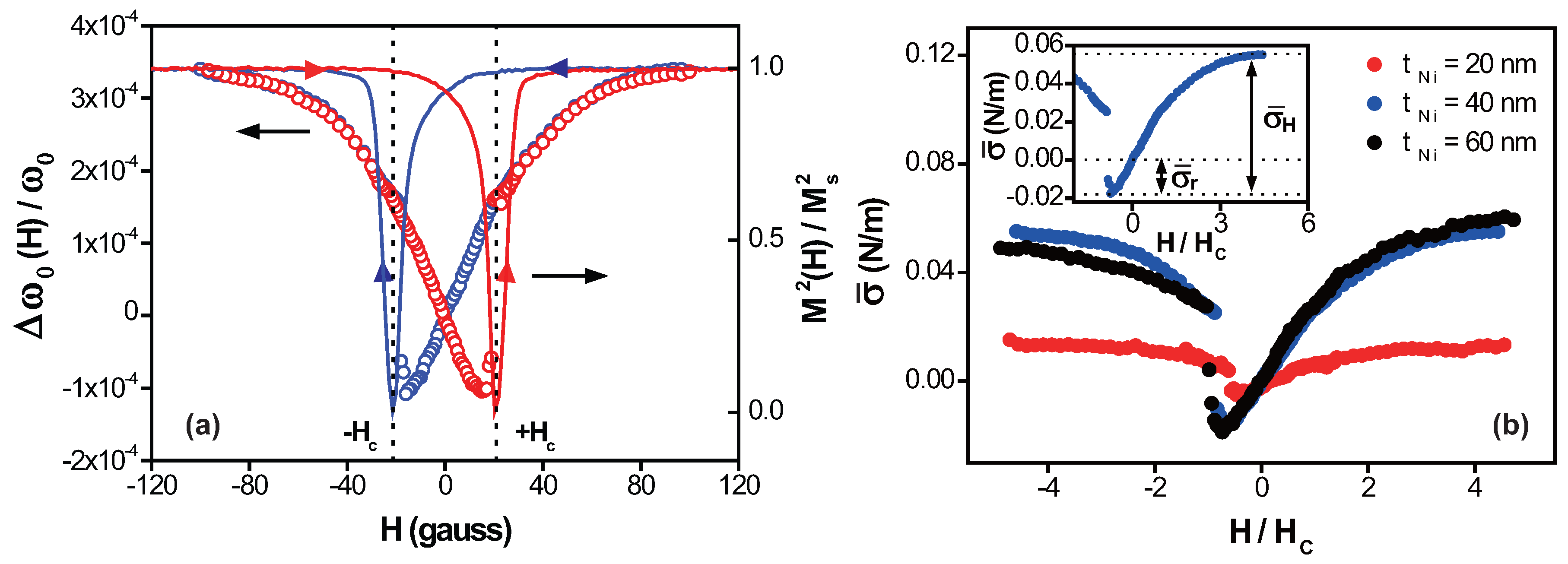
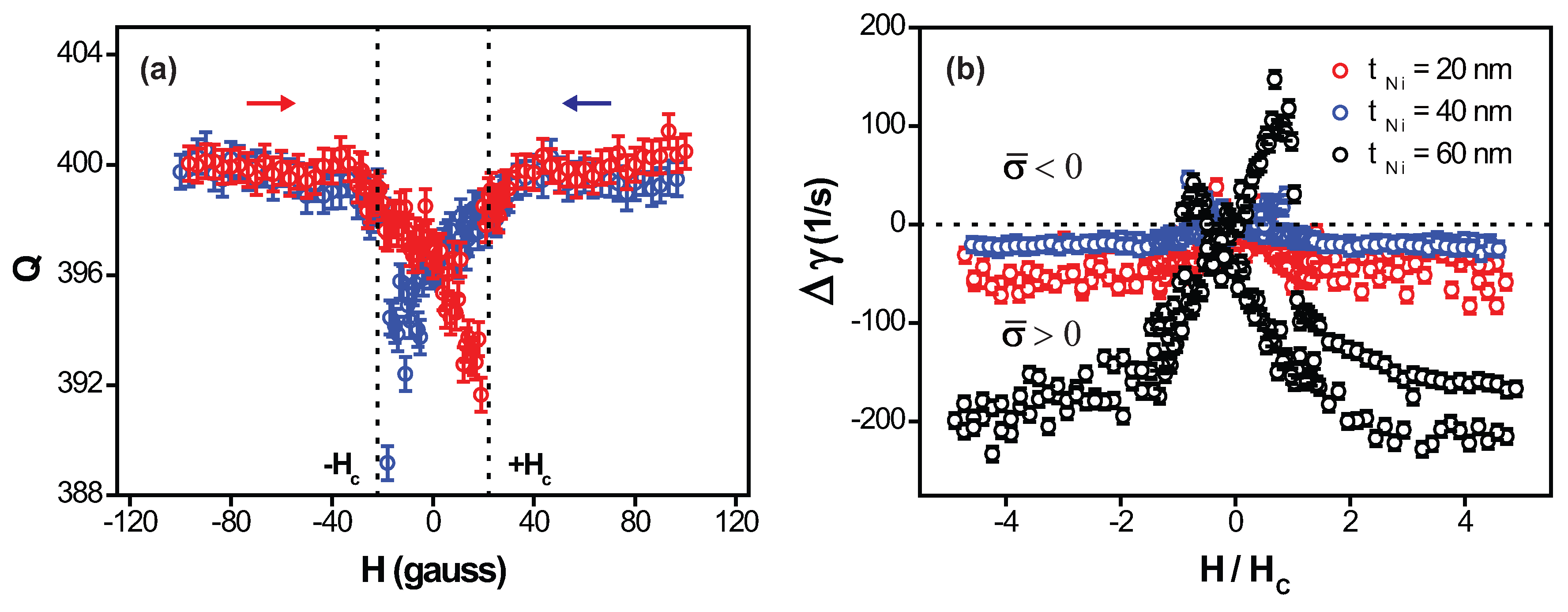
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| DC | Direct current |
| FWHM | Full width at half maximum |
| Ni | Nickel |
| Q | Q-factor: quality factor |
| Si | Silicon |
| VSM | Vibrating sample magnetometer |
References
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials, 2nd ed.; IEEE/Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Clark, A.E. Magnetostrictive rare earth-Fe2 compounds. In Power Sonic and Ultrasonic Transducers Design, Proceedings of the International Workshop, Lille, France, 26–27 May 1987; Hamonic, B., Decarpigny, J.N., Eds.; Springer: Berlin, Heidelberg, 1988; pp. 43–99. [Google Scholar]
- Teter, J.P.; Clark, A.E.; McMasters, O.D. Anisotropic magnetostriction in Tb0.27Dy0.73Fe1.95. J. Appl. Phys. 1987, 61, 3787. [Google Scholar] [CrossRef]
- Roukes, M. Nanoelectromechanical systems face the future. Phys. World 2001, 14, 25–32. [Google Scholar] [CrossRef]
- Masmanidis, S.C.; Tang, H.X.; Myers, E.B.; Li, M.; De Greve, K.; Vermeulen, G.; VanRoy, W.; Roukes, M.L. Nanomechanical measurement of magnetostriction and magnetic anisotropy in (Ga,Mn)As. Phys. Rev. Lett. 2005, 95, 187206. [Google Scholar] [CrossRef] [PubMed]
- Hunter, D.; Osborn, W.; Wang, K.; Kazantseva, N.; Hattrick-Simpers, J.; Suchoski, R.; Takahashi, R.; Young, M.L.; Mehta, A.; Bendersky, L.A.; et al. Giant magnetostriction in annealed Co1-xFex thin-films. Nat. Commun. 2011, 2, 518. [Google Scholar] [CrossRef] [PubMed]
- Gojdka, B.; Jahns, R.; Meurisch, K.; Greve, H.; Adelung, R.; Quandt, E.; Knöchel, R.; Faupel, F. Fully integrable magnetic field sensor based on delta-E effect. Appl. Phys. Lett. 2011, 99, 223502. [Google Scholar] [CrossRef]
- Nan, T.; Hui, Y.; Rinaldi, M.; Sun, N.X. Self-Biased 215MHz Magnetoelectric NEMS resonator for ultra-sensitive DC magnetic field detection. Sci. Rep. 2013, 3, 1985. [Google Scholar] [CrossRef] [PubMed]
- Du Trémolet de Lacheisserie, E.; Peuzin, J. Magnetostriction and internal stresses in thin films: The cantilever method revisited. J. Magn. Magn. Mater. 1994, 136, 189–196. [Google Scholar] [CrossRef]
- Weber, M.; Koch, R.; Rieder, K.H. UHV cantilever beam technique for quantitative measurements of magnetization, magnetostriction, and intrinsic stress of ultrathin magnetic films. Phys. Rev. Lett. 1994, 73, 1166–1169. [Google Scholar] [CrossRef] [PubMed]
- Löffler, M.; Kremer, R.; Sutor, A.; Lerch, R. Hysteresis of the resonance frequency of magnetostrictive bending cantilevers. J. Appl. Phys. 2015, 117, 17A907. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, E.J.; Cho, M.R.; Kim, C.S.; Park, Y.D.; Kouh, T. Photothermal effect and heat dissipation in a micromechanical resonator. Appl. Phys. Express 2012, 5, 075201. [Google Scholar] [CrossRef]
- Dapino, M.J.; Smith, R.C.; Flatau, A.B. Model for the ΔE effect in magnetostrictive transducers. Proc. SPIE 2000, 3985, 174–185. [Google Scholar]
- Pernpeintner, M.; Holländer, R.B.; Seitner, M.J.; Weig, E.M.; Gross, R.; Goennenwein, S.T.B.; Huebl, H. A versatile platform for magnetostriction measurements in thin films. J. Appl. Phys. 2016, 119, 093901. [Google Scholar] [CrossRef]
- Valladares, L.D.L.S.; Ionescu, A.; Holmes, S.; Barnes, C.H.W.; Domínguez, A.B.; Quispe, O.A.; González, J.C.; Milana, S.; Barbone, M.; Ferrari, A.C.; et al. Characterization of Ni thin films following thermal oxidation in air. J. Vac. Sci. Technol. B 2014, 32, 051808. [Google Scholar] [CrossRef]
- McFarland, A.W.; Poggi, M.A.; Doyle, M.J.; Bottomley, L.A.; Colton, J.S. Influence of surface stress on the resonance behavior of microcantilevers. Appl. Phys. Lett. 2005, 87, 053505. [Google Scholar] [CrossRef]
- Cleland, A.N. Foundation of Nanomechanics; Springer: Verlag/Berlin, Germany, 2003. [Google Scholar]
- Hornauer, H.; Patrikos, J.; Röll, K. Sensor head for measurement of stress anisotropy in thin films. Vacuum 1990, 41, 1302–1304. [Google Scholar] [CrossRef]
- Lee, E.W. Magnetostriction and magnetomechanical effects. Rep. Prog. Phys. 1955, 18, 184. [Google Scholar] [CrossRef]
- Verbridge, S.S.; Parpia, J.M.; Reichenbach, R.B.; Bellan, L.M.; Craighead, H.G. High quality factor resonance at room temperature with nanostrings under high tensile stress. J. Appl. Phys. 2006, 99, 124304. [Google Scholar] [CrossRef]
- Yang, J.; Ono, T.; Esashi, M. Surface effects and high quality factors in ultrathin single-crystal silicon cantilevers. Appl. Phys. Lett. 2000, 77, 3860–3862. [Google Scholar] [CrossRef]
- Feng, X.L.; Zorman, C.A.; Mehregany, M.; Roukes, M.L. Dissipation in single-crystal 3C-SiC ultra-high frequency nanomechanical resonators. In Proceedings of the Solid-State Sensors, Actuators, and Microsystems Workshop, Hilton Head Island, SC, USA, 4–8 June 2006; p. 86. [Google Scholar]
- Kumar, A.; Rajauria, S.; Huo, H.; Ozsun, O.; Rykaczewski, K.; Kumar, J.; Ekinci, K.L. Surface area enhancement of microcantilevers by femto-second laser irradiation. Appl. Phys. Lett. 2012, 100, 141607. [Google Scholar] [CrossRef]
| (nm) | (gauss) | (N/m) | (N/m) | |
|---|---|---|---|---|
| 20 | 21.2 | |||
| 40 | 21.8 | |||
| 60 | 20.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.; Lee, E.J.; Kouh, T. Field-Dependent Resonant Behavior of Thin Nickel Film-Coated Microcantilever. Micromachines 2017, 8, 109. https://doi.org/10.3390/mi8040109
Park Y, Lee EJ, Kouh T. Field-Dependent Resonant Behavior of Thin Nickel Film-Coated Microcantilever. Micromachines. 2017; 8(4):109. https://doi.org/10.3390/mi8040109
Chicago/Turabian StylePark, Yunhee, Eun Joong Lee, and Taejoon Kouh. 2017. "Field-Dependent Resonant Behavior of Thin Nickel Film-Coated Microcantilever" Micromachines 8, no. 4: 109. https://doi.org/10.3390/mi8040109
APA StylePark, Y., Lee, E. J., & Kouh, T. (2017). Field-Dependent Resonant Behavior of Thin Nickel Film-Coated Microcantilever. Micromachines, 8(4), 109. https://doi.org/10.3390/mi8040109





