Swimming Characteristics of Bioinspired Helical Microswimmers Based on Soft Lotus-Root Fibers
Abstract
:1. Introduction
2. Swimming Characteristic of the Helical Microswimmers
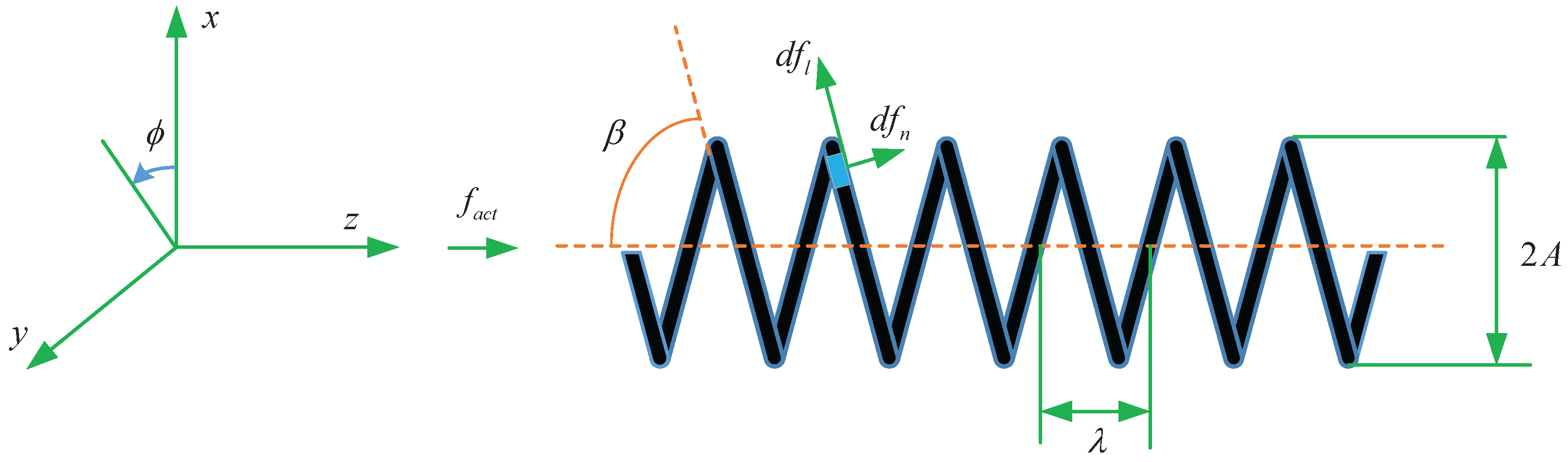
2.1. Theoretical Analysis of Rigid Helical Microswimmers
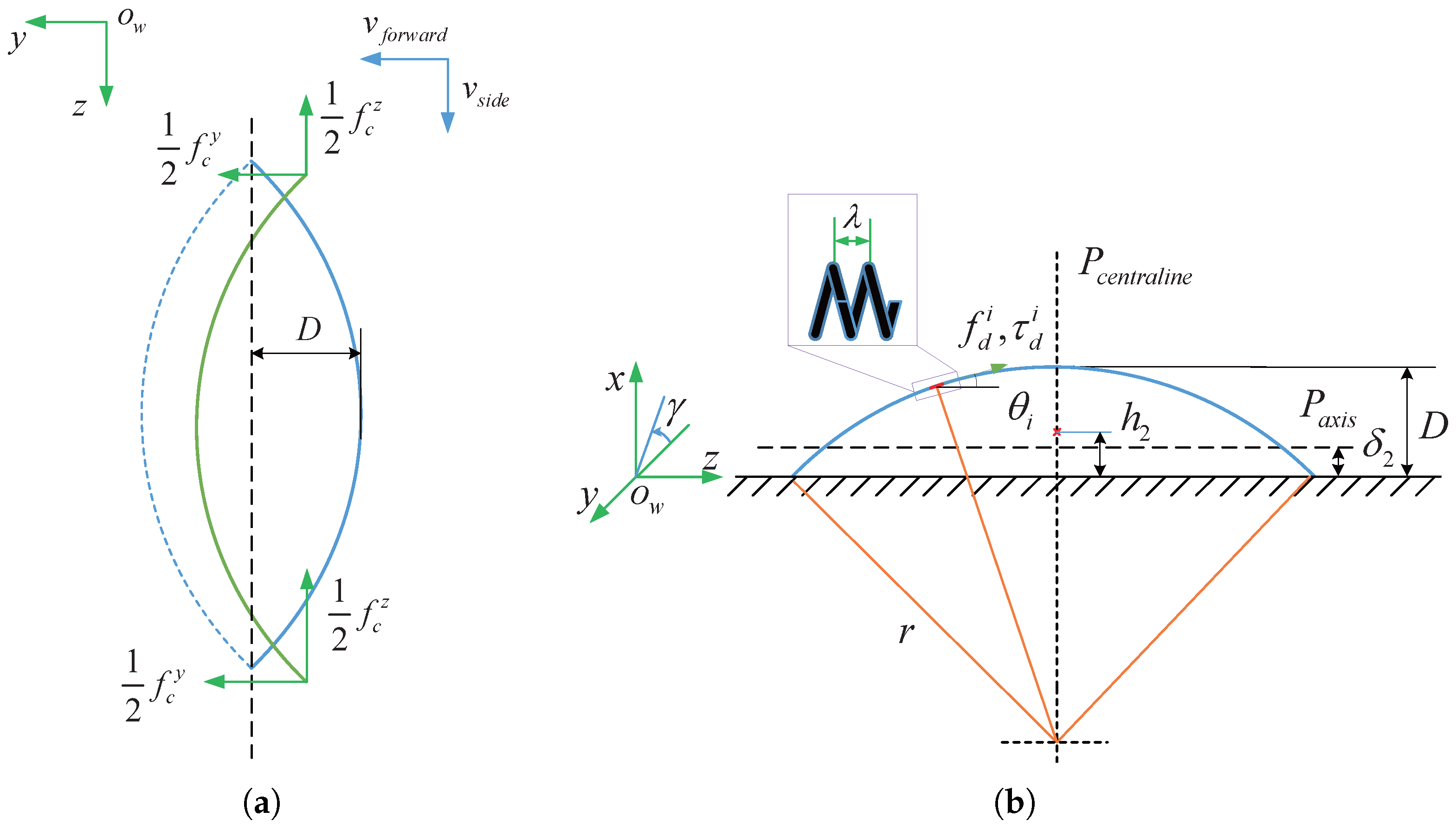
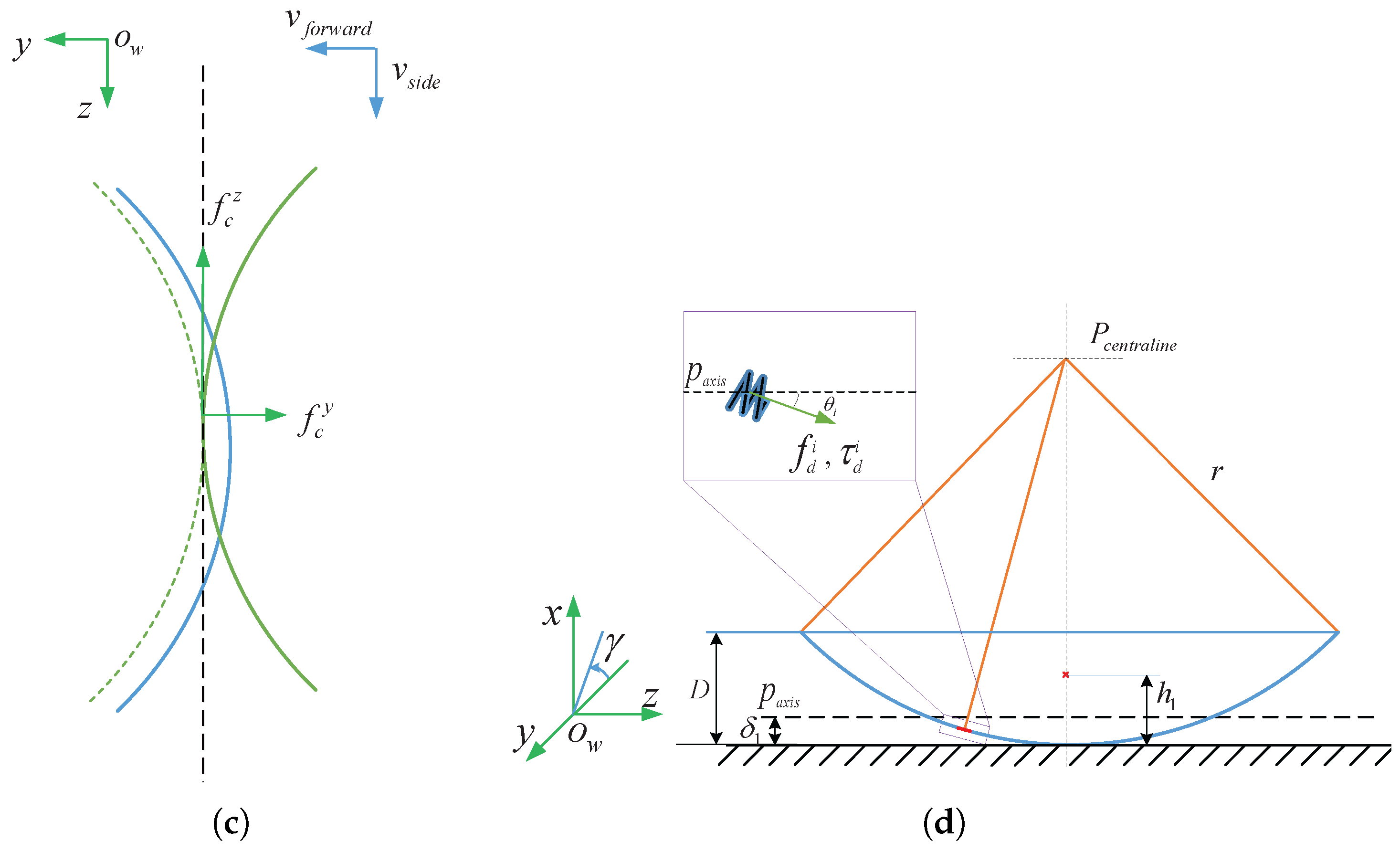
2.2. Analysis on Spindle-Like Rotation Locomotion Steps
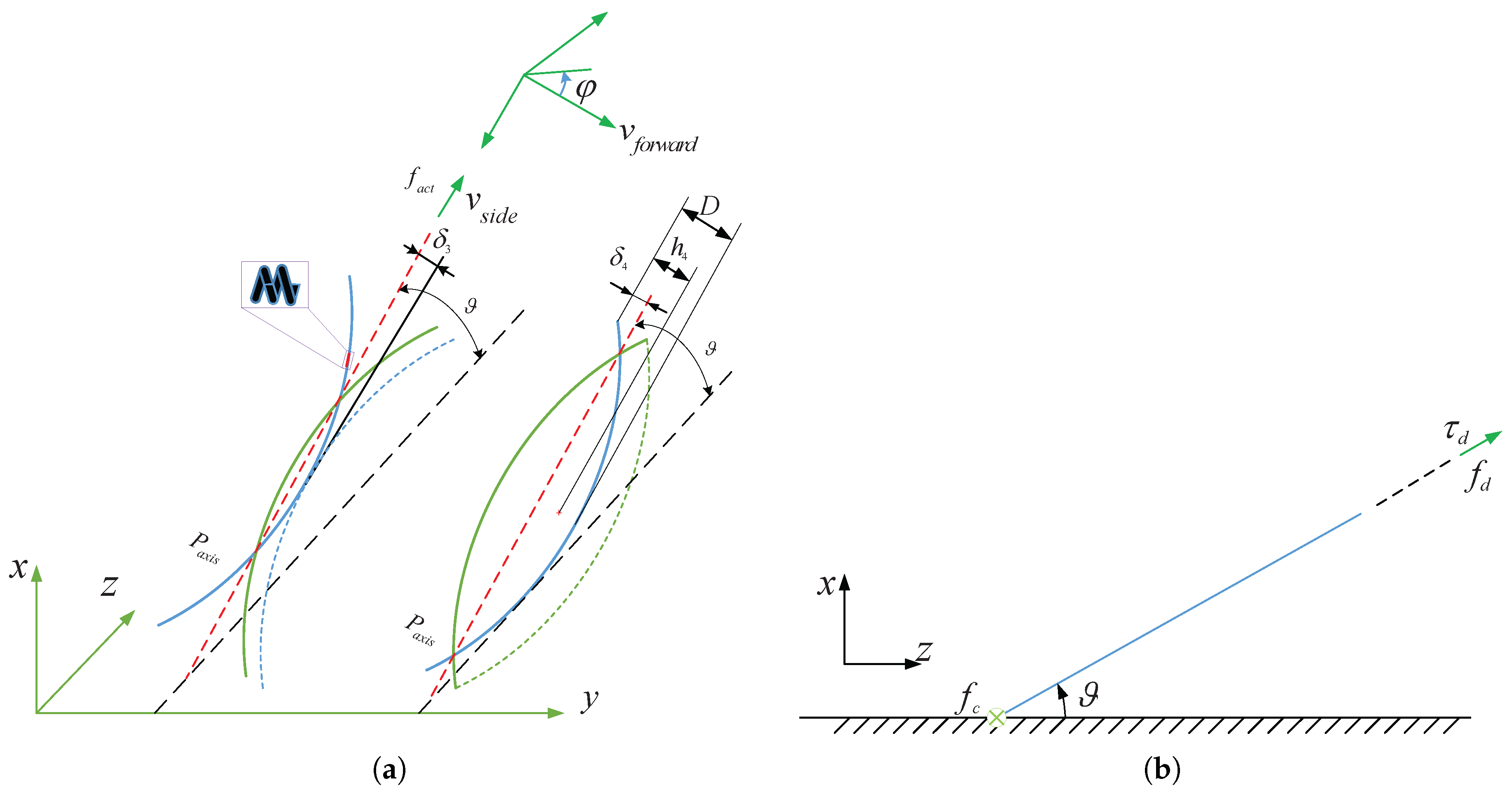
2.3. Theoretical Analysis of Soft Helical Microswimmers
3. Experimental Setup and Fabrication of the Helical Microswimmers
4. Results and Discussion
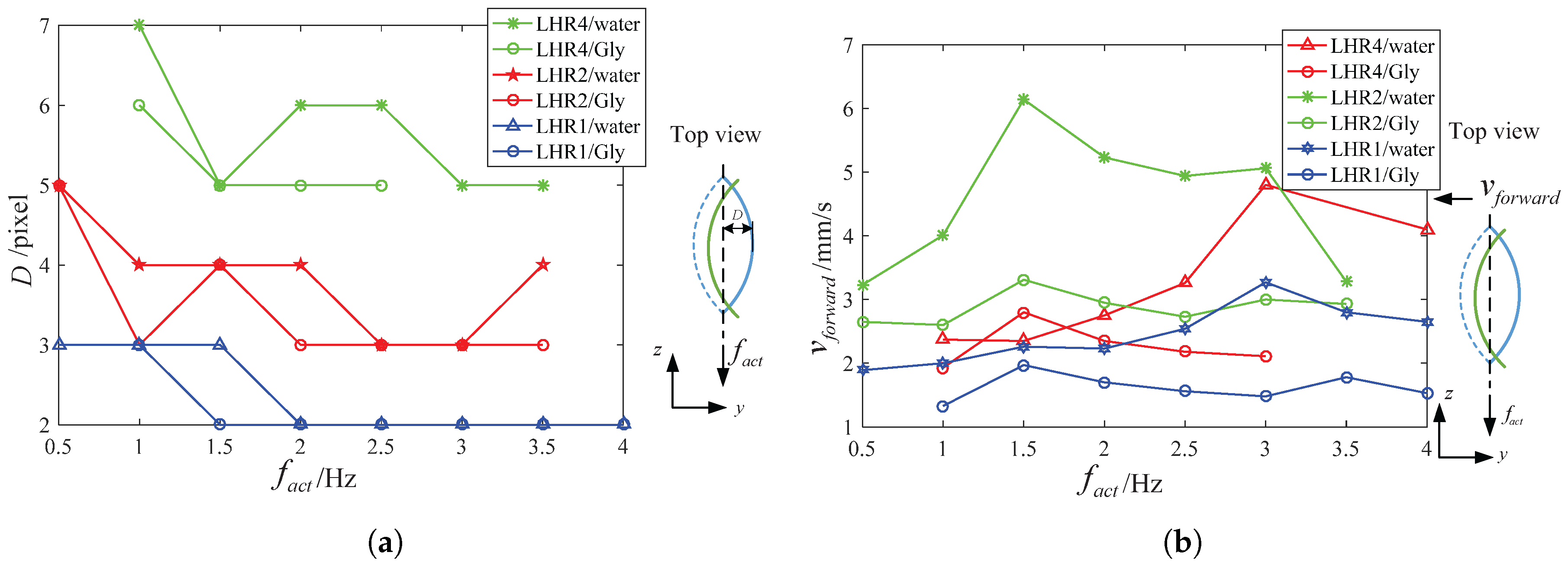
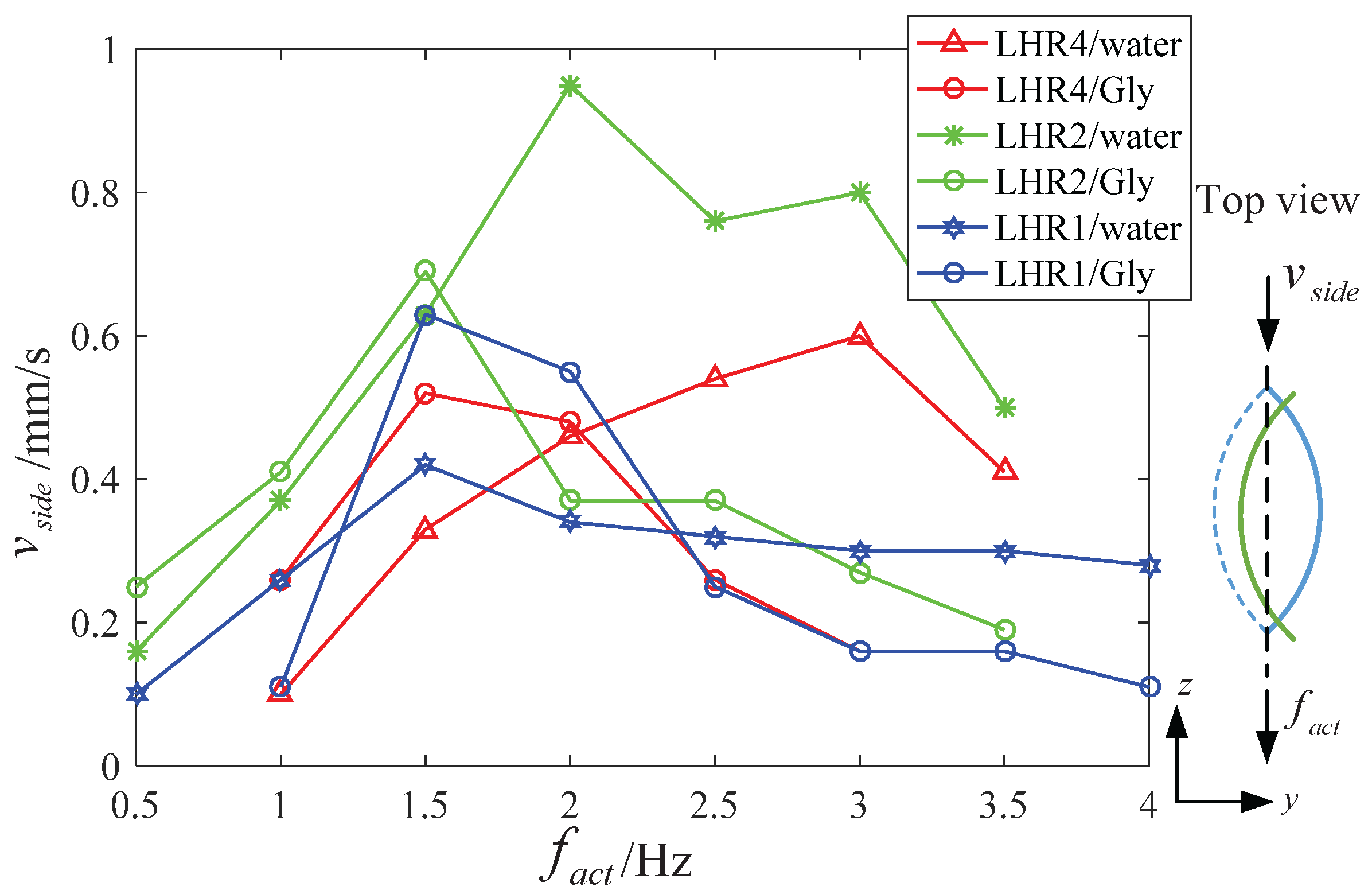
4.1. Experiments and Analysis on Spindle-like Rotation Locomotion
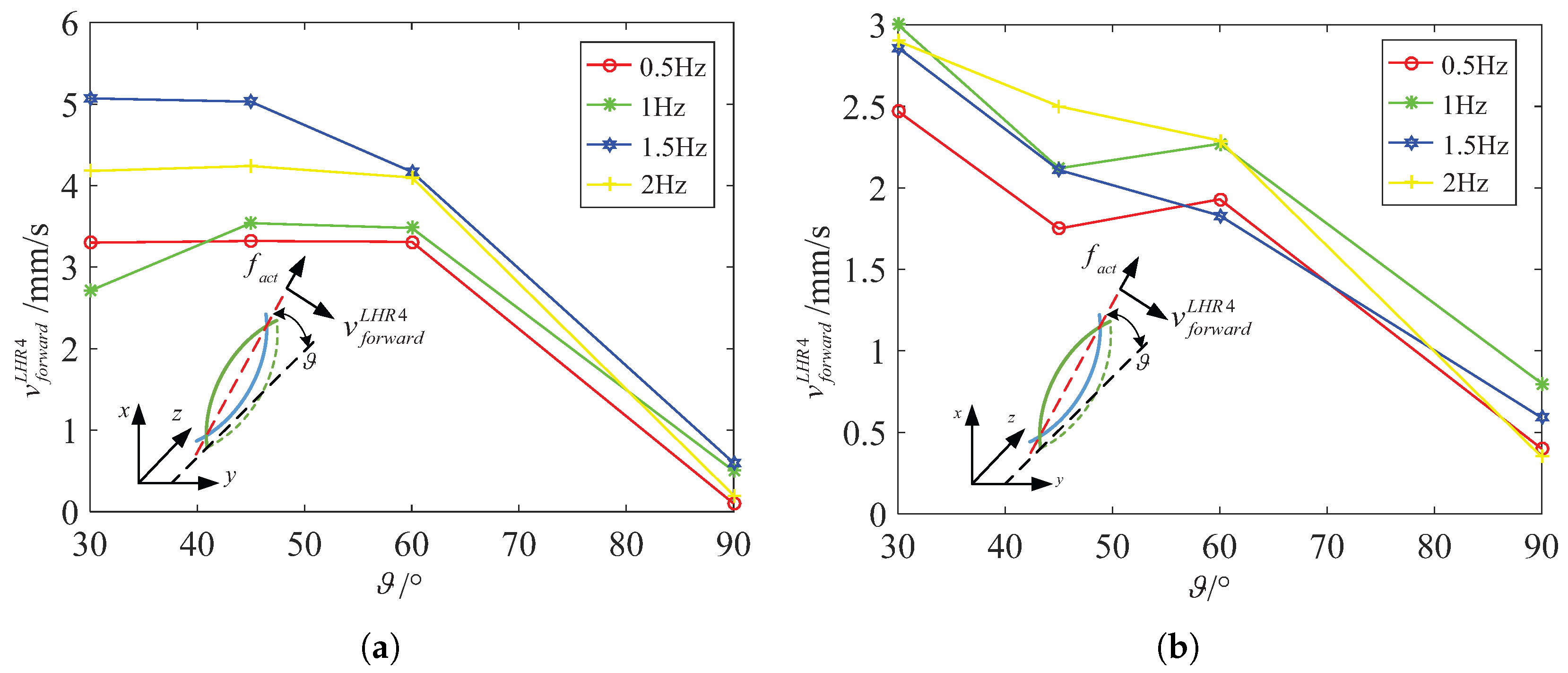
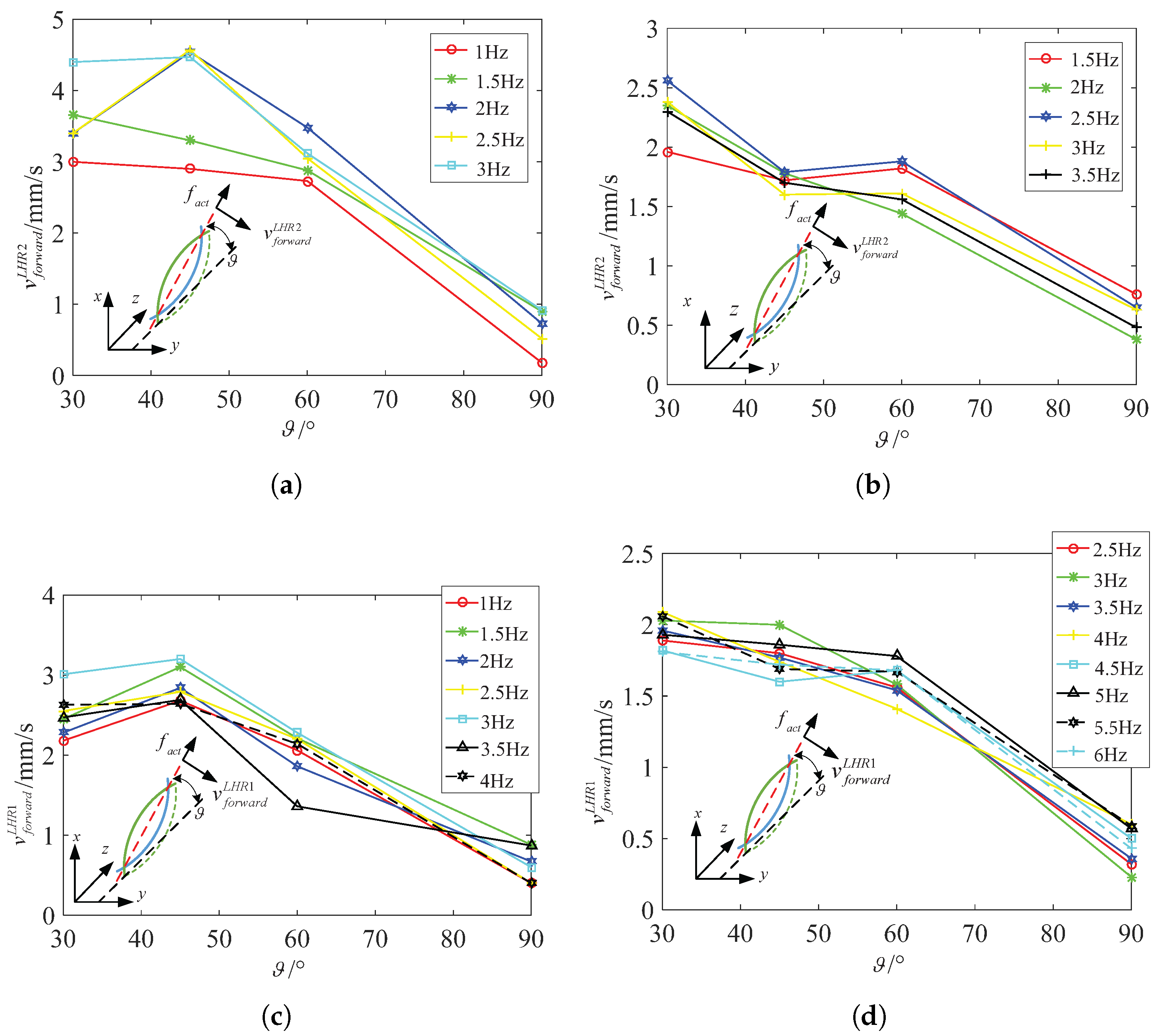
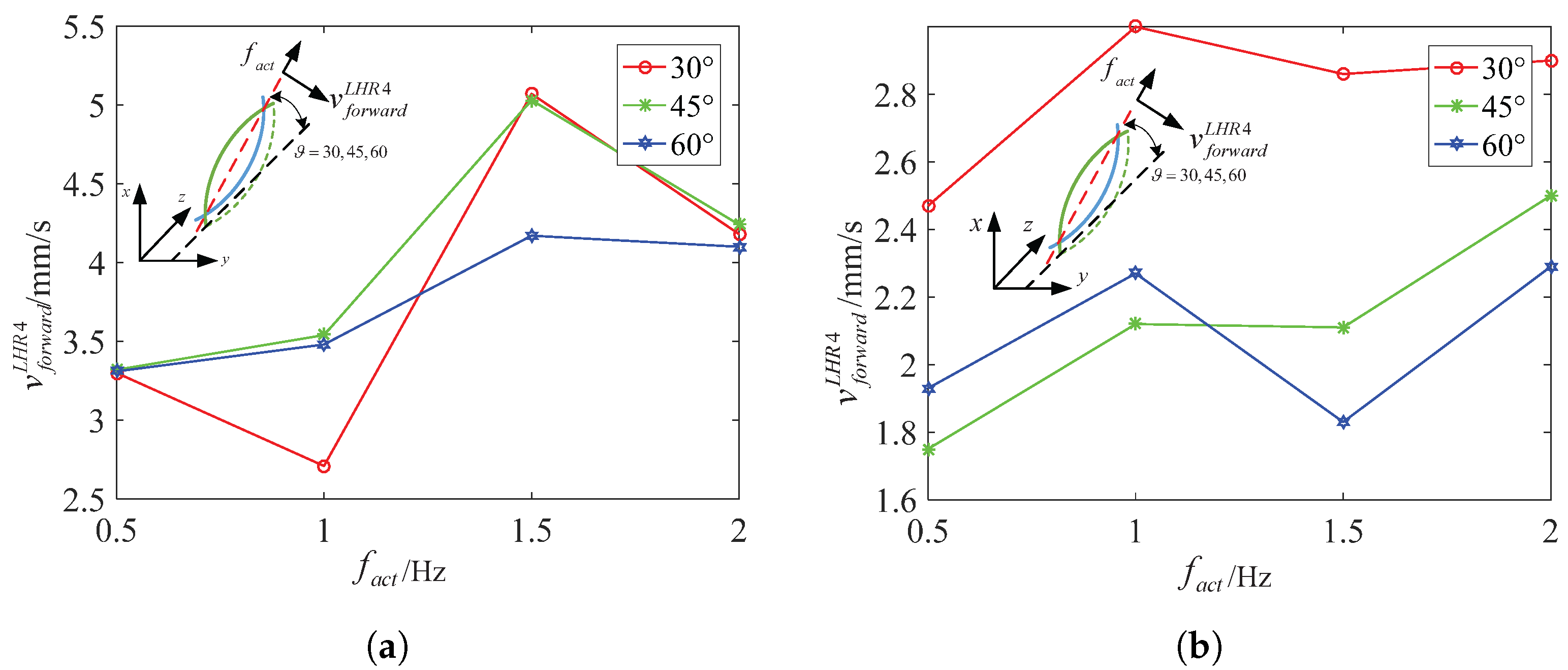
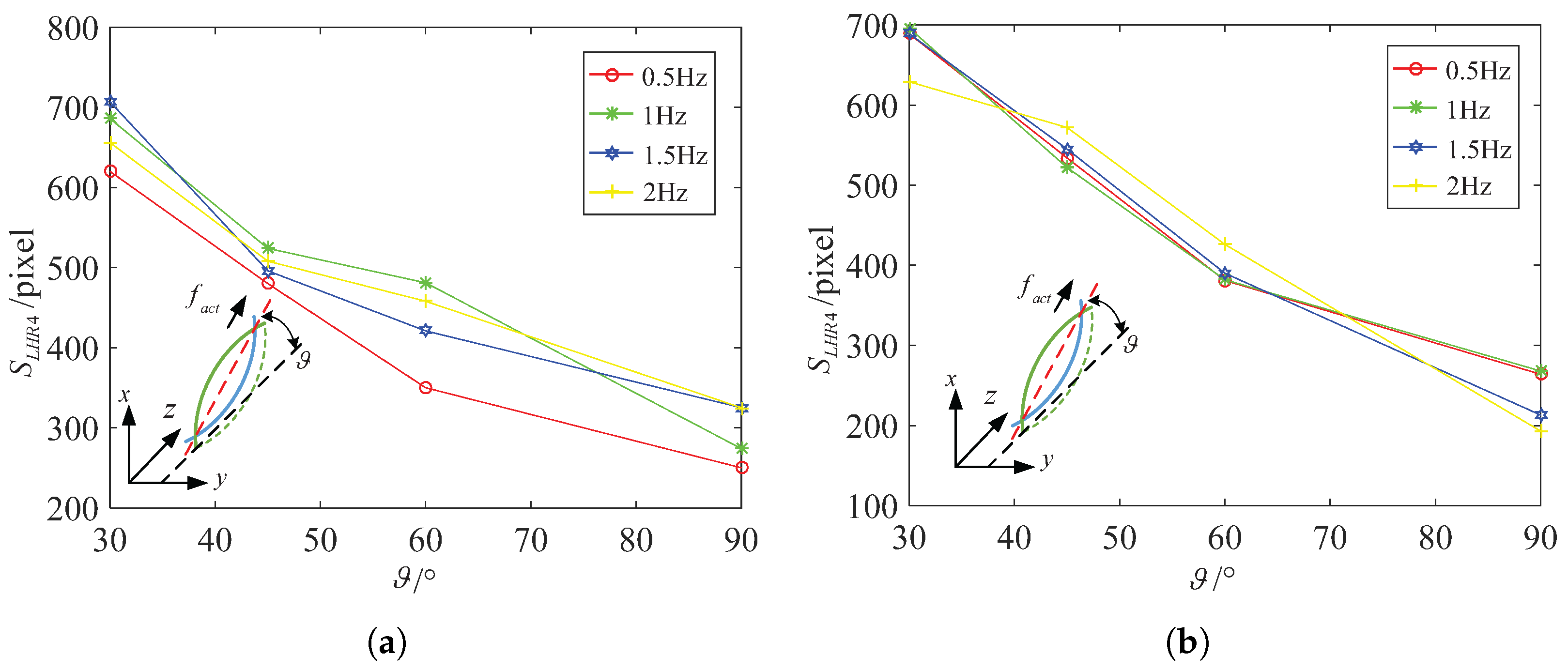
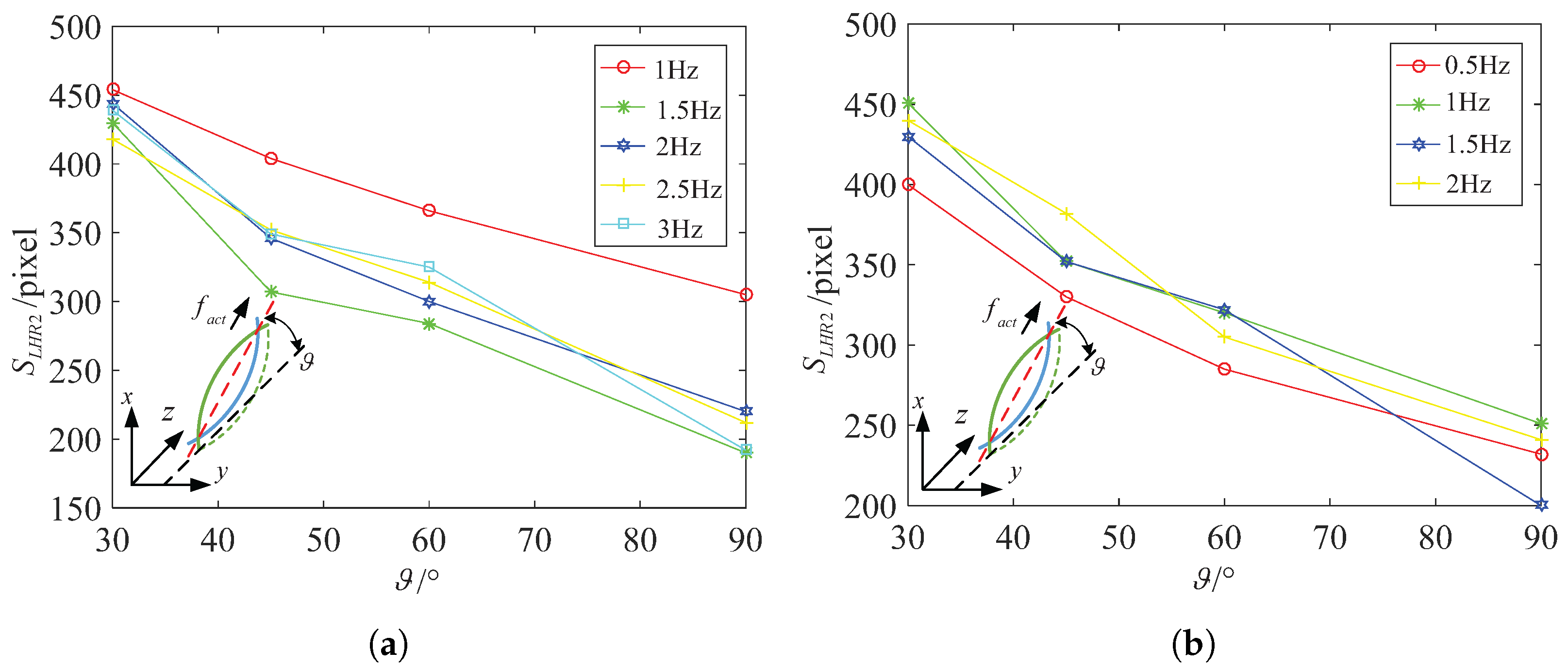
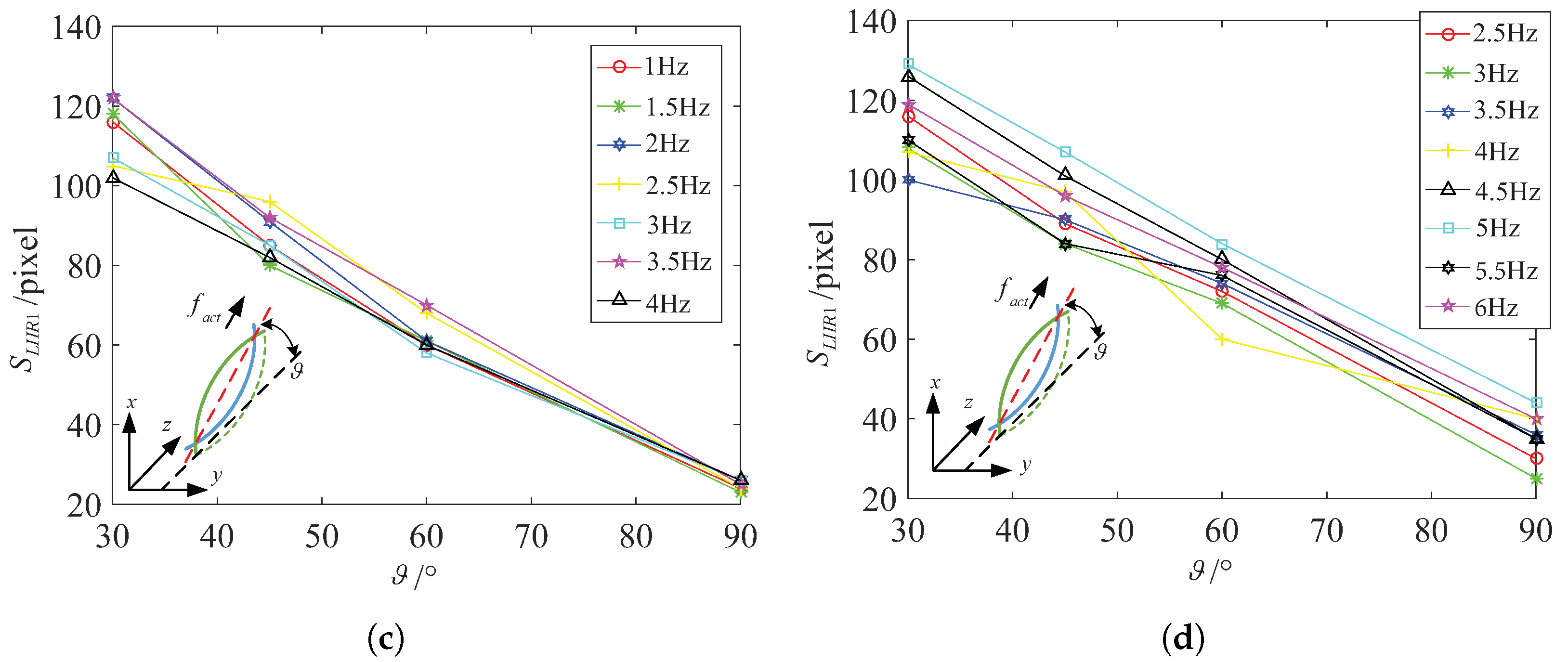
4.2. Experiments and Analysis on Spindle-Like Rotation Locomotion with an Inclination Angle
4.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nelson, B.; Kaliakatsos, I.; Abbott, J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef] [PubMed]
- Tottori, S.; Zhang, L.; Qiu, F.; Krawczyk, K.; Franco-Obregon, A.; Nelson, B. Magnetic helical micromachines: Fabrication, controlled swimming, and cargo transport. Adv. Mater. 2012, 24, 811–816. [Google Scholar] [CrossRef] [PubMed]
- Qiu, F.; Mhanna, R.; Zhang, L.; Ding, Y.; Fujita, S.; Nelson, B. Artificial bacterial flagella functionalized with temperature-sensitive liposomes for controlled release. Sens. Actuators B Chem. 2014, 196, 676–681. [Google Scholar] [CrossRef]
- Fischer, P.; Ghosh, A. Magnetically actuated propulsion at low Reynolds numbers: Towards nanoscale control. Nanoscale 2011, 3, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Hosseinidoust, Z.; Mostaghaci, B.; Yasa, O.; Park, B.; Singh, A.; Sitti, M. Bioengineered and biohybrid bacteria-based systems for drug delivery. Adv. Drug Deliv. Rev. 2016, 106, 27–44. [Google Scholar] [CrossRef] [PubMed]
- Park, B.; Zhuang, J.; Yasa, O.; Sitti, M. Multifunctional bacteria-driven microswimmers for targeted active drug delivery. ACS Nano 2017, 11, 8910–8923. [Google Scholar] [CrossRef] [PubMed]
- Stanton, M.; Park, B.; Vilela, D.; Bente, K.; Faivre, D.; Sitti, M. Magnetotactic bacteria powered biohybrids target E. Coli biofilms. ACS Nano 2017, 11, 9968–9978. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Gao, W.; Zhang, L.; Wang, J. Micro/nanorobots for biomedicine: Delivery, surgery, sensing, and detoxification. Sci. Robot. 2017, 2, eaam6431. [Google Scholar] [CrossRef]
- Peyer, K.; Zhang, L.; Nelson, B. Bio-inspired magnetic swimming microrobots for biomedical applications. Nanoscale 2013, 5, 1259–1272. [Google Scholar] [CrossRef] [PubMed]
- Peyer, K.; Tottori, S.; Qiu, F.; Zhang, L.; Nelson, B. Magnetic helical micromachines. Chem. A Eur. J. 2013, 19, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Khalil, I.; Tabak, A.; Sadek, K.; Mahdy, D.; Hamdi, N.; Sitti, M. Rubbing against blood clots using helical robots: Modeling and in vitro experimental validation. IEEE Robot. Autom. Lett. 2017, 2, 927–934. [Google Scholar] [CrossRef]
- Zhang, H.; Hutmacher, D.; Chollet, F.; Poo, A.; Burdet, E. Microrobotics and MEMS based fabrication techniques for scaffold based tissue engineering. Macromol. Biosci. 2005, 5, 477–489. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Peyer, K.; Nelson, B. Artificial bacterial flagella for micromanipulation. Lab Chip 2010, 10, 2203–2215. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Qiu, F.; Tung, H.; Peyer, K.; Shamsudhin, N.; Pokki, J.; Sakar, M.S. Cooperative manipulation and transport of microobjects using multiple helical microcarriers. RSC Adv. 2014, 4, 26771–26776. [Google Scholar] [CrossRef]
- Peyer, K.; Zhang, L.; Nelson, B. Localized non-contact manipulation using artificial bacterial flagella. Appl. Phys. Lett. 2011, 99, 174101. [Google Scholar] [CrossRef]
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef]
- Purcell, E. The efficiency of propulsion by a rotating flagellum. Proc. Natl. Acad. Sci. USA 1997, 94, 11307–11311. [Google Scholar]
- Qiu, T.; Lee, T.; Mark, A.; Morozov, K.; Munster, R.; Mierka, O.; Fischer, P. Swimming by reciprocal motion at low Reynolds number. Nat. Commun. 2014, 5, 5119. [Google Scholar] [CrossRef] [PubMed]
- Tottori, S.; Nelson, B. Artificial helical microswimmers with mastigoneme-inspired appendages. Biomicrofluidics 2013, 7, 061101. [Google Scholar] [CrossRef] [PubMed]
- Tabak, A.; Yesilyurt, S. Improved kinematic models for two-link helical micro/nanoswimmers. IEEE Trans. Robot. 2014, 30, 14–25. [Google Scholar]
- Erman, A.; Tabak, A. Resistive force theory based modeling and simulation of surface contact for swimming helical micro robots with channel flow. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Besacon, France, 8–11 July 2014; pp. 390–395. [Google Scholar]
- Nourmohammadi, H.; Keighobadi, J.; Bahrami, M. Design, dynamic modelling and control of a bio-inspired helical swimming microrobot with three-dimensional manoeuvring. Trans. Inst. Meas. Control 2016, 1, 1–10. [Google Scholar] [CrossRef]
- Mahoney, A.; Sarrazin, J.; Bamberg, E.; Abbott, J.J. Velocity control with gravity compensation for magnetic helical microswimmers. Adv. Robot. 2011, 25, 1007–1028. [Google Scholar] [CrossRef]
- Xu, T.; Hwang, G.; Andreff, N.; Régnier, S. Modeling and swimming property characterizations of scaled-up helical microswimmers. IEEE/ASME Trans. Mechatron. 2014, 19, 1069–1079. [Google Scholar] [CrossRef]
- Xu, T.; Hwang, G.; Andreff, N.; Régnier, S. Planar path following of 3-D steering scaled-up helical microswimmers. IEEE Trans. Robot. 2015, 31, 117–127. [Google Scholar] [CrossRef]
- Zhang, L.; Abbott, J.; Dong, L.; Kratochvil, B.; Bell, D.; Nelson, B. Artificial bacterial flagella: Fabrication and magnetic control. Appl. Phys. Lett. 2009, 94, 064107. [Google Scholar] [CrossRef]
- Tottori, S.; Zhang, L.; Peyer, K.; Nelson, B.J. Assembly, disassembly, and anomalous propulsion of microscopic helices. Nano Lett. 2013, 13, 4263–4268. [Google Scholar] [CrossRef] [PubMed]
- Schamel, D.; Mark, A.; Gibbs, J.; Miksch, C.; Morozov, K.; Leshansky, A.; Fischer, P. Nanopropellers and Their Actuation in Complex Viscoelastic Media. ACS Nano 2014, 8, 8794–8801. [Google Scholar] [CrossRef] [PubMed]
- Walker, D.; Kubler, M.; Morozov, K.; Fischer, P.; Leshansky, A. Optimal length of low reynolds number nanopropellers. Nano Lett. 2015, 15, 4412–4416. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Hwang, G.; Andreff, N.; Régnier, S. Influence of geometry on swimming performance of helical swimmers using doe. J. Micro-Bio Robot. 2016, 11, 57–66. [Google Scholar] [CrossRef]
- Qiu, F.; Fujita, S.; Mhanna, R.; Zhang, L.; Simona, B.; Nelson, B. Magnetic helical microswimmers functionalized with lipoplexes for targeted gene delivery. Adv. Funct. Mater. 2015, 25, 1666–1671. [Google Scholar] [CrossRef]
- Ghosh, A.; Fischer, P. Controlled propulsion of artificial magnetic nanostructured propellers. Nano Lett. 2009, 9, 2243–2245. [Google Scholar] [CrossRef] [PubMed]
- Qiu, F.; Zhang, L.; Peyer, K.; Casarosa, M.; Francoobregon, A.; Choi, H.; Nelson, B. Noncytotoxic artificial bacterial flagella fabricated from biocompatible ORMOCOMP and iron coating. J. Mater. Chem. B 2013, 2, 357–362. [Google Scholar] [CrossRef]
- Xu, T.; Yu, H.; Zhang, H.; Vong, C.I.; Zhang, L. Morphologies and swimming characteristics of rotating magnetic swimmers with soft tails at low Reynolds numbers. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1385–1390. [Google Scholar]
- Stanton, M.; Park, B.; Miguel, L.; Ma, X.; Sitti, M.; Sánchez, S. Biohybrid microtube swimmers driven by single captured bacteria. Small 2017, 13, 1603679. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Sattayasamitsathit, S.; Dong, R.; Gao, W.; Tam, R.; Feng, X. Template electrosynthesis of tailored-made helical nanoswimmers. Nanoscale 2014, 6, 9415–9420. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, T.; Xu, T.; Kiristi, M.; Liu, W.; Wu, Z. Magneto-acoustic hybrid nanomotor. Nano Lett. 2015, 15, 4814–4821. [Google Scholar] [CrossRef] [PubMed]
- Sitti, M.; Ceylan, H.; Hu, W.; Turan, M.; Yim, S.; Diller, E. Biomedical applications of untethered mobile milli/microrobots. Proc. IEEE 2015, 103, 205–224. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Feng, X.; Pei, A.; Kane, C.; Tam, R.; Hennessy, C.; Wang, J. Bioinspired helical microswimmers based on vascular plants. Nano Lett. 2013, 14, 305–310. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Zhou, Q.; Yu, J.; Xu, T.; Deng, Y.; Tang, T.; Feng, Q.; Bian, L.; Zhang, Y.; Ferreira, A.; et al. Magnetite nanostructured porous hollow helical microswimmers for targeted delivery. Adv. Funct. Mater. 2015, 25, 5333–5342. [Google Scholar] [CrossRef]
- Hancock, G. The self-propulsion of microscopic organisms through liquids. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; Royal Society: London, UK, 1953; Volume 217, pp. 96–121. [Google Scholar]
- Brennen, C.; Winet, H. Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 1977, 9, 339–398. [Google Scholar] [CrossRef]
- Smith, E.; Makarov, D.; Sanchez, S.; Fomin, V.; Schmidt, O. Magnetic microhelix coil structures. Phys. Rev. Lett. 2011, 107, 097204. [Google Scholar] [CrossRef] [PubMed]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Xu, T.; Guan, Y.; Yan, X.; Ye, C.; Wu, X. Swimming Characteristics of Bioinspired Helical Microswimmers Based on Soft Lotus-Root Fibers. Micromachines 2017, 8, 349. https://doi.org/10.3390/mi8120349
Liu J, Xu T, Guan Y, Yan X, Ye C, Wu X. Swimming Characteristics of Bioinspired Helical Microswimmers Based on Soft Lotus-Root Fibers. Micromachines. 2017; 8(12):349. https://doi.org/10.3390/mi8120349
Chicago/Turabian StyleLiu, Jia, Tiantian Xu, Yanming Guan, Xiaohui Yan, Chengwei Ye, and Xinyu Wu. 2017. "Swimming Characteristics of Bioinspired Helical Microswimmers Based on Soft Lotus-Root Fibers" Micromachines 8, no. 12: 349. https://doi.org/10.3390/mi8120349
APA StyleLiu, J., Xu, T., Guan, Y., Yan, X., Ye, C., & Wu, X. (2017). Swimming Characteristics of Bioinspired Helical Microswimmers Based on Soft Lotus-Root Fibers. Micromachines, 8(12), 349. https://doi.org/10.3390/mi8120349





