Design and Fabrication of Capacitive Silicon Nanomechanical Resonators with Selective Vibration of a High-Order Mode
Abstract
:1. Introduction
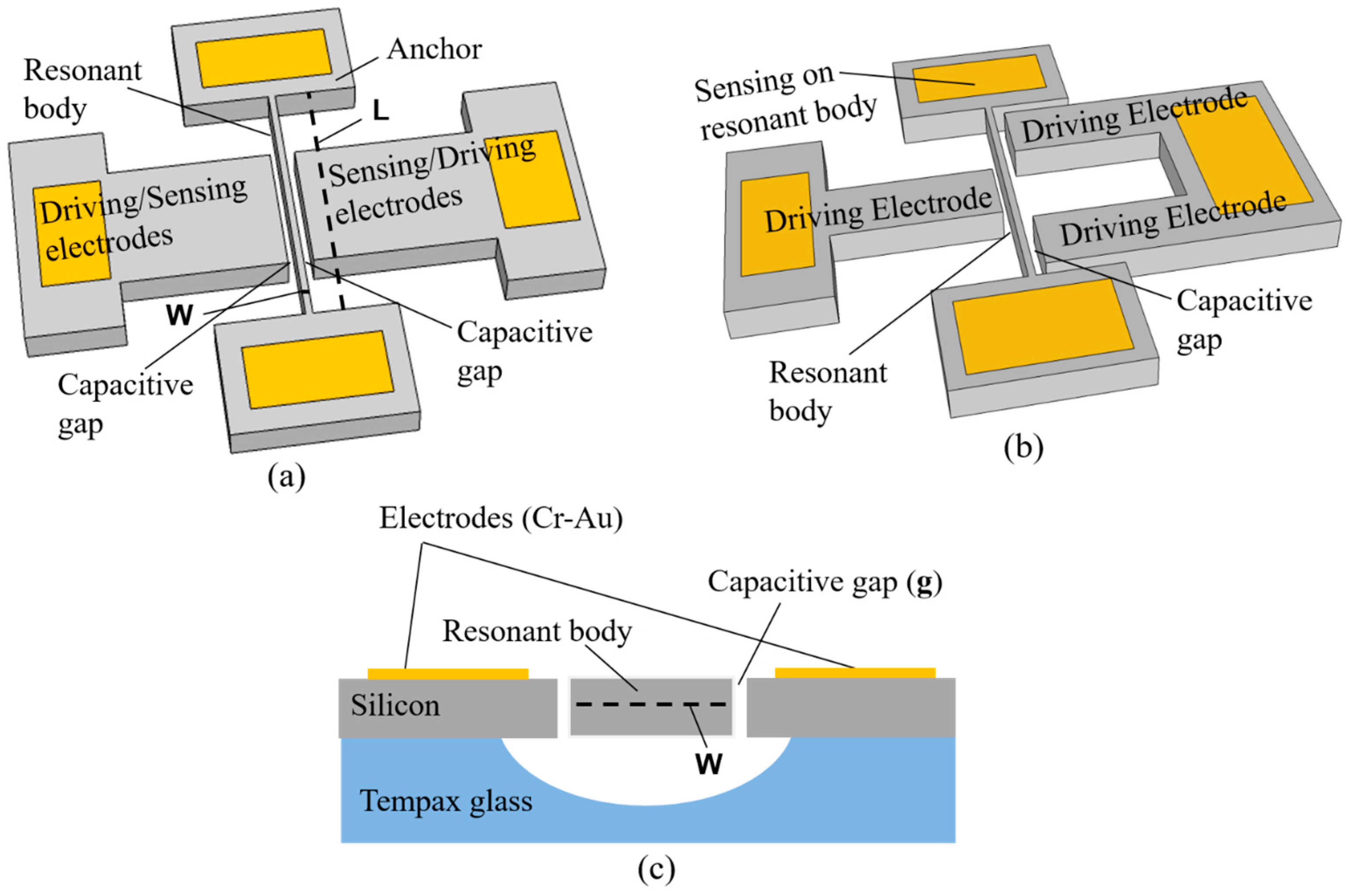
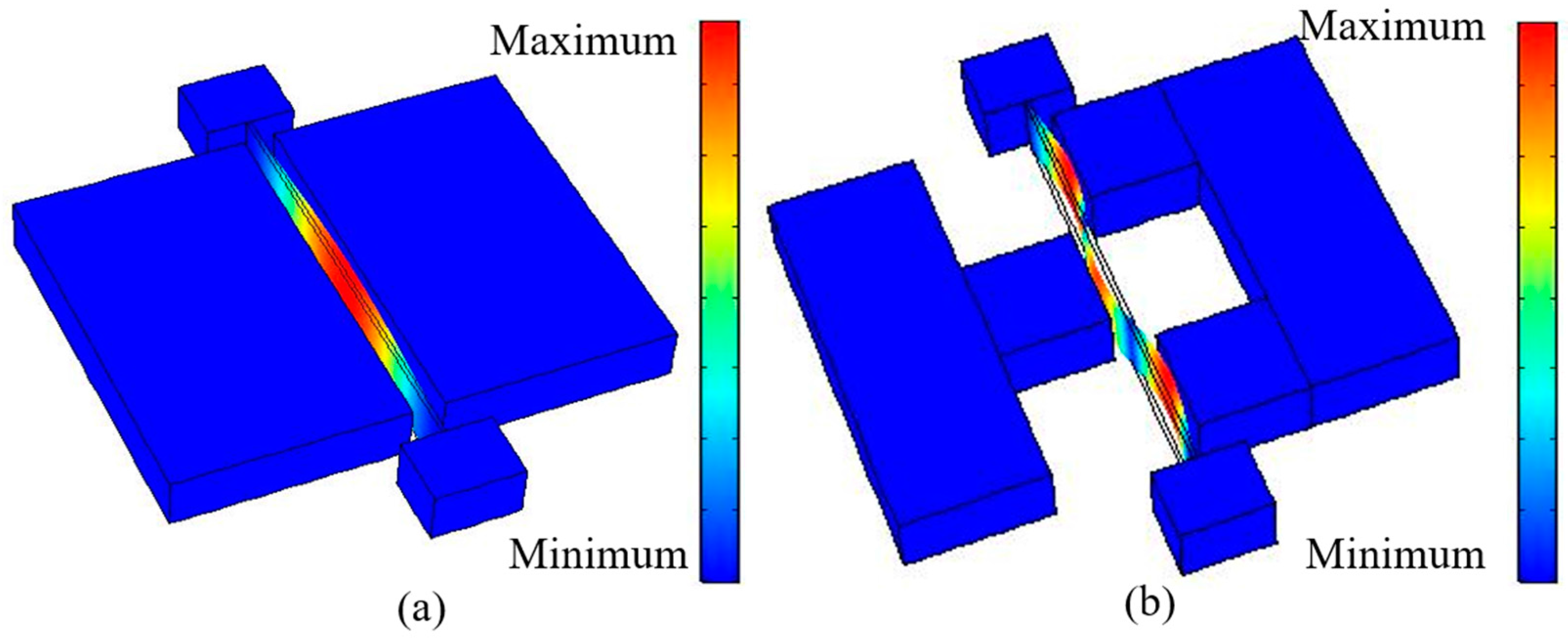
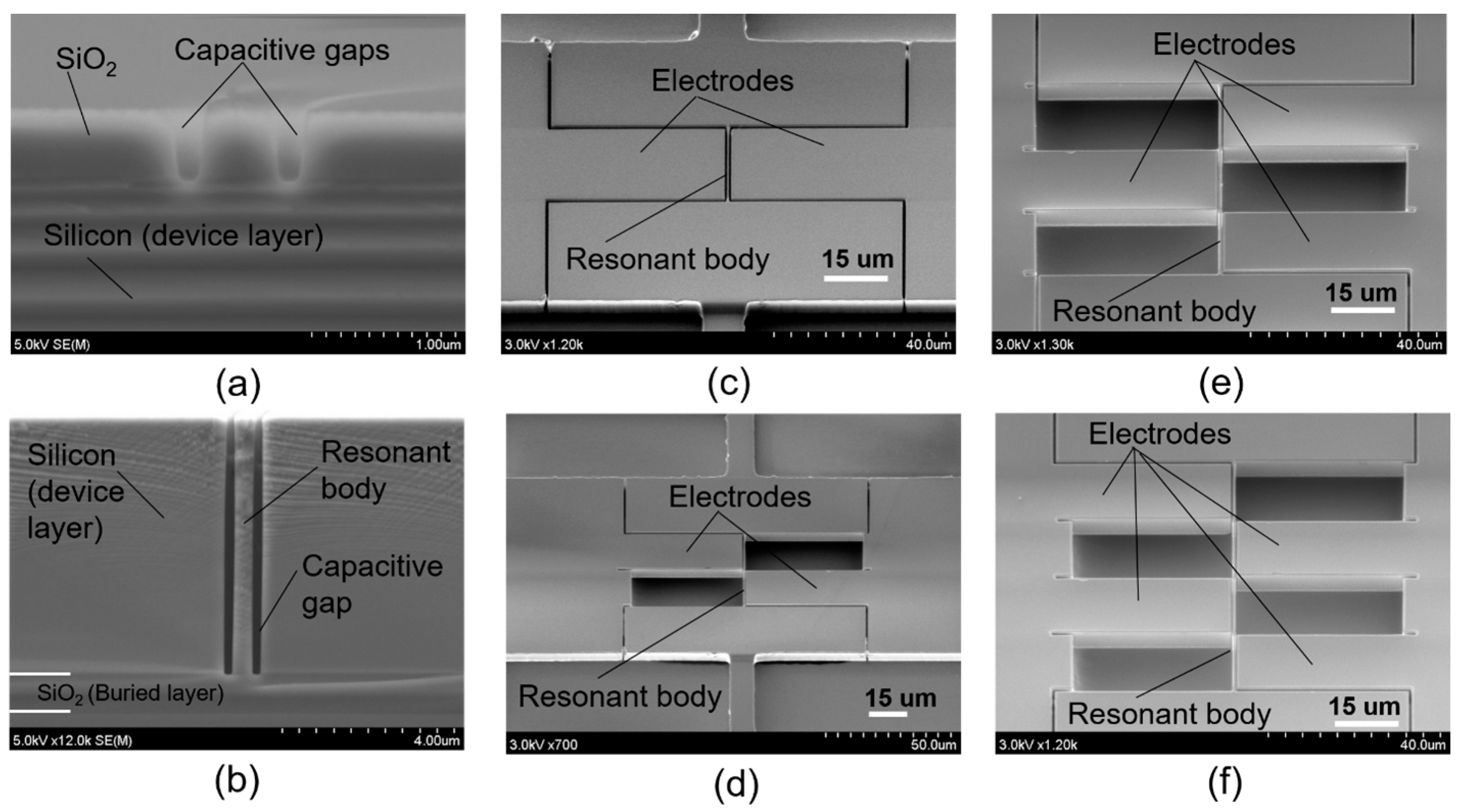
2. Device Description
3. Experiments
3.1. Experimental Methodology
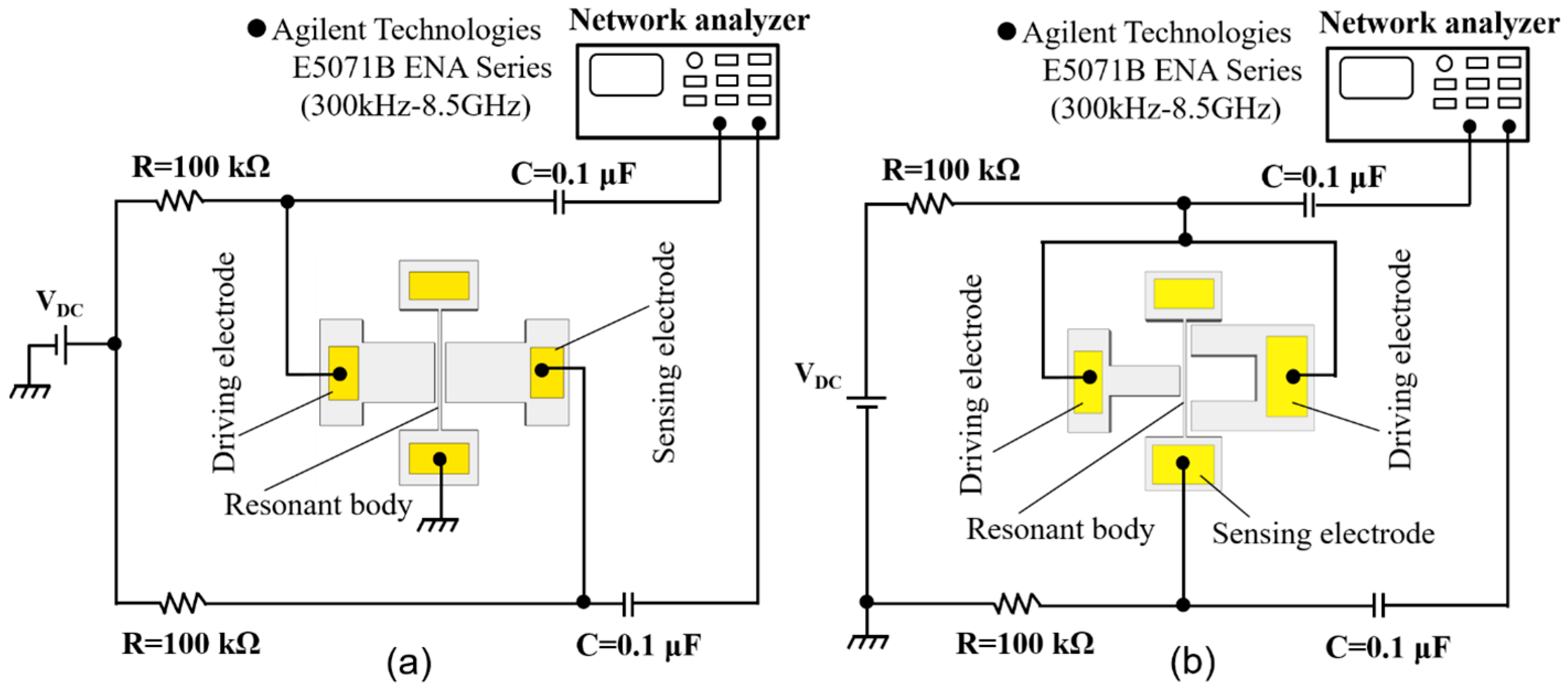
3.2. Measurement Setup
3.3. Measurement Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IoT Devices and Local Networks. Available online: https://www.micrium.com/iot/devices/ (accessed on 11 September 2017).
- Gallio, S.; Goryachev, M.; Abbe, P.; Vacheret, X.; Tobar, M.E.; Bourquin, R. Quality factor measurement of various type of quartz crystal resonator operating near 4K. IEEE Trans. Ulrtason. Ferroelectr. Freq. Control 2016, 63, 975–980. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, R.; Sakamoto, K.; Watanabe, Y. Method for improving quality factor in crystal oscillators with duplicated quartz resonator. In Proceedings of the 34th Symposium on Ultrasonic Electronics, Tokyo, Japan, 20–22 November 2013; Volume 34, pp. 259–260. [Google Scholar]
- Murizaki, Y.; Sakuma, S.; Arai, F. Microfabrication of wide-measurement-range load sensor using quartz crystal resonator. In Proceedings of the 28th IEEE International Conference on MEMS, Estoril, Portugal, 18–22 January 2015; pp. 833–836. [Google Scholar]
- Spassov, L.; Gadjanova, V.; Velcheva, R.; Dulmet, B. Short and long term stability of resonant quartz temperature sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 1626–1631. [Google Scholar] [CrossRef] [PubMed]
- Murozaki, Y.; Arai, F. Wide range load sensor using quartz crystal resonator for detection of biological signals. IEEE Sens. J. 2015, 15, 1913–1919. [Google Scholar] [CrossRef]
- Van Beek, J.T.M.; Puers, R. A review of MEMS oscillators for frequency reference and timing applications. J. Micromech. Microeng. 2011, 22, 013001. [Google Scholar] [CrossRef]
- Nguyen, C.T.C. MEMS technology for timing and frequency control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 251–270. [Google Scholar] [CrossRef] [PubMed]
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.Y.; Nabki, F. Micromachined resonators: A review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef]
- Toan, N.V.; Miyashita, H.; Toda, M.; Kawai, Y.; Ono, T. Fabrication of an hermetically packaged silicon resonator on LTCC substrate. Microsyst. Technol. 2013, 19, 1165–1175. [Google Scholar] [CrossRef]
- Toan, N.V.; Toda, M.; Kawai, Y.; Ono, T. A capacitive silicon resonator with movable electrode structure for gap width reduction. J. Micromech. Microeng. 2014, 24, 025006. [Google Scholar] [CrossRef]
- Toan, N.V.; Nha, N.V.; Song, Y.; Ono, T. Fabrication and evaluation of capacitive silicon resonators with piezoresistive heat engines. Sens. Actuator A Phys. 2017, 262, 99–107. [Google Scholar] [CrossRef]
- Toan, N.V.; Toda, M.; Kawai, Y.; Ono, T. A long bar type silicon resonator with a high quality factor. IEEJ Trans. Sens. Micromach. 2014, 134, 26–31. [Google Scholar] [CrossRef]
- Bahreyni, B. Fabrication and Design of Resonant Microdevices; William Andrew Inc.: Norwich, NY, USA, 2008. [Google Scholar]
- Ho, G.K.; Sundaresan, K.; Pourkamali, S.; Ayazi, F. Low motional impedance highly tunable I2 resonators for temperature compensated reference oscillators. In Proceedings of the 18th IEEE International Conference on MEMS, Miami Beach, FL, USA, 30 January–3 February 2005; pp. 116–120. [Google Scholar]
- Hao, Z.; Erbil, A.; Ayazi, F. An analytical model for support loss in micromachined beam resonators with in-plane flexural vibrations. Sens. Actuators A Phys. 2003, 109, 156–164. [Google Scholar] [CrossRef]
- Yasumura, K.Y.; Stowe, T.D.; Chow, E.M.; Pafman, T.; Kenny, T.W.; Stipe, B.C.; Rugar, D. Quality factor in micro-and submicron-thick cantilevers. J. Microelectromech. Syst. 2000, 9, 117–125. [Google Scholar] [CrossRef]
- Lifshitz, R.; Roukes, M.L. Thermoelastic damping in micro and nanomechanical systems. Phys. Rev. B 2000, 61, 5600. [Google Scholar] [CrossRef]
- Duwel, A.; Weinstein, M.; Gorman, J.; Borenstein, J.; Ward, P. Quality factors of MEMS gyros and the role of thermoelastic damping. In Proceedings of the 15th IEEE International Conference on MEMS, Las Vegas, NV, USA, 24 January 2000; pp. 214–219. [Google Scholar]
- Pourkamali, S.; Hashimura, A.; Abdolvand, R.; Ho, G.K.; Erbil, A.; Ayazi, F. High Q single crystal silicon HARPSS capacitive beam resonator with self-aligned sub-100 nm transduction gaps. J. Microelectromech. Syst. 2003, 12, 487–496. [Google Scholar] [CrossRef]
- Lee, J.E.Y.; Yan, J.; Seshia, A.A. Low loss HF band SOI wine glass bulk mode capacitive square-plate resonator. J. Micromech. Microeng. 2009, 19, 074003. [Google Scholar] [CrossRef]
- Toan, N.V.; Kubota, T.; Sekhar, H.; Samukawa, S.; Ono, T. Mechanical quality factor enhancement in a silicon micromechanical resonator by low-damage process using neutral beam etching technology. J. Micromech. Microeng. 2014, 24, 085005. [Google Scholar] [CrossRef]


| Resonator Structures | Vibration Modes | First Mode | Second Mode | Third Mode | Fourth Mode |
|---|---|---|---|---|---|
| Parameters | Resonant length | 21.3 μm | 35.5 μm | 49.3 μm | 63.3 μm |
| Resonant width | 0.5 μm | 0.5 μm | 0.5 μm | 0.5 μm | |
| Resonant thickness | 7 μm | 7 μm | 7 μm | 7 μm | |
| Capacitive gap | 0.3 μm | 0.3 μm | 0.3 μm | 0.3 μm | |
| Number of driving electrodes | 1 | 2 | 3 | 4 | |
| Calculation | Frequency | 9.66 MHz | 9.60 MHz | 9.73 MHz | 9.79 MHz |
| Finite element method (FEM) Simulation | Frequency | 9.71 MHz | 9.68 MHz | 9.73 MHz | 9.78 MHz |
| Vibration mode (resonant body only) |  |  |  |  |
| Resonator Structures | Vibration Modes | First Mode | Second Mode | Third Mode | Fourth Mode |
|---|---|---|---|---|---|
| Measurement conditions | VAC | 0 dBm | 0 dBm | 0 dBm | 0 dBm |
| VDC | 15 V | 15 V | 15 V | 15 V | |
| Pressure level | 0.01 Pa | 0.01 Pa | 0.01 Pa | 0.01 Pa | |
| Experimental results | Resonant frequency | 10.15 MHz | 10.85 MHz | 10.85 MHz | 10.36 MHz |
| Quality factor | 10078 | 8768 | 4255 | 844 | |
| Insertion loss | −75 dB | −71 dB | −65.6 dB | −51.5 dB | |
| Motional resistance | 281 kΩ | 181 kΩ | 95 kΩ | 18.7 kΩ |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toan, N.V.; Shimazaki, T.; Inomata, N.; Song, Y.; Ono, T. Design and Fabrication of Capacitive Silicon Nanomechanical Resonators with Selective Vibration of a High-Order Mode. Micromachines 2017, 8, 312. https://doi.org/10.3390/mi8100312
Toan NV, Shimazaki T, Inomata N, Song Y, Ono T. Design and Fabrication of Capacitive Silicon Nanomechanical Resonators with Selective Vibration of a High-Order Mode. Micromachines. 2017; 8(10):312. https://doi.org/10.3390/mi8100312
Chicago/Turabian StyleToan, Nguyen Van, Tsuyoshi Shimazaki, Naoki Inomata, Yunheub Song, and Takahito Ono. 2017. "Design and Fabrication of Capacitive Silicon Nanomechanical Resonators with Selective Vibration of a High-Order Mode" Micromachines 8, no. 10: 312. https://doi.org/10.3390/mi8100312
APA StyleToan, N. V., Shimazaki, T., Inomata, N., Song, Y., & Ono, T. (2017). Design and Fabrication of Capacitive Silicon Nanomechanical Resonators with Selective Vibration of a High-Order Mode. Micromachines, 8(10), 312. https://doi.org/10.3390/mi8100312






