Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems
Abstract
1. Introduction
2. Materials and Methods
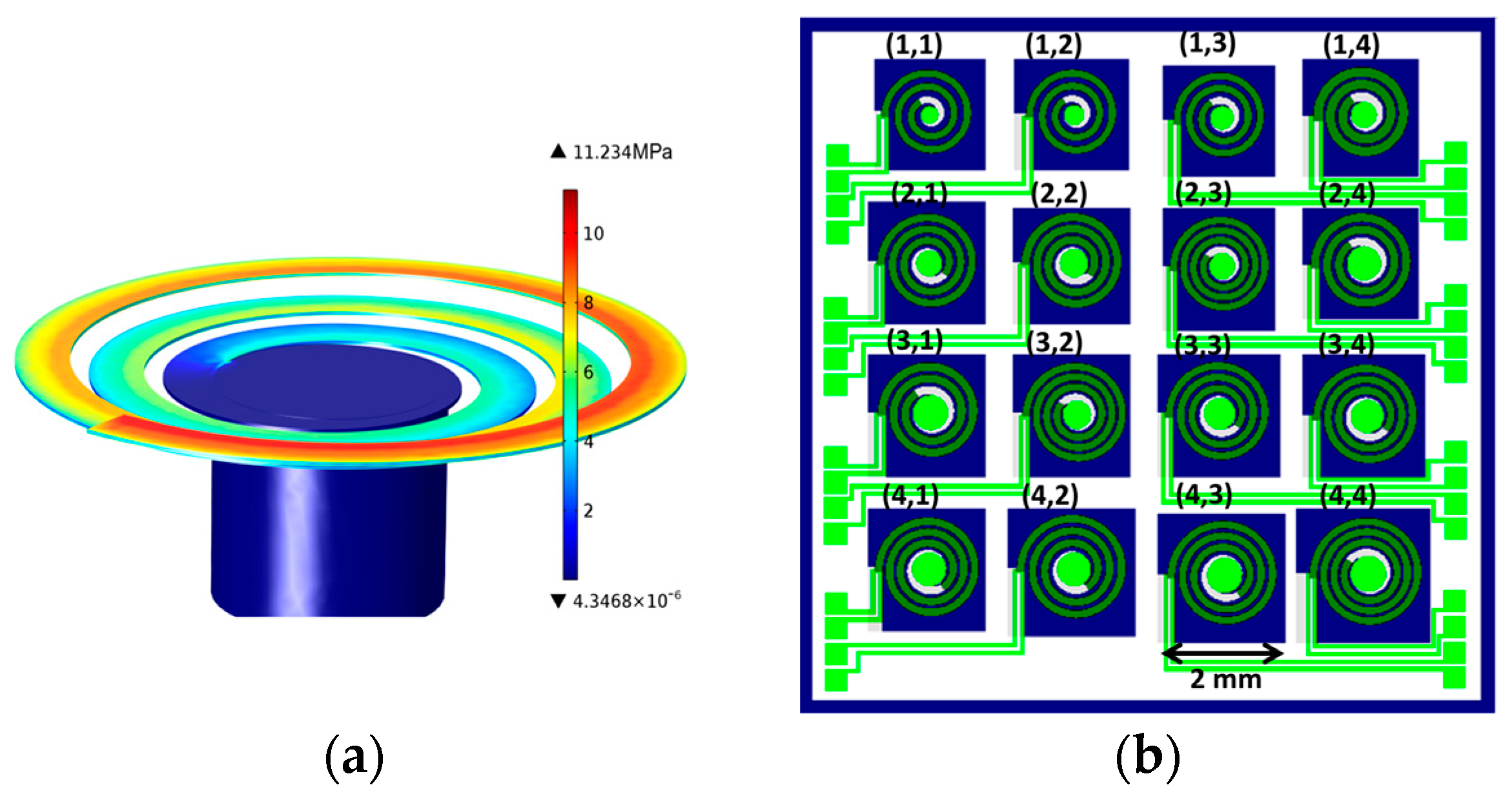
2.1. Cantilever Design
2.2. Analytical Model
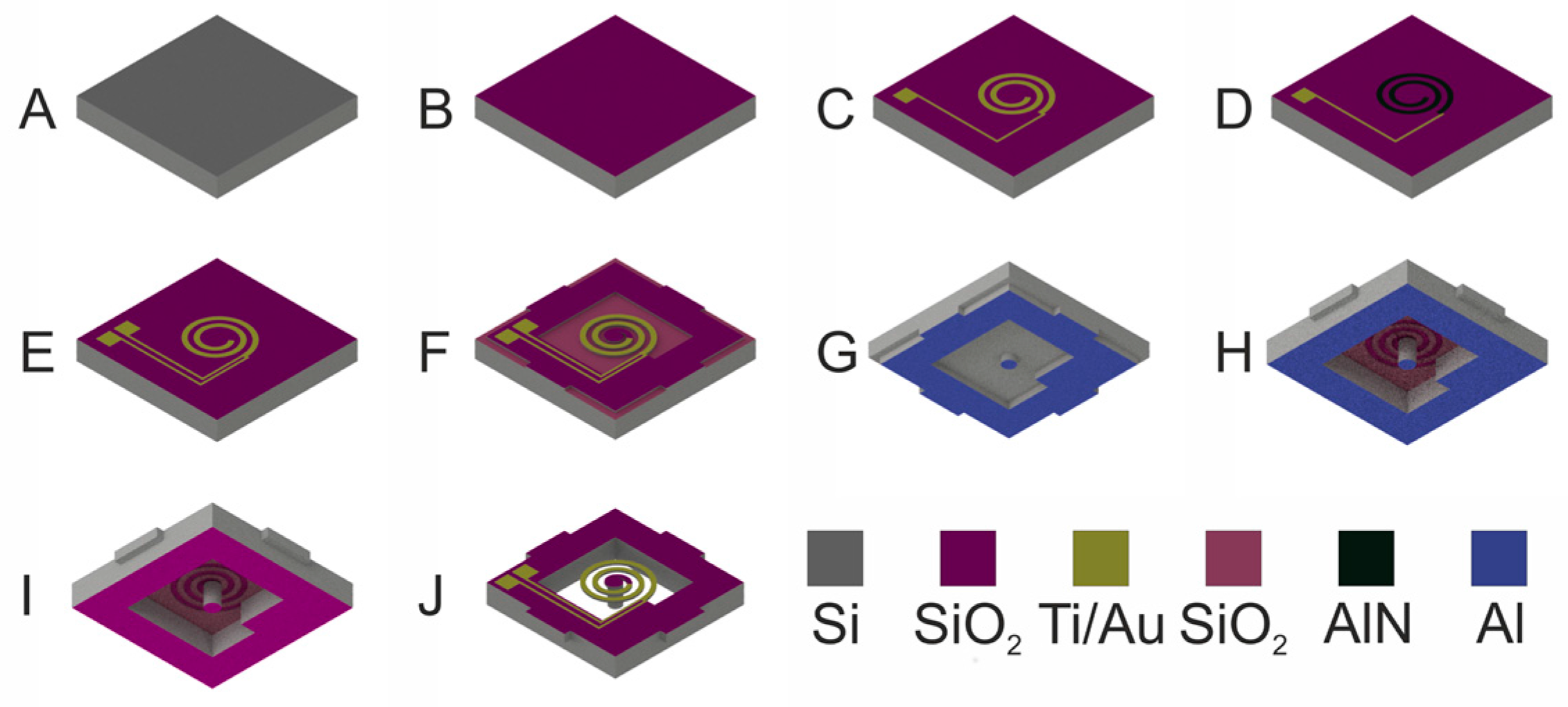
2.3. Fabrication
2.4. Characterization
3. Results and Discussion
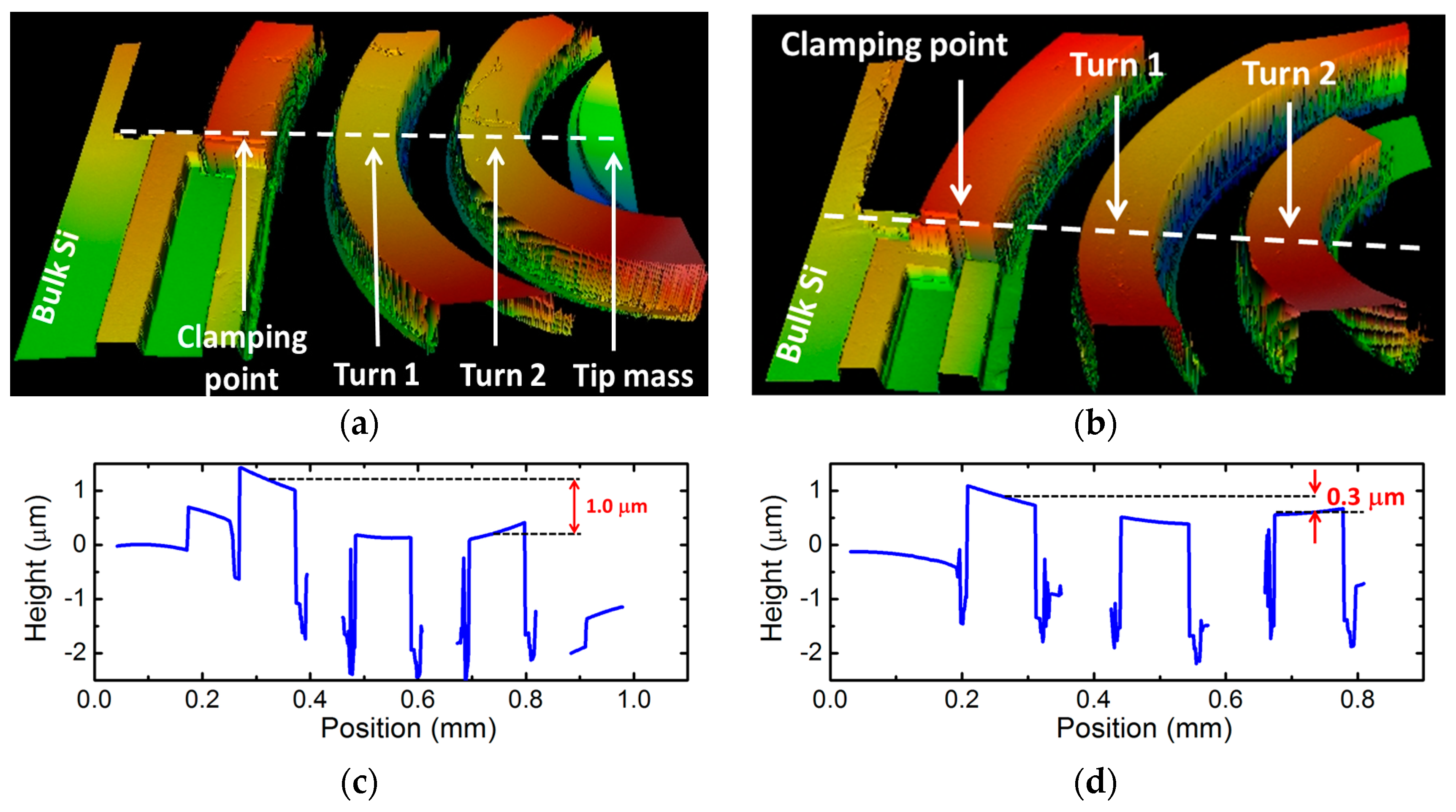
3.1. Structural Characterization
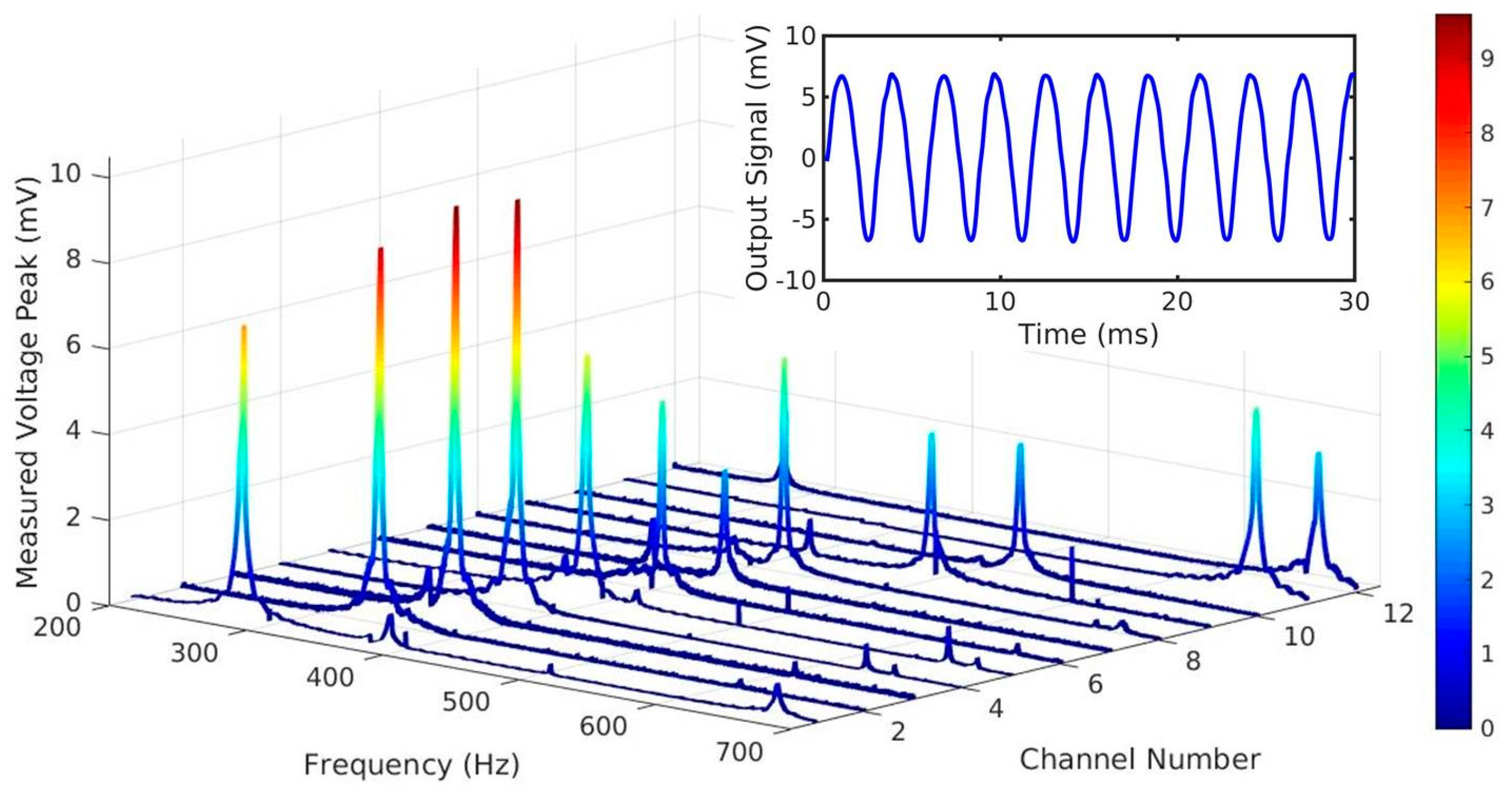
3.2. Vibration Tests and Validation of the Analytical Model
3.3. Resonant Modes
3.4. Applicability in FICI
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wilson, B.S.; Dorman, M.F. Cochlear implants: Current designs and future possibilities. J. Rehabil. Res. Dev. 2008, 45, 695–730. [Google Scholar] [CrossRef] [PubMed]
- Cohen, N. The totally implantable cochlear implant. Ear Hear. 2007, 28. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Bintz, L.; Anderson, D.Z.; Bright, K.E. A life-sized physical model of the human cochlea with optical holographic readout. J. Acoust. Soc. Am. 1993, 93, 1516–1523. [Google Scholar] [CrossRef] [PubMed]
- Wittbrodt, M.J.; Steele, C.R.; Puria, S. Developing a physical model of the human cochlea using microfabrication methods. Audiol. Neurotol. 2006, 11, 104–112. [Google Scholar] [CrossRef] [PubMed]
- White, R.D.; Grosh, K. Microengineered hydromechanical cochlear model. Proc. Natl. Acad. Sci. USA 2005, 102, 1296–1301. [Google Scholar] [CrossRef] [PubMed]
- Shintaku, H.; Nakagawa, T.; Kitagawa, D.; Tanujaya, H.; Kawano, S.; Ito, J. Development of piezoelectric acoustic sensor with frequency selectivity for artificial cochlea. Sens. Actuators Phys. 2010, 158, 183–192. [Google Scholar] [CrossRef]
- Inaoka, T.; Shintaku, H.; Nakagawa, T.; Kawano, S.; Ogita, H.; Sakamoto, T.; Hamanishi, S.; Wada, H.; Ito, J. Piezoelectric materials mimic the function of the cochlear sensory epithelium. Proc. Natl. Acad. Sci. USA 2011, 108, 18390–18395. [Google Scholar] [CrossRef] [PubMed]
- Harada, M.; Ikeuchi, N.; Fukui, S.; Ando, S. Fish-bone-structured acoustic sensor toward silicon cochlear systems. In Micromachined Devices and Components IV; SPIE: Bellingham, WA, USA, 1998; Volume 3514. [Google Scholar] [CrossRef]
- Xu, T.; Bachman, M.; Zeng, F.-G.; Li, G.-P. Polymeric micro-cantilever array for auditory front-end processing. Sens. Actuators Phys. 2004, 114, 176–182. [Google Scholar] [CrossRef]
- Jang, J.; Kim, S.; Sly, D.J.; O’leary, S.J.; Choi, H. MEMS piezoelectric artificial basilar membrane with passive frequency selectivity for short pulse width signal modulation. Sens. Actuators Phys. 2013, 203, 6–10. [Google Scholar] [CrossRef]
- Jang, J.; Lee, J.; Woo, S.; Sly, D.J.; Campbell, L.J.; Cho, J.-H.; O’Leary, S.J.; Park, M.-H.; Han, S.; Choi, J.-W.; et al. A microelectromechanical system artificial basilar membrane based on a piezoelectric cantilever array and its characterization using an animal model. Sci. Rep. 2015, 5, 12447. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.J.; Jeon, Y.; Jeong, J.-H.; Sood, R.; Kim, S.G. Energy harvesting MEMS device based on thin film piezoelectric cantilevers. J. Electroceram. 2006, 17, 543–548. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, J.; Takei, R.; Makimoto, N.; Itoh, T.; Kobayashi, T. S-shape spring sensor: Sensing specific low-frequency vibration by energy harvesting. Rev. Sci. Instrum. 2016, 87, 085005. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Zhang, L.; Yamashita, T.; Takei, R.; Makimoto, N.; Kobayashi, T. A silicon disk with sandwiched piezoelectric springs for ultra-low frequency energy harvesting. J. Phys. Conf. Ser. 2015, 660, 012093. [Google Scholar] [CrossRef]
- Jackson, N.; Keeney, L.; Mathewson, A. Flexible-CMOS and biocompatible piezoelectric AlN material for MEMS applications. Smart Mater. Struct. 2013, 22, 115033. [Google Scholar] [CrossRef]
- Heidrich, N.; Knöbber, F.; Sah, R.E.; Pletschen, W.; Hampl, S.; Cimalla, V.; Lebedev, V. Biocompatible AlN-based piezo energy harvesters for implants. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 1642–1644. [Google Scholar]
- Gan, R.Z.; Dai, C.; Wang, X.; Nakmali, D.; Wood, M.W. A totally implantable hearing system—Design and function characterization in 3D computational model and temporal bones. Hear. Res. 2010, 263, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Beker, L.; Zorlu, Ö.; Göksu, N.; Külah, H. Stimulating auditory nerve with MEMS harvesters for fully implantable and self-powered cochlear implants. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 1663–1666. [Google Scholar]
- Ansari, M.Z.; Cho, C. Deflection, Frequency, and Stress Characteristics of Rectangular, Triangular, and Step Profile Microcantilevers for Biosensors. Sensors 2009, 9. [Google Scholar] [CrossRef] [PubMed]
- Sharpe, W.N.; Yuan, B.; Vaidyanathan, R.; Edwards, R.L. Measurements of Young’s modulus, Poisson’s ratio, and tensile strength of polysilicon. In Proceedings of the IEEE Tenth Annual International Workshop on Micro Electro Mechanical Systems. An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Nagoya, Japan, 26–30 January 1997; pp. 424–429. [Google Scholar]
- Stokey, W.F. Vibration of systems having distributed mass and elasticity. In Harris’ Shock and Vibration Handbook, 5th ed.; McGraw-Hill Education: New York City, NY, USA, 2002; p. 7.5. [Google Scholar]
- Sooriakumar, K.; Chan, W.; Savage, T.S.; Fugate, C. A Comparative Study of Wet vs. Dry Isotropic Etch to Strengthen Silicon Micromachined Pressure Sensor. In A Comparative Study of Wet vs. Dry Isotropic Etch to Strengthen Silicon Micromachined Pressure Sensor; Electrochemical Society: Pennington, NJ, USA, 1995; pp. 259–265. ISBN 978-1-56677-123-8. [Google Scholar]
- Karami, M.A.; Yardimoglu, B.; Inman, D. Coupled Out of Plane Vibrations of Spiral Beams. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar]
- Shackelford, J.F.; Alexander, W. Mechanical Properties of Materials. In CRC Materials Science and Engineering Handbook, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2000; Table 407; ISBN 978-0-8493-2696-7. [Google Scholar]
- Timoshenko, S.; Young, D.H. Elements of Strength of Materials, 4th ed.; Affiliated East-West Press: Delhi, India, 1962. [Google Scholar]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectromech. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Zhong, H.; Xiao, Z.; Jiao, X.; Yang, J.; Wang, H.; Zhang, R.; Shi, Y. Residual stress of AlN films RF sputter deposited on Si(111) substrate. J. Mater. Sci. Mater. Electron. 2012, 23, 2216–2220. [Google Scholar] [CrossRef]
- Dubois, M.-A.; Muralt, P. Stress and piezoelectric properties of aluminum nitride thin films deposited onto metal electrodes by pulsed direct current reactive sputtering. J. Appl. Phys. 2001, 89, 6389–6395. [Google Scholar] [CrossRef]
- Pobedinskas, P.; Bolsée, J.-C.; Dexters, W.; Ruttens, B.; Mortet, V.; D’Haen, J.; Manca, J.V.; Haenen, K. Thickness dependent residual stress in sputtered AlN thin films. Thin Solid Films 2012, 522, 180–185. [Google Scholar] [CrossRef]



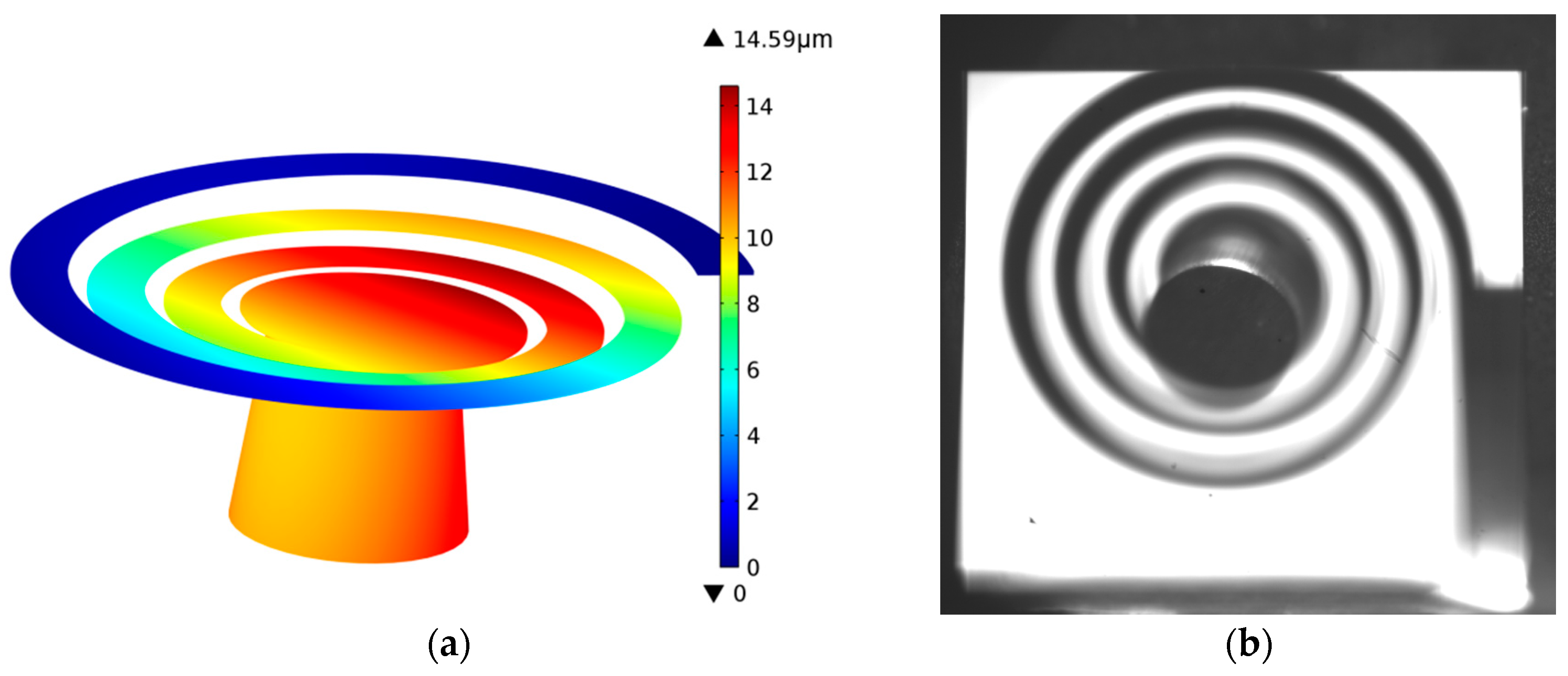
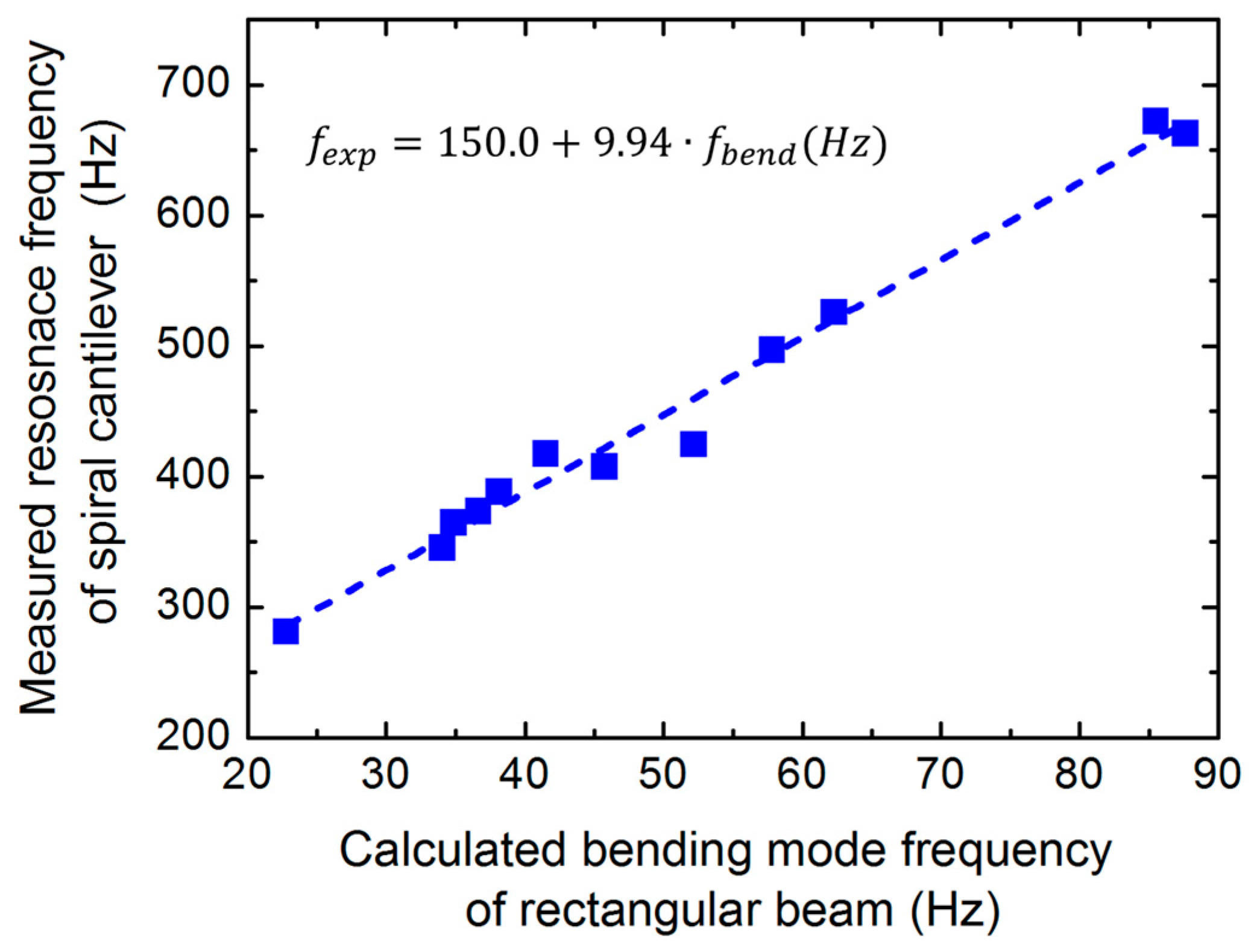
| Ch. | L | w | R0 | r | mbeam | mtm | Res. Freq. | Peak | Q | Res. Fr./Etched | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Exp. | Calc. | Voltage | Factor | Exp. | Calc. | ||||||
| (π/mm) | (μm) | (μm) | (μm) | (ng) | (ng) | (Hz) | (Hz) | (mV) | (Hz) | (Hz) | ||
| 1 | 8.0/11.8 | 145 | 870 | 315 | 50 | 320 | 281 | 283 | 6.89 | 145 | 241 | 240 |
| 2 | 7.0/9.4 | 150 | 850 | 300 | 41 | 287 | 345 | 337 | 8.80 | 133 | 289 | 295 |
| 3 | 7.0/9.2 | 150 | 800 | 300 | 40 | 287 | 365 | 366 | 9.60 | 148 | 311 | 312 |
| 4 | 7.0/9.2 | 150 | 800 | 290 | 40 | 266 | 374 | 348 | 9.53 | 254 | 321 | 319 |
| 5 | 7.0/9.1 | 145 | 800 | 280 | 38 | 246 | 389 | 377 | 5.71 | 117 | 335 | 332 |
| 6 | 6.5/7.4 | 160 | 760 | 310 | 36 | 309 | 408 | 379 | 4.47 | 218 | 343 | 348 |
| 7 | 8.0/10.3 | 145 | 800 | 250 | 40 | 190 | 417 | 424 | 2.64 | 176 | 352 | 357 |
| 8 | 6.0/7.4 | 160 | 760 | 300 | 33 | 287 | 425 | 473 | 5.02 | 216 | - 2 | 362 |
| 9 | 7.0/7.7 | 160 | 760 | 250 | 36 | 190 | 497 | 471 | 3.40 | 180 | 422 | 424 |
| 10 | 7.0/7.7 | 150 | 760 | 230 | 34 | 157 | 526 | 543 | 3.05 | 173 | 449 | 449 |
| 11 | 6.5/6.3 | 180 | 700 | 230 | 34 | 157 | 663 | 679 | 4.40 | 245 | 578 | 576 |
| 12 | 6.0/6.5 | 140 | 700 | 210 | 27 | 127 | 672 | 687 | 3.14 | 210 | 590 | 574 |
| 13 | 7.0/9.9 | 145 | 850 | 310 | 42 | 309 | 1 | 363 | - | - | 268 | - |
| 14 | 8.0/9.6 | 140 | 760 | 230 | 40 | 157 | 1 | 482 | - | - | 414 | - |
| 15 | 6.0/6.6 | 180 | 700 | 180 | 27 | 88 | 1 | 874 | - | - | 707 | - |
| 16 | 6.0/6.4 | 140 | 700 | 160 | 26 | 66 | 1 | 1058 | - | - | 2 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Udvardi, P.; Radó, J.; Straszner, A.; Ferencz, J.; Hajnal, Z.; Soleimani, S.; Schneider, M.; Schmid, U.; Révész, P.; Volk, J. Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems. Micromachines 2017, 8, 311. https://doi.org/10.3390/mi8100311
Udvardi P, Radó J, Straszner A, Ferencz J, Hajnal Z, Soleimani S, Schneider M, Schmid U, Révész P, Volk J. Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems. Micromachines. 2017; 8(10):311. https://doi.org/10.3390/mi8100311
Chicago/Turabian StyleUdvardi, Péter, János Radó, András Straszner, János Ferencz, Zoltán Hajnal, Saeedeh Soleimani, Michael Schneider, Ulrich Schmid, Péter Révész, and János Volk. 2017. "Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems" Micromachines 8, no. 10: 311. https://doi.org/10.3390/mi8100311
APA StyleUdvardi, P., Radó, J., Straszner, A., Ferencz, J., Hajnal, Z., Soleimani, S., Schneider, M., Schmid, U., Révész, P., & Volk, J. (2017). Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems. Micromachines, 8(10), 311. https://doi.org/10.3390/mi8100311






