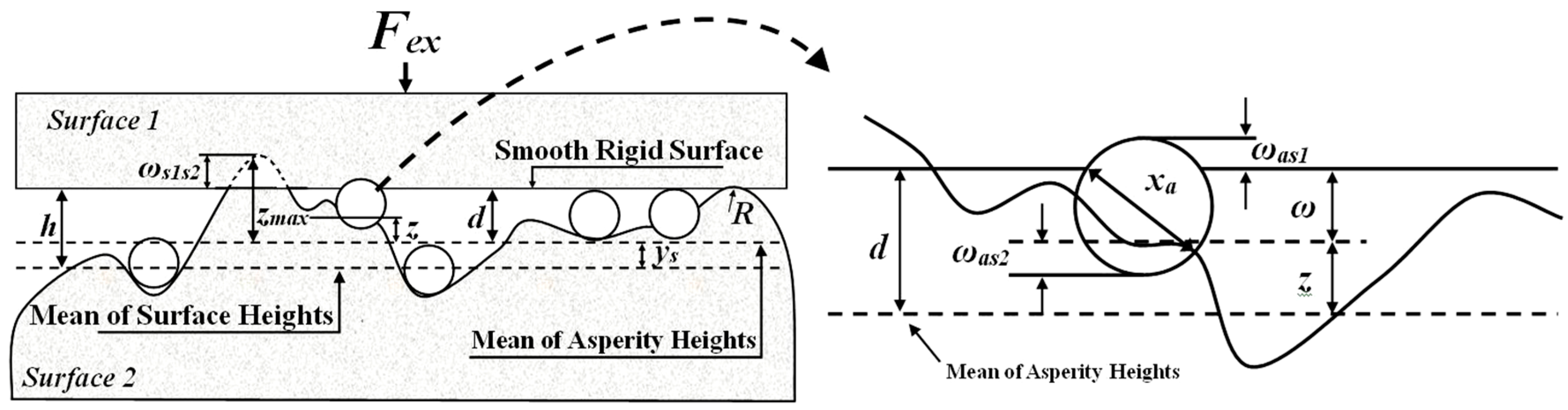
3. Results and Discussion
In the past, many analyses of heat flow with contact surfaces assumed that the coefficient of friction had to be fixed. For example, Bulsara [
25] analyzed the average contact temperature of abrasive particles and Rolland [
30] analyzed the case of the Swiss lever escapement mechanism. However, the coefficient of friction of the actual contact surface changes with the changing of the parameters, so the results of the analysis and the actual situation may contain errors. In this paper, the coefficient of friction is assumed to be fixed to 0.1 and the coefficient of friction changes with the contact conditions were analyzed, indicating the differences in the contact temperature. SUJ2 and CrMo steel were used for surfaces 1 and 2, and the particles in this analysis, and the properties are listed in
Table 1. Under the three-body contact situation, there are two kinds of contact temperature: surface peak with surface peak (
Ts1s2,ave), and particle with surface peak (
Ts1a,ave). The temperature characteristics are expressed as described in [
29]:
where
Ks2,
Hs2, and
αs2 are the thermal conductivity of surface 2, the hardness of surface 2, and the thermal diffusivity of surface 2, respectively.
αs2 =
Ks2/(
ρs2 ×
Cps2), where
ρs2 and
Cps2 are the density of surface 2 and specific heat capacity of surface 2, respectively. The material pair used in the analysis was SUJ2 and CrMo, which are types of steel commonly used for bearings, gears, and ball screws.
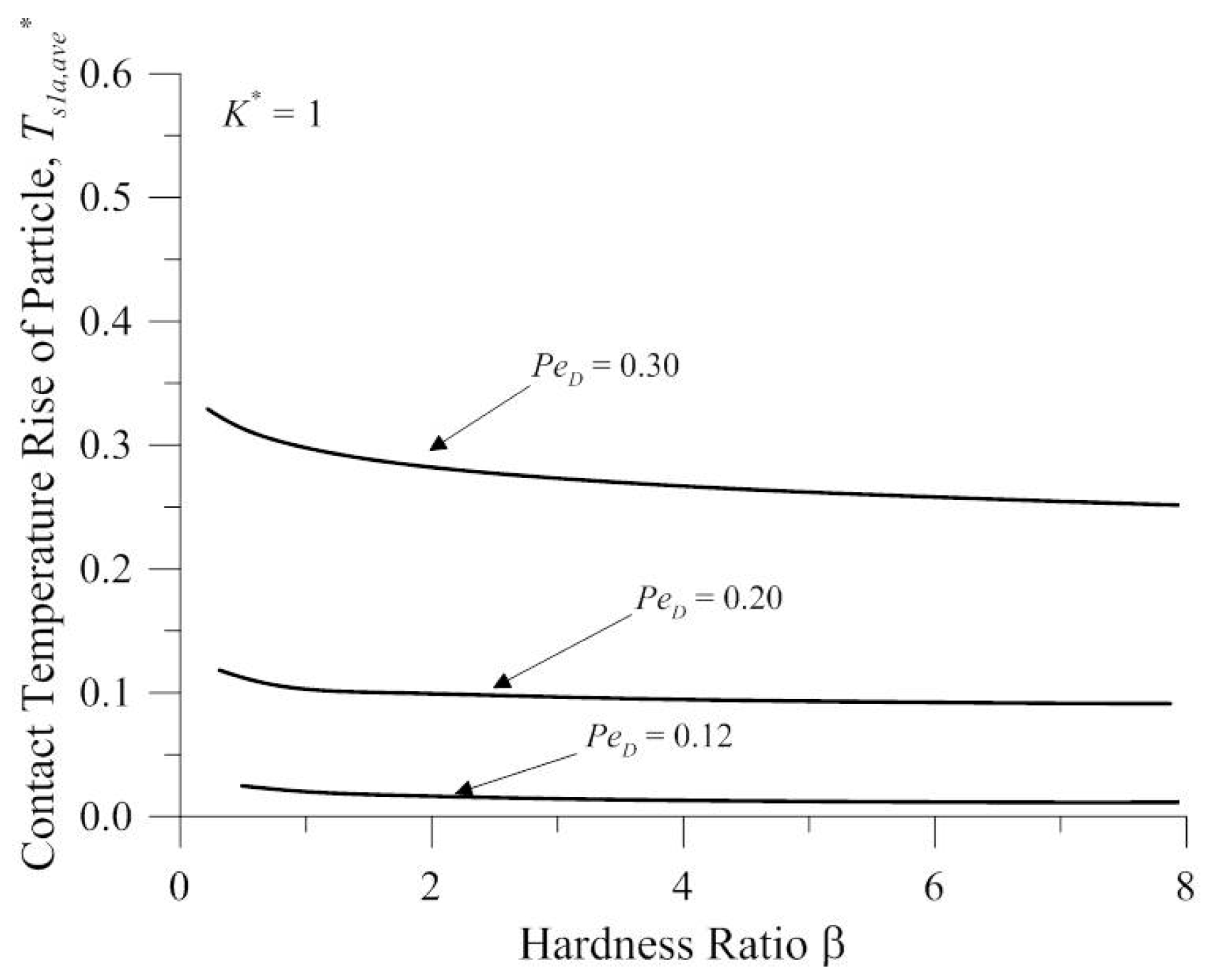
Figure 3 shows the contact temperature vs. the hardness ratio β at various Peclet numbers based on the particle diameter
PeD for the results from the present analysis. Where
K* =
Ks1/
Ka, the Peclet number is based on the particle diameter
PeD =
Vxa/
αs1, where
αs1 is the thermal diffusivity of surface 1, and the hardness ratio β =
Fai/(0.5 × π ×
ra2 ×
Hs2), where
ra is the contact radius of surface 1 and the particle. This Figure shows that the contact temperature rise of the particle increases with the increasing Peclet number based on the particle diameter
PeD, which decreases as the hardness ratio increases. The trend of the variation of
Tf is similar with the results of Khonsari et al. [
29]. However, the reference was to predict the scuffing phenomenon, so the operating conditions are relatively more severe than the conditions of present analysis.
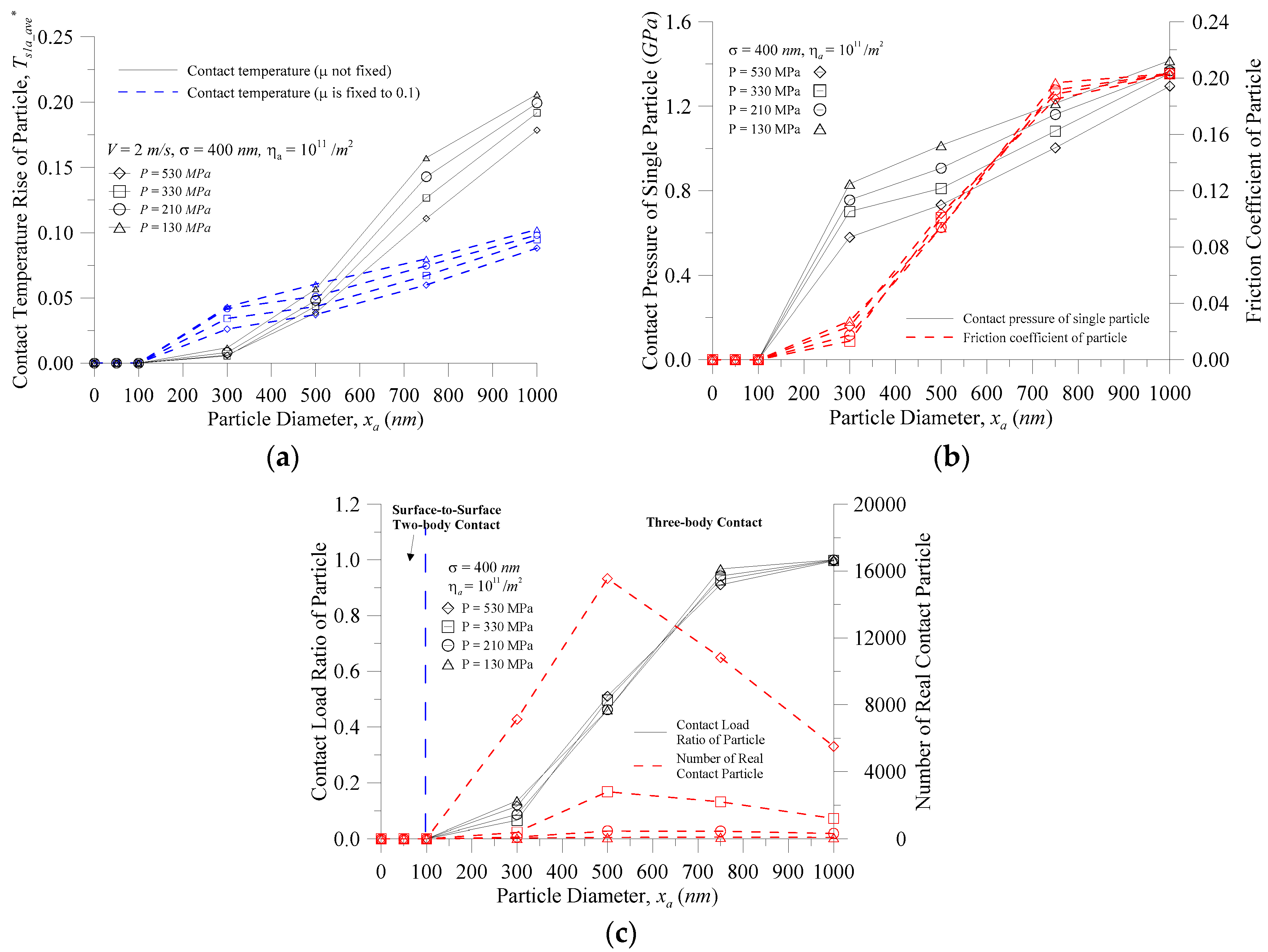
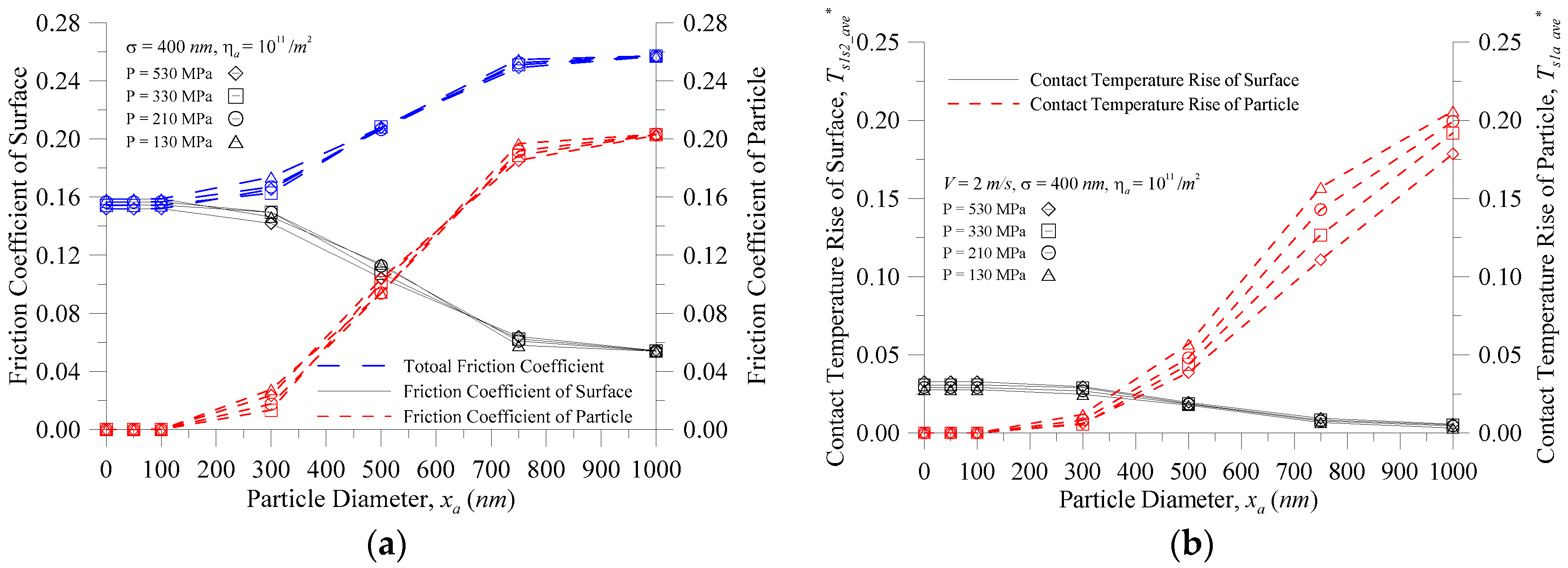
Figure 4 shows the characteristics of the particle vs. the particle diameter at various contact pressures for (a) the contact temperature rise; (b) the contact pressure of a single particle and the coefficient of friction; and (c) the contact load ratio of the particle (
Fs1a* =
Fs1a/
Ftotal) and the number of real contact particles when the equivalent RMS of the contacting surface roughness
σ = 400 nm,
ηa = 10
11/m
2, and
V = 2.0 m/s. As shown in
Figure 4a, however, whether the coefficient of friction was assumed to be fixed (
μ = 0.1) or variable, the contact temperature rise of the particles increased as the particle size increased. However, when the particle size was greater than 500 nm, the actual contact temperature was higher than the contact temperature when the coefficient of friction was assumed to be fixed, and the difference was larger as the particle size increased; at a particle size of 750 nm, the difference reached 85%–96%. The reason for this is that the contact temperature is varied and so can be illustrated in
Figure 4b where the friction heat flux is
μPV. At the same speed, the coefficient of friction of the particle and the contact pressure of a single particle (
Figure 4b) increased with the increasing particle size, and the main reason for the rapid increase in the contact temperature is the coefficient of friction of the particles.
Figure 4a also showed that with the same particle size, the greater the contact pressure, the smaller the contact temperature rise of the particle. The reason for this is that, at the smaller contact pressure, the particles easily distracted the two surfaces so that the external load was mainly borne by the minority particles, as shown in
Figure 4c. At the same time, as that shown in
Figure 4b, the contact pressure of a single particle increased with decreases in the contact pressure at the same particle size. Furthermore, at
xa < 100 nm, the contact pressure of a single particle was reduced to 0, and is explained in
Figure 4c, which shows that the contact load ratio of particles and number of contact particles were zero at
xa < 100 nm. As the space of the interface was much larger than the particle diameter, the particles sank into the trough, and there was no particle contact between the contact interfaces. As illustrated in
Figure 2, when the particle appeared in the interface, there are three kinds of contact behavior that can correspond to the contact load ratio of particles (
Fs1a*): (1) as
Fs1a* = 0, the surface-to-surface two-body contact appears; (2) as
Fs1a* = 1, the contact behavior is a particle-to-surface two-body contact; and (3) for 0 <
Fs1a* < 1, three-body contact exists. Under this operating condition, the black solid line in
Figure 4c displays that when
xa < 100 nm, the surface-to-surface two-body contact appeared; as the particle size increased, the contact behavior entered the three-body contact until the particle size reaches 1000 nm; and when the contact load ratio of a particle reached 100%, the contact behavior entered the particle-to-surface two-body contact zone. The red dotted line in
Figure 4c shows that the number of real contact particles increased as the contact pressure increased. With the same contact pressure, the number of real contact particles increased with an increase in the particle size, and the contact behavior entered the three-body contact zone at a particle size greater than 100 nm. However, when
xa > 500 nm, the number of real contact particles decreased. This is because the larger particles were more likely to separate the surfaces, and the in-contact particles only left larger ones in the particle distribution. When the total contact pressure was small in
Figure 4b, the contact pressure of a single particle then increased, which also describes one reason for the larger contact temperature rise of a particle than when the particle diameter was larger in
Figure 4a.
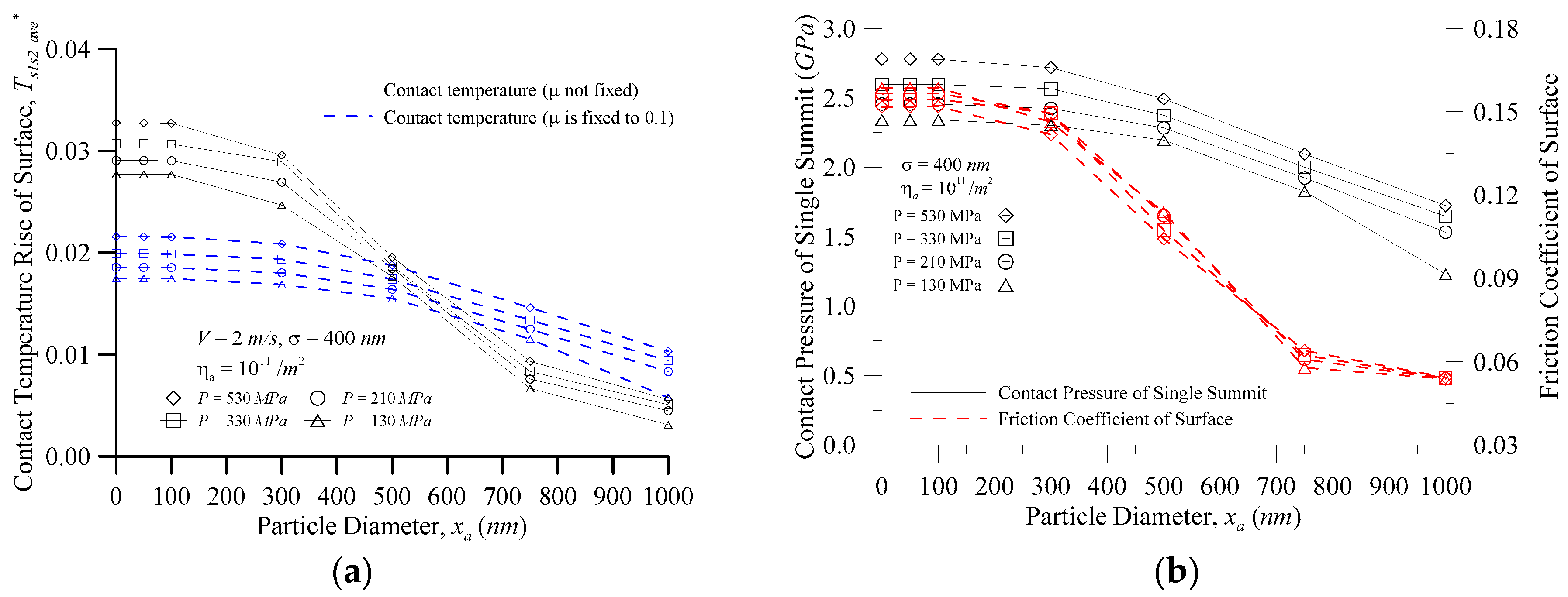
Figure 5 shows the characteristics of the surface vs. particle diameter at various contact pressures for (a) the contact temperature rise; and (b) the contact pressure of a single summit and the coefficient of friction when
σ = 400 nm,
ηa = 10
11/m
2, and
V = 2.0 m/s.
Figure 5a shows the temperature rise comparison between the coefficient of friction fixed at 0.1 and the non-fixed coefficient of friction. In the case of smaller particles, the change of the real contact temperature rise was greater than that of the contact temperature rise for the general assumption of
μ = 0.1; and the smaller the particle diameter, the greater the error of the surface temperature rise. When
xa = 0 nm (that is, two-body contact, no third particle),
P = 530 MPa
, T*s1s2_ave increased from 0.022 to 0.033 (i.e., 36.5 K to 55.3 K) because the unit friction heat flux input is
μPV, and the smaller particles easily sank into the trough of the surface so that the external load was borne by the surface peak, as illustrated in
Figure 5b. The contact pressure of the single summit
Ps1s2,i and the coefficient of friction of the surface
μs1s2 were larger, so the contact temperature rise of the surface was higher with the smaller particles, and the contact temperature rise of the surface decreased with an increase in particle size in
Figure 5a. In
Figure 5b, when the particle diameter was about 650 nm or more, the contact pressure of the single summit
Ps1s2,i and the coefficient of friction of surface
μs1s2 increased with increasing contact pressure, so the contact pressure increased, and the contact temperature rise of the surface increased. When the particle diameter was less than 650 nm, the coefficient of friction of the surface did not increase as the contact pressure increased, but each contact pressure of a single summit increased with the increasing contact pressure, so the greater the contact pressure, the greater the contact temperature rise of the surface. As seen in
Figure 4 and
Figure 5, the surface peak contact pressure was the main impact on the contact temperature rise trends of the surface, and the coefficient of friction of the surface mainly affected the contact temperature rise of the surface. The particle contact pressure was also the main influence on the contact temperature rise trends of the particle, and the coefficient of friction of the particle mainly affected the contact temperature rise of the particle.
Figure 6 shows the characteristics of the surface and particle vs. particle diameter at various contact pressures for (a) the coefficient of friction; and (b) the contact temperature rise when
σ = 400 nm,
ηa = 10
11/m
2, and
V = 2.0 m/s. As shown in
Figure 6a, the coefficient of friction of the surface decreased as the particle size increased, and the coefficient of friction of the particle increased as the particle size increased. When
xa < 500 nm, the total coefficient of friction was dominated by the coefficient of friction of the surface, and at
xa > 500 nm, the total coefficient of friction was dominated by the coefficient of friction of the particle.
Figure 6b shows that the changing trend of the contact temperature rise of the surface and the contact temperature rise of the particle with the increasing particle size was similar to that of the coefficient of friction. Based on the discussions of
Figure 4 and
Figure 6, the coefficient of friction was the main impact factor which affected the contact temperature rise in a three-body contact situation. In engineering applications, we try to seek the surface contact with the surface and the particle contact with the surface where the resulting heat balance is assigned to the particles and the surface, which is the ideal operating condition to avoid the interface from too high a contact temperature point.
Figure 6b shows that when the particle size was small, the contact temperature rise of the surface was higher; however, when the particle size was large, the contact temperature rise of the particle was too high. Thus, it can be seen from
Figure 6b that, under these operating conditions, the contact temperature equilibrium point was approximately
xa = 380 nm where, at this time, the temperature rise parameter was about 0.038 (a temperature rise of about 59.3 K). Therefore, an effective filter in the process of running debris particles or the foreign particles below a size of 400 nm is in the ideal range to avoid surface damage (wear, scuffing) caused by too high a contact temperature rise. Under these conditions, it is better to choose the filter of some component systems to filter out particles with a diameter of 500 nm or more (i.e., the temperature rise does not exceed about 85.8 K).
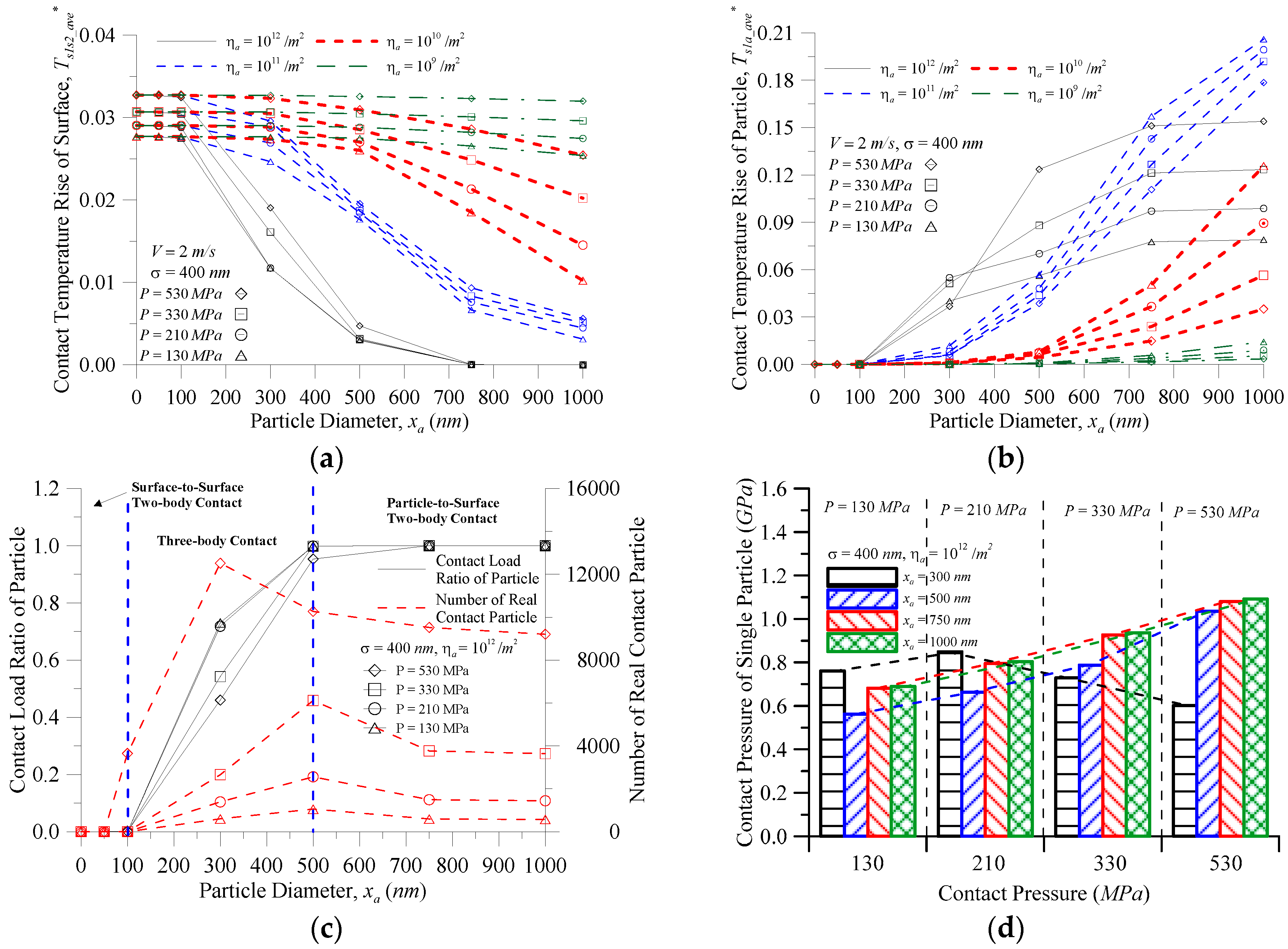
Figure 7 shows the characteristics of the particle and surface vs. the particle diameter at various contact pressures and the area density of particles for (a) the contact temperature rise of the surface; (b) the contact temperature rise of the particles; and (c) the contact load ratio of the particles and number of real contact particles when
σ = 400 nm and
V = 2.0 m/s.
Figure 7a shows that the contact temperature rise of the surface increased with increasing contact pressure at any area density of the particles when the particle size was the same. At
xa ≤ 100 nm, at the same contact pressure, with any area density of the particles, the contact temperature rise of the surface was almost overlapping. Under this condition, the particles had barely any effect, and the contact temperature rise of the surface was almost the same as that of the surface under two-body contact. At the same contact pressure, the contact temperature rise of the surface was affected by the particles, and decreased with increases in particle size and the area density of the particles where the larger the particle size or area density of the particles, the greater the decline level. As shown in
Figure 7b, when the area density of particles
ηa = 10
9–10
11/m
2 with the same particle size, the contact temperature rise of the particles decreased as the contact pressure increased. At the same contact pressure, the contact temperature rise of the particles increased with an increase in the area density of the particles. When the area density of the particles was reduced to 10
9/
m
2, the curve showed a steady trend given the sparse distribution of particles on the surface at such a low area density of particles. Most of the external load was still borne by the surface, so the particle size had a limited effect on the external load, and the impact on the temperature rise was also very small. When the area density of particles
ηa = 10
12/m
2 (at the same contact pressure), the contact temperature rise of the particles increased with an increase in the particle diameter, and rose before stabilizing. However, in the case of the same particle diameter, there was no certain trend of the contact pressure on the contact temperature rise of the particles until the particle diameter increased to 500 nm, then stabilized, and the contact temperature rise of the particles decreased with decreasing contact pressure. When
xa < 300 nm, the temperature rise of the particles showed no certain trend with contact pressure changes as seen in
Figure 7c. When the particle size increased from 300 nm to 500 nm, the particles were reduced and the contact load ratio was increased so that the contact pressure increased rapidly for
ηa = 10
12/m
2 and P = 530 MPa, but the number of real contact particles of other contact pressures still increased so the contact pressure of a single particle was less than
P = 530 MPa. When
xa > 750 nm, the contact temperature rise of particles
ηa = 10
11/m
2 was larger than the contact temperature rise of particles
ηa = 10
12/m
2 (as seen in
Figure 4c and
Figure 7c) as under the same total load, the area density of the particles increased, as did the number of real contact particles, resulting in a decrease to the contact pressure of a single particle. Therefore, in
Figure 7d, under
P = 130 and 210 MPa, the contact pressure
P became smaller, whereas the contact pressure of the single particle increased.
Figure 7d also shows that the contact pressure of a single particle changed with the contact pressure at the same particle size. This was the same as
Figure 7b where the contact temperature rise of the particles changed with the contact pressure. Therefore, the contact pressure of a single particle was the main factor influencing the changing trend in the contact temperature rise of the particles. According to the friction heat flux formula
μPV, the contact pressure of a single particle is also one of the main factors in producing friction heat between the particles and the surface contact. As indicated in
Figure 6, a temperature rise of not more than 85.8 K (with a temperature rise parameter value of 0.055), could be chosen as the filter aperture and also be used to schedule oil changes.
Figure 7 depicts that the greater particle size, the greater the area density of the particles, and the contact temperature rise of the particles becomes faster at greater than 0.055. Therefore, the optimum oil change period was when the area density of the particle exceeded 10
12/m
2 under this operating condition.
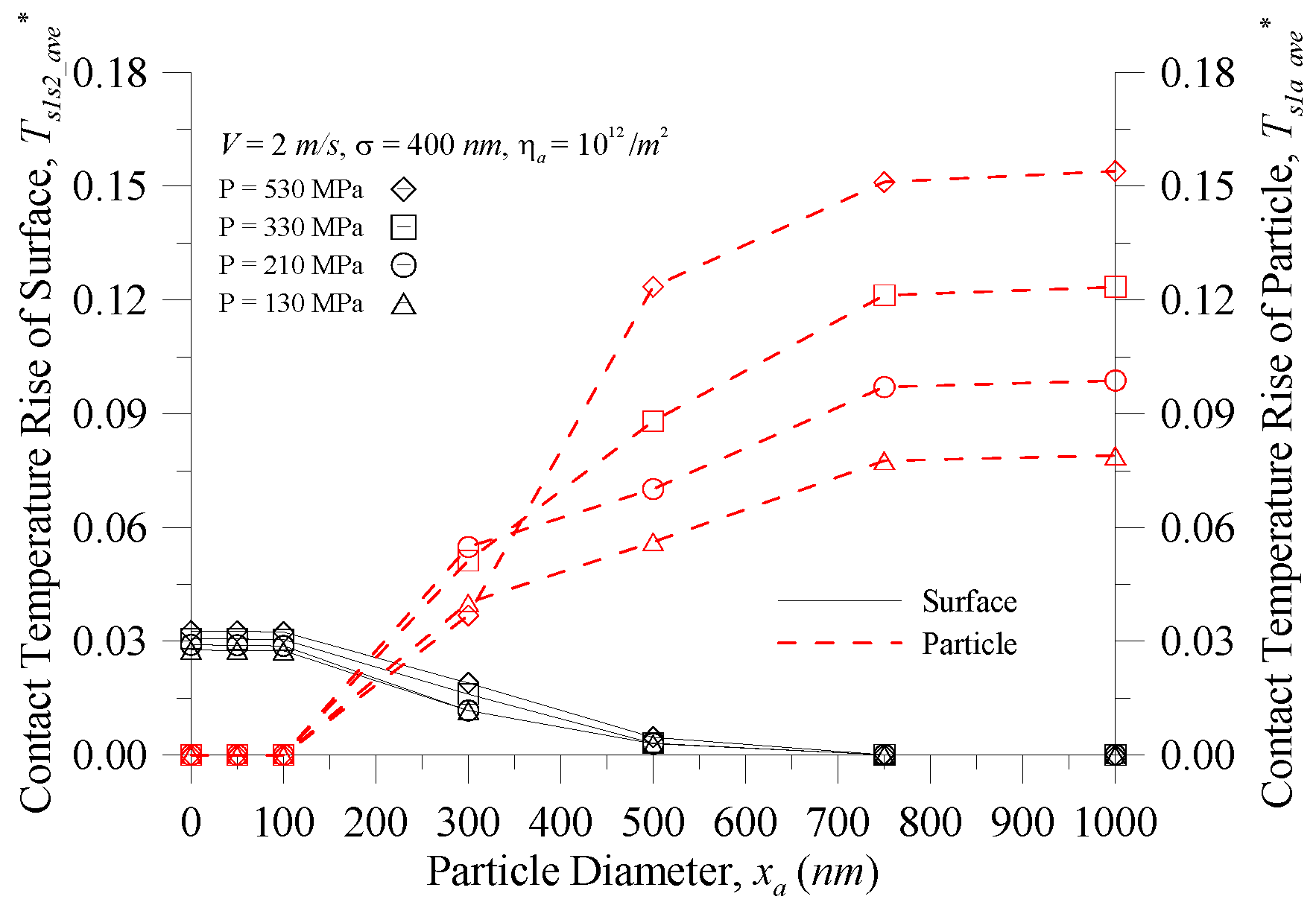
Figure 8 depicts the contact temperature of the surface and particle vs. particle diameter at various contact pressures for
σ = 400 nm,
V = 2 m/s, and
ηa = 10
12/m
2. As shown in
Figure 8, under contact pressure between 130–530 MPa, the equilibrium point between the contact temperature rise of the surface and the contact temperature rise of the particles varied with particle sizes at
xa = 175–225 nm. Therefore, theoretical analysis can predict that under the in-service process of the component, if the particle size can be effectively monitored and controlled, the contact temperature will reach the equilibrium point between the contact interfaces. The contact point will be able to avoid instantaneous excessively higher contact temperatures, resulting in the phenomenon of contact point wear. In addition, when compared with
Figure 6, when the area density of particles is increased (10
11/m
2 rises to 10
12/m
2), the filter is selected to filter out particle diameters of 300 nm or more (i.e., the temperature rise does not exceed ca. 85.8 K as displayed in
Figure 6).
From the results of
Figure 4 and
Figure 5, any relative movement of the components in a variety of operating conditions will have a different coefficient of friction and different frictional heat generation, thus affecting the micro-contact temperature. In the case of the contact temperature of the surface or contact temperature of the particle, there was a maximum error of about 150% under the non-fixed coefficient of friction and the fixed coefficient of friction, which may result in greater error in more severe operating conditions. Therefore, to make the predicted value of the analysis closer to the actual situation when analyzing the characteristics between the interfaces, the coefficient of friction must be considered in the analysis as the variation of the operating conditions.
The plasticity index is an important indicator of the rough surface contact characteristics, where the greater the value it represents, the higher the chance that plastic deformation will occur at the asperity of the rough surfaces. The plasticity index of the general engineering surface was between 0.7–2.55, and given as:
where
E* is the equivalent of Young’s modulus;
H is the hardness of the soft material; and
R* is the equivalent radius of curvature of an asperity.
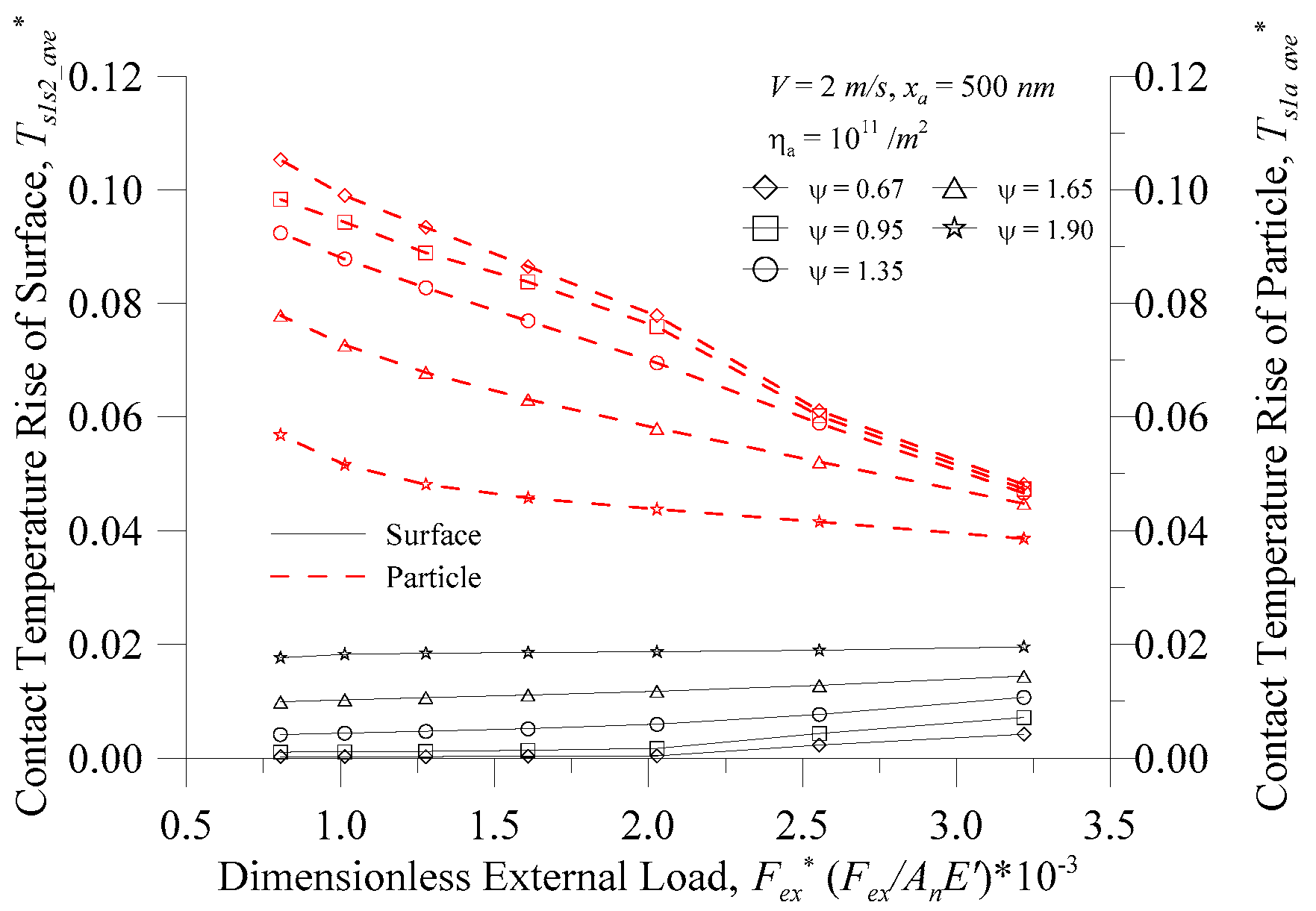
Figure 9 shows the surface and particle temperature rise versus the dimensionless external load (
Fex*) for
V = 2.0 m/s,
ηa = 10
11/m
2 and
xa = 500 nm at various plasticity indices (
ψ). The dimensionless external load and plasticity index are important indicators of micro-contact theory [
8]. The dimensionless external load is almost linear with the real contact area [
12], and the plasticity index
ψ is an indicator of the plastic deformation in the real contact area. The greater the value of the plasticity index, the greater the percentage of the plastic deformation area. As indicated in
Figure 9, the surface contact temperature increased as the dimensionless external force increased. Under the same external force, the surface contact temperature increased with the increase of the plasticity index. As the plastic index was larger, there was a greater possibility of plastic deformation at the surface peak contact point, and the temperature was higher. While at a low plasticity index value, the external force had little effect on the surface contact temperature, but the surface contact temperature still rose significantly at
Fex* > 2.0 × 10
−3.
Figure 9 also indicates that the particle contact temperature decreased as the dimensionless external force increased. Under the same external force, the particle contact temperature decreased with the increase of the plasticity index. The plasticity index
ψ is an important parameter of surface material and rough topography. Particle size and area density of particles are also the main particle properties, and the relationship is discussed below.
From the previous analysis, when the component is running, the contact pressure, the relative sliding speed, the surface roughness, the generated particle size, the area density of particles, and other operating conditions affect the micro-contact temperature prediction value.
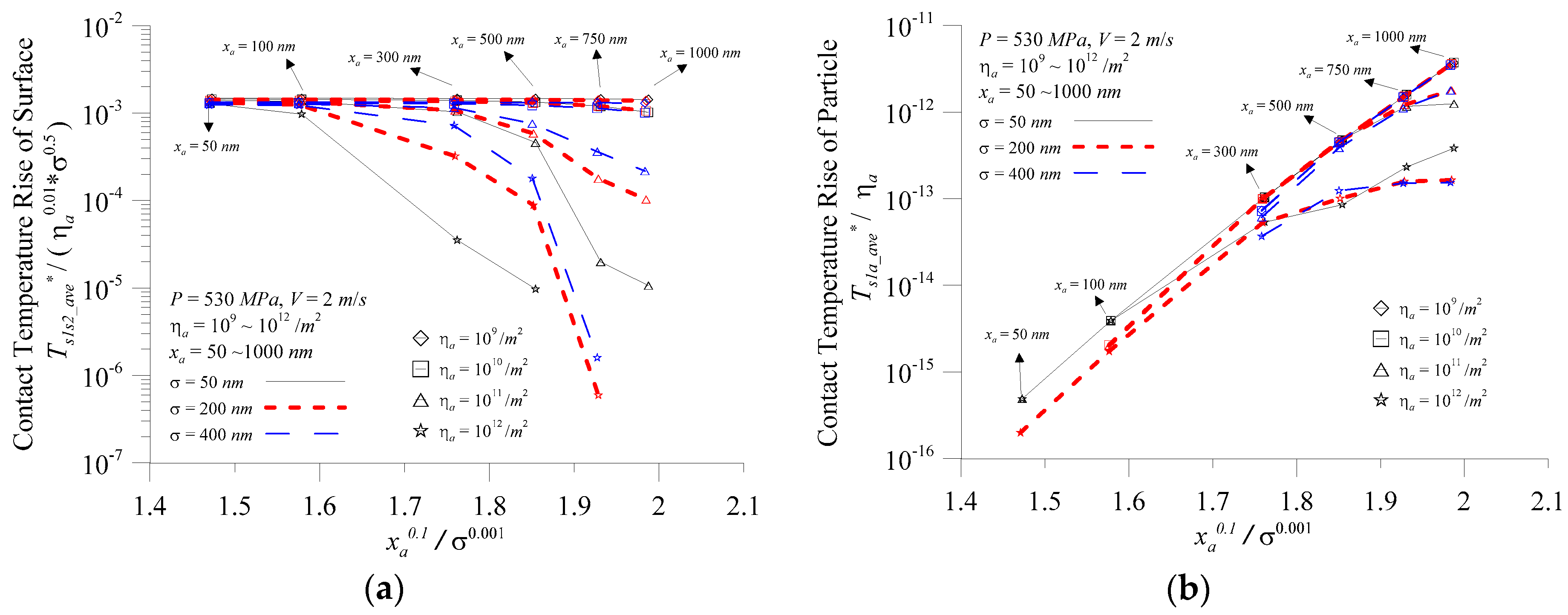
Figure 10 depicts the variation of contact temperature rise with the ratio of particle diameter to surface roughness at various surface roughness values and area density of particles for (a) the surface; and (b) the particles when
P = 530 MPa,
V = 2.0 m/s,
σ = 50–400 nm
, ηa = 10
9–10
11/m
2, and
xa = 50–1000 nm.
Figure 10a indicates
xa0.1/
σ0.001 and the predicted value of the surface contact temperature was converted to the surface temperature parameter (
Ts1s2_ave* /
ηa 0.01σ0.5) where the surface contact temperature almost overlapped the area density of particles of 10
9/m
2. The area density of particles increased to10
10/m
2 only in the large
xa0.1/
σ0.001, and the surface contact temperature showed a small decline. It showed that the particles affected the surface temperature less significantly and the root mean square roughness was the maximum influence factor of the surface contact temperature. When
ηa > 10
10/m
2 or more, the surface contact temperature parameter decreased significantly with the increase of the
xa0.1/
σ0.001 ratio. When the particle size was the same, the larger the area density of particles, the greater the decrease in surface contact temperature parameters.
Figure 10b indicates, except for abnormal
ηa = 10
10/m
2, the particle contact temperature was almost linear with
xa0.1/
σ0.001 when the predicted value of the particle contact temperature was converted to the temperature parameter (
Ts1a_ave*/
ηa). As the previous analysis showed, the interface particle temperature was extremely likely to damage the interface performance at
ηa = 10
10/m
2, but also required general lubrication maintenance to avoid the situation. It also indicated that, under normal circumstances,
xa0.1/
σ0.001 was an important influencing factor for particle contact temperature. The particle contact temperature parameter (
Ts1a_ave*/
ηa) increased with an increase of the
xa0.1/
σ0.001 ratio. However, at high particle concentrations, the rising trend changed slowly, while at a particle concentration of 10
9/m
2, there was almost a linear increase.