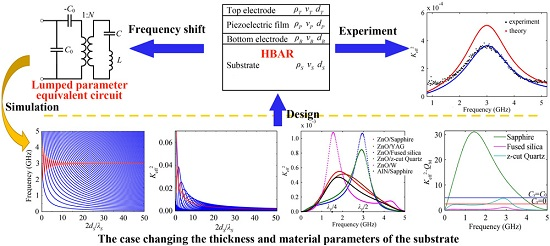
Resonance Spectrum Characteristics of Effective Electromechanical Coupling Coefficient of High-Overtone Bulk Acoustic Resonator
Abstract
:1. Introduction
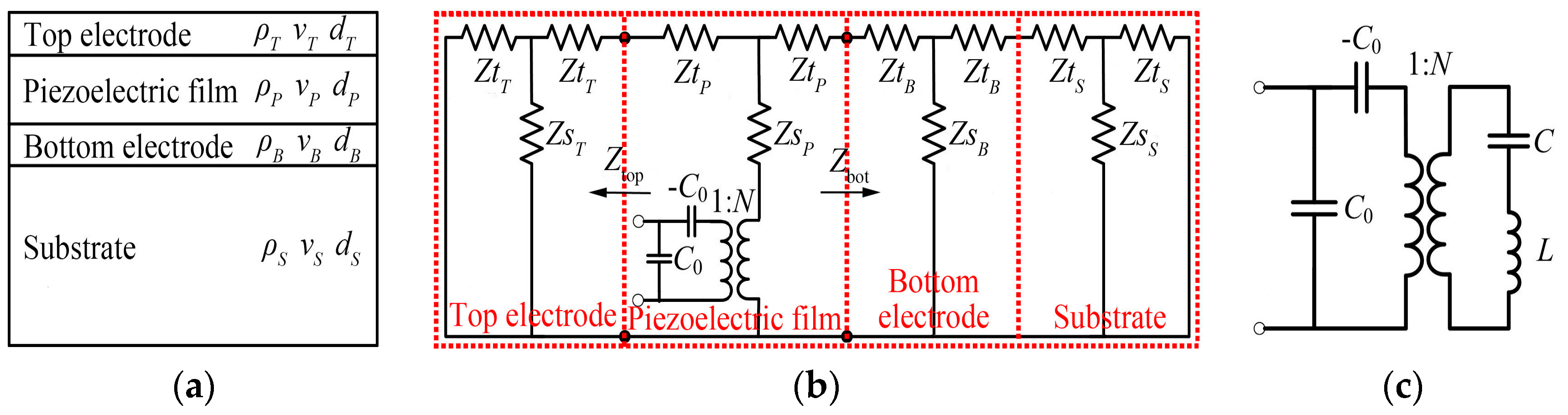
2. The Lumped Parameter Equivalent Circuit of HBAR
3. Relationship between the Effective Electromechanical Coupling Coefficient and the Substrate
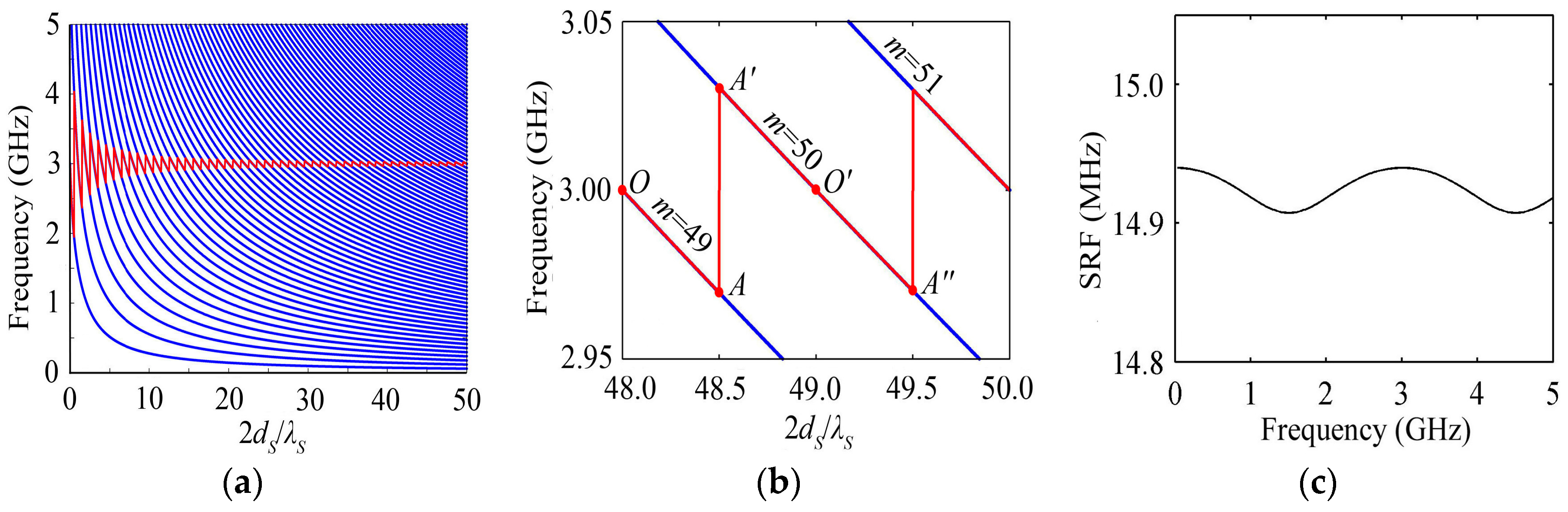
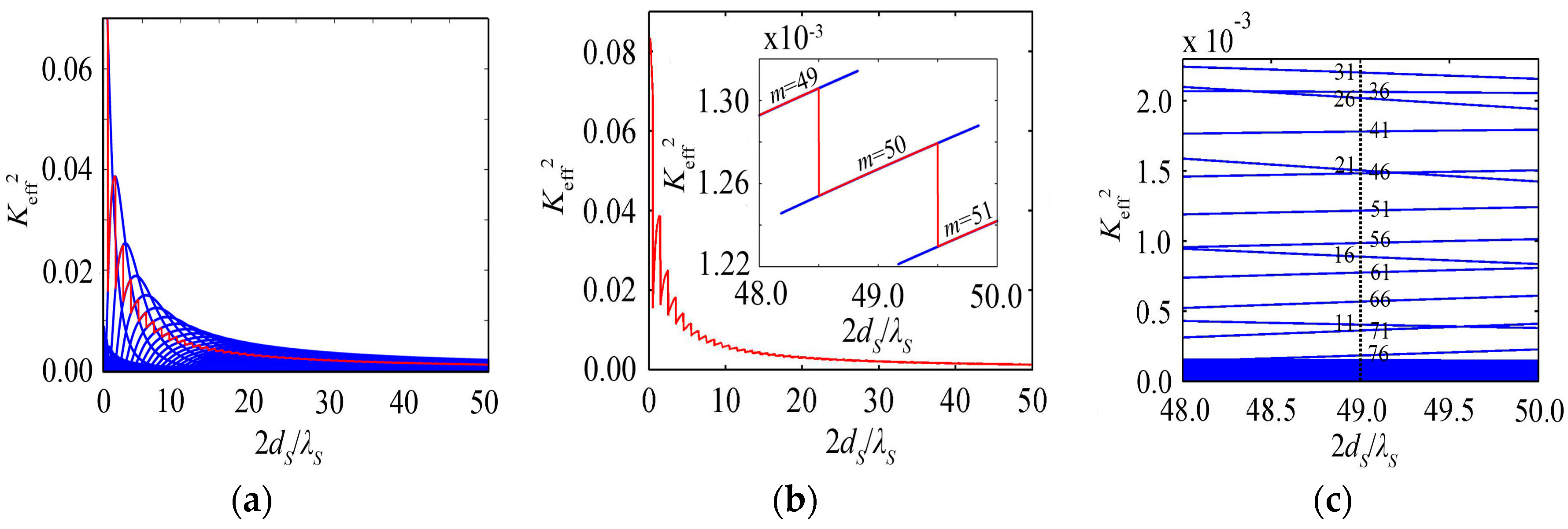
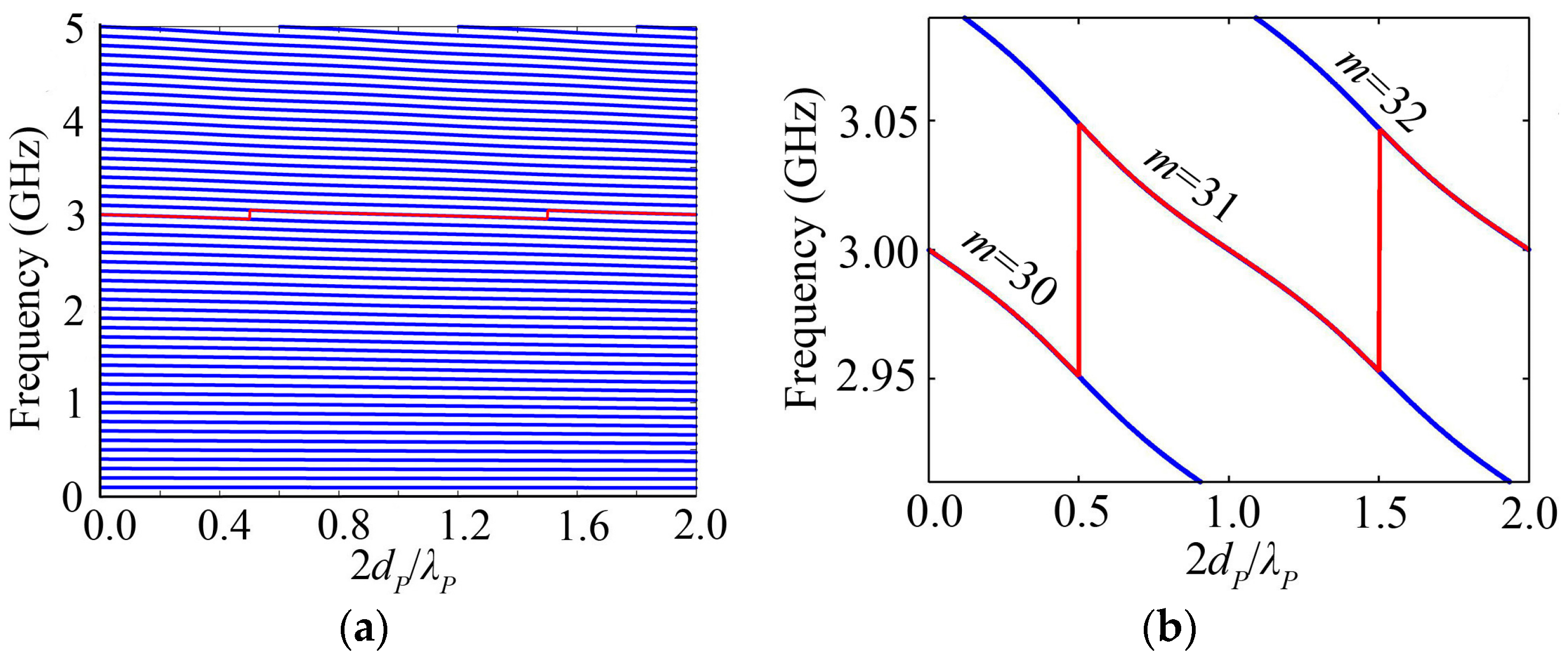
3.1. Keff2 Varies with the Substrate Thickness
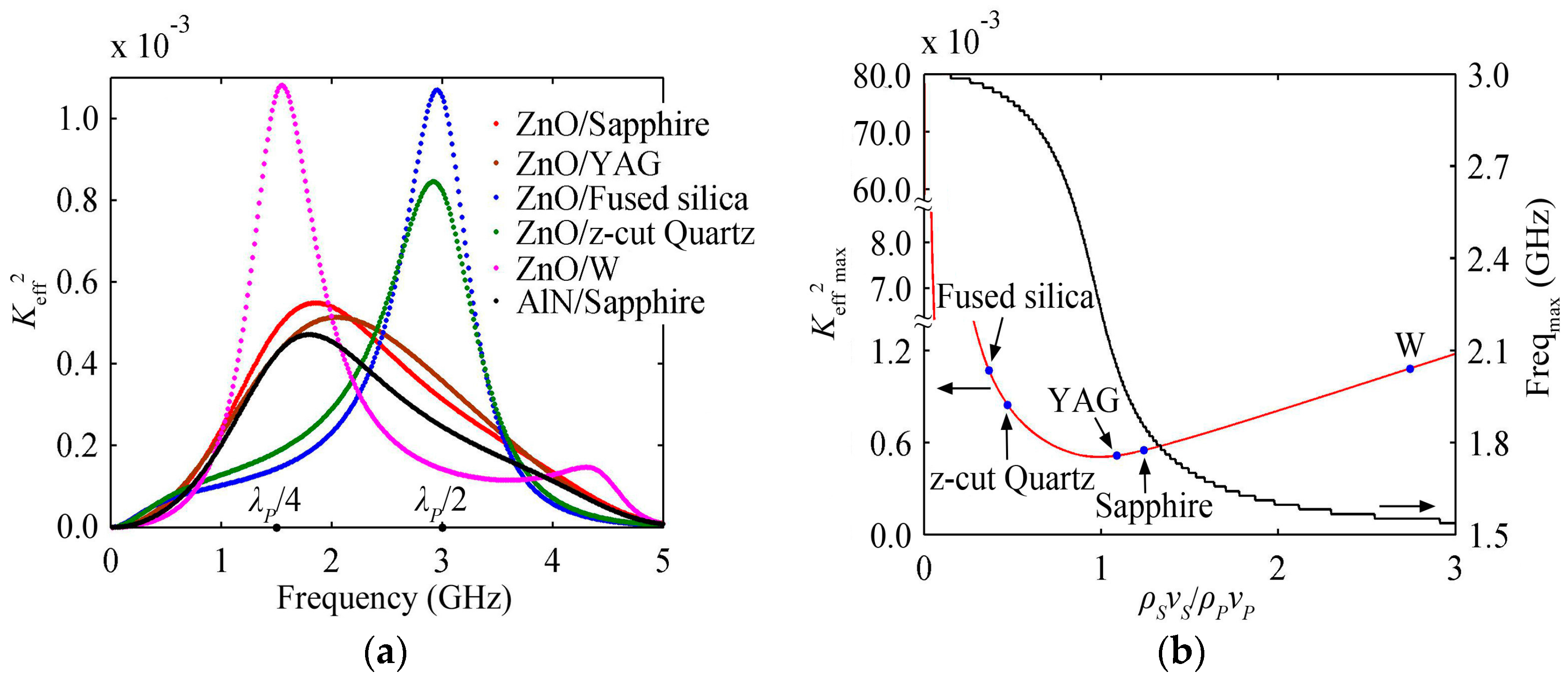
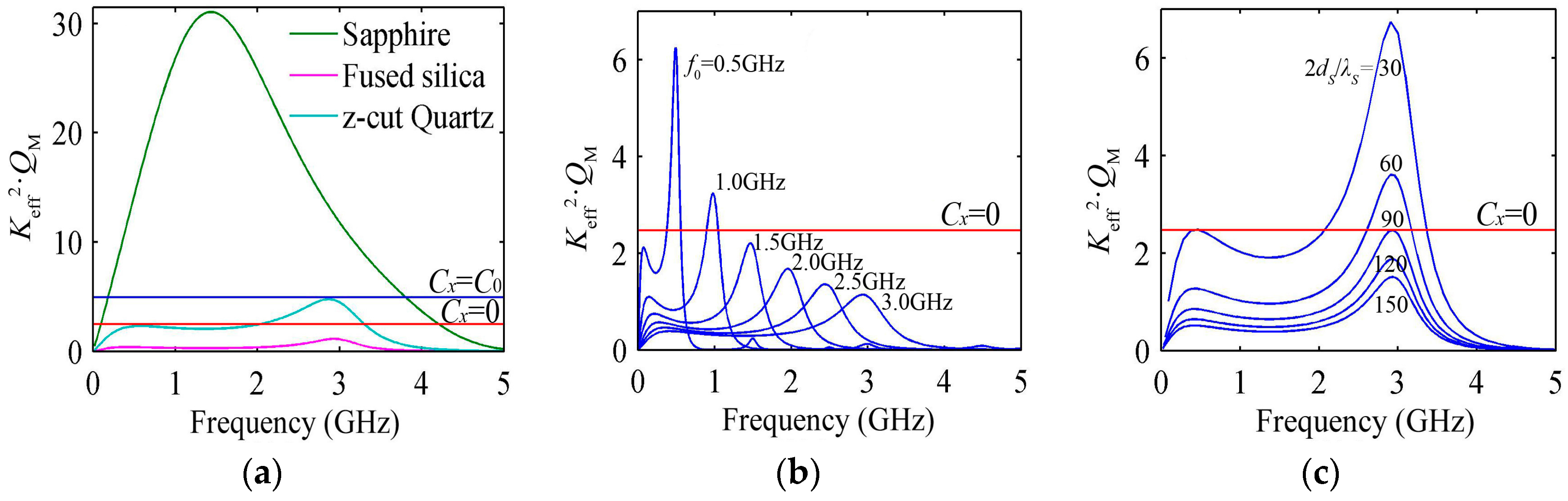
3.2. Keff2 Varies with the Substrate Materials
4. Relationship between the Effective Electromechanical Coupling Coefficient and the Piezoelectric Film
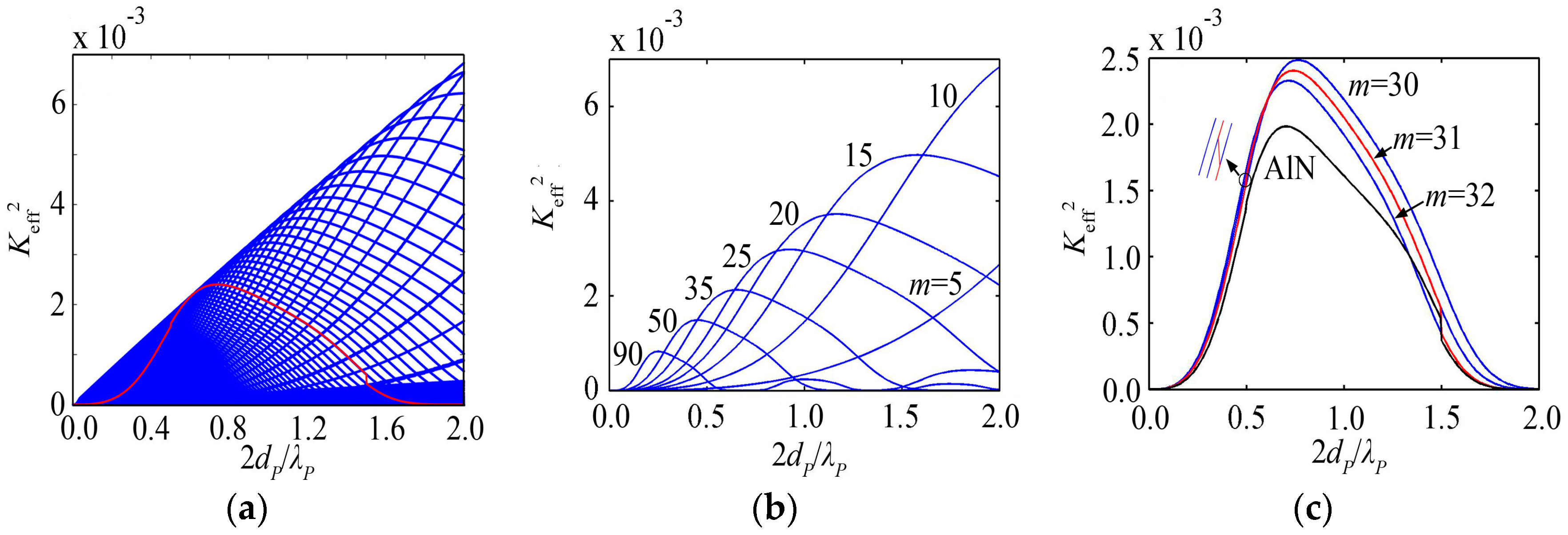
4.1. Keff2 Varies with the Piezoelectric Film Thickness
4.2. Keff2 Varies with the Piezoelectric Film Materials
5. Influence of the Electrode on the Effective Electromechanical Coupling Coefficient
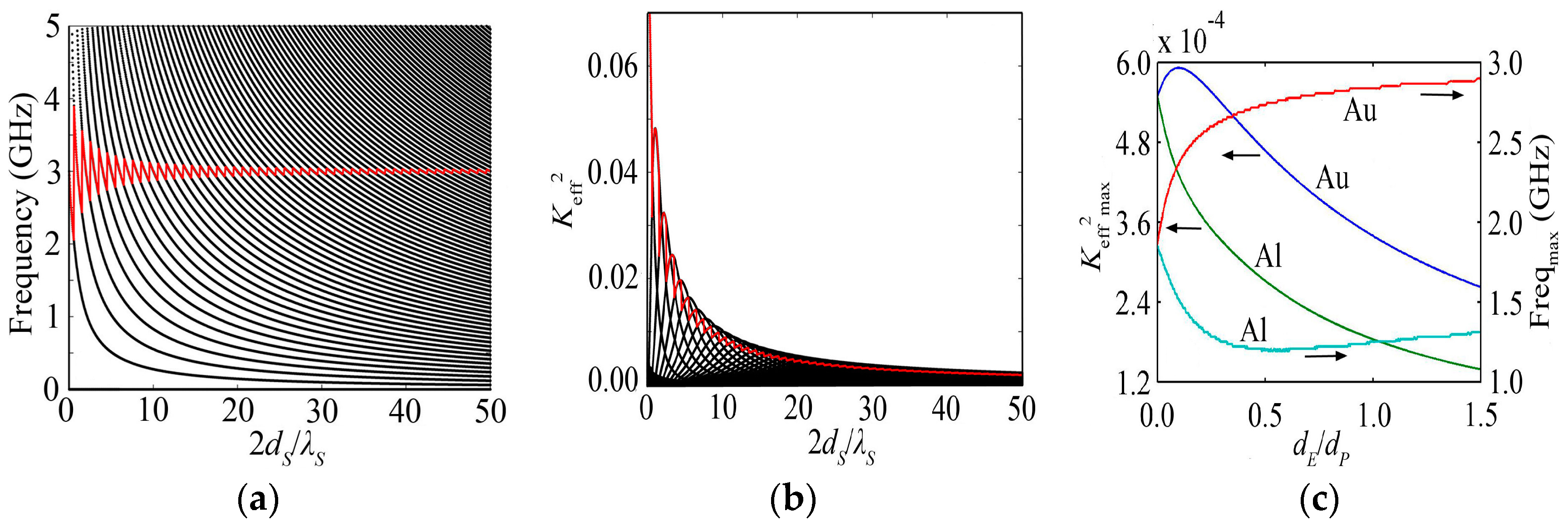
5.1. Keff2 Varies with the Substrate Thickness Considering the Effect of the Electrode
5.2. The Relationship between Keff2 and the Electrode Thickness and Materials
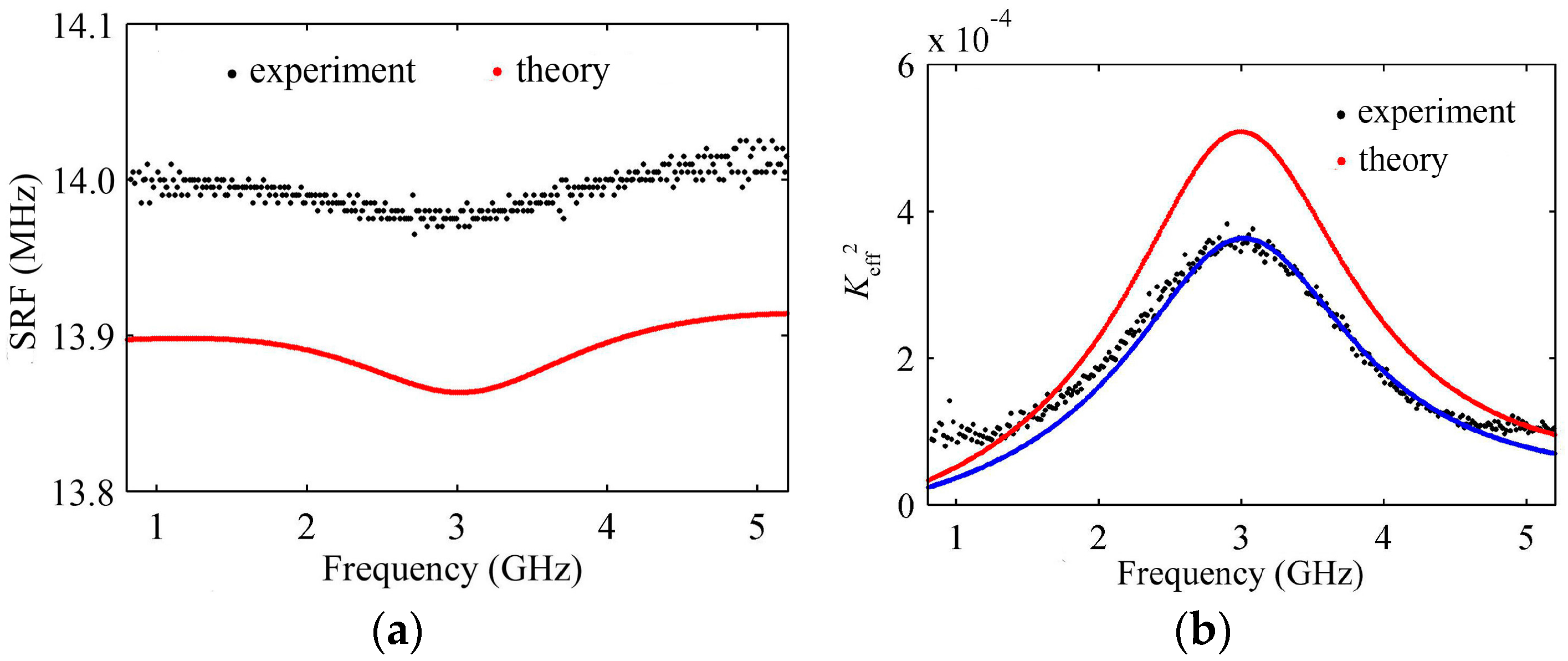
6. Experiment
7. Effects of Keff2 on the Function of the Crystal Oscillators Constructed with HBARs
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moore, R.A.; Haynes, J.T.; McAvoy, B.R. High Overtone Bulk Resonator Stabilized Microwave Sources. In Proceedings of the IEEE Ultrasonics Symposium (IUS), Chicago, IL, USA, 14–16 October 1981; pp. 414–424.
- Yu, H.; Lee, C.Y.; Pang, W.; Zhang, H. Low Phase Noise, Low Power Consuming 3.7 GHz Oscillator Based on High-Overtone Bulk Acoustic Resonator. In Proceedings of the IEEE Ultrasonics Symposium (IUS), New York, NY, USA, 28–31 October 2007; pp. 1160–1163.
- Driscoll, M.M.; Jelen, R.A.; Matthews, N. Extremely low phase noise UHF oscillators utilizing high-overtone, bulk-acoustic resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 774–779. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, Z.; Cheeke, J.D.N.; Hickernell, F.S. Direct characterization of ZnO films in composite resonators by the resonance spectrum method. In Proceedings of the IEEE Ultrasonics Symposium (IUS), Caesars Tahoe, NV, USA, 17–20 October 1999; pp. 991–994.
- Wang, Z.; Zhang, Y.; Cheeke, J.N. Characterization of electromechanical coupling coefficients of piezoelectric films using composite resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1327–1330. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, Z.; Cheeke, J.D. Resonant spectrum method to characterize piezoelectric films in composite resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 321–333. [Google Scholar] [CrossRef] [PubMed]
- Pao, S.Y.; Chao, M.C.; Wang, Z.; Chiu, C.H. Analysis and experiment of HBAR frequency spectra and applications to characterize the piezoelectric thin film and to HBAR design. In Proceedings of the IEEE International Frequency Control Symposium and PDA Exhibition, New Orleans, LA, USA, 29–31 May 2002; pp. 27–35.
- Zhou, Q.B.; Lu, Y.K.; Zhang, S.Y. Extraction of electromechanical coupling coefficient of piezoelectric thin films deposited on substrates. Ultrasonics 2001, 39, 377–382. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.Y.; Zheng, K. Parameter characterization of high-overtone bulk acoustic resonators by resonant spectrum method. Ultrasonics 2005, 43, 635–642. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, Z.; Zhang, S.Y. Electrode effects on frequency spectra and electromechanical coupling factors of HBAR. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1020–1025. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, Z.; Zhang, S.Y. Study on resonance frequency distribution of high-overtone bulk acoustic resonators. Chin. J. Acoust. 2005, 24, 146–154. [Google Scholar]
- Zhang, H.; Zhang, S.Y.; Zheng, K. Electrode effects on general modes in high-overtone bulk acoustic resonators. Ultrasonics 2007, 44, e737–e740. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wang, C.H.; Liu, M.W. Effective electromechanical coupling coefficient of high-overtone bulk acoustic resonator. Chin. J. Acoust. 2016, in press. [Google Scholar]
- Sittig, E.K. Design and technology of piezoelectric transducers for frequencies above 100 MHz. In Physical Acoustics; Mason, W.P., Thurston, R.N., Eds.; Academic Press: New York, NY, USA, 1972; Volume IX, pp. 221–275. [Google Scholar]
- Berlincourt, D.A.; Curran, D.R.; Jaffe, H. Piezoelectric and piezomagnetic materials and their function in transducers. In Physical Acoustics; Mason, W.P., Ed.; Academic Press: New York, NY, USA, 1964; Part A; Volume 1, pp. 239–242. [Google Scholar]
- Auld, B.A. Appendix 2: Properties of materials. In Acoustic Fields and Waves in Solids; Wiley: New York, NY, USA, 1973; Volume 1, pp. 95–96. [Google Scholar]
- Zhang, Y.F.; Chen, D. Multilayer Integrated Film Bulk Acoustic Resonators; Springer: Berlin, Germany, 2013; p. 46. [Google Scholar]
- Li, J.; Liu, M.W.; Li, J.H.; Ma, J.; Wang, C.H. Mechanical quality factor of high-overtone bulk acoustic resonator. Chin. J. Acoust. 2016, 35, 193–211. [Google Scholar]
- Molarius, J.; Kaitila, J.; Pensala, T.; Ylilammi, M. Piezoelectric ZnO films by R.F. sputtering. J. Mater. Sci. Mater. Electron. 2003, 14, 431–435. [Google Scholar] [CrossRef]
- Hashimoto, K.Y. Surface Acoustic Wave Devices in Telecommunications: Modelling and Simulation; Springer: Berlin, Germany, 2000. [Google Scholar]
- Virgil, E.B. Introduction to Quartz Crystal Unit Design; Van Nostrand Reinhold Company: New York, NY, USA, 1982; pp. 101–133. [Google Scholar]
| Structure | Material | ν (m/s) | ρ (kg/m3) | kt2 | ρν (×107 kg·m−2·s−1) |
|---|---|---|---|---|---|
| Piezoelectric film | ZnO | 6301 | 5680 | 0.0784 | 3.5790 |
| AlN | 10,400 | 3260 | 0.065 | 3.3904 | |
| Substrate | Fused silica | 5973 | 2200 | - | 1.3141 |
| z-cut Quartz | 6359 | 2651 | - | 1.6858 | |
| Yttrium aluminum garnet (YAG) | 8558 | 4550 | - | 3.8939 | |
| Sapphire | 11,155 | 3986 | - | 4.4464 | |
| Tungsten (W) 1 | 5113 | 19,200 | - | 9.8170 | |
| Electrode | Al | 6330 | 2695 | - | 1.7059 |
| Au | 3104 | 19,300 | - | 5.9907 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, M.; Wang, C. Resonance Spectrum Characteristics of Effective Electromechanical Coupling Coefficient of High-Overtone Bulk Acoustic Resonator. Micromachines 2016, 7, 159. https://doi.org/10.3390/mi7090159
Li J, Liu M, Wang C. Resonance Spectrum Characteristics of Effective Electromechanical Coupling Coefficient of High-Overtone Bulk Acoustic Resonator. Micromachines. 2016; 7(9):159. https://doi.org/10.3390/mi7090159
Chicago/Turabian StyleLi, Jian, Mengwei Liu, and Chenghao Wang. 2016. "Resonance Spectrum Characteristics of Effective Electromechanical Coupling Coefficient of High-Overtone Bulk Acoustic Resonator" Micromachines 7, no. 9: 159. https://doi.org/10.3390/mi7090159
APA StyleLi, J., Liu, M., & Wang, C. (2016). Resonance Spectrum Characteristics of Effective Electromechanical Coupling Coefficient of High-Overtone Bulk Acoustic Resonator. Micromachines, 7(9), 159. https://doi.org/10.3390/mi7090159