Microfluidic 3D Helix Mixers
Abstract
:1. Introduction
2. Experimental Section
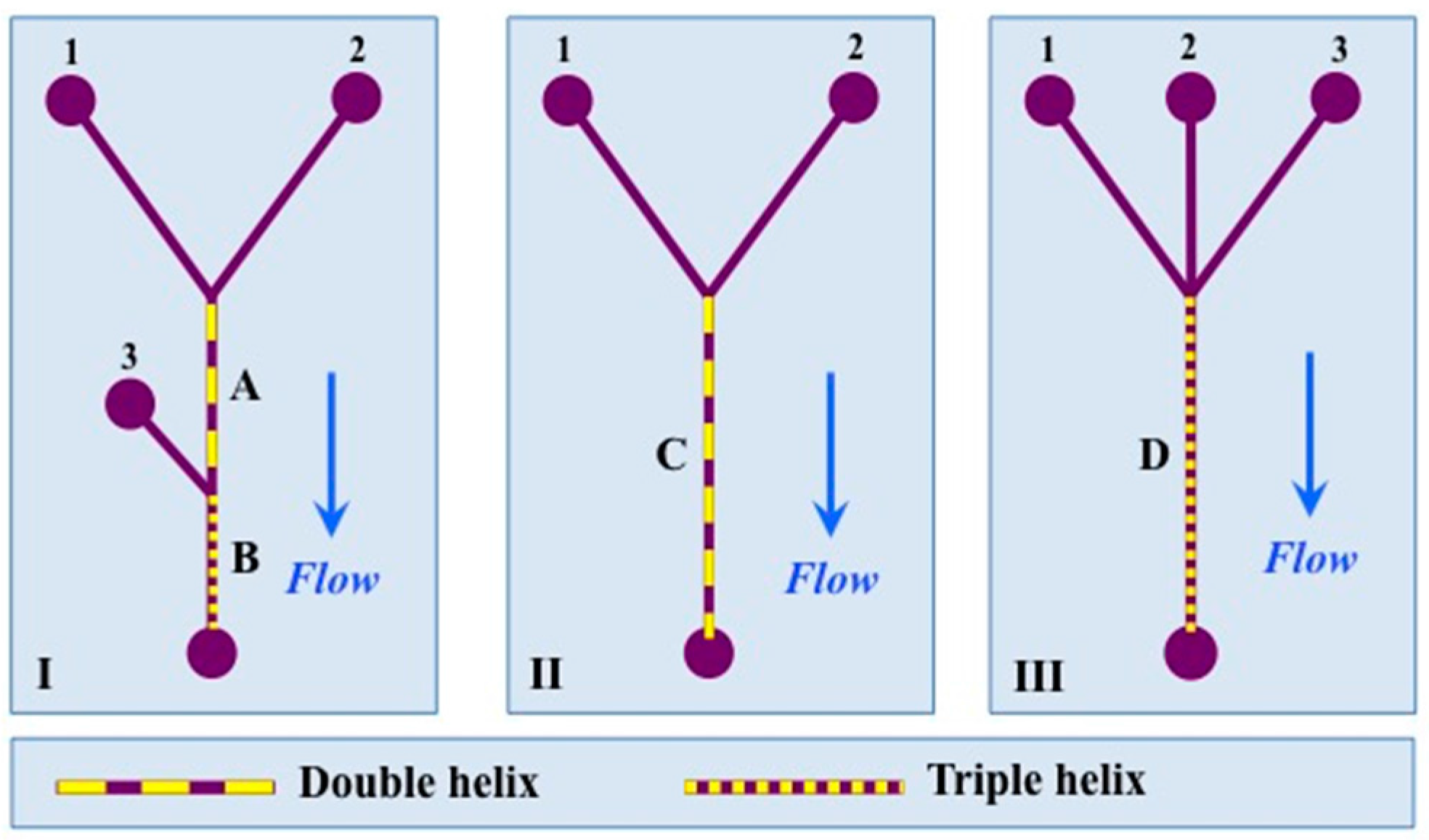
2.1. Thread Helices and PDMS Cast
2.2. Imaging
2.3. Pressure Drop Along the Microchannels
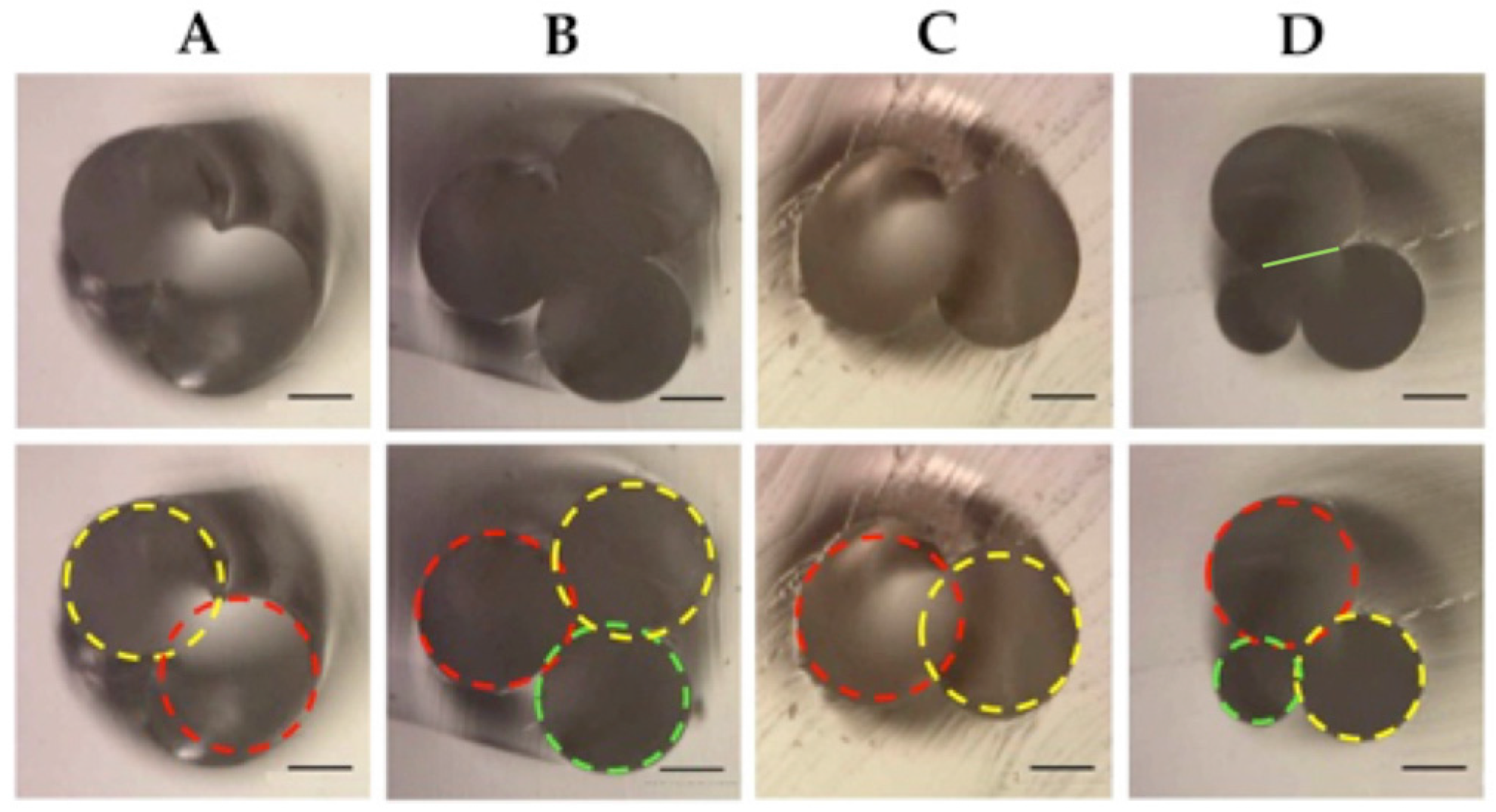
2.4. Helix Characteristics
- (1)
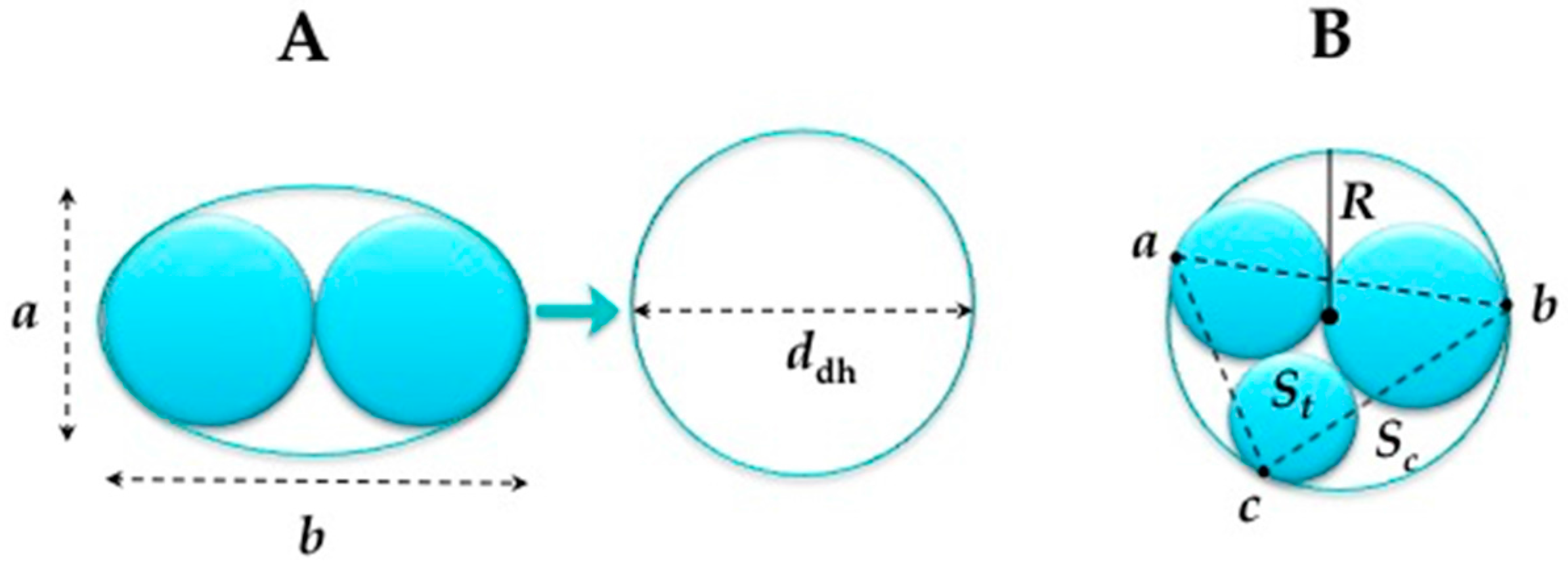
- For the double helices the equivalent circular diameter was calculated using the following equation (see Figure 5A):where A = the cross-sectional area of the oval (m2); = πab/4 (a = major dimension of oval, b = minor dimension oval) andddh = 1.55 A0.625/P0.25P = approximate perimeter of oval (m) = 2π (1/2 ((a/2)2 + (b/2)2))1/2
- (2)
- When the radii of the threads are all unequal as presented in Figure 5B, the radius is estimated by the circumcircle radius using Heron’s formula.where s = (a + b + c)/2, the triangle area and the circumcircle area Sc = πR2.
- (3)
- The Reynolds number (Re)where ρ is the density of the fluid (kg/m3), η the kinematic viscosity (m2/s). The kinematic viscosity for water at room temperature is 1.004 m2/s.Re = (ρVd)/η
- (4)
- The Schmidt number (Sc)where, D is mass diffusivity (m2/s), μ the dynamic viscosity of the fluid (Pa·s or N·s/m2 or kg/m·s) and ρ is the density of the fluid (kg/m3). Sc is assumed to be 340 for a dilute solution in water.Sc = η/D = μ/(ρD)
- (5)
- The Péclet number (Pe)Pe = Sc × Re
- (6)
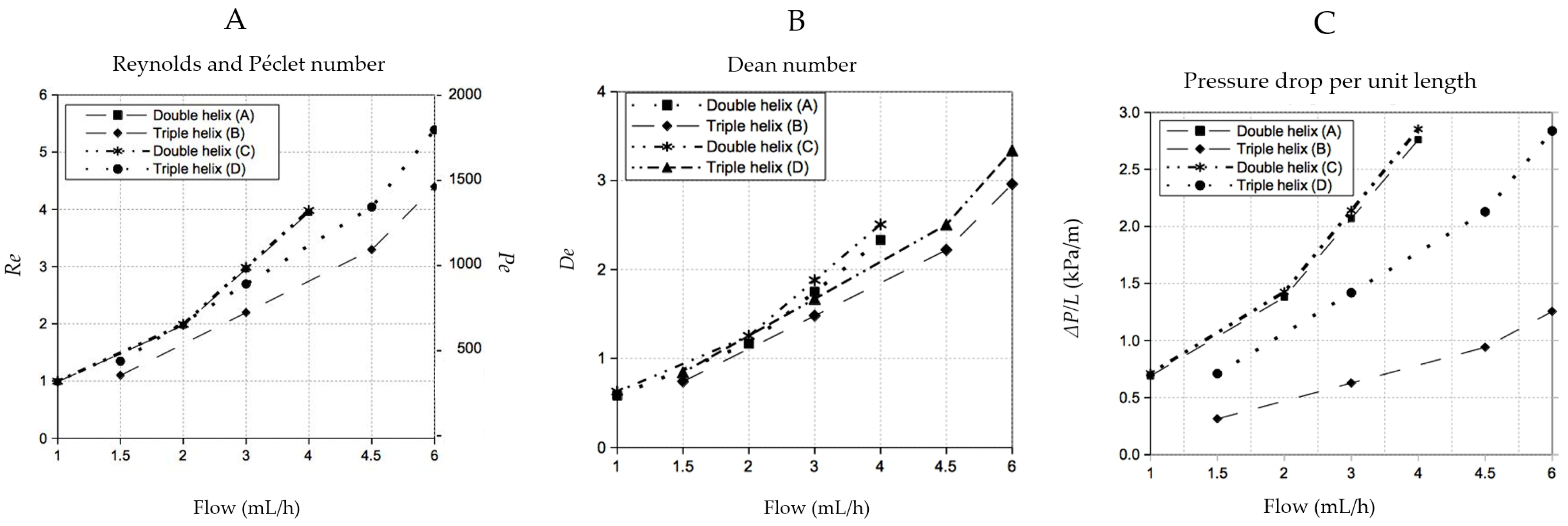
- The radius of curvature of the helices (Rc) is larger than the radius of the channel (R) leading to the secondary Dean flow, which is due to the inhomogeneous flow inside the helices and is quantified by the Dean number (De).where Re = the Reynolds number, d = the diameter of the helix and Rc = the radius of curvature.De ~ Re (d/2Rc)1/2whereRc = 1/curvatureandcurvature = R/R2 + c2c = total length/2π × total number of pitches.Related to this is the curvature ratio λ = Rc/R used by others to study the mixing performance (e.g., [14]).
- (7)
- For a circular channel with diameter d (μm), the time required for mixing due to molecular diffusion in a laminar flow across the channel is approximately: tmix (s) = d2/D. The diffusion coefficient D is known to range from 9.3 × 10−9 m2/s at 300 K for protons (including water), to 2.3 × 10−9 m2/s for water, to ~4 × 10−10 m2/s for small molecular dyes, to ~4 × 10−12 m2/s for 100 nm particles. The length required for mixing due to molecular diffusion in a laminar flow Lmix (m) = tmix × V, with the average velocity in V (m/s).
- (8)
- The equation (diffusion equation) for incompressible flowwhere ε is the variable of interest and V the average velocity of the fluid was used.
2.5. Microchannel Chemical Reaction
2.6. Assembly of Nanoparticles
2.7. Computational Modeling
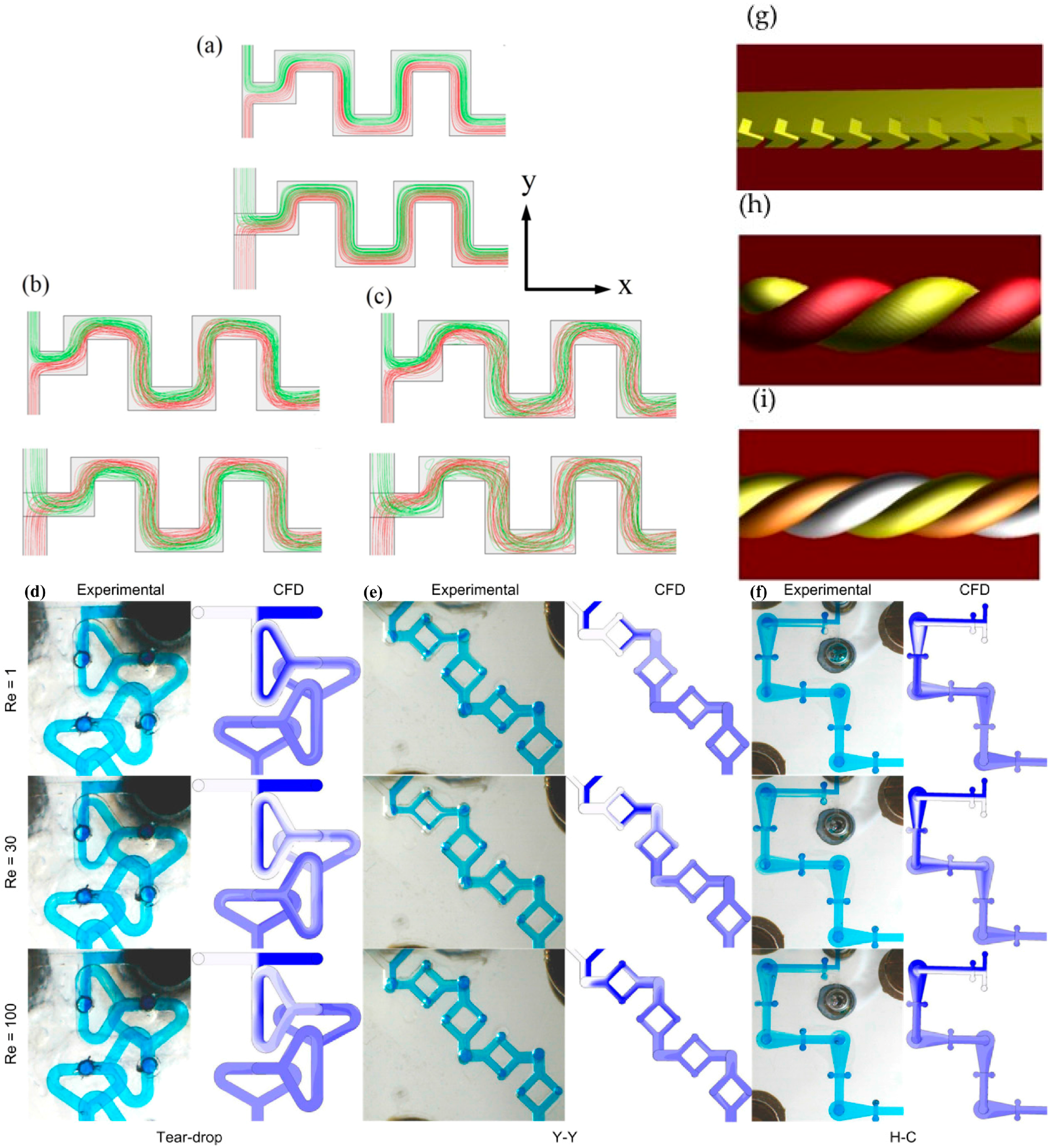
3. Results and Discussion
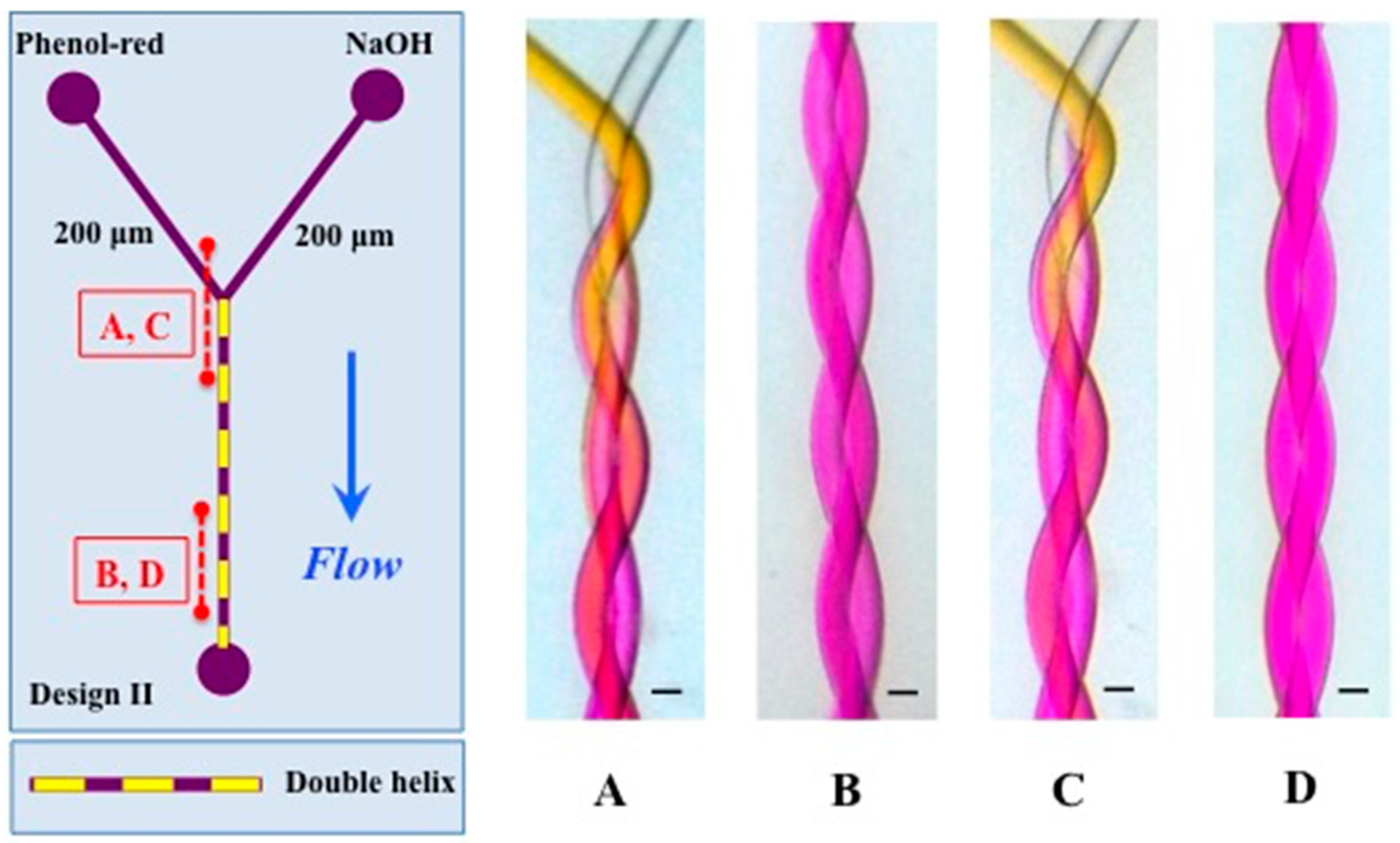
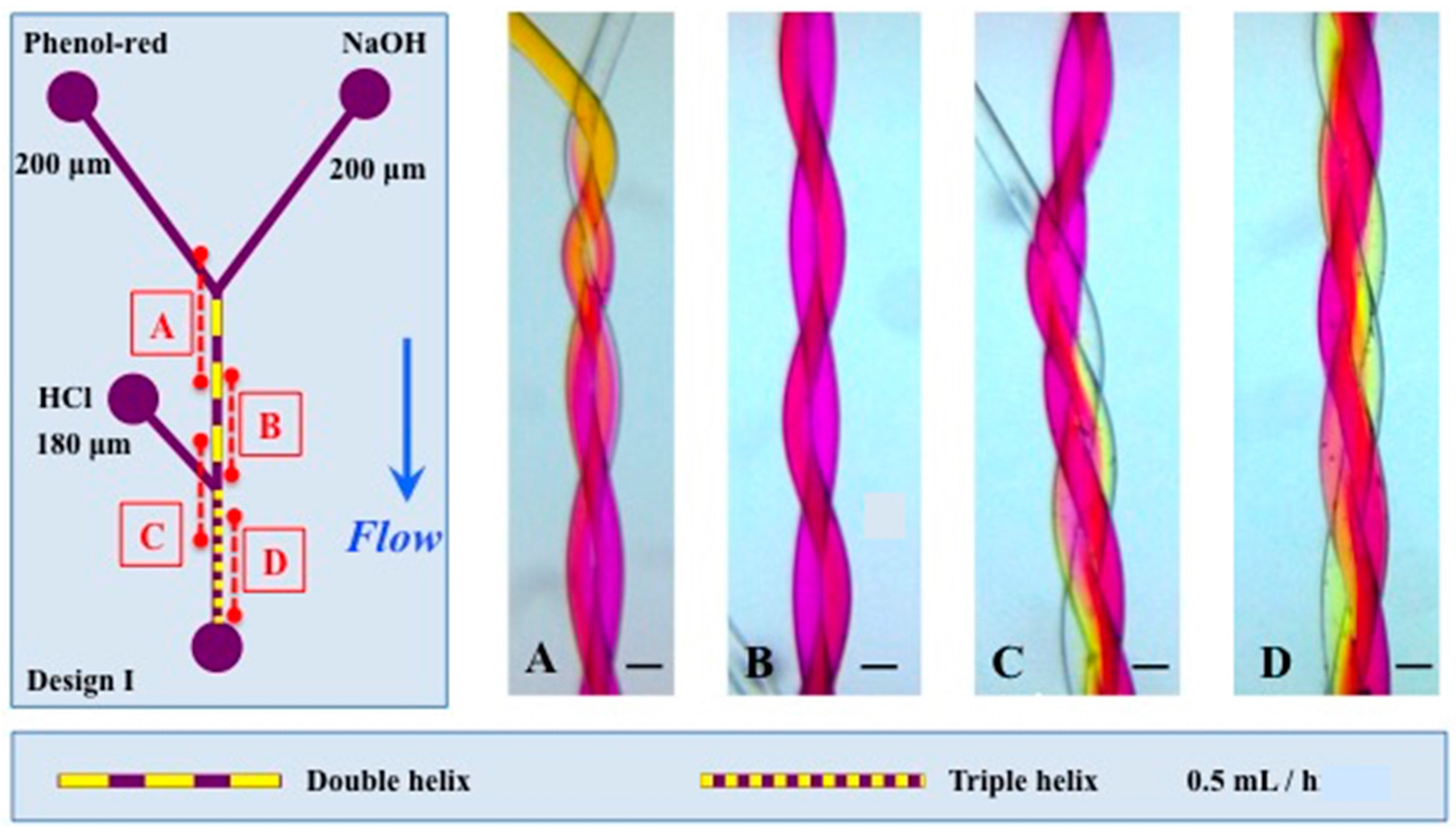
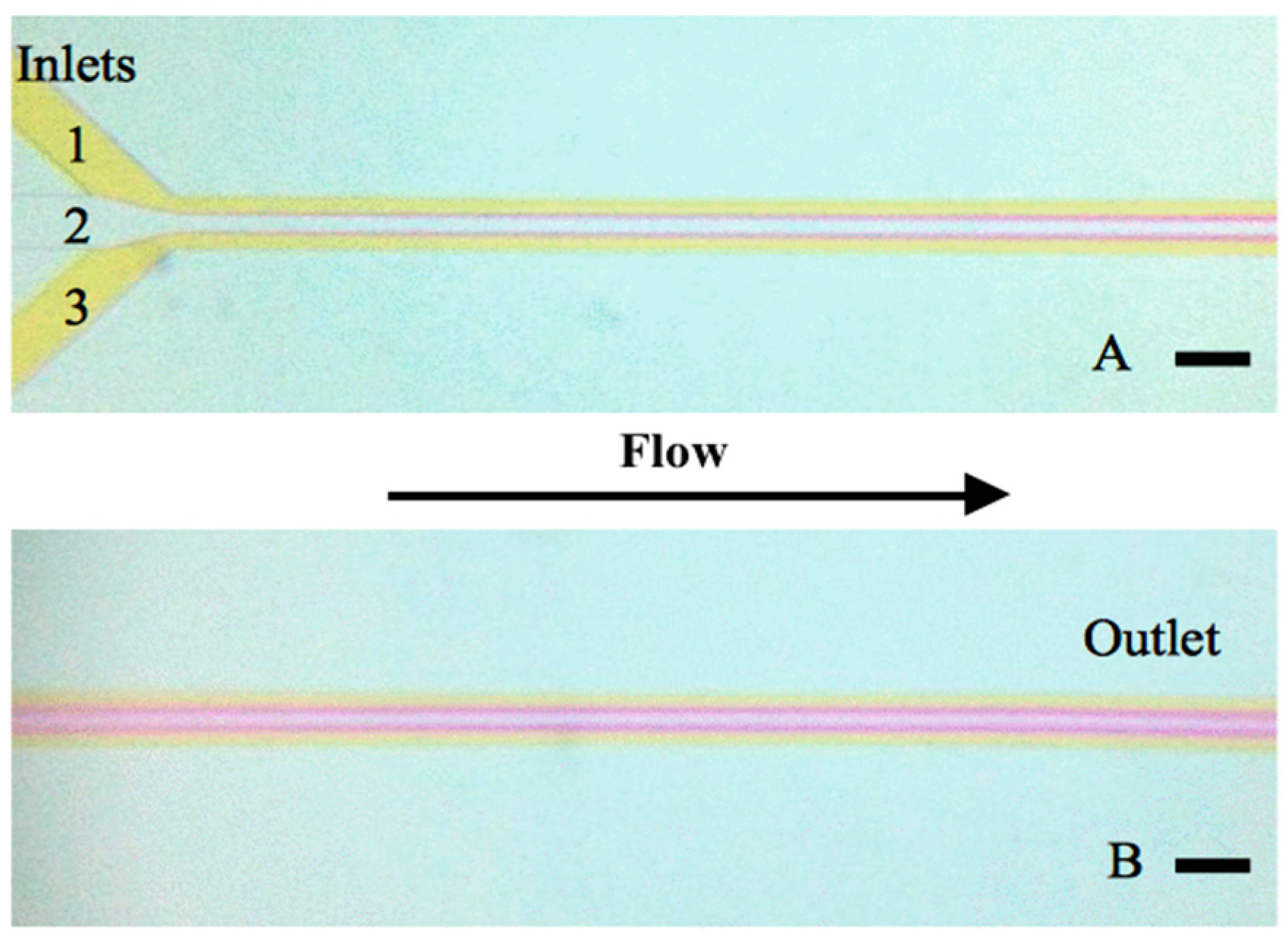
3.1. Mixing
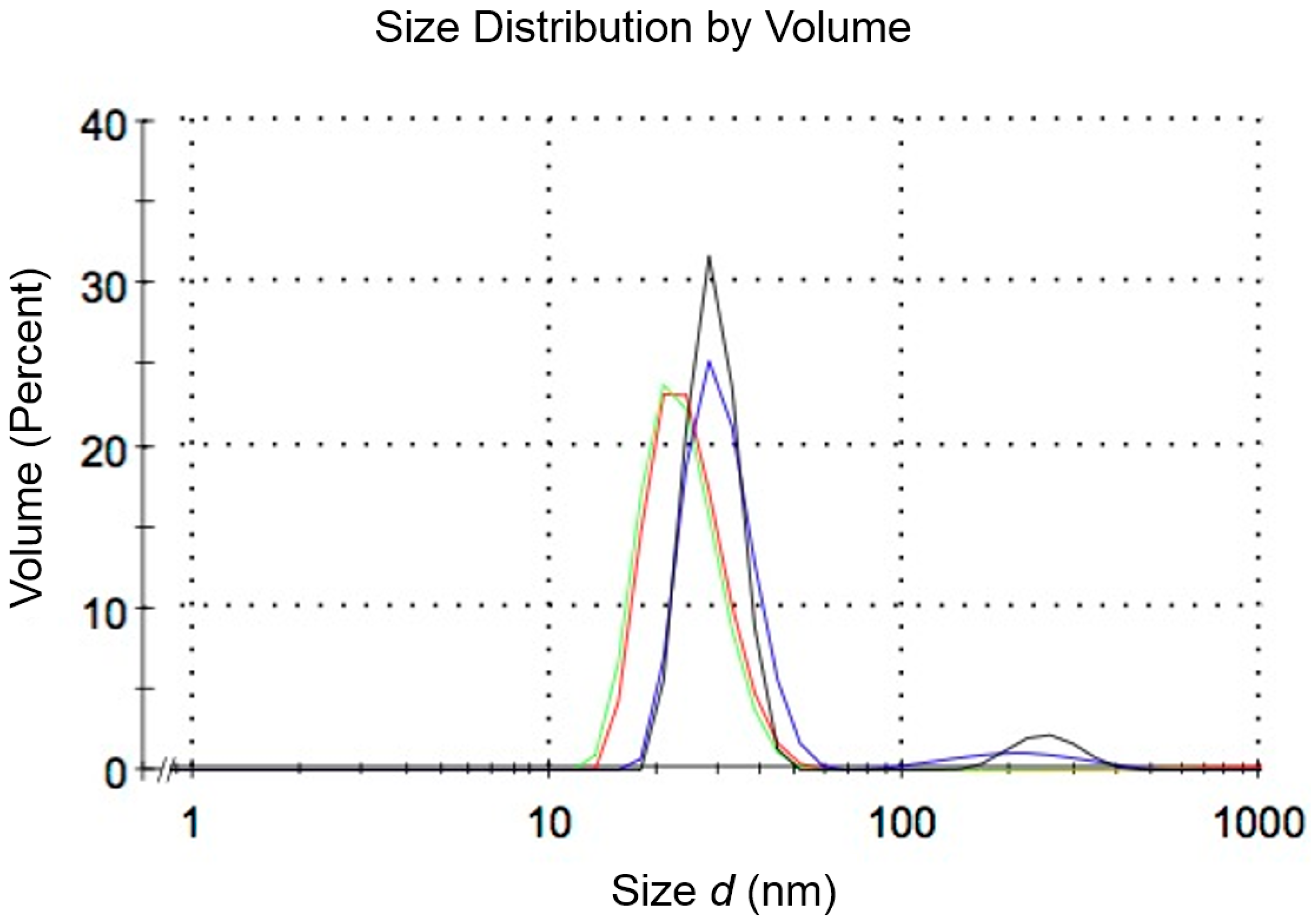
3.2. Assembly of Nanoparticles
3.3. Comparison with Other 3D Mixers
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Salieb-Beugelaar, G.B.; Simone, G.; Arura, A.; Philippi, A.; Manz, A. Latest developments in microfluidic cell biology & analysis systems. Anal. Chem. 2010, 82, 4848–4864. [Google Scholar] [PubMed]
- Salieb-Beugelaar, G.B.; Hunziker, P.R. Towards nano-diagnostics for rapid diagnosis of infectious diseases-current technological state. Eur. J. Nanomed. 2014, 6, 11–28. [Google Scholar] [CrossRef]
- Zhang, B.; Salieb-Beugelaar, G.B.; Nigo, M.M.; Weidmann, M.; Hunziker, P. Diagnosing dengue virus infection: Rapid tests and the role of micro/nanotechnologies. Nanomed. Nanotechnol. Biol. Med. 2015, 11, 1745–1761. [Google Scholar] [CrossRef] [PubMed]
- Salieb-Beugelaar, G.B.; Zhang, B.; Nigo, M.M.; Frischmann, S.; Hunziker, P.R. Improving diagnosis of pneumococcal disease by multiparameter testing and micro/nanotechnologies. Eur. J. Nanomed. 2016, 8, 115–128. [Google Scholar] [CrossRef]
- Parekh, P.D.; Ladd, C.; Panich, L.; Moussa, K.; Dickey, M.D. 3D printing of liquid metals as fugitive inks for fabrication of 3D microfluidic channels. Lab Chip 2016, 16, 1812–1820. [Google Scholar] [CrossRef] [PubMed]
- Jue, E.; Schoepp, N.G.; Witters, D.; Ismagilov, R.F. Evaluating 3D printing to solve the sample-to-device interface for LRS and POC diagnostics: Example of an interlock meter-mix device for metering and lysing clinical urine samples. Lab Chip 2016, 16, 1852–1860. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.M.; Ng, S.H.; Li, K.H.; Yoon, Y.J. 3D printed microfluidics for biological applications. Lab Chip 2015, 15, 3627–3637. [Google Scholar] [CrossRef] [PubMed]
- Tsao, T.R.; Morony, R.M.; Martin, B.A.; White, R.M. Electrochemical detection of localization mixing produced by ultrasonic fluxural waves. In Proceedings of the IEEE 1991 Ultrasonics Symposium, Orlando, FL, USA, 8–11 December 1991.
- Suzuki, H.; Ho, C.M. A magnetic force driven chaotic micro-mixer. In Proceedings of the Fifteenth IEEE International Conference on Micro Electro Mechanical Systems, Las Vegas, NE, USA, 20–24 January 2002; pp. 40–43.
- Hossain, S.; Kim, K.-Y. Mixing performance of a serpentine micromixer with non-aligned inputs. Micromachines 2015, 6, 842–854. [Google Scholar] [CrossRef]
- Viktorov, V.; Mahmud, R.; Visconte, C. Comparative analysis of passive micromixers at a wide range of Reynolds numbers. Micromachines 2015, 6, 1166–1179. [Google Scholar] [CrossRef]
- Liu, R.H.; Stremler, M.A.; Sharp, K.V.; Olsen, M.G.; Santiago, J.G.; Adrian, R.J.; Aref, H.; Beede, D.J. Passive mixing in a three dimensional serpentine microchannel. J. Microelectromech. Syst. 2000, 9, 190–197. [Google Scholar] [CrossRef]
- Chen, H.C.; Meiners, J.-C. Topologic mixing on a microfluidic chip. Appl. Phys. Lett. 2004, 84, 2193–2195. [Google Scholar] [CrossRef]
- Kumar, V.; Aggerwal, M.; Nigam, K.D.P. Mixing in curved tubes. Chem. Eng. Sci. 2006, 61, 5742–5753. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, D.S.; Lee, S.S.; Kwon, T.H. A split and recombination micromixer fabricated in a PDMS three-dimensional structure. J. Micromech. Microeng. 2006, 16, 1067–1072. [Google Scholar] [CrossRef]
- Viktorov, V.; Nimafar, M. A novel generation of 3D SAR-based passive micromixer: Efficient mixing and low pressure drop at a low Reynolds number. J. Micromech. Microeng. 2013, 23, 055023. [Google Scholar] [CrossRef]
- Ansari, M.A.; Kim, K.-Y.; Anwar, K.; Kim, S.M. A novel passive micromixer based on unbalanced splits and collisions of fluid streams. J. Micromech. Microeng. 2010, 20, 1–10. [Google Scholar] [CrossRef]
- Lim, T.W.; Son, Y.; Jeong, Y.J.; Kong, H.-J.; Lee, K.-S.; Kim, D.-P. Three-dimensionally crossing manifold micro-mixer for fast mixing in a short channel length. Lab Chip 2011, 11, 100–103. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Odom, T.W.; Chiu, D.T.; Whitesides, G.M. Fabrication of complex three-dimensional systems in PDMS. J. Am. Chem. Soc. 2003, 125, 554–559. [Google Scholar] [CrossRef] [PubMed]
- Hunziker, P.R.; Wolf, M.P.; Wang, X.; Zhang, B.; Marsch, S.; Salieb-Beugelaar, G.B. Construction of programmable interconnected 3D microfluidic networks. J. Micromech. Microeng. 2015, 25, 025018. [Google Scholar] [CrossRef]
- Hwang, Y.; Seo, D.; Roy, M.; Han, E.; Candler, R.N.; Seo, S. Capillary flow in PDMS cylindrical microfluidic channel using 3-D printed mold. J. Microelectromech. Syst. 2016, 25, 238–240. [Google Scholar] [CrossRef]
- Parker, B.; Samanipour, R.; Ahmadi, A.; Kim, K. Rapid fabrication of circular channel microfluidic flow-focusing devices for hydrogel droplet generation. Micro&Nano Lett. 2016, 11, 41–45. [Google Scholar]
- Song, S.-H.; Lee, C.-K.; Kim, T.-J. A rapid and simple fabrication method for 3-dimensional circular microfluidic channel using metal wire removal process. Microfluid. Nanofluid. 2010, 9, 533–540. [Google Scholar] [CrossRef]
- Verma, M.K.S.; Majumber, A.; Ghatak, A. Embedded template-assisted fabrication of complex microchannels in PDMS and design of a microfluidic adhesive. Langmuir 2006, 22, 10291–10295. [Google Scholar] [CrossRef] [PubMed]
- Verma, M.K.S.; Ganneboyina, S.R.; Rakshit, V.; Ghatak, A. Three-dimensional multihelical microfluidic mixers for rapid mixing of liquids. Langmuir 2008, 24, 2248–2251. [Google Scholar] [CrossRef] [PubMed]
- Gompper, G.; Fedosov, D.A. Modeling microcirculatory blood flow: Current state and future perspectives. WIREs Syst. Biol. Med. 2016, 8, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Ben-Haim, N.; Broz, P.; Marsch, S.; Meier, W.; Hunziker, P. Cell-specific integration of artificial organelles based on functionalized polymer vesicles. Nano Lett. 2008, 8, 1368–1373. [Google Scholar] [CrossRef] [PubMed]
- Broz, P.; Benito, S.M.; Saw, C.; Burger, P.; Heider, H.; Pfisterer, M.; Marsch, S.; Meier, W.; Hunziker, P. Cell targeting by a generic receptor-targeted polymer nanocontainer platform. J. Control. Release 2005, 102, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhu, Z.; Wang, X.; Gonçalves, D.; Zhang, B.; Hierlemann, A.; Hunziker, P. Microfluidics-based single-step preparation of injection-ready polymeric nanosystems for medical imaging and drug delivery. Nanoscale 2015, 7, 16983–16993. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Ranquin, A.; Versees, W.; Meier, W.; Steyaert, J.; Van Gelder, P. Therapeutic nanoreactors: Combining chemistry and biology in a novel triblock copolymer drug delivery system. Nano Lett. 2005, 5, 2220–2224. [Google Scholar] [CrossRef] [PubMed]
- Langowska, K.; Palivan, C.G.; Meier, W. Polymer nanoreactors shown to produce and release antibiotics locally. Chem. Commun. 2013, 49, 128–130. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, F.; Gutknecht, J.; Morozov, O.; Hunziker, P. A mathematical programming language extension for multilinear algebra. In Proceedings of the Kolloqium über Programmiersprachen und Grundlagen der Programmierung, Timmendorfer Strand, Lübeck, Germany, 10–12 October 2007.
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 17, 549–560. [Google Scholar] [CrossRef]
- Nguyen, N.-T. Micromixers: Fundamentals, Design and Fabrication, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezić, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]



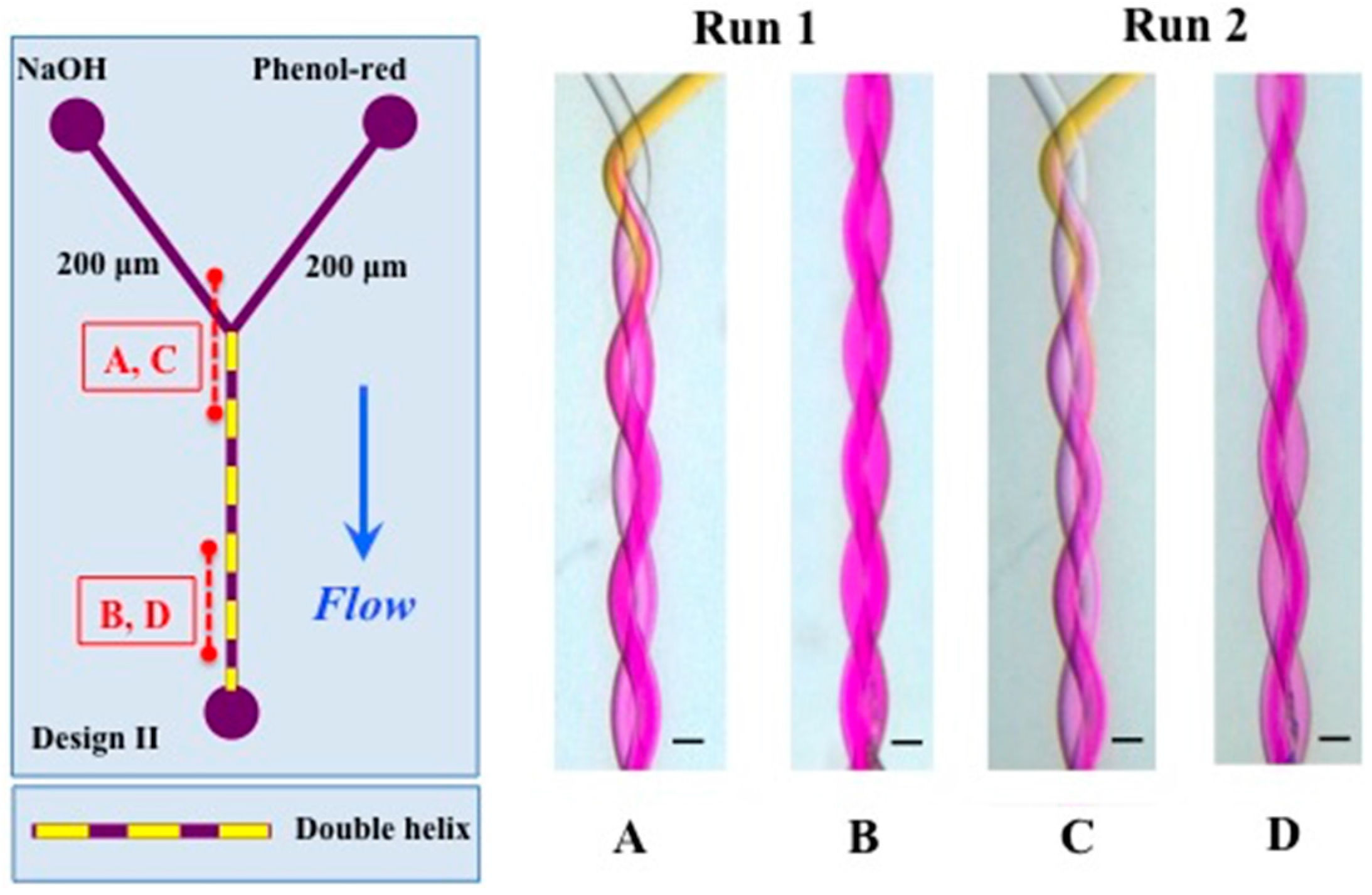
| Run | 1 | 2 |
|---|---|---|
| Qaq (mL/h) | 1.00 | 4.00 |
| Qorg (mL/h) | 0.03 | 0.59 |
| QT (mL/h) | 1.03 | 4.59 |
| FRR | 33.30 | 6.78 |
| %EtOH | 3.00 | 15.00 |
| Type Helix | dchannels (μm) | R (m) | Rcurvature (m) | λ | Lpitch (m) | Tmix (s) |
|---|---|---|---|---|---|---|
| Double helix (I/A) | 200/200 | 1.79 × 10−4 | 1.03 × 10−3 | 5.73 | 2.44 × 10−3 | 128 |
| Triple helix (I /B) | 180/200/200 | 2.41 × 10−4 | 1.07 × 10−3 | 4.41 | 2.80 × 10−3 | 232 |
| Double helix (II /C) | 200/200 | 1.77 × 10−4 | 8.94× 10−4 | 5.04 | 2.24 × 10−3 | 126 |
| Triple helix (III /D) | 120/180/200 | 1.97 × 10−4 | 1.00 × 10−3 | 5.10 | 2.50 × 10−3 | 155 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salieb-Beugelaar, G.B.; Gonçalves, D.; Wolf, M.P.; Hunziker, P. Microfluidic 3D Helix Mixers. Micromachines 2016, 7, 189. https://doi.org/10.3390/mi7100189
Salieb-Beugelaar GB, Gonçalves D, Wolf MP, Hunziker P. Microfluidic 3D Helix Mixers. Micromachines. 2016; 7(10):189. https://doi.org/10.3390/mi7100189
Chicago/Turabian StyleSalieb-Beugelaar, Georgette B., Daniel Gonçalves, Marc P. Wolf, and Patrick Hunziker. 2016. "Microfluidic 3D Helix Mixers" Micromachines 7, no. 10: 189. https://doi.org/10.3390/mi7100189
APA StyleSalieb-Beugelaar, G. B., Gonçalves, D., Wolf, M. P., & Hunziker, P. (2016). Microfluidic 3D Helix Mixers. Micromachines, 7(10), 189. https://doi.org/10.3390/mi7100189






