Abstract
The ability to elicit distinct duty cycles from the same self-regulating microfluidic oscillator device would greatly enhance the versatility of this micro-machine as a tool, capable of recapitulating in vitro the diverse oscillatory processes that occur within natural systems. We report a novel approach to realize this using the coordinated modulation of input volumetric flow rate ratio and fluidic capacitance ratio. The demonstration uses a straightforward experimental system where fluid inflow to the oscillator is provided by two syringes (of symmetric or asymmetric cross-sectional area) mounted upon a single syringe pump applying pressure across both syringes at a constant linear velocity. This produces distinct volumetric outflow rates from each syringe that are proportional to the ratio between their cross-sectional areas. The difference in syringe cross-sectional area also leads to differences in fluidic capacitance; this underappreciated capacitive difference allows us to present a simplified expression to determine the microfluidic oscillators duty cycle as a function of cross-sectional area. Examination of multiple total volumetric inflows under asymmetric inflow rates yielded predictable and robust duty cycles ranging from 50% to 90%. A method for estimating the outflow duration for each inflow under applied flow rate ratios is provided to better facilitate the utilization of this system in experimental protocols requiring specific stimulation and rest intervals.
1. Introduction
Emerging interest in microfluidic machines that directly utilize fluidic energy to execute core operations has prompted the development of self-regulated machines that, by virtue of their autonomous operation, have also garnered much attention as potential platforms for basic biomedical research [1,2,3].
Biological and physiological systems are fundamentally regulated by oscillatory processes operating at discrete spatial and temporal scales. Our understanding of these systems, consequently, has benefited from the development of pulsatile stimulation techniques capable of manipulating the temporal dynamics of these processes and investigating the role of timing within them. Historically, the in vitro study of these processes in cultured cells was advanced primarily by two types of assays: one in which a single stimulus is bath-applied and later washed off (e.g., pulse-chase analysis [4,5], and BrdU “birth dating” [6]); and one in which a continuous long-term temporal stimulation pattern is applied by way of an external control apparatus [7]. Advancements in microfluidic technology have catalyzed the translation of such assays, in parallel with the development of novel counterparts, to forms supported by these emerging micro-scale—“lab-on-a-chip”—platforms [8,9,10,11].
Microfluidic devices often emulate electronic circuitry and utilize integrated conduits and embedded valves to direct and manipulate fluid flows. The control systems underlying their operation, however, have typically remained external from the fluidic devices themselves [12,13,14]. An awareness that this rise in peripheral equipment cost may limit “next-generation” microfluidic systems has motivated the development of autonomous, pre-programmed, fluidic systems [1,12,13,14,15,16,17]. Foremost among these is the microfluidic oscillator [18].
Not unlike how electronic oscillators were among the first broadly adopted automated electrical circuits; self-oscillating microfluidic devices provide a simple, yet useful, first target for microfluidic automation [1,2] as evidenced by the growing body of literature describing experimental methods, wherein cells cultured within micro-devices are chemically stimulated in a pulsatile, rather than continuous, manner [8,10,19,20]. One such method for cellular interrogation modifies stimulation events by altering the duration of an applied stimulus and/or rest period; effectively manipulating the oscillation frequency and duty cycle of the stimulatory system [19]. Through this approach, it has been observed that different responses may be elicited from the same population of cells by manipulating these stimulatory parameters.
The work presented here was motivated by the questions: how can a single microfluidic oscillator circuit be designed to best support multiple stimulatory frequencies and rest periods; and how can this be done in a manner that is easy to understand and perform by non-microfluidic experts? We have previously demonstrated the ability to alter oscillation frequency by modifying flow rate, and to alter duty cycle by modifying the device itself [1,2]. As the technical burden of repeatedly designing and fabricating different devices for each desired duty cycle is both difficult and tedious; we asked if a continuous and predictable modification of duty cycle could be achieved by simply modifying the syringes used to provide volumetric inflow.
The challenge associated with modifying volumetric inflow rate lies in the effect this may have upon the threshold opening pressure of each valve [21]. Due to the complexity of the relationship between volumetric flow rate and duty cycle, predicting the duty cycle resulting from a change in volumetric flow rate is not trivial. Additional challenges arise if two syringe pumps are used to generate differing volumetric inflows, owing largely to inherent pump-to-pump variability and general inflow rate unsteadiness that may produce unstable oscillations [22]. Here we report the predictable modulation of duty cycle using two syringes mounted upon a single syringe pump such that volumetric flow rate ratio and fluidic capacitance are coupled. This setup is advantageous in that it allows duty cycle to be considered simply as a function of the volumetric inflow rate ratio; requiring no modifications of the microfluidic circuit to robustly produce distinct duty cycles.
2. Working Principle
The microfluidic oscillator functions by converting two constant volumetric flow rate inflows to one oscillatory outflow through the activity of two normally-closed three-way valves that generate oscillations in fluid outflow through the alternate obstruction of each inflow (Figure 1).
Briefly, if we denote the two valves valve 1 and valve 2, and arbitrarily assume that valve 2 is initially in an open position—allowing fluid to flow across it; a portion of the outflow from valve 2 will be diverted from its drain terminal to the gate terminal of valve 1. The gate terminal refers to the conduit leading to the region below the membrane valve unit. The accumulation of fluid within this region supplies the gate pressure of valve 1 (PG1); preventing the downward deflection of the membrane, and consequently preventing valve 1 from transitioning to an open position while PG1 exceeds the source pressure of valve 1 (PS1) generated by the accumulation of fluid in the portion of the valve upstream from the valve 1 gate.
When PS1 has surpassed the sum of PG1 and the inherent pressure threshold of valve 1 (Pth1), determined by the specific mechanical properties of the membrane, the membrane is deflected downward, and fluid is allowed to travel through valve 1. A portion of this outflow is then diverted from its drain terminal to the gate terminal of valve 2, as the outflow from valve 1 had been diverted previously, and supplies the gate pressure necessary to force the accumulation of fluid upstream of valve 2, until the difference between PS2 and PG2 has exceeded Pth2 (Figure 1a,b). The coordination of these processes, resulting in the anti-synchronized opening and closing of both valve units, produces an oscillatory outflow (described in greater detail in previous work [2,21]).
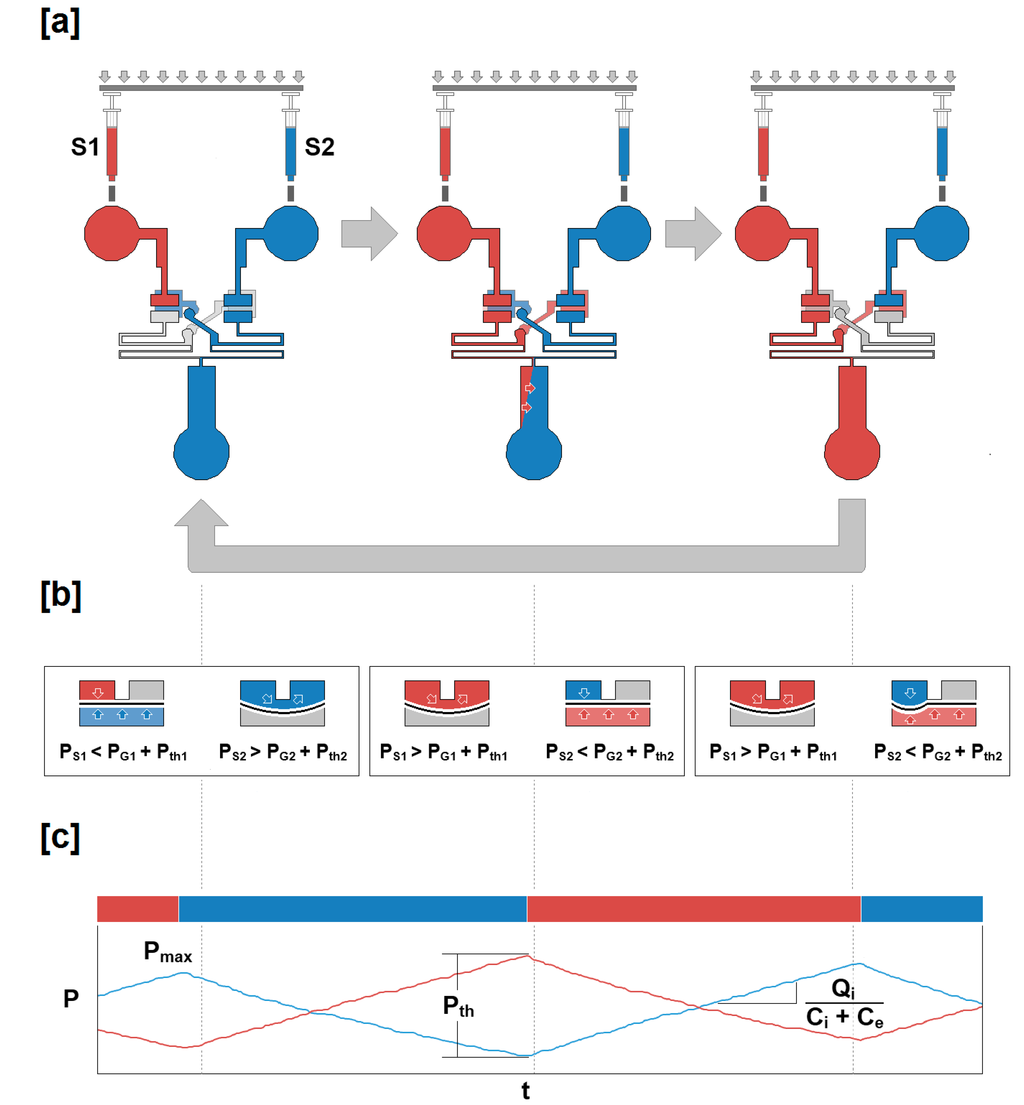
Figure 1.
Schematic for the experimental system. The three panels displayed represent the behavior of the microfluidic oscillator at three time points during operation under symmetric flow conditions. (a) Two fluids (blue and red) are introduced through two syringes mounted on a single syringe pump. The fluids enter the device at a constant rate, but are converted into an oscillatory outflow when passing through the valves. (b) A cross section of each valve unit at the time points displayed in panel (a). Initially, the source pressure (PS1) is insufficient (PS1 < PG1 + Pth1) to displace the membrane downward, allowing the blue fluid to outflow. When the pressure has reached its maximum value (Pmax), the membrane is displaced (PS1 > PG1 + Pth1), allowing the red fluid to outflow until sufficient source pressure (PS2) has accumulated within the chamber above the opposite membrane (PS2 > PG2 + Pth2) allowing the blue fluid to outflow. (c) The time points within the pressure data time series corresponding to the valve and outflow profiles presented in panels (a) and (b) are indicated. A sample Pmax and Pth are also represented, as well as the relationship between inflow rate (Qi), internal capacitance (Ci), and external capacitance (Ce).
Functionally, as the gate pressure of the valve regulating one flow is itself regulated by the volumetric outflow rate across the other, we assume the following characteristic:
This expression, where Qin, C and P represent inflow rate, fluidic capacitance, and pressure respectively, may be expanded to describe the threshold-dependent mechanism underlying the functionality of the valves. Conceptually, the transition between a closed-to-open or open-to-closed valve-state is governed by the values of Pth and PG set by the mechanical properties of the membrane and buildup of fluid pressure below the membrane (Figure 1b), respectively, and the rate at which fluid pressure builds within the valve region above the membrane (PS) [2]. The relationship between inflow rate and capacitance, thus, may be used to determine duty cycle as a function of time:
Under symmetric flow conditions, Q1 ≅ Q2, where the mechanical properties of the membrane and valve compartments are preserved across both valves, the assumption is Pth1 ≅ Pth2 and C1 ≅ C2, allowing us to consequently define duty cycle solely as a function of volumetric flow rate.
Equation (4) depicts an attractive relationship that relates duty cycles simply to volumetric inflow ratios. By this definition, the introduction of asymmetry to the volumetric inflow rates of each fluid, Qi, would produce asymmetric duty cycles. However, in asymmetric conditions where Q1 ≠ Q2 (e.g., Q1 < Q2), the syringe supplying the greater volumetric inflow (Q2) will result in a greater threshold pressure for the valve regulating the lesser volumetric inflow, and consequently, Pth1 > Pth2. The presence of this asymmetry suggests that the use of two identical syringes, evacuated at asymmetric linear velocities, would rely upon a complex balance between Qin, C, and P such that the duty cycles produced may not be accurately modeled by Equation (4). One way to maintain the relationship shown in Equation (4) would be to modulate Ci together with Qi so that Pthi × Ci ≈ constant. One way to achieve this conveniently is by mounting two plastic syringes of different cross-sectional area on one syringe pump (Figure 2), and utilizing the compliance of the syringe components [23] and resulting capacitive differences of the syringes [12]. Within the described system, as syringe outflow rate is a function of velocity and syringe cross-sectional area, and as both syringes are evacuated at the same linear velocity, we may further refine our definition of duty cycle as being a function of syringe diameter (Figure 2b). By using syringes of different diameters, we apply Equation (4) and demonstrate predictability of duty cycle values as a function of the combination of syringes used (Table 1).
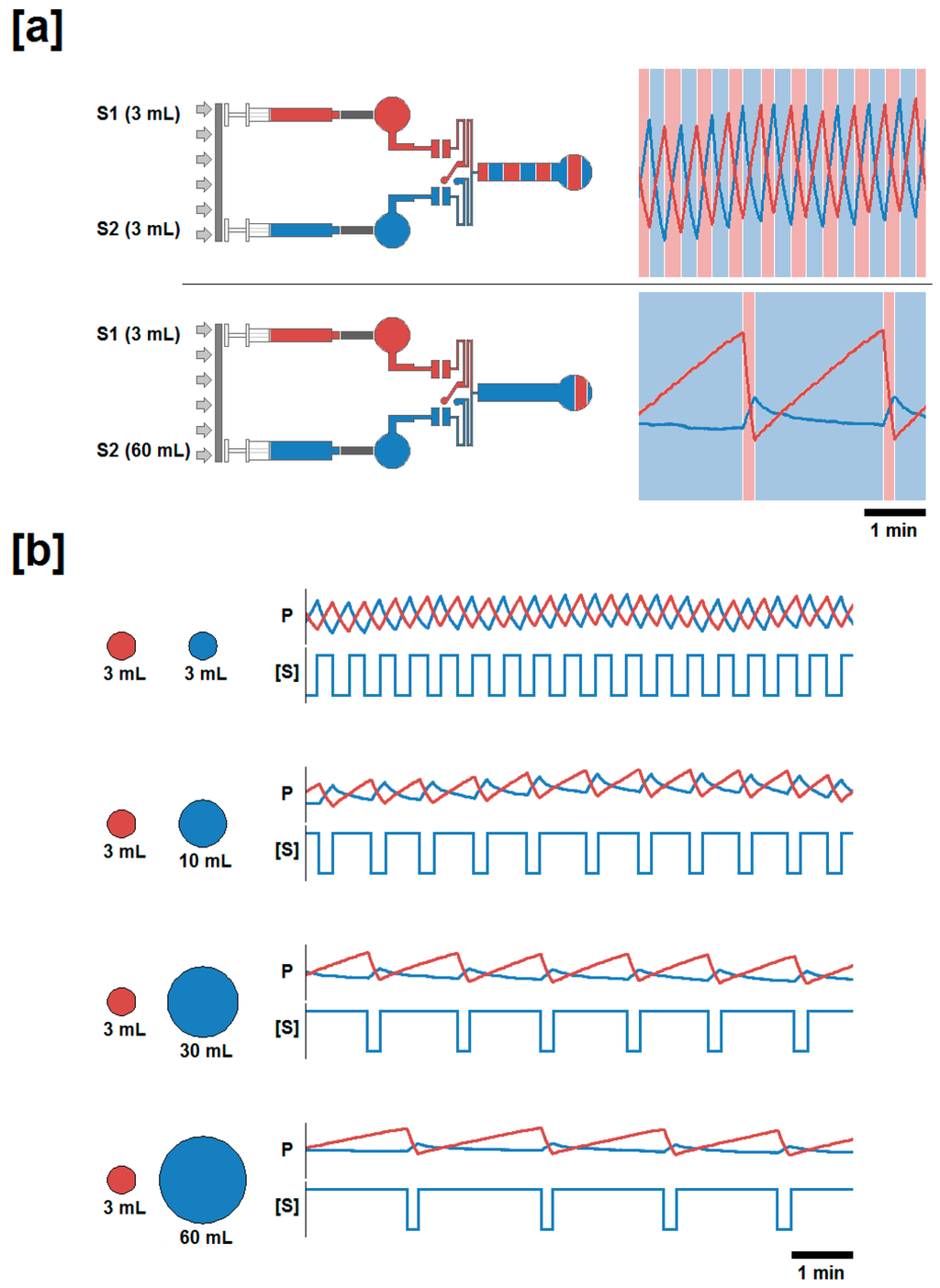
Figure 2.
Schematic for the experimental generation of symmetric and asymmetric volumetric flow rates, and changes in duty cycle and pressure profile produced as a function of syringe diameter. (a) Two sample conditions where Syringe 1, (red), and Syringe 2, (blue), are mounted on a single syringe pump. The ratios illustrated are the symmetric 3 mL:3 mL (upper) and asymmetric 3 mL:60 mL (lower). Within the experimental protocol , Syringe 1 was held constant in all pairings while Syringe 2 was varied to achieve symmetric (50%) and asymmetric (>50%) duty cycles; and total volumetric inflow rate remained constant. Experimentally generated pressure profile waveforms are presented against alternating background bands representing the fluid outflow profile. (b) Pressure profile and stimulation period for the four inflow ratio regimes. Pressure profiles were generated while the syringe pump was moving at a constant linear velocity such that the total volumetric inflow rate (the sum of the inflows supplied by each syringe) was maintained at a volumetric flow rate of 20 μL/min. The pressure profiles recorded (P) are presented above each trace representing the concentration of a fluidic stimulant ([S]) provided via Syringe 2, in the outflow.
3. Materials and Methods
3.1. Master Mold Fabrication
Microfluidic oscillator master molds were fabricated upon 4″-silicon wafers using the negative photoresist, SU-8 (MicroChem, Newton, MA, USA). Following air-cleaning of the wafer, SU-8 2075 photoresist was deposited on the wafer and spin-coated at 500 rpm (acceleration of 440 rpm/s) for 10 s and at 2100 rpm (acceleration of 440 rpm/s) for 30 s. The coated wafer was then placed on a hotplate for pre-exposure baking at 65 °C for 5 min, 95 °C for 20 min and then allowed to gradually cool to room temperature by allowing it to remain on the hotplate after the plate was turned off. The SU-8 substrate was then exposed with conventional UV (~17 mJ/cm²) for 30 s using a mask aligner (Hybrid Technology Group), and then placed on a hotplate for post-exposure baking at 65 °C for 5 min, 95 °C for 10 min and then allowed to gradually cool to room temperature as before. Unexposed regions of photoresist were dissolved by repeatedly immersing the wafer in fresh SU-8 developer solution (MicroChem, Newton, MA, USA) for 60 s intervals until all non-exposed/cross-linked regions of SU-8 were removed. The completed mold was then placed within a gravity convection oven (DX-400, Yamato Scientific America, Santa Barbara, CA, USA) for 15 min at 120 °C and, upon returning to room temperature, was treated (silanized) in a desiccator for 1 h in the presence of vaporized tridecafluoro-1,1,2,2-tetrahydrooctyl-1-trichlorosilane (United Chemical Tech., Bristol, PA, USA).
3.2. Microfluidic Oscillator Fabrication
The microfluidic oscillator device consists of three polydimethylsiloxane (PDMS) layers assembled as previously described [1,2]. Briefly, the device features (100 μm height) were imprinted in the top and bottom layers, and a PDMS membrane (target thickness: 20 μm) was positioned between them (Figure 1).
1:10 PDMS (Sylgard 184, Dow Corning, Midland, MI, USA) was poured onto the master mold and allowed to cure within a gravity convection oven at 60 °C for 6 h. The cured PDMS slab was then removed from the mold and cut into individual device layers. Concurrently, PDMS membranes were fabricated by spin-coating 1:10 PDMS onto glass slides pre-treated with silane as before. PDMS membranes were then cured within a gravity convection oven for 5 min at 120 °C and 10 min at 60 °C. Prior to final assembly, a 2-mm biopsy punch was used to remove PDMS from the inlet and outlet ports of the top device layer. The bottom layer and membrane were then treated by plasma oxidation (Covance MP, FemtoScience, Hwaseong-si, Gyeonggi-do, South Korea) to facilitate bonding and, following bonding, were then placed in a gravity convection oven at 120 °C for 5 min and at 60 °C for 10 min. Thru-holes were then made in the membrane to allow fluid communication between the top and bottom device layers, using a 350-μm biopsy punch (Ted Pella Inc., Redding, CA, USA). The top layer was then treated by plasma oxidation to facilitate bonding with the membrane-bottom layer assembly. Following treatment, but preceding bonding, the normally closed region of the top layer was “deactivated” by being brought into direct contact with an unoxidized PDMS “stamp”. Following final bonding, assembled devices were incubated for 2 min within a gravity convection oven at 120 °C.
3.3. Microfluidic Oscillator Testing and Data Processing
Microfluidic oscillators were tested by connecting pressure sensors (Model 142PC05D, Honeywell, NJ, USA) at the device inlets via Tygon tubing (Saint-Gobain™ Tygon™ R-3603 Clear Laboratory Tubing, Saint-Gobain Performance Plastics, Akron, OH, USA) to measure source pressure. Source pressure data was collected for both valves to quantify pressure buildup and release corresponding to fluid accumulation and evacuation, respectively, through the valves; our previous work highlighted the relationship between source pressure and drain pressure [24]. The occurrence of fluidic oscillations and the coincident timing of these oscillations relative to source pressure profiles were verified visually. All subsequent quantification and assessment, however, was performed using source pressure data. Data was obtained at a sampling rate of 1000 Hz, every 100 data points were averaged (resulting in 1 data point per 100 ms), and stored using LabVIEW (National Instruments, Austin, TX, USA). Data was recorded for a minimum of four hours, of which the data acquired during the first hour for each condition was examined and discarded to ensure the volumetric flow and capacitance of the fluidic system had stabilized, and only the subsequent time (three hours) was assessed. Syringe pumps (Model KDS220, KD Scientific, Holliston, MA, USA and Model Fusion 200, Chemyx, Stafford, TX, USA) were used to provide constant volumetric flow to the device. One input, a 3 mL syringe (Syringe 1) remained connected to one inlet port for the entirety of the study, while the second (Syringe 2) was allowed to alternate between 3 mL, 10 mL, 30 mL and 60 mL plastic syringes (Becton, Dickinson and Company, Franklin Lakes, NJ, USA). The syringe pump was programmed with total volumetric inflow rates appropriate for each syringe pairing, such that Q2 ≥ Q1 and Q2 + Q1 = Qtotal.
Voltage data were collected using LabVIEW and processed, in part, using the open-source peakdet [25].
4. Results and Discussion
4.1. Predictive Duty Cycle Control
Using Equation (4), we calculated and experimentally measured duty cycle as a function of volumetric flow rate ratios achieved through the simple utilization of two plastic syringes of different cross-sectional area mounted on a single syringe pump (Table 1). The estimates generated by Equation (4) agreed with experimental observations.

Table 1.
Different syringe pairings on a single syringe pump enables different duty cycles to be achieved, while maintaining a constant total volumetric inflow rate of 20 μL/min.
| Syringe 1 | Syringe 2 | Duty Cycle (Expected) | Duty Cycle (Observed) | ||||
|---|---|---|---|---|---|---|---|
| Volume (mL) | Diameter (mm) | Inflow Rate (μL/min) | Volume (mL) | Diameter (mm) | Inflow Rate (μL/min) | ||
| 3 | 8.66 | 15.33 | 1 | 4.78 | 4.67 | 23.35% | - |
| 3 | 8.66 | 10.00 | 3 | 8.66 | 10.00 | 50.00% | 48.71% |
| 3 | 8.66 | 6.80 | 5 | 12.06 | 13.20 | 65.98% | - |
| 3 | 8.66 | 5.26 | 10 | 14.5 | 14.74 | 73.71% | 74.59% |
| 3 | 8.66 | 3.40 | 20 | 19.13 | 16.60 | 82.99% | - |
| 3 | 8.66 | 2.75 | 30 | 21.7 | 17.25 | 86.26% | 86.00% |
| 3 | 8.66 | 1.90 | 60 | 26.7 | 18.10 | 90.48% | 90.82% |
| 3 | 8.66 | 0.97 | 140 | 38.4 | 19.03 | 95.16% | - |
Highlighted values represent syringe combinations studied experimentally. The duty cycle values presented are calculated with respect to Syringe 2. Utilizing this system, we succeeded in achieving duty cycles ranging from 50% to 90% (Figure 3a), reproducible across multiple devices (n = 3) (Figure 3b).
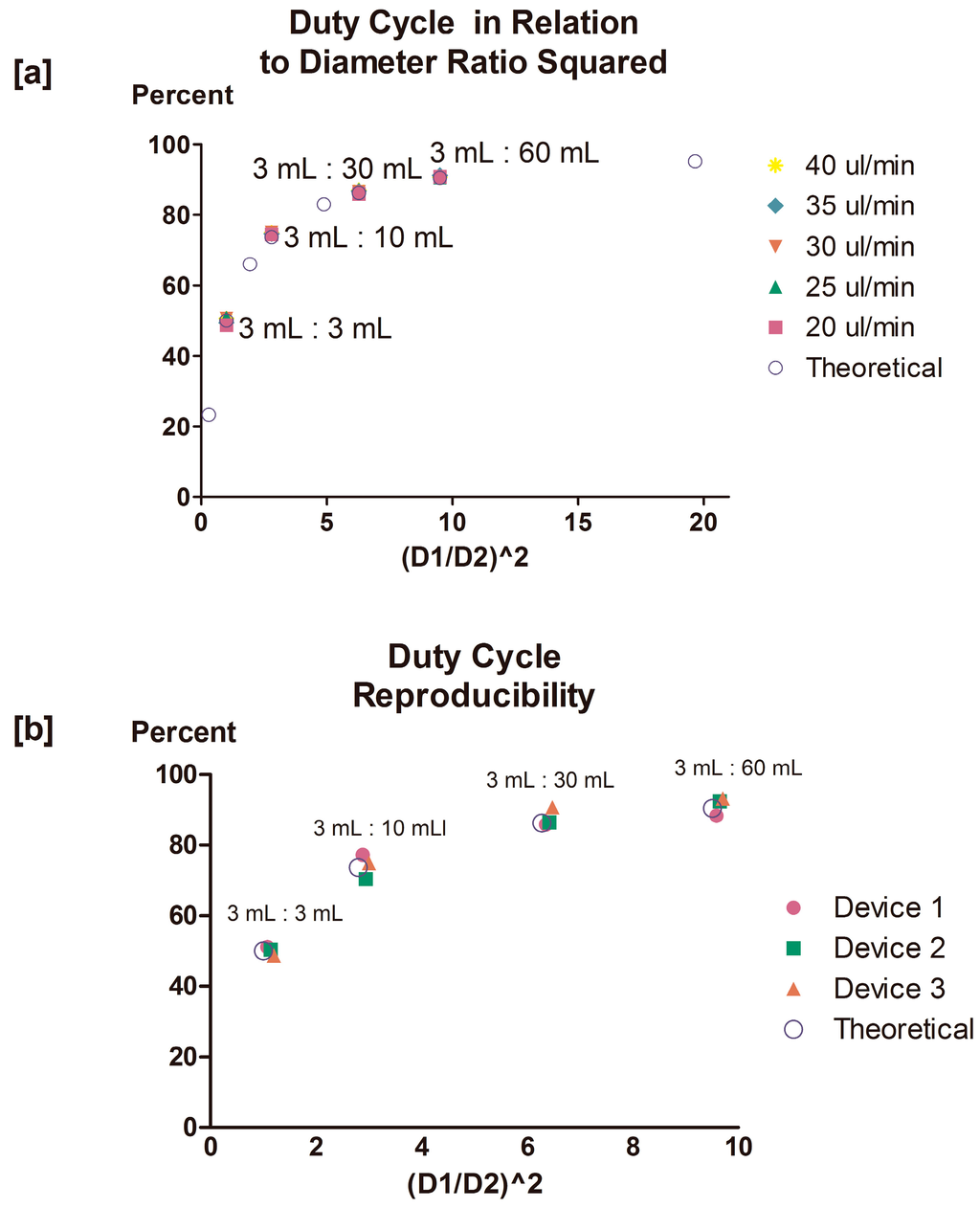
Figure 3.
Experimental duty cycles overlap predicted values; flow rate ratio manipulation stably and reproducibly regulates duty cycle across multiple devices. (a) Filled symbols represent duty cycle values observed and averaged across four syringe combinations and at five different total volumetric inflow rates. Unfilled blue circles represent predicted duty cycle values. All values are derived from time series data containing >6 oscillations. Duty cycle values are plotted against the squared ratio between syringe diameter (Syringe 2:Syringe 1) to illustrate the general trend observed. (b) Duty cycle data collected from multiple devices (n = 3) is presented against the squared ratio between syringe diameter (Syringe 2:Syringe 1). Filled symbols represent duty cycle values recorded and averaged across four syringe combinations for total volumetric inflow rates ranging from 5 to 40 μL/min. Unfilled circles represent theoretical (predicted) duty cycle values. All averaged values are derived from time series data containing >6 oscillations. Error bars represent the calculated standard deviation for all duty cycle values recorded from each of three devices for all tested inflow rate ranges.
4.2. Mounting Syringes on Separate Syringe Pumps Produces Unstable Duty Cycles
To verify that Equation (4) did not accurately predict duty cycles produced through the sole modification of volumetric flow rate; two identical syringes were mounted on two independent syringe pumps and tested for their ability to produce predictable duty cycles. Flow was initiated at a total volumetric flow rate of 20 μL/min, and the resulting duty cycles were recorded and analyzed. The duty cycles produced via this setup deviated from their predicted values and were unstable, appearing to shift sporadically from one oscillation pattern to another, interspersed by brief periods during which the oscillations would appear stable. This instability was also present at additional total volumetric inflow rates (data not shown), and ultimately affected the predictability of the duty cycles produced (Figure 4).
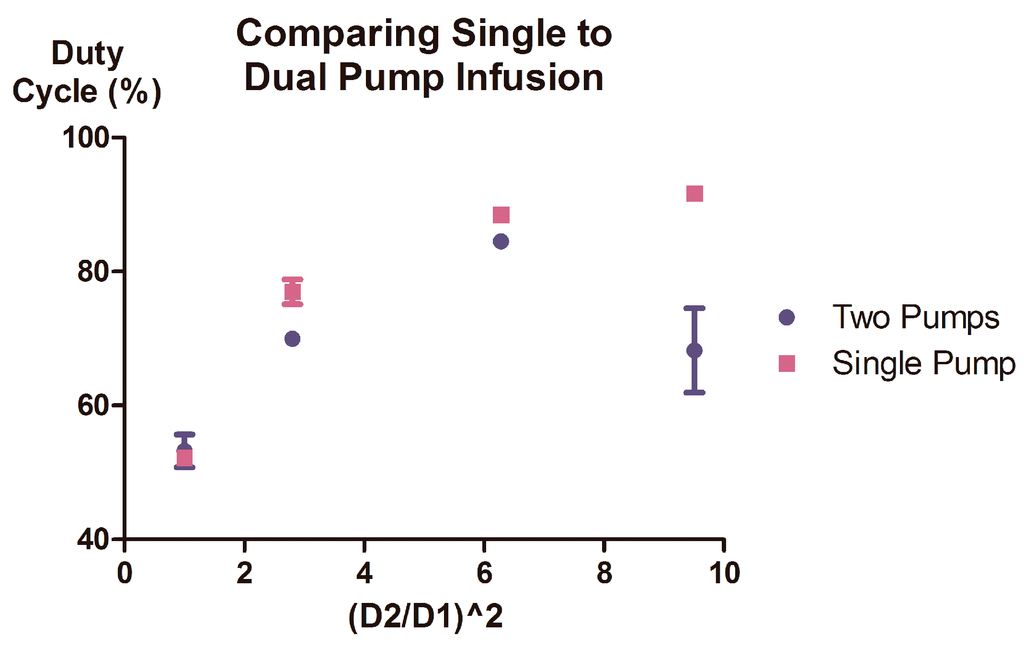
Figure 4.
Single syringe pump setup results in more robust duty cycle control than two pump setup. A minimum of 7 sequential oscillations were observed using two experimental setups (either comprised of a multiple syringes mounted upon a single pump or single syringes mounted upon multiple pumps) to identify reproducibility and consistency of duty cycle. The data presented was acquired using both experimental setups at a total volumetric inflow rate of 20 μL/min. Error bars represent the 95% confidence intervals for experimentally observed results. Two different syringe pump models were utilized in the multiple syringe pump setup.
The sources of the observed deviation and instability are likely two-fold. The deviation likely arises as a consequence of the asymmetric linear pressures experienced by each syringe that result in a change in relative Pth, but not in C; necessary for performing the reduction yielding Equation (4), and consequently, for the simplified and accurate prediction of duty cycle. The source of the observed instability at a specific flow rate ratio may be multifaceted; deriving from differences in manufacturing of the pumps themselves, differences in their calibration or age, and general unsteadiness inherently observed in syringe pumps [22,26]. As the presence of variability between syringe pumps is unavoidable, the use of multiple syringe pumps presents an inherent risk that predictability of the resulting duty cycle will be adversely effected due to an uncoupling between the pump-derived variability experienced by each individual syringe. Mounting multiple syringes upon a single syringe pump, however, ensures that each syringe experiences similar pump-derived variability. This coupling then ensures that slight instabilities in linear output are experienced simultaneously by both syringes; resulting in a predictable and stable duty cycle.
4.3. Maximum Pressure Profile Remains Relatively Constant
The use of asymmetric inflow rates generated by mounting two syringes of varying diameter onto a single syringe pump alters the pressure profiles generated from each valve (Figure 2b). As we are unable to directly measure gate pressure within our experimental system, we use the previously established approximation, where
and
at the time of an open-to-close transition [2]. By this approximation, we conclude the asymmetric Pth values observed, even under extreme asymmetric conditions (
kPa), are far below those reported in previous work (
kPa) utilizing asymmetric valve units [8].
The Pmax values recorded for each valve under the examined flow conditions are equivalent under symmetric volumetric inflow rates, but diverge from these values as the asymmetry between the two inflow rates is increased (Table 2).
Because the transition of each valve from a closed-to-open state is triggered by the accumulation of sufficient fluidic pressure (Pmax); the initial outflow velocity from each valve is higher (Qmax) relative to the stabilized baseline velocity subsequently achieved [24]. The lower Pmax values observed within this system, relative to values previously-reported [2], suggests a reduction in Qmax and, thus, in the magnitude of the transient fluctuation in flow velocity accompanying the transition of each valve from a closed-to-open state. Despite this reduction, as fluidic shear is known to influence the morphological and phenotypical properties of cultured cells and tissues, the mere presence of this fluctuation may nonetheless represent a parameter which must be considered when utilizing this device for the performance of biological analyses.
A comparison of Pmax values across both valves in one device demonstrates Pmax values for valve 1 increase relative to Pmax values for valve 2 in proportion to the degree of asymmetry between the inflow rate ratios across the two valves. All data presented is derived from one device, as inter-device variability led to differing absolute Pmax values across devices. Similar trends, however, were observed across all devices examined.

Table 2.
Larger maximum pressures observed in valve receiving smaller inflow rate.
| Total Volumetric Inflow Rate (μL/min) | 3 mL:3 mL | 3 mL:10 mL | 3 mL:30 mL | 3 mL:60 mL | ||||
|---|---|---|---|---|---|---|---|---|
| Valve 1 (kPa) | Valve 2 (kPa) | Valve 1 (kPa) | Valve 2 (kPa) | Valve 1 (kPa) | Valve 2 (kPa) | Valve 1 (kPa) | Valve 2 (kPa) | |
| 20 | 3.30 | 3.34 | 3.49 | 3.32 | 3.51 | 2.76 | 3.67 | 3.04 |
| 25 | 4.08 | 4.16 | 4.20 | 4.01 | 4.28 | 3.48 | 4.53 | 3.80 |
| 30 | 4.77 | 4.92 | 5.03 | 4.83 | 5.20 | 4.28 | 5.44 | 4.58 |
| 35 | 5.52 | 5.70 | 5.72 | 5.54 | 6.11 | 5.08 | 6.34 | 5.35 |
| 40 | 6.31 | 6.52 | 6.52 | 6.29 | 6.98 | 5.86 | 7.18 | 5.94 |
4.4. Syringe Properties Influence Capacitance
Syringe size has previously been shown to impact overall compliance in a syringe-driven system, where, independent of material and design, increases in syringe diameter are correlated with increases in syringe compliance [27]. This effect, underappreciated within the field of microfluidics, was observed within our experimental system (Figure 5), and presented a source for concern, as external capacitance could influence the period of the oscillatory output [24]. The good agreement between the duty cycles predicted by the simplified Equation (4) and the actual observed duty cycles are explained by looking at Equation (3), where there is an approximate inverse relationship between C and Pth observed under asymmetric inflow rates (described in greater detail below).
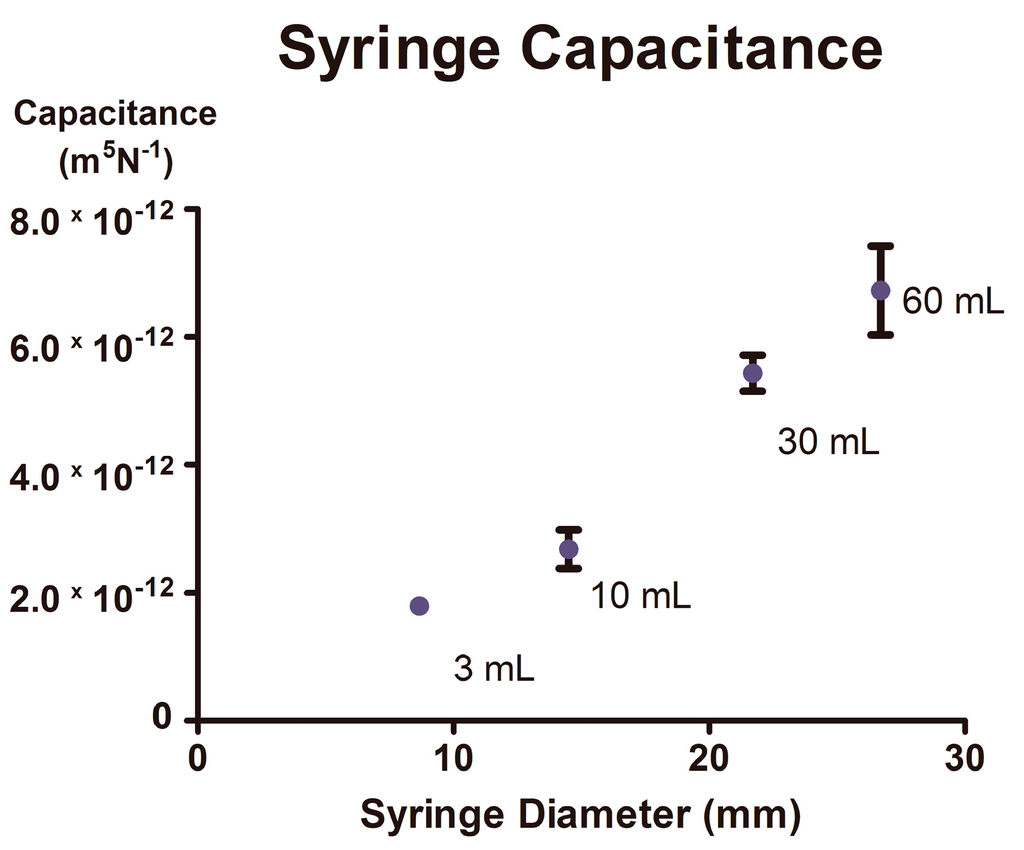
Figure 5.
Fluidic capacitance increases significantly with increasing syringe volume. Capacitance values were averaged for individual syringes using data collected at multiple volumetric flow rates (ranging from 10 to 40 μL/min). All values are derived from time series data containing >6 oscillations, with five replicates (p < 0.0002). Error bars represent the 95% confidence intervals of all capacitance values obtain over multiple inflow rate ranges.
4.5. Different Asymmetric Inflow Rates at Constant Total Volumetric Inflow Rate Produce Distinct Periods
Previous work provides an approximation of the off-time for each valve that can be used to estimate oscillatory period [2], thereby assisting in contextualizing any observed shift in period:
We calculated Pth using experimental data collected under multiple inflow conditions. We found that under asymmetric flow regimes, Pth and C exhibit an inverse relationship, where Pth is higher for the valve experiencing the lower flow rate (valve 1), lower for the valve experiencing the higher flow rate (valve 2) and where the absolute difference between Pth (i.e., ) increases with the degree of asymmetry between the syringes used. As C is proportional to the size of a given syringe, it is consequently proportional to Qin, which increases with the size of the syringe used. This finding is in agreement with previous results reported for four-way valves, where an increase in volumetric inflow rate through one valve increases calculated Pth for the opposite valve [21].
From Equation (5), we infer that increasing Pth in conditions with lower Qin, will produce higher toff; and that as the asymmetry between the flow rate across each valve increases, toff will increase for the valve with a lower inflow rate, producing larger oscillation periods.
Using the averaged values of Pth and C for each respective syringe pairing, we approximated toff for both valves. We then compared the calculated period approximation with experimental data (Figure 6), and observed that the relationship between volumetric flow rate and period is preserved. We limited the presented period data to one device, as all devices tested exhibited similar trends, with slight variations in absolute values. Such variations may originate from differences in device size (e.g., thickness of the PDMS membrane), fabrication procedure or material batch characteristics. In addition, larger standard deviations in the period, prominent at greater asymmetric inflow rates, may also originate from fluctuations in syringe pump pressure [26].
This observation highlights the utility of our approach and underscores the motivation for this work. Mounting two syringes of the same size on two independent syringe pumps and evacuating them at two different volumetric flow rates will produce changes in Pth, but not in C, introducing a source of complexity to the relationship between volumetric flow rate ratio and duty cycle. Practically, this would result in the inability to reduce down to Equation (4). However, by utilizing syringes of differing diameter, volumetric flow rate-dependent changes in Pth are counteracted, allowing one to perform straightforward prediction of duty cycle as a function of volumetric flow rate ratio.
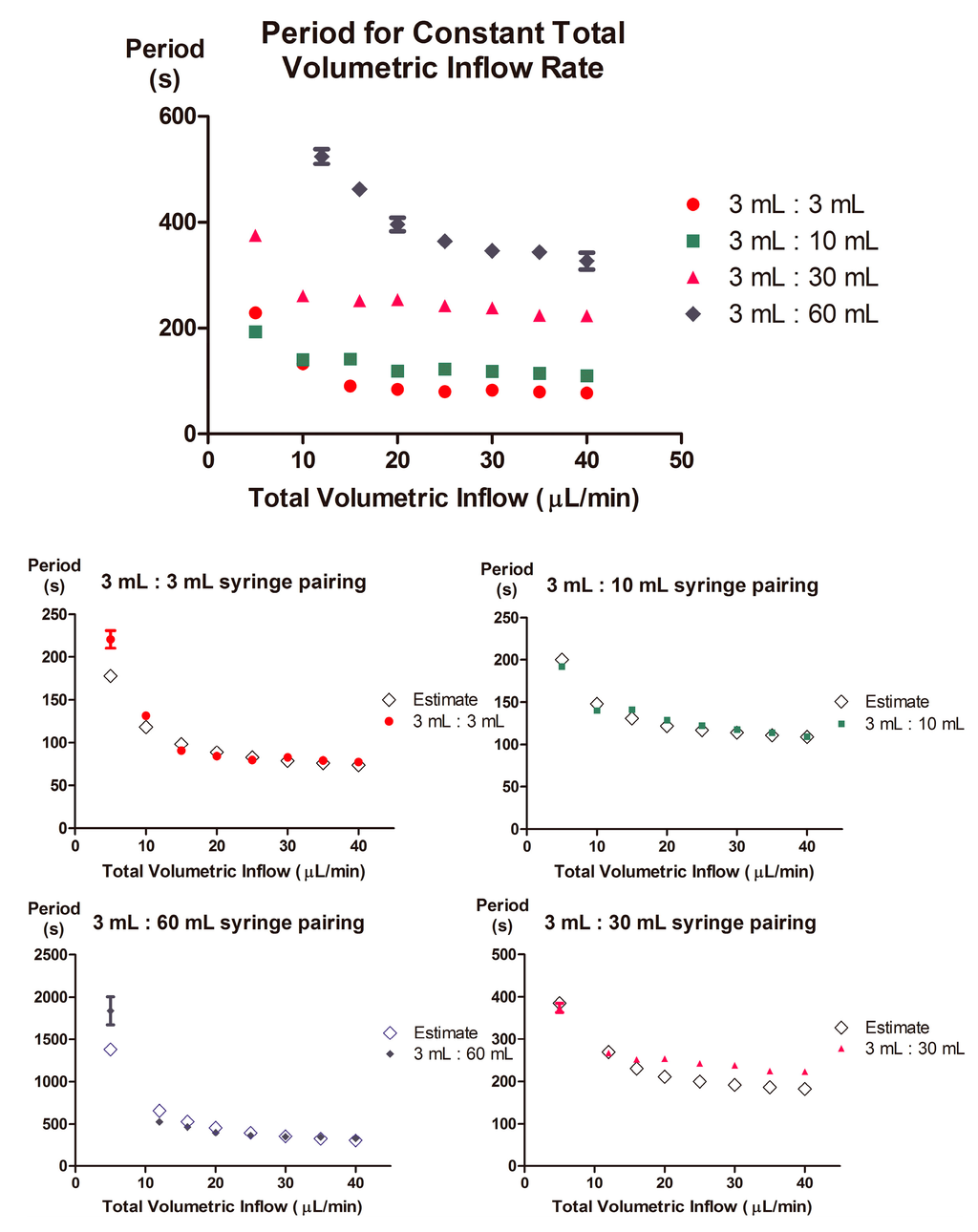
Figure 6.
Asymmetric inflow rates produce markedly different periodicity, yet can be estimated relatively-well. Observed period values for each syringe combination demonstrate the range of periodicities generated for each of the four combinations tested. The estimated oscillatory period was calculated by applying Equation (5) for each syringe combination; values for C and Pth were derived from the minimal and maximal volumetric inflow rates tested, and were used to establish a linear relationship for Pth−i where Pth−i = m × Qi + b. Predicted period values (unfilled) were then compared to the averaged measured period values (filled). All values are derived from time series data containing >12 oscillations, and error bars represent 95% confidence intervals for experimentally observed results.
4.6. Estimating Rest and Stimulation Pulse Duration for Control of Rhythmic Stimulation
The described microfluidic oscillator is designed to translate two independent fluid inputs into a single oscillatory fluid output. In practice, if one input contains a fluid stimulant, and the other a neutral “wash” solution, this system may be utilized to conduct biological experiments in which a population of cells (or tissue explant) cultured downstream is presented with this fluid stimulant at a fixed concentration, and for a pre-determined period of time—referred to as the stimulation duration (D); followed by a “wash”—or rest period (R). The functional significance of the presented asymmetric operating technique is that it allows the user to dynamically control the duty cycle of this oscillatory outflow, and in doing so, to characterize biological responses to multiple stimulation regimes characterized by variations in D and R (e.g., fixed D separated by variable R). Within a biological context, control of these parameters is critical as both have been reported to elicit distinct cellular responses [19].
Within the context of the presented device system, D and R may be calculated as a function of relative inflow rates. To do so, C and Pth for each valve must be measured with respect to its corresponding syringe and input Qi values, respectively. Measurements of Pth for each valve must be conducted at two total volumetric inflow rates (we used 5 μL/min and 40 μL/min, the minimal and maximal total volumetric inflow rates, respectively) to approximate the linear relationship Pth−i = m × Qi + b. This relationship may then be used to approximate intermediate Pth−i values for different inflow rates, and for each syringe pairing. The Pth−i, C, and Qi values may then be used, in equation (5), to determine the off-time for each valve. The sum of the off-times will estimate the periodicity of the device for a given syringe combination. By this method, a curve in general agreement with empirical data, and representing the periodicity as a function of the ratio between syringe diameters, may be generated (Figure 6). This curve may then be utilized to identify an appropriate total volumetric inflow to produce a desired D and R for the specific syringe combination being used. Conversely, this curve may also be utilized to identify the appropriate combination of syringes necessary to modify the length of D or R.
5. Conclusions
The volumetric flow-regulated microfluidic oscillator system described herein greatly increases the versatility and utility of our previously described micro-machine as a tool for generating and delivering pulsatile stimulation. Furthermore, in allowing users to reliably produce a desired duty cycle through the simple manipulation of volumetric inflow rate, the system described greatly reduces the barrier for adoption otherwise presented by placing the burden for “programming” the device upon the end-user. Notably, the benefit of using one syringe pump to drive both syringes is that inherent syringe pump unsteadiness and subsequent inflow fluctuations are applied to both syringes simultaneously; negating their impact on duty cycle, and resulting in a more consistent and stable oscillation.
Acknowledgments
The authors would like to thank the National Institutes of Health (GM096040), the National Science Foundation Graduate Research Fellowship Program and the National Institutes of Health Cellular Biotechnology Training Program (to Sasha Cai Lesher-Perez) under Grant No. DGE 1256260 (ID: 2011101670) and Grant No. NIH GM008353, respectively; as well as the Wayne State University Interdisciplinary Biomedical Sciences Competitive Research Fellowship (to Priyan Weerappuli); and the National Natural Science Foundation of China (No. 51136007), the Natural Science Foundation of Chongqing, China (No. cstc2013jjB9004), the Research Project of the Chinese Ministry of Education (No. 113053A) and the China Scholarship Council (to Chao Zhang); for financial support.
Author Contributions
Sasha Cai Lesher-Perez, Priyan Weerappuli, Sung-Jin Kim and Shuichi Takayama conceived of and designed the experiments. Sasha Cai Lesher-Perez and Priyan Weerappuli performed all experiments. Sasha Cai Lesher-Perez, Priyan Weerappuli, Sung-Jin Kim and Chao Zhang analyzed and interpreted the data and results. Sasha Cai Lesher-Perez, Priyan Weerappuli and Shuichi Takayama wrote the paper. Sasha Cai Lesher-Perez, Priyan Weerappuli, Sung-Jin Kim, Chao Zhang and Shuichi Takayama assisted in the preparation and approval of the submitted manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mosadegh, B.; Kuo, C.H.; Tung, Y.C.; Torisawa, Y.S.; Bersano-Begey, T.; Tavana, H.; Takayama, S. Integrated elastomeric components for autonomous regulation of sequential and oscillatory flow switching in microfluidic devices. Nat. Phys. 2010, 6, 433–437. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.J.; Yokokawa, R.; Lesher-Perez, S.C.; Takayama, S. Constant flow-driven microfluidic oscillator for different duty cycles. Anal. Chem. 2012, 84, 1152–1156. [Google Scholar] [CrossRef] [PubMed]
- Walker, G.M.; Beebe, D.J. A passive pumping method for microfluidic devices. Lab Chip 2002, 2, 131–134. [Google Scholar] [CrossRef] [PubMed]
- Jamieson, J.D.; Palade, G.E. Intracellular transport of secretory proteins in the pancreatic exocrine cell. I. Role of the peripheral elements of the Golgi complex. J. Cell Biol. 1967, 34, 577–596. [Google Scholar]
- Jamieson, J.D.; Palade, G.E. Intracellular transport of secretory proteins in the pancreatic exocrine cell. II. Transport to condensing vacuoles and zymogen granules. J. Cell Biol. 1967, 34, 597–615. [Google Scholar] [CrossRef] [PubMed]
- Gratzner, H.G. Monoclonal antibody to 5-bromo- and 5-iododeoxyuridine: A new reagent for detection of DNA replication. Science 1982, 218, 474–475. [Google Scholar] [CrossRef] [PubMed]
- Dolmetsch, R.E.; Xu, K.; Lewis, R.S. Calcium oscillations increase the efficiency and specificity of gene expression. Nature 1998, 392, 933–936. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.J.; Falconnet, D.; Niemistö, A.; Ramsey, S.A.; Prinz, S.; Shmulevich, I.; Galitski, T.; Hansen, C.L. Dynamic analysis of MAPK signaling using a high-throughput microfluidic single-cell imaging platform. Proc. Natl. Acad. Sci. USA 2009, 106, 3758–3763. [Google Scholar] [CrossRef] [PubMed]
- Tay, S.; Hughey, J.J.; Lee, T.K.; Lipniacki, T.; Quake, S.R.; Covert, M.W. Single-cell NF-κB dynamics reveal digital activation and analogue information processing. Nature 2010, 466, 267–271. [Google Scholar] [CrossRef] [PubMed]
- Cheong, R.; Wang, C.J.; Levchenko, A. High content cell screening in a microfluidic device. Mol. Cell. Proteomics 2009, 8, 433–442. [Google Scholar] [CrossRef] [PubMed]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Mosadegh, B.; Bersano-Begey, T.; Park, J.Y.; Burns, M.A.; Takayama, S. Next-generation integrated microfluidic circuits. Lab Chip 2011, 11, 2813–2818. [Google Scholar] [CrossRef] [PubMed]
- Leslie, D.C.; Easley, C.J.; Seker, E.; Karlinsey, J.M.; Utz, M.; Begley, M.R.; Landers, J.P. Frequency-specific flow control in microfluidic circuits with passive elastomeric features. Nat. Phys. 2009, 5, 231–235. [Google Scholar] [CrossRef]
- Duncan, P.N.; Nguyen, T.V.; Hui, E.E. Pneumatic oscillator circuits for timing and control of integrated microfluidics. Proc. Natl. Acad. Sci. USA 2013, 110, 18104–18109. [Google Scholar] [CrossRef] [PubMed]
- Rhee, M.; Burns, M.A. Microfluidic pneumatic logic circuits and digital pneumatic microprocessors for integrated microfluidic systems. Lab Chip 2009, 9, 3131–3143. [Google Scholar] [CrossRef] [PubMed]
- Collino, R.R.; Reilly-Shapiro, N.; Foresman, B.; Xu, K.; Utz, M.; Landers, J.P.; Begley, M.R. Flow switching in microfluidic networks using passive features and frequency timing. Lab Chip 2013, 13, 3668–3674. [Google Scholar] [CrossRef] [PubMed]
- Toepke, M.W.; Abhyankar, V.V.; Beebe, D.J. Microfluidic logic gates and timers. Lab Chip 2007, 7, 1449–1453. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Lai, D.; Park, J.Y.; Yokokawa, R.; Takayama, S. Microfluidic automation using elastomeric valves and droplets: Reducing reliance on external controllers. Small 2012, 8, 2925–2934. [Google Scholar] [CrossRef] [PubMed]
- Jovic, A.; Howell, B.; Cote, M.; Wade, S.M.; Mehta, K.; Miyawaki, A.; Neubig, R.R.; Linderman, J.J.; Takayama, S. Phase locked signals elucidate circuit architecture of an oscillatory pathway. PLoS Comput. Biol. 2010, 6, e1001040. [Google Scholar] [CrossRef] [PubMed]
- Jovic, A.; Howell, B.; Takayama, S. Timing is everything: using fluidics to understand the role of temporal dynamics in cellular systems. Microfluid. Nanofluid. 2009, 6, 717–729. [Google Scholar] [CrossRef]
- Kim, S.J.; Yokokawa, R.; Takayama, S. Analyzing threshold pressure limitations in microfluidic transistors for self-regulated microfluidic circuits. Appl. Phys. Lett. 2012, 101, 234107. [Google Scholar] [CrossRef] [PubMed]
- Korczyk, P.M.; Cybulski, O.; Makulska, S.; Garstecki, P. Effects of unsteadiness of the rates of flow on the dynamics of formation of droplets in microfluidic systems. Lab Chip 2011, 11, 173–175. [Google Scholar] [CrossRef] [PubMed]
- Rooke, G.A.; Bowdle, T.A. Syringe pumps for infusion of vasoactive drugs: mechanical idiosyncrasies and recommended operating procedures. Anesth. Analg. 1994, 78, 150–156. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.J.; Yokokawa, R.; Takayama, S. Microfluidic oscillators with widely tunable periods. Lab Chip 2013, 13, 1644–1648. [Google Scholar] [CrossRef] [PubMed]
- Peakdet: Peak Detection Using MATLAB. Available online: http://billauer.co.il/peakdet.html (accessed on 24 November 2014).
- Li, Z.; Mak, S.Y.; Sauret, A.; Shum, H.C. Syringe-pump-induced fluctuation in all-aqueous microfluidic system implications for flow rate accuracy. Lab Chip 2014, 14, 744–749. [Google Scholar] [CrossRef] [PubMed]
- Weiss, M.; Hug, M.I.; Neff, T.; Fischer, J. Syringe size and flow rate affect drug delivery from syringe pumps. Can. J. Anaesth. 2000, 47, 1031–1035. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).