High-Order Exponentially Fitted Methods for Accurate Prediction of Milling Stability
Abstract
1. Introduction
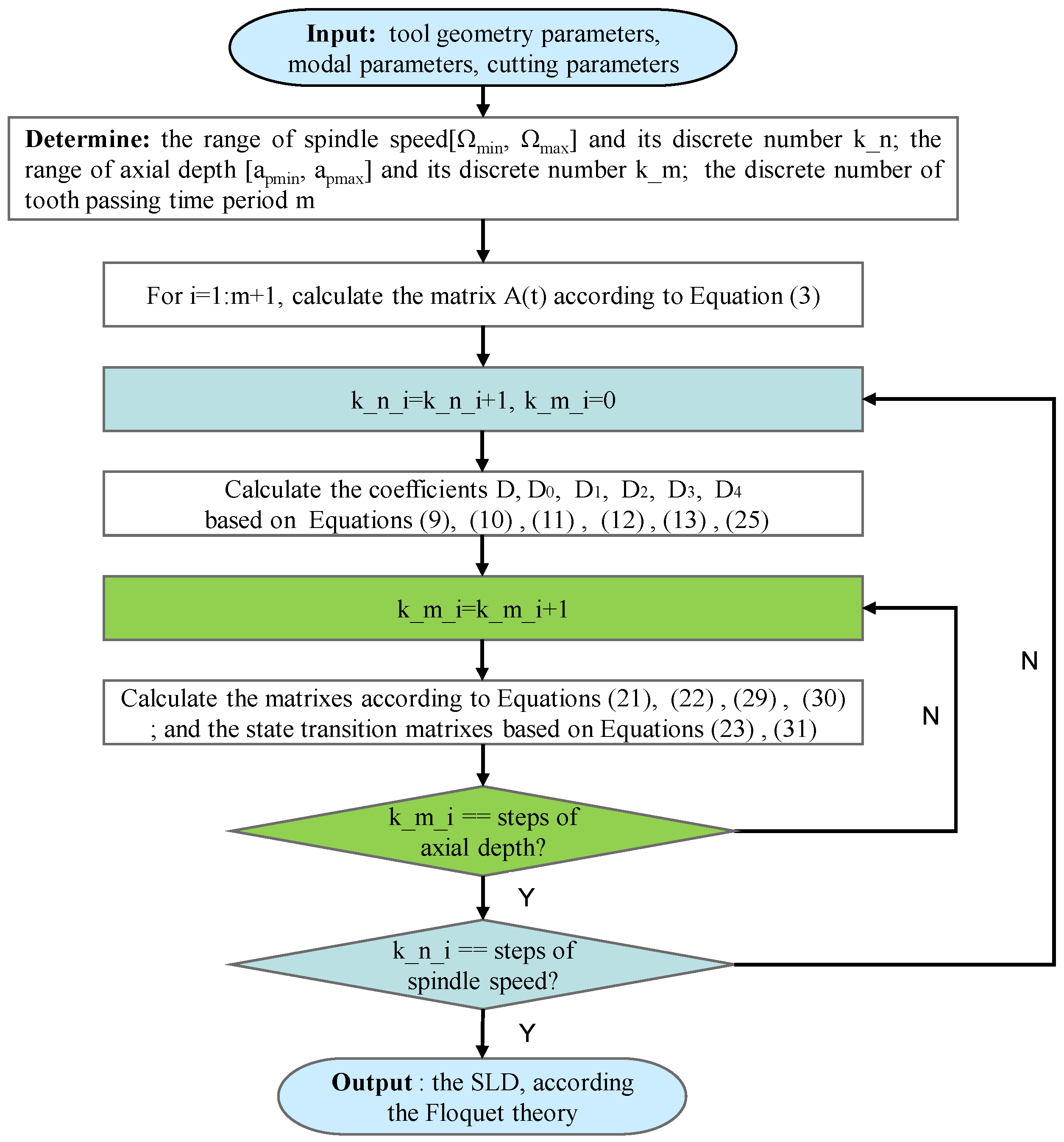
2. Dynamics Modeling of Milling Operations and Numerical Algorithms
2.1. Third-Order Implicit Exponentially Fitted Method (3rd IEM)
2.2. Fourth-Order Implicit Exponentially Fitted Method (4th IEM)
3. Numerical Analysis and Discussion
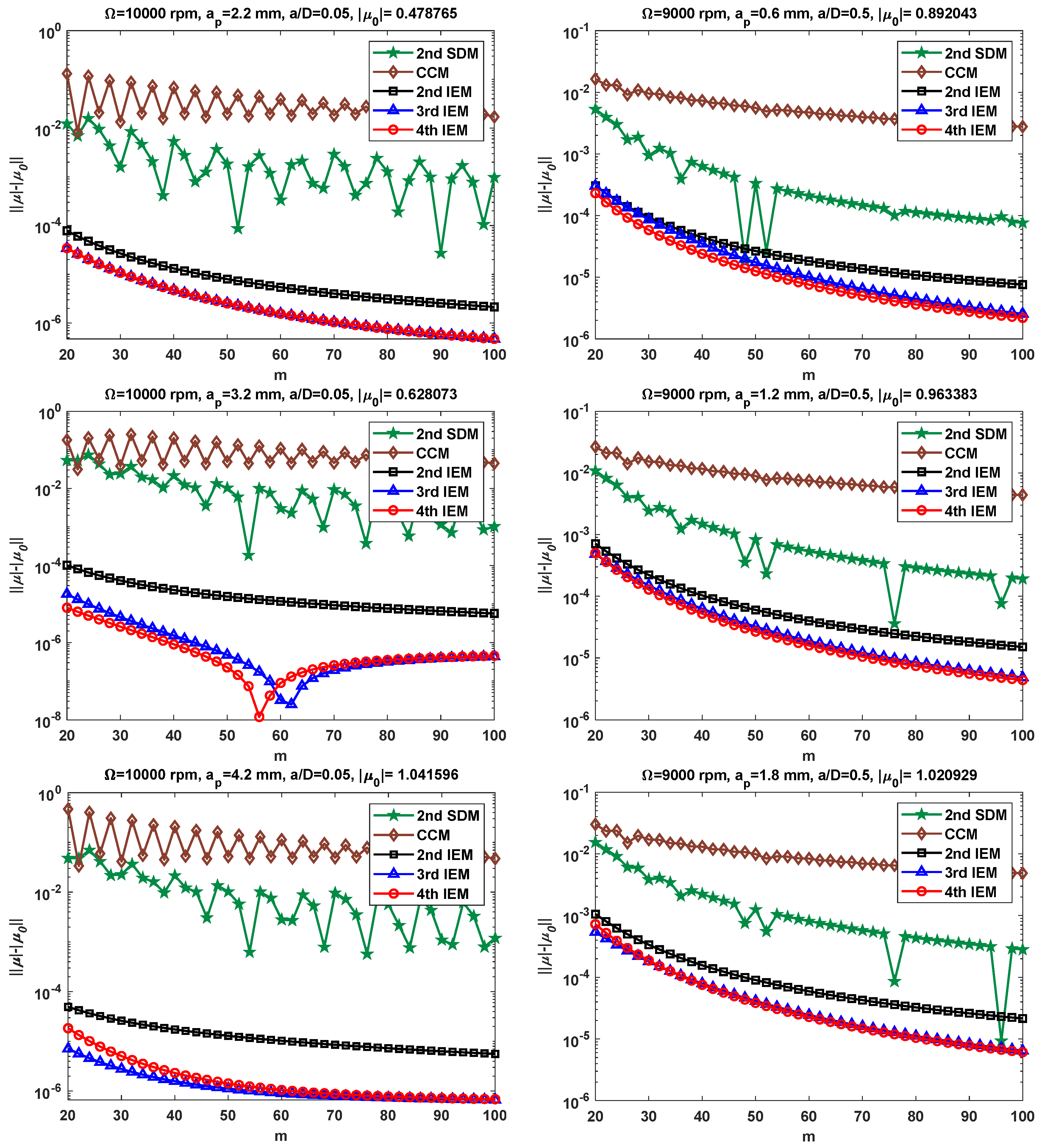
3.1. Convergence Rate Verification
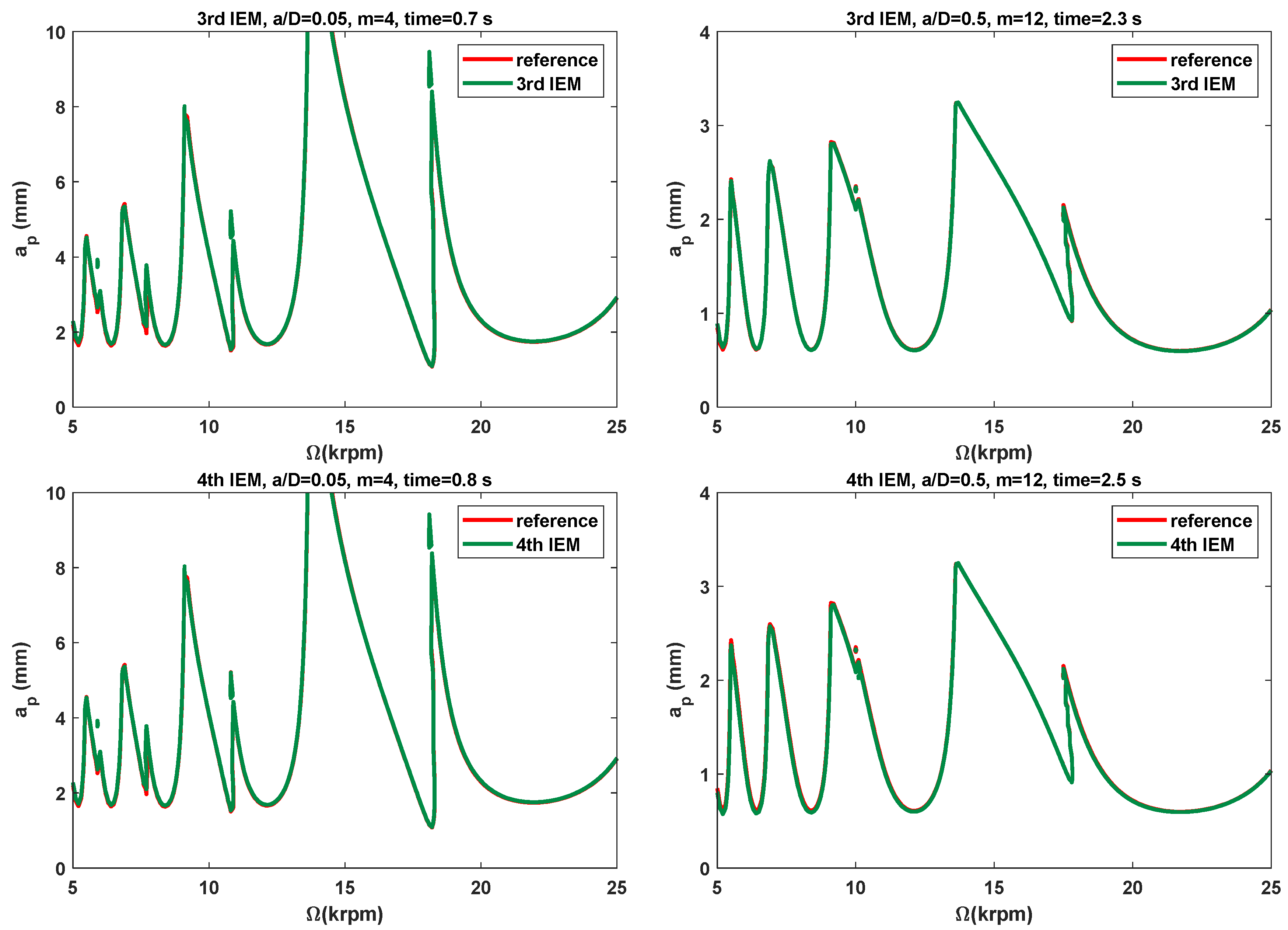
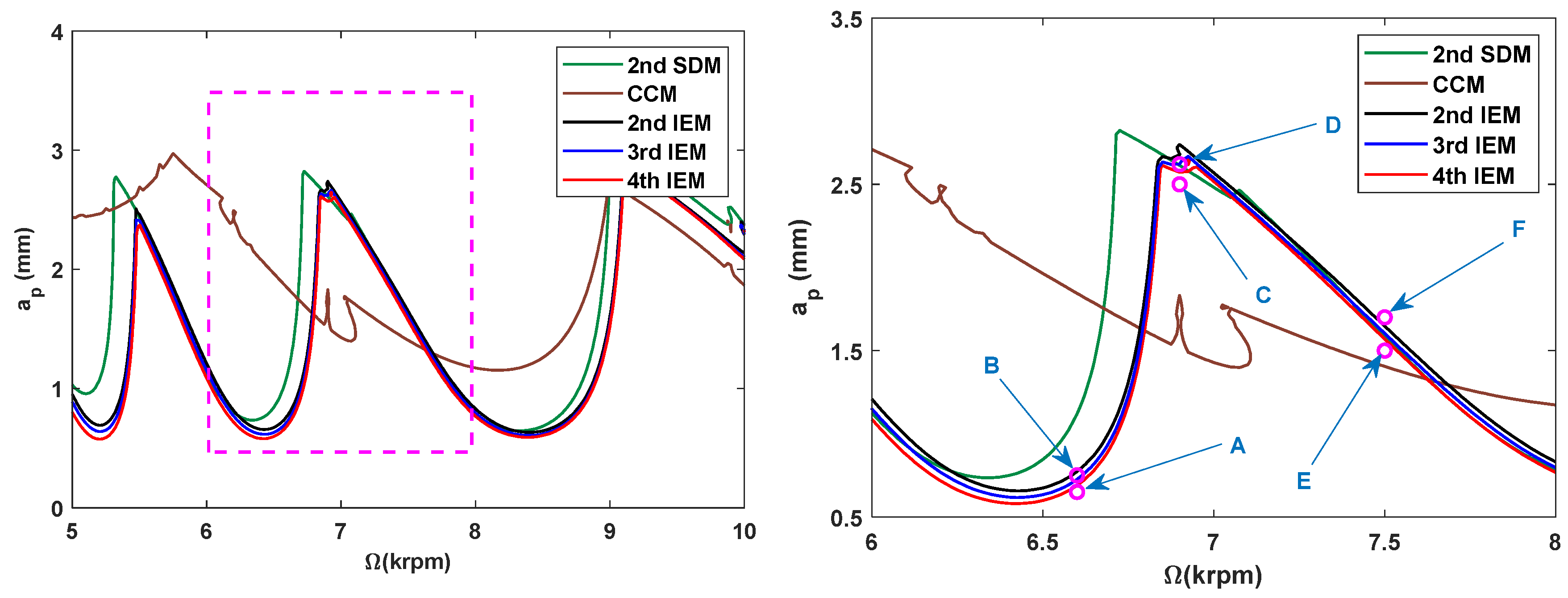
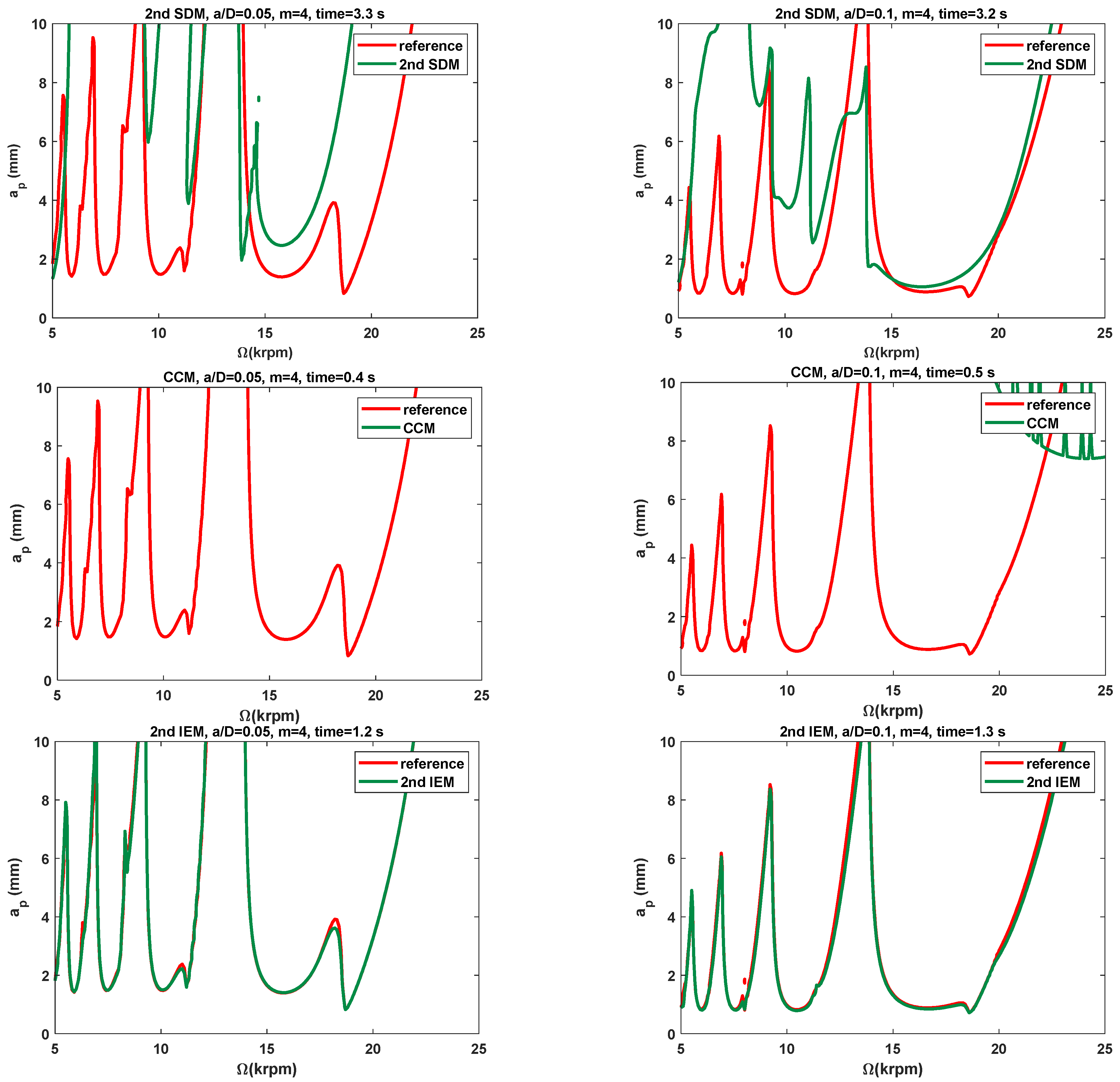
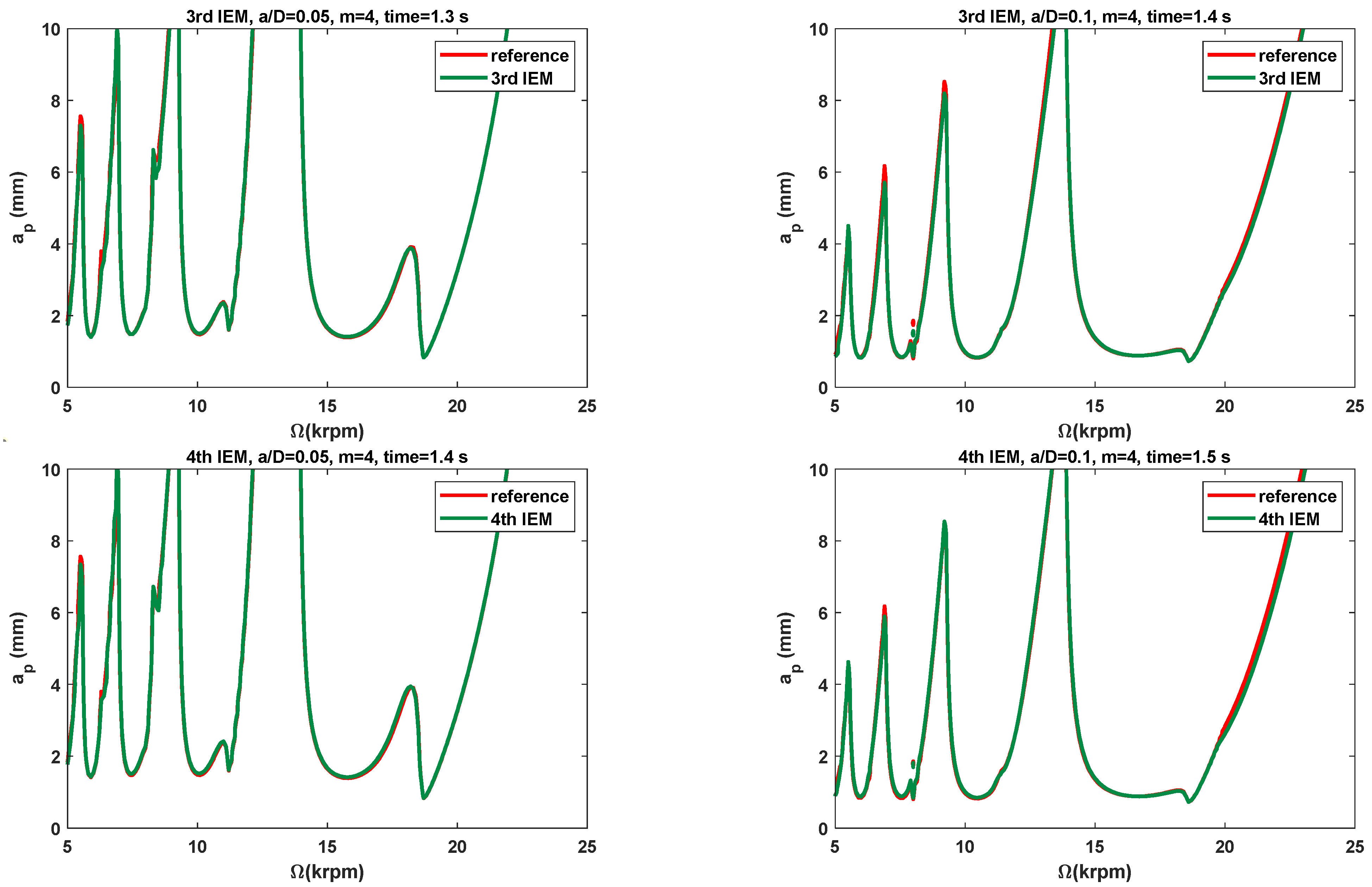
3.2. Stability Lobes Prediction and Comparison
3.2.1. Single-DOF Milling Operation
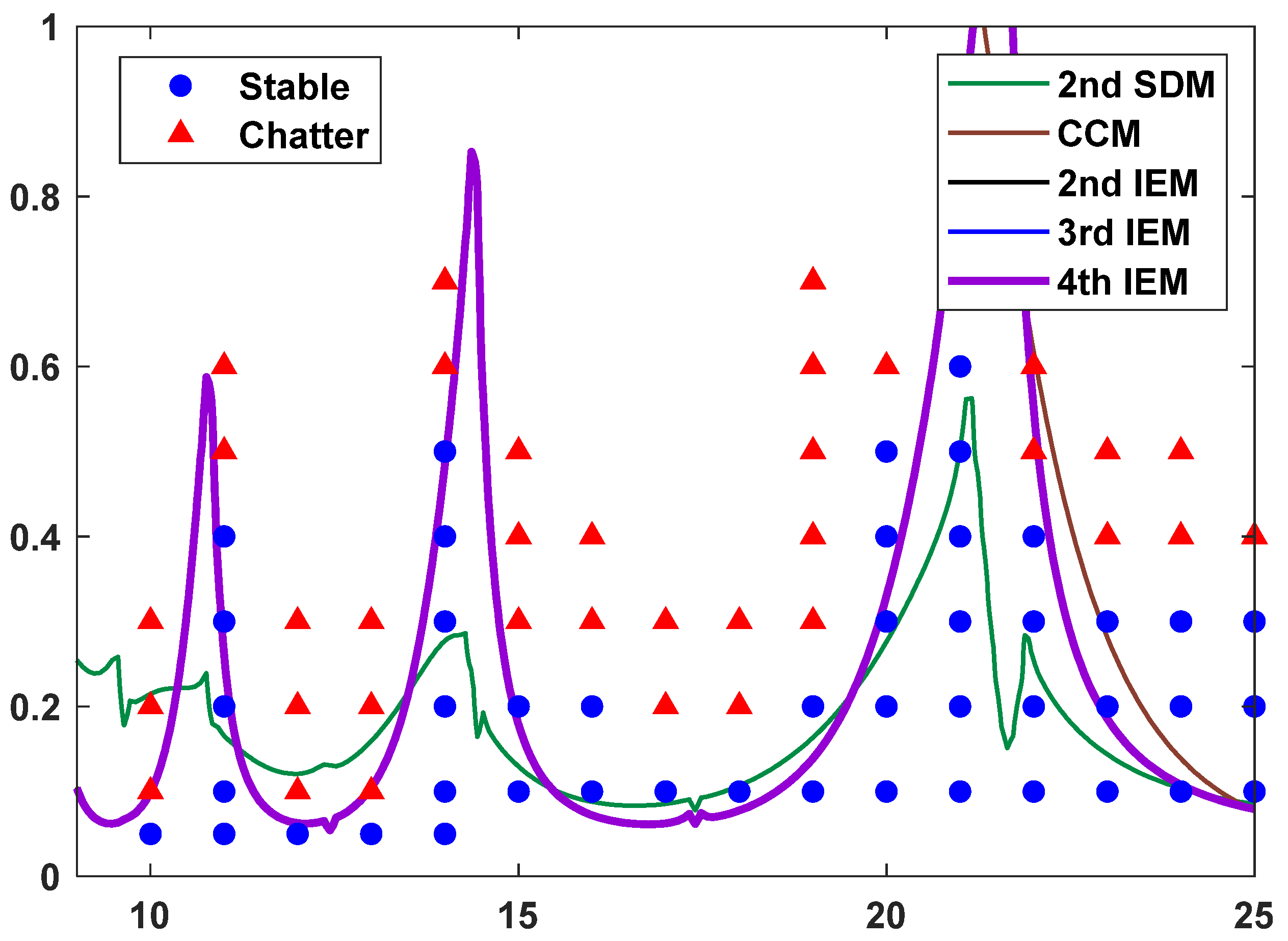
3.2.2. Two-DOF Milling Operation
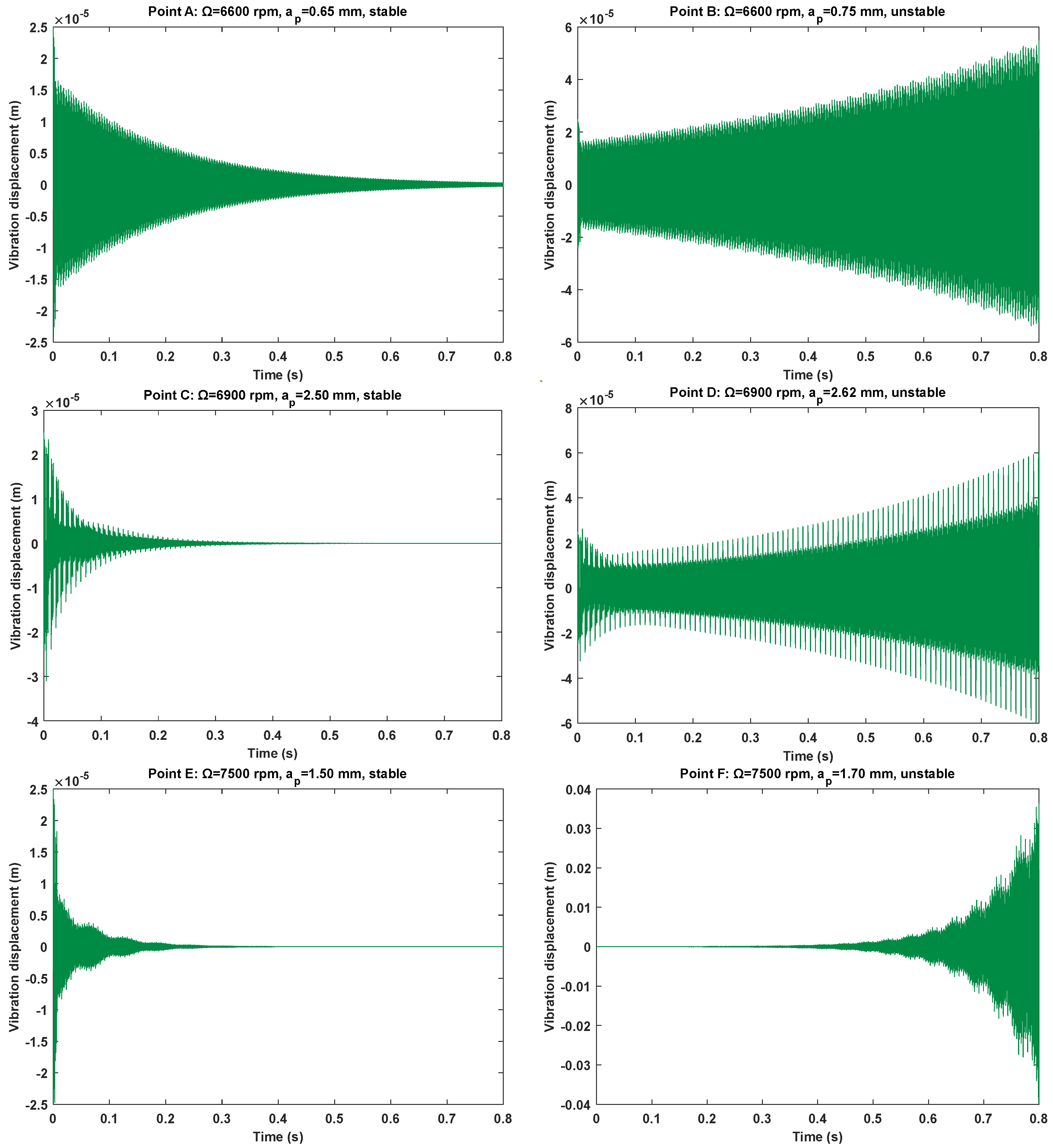
4. Experimental Verification and Analysis
4.1. Experimental Verification Based on Benchmark Example
4.2. Experimental Verification Based on Actual Cutting Process
5. Conclusions
- (1)
- To construct the Floquet transition matrix, the principal period of the coefficient matrix is decomposed into two different subintervals, and the fourth-step and five-step implicit exponential fitting schemes are applied to more accurately estimate the state term.
- (2)
- Compared with the three conventional methods, the convergence rates of the high-order exponentially fitted methods are analyzed for the single-DOF milling system. The numerical results demonstrate that the 3rd IEM and 4th IEM achieve much higher convergence rates than the 2nd SDM, the CCM, and the 2nd IEM under different radial immersion conditions.
- (3)
- In comparison with the three existing methods, the SLDs determined by the proposed IEMs are mostly consistent with the reference stability lobes under the identical discrete number. When compared with the 2nd SDM, the calculation time of the 3rd IEM and the 4th IEM can be saved by approximately 56% and 53%, respectively. The calculation speeds of the 3rd IEM and the 4th IEM are nearly comparable to that of the 2nd IEM. Therefore, the 3rd IEM and the 4th IEM are proved to have better performances without sacrificing computational efficiency for predicting milling stability lobes.
- (4)
- The experimental verifications with the two-DOF milling operation demonstrate the applicability and effectiveness of the 3rd IEM and the 4th IEM. The prediction results of the proposed IEMs exhibit excellent agreement with the experimental results, which indicates that the proposed IEMs have the ability to ascertain chatter-free conditions for actual milling processes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| M | The mass matrix |
| C | The damping matrix |
| K | The stiffness matrix |
| The modal displacement vector at the current moment | |
| The modal displacement vector at the previous tooth-passing period | |
| The axial of the depth cut | |
| The coefficient matrix | |
| T | The principal period of the system |
| N | The number of cutter teeth |
| The spindle speed | |
| The forced vibration time period | |
| The initial time point | |
| The constant matrix | |
| The state transition matrix | |
| The reference spectral radius | |
| The approximate spectral radius | |
| m | The discrete number |
| The radial immersion ratio | |
| The modal mass | |
| The relative damping ratio | |
| c | The damping |
| k | The stiffness |
| The angular natural frequency | |
| The tangential cutting force coefficient | |
| The normal cutting force coefficient | |
| DDE | Delay differential equation |
| SLD | Stability lobe diagram |
| DDS | Direct difference scheme |
| DIS | Direct integration scheme |
| DOF | Degree of freedom |
| LED | Local discretization error |
References
- Altintas, Y.; Weck, M. Chatter stability of metal cutting and grinding. CIRP Ann. 2004, 53, 619–642. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. Stability analysis for milling operations using an Adams-Simpson-based method. Int. J. Adv. Manuf. Technol. 2017, 92, 969–979. [Google Scholar] [CrossRef]
- Yue, C.; Gao, H.; Liu, X.; Liang, S.Y.; Wang, L. A review of chatter vibration research in milling. Chin. J. Aeronaut. 2019, 32, 215–242. [Google Scholar] [CrossRef]
- Altintas, Y.; Stepan, G.; Merdol, D.; Dombovari, Z. Chatter stability of milling in frequency and discrete time domain. CIRP J. Manuf. Sci. Technol. 2008, 1, 35–44. [Google Scholar] [CrossRef]
- Tao, J.; Qin, C.; Liu, C. A synchroextracting-based method for early chatter identification of robotic drilling process. Int. J. Adv. Manuf. Technol. 2018, 100, 273–285. [Google Scholar] [CrossRef]
- Altintas, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann.-Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Merdol, S.D.; Altintas, Y. Multi frequency solution of chatter stability for low immersion milling. J. Manuf. Sci. Eng. 2004, 126, 459–466. [Google Scholar] [CrossRef]
- Bayly, P.V.; Halley, J.E.; Mann, B.P.; Davies, M.A. Stability of interrupted cutting by temporal finite element analysis. J. Manuf. Sci. Eng. 2003, 125, 220–225. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Semi-discretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Butcher, E.A.; Bobrenkov, O.A.; Bueler, E.; Nindujarla, P. Analysis of milling stability by the Chebyshev collocation method: Algorithm and optimal stable immersion levels. J. Comput. Nonlinear Dyn. 2009, 4, 031003. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Olvera, D.; Elías-Zúñiga, A.; Martínez-Alfaro, H.; López de Lacalle, L.N.; Rodríguez, C.A.; Campa, F.J. Determination of the stability lobes in milling operations based on homotopy and simulated annealing techniques. Mechatronics 2014, 24, 177–185. [Google Scholar] [CrossRef]
- Li, M.; Zhang, G.; Huang, Y. Complete discretization scheme for milling stability prediction. Nonlinear Dyn. 2013, 71, 187–199. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Z.; Peng, Y.; Zhu, F.; Ming, X. Prediction of chatter stability for milling process using Runge-Kutta-based complete discretization method. Int. J. Adv. Manuf. Technol. 2016, 86, 943–952. [Google Scholar] [CrossRef]
- Dai, Y.; Li, H.; Xing, X.; Hao, B. Prediction of chatter stability for milling process using precise integration method. Precis. Eng. 2018, 52, 152–157. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. A novel stability prediction method for milling operations using the holistic-interpolation scheme. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4463–4475. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, C.; Ding, Y.; Ding, H. Prediction of chatter stability in high speed milling using the numerical differentiation method. Int. J. Adv. Manuf. Technol. 2017, 89, 2535–2544. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Numerical integration method for prediction of milling stability. J. Manuf. Sci. Eng. 2011, 133, 031005. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Meng, G.; Liu, C. A novel approach for the prediction of the milling stability based on the Simpson method. Int. J. Mach. Tools Manuf. 2015, 99, 43–47. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Li, L. An Adams-Moulton-based method for stability prediction of milling processes. Int. J. Adv. Manuf. Technol. 2017, 89, 3049–3058. [Google Scholar] [CrossRef]
- Wu, Y.; You, Y.; Liu, A.; Deng, B.; Liu, W. An implicit exponentially fitted method for chatter stability prediction of milling processes. Int. J. Adv. Manuf. Technol. 2020, 106, 2189–2204. [Google Scholar] [CrossRef]
- Long, X.H.; Balachandran, B.; Mann, B.P. Dynamics of Milling Processes with Variable Time Delays. Nonlinear Dyn. 2007, 47, 49–63. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.; Dang, J.; Yang, Y. A unified stability prediction method for milling process with multiple delays. Int. J. Mach. Tools Manuf. 2010, 50, 29–41. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, Y.; Yuan, X.; Liu, W. A second-order semi-discretization method for the efficient and accurate stability prediction of milling process. Int. J. Adv. Manuf. Technol. 2017, 92, 583–595. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Jia, J.; Ma, B.; Jiang, X.; Wang, D.; Zhu, T. High-order semi-discretization methods for stability analysis in milling based on precise integration. Precis. Eng. 2022, 73, 71–92. [Google Scholar] [CrossRef]
- Totis, G.; Albertelli, P.; Sortino, M.; Monno, M. Efficient evaluation of process stability in milling with spindle speed variation by using the Chebyshev collocation method. J. Sound Vib. 2014, 333, 646–668. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Second-order full-discretization method for milling stability prediction. Int. J. Mach. Tools Manuf. 2010, 50, 926–932. [Google Scholar] [CrossRef]
- Quo, Q.; Sun, Y.; Jiang, Y. On the accurate calculation of milling stability limits using third-order full-discretization method. Int. J. Mach. Tools Manuf. 2012, 62, 61–66. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Wu, B. An efficient full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2012, 63, 44–48. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Liu, Z.; Wang, H.; Yan, Z. An updated full-discretization milling stability prediction method based on the higher-order Hermite–Newton interpolation polynomial. Int. J. Adv. Manuf. Technol. 2018, 95, 2227–2242. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. Least squares approximated stability boundaries of milling process. Int. J. Mach. Tools Manuf. 2014, 79, 24–30. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. High order vector numerical integration schemes applied in state space milling stability analysis. Appl. Math. Comput. 2016, 273, 1025–1040. [Google Scholar] [CrossRef]
- De la Luz Sosa, J.; Olvera-Trejo, D.; Urbikain, G.; Martinez-Romero, O.; Elías-Zúñiga, A.; Lacalle, L.N.L.d. Uncharted Stable Peninsula for Multivariable Milling Tools by High-Order Homotopy Perturbation Method. Appl. Sci. 2020, 10, 7869. [Google Scholar] [CrossRef]
- Tang, X.; Peng, F.; Yan, R.; Gong, Y.; Li, Y.; Jiang, L. Accurate and efficient prediction of milling stability with updated full-discretization method. Int. J. Adv. Manuf. Technol. 2017, 88, 2357–2368. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, X.; Liu, Z.; Wang, D.; Li, J.; Ji, Y. Third-order updated full-discretization method for milling stability prediction. Int. J. Adv. Manuf. Technol. 2017, 92, 2299–2309. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y.; Zhang, D.; Zhao, B.; Wang, G.; Pang, X. A Novel Updated Full-Discretization Method for Prediction of Milling Stability. Micromachines 2022, 13, 160. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. A refined and accurate method for stability analysis of milling process. Alex. Eng. J. 2025, 116, 306–320. [Google Scholar] [CrossRef]
- Xie, Q. Milling stability prediction using an improved complete discretization method. Int. J. Adv. Manuf. Technol. 2016, 83, 815–821. [Google Scholar] [CrossRef]
- Xia, Y.; Wan, Y.; Du, J.; Zhang, P.; Su, G. Fast prediction of chatter stability in milling process based on an updated numerical solution scheme. Int. J. Adv. Manuf. Technol. 2022, 123, 4041–4050. [Google Scholar] [CrossRef]
- Niu, J.; Ding, Y.; Zhu, L.; Ding, H. Runge–Kutta methods for a semi-analytical prediction of milling stability. Nonlinear Dyn. 2014, 76, 289–304. [Google Scholar] [CrossRef]
- Li, H.; Dai, Y.; Fan, Z. Improved precise integration method for chatter stability prediction of two-DOF milling system. Int. J. Adv. Manuf. Technol. 2018, 101, 1235–1246. [Google Scholar] [CrossRef]
- Dai, Y.; Li, H.; Wei, Z. Chatter stability prediction for five axis ball-end milling with precise integration method. J. Manuf. Process. 2018, 32, 20–31. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Liu, C. A predictor-corrector-based holistic-discretization method for accurate and efficient milling stability analysis. Int. J. Adv. Manuf. Technol. 2018, 96, 2043–2054. [Google Scholar] [CrossRef]
- Dong, X.; Qiu, Z. Stability analysis in milling process based on updated numerical integration method. Mech. Syst. Signal Process. 2020, 137, 106435. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Yu, G. An accurate and fast milling stability prediction approach based on the Newton-Cotes rules. Int. J. Mech. Sci. 2020, 177, 105469. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Shi, H.; Xiao, D.; Li, B.; Liu, C. A novel Chebyshev-wavelet-based approach for accurate and fast prediction of milling stability. Precis. Eng. 2020, 62, 244–255. [Google Scholar] [CrossRef]
- Zhi, H.; Zhang, T.; Du, J.; Yan, X. An Efficient Full-Discretization Method for Milling Stability Prediction. Int. J. Adv. Manuf. Technol. 2020, 107, 4955–4967. [Google Scholar] [CrossRef]
- Tang, C.; Yan, H.; Zhang, H.; Chen, Z.; Li, W.; Zhang, G. The arbitrary order implicit multistep schemes of exponential fitting and their applications. J. Comput. Appl. Math. 2005, 173, 155–168. [Google Scholar] [CrossRef]
- Gradišek, J.; Kalveram, M.; Insperger, T.; Weinert, K.; Stepan, G.; Govekar, E.; Grabec, I. On stability prediction for milling. Int. J. Mach. Tools Manuf. 2005, 45, 769–781. [Google Scholar] [CrossRef]





| Modal Parameters | Cutting Parameters |
|---|---|
| = 0.03993 kg | = |
| = 0.011 | = |
| = | N = 2 |
| Models | Single-DOF Milling Model | Two-DOF Milling Model | |||
|---|---|---|---|---|---|
| Methods | = 0.05, m = 4 | = 0.5, m = 12 | = 0.05, m = 4 | = 0.1, m = 4 | |
| 2nd SDM | 1.0 | 2.9 | 3.3 | 3.2 | |
| CCM | 0.2 | 0.7 | 0.4 | 0.5 | |
| 2nd IEM | 0.6 | 2.1 | 1.2 | 1.3 | |
| 3rd IEM | 0.7 | 2.3 | 1.3 | 1.4 | |
| 4th IEM | 0.8 | 2.5 | 1.4 | 1.5 | |
| Modal Parameters | Cutting Parameters |
|---|---|
| = , = | = |
| = 0.018, = 0.014 | = |
| = , = , | N = 2 |
| Modal Parameters | Cutting Parameters |
|---|---|
| = , = | = |
| = 1.56 kg/s, = 1.60 kg/s | = |
| = 0.0201 kg, = 0.0199 kg | N = 1 |
| Modal Parameters | Cutting Parameters |
|---|---|
| = , = | = |
| = 0.02496, = 0.03322 | = |
| = 0.03253 kg, = 0.02959 kg | N = 4 |
| Group | Time Domain | Frequency Domain |
|---|---|---|
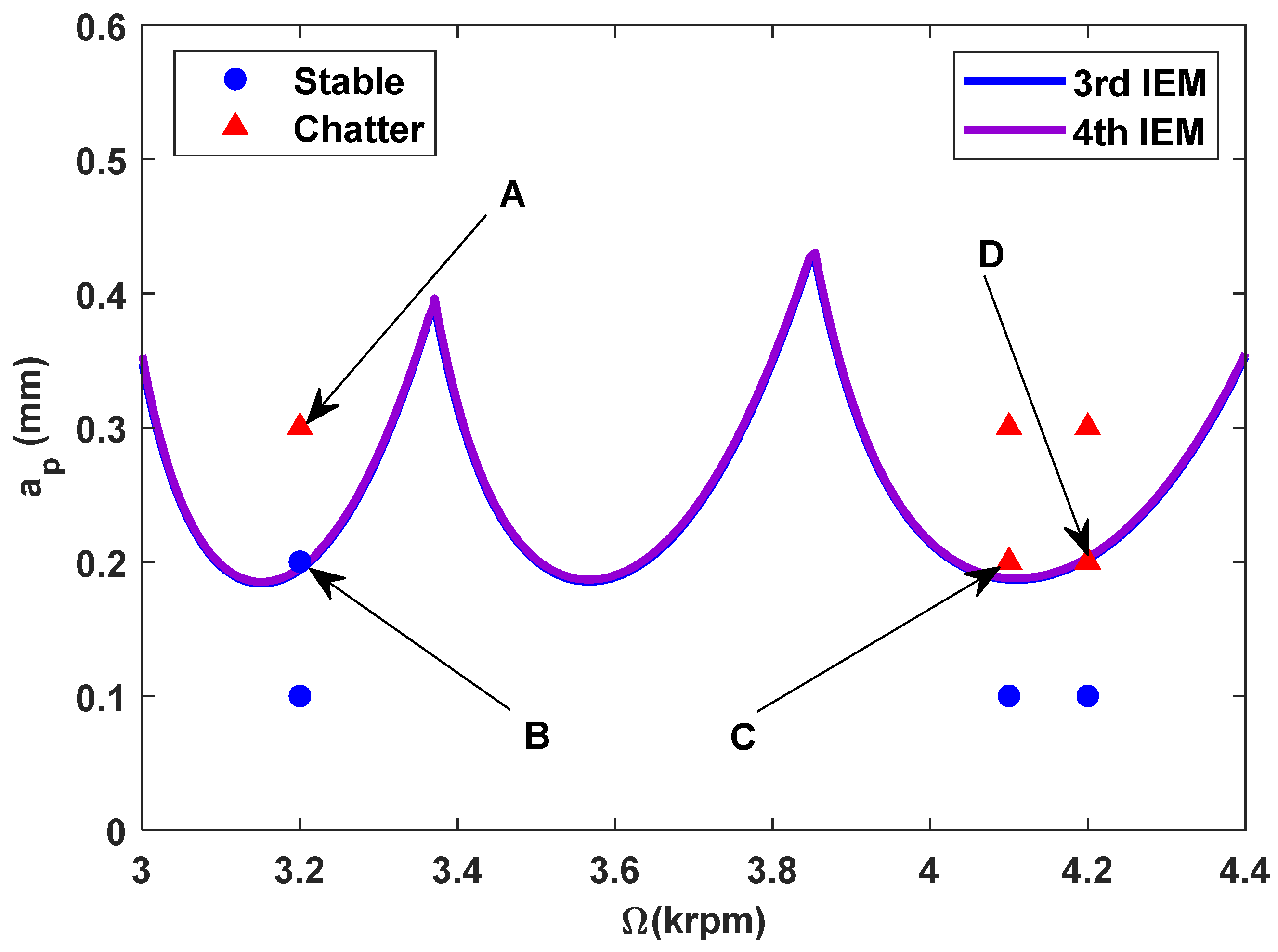
| Point A (Chatter) | 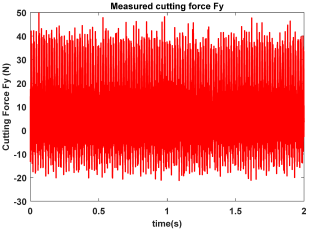 | 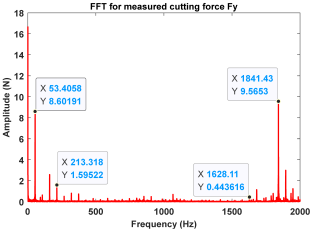 |
| Point B (Stable) |  | 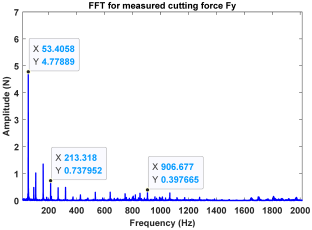 |
| Point C (Chatter)) |  | 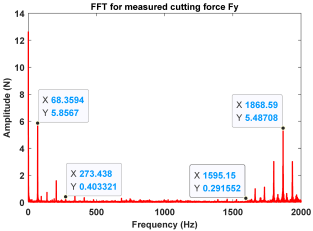 |
| Point D (Chatter) | 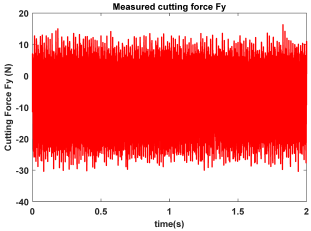 | 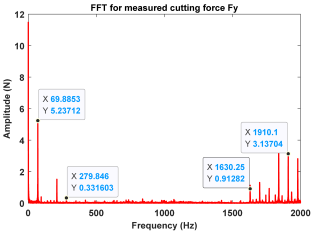 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Deng, B.; Zhao, Q.; Ye, T.; Liu, A.; Jiang, W. High-Order Exponentially Fitted Methods for Accurate Prediction of Milling Stability. Micromachines 2025, 16, 997. https://doi.org/10.3390/mi16090997
Wu Y, Deng B, Zhao Q, Ye T, Liu A, Jiang W. High-Order Exponentially Fitted Methods for Accurate Prediction of Milling Stability. Micromachines. 2025; 16(9):997. https://doi.org/10.3390/mi16090997
Chicago/Turabian StyleWu, Yi, Bin Deng, Qinghua Zhao, Tuo Ye, Anmin Liu, and Wenbo Jiang. 2025. "High-Order Exponentially Fitted Methods for Accurate Prediction of Milling Stability" Micromachines 16, no. 9: 997. https://doi.org/10.3390/mi16090997
APA StyleWu, Y., Deng, B., Zhao, Q., Ye, T., Liu, A., & Jiang, W. (2025). High-Order Exponentially Fitted Methods for Accurate Prediction of Milling Stability. Micromachines, 16(9), 997. https://doi.org/10.3390/mi16090997






