Advances in Laser Linewidth Measurement Techniques: A Comprehensive Review
Abstract
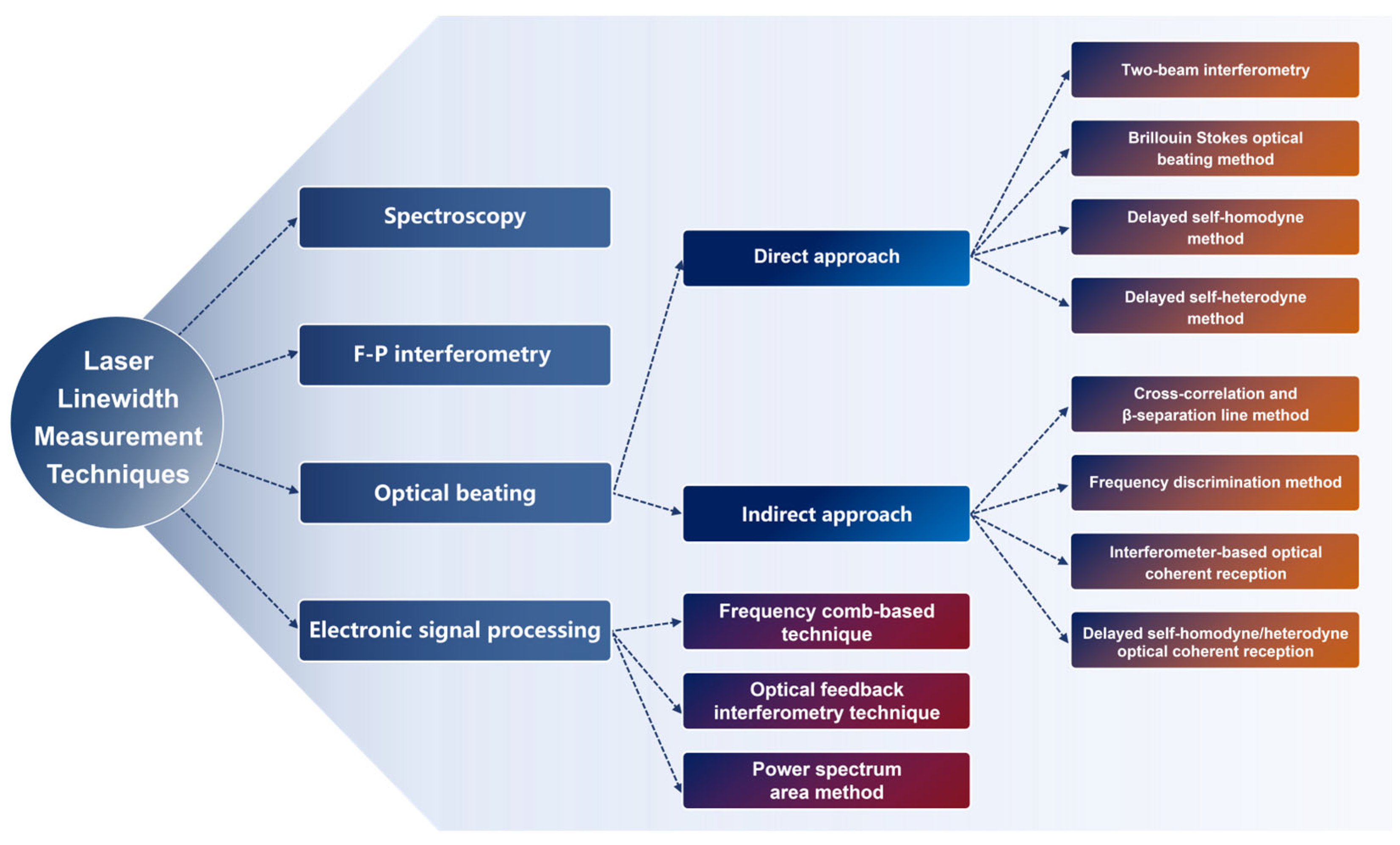
1. Introduction
2. Basic Concept of Linewidth
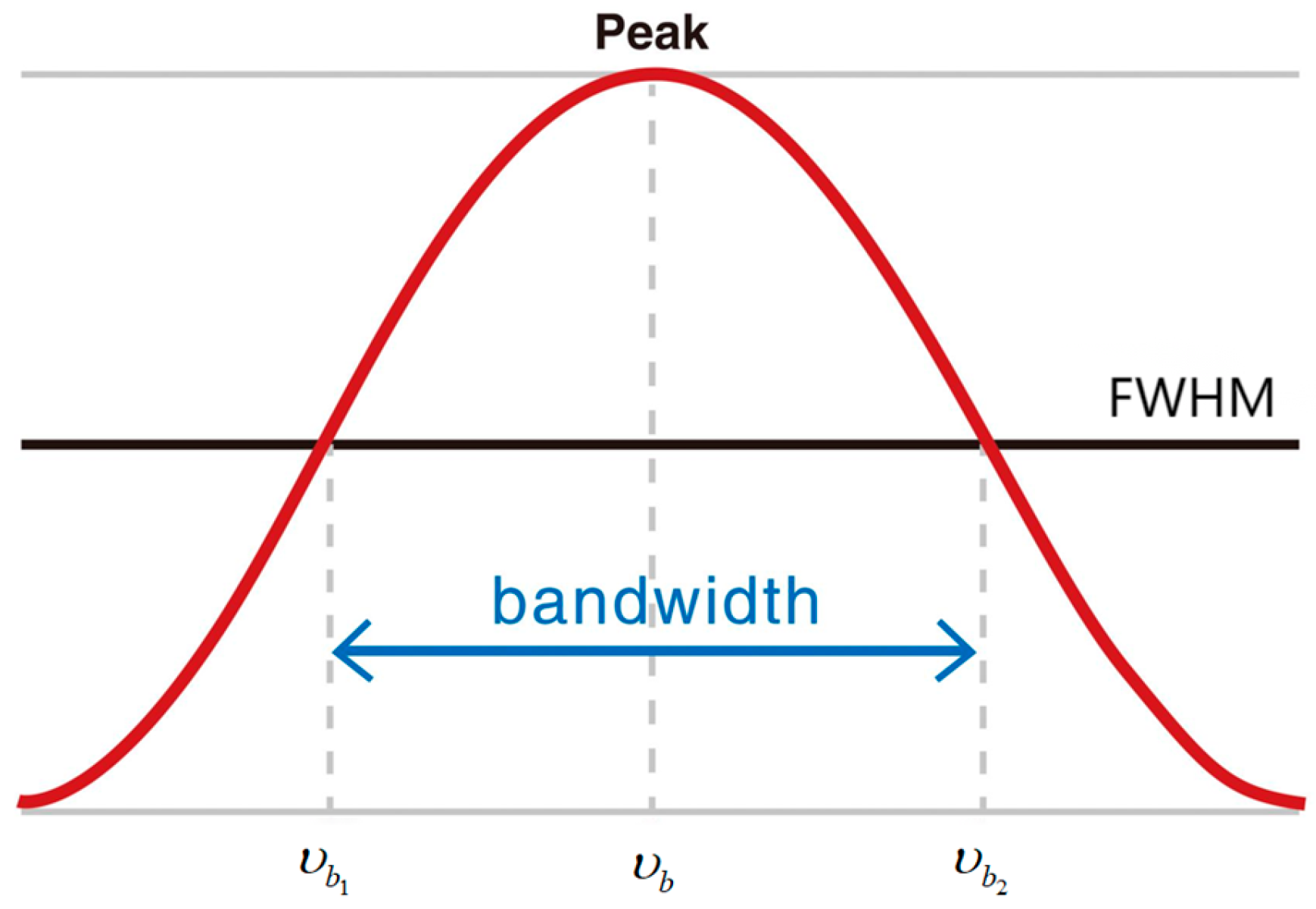
2.1. What Is Linewidth?
2.2. How to Measure Linewidth?
3. Spectroscopic Method
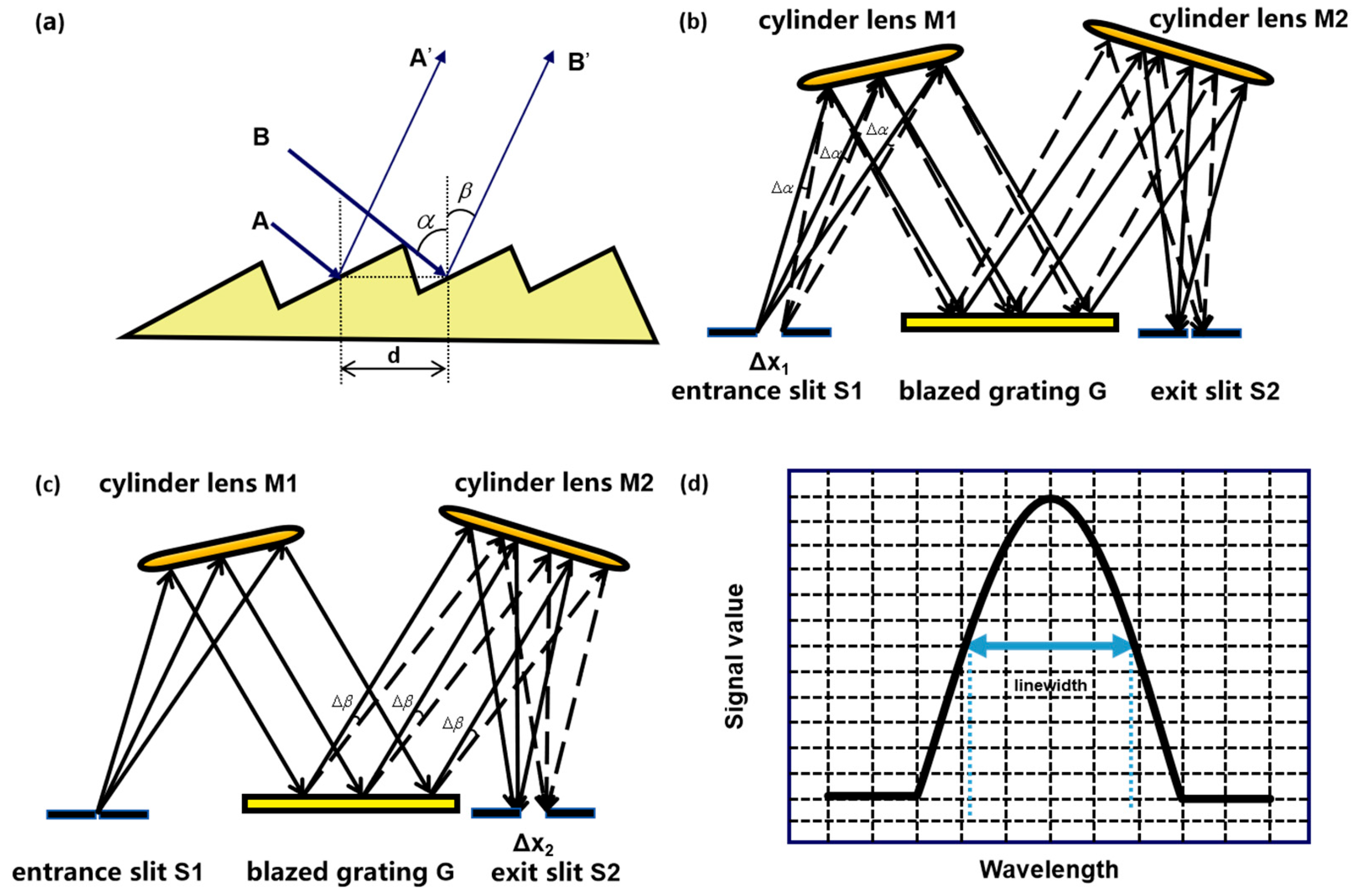
3.1. Effect of Incident Slit Width on Spectral Linewidth
3.2. Effect of Exit Slit Width on Spectral Line Width
3.3. Effect of Slit Width on Spectrometer Resolution
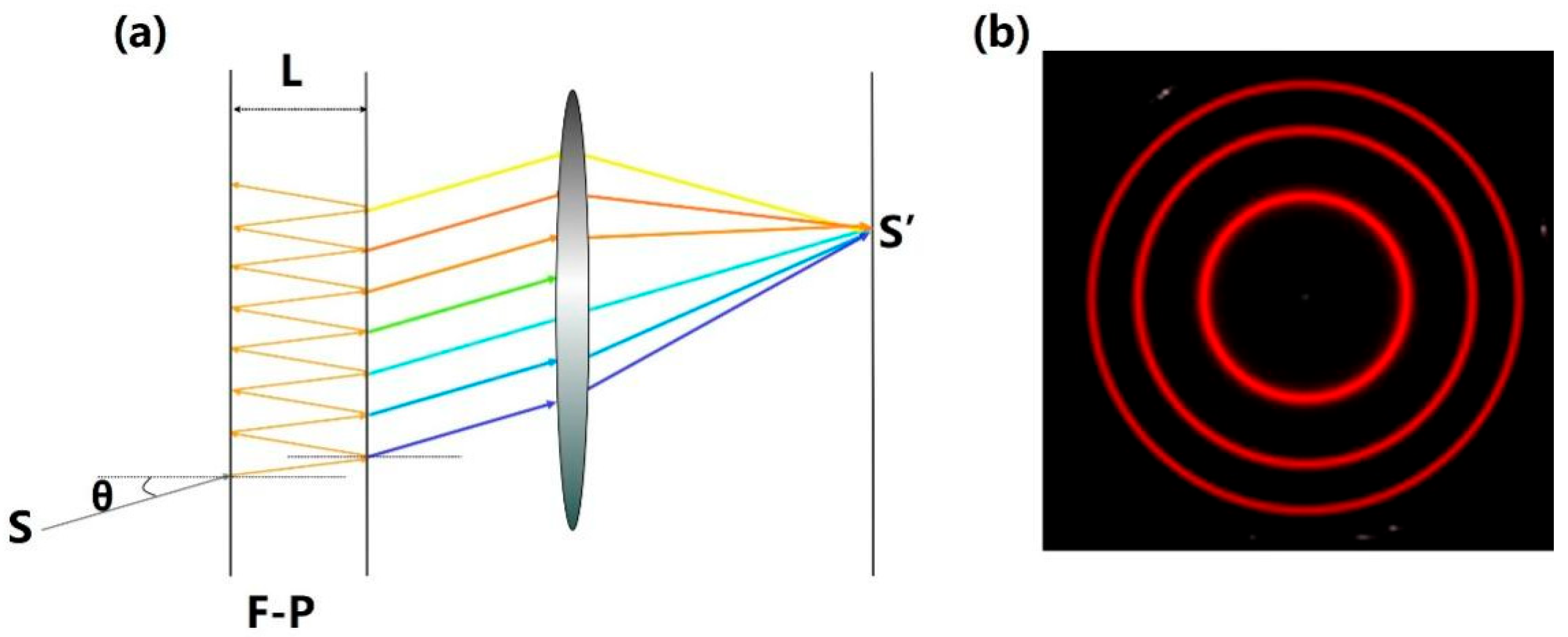
4. F-P Interferometry
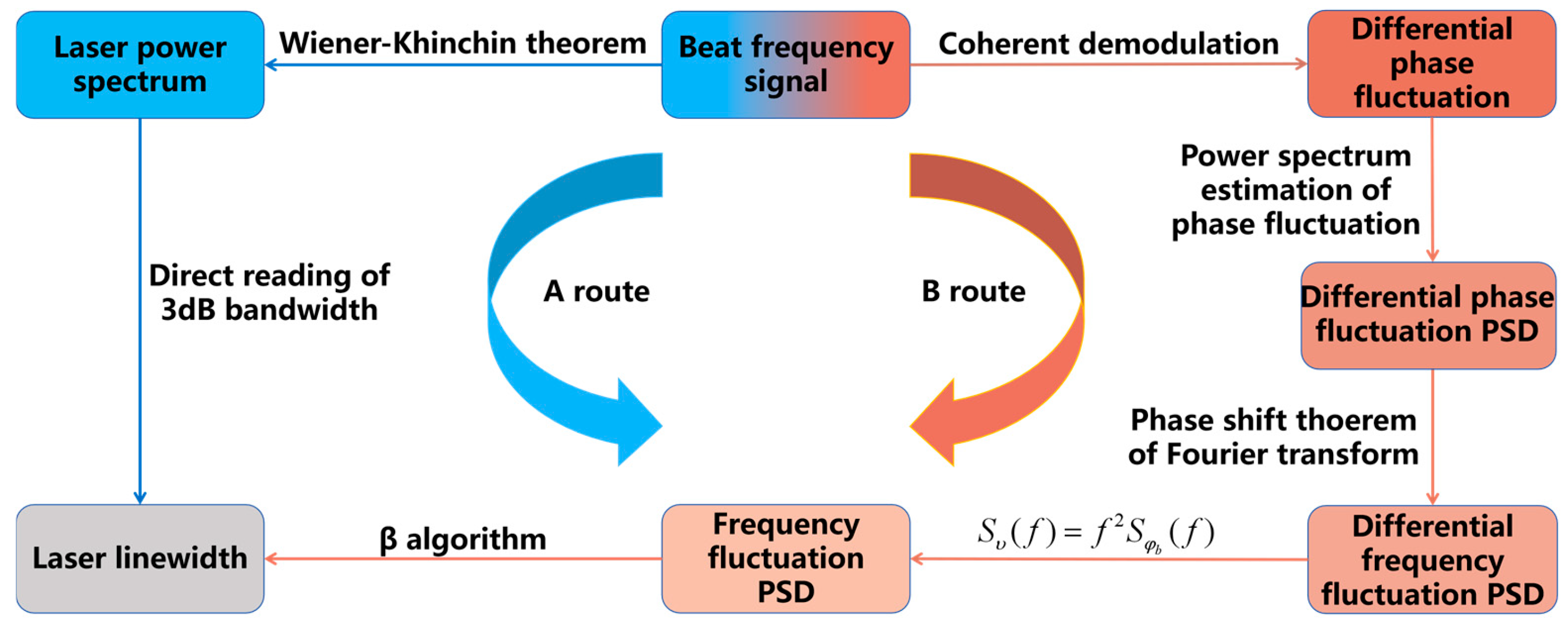
5. Optical Beating Method
5.1. Laser Linewidth Measurement Based on the Signal Power Spectrum (Direct Measurement)
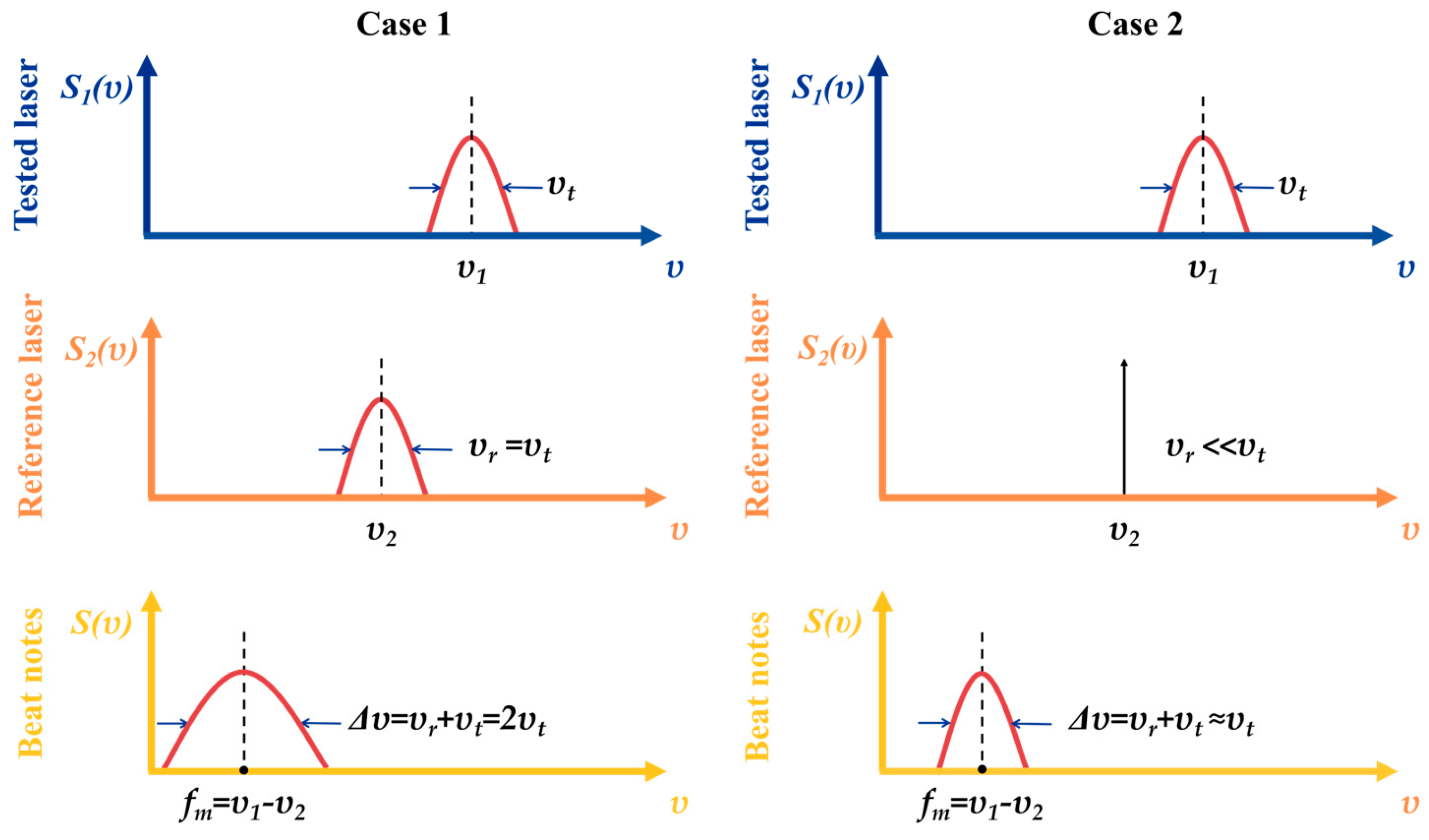
5.2. Linewidth Measurement Based on Phase Noise (Indirect Measurement)
| Measuring Equipment | Description | Case | Main Hallmarks | Reference | |
|---|---|---|---|---|---|
| Two-beam interferometry | 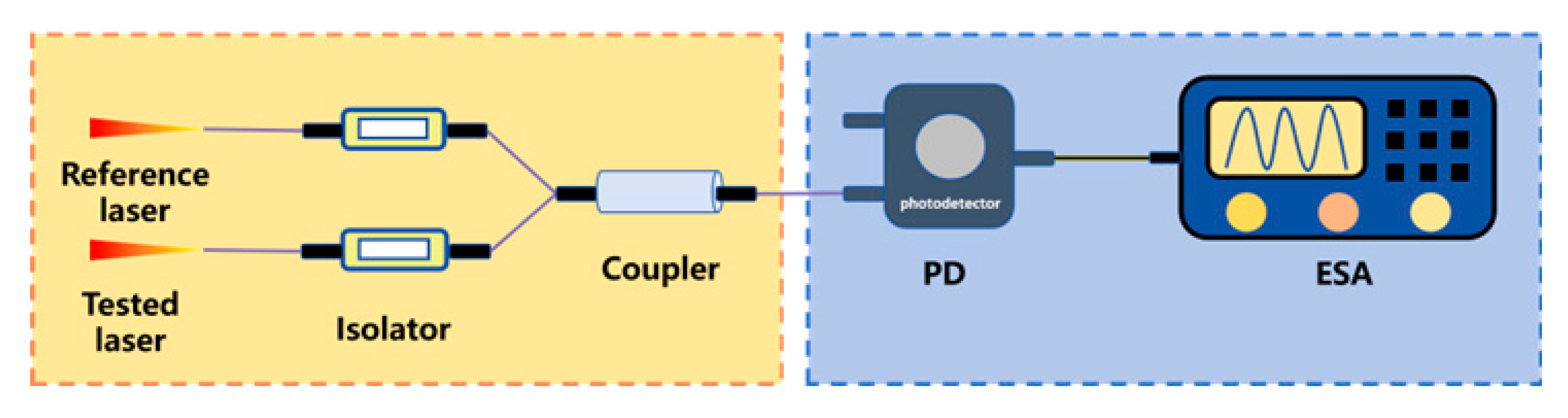 | This method determines the laser linewidth by interfering the test laser with a stabilized reference laser, precisely tuning their frequency offset, detecting the beat signal with a photodetector, and analyzing it using an electrical spectrum analyzer. | 1 | High-resolution and high-sensitivity Strict requirements for reference light sources | 0.6 Hz [228] 40 mHz [229] 100 Hz [230] |
| Brillouin stokes optical beating method | 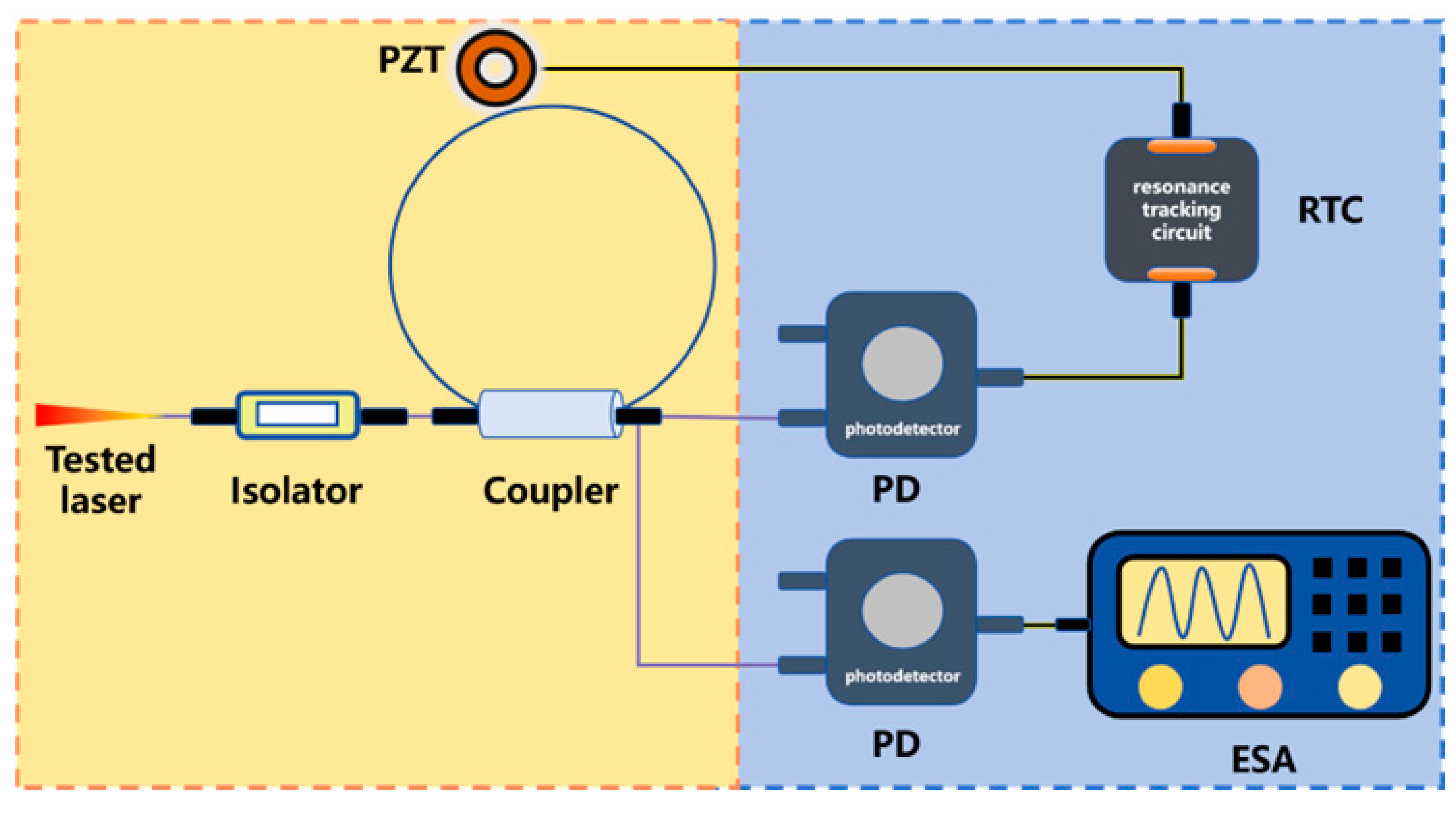 | This technology measures the laser linewidth by using second-order Stokes waves in a fiber resonator as intrinsic references, generating same-direction second-order Stokes via pump excitation, coupling for beat frequency, analyzing FWHM of the spectrum, and controlling resonator length with resonant tracking and piezoelectric ceramics. | 2 | High-resolution Simple system (only one laser needed) Sensitive to environment Beat signal frequency range limitation due to large Brillouin shift | 4.2 kHz [231] 100 kHz [232] 300 Hz [233] 5.5 kHz [234] 860 Hz [235] 3.84 kHz [236] |
| Delayed self-homodyne method |  | This technology uses an unbalanced Mach-Zehnder interferometer architecture to split the tested laser into a time-delayed signal via a fiber delay line and a reference signal, generating an optical beat signal through coherent interference, converting it into an electrical signal, and extracting the laser linewidth by analyzing the PSD of the electrical signal. | 1 | Avoiding dependence on the reference laser Zero frequency interference | 18 MHz [237] 460 kHz [238] |
| Delayed self-heterodyne method |  Mach-Zehnder interferometer-based delayed self-heterodyne method Mach-Zehnder interferometer-based delayed self-heterodyne method | The tested laser is split at Coupler1. One arm incorporates a delay fiber, to induce controlled decoherence, while the other arm routes light through an AOM generating a frequency shift. The obtained delayed beam and frequency-shifted beam are coupled at Coupler2 and detected by PD. Finally, ESA is used to collect data and display the detected signal. | 1 | Avoiding interference from zero frequency Long fiber length can introduce 1/f noise | 120 kHz [239] 2.58 kHz [240] |
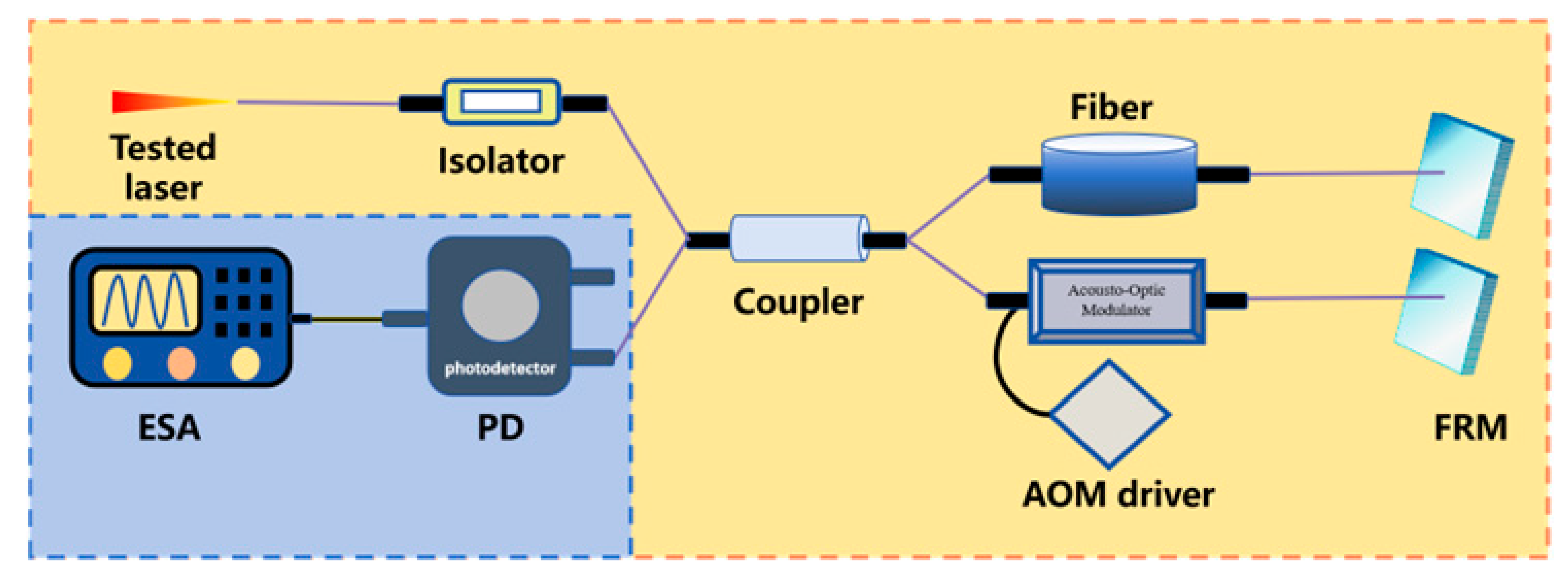 Michelson interferometer-based delayed self-heterodyne method Michelson interferometer-based delayed self-heterodyne method | The system splits the tested laser via a coupler, introducing Faraday Rotator Mirror (FRM) to stabilize polarization and reduce noise. After passing through delay fiber, the laser is reflected by FRM, redoing the optical path, then interferes at the coupler for 2 times the fiber-length delay. Finally, PD detects and ESA acquires data. | 1 | FRM is introduced, maintaining the stability of polarization state and reducing the noise caused by random polarization state drift. Long fiber length can introduce 1/f noise. | [241] | |
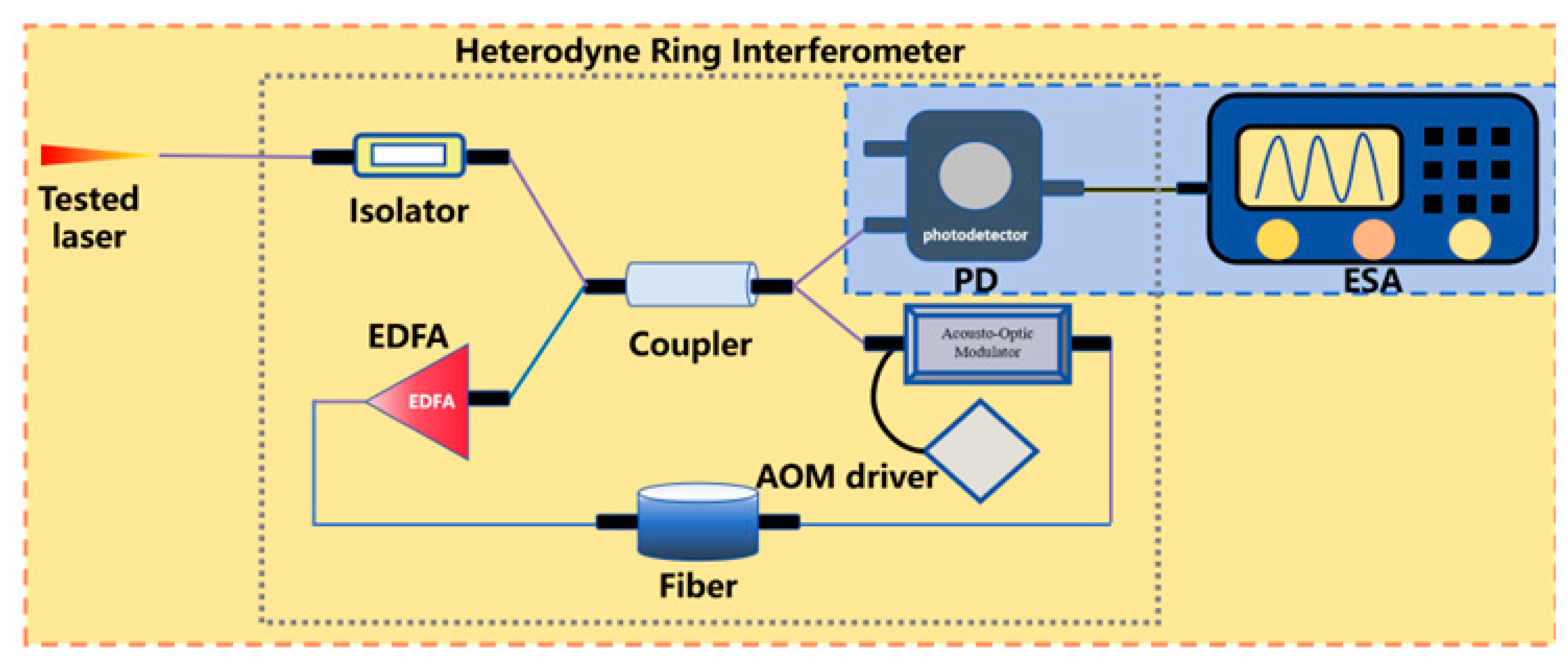 Gain compensation loop delay self-heterodyne method Gain compensation loop delay self-heterodyne methodEDFA: erbium-doped optical fiber amplifier | This method uses a fiber ring’s multipass transmission to amplify delay time, reducing required delay fiber length. Resolving beams with different circulation cycles from the fiber ring enables acquiring theoretically infinite photocurrent spectral lines via ESA, with its architecture multiplying temporal delay between beams. | 1 | Can measure wide range of laser bands Sensitive to the environmental noise Unable to eliminate the impact of 1/f noise | 680 Hz [242] | |
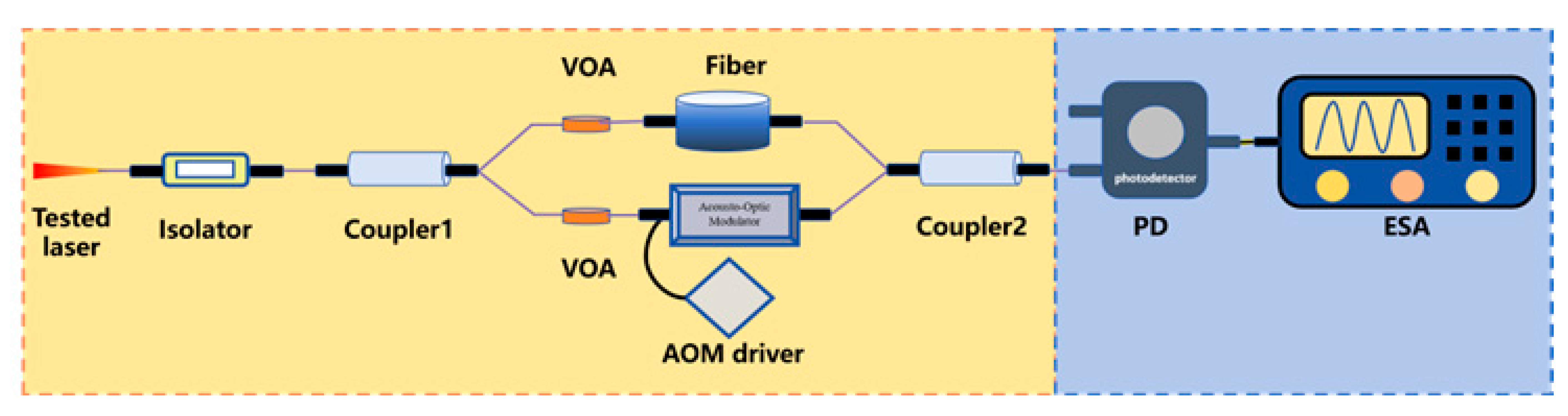 High-coherence envelope self-coherence detection High-coherence envelope self-coherence detectionVOA: Variable Optical Attenuator | This approach introduces two variable optical attenuators into the modified MZI-based delayed self-heterodyne method system. By establishing a quantitative mapping relationship between the contrast difference between the second spectral peak and the second trough (CDSPST) and the laser linewidth, the linewidth is calculated. | 1 | suppressing the spectral broadening induced by 1/f noise in the Gaussian linewidth of laser output | 150 Hz [243,244] 98 Hz [245] 609 Hz [246] | |
 Dual-parameter acquisition (DPA) method Dual-parameter acquisition (DPA) methodSMF: Single-Mode Fiber | This method transforms conventional Lorent-zian fitting based on incoherent interference into dynamic modeling utilizing partially co-herent interference. By extracting the power difference between adjacent extrema in the first-order sidelobe and the frequency deviation between the central frequency and the zeroth-order minimum, the linewidth is measured. | 1 | No precise delay fiber length data needed | 458 Hz [247] | |
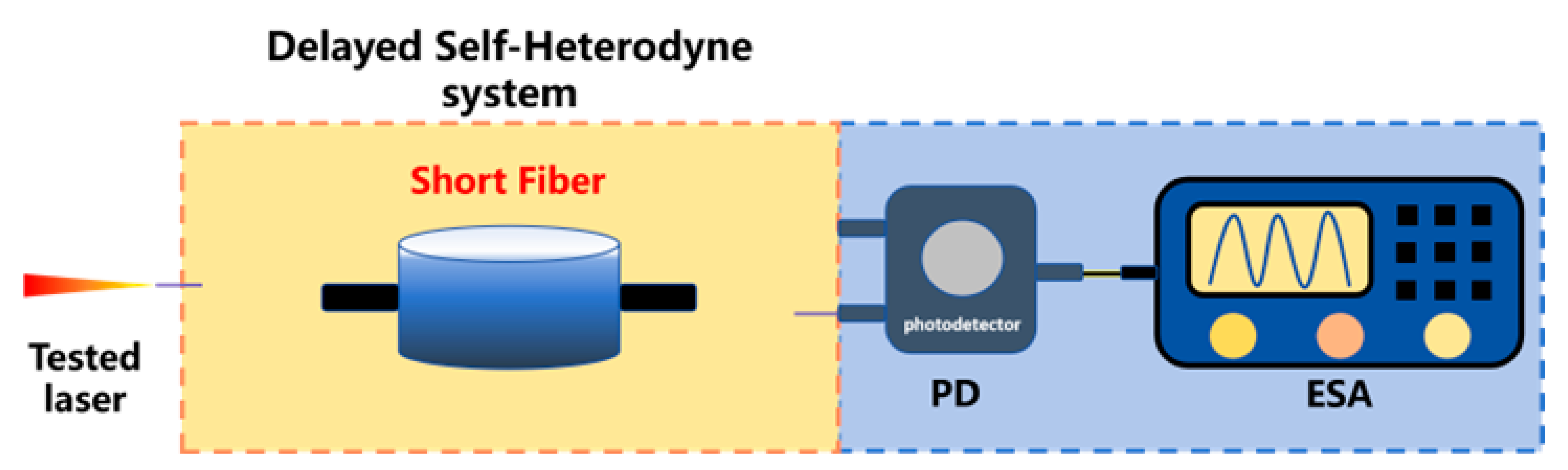 Linewidth measurement based on short-fiber delayed self-heterodyne Linewidth measurement based on short-fiber delayed self-heterodyne | In order to completely eliminate the influence of 1/f noise from the root, a linewidth measurement method using short optical fibers for delayed autoheterodyne has emerged in recent years. When the delay fiber is short, the broadening of the measured power spectrum can be effectively suppressed. | 1 | eliminate the influence of 1/f noise | 151 Hz [248] 944 Hz [249,250] 8 kHz [251] 2.53 kHz [252] 6.1 kHz [253,254] 1.753 kHz [255] 100 Hz [256] |
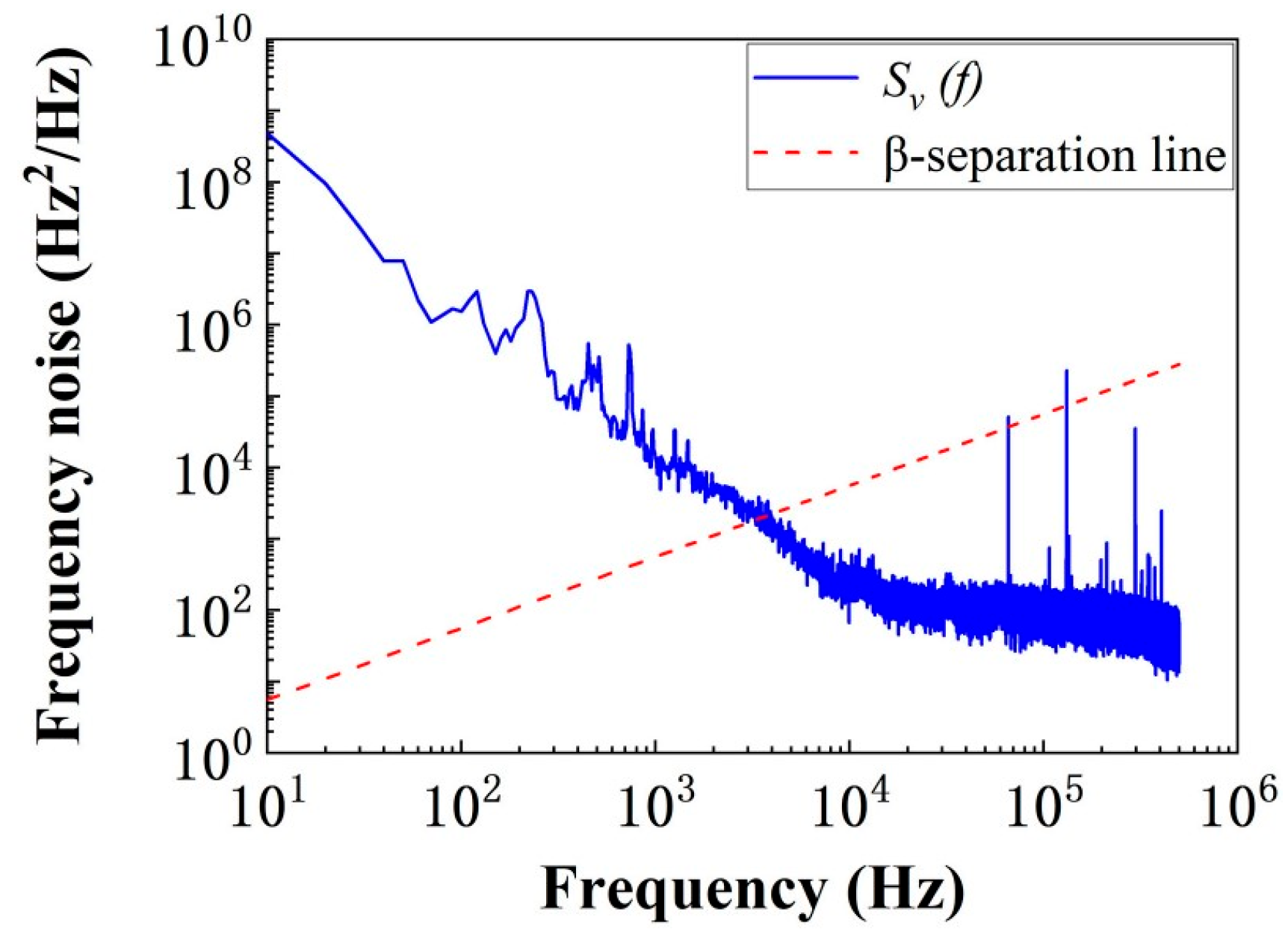
| Measuring Equipment | Description | Main Hallmarks | Reference | |
|---|---|---|---|---|
| Cross-correlation method and β algorithm | 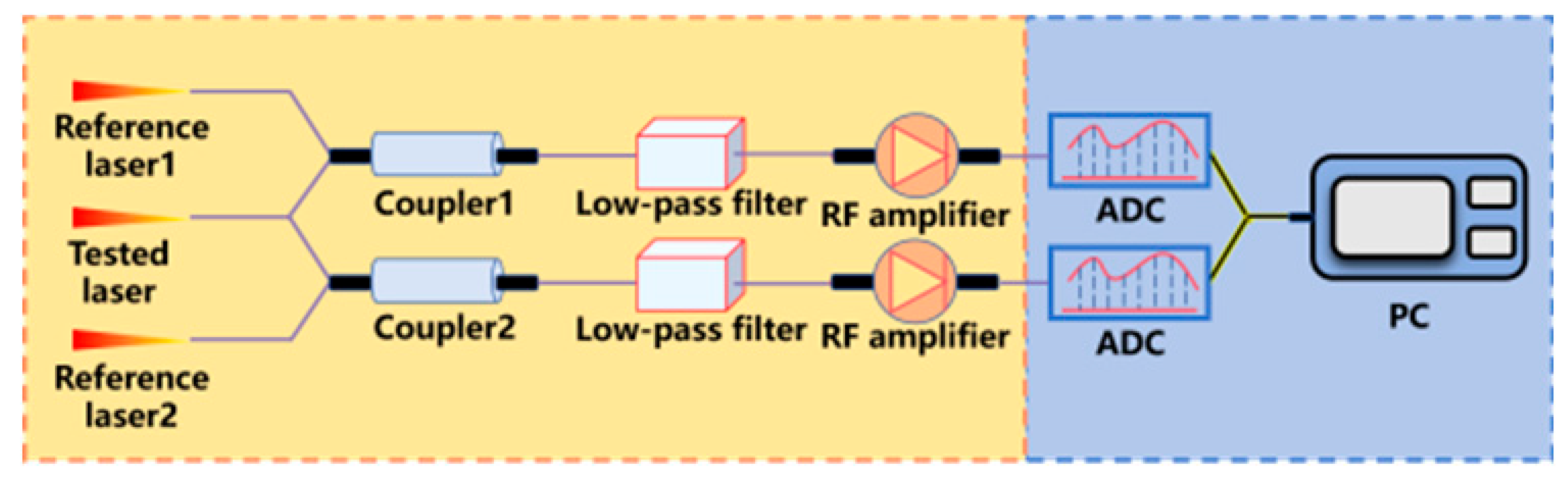 ADC:Analog-to-Digital Converter ADC:Analog-to-Digital Converter | The innovation of this methodology lies in the integration of the radio-frequency-domain cross-correlation frequency noise characterization technique with the β full-frequency-domain demodulation algorithm. The cross-correlation method iteratively suppresses system noise through multiple computational operations, while the β-algorithm achieves full-bandwidth linewidth resolution via frequency noise integration. | Avoiding linear fitting Suitable for any noise Complex calculation | 26.9 kHz [159] |
| Frequency discrimination method | 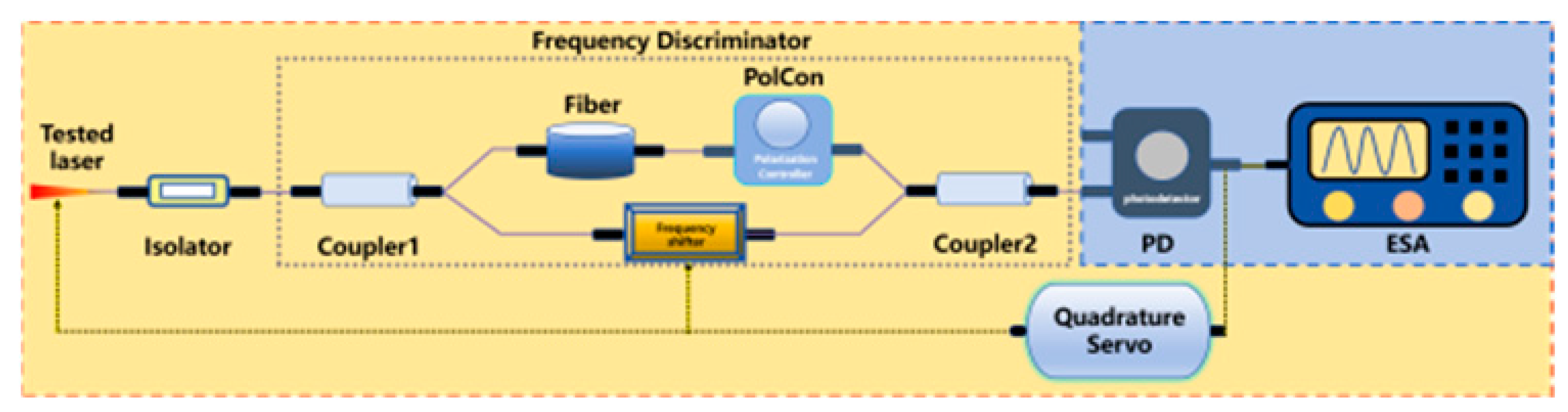 Polarization Controller: PolCon Polarization Controller: PolCon | Frequency discrimination is to characterize frequency noise by changing laser frequency fluctuations into intensity variations via a frequency discriminator, where the resulting intensity changes are monitored to derive frequency deviations. A quadrature servo control adjusts laser frequency dynamically via discriminator feedback, maintaining quadrature operation for optimal sensitivity and compensating drift for frequency stabilization. | Avoiding interference from zero frequency Frequency range is limited Precise control is necessary | 0.7 Hz [160] 269 Hz [274] 45 Hz [275] |
| Optical coherent reception method | 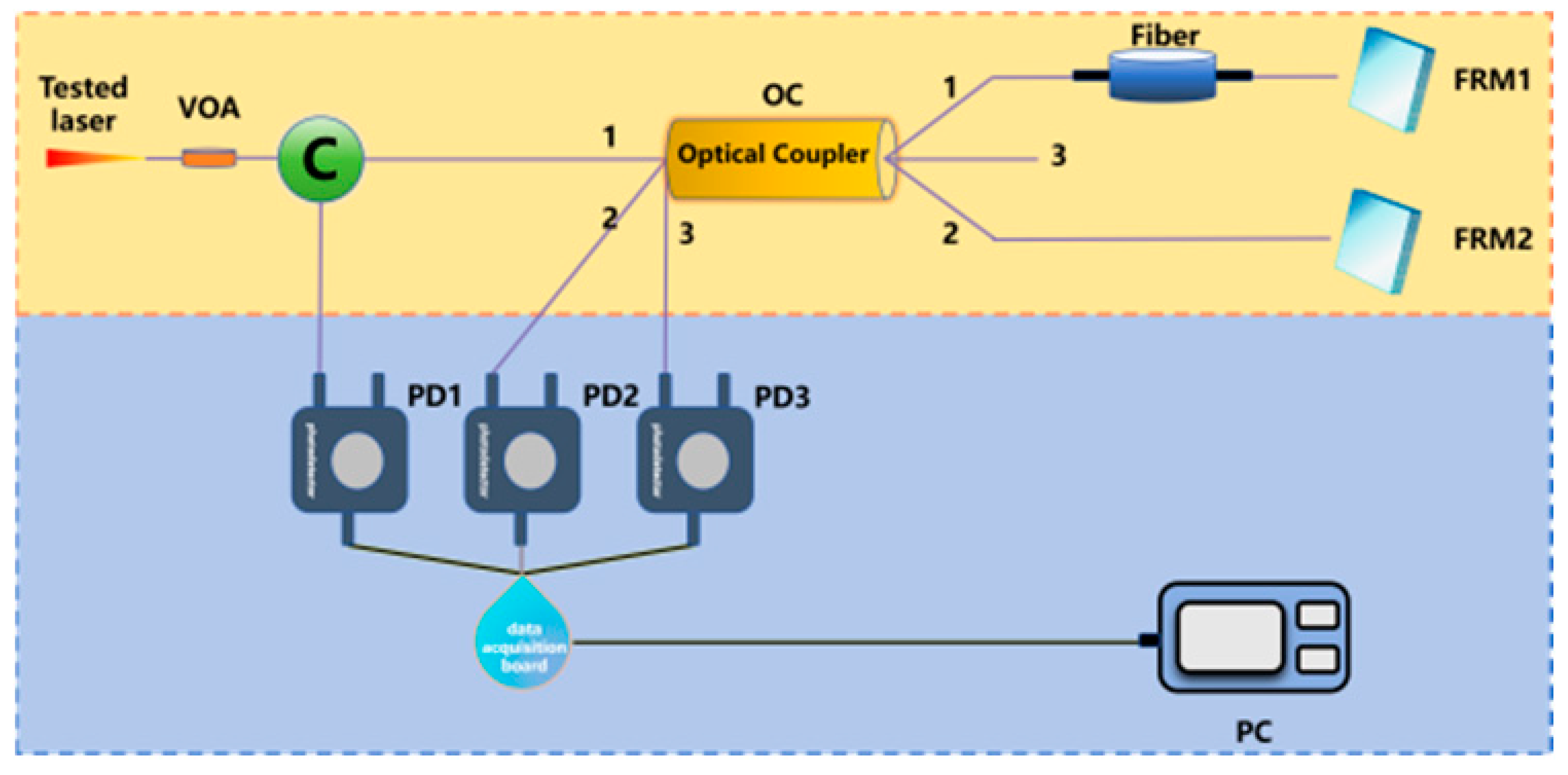 Based on an 120° interferometer Based on an 120° interferometer | This method determines laser linewidth by establishing the quantitative relationship between interferometric phase noise and the laser’s frequency noise PSD. After signal collection via an analog card, the phase noise PSD is obtained by analyzing frequency-phase characteristics and linear fitting curve deviation from linear scanning, demodulating phase information, and calculating the laser linewidth using the β algorithm. | Measure instantaneous phase change directly Complex structure High cost | 4.36 kHz [265] (minimum integrated linewidth) 3.58 kHz [265] (minimum Lorentzian linewidth) |
| Optical coherent reception method |  Based on delayed self-homodyne/self-heterodyne Based on delayed self-homodyne/self-heterodyne | The tested laser is split via a coupler into two beams. One propagates directly, while the other undergoes a time delay. Both beams are then routed through a PolCon before entering the incorporating an ICR for generating I/Q signals. The amplified signals are fed into a DSP system to extract phase noise characteristics, ultimately computing the linewidth. | Measure instantaneous phase change directly Complex structure High cost | 50 kHz [276] 20 kHz ~ 2 MHz [277] |
6. Linewidth Measurement Method Based on Electronic Information Processing
6.1. Frequency Comb-Based Method
6.2. Optical Feedback Interferometry-Based Method
6.3. Power Area Method (PAM)
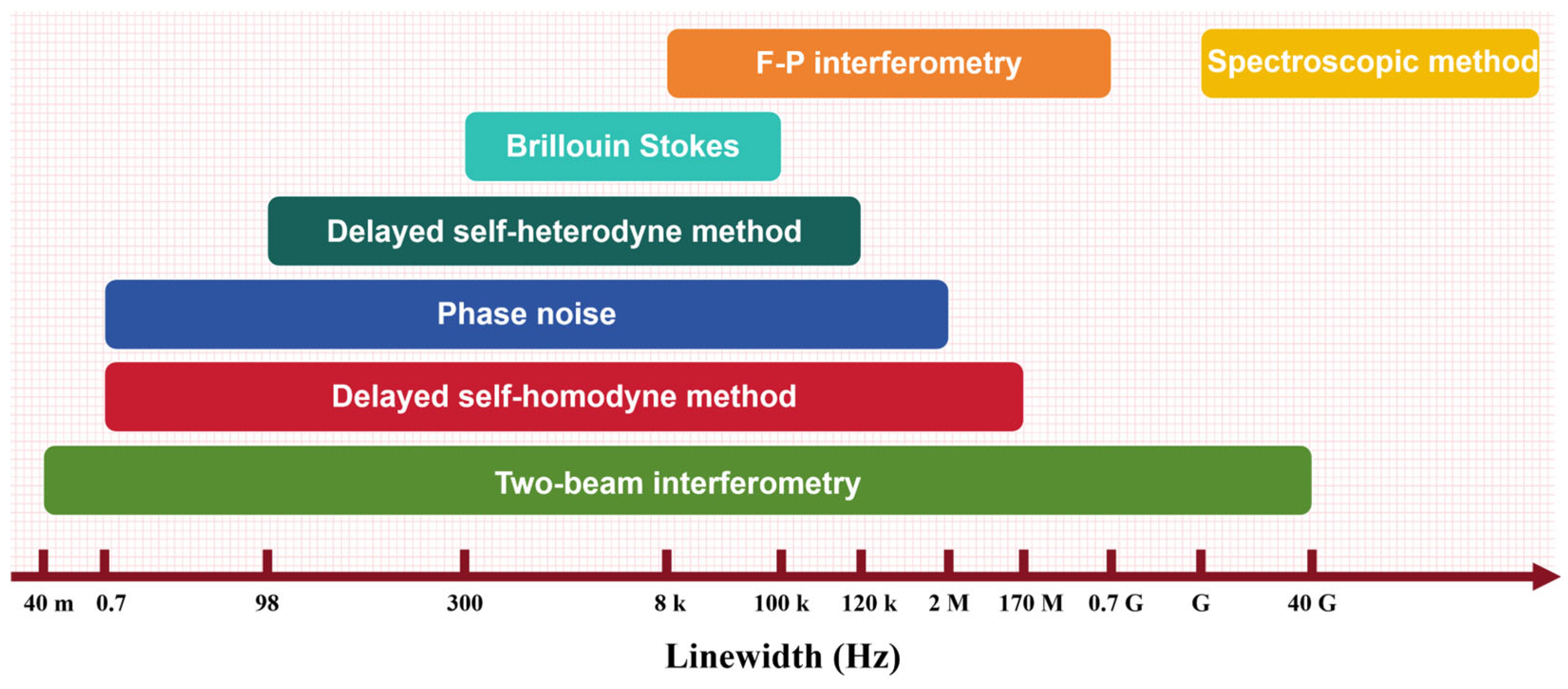
7. Comparative Analysis of Laser Linewidth Measurement Techniques
8. Conclusions and Perspectives
Funding
Data Availability Statement
Conflicts of Interest
References
- Einstein, A. On the Quantum Mechanics of Radiation. Phys. Z. 1917, 18, 121–128. [Google Scholar]
- Schawlow, A.L.; Townes, C.H. Infrared and Optical Masers. Phys. Rev. 1958, 112, 1940–1949. [Google Scholar] [CrossRef]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Maiman, T.H. Optical and Microwave-Optical Experiments in Ruby. Phys. Rev. Lett. 1960, 4, 564–566. [Google Scholar] [CrossRef]
- Zeng, X.; Cui, S.; Jiang, H.; Ruan, B.; Cheng, X.; Zhou, J.; Lin, Z.; Yang, X.; Chen, W.; Feng, Y. Single-Frequency Upconverted Laser Generation by Phase Summation. High Power Laser Sci. Eng. 2023, 11, e18. [Google Scholar] [CrossRef]
- Legero, T.; Matei, D.G.; Haefner, S.; Grebing, C.; Weyrich, R.; Riehle, F.; Sterr, U.; Zhang, W.; Robinson, J.; Sonderhouse, L.; et al. 1.5 μm Lasers with Sub 10 mHz Linewidth. In Proceedings of the 2017 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 14–19 May 2017. [Google Scholar]
- Mercer, L.B. 1/f Frequency Noise Effects on Self-Heterodyne Linewidth Measurements. J. Light. Technol. 1991, 9, 485–493. [Google Scholar] [CrossRef]
- Pixley, N.C.; Correll, T.L.; Pappas, D.; Matveev, O.I.; Smith, B.W.; Winefordner, J.D. Tunable Resonance Fluorescence Monochromator with Sub-Doppler Spectral Resolution. Opt. Lett. 2001, 26, 1946–1948. [Google Scholar] [CrossRef]
- Račiukaitis, G. Ultra-Short Pulse Lasers for Microfabrication: A Review. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1100112. [Google Scholar] [CrossRef]
- Wei-Lian, S. The Development of Laser Processing Technology. Laser Infrared 2006, 36, 755–758. [Google Scholar]
- Murray, K.K.; Seneviratne, C.A.; Ghorai, S. High Resolution Laser Mass Spectrometry Bioimaging. Methods 2016, 104, 118–126. [Google Scholar] [CrossRef]
- Najda, S.P.; Perlin, P.; Leszczyński, M.; Slight, T.J.; Meredith, W.; Schemmann, M.; Moseley, H.; Woods, J.A.; Valentine, R.; Kalra, S. A Multi-Wavelength (Uv to Visible) Laser System for Early Detection of Oral Cancer. In Proceedings of the Imaging, Manipulation, and Analysis of Biomolecules, Cells, and Tissues XIII, San Francisco, CA, USA, 9–11 February 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9328, pp. 32–37. [Google Scholar]
- Kalisky, Y.; Kalisky, O. The Status of High-Power Lasers and Their Applications in the Battlefield. Opt. Eng. 2010, 49, 91003. [Google Scholar] [CrossRef]
- Wang, R.-F.; Zhang, Y.-P.; Xu, Z.-Y. Present Situation and Developing Trend of Application of Laser Technique to Military. Infrared Laser Eng. 2007, S1, 308–311. [Google Scholar]
- Predehl, K.; Grosche, G.; Raupach, S.M.F.; Droste, S.; Terra, O.; Alnis, J.; Legero, T.; Haensch, T.W.; Udem, T.H.; Holzwarth, R.; et al. A 920-Kilometer Optical Fiber Link for Frequency Metrology at the 19th Decimal Place. Science 2012, 336, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast Physical Random Bit Generation with Chaotic Semiconductor Lasers. Nat. Photonics 2008, 2, 728–732. [Google Scholar] [CrossRef]
- Marcu, A.; Stafe, M.; Barbuta, M.; Ungureanu, R.; Serbanescu, M.; Calin, B.; Puscas, N. Photon Energy Transfer on Titanium Targets for Laser Thrusters. High Power Laser Sci. Eng. 2022, 10, e27. [Google Scholar] [CrossRef]
- Duan, Y.; Sun, Y.; Zhu, H.; Mao, T.; Zhang, L.; Chen, X. YVO4 Cascaded Raman Laser for Five-Visible-Wavelength Switchable Emission. Opt. Lett. 2020, 45, 2564–2567. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Bai, Z.; Chen, J.; Li, X.; Zhu, Z.-H.; Wang, Y.; Omatsu, T.; Mildren, R.P.; Lu, Z. Diamond Raman Vortex Lasers. ACS Photonics 2024, 12, 864–869. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Chauhan, N.; Harrington, M.W.; Nelson, K.D.; Blumenthal, D.J. Integrated Photonic Molecule Brillouin Laser with a High-Power Sub-100-mHz Fundamental Linewidth. Opt. Lett. 2023, 49, 45–48. [Google Scholar] [CrossRef]
- Jin, D.; Bai, Z.; Zhao, Z.; Chen, Y.; Fan, W.; Wang, Y.; Mildren, R.P.; Lü, Z. Linewidth Narrowing in Free-Space-Running Diamond Brillouin Lasers. High Power Laser Sci. Eng. 2023, 11, e47. [Google Scholar] [CrossRef]
- Alouini, M.; Danion, G.; Vallet, M. Self-Linewidth-Narrowing Photonic Oscillator. Opt. Express 2025, 33, 1021–1033. [Google Scholar] [CrossRef]
- Li, L.; Zhao, Z.; Yu, Q.; Sheng, L.; Qi, Y.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z.; Bai, Z. Multistage Cyclic Filtering System Utilizing a Single-Longitudinal-Mode Brillouin Fiber Laser with a Fiber Ring and Reflective Saturable Absorber. Opt. Commun. 2025, 577, 131434. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Shaashoua, R.; Kasuker, L.; Kishner, M.; Levy, T.; Rotblat, B.; Ben-Zvi, A.; Bilenca, A. Brillouin Gain Microscopy. Nat. Photonics 2024, 18, 836–841. [Google Scholar] [CrossRef]
- Chen, H.; Bai, Z.; Cai, Y.; Yang, X.; Ding, J.; Qi, Y.; Yan, B.; Li, Y.; Wang, Y.; Lu, Z. Order Controllable Enhanced Stimulated Brillouin Scattering Utilizing Cascaded Diamond Raman Conversion. Appl. Phys. Lett. 2023, 122, 092202. [Google Scholar] [CrossRef]
- Nishigata, Y.; Sasaki, S.; Miyamoto, K.; Omatsu, T. Cascaded Vector Vortex Mode Generation from a Solid-State Raman Laser. Appl. Opt. 2021, 60, 10638–10642. [Google Scholar] [CrossRef]
- Pask, H.M. The Design and Operation of Solid-State Raman Lasers. Prog. Quantum Electron. 2003, 27, 3–56. [Google Scholar] [CrossRef]
- Xuan, C.; Zhou, Y.; Yang, X.; Ma, Y.; Rao, A.S.; Omatsu, T.; Bai, Z.; Wan, Y.; Wen, J.; Yusufu, T. Generation of High-order Laguerre-gaussian Modes from an Optical Vortex Pumped Diamond Raman Laser. Laser Photonics Rev. 2024, 18, 2400081. [Google Scholar] [CrossRef]
- Antipov, S.; Sabella, A.; Williams, R.J.; Kitzler, O.; Spence, D.J.; Mildren, R.P. 1.2 kW Quasi-Steady-State Diamond Raman Laser Pumped by an M2 = 15 Beam. Opt. Lett. 2019, 44, 2506–2509. [Google Scholar] [CrossRef]
- Pahlavani, R.L.; Spence, D.J.; Sharp, A.O.; Mildren, R.P. Linewidth Narrowing in Raman Lasers. APL Photonics 2025, 10, 076107. [Google Scholar] [CrossRef]
- Liu, Z.; Fan, R.; Jin, D.; Luo, T.; Li, S.; Li, N.; Li, S.; Wang, Y.; Lu, Z. Quarter Acoustic Period Pulse Compression Using Stimulated Brillouin Scattering in PF-5060. Opt. Express 2022, 30, 12586–12595. [Google Scholar] [CrossRef]
- Zhu, L.; Bai, Z.; Chen, Y.; Jin, D.; Fan, R.; Qi, Y.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z. The Effect of Pump Beam Focusing Characteristics on Stimulated Brillouin Scattering. Opt. Commun. 2022, 515, 128205. [Google Scholar] [CrossRef]
- Gyger, F.; Liu, J.; Yang, F.; He, J.; Raja, A.S.; Wang, R.N.; Bhave, S.A.; Kippenberg, T.J.; Thévenaz, L. Observation of Stimulated Brillouin Scattering in Silicon Nitride Integrated Waveguides. Phys. Rev. Lett. 2020, 124, 13902. [Google Scholar] [CrossRef]
- Tao, Y.; Jiang, M.; Liu, L.; Li, C.; Zhou, P.; Jiang, Z. More than 20 W, High Signal-to-Noise Ratio Single-Frequency All-Polarization-Maintaining Hybrid Brillouin/Ytterbium Fiber Laser. J. Light. Technol. 2022, 41, 678–683. [Google Scholar] [CrossRef]
- Deroh, M.; Lucas, E.; Hammani, K.; Millot, G.; Kibler, B. Stabilized Single-Frequency Sub-kHz Linewidth Brillouin Fiber Laser Cavity Operating at 1 μm. Appl. Opt. 2023, 62, 8109–8114. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Gao, F.; Chen, H.; Yang, X.; Bai, Z.; Qi, Y.; Wang, Y.; Lu, Z.; Ding, J. Continuous-Wave Diamond Laser with a Tunable Wavelength in Orange–Red Wavelength Band. Opt. Commun. 2023, 528, 128985. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, X.; Li, M.; Zeng, X.; Jiang, H.; Feng, Y. Diamond Guide Star Laser Pulsed at a Larmor Frequency. Opt. Express 2024, 32, 46345–46352. [Google Scholar] [CrossRef]
- Zhang, W.; Kittlaus, E.; Savchenkov, A.; Iltchenko, V.; Yi, L.; Papp, S.B.; Matsko, A. Monolithic Optical Resonator for Ultrastable Laser and Photonic Millimeter-Wave Synthesis. Commun. Phys. 2024, 7, 177. [Google Scholar] [CrossRef]
- Matsui, Y.; Eriksson, U.; Wesstrom, J.-O.; Liu, Y.; Hammerfeldt, S.; Hassler, M.; Stoltz, B.; Carlsson, N.; Siraj, S.; Goobar, E.; et al. Narrow Linewidth Tunable Semiconductor Laser. In Proceedings of the 2016 Compound Semiconductor Week (CSW) Includes 28th International Conference on Indium Phosphide & Related Materials (IPRM) & 43rd International Symposium on Compound Semiconductors (ISCS), Toyama, Japan, 26–30 June 2016. [Google Scholar]
- Wang, Q.; Guo, J.; Chen, W.; Liu, J.; Zhu, N. Widely Tunable Distributed Feedback Semiconductor Lasers with Constant Power and Narrow Linewidth. Chin. J. Lasers 2017, 44, 0101004. [Google Scholar] [CrossRef]
- Glebov, A.L.; Leisher, P.O.; Wicht, A.; Bawamia, A.; Krüger, M.; Kürbis, C.; Schiemangk, M.; Smol, R.; Peters, A.; Tränkle, G. Narrow Linewidth Diode Laser Modules for Quantum Optical Sensor Applications in the Field and in Space. Soc. Photo-Opt. Instrum. Eng. (SPIE) Conf. Ser. 2017, 10085, 100850F. [Google Scholar]
- Ishii, H.; Fujiwara, N.; Watanabe, K.; Kanazawa, S.; Itoh, M.; Takenouchi, H.; Miyamoto, Y.; Kasai, K.; Nakazawa, M. Narrow Linewidth Tunable DFB Laser Array Integrated with Optical Feedback Planar Lightwave Circuit (PLC). IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1501007. [Google Scholar] [CrossRef]
- Argence, B.; Chanteau, B.; Lopez, O.; Nicolodi, D.; Abgrall, M.; Chardonnet, C.; Daussy, C.; Darquie, B.; Le Coq, Y.; Amy-Klein, A. Quantum Cascade Laser Frequency Stabilization at the Sub-Hz Level. Nat. Photonics 2015, 9, 456–460. [Google Scholar] [CrossRef]
- Deng, X.; Liu, J.; Zang, Q.; Jiao, D.; Gao, J.; Zhang, X.; Wang, D.; Dong, R.; Liu, T. Coherent Phase Transfer via Fiber Using Heterodyne Optical Phase Locking as Optical Amplification. Appl. Opt. 2018, 57, 9620–9624. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.-C.; Chi, Y.-C.; Wang, H.-Y.; Tsai, C.-T.; Lin, G.-R. Blue Laser Diode Enables Underwater Communication at 12.4 Gbps. Sci. Rep. 2017, 7, 40480. [Google Scholar] [CrossRef] [PubMed]
- Giuliano, G.; Laycock, L.; Rowe, D.; Kelly, A.E. Solar Rejection in Laser Based Underwater Communication Systems. Opt. Express 2017, 25, 33066–33077. [Google Scholar] [CrossRef]
- Agrell, E.; Karlsson, M.; Chraplyvy, A.R.; Richardson, D.J.; Krummrich, P.M.; Winzer, P.; Roberts, K.; Fischer, J.K.; Savory, S.J.; Eggleton, B.J. Roadmap of Optical Communications. J. Opt. 2016, 18, 63002. [Google Scholar] [CrossRef]
- Biswas, A.; Kovalik, J.M.; Srinivasan, M.; Shaw, M.; Piazzolla, S.; Wright, M.W.; Farr, W.H. Deep Space Laser Communications. In Proceedings of the Free-Space Laser Communication and Atmospheric Propagation XXVIII, San Francisco, CA, USA, 13–18 February 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9739, pp. 209–223. [Google Scholar]
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tuts. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Mansour, A.; Mesleh, R.; Abaza, M. New Challenges in Wireless and Free Space Optical Communications. Opt. Lasers Eng. 2017, 89, 95–108. [Google Scholar] [CrossRef]
- Liu, L. Laser Communications in Space I Optical Link and Terminal Technology. Chin. J. Lasers 2007, 34, 3. [Google Scholar]
- Liang, J.; Chaudhry, A.U.; Yanikomeroglu, H. Phasing Parameter Analysis for Satellite Collision Avoidance in Starlink and Kuiper Constellations. In Proceedings of the 2021 IEEE 4th 5G World Forum (5GWF), Montreal, QC, Canada, 13–15 October 2021; IEEE: New York, NY, USA, 2021; pp. 493–498. [Google Scholar]
- Chaudhry, A.U.; Yanikomeroglu, H. Laser Intersatellite Links in a Starlink Constellation: A Classification and Analysis. IEEE Veh. Technol. Mag. 2021, 16, 48–56. [Google Scholar] [CrossRef]
- Zhai, H.; Zhang, Z.; Zhang, H.; Wang, B.; Zhao, Y.; Zhang, J. Design and Implementation of the Hardware Platform of Satellite Optical Switching Node. In Proceedings of the 2021 19th International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 23–27 August 2021; IEEE: New York, NY, USA, 2021; pp. 1–3. [Google Scholar]
- Guan, H.; Novack, A.; Galfsky, T.; Ma, Y.; Fathololoumi, S.; Horth, A.; Huynh, T.N.; Roman, J.; Shi, R.; Caverley, M.; et al. Widely-Tunable, Narrow-Linewidth III-V/Silicon Hybrid External-Cavity Laser for Coherent Communication. Opt. Express 2018, 26, 7920–7933. [Google Scholar] [CrossRef]
- Zhou, K.; Zhao, Q.; Huang, X.; Yang, C.; Li, C.; Zhou, E.; Xu, X.; Wong, K.K.Y.; Cheng, H.; Gan, J.; et al. kHz-Order Linewidth Controllable 1550 nm Single-Frequency Fiber Laser for Coherent Optical Communication. Opt. Express 2017, 25, 19752–19759. [Google Scholar] [CrossRef]
- Li, R.; Lin, B.; Liu, Y.; Dong, M.; Zhao, S. A Survey on Laser Space Network: Terminals, Links, and Architectures. IEEE Access 2022, 10, 34815–34834. [Google Scholar] [CrossRef]
- Chen, Q.; Lu, Q.; Guo, W. Theory and Simulation of Multi-Channel Interference (MCI) Widely Tunable Lasers. Opt. Express 2015, 23, 18040–18051. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Chen, Q.; Wang, K.; Lu, Q.; Lu, M.; Guo, W. Narrow-Linewidth Thermally Tuned Multi-Channel Interference Laser Integrated with a SOA and Spot Size Converter. Opt. Express 2021, 29, 13246–13255. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, C.; Wang, K.; Zhang, M.; Ma, X.; Liu, Y.; Lu, Q.; Guo, W. Narrow-Linewidth Thermally Tuned Multi-Channel Interference Widely Tunable Semiconductor Laser with Thermal Tuning Power below 50 mW. Photonics Res. 2020, 8, 671–676. [Google Scholar] [CrossRef]
- Otuya, D.O.; Kasai, K.; Hirooka, T.; Yoshida, M.; Nakazawa, M. 1.92 Tbit/s, 64 QAM Coherent Nyquist Pulse Transmission over 150 km with a Spectral Efficiency of 7.5 Bit/s/Hz. In Proceedings of the OFC 2014, San Francisco, CA, USA, 9–13 March 2014; IEEE: New York, NY, USA, 2014; pp. 1–3. [Google Scholar]
- Schuh, K.; Buchali, F.; Idler, W.; Eriksson, T.A.; Schmalen, L.; Templ, W.; Altenhain, L.; Dümler, U.; Schmid, R.; Möller, M. Single Carrier 1.2 Tbit/s Transmission over 300 Km with PM-64 QAM at 100 Gbaud. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017; Optica Publishing Group: Washington, DC, USA, 2017; p. Th5B.5. [Google Scholar]
- Kazovsky, L. Performance Analysis and Laser Linewidth Requirements for Optical PSK Heterodyne Communications Systems. J. Light. Technol. 1986, 4, 415–425. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Kavanagh, N.; Zhao, J.; Ye, N.; Chen, Y.; Wheeler, N.V.; Wooler, J.P.; Hayes, J.R.; Sandoghchi, S.R.; et al. 81 Gb/s WDM Transmission at 2μm over 1.15 km of Low-Loss Hollow Core Photonic Bandgap Fiber. In Proceedings of the 2014 the European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014. [Google Scholar]
- Gwyn, S.; Watson, S.; Slight, T.; Knapp, M.; Viola, S.; Ivanov, P.; Zhang, W.; Yadav, A.; Rafailov, E.; Haji, M.; et al. Dynamic Device Characteristics and Linewidth Measurement of InGaNGaN Laser Diodes. IEEE Photonics J. 2021, 13, 1500510. [Google Scholar] [CrossRef]
- Ip, E.; Kahn, J.M. Addendum to “Feedforward Carrier Recovery for Coherent Optical Communications”. J. Light. Technol. 2009, 27, 2552–2553. [Google Scholar] [CrossRef]
- Pfau, T.; Hoffmann, S.; Noe, R. Hardware-Efficient Coherent Digital Receiver Concept with Feedforward Carrier Recovery for M-QAM Constellations. J. Light. Technol. 2009, 27, 989–999. [Google Scholar] [CrossRef]
- Kikuchi, K. Fundamentals of Coherent Optical Fiber Communications. J. Light. Technol. 2016, 34, 157–179. [Google Scholar] [CrossRef]
- Nakazawa, M.; Okamoto, S.; Omiya, T.; Kasai, K.; Yoshida, M. 256 QAM (64 Gbit/s) Coherent Optical Transmission over 160 km with an Optical Bandwidth of 5.4 GHz. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 21–25 March 2010; Optica Publishing Group: Washington, DC, USA, 2010; p. OMJ5. [Google Scholar]
- Ip, E.; Kahn, J. Carrier Synchronization for 3-and 4-Bit-per-Symbol Optical Transmission. J. Light. Technol. 2005, 23, 4110–4124. [Google Scholar] [CrossRef]
- Barry, J.R.; Kahn, J.M. Carrier Synchronization for Homodyne and Heterodyne Detection of Optical Quadriphase-Shift Keying. J. Light. Technol. 1992, 10, 1939–1951. [Google Scholar] [CrossRef]
- Al-Dabbagh, M.D.; Smith, J.; Kleine-Ostmann, T.; Naftaly, M.; Fatadin, I. Characterization of Photonic-Assisted Free-Space Sub-THz Data Transmission. In Proceedings of the 2023 48th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Montreal, QC, Canada, 17–22 September 2023; IEEE: New York, NY, USA, 2023. [Google Scholar]
- Chen, Z.; Wang, K.; Chen, Q.; Jiang, C.; Wei, Y.; Liu, H.; Lu, M.; Lu, Q.; Guo, W. Nano-ITLA Based on Thermo-Optically Tuned Multi-Channel Interference Widely Tunable Laser. J. Light. Technol. 2023, 41, 5405–5411. [Google Scholar] [CrossRef]
- Seimetz, M. Osa Laser Linewidth Limitations for Optical Systems with High-Order Modulation Employing Feed Forward Digital Carrier Phase Estimation. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 February 2008; pp. 2470–2472. [Google Scholar]
- Li, M.; Guo, Y.; Wang, X.; Fu, W.; Zhang, Y.; Wang, Y. Researching Pointing Error Effect on Laser Linewidth Tolerance in Space Coherent Optical Communication Systems. Opt. Express 2022, 30, 5769–5787. [Google Scholar] [CrossRef] [PubMed]
- Lowery, A.J. Amplified-Spontaneous Noise Limit of Optical OFDM Lightwave Systems. Opt. Express 2008, 16, 860–865. [Google Scholar] [CrossRef] [PubMed]
- Ferrero, V.; Camatel, S. Optical Phase Locking Techniques: An Overview and a Novel Method Based on Single Side Sub-Carrier Modulation. Opt. Express 2008, 16, 818–828. [Google Scholar] [CrossRef]
- Li, Y.; Lin, X.; Yang, Y.; Xia, Y.; Xiong, J.; Song, S.; Liu, L.; Chen, Z.; Cheng, X.; Li, F. Temperature Characteristics at Altitudes of 5–80 km with a Self-Calibrated Rayleigh–Rotational Raman Lidar: A Summer Case Study. J. Quant. Spectrosc. Radiat. Transf. 2017, 188, 94–102. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, Z.L.; Cheng, X.W.; Yang, G.T.; Du, L.F.; Wang, J.H.; Yang, Y.; Li, Y.J.; Xiong, J.; Li, F.Q.; et al. All-Solid-State Narrowband Sodium Lidar System and Preliminary Result. Chin. J. Lasers 2015, 42, S113003. [Google Scholar] [CrossRef]
- Yang, F.; Ye, Q.; Pan, Z.; Chen, D.; Cai, H.; Qu, R.; Yang, Z.; Zhang, Q. 100-mW Linear Polarization Single-Frequency All-Fiber Seed Laser for Coherent Doppler Lidar Application. Opt. Commun. 2012, 285, 149–152. [Google Scholar] [CrossRef]
- Hostetler, C.A.; Behrenfeld, M.J.; Hu, Y.; Hair, J.W.; Schulien, J.A. Spaceborne Lidar in the Study of Marine Systems. In Annual Review of Marine Science; Carlson, C., Giovannoni, S., Eds.; Annual Review: San Mateo, CA, USA, 2018; Volume 10, pp. 121–147. ISBN 1941-1405. [Google Scholar]
- Edner, H.; Sunesson, A.; Svanberg, S. NO Plume Mapping by Laser-Radar Techniques. Opt. Lett. 1988, 13, 704–706. [Google Scholar] [CrossRef]
- Carlson, C.G.; Dragic, P.D.; Price, R.K.; Coleman, J.J.; Swenson, G.R. A Narrow-Linewidth, Yb Fiber-Amplifier-Based Upper Atmospheric Doppler Temperature Lidar. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 451–461. [Google Scholar] [CrossRef]
- Geng, J.; Spiegelberg, C.; Jiang, S. Narrow Linewidth Fiber Laser for 100-km Optical Frequency Domain Reflectometry. Photonics Technol. Lett. IEEE 2005, 17, 1827–1829. [Google Scholar] [CrossRef]
- Hu, X.; Yan, Z.A.; Guo, S.Y.; Cheng, Y.Q.; Gong, J.C. Sodium Fluorescence Doppler Lidar to Measure Atmospheric Temperature in the Mesopause Region. Chin. Sci. Bull. 2011, 56, 417–423. [Google Scholar] [CrossRef]
- Li, T.; Fang, X.; Liu, W.; Gu, S.-Y.; Dou, X. Narrowband Sodium Lidar for the Measurements of Mesopause Region Temperature and Wind. Appl. Opt. 2012, 51, 5401–5411. [Google Scholar] [CrossRef]
- Chen, T.-H.; Huang, C.-Y.; Shia, T.K.; Wun, S.-J.; Hsu, C.-H.; Ku, K.-N.; Lee, C.-S.; Lin, C.-Y.; Chang, P.-C.; Wang, C.-C. A Frequency Digital Pre-Distortion Compensation Method for FMCW LiDAR System. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 8–12 March 2020; Optica Publishing Group: Washington, DC, USA, 2020; p. Th2A.23. [Google Scholar]
- Sun, J.; Hosseini, E.S.; Yaacobi, A.; Cole, D.B.; Leake, G.; Coolbaugh, D.; Watts, M.R. Two-Dimensional Apodized Silicon Photonic Phased Arrays. Opt. Lett. 2014, 39, 367–370. [Google Scholar] [CrossRef] [PubMed]
- Suh, M.-G.; Vahala, K.J. Soliton Microcomb Range Measurement. Science 2018, 359, 884–887. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hua, Z.; Shi, J.; Dai, Z.; Wang, J.; Shao, L.; Tan, Y. Laser Feedback Frequency-Modulated Continuous-Wave LiDAR and 3-D Imaging. IEEE Trans. Instrum. Meas. 2023, 72, 9. [Google Scholar] [CrossRef]
- Liu, C.; Guo, Y.; Zhou, Y.; Li, X.; Lu, L.; Li, Y.; Bao, W.; Chen, J.; Zhou, L. Fast-tuning and Narrow-linewidth Hybrid Laser for FMCW Ranging. Laser Photonics Rev. 2025, 19, 2401338. [Google Scholar] [CrossRef]
- Morton, P.A.; Xiang, C.; Khurgin, J.B.; Morton, C.D.; Tran, M.; Peters, J.; Guo, J.; Morton, M.J.; Bowers, J.E. Integrated Coherent Tunable Laser (ICTL) with Ultra-Wideband Wavelength Tuning and Sub-100 Hz Lorentzian Linewidth. J. Light. Technol. 2022, 40, 1802–1809. [Google Scholar] [CrossRef]
- Li, B.; Luo, S.; Yu, A.; Gao, J.; Sun, P.; Wang, X.; Zuo, D. Sensitive Raman Gas Analysis Using a 500 mW External Cavity Diode Laser at 410 nm. Laser Phys. Lett. 2017, 14, 95701. [Google Scholar] [CrossRef]
- Al-Taiy, H.; Wenzel, N.; PreußLer, S.; Klinger, J.; Schneider, T. Ultra-Narrow Linewidth, Stable and Tunable Laser Source for Optical Communication Systems and Spectroscopy. Opt. Lett. 2014, 39, 5826–5829. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Pilgram, N.H.; Kłos, J.; Kotochigova, S.; Hutzler, N.R. Enhanced Molecular Yield from a Cryogenic Buffer Gas Beam Source via Excited State Chemistry. New J. Phys. 2020, 22, 22002. [Google Scholar] [CrossRef]
- Mitra, D.; Vilas, N.B.; Hallas, C.; Anderegg, L.; Augenbraun, B.L.; Baum, L.; Miller, C.; Raval, S.; Doyle, J.M. Direct Laser Cooling of a Symmetric Top Molecule. Science 2020, 369, 1366–1369. [Google Scholar] [CrossRef]
- Anderegg, L.; Cheuk, L.W.; Bao, Y.; Burchesky, S.; Ketterle, W.; Ni, K.-K.; Doyle, J.M. An Optical Tweezer Array of Ultracold Molecules. Science 2019, 365, 1156–1158. [Google Scholar] [CrossRef] [PubMed]
- Feng, K.; Cui, J.; Dang, H.; Zhao, S.; Wu, W.; Tan, J. Investigation and Development of a High Spectral Resolution Coherent Optical Spectrum Analysis System. Opt. Express 2016, 24, 25389–25402. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Jiang, T.; Teng, L.; Zhang, H.; Chen, L.; Bao, X.; Lu, Z. Sub-MHz Ultrahigh-Resolution Optical Spectrometry Based on Brillouin Dynamic Gratings. Opt. Lett. 2014, 39, 2967–2970. [Google Scholar] [CrossRef] [PubMed]
- Verma, M.; Jayich, A.M.; Vutha, A.C. Electron Electric Dipole Moment Searches Using Clock Transitions in Ultracold Molecules. Phys. Rev. Lett. 2020, 125, 153201. [Google Scholar] [CrossRef]
- Yu, P.; Hutzler, N.R. Probing Fundamental Symmetries of Deformed Nuclei in Symmetric Top Molecules. Phys. Rev. Lett. 2021, 126, 023003. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine; Division on Engineering and Physical Sciences; Board on Physics and Astronomy; Committee on Decadal Assessment and Outlook Report on Atomic, Molecular, and Optical Science. Manipulating Quantum Systems: An Assessment of Atomic, Molecular, and Optical Physics in the United States; National Academies Press: Washington, DC, USA, 2020; ISBN 0-309-49951-8. [Google Scholar]
- Wang, J.; Qi, K.Q.; Wang, S.X.; Gao, R.; Li, P.; Yang, R.; Liu, H.; Luo, Z. Advance and prospect in the study of laser interferometry technology for space gravitational wave detection. Sci. Sin-Phys Mech. Astron. 2024, 54, 109–127. (In Chinese) [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C. Binary Black Hole Population Properties Inferred from the First and Second Observing Runs of Advanced LIGO and Advanced Virgo. Astrophys. J. Lett. 2019, 882, L24. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 31040. [Google Scholar] [CrossRef]
- Kapasi, D.P.; Eichholz, J.; McRae, T.; Ward, R.L.; Slagmolen, B.J.J.; Legge, S.; Hardman, K.S.; Altin, P.A.; McClelland, D.E. Tunable Narrow-Linewidth Laser at 2 μm Wavelength for Gravitational Wave Detector Research. Opt. Express 2020, 28, 3280–3288. [Google Scholar] [CrossRef] [PubMed]
- Harry, G.M.; LIGO Sci Collaboration. Advanced LIGO: The next Generation of Gravitational Wave Detectors. Class. Quantum Gravity 2010, 27, 084006. [Google Scholar] [CrossRef]
- Kwee, P.; Bogan, C.; Danzmann, K.; Frede, M.; Kim, H.; King, P.; Poeld, J.; Puncken, O.; Savage, R.L.; Seifert, F.; et al. Stabilized High-Power Laser System for the Gravitational Wave Detector Advanced LIGO. Opt. Express 2012, 20, 10617–10634. [Google Scholar] [CrossRef]
- Nicholson, T.L.; Campbell, S.L.; Hutson, R.B.; Marti, G.E.; Bloom, B.J.; McNally, R.L.; Zhang, W.; Barrett, M.D.; Safronova, M.S.; Strouse, G.F.; et al. Systematic Evaluation of an Atomic Clock at 2 × 10−18 Total Uncertainty. Nat. Commun. 2015, 6, 6896. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical Atomic Clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Bloom, B.J.; Nicholson, T.L.; Williams, J.R.; Campbell, S.L.; Bishof, M.; Zhang, X.; Zhang, W.; Bromley, S.L.; Ye, J. An Optical Lattice Clock with Accuracy and Stability at the 10−18 Level. Nature 2014, 506, 71–75. [Google Scholar] [CrossRef]
- Ushijima, I.; Takamoto, M.; Das, M.; Ohkubo, T.; Katori, H. Cryogenic Optical Lattice Clocks. Nat. Photonics 2015, 9, 185–189. [Google Scholar] [CrossRef]
- Huntemann, N.; Sanner, C.; Lipphardt, B.; Tamm, C.; Peik, E. Single-Ion Atomic Clock with 3 × 10−18 Systematic Uncertainty. Phys. Rev. Lett. 2016, 116, 63001. [Google Scholar] [CrossRef]
- Takamoto, M.; Takano, T.; Katori, H. Frequency Comparison of Optical Lattice Clocks beyond the Dick Limit. Nat. Photonics 2011, 5, 288–292. [Google Scholar] [CrossRef]
- Young, A.W.; Eckner, W.J.; Milner, W.R.; Kedar, D.; Norcia, M.A.; Oelker, E.; Schine, N.; Ye, J.; Kaufman, A.M. Half-Minute-Scale Atomic Coherence and High Relative Stability in a Tweezer Clock. Nature 2020, 588, 408–413. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Drake, T.; Stone, J.R.; Briles, T.C.; Spencer, D.T.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R. Architecture for the Photonic Integration of an Optical Atomic Clock. Optica 2019, 6, 680–685. [Google Scholar] [CrossRef]
- Zhu, T.; He, Q.; Xiao, X.; Bao, X. Modulated Pulses Based Distributed Vibration Sensing with High Frequency Response and Spatial Resolution. Opt. Express 2013, 21, 2953–2963. [Google Scholar] [CrossRef] [PubMed]
- Juarez, J.C.; Taylor, H.F. Field Test of a Distributed Fiber-Optic Intrusion Sensor System for Long Perimeters. Appl. Opt. 2007, 46, 1968–1971. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Du, Y.; Ding, Z.; Liu, K.; Zhou, Y.; Jiang, J. 40-km OFDR-Based Distributed Disturbance Optical Fiber Sensor. IEEE Photon. Technol. Lett. 2015, 28, 771–774. [Google Scholar] [CrossRef]
- Wang, Z.N.; Zeng, J.J.; Li, J.; Fan, M.Q.; Wu, H.; Peng, F.; Zhang, L.; Zhou, Y.; Rao, Y.J. Ultra-Long Phase-Sensitive OTDR with Hybrid Distributed Amplification. Opt. Lett. 2014, 39, 5866–5869. [Google Scholar] [CrossRef]
- Harris, M.; Pearson, G.; Vaughan, J.; Letalick, D.; Karlsson, C. The Role of Laser Coherence Length in Continuous-Wave Coherent Laser Radar. J. Mod. Opt. 1998, 45, 1567–1581. [Google Scholar] [CrossRef]
- Scully, M.O.; Lamb, W.E. Quantum Theory of an Optical Maser. I. General Theory. Phys. Rev. 1967, 159, 208–226. [Google Scholar] [CrossRef]
- Krawinkel, T. Improved GNSS Navigation with Chip-Scale Atomic Clocks; Verlag der Bayerischen Akademie der Wissenschaften: Munich, Germany, 2018; ISBN 3-7696-5235-5. [Google Scholar]
- Henderson, S.W.; Suni, P.J.; Hale, C.P.; Hannon, S.M.; Magee, J.R.; Bruns, D.L.; Yuen, E.H. Coherent Laser Radar at 2 mu m Using Solid-State Lasers. IEEE Trans. Geosci. Remote Sens. 1993, 31, 4–15. [Google Scholar] [CrossRef]
- Koch, G.J.; Beyon, J.Y.; Barnes, B.W.; Petros, M.; Yu, J.; Amzajerdian, F.; Kavaya, M.J.; Singh, U.N. High-Energy 2 μm Doppler Lidar for Wind Measurements. Opt. Eng. 2007, 46, 116201. [Google Scholar] [CrossRef]
- Koch, G.J.; Beyon, J.Y.; Petzar, P.J.; Petros, M.; Yu, J.; Trieu, B.C.; Kavaya, M.J.; Singh, U.N.; Modlin, E.A.; Barnes, B.W.; et al. Field Testing of a High-Energy 2-μm Doppler Lidar. J. Appl. Remote Sens. 2010, 4, 043512. [Google Scholar] [CrossRef]
- Fan, Y.; Oldenbeuving, R.M.; Roeloffzen, C.G.; Hoekman, M.; Geskus, D.; Heideman, R.G.; Boller, K.-J. 290 Hz Intrinsic Linewidth from an Integrated Optical Chip-Based Widely Tunable InP-Si3N4 Hybrid Laser. In Proceedings of the 2017 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 14–19 May 2017; IEEE: New York, NY, USA, 2017; pp. 1–2. [Google Scholar]
- Sun, G.W.; Wei, F.; Zhang, L. Low-Noise External Cavity Semiconductor Lasers Based on Polarization-Maintaining Fiber Bragg Gratings. Chin. J. Laser 2018, 45, 0601004. [Google Scholar]
- Fan, Y.; Epping, J.P.; Oldenbeuving, R.M.; Roeloffzen, C.G.; Hoekman, M.; Dekker, R.; Heideman, R.G.; van der Slot, P.J.; Boller, K.-J. Optically Integrated InP-Si3N4 Hybrid Laser. IEEE Photonics J. 2016, 8, 1505111. [Google Scholar] [CrossRef]
- Ding, D.; Lv, X.; Chen, X.; Wang, F.; Zhang, J.; Che, K. Tunable High-Power Blue External Cavity Semiconductor Laser. Opt. Laser Technol. 2017, 94, 1–5. [Google Scholar] [CrossRef]
- Yu, L.; Lu, D.; Pan, B.; Zhang, L.; Guo, L.; Li, Z.; Zhao, L.J. Widely Tunable Narrow-Linewidth Lasers Using Self-Injection DBR Lasers. IEEE Photonics Technol. Lett. 2014, 27, 50–53. [Google Scholar] [CrossRef]
- Shin, D.K.; Henson, B.M.; Khakimov, R.I.; Ross, J.A.; Dedman, C.J.; Hodgman, S.S.; Baldwin, K.G.H.; Truscott, A.G. Widely Tunable, Narrow Linewidth External-Cavity Gain Chip Laser for Spectroscopy between 1.0-1.1 μm. Opt. Express 2016, 24, 27403–27414. [Google Scholar] [CrossRef]
- Luvsandamdin, E.; Spieberger, S.; Schiemangk, M.; Sahm, A.; Mura, G.; Wicht, A.; Peters, A.; Erbert, G.; Trankle, G. Development of Narrow Linewidth, Micro-Integrated Extended Cavity Diode Lasers for Quantum Optics Experiments in Space. Appl. Phys. B 2013, 111, 255–260. [Google Scholar] [CrossRef]
- Aoyama, K.; Yoshioka, R.; Yokota, N.; Kobayashi, W.; Yasaka, H. Experimental Demonstration of Linewidth Reduction of Laser Diode by Compact Coherent Optical Negative Feedback System. Appl. Phys. Express 2014, 7, 122701. [Google Scholar] [CrossRef]
- Guo, Y.; Li, X.; Xu, W.; Liu, C.; Jin, M.; Lu, L.; Xie, J.; Stroganov, A.; Chen, J.; Zhou, L. A Hybrid-Integrated External Cavity Laser with Ultra-Wide Wavelength Tuning Range and High Side-Mode Suppression. In Proceedings of the 2022 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 6–10 March 2022; IEEE: New York, NY, USA, 2022; pp. 1–3. [Google Scholar]
- Daiber, A. Narrow-Linewidth Tunable External Cavity Laser for Coherent Communication. In Proceedings of the 2014 IEEE Photonics Conference, San Diego, CA, USA, 12–16 October 2014; IEEE: New York, NY, USA, 2014; pp. 447–448. [Google Scholar]
- Guo, Y.; Li, X.; Jin, M.; Lu, L.; Xie, J.; Chen, J.; Zhou, L. Hybrid Integrated External Cavity Laser with a 172-nm Tuning Range. APL Photonics 2022, 7, 066101. [Google Scholar] [CrossRef]
- Tang, L.; Yang, S.; Chen, H.; Chen, M. Hybrid Integrated Low Noise Optical Phase-Locked Loop Based on Self-Injection Locked Semiconductor Laser. J. Light. Technol. 2021, 40, 2033–2039. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, L.; Xie, W.; Cheng, R.; Liu, Z.; Wei, W.; Dong, Y. Ultra-Long Range Optical Frequency Domain Reflectometry Using a Coherence-Enhanced Highly Linear Frequency-Swept Fiber Laser Source. Opt. Express 2019, 27, 19359–19368. [Google Scholar] [CrossRef] [PubMed]
- Binaie, A.; Ahasan, S.; Krishnaswamy, H. A Spurless and Wideband Continuous-Time Electro-Optical Phase Locked Loop (CT-EOPLL) for High Performance LiDAR. IEEE Open J. Solid-State Circuits Soc. 2021, 1, 235–246. [Google Scholar] [CrossRef]
- Idjadi, M.H.; Aflatouni, F. Integrated Pound−Drever−Hall Laser Stabilization System in Silicon. Nat. Commun. 2017, 8, 1209. [Google Scholar] [CrossRef] [PubMed]
- Lihachev, G.; Riemensberger, J.; Weng, W.; Liu, J.; Tian, H.; Siddharth, A.; Snigirev, V.; Shadymov, V.; Voloshin, A.; Wang, R.N. Low-Noise Frequency-Agile Photonic Integrated Lasers for Coherent Ranging. Nat. Commun. 2022, 13, 3522. [Google Scholar] [CrossRef]
- Far Brusatori, M.; Duplat, D.N.; Degli-Eredi, I.; Nielsen, L.; Tønning, P.L.; Castera, P.; Volet, N.; Heck, M.J. Ultralow-Linewidth Ring Laser Using Hybrid Integration and Generic Foundry Platforms. Opt. Lett. 2022, 47, 2686–2689. [Google Scholar] [CrossRef]
- Snigirev, V.; Riedhauser, A.; Lihachev, G.; Churaev, M.; Riemensberger, J.; Wang, R.N.; Siddharth, A.; Huang, G.; Möhl, C.; Popoff, Y. Ultrafast Tunable Lasers Using Lithium Niobate Integrated Photonics. Nature 2023, 615, 411–417. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Chen, X.; Jiang, D.; Huang, J. Fabrication of Distributed Feedback Bragg Fiber Laser on Regular Er-Doped Fiber. Chin. J. Lasers 2006, 33, 873–876. [Google Scholar]
- Hill, K.O.; Bilodeau, F.; Malo, B.; Kitagawa, T.; Theriault, S.; Johnson, D.C.; Albert, J.; Takiguchi, K. Chirped In-Fiber Bragg Gratings for Compensation of Optical-Fiber Dispersion. Opt. Lett. 1994, 19, 1314–1316. [Google Scholar] [CrossRef]
- Hill, K.O.; Malo, B.; Bilodeau, F.; Johnson, D.C.; Albert, J. Bragg Gratings Fabricated in Monomode Photosensitive Optical Fiber by UV Exposure through a Phase Mask. Appl. Phys. Lett. 1993, 62, 1035–1037. [Google Scholar] [CrossRef]
- Song, Z.; Qi, H.; Peng, G.; Li, S.; Guo, J.; Wang, C. Research on Fabrication Technology of Fiber Bragg Grating by Phase Mask Moving. J. Optoelectron. 2014, 25, 1294–1297. [Google Scholar]
- Song, Z.; Wang, W.; Qi, H.; Guo, J.; Ni, J.; Wang, C. Packaging Technology of Distributed Feedback Fiber Laser. Acta Photonica Sin. 2016, 45, 0814005. [Google Scholar] [CrossRef]
- Vivek, K.; Rajesh, R.; Sreehari, C.V.; Kumar, S.S.; Shajahan, K.; Praveen, T.V.; Santhanakrishnan, T.; Moosad, K.P.B. A New Approach of Large Diameter Polymer-Coated Fiber Laser Hydrophone. J. Light. Technol. 2017, 35, 4097–4104. [Google Scholar] [CrossRef]
- Launay, F.-X.; Bouffaron, R.; Lardat, R.; Roux, G.; Doisy, M.; Bergogne, C. Acoustic Antenna Based on Fiber Laser Hydrophones; LopezHiguera, J., Jones, J., LopezAmo, M., Santos, J., Eds.; SPIE: Bellingham, WA, USA, 2014; Volume 9157. [Google Scholar]
- Ishii, H.; Kasaya, K.; Oohashi, H. Narrow Spectral Linewidth Operation (<160 kHz) in Widely Tunable Distributed Feedback Laser Array. Electron. Lett. 2010, 46, 714–715. [Google Scholar] [CrossRef]
- Kasukawa, A.; Mukaihara, T. High Power, Narrow Linewidth Tunable Lasers. In Proceedings of the 2014 OptoElectronics and Communication Conference and Australian Conference on Optical Fibre Technology, Melbourne, Australia, 6–10 July 2014; IEEE: New York, NY, USA, 2014; pp. 965–966. [Google Scholar]
- Panyaev, I.S.; Itrin, P.A.; Korobko, D.A.; Fotiadi, A.A. Sub-100-Hz DFB Laser Injection-Locked to PM Fiber Ring Cavity. Light. Technol. IEEE/OSA J. Light. Technol. 2024, 42, 2928–2937. [Google Scholar] [CrossRef]
- Yang, D.; Yan, F.; Feng, T. Narrow-Linewidth and Low RIN Tm/Ho Co-Doped Fiber Laser Based on Self-Injection Locking. Opt. Express 2024, 32, 12172–12180. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Xiong, B.; Sun, C.; Ke, X.; Hao, Z.; Wang, L.; Wang, J.; Han, Y.; Li, H.; Luo, Y. Laser Frequency Noise Characterization by Self-Heterodyne with Both Long and Short Delay. Appl. Opt. 2019, 58, 3555–3563. [Google Scholar] [CrossRef]
- Li, Y.; Fu, Z.; Zhu, L.; Fang, J.; Zhu, H.; Zhong, J.; Xu, P.; Chen, X.; Wang, J.; Zhan, M. Laser Frequency Noise Measurement Using an Envelope-Ratio Method Based on a Delayed Self-Heterodyne Interferometer. Opt. Commun. 2019, 435, 244–250. [Google Scholar] [CrossRef]
- Gundavarapu, S.; Brodnik, G.M.; Puckett, M.; Huffman, T.; Bose, D.; Behunin, R.; Wu, J.; Qiu, T.; Pinho, C.; Chauhan, N.; et al. Sub-Hertz Fundamental Linewidth Photonic Integrated Brillouin Laser. Nat. Photonics 2019, 13, 60–67. [Google Scholar] [CrossRef]
- Day, T.; Gustafson, E.K. Sub-Hertz Relative Frequency Stabilization of Two-Diode Laser-Pumped Nd:YAG Lasers Locked to a Fabry-Perot Interferometer. IEEE J. Quantum Electron. 1992, 28, 1106–1117. [Google Scholar] [CrossRef]
- Sane, S.S.; Bennetts, S.; Debs, J.E.; Kuhn, C.C.N.; McDonald, G.D.; Altin, P.A.; Close, J.D.; Robins, N.P. 11 W Narrow Linewidth Laser Source at 780nm for Laser Cooling and Manipulation of Rubidium. Opt. Express 2012, 20, 8915–8919. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Qi, Y.; Ding, Y.; Zhou, J.; Dong, J.; Wei, Y.; Lou, Q. All-Fiber, High Power Single-Frequency Linearly Polarized Ytterbium-Doped Fiber Amplifier. Chin. Opt. Lett. 2011, 9, 031402. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, J.; Bi, D.; Zhou, J.; Diao, W.; Chen, W. Development of All-Solid Coherent Doppler Wind Lidar. Chin. Opt. Lett. 2012, 10, 012801. [Google Scholar] [CrossRef]
- Jiang, M.; Xu, H.; Zhou, P.; Zhao, G.; Gu, X. All-Fiber, Narrow Linewidth and Linearly Polarized Fiber Laser in a Single-Mode-Multimode-Single-Mode Cavity. Appl. Opt. 2016, 55, 6121–6124. [Google Scholar] [CrossRef]
- Wright, M.W.; Yao, H.; Marciante, J.R. Resonant Pumping of Er-Doped Fiber Amplifiers for Improved Laser Efficiency in Free-Space Optical Communications. NASA/JPL Interplanet. Netw. (IPN) Prog. Rep. 2012, 42–189, 1–20. [Google Scholar]
- Psaltis, D. Coherent Optical Information Systems. Science 2002, 298, 1359–1363. [Google Scholar] [CrossRef]
- Ricciardi, I.; De Tommasi, E.; Maddaloni, P.; Mosca, S.; Rocco, A.; Zondy, J.-J.; De Rosa, M.; De Natale, P. A Narrow-Linewidth, Frequency-Stabilized OPO for Sub-Doppler Molecular Spectroscopy around 3 μm. In Proceedings of the Nonlinear Optics and Applications VI, Brussels, Belgium, 16–18 April 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8434, pp. 389–397. [Google Scholar]
- Li, C.; Xu, S.; Feng, Z.; Xiao, Y.; Mo, S.; Yang, C.; Zhang, W.; Chen, D.; Yang, Z. The ASE Noise of a Yb3+-Doped Phosphate Fiber Single-Frequency Laser at 1083 nm. Laser Phys. Lett. 2014, 11, 025104. [Google Scholar] [CrossRef]
- Li, C.; Xu, S.; Yang, C.; Wei, X.; Yang, Z. Frequency Noise of High-Gain Phosphate Fiber Single-Frequency Laser. Laser Phys. 2013, 23, 045107. [Google Scholar] [CrossRef]
- Ronnekleiv, E. Frequency and Intensity Noise of Single Frequency Fiber Bragg Grating Lasers. Opt. Fiber Technol. 2001, 7, 206–235. [Google Scholar] [CrossRef]
- Foster, S.; Tikhomirov, A.; Milnes, M. Fundamental Thermal Noise in Distributed Feedback Fiber Lasers. IEEE J. Quantum Electron. 2007, 43, 378–384. [Google Scholar] [CrossRef]
- Ma, L.; Hu, Z.; Liang, X.; Meng, Z.; Hu, Y. Relaxation Oscillation in Er3+-Doped and Yb3+/Er3+ Co-Doped Fiber Grating Lasers. Appl. Opt. 2010, 49, 1979–1985. [Google Scholar] [CrossRef]
- Gordon, J.P.; Zeiger, H.J.; Townes, C.H. The Maser—New Type of Microwave Amplifier, Frequency Standard, and Spectrometer. Phys. Rev. 1955, 99, 1264–1274. [Google Scholar] [CrossRef]
- Henry, C. Theory of the Linewidth of Semiconductor Lasers. IEEE J. Quantum Electron. 1982, 18, 259–264. [Google Scholar] [CrossRef]
- Haken, H. Theory of Intensity and Phase Fluctuations of a Homogeneously Broadened Laser. Z. Für Phys. 1966, 190, 327–356. [Google Scholar] [CrossRef]
- Lax, M. Quantum Noise v: Phase Noise in a Homogeneously Broadened Maser. Phys. Quantum Electron. 1966, 65, 735. [Google Scholar]
- Manes, K.R.; Siegman, A.E. Observation of Quantum Phase Fluctuations in Infrared Gas Lasers. Phys. Rev. A 1971, 4, 373–386. [Google Scholar] [CrossRef]
- Zhu, T.; Wei, D.; Shi, L.; Huang, L.; Li, J.; Xu, M. Research Progress in Narrow Linewidth Laser Technology (Invited). Laser Optoelectron. Prog. 2024, 61, 0114003. [Google Scholar] [CrossRef]
- Hao, S.; Jian-Wen, H.; Xiang, X.; Tao, L.I. Design of Digital Frequency Multiplier for near Infrared and Visible Light Fourier Transform Spectrometer. Infrared 2014, 35, 29–33. [Google Scholar]
- Hongbo, W. Research on In-Orbit Spectral Calibration and Polarization Correction Technology of Visible/near-Infrared Push Broom Imaging Spectrometer. Ph.D. Thesis, Graduate School of Chinese Academy of Sciences (Shanghai Institute of Technical Physics), Shanghai, China, 2016. [Google Scholar]
- Yin, Y. Research on High Precision CCD Circuit System of Portable Raman Spectrometer. Master’s Thesis, Zhejiang University, Hangzhou, China, 2014. [Google Scholar]
- Zheng, Y.; Han, Z.; Li, Y.; Li, F.; Wang, H.; Zhu, R. 3.1 kW 1050 nm Narrow Linewidth Pumping-Sharing Oscillator-Amplifier with an Optical Signal-to-Noise Ratio of 45.5 dB. Opt. Express 2022, 30, 12670–12683. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Peng, W.; Feng, Y.; Wang, J.; Ma, Y.; Gao, Q.; Zhu, R.; Tang, C. 3.25 kW All-Fiberized and Polarization-Maintained Yb-Doped Amplifier with a 20 GHz Linewidth and near-Diffraction-Limited Beam Quality. Appl. Opt. 2021, 60, 6331–6336. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Ma, Y.; Chang, Z.; Peng, W.; Sun, Y.; Gao, Q.; Zhu, R.; Tang, C. 2.5 kW Narrow Linewidth Linearly Polarized All-Fiber MOPA with Cascaded Phase-Modulation to Suppress SBS Induced Self-Pulsing. IEEE Photon. J. 2020, 12, 1502815. [Google Scholar] [CrossRef]
- Bradberry, G.W.; Vaughan, J.M. Measurement of Narrow Linewidth with a Fabry-Perot Interferometer of Limited Resolution. Opt. Commun. 1977, 20, 307–310. [Google Scholar] [CrossRef]
- Takakura, T.; Iga, K.; Tako, T. Linewidth Measurement of a Single Longitudinal Mode AlGaAs Laser with a Fabry-Perot Interferometer. Jpn. J. Appl. Phys. 1980, 19, L725. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Mukai, T.; Saito, S. Quantum Phase Noise and Linewidth of a Semiconductor Laser. Electron. Lett. 1981, 17, 327–329. [Google Scholar] [CrossRef]
- Fleming, M.; Mooradian, A. Spectral Characteristics of External-Cavity Controlled Semiconductor Lasers. IEEE J. Quantum Electron. 1981, 17, 44–59. [Google Scholar] [CrossRef]
- Goodno, G.D.; Book, L.D.; Rothenberg, J.E. Low-Phase-Noise, Single-Frequency, Single-Mode 608 W Thulium Fiber Amplifier. Opt. Lett. 2009, 34, 1204–1206. [Google Scholar] [CrossRef]
- Drever, R.W.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser Phase and Frequency Stabilization Using an Optical Resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Shaykin, A.A.; Burdonov, K.F.; Khazanov, E.A. A Novel Technique for Longitudinal Mode Selection in Q-Switched Lasers. Laser Phys. Lett. 2015, 12, 125001. [Google Scholar] [CrossRef]
- Yang, X.; Li, Z.; Li, H.; Zhou, J.; Zhong, Y. Investigation on the Entrance Slit Width and Exit Slit Width of Grating Spectrometer on the Measured Spectral Line Width. J. Jiaying Univ. (Nat. Sci.) 2008, 26, 38–41. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Q.; Tang, Y.; Yan, X. Spectral Linewidth Measurement Enhancement by Two United Spectrometers. Acta Opt. Sin. 2008, 28, 710–714. [Google Scholar] [CrossRef]
- Liu, M.; Yang, M.; Zhu, J.; Zhu, H.; Wang, Y.; Ren, Z.; Zhai, Y.; Zhu, H.; Shan, Y.; Qi, H.; et al. High-Sensitivity Computational Miniaturized Terahertz Spectrometer Using a Plasmonic Filter Array and a Modified Multilayer Residual CNN. Nanophotonics 2023, 12, 4375–4385. [Google Scholar] [CrossRef]
- Live Lecture Notes: Principles and Selection Guidelines for Different Types of Spectrometers. Available online: https://mp.weixin.qq.com/s/2oauTfHypSLiZei2rlgidQ (accessed on 20 February 2025).
- Yokogawa Test & Measurement Corporation. Available online: https://tmi.yokogawa.com/cn/solutions/products/optical-measuring-instruments/optical-spectrum-analyzer/ (accessed on 1 June 2025).
- Huang, W.; Xie, J.; Lu, L.; Chen, X.; Ming, H.; Lu, Y.; Wang, A. Spectrum Method of F-P Etalon Spacing High Precision Measurement. Chin. J. Lasers 2003, 30, 739–742. [Google Scholar]
- Wang, Y.; Hua, D.; Mao, J. Effect of Propagation Properties of Gaussian Beam on Fabry-Perot Etalon in Lidar. Chin. J. Lasers 2010, 37, 3013–3018. [Google Scholar] [CrossRef]
- Gao, W.; Lu, Z.W.; He, W.M.; Dong, Y.K.; Hasi, W.L.J. Characteristics of Amplified Spectrum of a Weak Frequency-Detuned Signal in a Brillouin Amplifier. Laser Part. Beams 2009, 27, 465–470. [Google Scholar] [CrossRef]
- Vorobiev, N.; Glebov, L.; Smirnov, V. Single-Frequency-Mode Q-Switched Nd:YAG and Er:Glass Lasers Controlled by Volume Bragg Gratings. Opt. Express 2008, 16, 9199–9204. [Google Scholar] [CrossRef] [PubMed]
- Mejia, E.B.; Starodumov, A.N.; Barmenkov, Y.O. Blue and Infrared Up-Conversion in Tm3+-Doped Fluorozirconate Fiber Pumped at 1.06, 1.117, and 1.18 μm. Appl. Phys. Lett. 1999, 74, 1540–1542. [Google Scholar] [CrossRef]
- Gurevich, Y.V.; Stürmer, J.; Schwab, C.; Führer, T.; Lamoreaux, S.K.; Quirrenbach, A.; Walther, T. A Laser Locked Fabry-Perot Etalon with 3 cm/s Stability for Spectrograph Calibration. Int. Soc. Opt. Photonics 2014, 9147, 2414–2430. [Google Scholar] [CrossRef]
- Thorlabs. Available online: https://www.thorlabs.com (accessed on 1 June 2025).
- Ratkoceri, J.; Batagelj, B. Injection-Locked Range and Linewidth Measurements at Different Seed-Laser Linewidths Using a Fabry-Perot Laser-Diode. Opt. Quantum Electron. 2018, 50, 402. [Google Scholar] [CrossRef]
- Hun, X.; Bai, Z.; Chen, B.; Wang, J.; Cui, C.; Qi, Y.; Ding, J.; Wang, Y.; Lu, Z. Fabry-Perot Based Short Pulsed Laser Linewidth Measurement with Enhanced Spectral Resolution. Results Phys. 2022, 37, 105510. [Google Scholar] [CrossRef]
- Hercher, M. The Spherical Mirror Fabry-Perot Interferometer. Appl. Opt. 1968, 7, 951. [Google Scholar] [CrossRef]
- Stone, J.; Marcuse, D. Ultrahigh Finesse Fiber Fabry-Perot Interferometers. J. Light. Technol. 1986, 4, 382–385. [Google Scholar] [CrossRef]
- Hsu, K.; Miller, C.M.; Miller, J.W. Speed-of-Light Effects in High-Resolution Long-Cavity Fiber Fabry–Perot Scanning Interferometers. Opt. Lett. 1993, 18, 235–237. [Google Scholar] [CrossRef]
- Xue, J.; Chen, W.; Pan, Y.; Shi, J.; Fang, Y.; Xie, H.; Xie, M.; Sun, L.; Su, B. Pulsed Laser Linewidth Measurement Using Fabry–Pérot Scanning Interferometer. Results Phys. 2016, 6, 698–703. [Google Scholar] [CrossRef]
- Hun, X.; Bai, Z.X.; Wang, J.; Chen, B.; Cui, C.; Wang, Y.; Lu, Z. Convolution Error Reduction for a Fabry–Pérot-Based Linewidth Measurement: A Theoretical and Experimental Study. Photonics 2022, 9, 1004. [Google Scholar] [CrossRef]
- Liu, W.; Hu, C.; Jiang, P.; Wu, B.; Shen, Y. Ultra-High-Resolution Spectrometry Incorporating Two-Dimension Dispersing Spectrometer and Tunable Fabry-Perot Filter. Acta Opt. Sin. 2015, 35, 063007. [Google Scholar]
- Cohen, L. Generalization of the Wiener-Khinchin Theorem. IEEE Signal Process. Lett. 1998, 5, 292–294. [Google Scholar] [CrossRef]
- Cui, M.; Huang, J.; Yang, X. Review on Methods for Laser Linewidth Measurement. Laser Optoelectron. Prog. 2021, 58, 0900005. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Z.; Qi, Y.; Ding, J.; Li, S.; Yan, X.; Wang, Y.; Lu, Z. Narrow-Linewidth Laser Linewidth Measurement Technology. Front. Phys. 2021, 9, 768165. [Google Scholar] [CrossRef]
- Mach, L. Ueber Einen Interferenzrefraktor. Z. Für Instrumentenkunde 1982, 12, 89–93. [Google Scholar]
- Okoshi, T.; Kikuchi, K.; Nakayama, A. Novel Method for High Resolution Measurement of Laser Output Spectrum. Electron. Lett. 1980, 16, 630–631. [Google Scholar] [CrossRef]
- Gallion, P.; Debarge, G. Quantum Phase Noise and Field Correlation in Single Frequency Semiconductor Laser Systems. IEEE J. Quantum Electron. 1984, 20, 343–349. [Google Scholar] [CrossRef]
- Saito, S.; Yamamoto, Y. Direct Observation of Lorentzian Lineshape of Semiconductor Laser and Linewidth Reduction with External Grating Feedback. Electron. Lett. 1981, 17, 325–327. [Google Scholar] [CrossRef]
- Richter, L.; Mandelberg, H.; Kruger, M.; McGrath, P. Linewidth Determination from Self-Heterodyne Measurements with Subcoherence Delay Times. IEEE J. Quantum Electron. 1986, 22, 2070–2074. [Google Scholar] [CrossRef]
- Peng, Y. A Novel Scheme for Hundred-Hertz Linewidth Measurements with the Self-Heterodyne Method. Chin. Phys. Lett. 2013, 30, 084208. [Google Scholar] [CrossRef]
- Yue, Y.; Qin, B.; Lv, H.; Ouyang, H. Comparison of Several Ultra-Narrow Laser Linewidth Measurement. Opt. Commun. Technol. 2013, 37, 15–17. [Google Scholar]
- Okusaga, O.; Cahill, J.; Docherty, A.; Zhou, W.; Menyuk, C.R. Guided Entropy Mode Rayleigh Scattering in Optical Fibers. Opt. Lett. 2012, 37, 683–685. [Google Scholar] [CrossRef]
- Moloney, J.V.; Newell, A.C. Nonlinear Optics. Phys. D Nonlinear Phenom. 1990, 44, 1–37. [Google Scholar] [CrossRef]
- Camatel, S.; Ferrero, V. Narrow Linewidth CW Laser Phase Noise Characterization Methods for Coherent Transmission System Applications. J. Light. Technol. 2008, 26, 3048–3055. [Google Scholar] [CrossRef]
- Murakami, M.; Saito, S. Evolution of Field Spectrum Due to Fiber-Nonlinearity-Induced Phase Noise in in-Line Optical Amplifier Systems. IEEE Photon. Technol. Lett. 1992, 4, 1269–1272. [Google Scholar] [CrossRef]
- Olivero, J.J.; Longbothum, R.L. Empirical Fits to the Voigt Line Width: A Brief Review. J. Quant. Spectrosc. Radiat. Transf. 1977, 17, 233–236. [Google Scholar] [CrossRef]
- Young, B.C.; Cruz, F.C.; Itano, W.M.; Bergquist, J.C. Visible Lasers with Subhertz Linewidths. Phys. Rev. Lett. 1999, 82, 3799. [Google Scholar] [CrossRef]
- Kessler, T.; Hagemann, C.; Grebing, C.; Legero, T.; Sterr, U.; Riehle, F.; Martin, M.J.; Chen, L.; Ye, J. A Sub-40-mHz-Linewidth Laser Based on a Silicon Single-Crystal Optical Cavity. Nat. Photonics 2012, 6, 687–692. [Google Scholar] [CrossRef]
- Lee, H.; Suh, M.-G.; Chen, T.; Li, J.; Diddams, S.A.; Vahala, K.J. Spiral Resonators for On-Chip Laser Frequency Stabilization. Nat. Commun. 2013, 4, 2468. [Google Scholar] [CrossRef]
- Kueng, A.; Thevenaz, L.; Robert, P. Telenor Laser Linewidth Determination in the Sub-Megahertz Range Using a Brillouin Fibre Laser. In Proceedings of the European Conference on Optical Communication, Oslo, Norway, 19 September 1996; pp. B305–B308. [Google Scholar]
- Dong, Y.-K.; Lu, Z.-W.; Lu, Y.-L.; He, W.-M. A New Method of Measuring Ultra-Narrow Laser Line-Width. Harbin Gongye Daxue Xuebao (J. Harbin Inst. Technol.) 2005, 37, 670–673. [Google Scholar]
- Sevillano, P.; Subías, J.; Heras, C.; Pelayo, J.; Villuendas, F. Brillouin Induced Self-Heterodyne Technique for Narrow Line Width Measurement. Opt. Express 2010, 18, 15201–15206. [Google Scholar] [CrossRef]
- Roy, A.S.; Kumar K., P. Low Jitter Measurement of Laser Linewidth Using Brillouin Induced Self-Heterodyne Method. In Proceedings of the Frontiers in Optics 2017, Washington, DC, USA, 18–21 September 2017. [Google Scholar] [CrossRef]
- Xu, Y.; Xiang, D.; Ou, Z.; Lu, P.; Bao, X. Random Fabry–Perot Resonator-Based Sub-kHz Brillouin Fiber Laser to Improve Spectral Resolution in Linewidth Measurement. Opt. Lett. 2015, 40, 1920–1923. [Google Scholar] [CrossRef]
- Boschung, J.; Thévenaz, L.; Robert, P.A. High-Accuracy Measurement of the Linewidth of a Brillouin Fibre Ring Laser. Electron. Lett. 1994, 30, 1488–1489. [Google Scholar] [CrossRef]
- Iiyama, K.; Hayashi, K. Delayed Self-Homodyne Method Using Solitary Monomode Fibre for Laser Linewidth Measurements. Electron. Lett. 1989, 25, 1589–1590. [Google Scholar] [CrossRef]
- Ludvigsen, H.; Tossavainen, M.; Kaivola, M. Laser Linewidth Measurements Using Self-Homodyne Detection with Short Delay. Opt. Commun. 1998, 155, 180–186. [Google Scholar] [CrossRef]
- Kojima, K.; Horiguchi, Y.; Koike-Akino, T.; Shimakura, Y.; Enoki, K.; Yagyu, E. Separation of Semiconductor Laser Intrinsic Linewidth and 1/f Noise Using Multiple Fiber Length for Self-Heterodyne Method. In Proceedings of the Optical Fiber Communication Conference 2015, Los Angeles, CA, USA, 22–26 March 2015. [Google Scholar]
- Chen, J.; Chen, C.; Guo, Q.; Sun, J.; Zhang, J.; Zhou, Y.; Liu, Z.; Yu, Y.; Qin, L.; Ning, Y. Linear Polarization and Narrow-Linewidth External-Cavity Semiconductor Laser Based on Birefringent Bragg Grating Optical Feedback. Opt. Laser Technol. 2024, 170, 110211. [Google Scholar] [CrossRef]
- Canagasabey, A.; Michie, A.; Canning, J.; Holdsworth, J.; Fleming, S.; Wang, H.-C.; Aslund, M.L. A Comparison of Delayed Self-Heterodyne Interference Measurement of Laser Linewidth Using Mach-Zehnder and Michelson Interferometers. Sensors 2011, 11, 9233–9241. [Google Scholar] [CrossRef]
- Chen, X.; Han, M.; Zhu, Y.; Dong, B.; Wang, A. Implementation of a Loss-Compensated Recirculating Delayed Self-Heterodyne Interferometer for Ultranarrow Laser Linewidth Measurement. Appl. Opt. 2006, 45, 7712. [Google Scholar] [CrossRef]
- Huang, S.; Zhu, T.; Liu, M.; Huang, W. Precise Measurement of Ultra-Narrow Laser Linewidths Using the Strong Coherent Envelope. Sci. Rep. 2017, 7, 41988. [Google Scholar] [CrossRef]
- Huang, S.; Zhu, T.; Cao, Z.; Liu, M.; Deng, M.; Liu, J.; Li, X. Laser Linewidth Measurement Based on Amplitude Difference Comparison of Coherent Envelope. IEEE Photonics Technol. Lett. 2016, 28, 759–762. [Google Scholar] [CrossRef]
- Bai, Q.; Yan, M.; Xue, B.; Gao, Y.; Wang, D.; Wang, Y.; Zhang, M.; Zhang, H.; Jin, B. The Influence of Laser Linewidth on the Brillouin Shift Frequency Accuracy of BOTDR. Appl. Sci. 2019, 9, 58. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, L.; Liao, Z.; Zhang, P.; Dai, S. Ultra-High Signal-to-Noise Ratio and Ultra-Narrow Linewidth Brillouin Fiber Laser for Linewidth Measurement at 2 μm. J. Light. Technol. 2025, 43, 2759–2763. [Google Scholar] [CrossRef]
- Wang, Z.; Ke, C.; Zhong, Y.; Xing, C.; Wang, H.; Yang, K.; Cui, S.; Liu, D. Ultra-Narrow-Linewidth Measurement Utilizing Dual-Parameter Acquisition through a Partially Coherent Light Interference. Opt. Express 2020, 28, 8484–8493. [Google Scholar] [CrossRef]
- Xue, M.; Zhao, J. Laser Linewidth Measurement Based on Long and Short Delay Fiber Combination. Opt. Express 2021, 29, 27118–27126. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Jiao, D.; Liu, J.; Deng, X.; Zang, Q.; Zhang, X.; Wang, D.; Zhang, X.; Liu, T. Laser Linewidth Measurement Based on Recirculating Self-Heterodyne Method with Short Fiber. Acta Opt. Sin. 2021, 41, 0712002. [Google Scholar] [CrossRef]
- Gao, J.; Jiao, D.; Deng, X.; Liu, J.; Zhang, L.; Zang, Q.; Zhang, X.; Liu, T.; Zhang, S. A Polarization-Insensitive Recirculating Delayed Self-Heterodyne Method for Sub-Kilohertz Laser Linewidth Measurement. Photonics 2021, 8, 137. [Google Scholar] [CrossRef]
- Jia, Y.; Ou, P.; Yang, Y.; Zhang, C. Short Fibre Delayed Self-Heterodyne Interferometer for Ultranarrow Laser Linewidth Measurement. J. Beijing Univ. Aeronaut. Astronaut. 2008, 34, 568. [Google Scholar]
- He, Y.; Hu, S.; Liang, S.; Li, Y. High-Precision Narrow Laser Linewidth Measurement Based on Coherent Envelope Demodulation. Opt. Fiber Technol. 2019, 50, 200–205. [Google Scholar] [CrossRef]
- Zhao, Z.; Bai, Z.; Jin, D.; Qi, Y.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z.; Mildren, R.P. Narrow Laser-Linewidth Measurement Using Short Delay Self-Heterodyne Interferometry. Opt. Express 2022, 30, 30600–30610. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Z.; Chen, X.; Qi, Y.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z.; Mildren, R.P. A Lorentzian Narrow-Linewidth Demodulation Scheme Based on a Short Fiber Delayed Self-Heterodyne Technique. Appl. Phys. Express 2022, 15, 106502. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, L.; Guan, T.; Mao, Y.; Dang, L.; Lan, T.; Shi, L.; Gao, L.; Zhu, T. Laser Coherence Linewidth Measurement Based on Deterioration of Coherent Envelope. Opt. Laser Technol. 2024, 172, 110498. [Google Scholar] [CrossRef]
- Wu, L.; Ji, Z.; Ma, W.; Su, D.; Zhao, Y.; Xiao, L.; Jia, S. Narrow Laser Linewidth Measurement with the Optimal Demodulated Lorentzian Spectrum. Appl. Opt. 2024, 63, 1847–1853. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Lu, B.; Yang, F.; Chen, D.; Cai, H.; Qu, R. Narrow Linewidth Single-Frequency Laser Noise Measurement Based on a 3 × 3 Fiber Coupler. Chin. J. Lasers 2016, 43, 0102004. [Google Scholar]
- Stéphan, G.M.; Tam, T.T.; Blin, S.; Besnard, P.; Têtu, M. Laser Line Shape and Spectral Density of Frequency Noise. Phys. Rev. A—At. Mol. Opt. Phys. 2005, 71, 43809. [Google Scholar] [CrossRef]
- Von Bandel, N.; Myara, M.; Sellahi, M.; Souici, T.; Dardaillon, R.; Signoret, P. Time-Dependent Laser Linewidth: Beat-Note Digital Acquisition and Numerical Analysis. Opt. Express 2016, 24, 27961–27978. [Google Scholar] [CrossRef]
- Bai, Y.; Yan, F.; Feng, T.; Han, W.; Zhang, L.; Cheng, D.; Bai, Z.; Wen, X. Demonstration of Linewidth Measurement Based on Phase Noise Analysis for a Single Frequency Fiber Laser in the 2 μm Band. Laser Phys. 2019, 29, 075102. [Google Scholar] [CrossRef]
- Schilt, S.; Bucalovic, N.; Tombez, L.; Dolgovskiy, V.; Schori, C.; Di Domenico, G.; Zaffalon, M.; Thomann, P. Frequency Discriminators for the Characterization of Narrow-Spectrum Heterodyne Beat Signals: Application to the Measurement of a Sub-Hertz Carrier-Envelope-Offset Beat in an Optical Frequency Comb. Rev. Sci. Instrum. 2011, 82, 123116. [Google Scholar] [CrossRef] [PubMed]
- Walls, W.F. Cross-Correlation Phase Noise Measurements. In Proceedings of the Frequency Control Symposium, Hershey, PA, USA, 27–29 May 1992. [Google Scholar]
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple Approach to the Relation between Laser Frequency Noise and Laser Line Shape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef] [PubMed]
- Bucalovic, N.; Dolgovskiy, V.; Schori, C.; Thomann, P.; Domenico, G.D.; Schilt, S. Experimental Validation of a Simple Approximation to Determine the Linewidth of a Laser from Its Frequency Noise Spectrum. Appl. Opt. 2012, 51, 4582–4588. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Chen, C.; Ning, Y.; Zhang, J.; Chen, J.; Zhang, X.; Li, L.; Wu, H.; Zhou, Y.; Qin, L. Single Polarization, Narrow Linewidth Hybrid Laser Based on Selective Polarization Mode Feedback. Opt. Laser Technol. 2022, 154, 108340. [Google Scholar] [CrossRef]
- Bava, E.; Galzerano, G.; Svelto, C. Frequency-Noise Sensitivity and Amplitude-Noise Immunity of Discriminators Based on Fringe-Side Fabry-Perot Cavities. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 1150–1159. [Google Scholar] [CrossRef]
- Sorin, W.V.; Chang, K.W. Frequency Domain Analysis of an Optical FM Discriminator. J. Light. Technol. 1992, 10, 787–793. [Google Scholar] [CrossRef]
- Kikuchi, K.; Okoshi, T. Measurement of FM Noise, AM Noise, and Field Spectra of 1.3 μm InGaAsP DFB Lasers and Determination of the Linewidth Enhancement Factor. IEEE J. Quantum Electron. 1985, 21, 1814–1818. [Google Scholar] [CrossRef]
- Li, J.; Lee, H.; Chen, T.; Vahala, K.J. Characterization of a High Coherence, Brillouin Microcavity Laser on Silicon. Opt. Express 2012, 20, 20170–20180. [Google Scholar] [CrossRef]
- Van Exter, M.P.; Kuppens, S.J.M.; Woerdman, J.P. Excess Phase Noise in Self-Heterodyne Detection. IEEE J. Quantum Electron. 1992, 28, 580–584. [Google Scholar] [CrossRef]
- Huynh, T.N.; Smyth, F.; Nguyen, L.; Barry, L.P. Effects of Phase Noise of Monolithic Tunable Laser on Coherent Communication Systems. Opt. Express 2012, 20, B244–B249. [Google Scholar] [CrossRef]
- Huynh, T.N.; Nguyen, L.; Barry, L.P. Delayed Self-Heterodyne Phase Noise Measurements with Coherent Phase Modulation Detection. IEEE Photon. Technol. Lett. 2011, 24, 249–251. [Google Scholar] [CrossRef]
- Taylor, M.G. Phase Estimation Methods for Optical Coherent Detection Using Digital Signal Processing. J. Light. Technol. 2009, 27, 901–914. [Google Scholar] [CrossRef]
- Chauhan, N.; Isichenko, A.; Liu, K.; Wang, J.; Zhao, Q.; Behunin, R.O.; Rakich, P.T.; Jayich, A.M.; Fertig, C.; Hoyt, C.W.; et al. Visible Light Photonic Integrated Brillouin Laser. Nat. Commun. 2021, 12, 4685. [Google Scholar] [CrossRef]
- Yang, D.; Li, T.; Yan, F.; Feng, T.; Yu, C.; Qin, Q.; Wang, X.; Guo, H.; Jiang, Y.; Cai, Y.; et al. Demonstration of an Ultra-Wideband Wavelength Self-Adaptive and High-Precision Single-Frequency Laser Linewidth Measurement System. Opt. Express 2024, 32, 40488. [Google Scholar] [CrossRef] [PubMed]
- Duthel, T.; Clarici, G.; Fludger, C.R.; Geyer, J.C.; Schulien, C.; Wiese, S. Laser Linewidth Estimation by Means of Coherent Detection. IEEE Photon. Technol. Lett. 2009, 21, 1568–1570. [Google Scholar] [CrossRef]
- Sutili, T.; Figueiredo, R.C.; Conforti, E. Laser Linewidth and Phase Noise Evaluation Using Heterodyne Offline Signal Processing. J. Light. Technol. 2016, 34, 4933–4940. [Google Scholar] [CrossRef]
- Ravaro, M.; Barbieri, S.; Santarelli, G.; Jagtap, V.; Linfield, E.H. Measurement of the Intrinsic Linewidth of Terahertz Quantum Cascade Lasers Using a Near-Infrared Frequency Comb. Opt. Express 2013, 20, 25654–25661. [Google Scholar] [CrossRef]
- Ravaro, M.; Manquest, C.; Sirtori, C.; Barbieri, S.; Santarelli, G.; Blary, K.; Lampin, J.-F.; Khanna, S.P.; Linfield, E.H. Phase-Locking of a 2.5 THz Quantum Cascade Laser to a Frequency Comb Using a GaAs Photomixer. Opt. Lett. 2011, 36, 3969–3971. [Google Scholar] [CrossRef]
- Barbieri, S.; Gellie, P.; Santarelli, G.; Ding, L.; Maineult, W.; Sirtori, C.; Colombelli, R.; Beere, H.; Ritchie, D. Phase-Locking of a 2.7-THz Quantum Cascade Laser to a Mode-Locked Erbium-Doped Fibre Laser. Nat. Photonics 2010, 4, 636–640. [Google Scholar] [CrossRef]
- Giuliani, G.; Norgia, M. Laser Diode Linewidth Measurement by Means of Self-Mixing Interferometry. IEEE Photonics Technol. Lett. 2000, 2, 1028–1030. [Google Scholar] [CrossRef]
- Cardilli, M.C.; Dabbicco, M.; Mezzapesa, F.P.; Scamarcio, G. Linewidth Measurement of Mid Infrared Quantum Cascade Laser by Optical Feedback Interferometry. Appl. Phys. Lett. 2016, 108, 6165–6206. [Google Scholar] [CrossRef]
- Tombez, L.; Francesco, J.D.; Schilt, S.; Domenico, G.D.; Hofstetter, D. Frequency Noise of Free-Running 4.6 μm Distributed Feedback Quantum Cascade Lasers near Room Temperature. Opt. Lett. 2011, 36, 3109–3111. [Google Scholar] [CrossRef]
- Zhou, Q.; Qin, J.; Xie, W.; Liu, Z.; Tong, Y.; Dong, Y.; Hu, W. Power-Area Method to Precisely Estimate Laser Linewidth from Its Frequency-Noise Spectrum. Appl. Opt. 2015, 54, 8282–8289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zheng, H.; Li, C.; Qi, Z.; Zhang, C.; Li, T.; Bai, Z. Advances in Laser Linewidth Measurement Techniques: A Comprehensive Review. Micromachines 2025, 16, 990. https://doi.org/10.3390/mi16090990
Liu Z, Zheng H, Li C, Qi Z, Zhang C, Li T, Bai Z. Advances in Laser Linewidth Measurement Techniques: A Comprehensive Review. Micromachines. 2025; 16(9):990. https://doi.org/10.3390/mi16090990
Chicago/Turabian StyleLiu, Zhongtian, Hao Zheng, Chunwei Li, Zunhan Qi, Cunwei Zhang, Tie Li, and Zhenxu Bai. 2025. "Advances in Laser Linewidth Measurement Techniques: A Comprehensive Review" Micromachines 16, no. 9: 990. https://doi.org/10.3390/mi16090990
APA StyleLiu, Z., Zheng, H., Li, C., Qi, Z., Zhang, C., Li, T., & Bai, Z. (2025). Advances in Laser Linewidth Measurement Techniques: A Comprehensive Review. Micromachines, 16(9), 990. https://doi.org/10.3390/mi16090990







