Research on GNSS/MEMS IMU Array Fusion Localization Method Based on Improved Grey Prediction Model
Abstract
1. Introduction
- (1)
- Multi-feature fusion GNSS confidence assessment algorithm: Designed a GNSS data quality evaluation system that integrates multiple indicators such as signal strength, satellite visibility, geometric accuracy factors, and solution consistency, enabling real-time dynamic assessment of GNSS data reliability and providing a reliable basis for subsequent adaptive fusion strategies.
- (2)
- Dynamic background value optimization method based on vehicle motion characteristics: Breaks through the limitations of the traditional grey model’s fixed background value construction, proposing an innovative method to dynamically adjust the weighting coefficients in the background value construction based on real-time vehicle speed, acceleration, and road curvature, significantly improving the model’s sensitivity and adaptability to changes in vehicle motion states.
- (3)
- Residual sequence compensation mechanism: Addressing the nonlinear trajectory characteristics of vehicles, established a prediction error correction model based on historical residual sequence analysis, exploiting residual variation patterns to achieve precise compensation of prediction results, effectively enhancing the model’s prediction accuracy in complex motion scenarios.
- (4)
- Adaptive fusion framework: Constructed an intelligent switching fusion architecture for GNSS normal/rejection scenarios, achieving optimal fusion of multi-source information when GNSS signals are reliable, and seamlessly switching to a virtual measurement fusion mode based on the improved grey model during signal rejection, ensuring continuous and stable positioning performance.
2. Confidence Algorithm and Improved Grey Prediction Model
2.1. GNSS Confidence Level Evaluation Algorithm
2.1.1. GNSS Signal Status Analysis and Classification
2.1.2. Multidimensional Confidence Level Evaluation Model Design
2.1.3. Comprehensive Evaluation
2.2. Improved Grey Prediction Model
2.2.1. Traditional Grey Prediction Model
2.2.2. Dynamic Adjustment Optimization Method
2.2.3. Residual Sequence Compensation Mechanism
2.3. MEMS-INS/GNSS Adaptive Fusion Strategy
2.3.1. Overall Fusion Framework Design
2.3.2. Fusion Strategy Under Normal GNSS Conditions
2.3.3. Fusion Strategy During GNSS Denial
3. Experiments and Simulations
3.1. Simulation Experiment Verification
3.1.1. Validation of the Improved Grey Prediction Model
3.1.2. GNSS Confidence Level Assessment Algorithm Verification
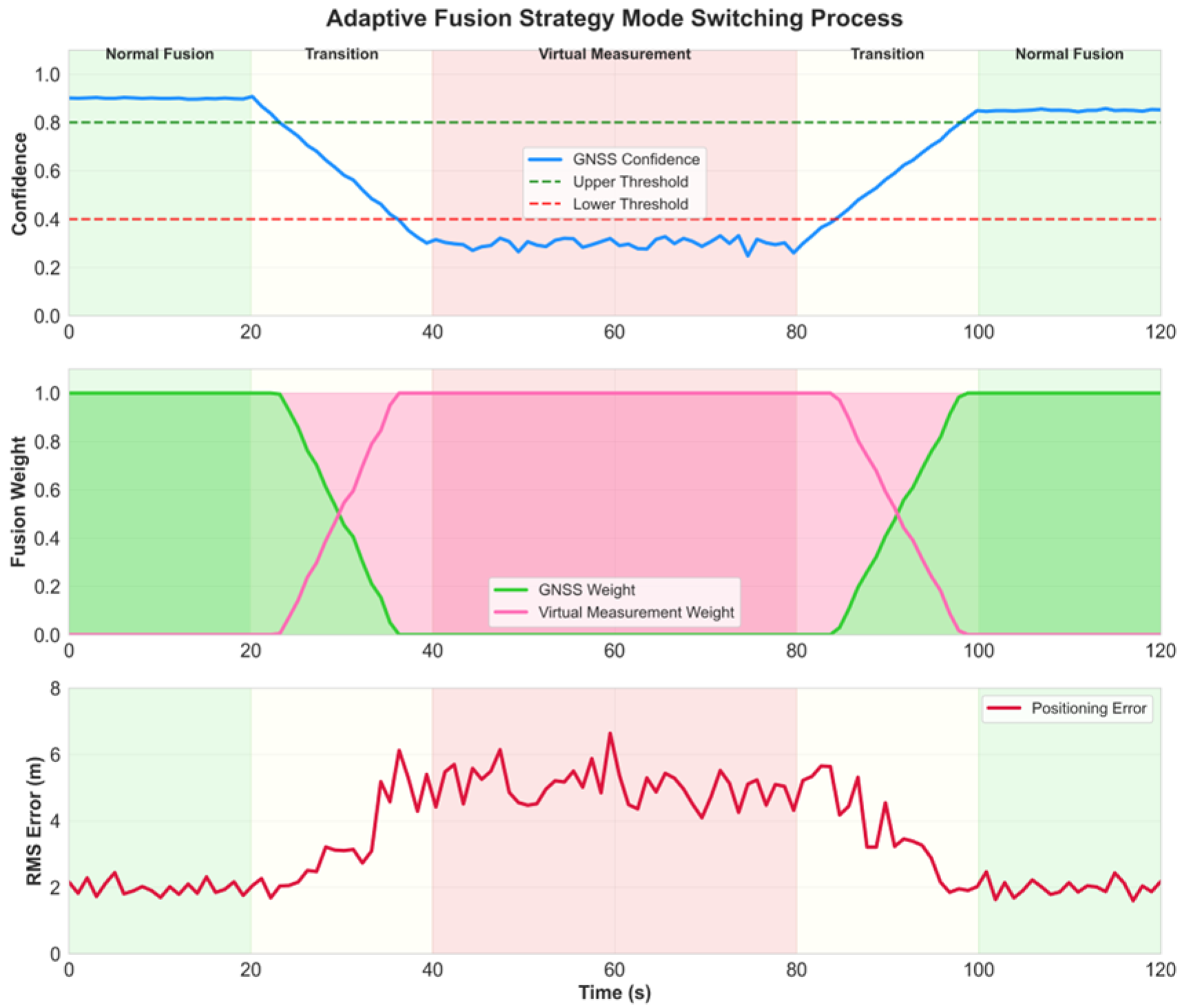
3.1.3. Adaptive Fusion Strategy Verification
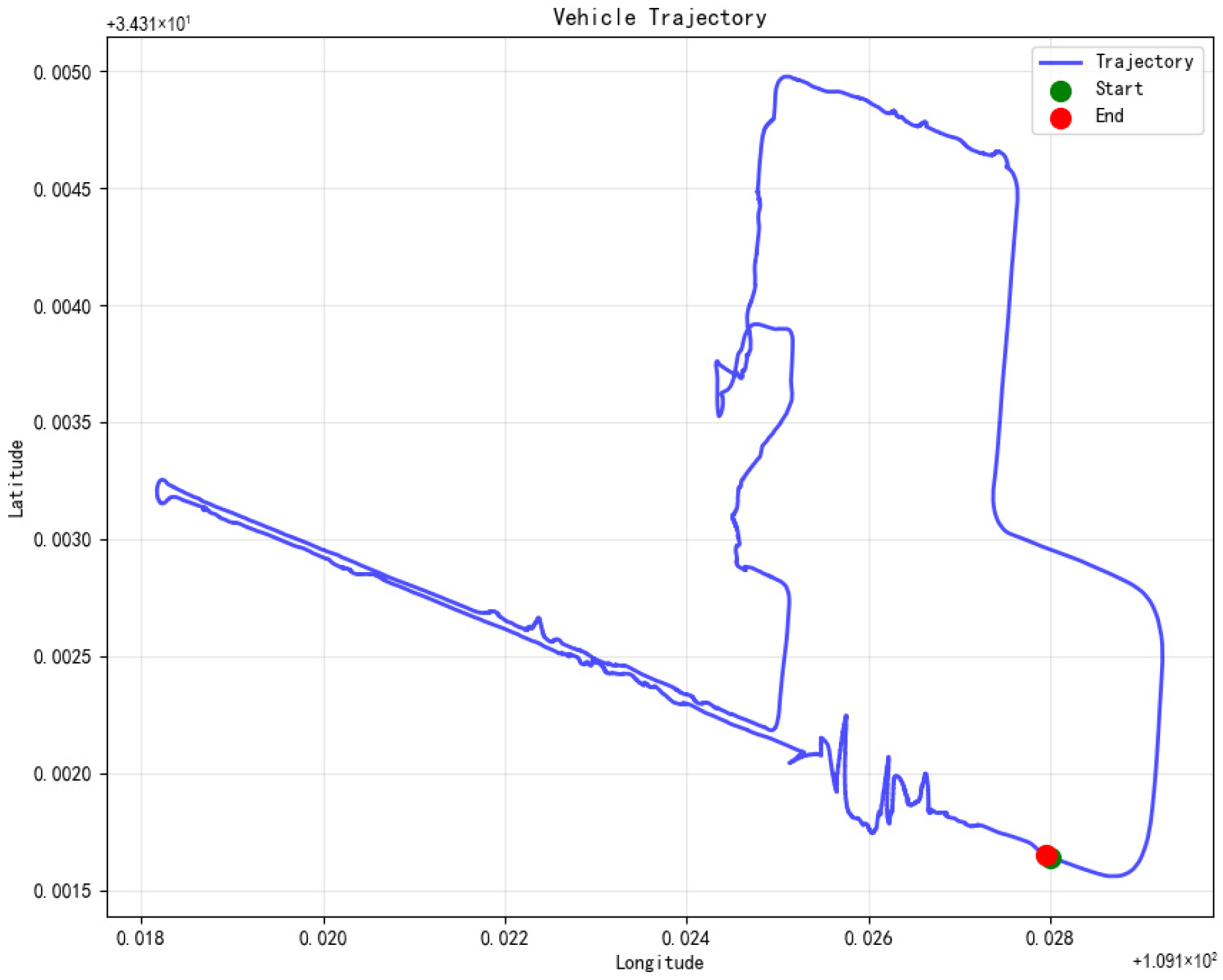
3.2. Vehicle Experiment Validation
3.2.1. Detailed Experimental Protocol
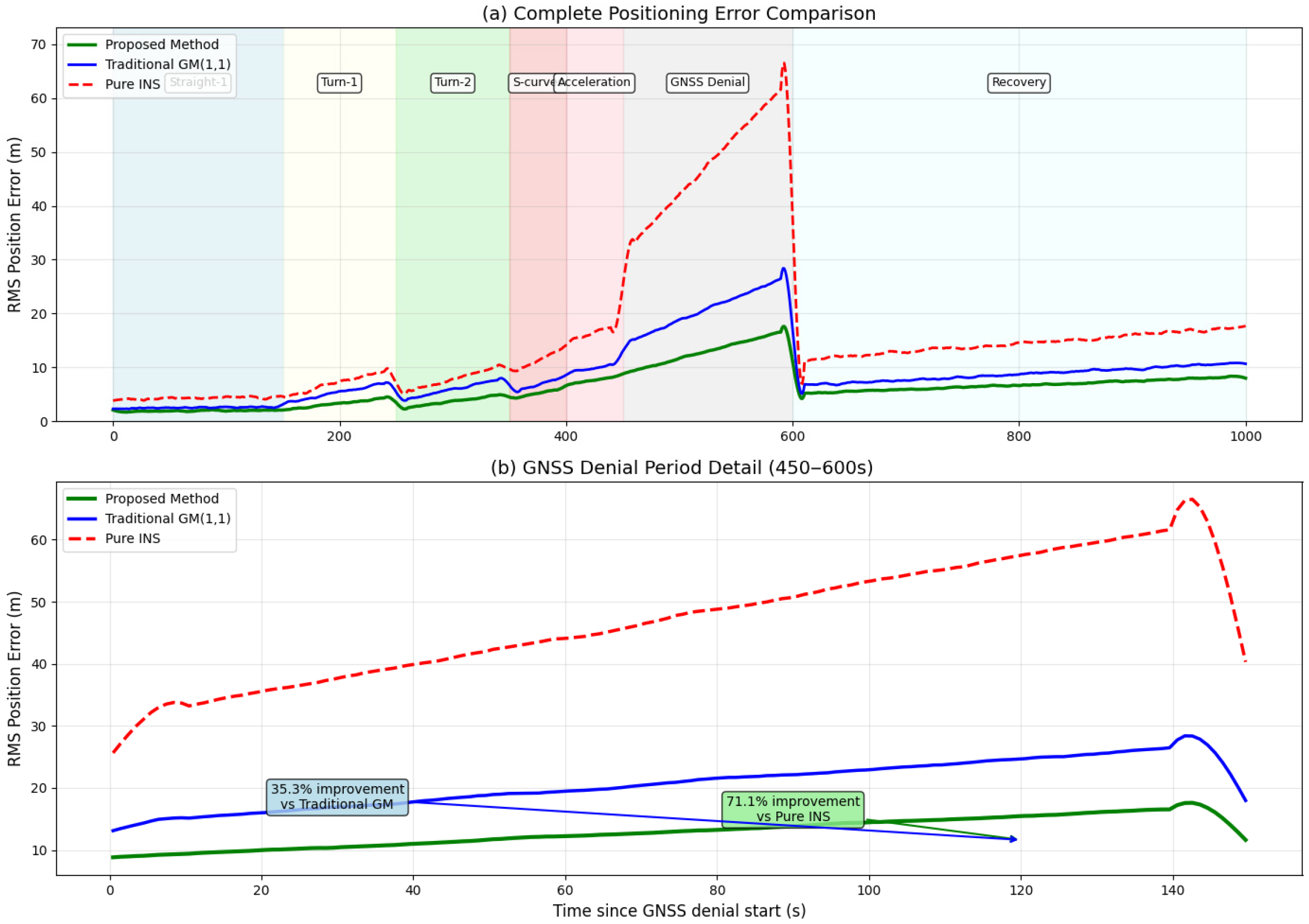
3.2.2. Experimental Results and Performance Comparison
4. Discussion
4.1. Performance Analysis of the Improved Grey Prediction Model
4.2. Analysis of GNSS Confidence Assessment Algorithm
4.3. Performance Analysis of Adaptive Fusion Strategy
4.4. Comparative Analysis with Existing Methods
4.5. Future Research Directions
5. Conclusions
- (1)
- The multi-feature fusion GNSS confidence evaluation algorithm effectively assesses signal reliability in real-time, providing reliable basis for adaptive fusion strategies.
- (2)
- The improved grey prediction model with dynamic background value optimization and residual sequence compensation achieves 31%, 52%, and 45% accuracy improvements in straight, turning, and acceleration scenarios respectively.
- (3)
- The adaptive fusion framework ensures seamless switching between normal and GNSS-denied conditions, maintaining over 79% accuracy improvement compared to pure INS methods during 30-s denial periods.
- (4)
- Vehicle experiments validate the practical effectiveness of the proposed method in real-world scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGC | Automatic Gain Control |
| C/N0 | Carrier-to-Noise Density Ratio |
| EKF | Extended Kalman Filter |
| GDOP | Geometric Dilution of Precision |
| GM(1,1) | Grey Model (1,1) |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| INS | Inertial Navigation System |
| LSTM | Long Short-Term Memory |
| MEMS | Microelectromechanical System |
| RMS | Root Mean Square |
| RNN | Recurrent Neural Network |
| SLAM | Simultaneous Localization and Mapping |
| UKF | Unscented Kalman Filter |
| V2I | Vehicle-to-Infrastructure |
| V2V | Vehicle-to-Vehicle |
References
- Wang, P.; Gao, Y.; Zhao, Q.; Wang, Y.; Zhou, F.; Zhang, D. An Enhanced, Real-Time, Low-Cost GNSS/INS Integrated Navigation Algorithm and Its Platform Design. Sensors 2025, 25, 2119. [Google Scholar] [CrossRef]
- Suvorkin, V.; Garcia-Fernandez, M.; González-Casado, G.; Li, M.; Rovira-Garcia, A. Assessment of Noise of MEMS IMU Sensors of Different Grades for GNSS/IMU Navigation. Sensors 2024, 24, 1953. [Google Scholar] [CrossRef]
- Quinchia, A.G.; Falco, G.; Falletti, E.; Dovis, F.; Ferrer, C. A Comparison between Different Error Modeling of MEMS Applied to GPS/INS Integrated Systems. Sensors 2013, 13, 9549–9588. [Google Scholar] [CrossRef]
- Zheng, S.; Zeng, K.; Li, Z.; Wang, Q.; Xie, K.; Liu, M.; Xie, S. Improving the prediction of GNSS satellite visibility in urban canyons based on a graph transformer. Navigation 2024, 71, 676. [Google Scholar] [CrossRef]
- Weng, D.; Hou, Z.; Meng, Y.; Cai, M.; Chan, Y. Characterization and mitigation of urban GNSS multipath effects on smartphones. Measurement 2023, 223, 113766. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Liu, P. Statistical Multipath Model Based on Experimental GNSS Data in Static Urban Canyon Environment. Sensors 2018, 18, 1149. [Google Scholar] [CrossRef]
- Jarraya, I.; Al-Batati, A.; Kadri, M.B.; Abdelkader, M.; Ammar, A.; Boulila, W.; Koubaa, A. Gnss-denied unmanned aerial vehicle navigation: Analyzing computational complexity, sensor fusion, and localization methodologies. Satell. Navig. 2025, 6, 9. [Google Scholar] [CrossRef]
- Hansen, J.M.; Johansen, T.A.; Sokolova, N.; Fossen, T.I. Nonlinear observer for tightly coupled integrated inertial navigation aided by RTK-GNSS measurements. IEEE Trans. Control Syst. Technol. 2018, 27, 1084–1099. [Google Scholar] [CrossRef]
- Bitar, N.A.; Gavrilov, A.I. Comparative analysis of fusion algorithms in a loosely-coupled integrated navigation system on the basis of real data processing. Gyroscopy Navig. 2019, 10, 231–244. [Google Scholar] [CrossRef]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L. Factor graph optimization for GNSS/INS integration: A comparison with the extended Kalman filter. Navigation 2021, 68, 315–331. [Google Scholar] [CrossRef]
- Hu, Y.; Li, H.; Liu, W. Robust factor graph optimisation method for shipborne GNSS/INS integrated navigation system. IET Radar Sonar Navig. 2024, 18, 782–798. [Google Scholar] [CrossRef]
- Jia, X.X.; Zhao, D.Q.; Xiao, G.R. GNSS/INS/Visual Integrated Navigation Algorithm and Performance Analysis Based on Factor Graph Optimization. In Proceedings of the 2024 9th International Conference on Cyber Security and Information Engineering, Istanbul, Turkey, 15–17 September 2024; pp. 289–295. [Google Scholar]
- Pannekoucke, O.; Richard, M.; Aabaribaoune, M.E.; Plu, M. A methodology to obtain model-error covariances due to the dis-cretization scheme from the parametric Kalman filter perspective. Nonlinear Process. Geophys. 2021, 28, 1–22. [Google Scholar] [CrossRef]
- Koroglu, M.T.; Yigit, C.O.; Konukseven, E.I.; Zaki, A. A survey of machine learning techniques for improving Global Navigation Satellite Systems. EURASIP J. Adv. Signal Process. 2024, 2024, 73. [Google Scholar] [CrossRef]
- Dai, H.; Bian, H.; Wang, R.; Ma, H. An INS/GNSS integrated navigation in GNSS denied environment using recurrent neural network. Def. Technol. 2020, 16, 334–340. [Google Scholar] [CrossRef]
- Song, L.; Xu, P.; He, X.; Li, Y.; Hou, J.; Feng, H. Improved LSTM Neural Network-Assisted Combined Vehicle-Mounted GNSS/SINS Navigation and Positioning Algorithm. Electronics 2023, 12, 3726. [Google Scholar] [CrossRef]
- Alaeiyan, H.; Mosavi, M.R.; Ayatollahi, A. Improving the performance of GPS/INS integration during GPS outage with incremental regularized LSTM learning. Alex. Eng. J. 2024, 105, 137–155. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, K.; Jiang, C.; Li, Z.; Yang, C.; Liu, D.; Zhang, H. Motion-Constrained GNSS/INS Integrated Navigation Method Based on BP Neural Network. Remote Sens. 2023, 15, 154. [Google Scholar] [CrossRef]
- Balochian, S.; Baloochian, H. Improving grey prediction model and its application in predicting the number of users of a public road transportation system. J. Intell. Syst. 2020, 30, 104–114. [Google Scholar] [CrossRef]
- Tan, X.; Xu, J.; Li, F.; Wu, M.; Liang, Y.; Chen, D.; Zhu, B. Grey modelling and real-time forecasting for the approximate non-homogeneous white exponential law BDS clock bias sequences. Sci. Rep. 2024, 14, 17897. [Google Scholar] [CrossRef]
- Li-Dong, W.; Lin, C.; Jun, L.U.; Qing, G. SINS/GPS integrated navigation system based on improved grey forecasting model. J. Chin. Inert. Technol. 2015, 23, 248–251, 257. [Google Scholar]
- Zheng, Z.; Lu, X.; Chen, Y. Improved Grey Model and Application in Real-Time GPS Satellite Clock Bias Prediction. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; pp. 419–423. [Google Scholar]
- Li, C.; Shen, Q.; Wang, L.; Zuo, K.; Tian, Y. Low-cost MEMS-INS/GPS loosely coupled navigation under insufficient satellite conditions. J. Beijing Univ. Aeronaut. Astronaut. 2023, 49, 10. [Google Scholar]
- Urrutia, J.D.; Meneses, J.L.; Antonio, G.V.A. Predicting future monthly electricity consumption in the philippines using markov-chain grey model. Indian J. Sci. Technol. 2019, 12, 1–44. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L. A Hybrid Intelligent Algorithm DGP-MLP for GNSS/INS Integration during GNSS Outages. J. Navig. 2019, 72, 375–388. [Google Scholar] [CrossRef]
- Jeutsa, A.K.; Kibong, M.T.; Diboma, B.S.; Sapnken, F.E.; Noumo, P.G.; Tamba, J.G. On the Limitations of Univariate Grey Prediction Models: Findings and Failures. Comput. Math. Methods 2024, 2024, 9961208. [Google Scholar] [CrossRef]
- Jafari, M. Optimal redundant sensor configuration for accuracy increasing in space inertial navigation system. Aerosp. Sci. Technol. 2015, 47, 467–472. [Google Scholar] [CrossRef]
- Feng, X.; Qiu, M.; Wang, T.; Yao, X.; Cong, H.; Zhang, Y. Noise-Adaptive GNSS/INS Fusion Positioning for Autonomous Driving in Complex Environments. Vehicles 2025, 7, 77. [Google Scholar] [CrossRef]
- Wen, W.; Hsu, L.T.; Zhang, G. Performance analysis of NDT-based graph slam for autonomous vehicle in diverse typical driving scenarios of Hong Kong. Sensors 2018, 18, 3928. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, L.; Li, B.; Liu, Z.; Li, Z.; Lu, Z. Development status and challenges of anti-spoofing technology of GNSS/INS integrated navigation. Front. Phys. 2024, 12, 1425084. [Google Scholar] [CrossRef]










| Parameter Category | Parameter | Dataset Range | Simulation Value | Justification |
|---|---|---|---|---|
| Motion Scenarios | Straight-line motion | 60% occurrence | 40 km/h ± 2 m/s2 | Highway/arterial roads |
| Turning maneuvers | 25% occurrence | 20 km/h, 3.2 m/s2 | Urban intersections | |
| Acceleration phases | 15% occurrence | 0–40 km/h, 4.5 m/s2 | Traffic scenarios | |
| GNSS Signal Quality | Open-sky C/N0 (dB-Hz) | 45–50 | 47 | Highway conditions |
| Urban canyon C/N0 (dB-Hz) | 25–40 | 32 | Downtown areas | |
| Severe obstruction GDOP | >8.0 | 10 | Tunnel/dense buildings | |
| IMU Specifications | Accelerometer bias (μg) | 20–50 | 35 | Bosch BMI088 equivalent |
| Gyroscope bias (deg/h) | 10–30 | 20 | MEMS grade sensors | |
| Sampling rate (Hz) | 100 | 100 | Standard output rate |
| Prediction Time (s) | Traditional RMS (m) | Improved Model RMS (m) | Accuracy Improvement (%) |
|---|---|---|---|
| 5 | 0.52 | 0.31 | 40.4 |
| 10 | 1.24 | 0.89 | 28.2 |
| 15 | 2.18 | 1.56 | 28.4 |
| 20 | 3.35 | 2.41 | 28.1 |
| 30 | 5.93 | 4.12 | 30.5 |
| Prediction Time (s) | Traditional RMS (m) | Improved Model RMS (m) | Accuracy Improvement (%) |
|---|---|---|---|
| 5 | 1.23 | 0.58 | 52.8 |
| 10 | 3.45 | 1.67 | 51.6 |
| 15 | 6.78 | 3.21 | 52.7 |
| 20 | 11.2 | 5.34 | 52.3 |
| Prediction Time (s) | Traditional RMS (m) | Improved Model RMS (m) | Accuracy Improvement (%) |
|---|---|---|---|
| 5 | 0.89 | 0.43 | 51.7 |
| 10 | 2.34 | 1.28 | 45.3 |
| 15 | 4.56 | 2.67 | 41.4 |
| 20 | 7.83 | 4.89 | 37.5 |
| Scene Description | Visible Number of Stars | Average C/NO (dB-Hz) | GDOP | Assessment Confidence |
|---|---|---|---|---|
| Slight Obstruction | 6–7 | 35–38 | 3–4 | 0.72 ± 0.05 |
| Moderate Obstruction | 4–5 | 28–32 | 5–7 | 0.48 ± 0.08 |
| Severe Obstruction | 3–4 | 22–26 | 8–12 | 0.23 ± 0.12 |
| Test Phase | Time Period (s) | Motion Characteristics | Pure INS Method (RMS Error m) | Traditional GM(1,1) (RMS Error m) | Proposed Method (RMS Error m) | Performance Improvement (INS %/GM %) |
|---|---|---|---|---|---|---|
| Straight Motion 1 | 0–150 | Uniform linear motion | 2.34 ± 0.41 | 1.82 ± 0.31 | 1.63 ± 0.24 | 30.3/10.4 |
| Urban Turn 1 | 150–220 | 90° left turn | 5.78 ± 0.82 | 3.71 ± 0.53 | 2.12 ± 0.35 | 63.3/42.9 |
| Urban Turn 2 | 220–290 | 90° right turn | 6.23 ± 0.91 | 4.08 ± 0.64 | 2.31 ± 0.42 | 62.9/43.4 |
| S-curve Section | 290–350 | Continuous S-turns | 8.67 ± 1.24 | 5.82 ± 0.87 | 4.08 ± 0.61 | 52.9/29.9 |
| U-turn Maneuver | 350–400 | 180° U-turn | 7.45 ± 1.15 | 4.97 ± 0.72 | 3.21 ± 0.55 | 56.9/35.4 |
| Acceleration Phase | 400–450 | 20–40 km/h acceleration | 12.41 ± 2.15 | 8.93 ± 1.52 | 6.79 ± 1.08 | 45.3/24.0 |
| GNSS Denial Period | 450–600 | Complex mixed motion | 25.64 ± 3.82 | 18.23 ± 2.91 | 8.91 ± 1.43 | 65.2/51.1 |
| Recovery Phase | 600–700 | Post-denial stabilization | 15.23 ± 2.31 | 11.47 ± 1.89 | 5.12 ± 0.83 | 66.4/55.4 |
| Straight Motion 2 | 700–1000 | Final straight section | 3.21 ± 0.52 | 2.45 ± 0.38 | 2.03 ± 0.31 | 36.8/17.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Liu, J.; Qin, W.; Li, C. Research on GNSS/MEMS IMU Array Fusion Localization Method Based on Improved Grey Prediction Model. Micromachines 2025, 16, 1040. https://doi.org/10.3390/mi16091040
Chen Y, Liu J, Qin W, Li C. Research on GNSS/MEMS IMU Array Fusion Localization Method Based on Improved Grey Prediction Model. Micromachines. 2025; 16(9):1040. https://doi.org/10.3390/mi16091040
Chicago/Turabian StyleChen, Yihao, Jieyu Liu, Weiwei Qin, and Can Li. 2025. "Research on GNSS/MEMS IMU Array Fusion Localization Method Based on Improved Grey Prediction Model" Micromachines 16, no. 9: 1040. https://doi.org/10.3390/mi16091040
APA StyleChen, Y., Liu, J., Qin, W., & Li, C. (2025). Research on GNSS/MEMS IMU Array Fusion Localization Method Based on Improved Grey Prediction Model. Micromachines, 16(9), 1040. https://doi.org/10.3390/mi16091040





