Gate-Induced Static and Dynamic Nonlinearity Characteristics of Bilayer Graphene Field-Effect Transistors (Bi-GFETs)
Abstract
1. Introduction
2. Nonlinearity Model of Bi-GFETs
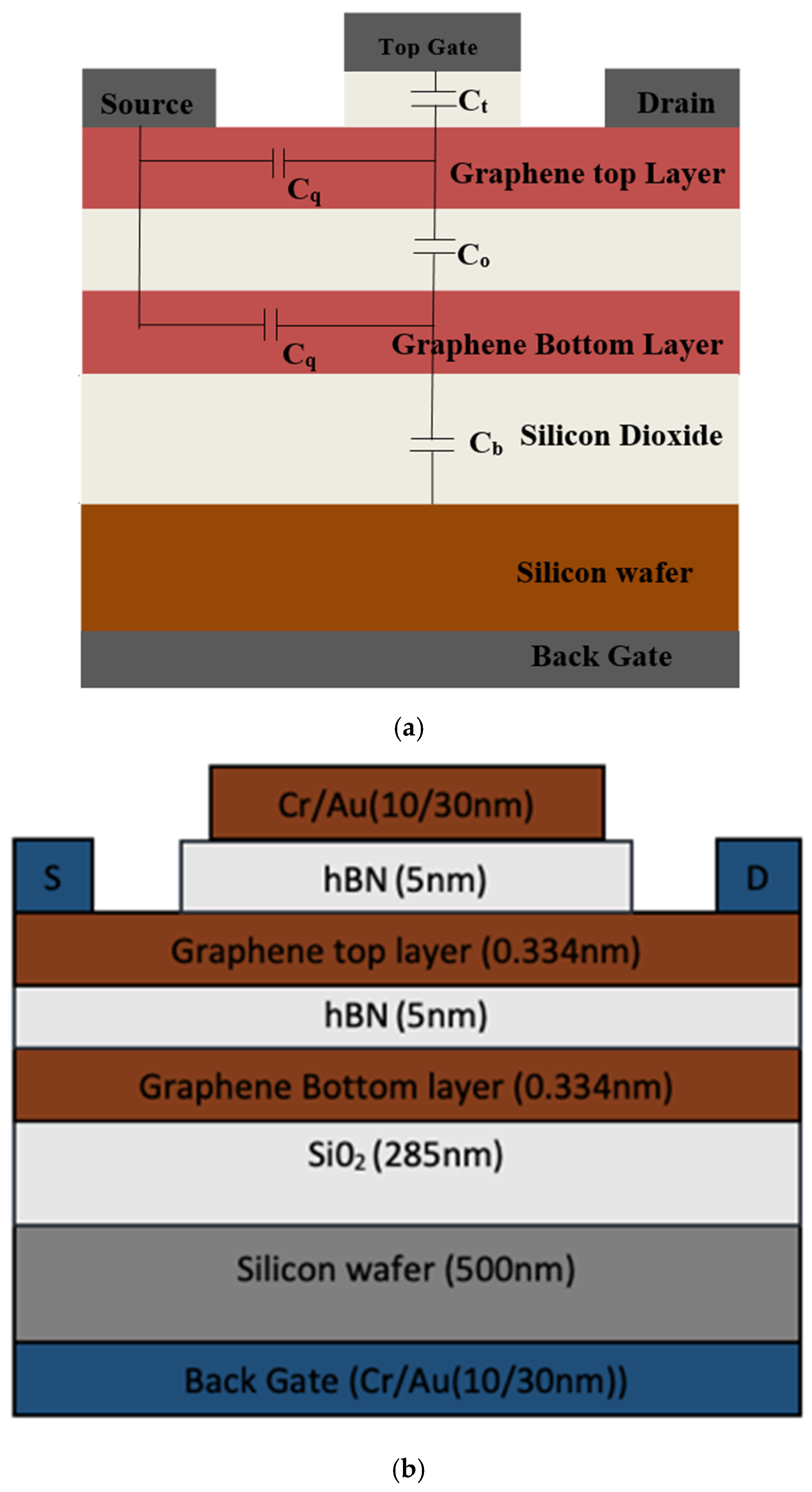
2.1. Drain Current and Energy Bandgap Model
2.2. Calculation of Harmonic and Intermodulation Distortion
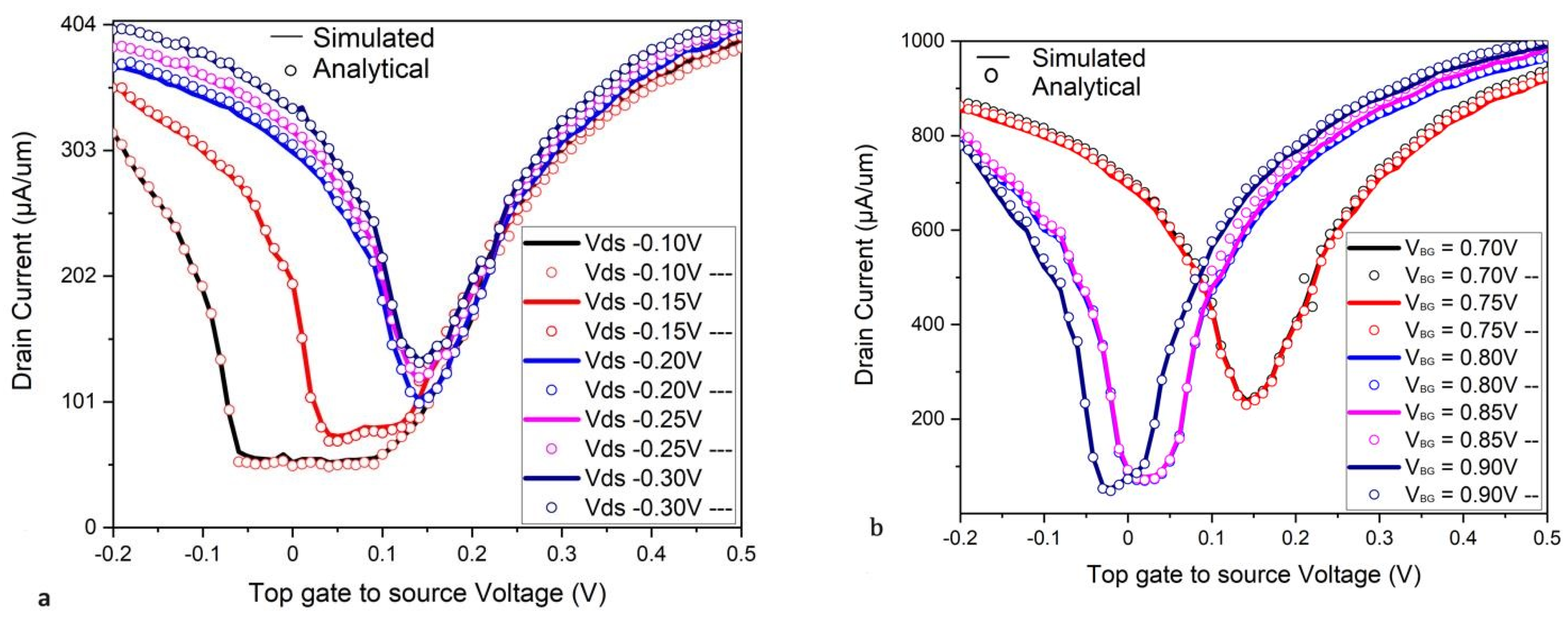
3. Results and Discussion
- Direct Measurement: Measuring the amplitude and phase of the fundamental and harmonic components using spectrum analyzers or network analyzers.
- Simulation: Employing circuit simulators to model the device and predict its harmonic response.
- Analytical Models: Developing physics-based models of the device to predict its nonlinear behavior and harmonic generation.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Shih, C.-J.; Vijayaraghavan, A.; Krishnan, R.; Sharma, R.; Han, J.-H.; Ham, M.-H.; Jin, Z.; Lin, S.; Paulus, G.L.; Reuel, N.F.; et al. Bi-and trilayer graphene solutions. Nat. Nanotechnol. 2011, 6, 439–445. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Yu, W.J.; Liu, L.; Cheng, R.; Chen, Y.; Huang, X.; Liu, Y.; Wang, Y.; Huang, Y.; Duan, X. Chemical vapour deposition growth of large single crystals of monolayer and bilayer graphene. Nat. Commun. 2013, 4, 2096. [Google Scholar] [CrossRef] [PubMed]
- Frank, S. Graphene transistors. Nat. Nanotechnol. 2010, 5, 487–496. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Kum, H.; Bae, S.-H.; Shim, J.; Kim, H.; Kong, L.; Meng, Y.; Wang, K.; Kim, C.; Kim, J. Path towards graphene commercialization from lab to market. Nat. Nanotechnol. 2019, 14, 927–938. [Google Scholar] [CrossRef]
- Giuseppe, I.; Bonaccorso, F.; Colombo, L.; Fiori, G. Quantum engineering of transistors based on 2D materials heterostructures. Nat. Nanotechnol. 2018, 13, 183–191. [Google Scholar]
- Novoselov, K.S.; Fal′Ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Gianluca, F.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerjee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768–779. [Google Scholar]
- Liu, Y.; Rodrigues, J.N.B.; Luo, Y.Z.; Li, L.; Carvalho, A.; Yang, M.; Laksono, E.; Lu, J.; Bao, Y.; Xu, H.; et al. Tailoring sample-wide pseudo-magnetic fields on a graphene–black phosphorus heterostructure. Nat. Nanotechnol. 2018, 13, 828–834. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, S.-E.; Hei, J.; Zeng, L.; Lin, P.; Shi, Z.; Chen, Q.; Li, X.; Yu, X.; Wu, D. Van der Waals integration inch-scale 2D MoSe2 layers on Si for highly sensitive broadband photodetection and imaging. Nano Res. 2023, 16, 11422–11429. [Google Scholar] [CrossRef]
- Kajale, S.N.; Hanna, J.; Jang, K.; Sarkar, D. Two-dimensional magnetic materials for spintronic applications. Nano Res. 2024, 17, 743–762. [Google Scholar] [CrossRef]
- Gao, L.; Chen, Z.; Chen, C.; Zhang, X.; Zhang, Z.; Zhang, Y. Silicon-processes-compatible contact engineering for two-dimensional materials integrated circuits. Nano Res. 2023, 16, 12471–12490. [Google Scholar] [CrossRef]
- Liu, Z.; Tao, Y.; Cui, Z.; Ji, Y.; Zhou, X.; Li, P.; Zhang, Y.; Zhong, D. A two-dimensional tetragonal structure of vanadium telluride. Nano Res. 2023, 16, 7749–7755. [Google Scholar] [CrossRef]
- Kliros George, S. Quantum capacitance of graphene sheets and nanoribbons. In Graphene Science Handbook: Size-Dependent Properties; CRC Press: Boca Raton, FL, USA, 2015; Chapter 13; pp. 171–183. [Google Scholar]
- Hong, T.Y.; Park, J.K.; Hong, S.K. Reducing Interface Resistance in Semiconductor System Through the Integration of Graphene. Electronics 2024, 13, 4305. [Google Scholar] [CrossRef]
- Yuanbo, Z.; Tang, T.-T.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 2009, 459, 820–823. [Google Scholar] [CrossRef]
- Chen, S.; He, M.; Zhang, Y.H.; Hsieh, V.; Fei, Z.; Watanabe, K.; Taniguchi, T.; Cobden, D.H.; Xu, X.; Dean, C.R.; et al. Electrically tunable correlated and topological states in twisted monolayer-bilayer graphene. Nat. Phys. 2020, 17, 374–380. [Google Scholar] [CrossRef]
- Jangyup, S.; Lee, S.; Kim, S.J.; Park, B.C.; Lee, H.-K.; Kim, S.; Kim, J.H.; Hong, B.H.; Hong, J. Hydrogenated monolayer graphene with reversible and tunable wide band gap and its field-effect transistor. Nat. Commun. 2016, 7, 13261. [Google Scholar] [CrossRef]
- Max, C.L.; Baus, M.; Kurz, H. A graphene field-effect device. IEEE Electron Device Lett. 2007, 28, 282–284. [Google Scholar] [CrossRef]
- Gianluca, F.; Iannaccone, G. On the possibility of tunable-gap bilayer graphene FET. IEEE Electron Device Lett. 2009, 30, 261–264. [Google Scholar] [CrossRef]
- Gianluca, F.; Iannaccone, G. Ultralow-voltage bilayer graphene tunnel FET. IEEE Electron Device Lett. 2009, 30, 1096–1098. [Google Scholar] [CrossRef]
- Sanjay, K.B.; Leonard; Register, F.; Tutuc, E.; Reddy, D.; MacDonald, A.H. Bilayer pseudospin field-effect transistor (BiSFET): A proposed new logic device. IEEE Electron Device Lett. 2008, 30, 158–160. [Google Scholar]
- Martina, C.; Fiori, G.; Iannaccone, G. A semianalytical model of bilayer-graphene field-effect transistor. IEEE Trans. Electron Devices 2009, 56, 2979–2986. [Google Scholar]
- Umoh, I.J.; Kazmierski, T.J.; Al-Hashimi, B.M. Multilayer graphene FET compact circuit-level model with temperature effects. IEEE Trans. Nanotechnol. 2014, 13, 805–813. [Google Scholar] [CrossRef]
- Szafranek, B.N.; Fiori, G.; Schall, D.; Neumaier, D.; Kurz, H. Current saturation and voltage gain in bilayer graphene field effect transistors. Nano Lett. 2012, 12, 1324–1328. [Google Scholar] [CrossRef]
- Himadri, P.; Kataria, S.; Gahoi, A.; Lemme, M.C. High voltage gain inverters from artificially stacked bilayer CVD graphene FETs. IEEE Electron Device Lett. 2017, 38, 1747–1750. [Google Scholar] [CrossRef]
- Kang, S.; Fallahazad, B.; Lee, K.; Movva, H.; Kim, K.; Corbet, C.M.; Taniguchi, T.; Watanabe, K.; Colombo, L.; Register, L.F.; et al. Bilayer graphene-hexagonal boron nitride heterostructure negative differential resistance interlayer tunnel FET. IEEE Electron Device Lett. 2015, 36, 405–407. [Google Scholar] [CrossRef]
- Aguirre-Morales; Jorge-Daniel; Fregonese, S.; Mukherjee, C.; Maneux, C.; Zimmer, T. An accurate physics-based compact model for dual-gate bilayer graphene FETs. IEEE Trans. Electron Devices 2015, 62, 4333–4339. [Google Scholar] [CrossRef]
- Mengchuan, T.; Li, X.; Gao, Q.; Xiong, X.; Zhang, Z.; Wu, Y. Improvement of conversion loss of resistive mixers using Bernal-stacked bilayer graphene. IEEE Electron Device Lett. 2018, 40, 325–328. [Google Scholar] [CrossRef]
- Ching-Tzu, C.; Low, T.; Chiu, H.-Y.; Zhu, W. Graphene-side-gate engineering. IEEE Electron Device Lett. 2012, 33, 330–332. [Google Scholar]
- Xu, T.; Wu, Y.; Zhao, M.; Wang, Z.; Zhao, C.; Yu, Y.; Liu, H.; Gu, X.; Cao, Z.; Chen, J.; et al. Electrical kinetic model of a hydroxylated graphene FET gas sensor. ACS Sens. 2024, 9, 4851–4859. [Google Scholar] [CrossRef]
- Khan, M.F.; Elahi, E.; Hassan, N.U.; Rehman, M.A.; Khalil, H.W.; Khan, M.A.; Rehman, S.; Hao, A.; Noh, H.; Khan, K.; et al. Bipolar photoresponse of a graphene field-effect transistor induced by photochemical reactions. ACS Appl. Electron. Mater. 2023, 5, 5111–5119. [Google Scholar] [CrossRef]
- Alam, A.U.; Holland, K.D.; Wong, M.; Ahmed, S.; Kienle, D.; Vaidyanathan, M. RF Linearity Performance Potential of Short-Channel Graphene Field Effect Transistors. IEEE Trans. Microw. Theory Tech. 2015, 63, 3874–3887. [Google Scholar] [CrossRef]
- Rodriguez, S.; Smith, A.; Vaziri, S.; Ostling, M.; Lemme, M.C.; Rusu, A. Static Nonlinearity in Graphene Field Effect Transistors. IEEE Trans. Electron Devices 2014, 61, 3001–3003. [Google Scholar] [CrossRef]
- Alam, A.U.; Rogers, C.M.S.; Paydavosi, N.; Holland, K.D.; Ahmed, S.; Vaidyanathan, M. RF Linerity Potential of Carbon-Nanotube Transistors Versus MOSFETs. IEEE Trans. Nanotechnol. 2013, 12, 340–351. [Google Scholar] [CrossRef]
- Dutta, A.; Koley, K.; Saha, S.K.; Sarkar, C.K. Analysis of Harmonic Distortion in UDG-MOSFETs. IEEE Trans. Electron Devices 2014, 61, 998–1005. [Google Scholar] [CrossRef]
- Khan, M.I.W.; Kim, S.; Park, D.-W.; Kim, H.-J.; Han, S.-K.; Lee, S.-G. Nonlinear Analysis of Nonresoanat THz Response of MOSFET and Implementation of a High-Resposnivity Cross-Coupled THz Detector. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 108–120. [Google Scholar] [CrossRef]
- Zhu, W.; Perebeinos, V.; Freitag, M.; Avouris, P. Carrier scattering, mobilities, and electrostatic potential in monolayer, bilayer, and trilayer graphene. Phys. Rev. B 2009, 80, 235402. [Google Scholar] [CrossRef]
- Munindra; Nand, D. Nonlinearity Analysis of Quantum Capacitance and its Effect on Nano-Graphene Field Effect Transistor Characteristics. J. Electron. Mater. 2022, 51, 4616–4624. [Google Scholar] [CrossRef]
- Nathawat, J.; Zhao, M.; Kwan, C.P.; Yin, S.; Arabchigavkani, N.; Randle, M.; Ramamoorthy, H.; He, G.; Somphonsane, R.; Matsumoto, N.; et al. Transient response of h-BN-encapsulated graphene transistors: Signatures of self-heating and hot-carrier trapping. ACS Omega 2019, 4, 4082–4090. [Google Scholar] [CrossRef]
- Kedzierski, J.; Hsu, P.-L.; Healey, P.; Wyatt, P.W.; Keast, C.L.; Sprinkle, M.; Berger, C.; de Heer, W.A. Epitaxial graphene transistors on SiC substrates. IEEE Trans. Electron Devices 2008, 55, 2078–2085. [Google Scholar] [CrossRef]
- Kedzierski, J.; Hsu, P.-L.; Reina, A.; Kong, J.; Healey, P.; Wyatt, P.; Keast, C. Graphene-on-insulator transistors made using C on Ni chemical-vapor deposition. IEEE Electron Device Lett. 2009, 30, 745–747. [Google Scholar] [CrossRef]
- Han, W.; Hsu, A.; Wu, J.; Kong, J.; Palacios, T. Graphene-based ambipolar RF mixers. IEEE Electron Device Lett. 2010, 31, 906–908. [Google Scholar] [CrossRef]
- Omid, H.; Vukusic, J.; Stake, J. A 30-GHz integrated subharmonic mixer based on a multichannel graphene FET. IEEE Trans. Microw. Theory Tech. 2013, 61, 841–847. [Google Scholar] [CrossRef]
- Michael, A.; Habibpour, O.; Vukusic, J.; Stake, J. Resistive graphene FET subharmonic mixers: Noise and linearity assessment. IEEE Trans. Microw. Theory Tech. 2012, 60, 4035–4042. [Google Scholar]
- Moon, J.S.; Seo, H.-C.; Antcliffe, M.; Le, D.; McGuire, C.; Schmitz, A.; Nyakiti, L.O.; Gaskill, D.K.; Campbell, P.M.; Lee, K.-M.; et al. Graphene FETs for zero-bias linear resistive FET mixers. IEEE Electron Device Lett. 2013, 34, 465–467. [Google Scholar] [CrossRef]
- Madan, H.; Hollander, M.J.; LaBella, M.; Cavalero, R.; Snyder, D.; Robinson, J.A.; Datta, S. Record high conversion gain ambipolar graphene mixer at 10 GHz using scaled gate oxide. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012. [Google Scholar]
- Madan, H.; Hollander, M.J.; Robinson, J.A.; Datta, S. Analysis and benchmarking of graphene based RF low noise amplifiers. In Proceedings of the 71st Device Research Conference, South Bend, IN, USA, 23–26 June 2013; pp. 41–42. [Google Scholar]
- Jenkins, K.A.; Farmer, D.B.; Han, S.J.; Dimitrakopoulos, C.; Oida, S.; Valdes-Garcia, A. Linearity of graphene field-effect transistors. Appl. Phys. Lett. 2013, 103, 173115. [Google Scholar] [CrossRef]
- Parrish, K.N.; Akinwande, D. Impact of contact resistance on the transconductance and linearity of graphene transistors. Appl. Phys. Lett. 2011, 98, 183505. [Google Scholar] [CrossRef]



| Operating Frequency [Ref.] | IIP3 (dBm) | Conversion Loss (dB) | L (µm) |
|---|---|---|---|
| 10 MHz [43] | 13.8 | ~30 to 40 (~38.89) | 2 |
| 30 GHz [44] | 12.8 | 19 | 0.5 |
| NA [45] | 4.9 | 20–22 (~21.10) | 1 |
| NA [46] | 22 | ~15 | 0.25 |
| NA [47] | 27 | 10 | 2 |
| 2 GHz [48] | 19 | 5 | 0.75 |
| 4.3 GHz [49] | 30 | 10 | 0.25 |
| 300 MHz [50] | 20 | 15 | 0.5 |
| 30 GHz [proposed with back gate unbiased] | 11.92 | 17 | 2.4 |
| 40 GHz [proposed with back gate biased] | 10.88 | 11.28 | 0.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakar, V.K.; Munindra; Pal, P.K. Gate-Induced Static and Dynamic Nonlinearity Characteristics of Bilayer Graphene Field-Effect Transistors (Bi-GFETs). Micromachines 2025, 16, 1031. https://doi.org/10.3390/mi16091031
Kakar VK, Munindra, Pal PK. Gate-Induced Static and Dynamic Nonlinearity Characteristics of Bilayer Graphene Field-Effect Transistors (Bi-GFETs). Micromachines. 2025; 16(9):1031. https://doi.org/10.3390/mi16091031
Chicago/Turabian StyleKakar, Varun Kumar, Munindra, and Pankaj Kumar Pal. 2025. "Gate-Induced Static and Dynamic Nonlinearity Characteristics of Bilayer Graphene Field-Effect Transistors (Bi-GFETs)" Micromachines 16, no. 9: 1031. https://doi.org/10.3390/mi16091031
APA StyleKakar, V. K., Munindra, & Pal, P. K. (2025). Gate-Induced Static and Dynamic Nonlinearity Characteristics of Bilayer Graphene Field-Effect Transistors (Bi-GFETs). Micromachines, 16(9), 1031. https://doi.org/10.3390/mi16091031






