Design and Parameter Optimization of Quasi-Zero-Stiffness Structures Based on Cosine-Curve Compliant Beams
Abstract
1. Introduction
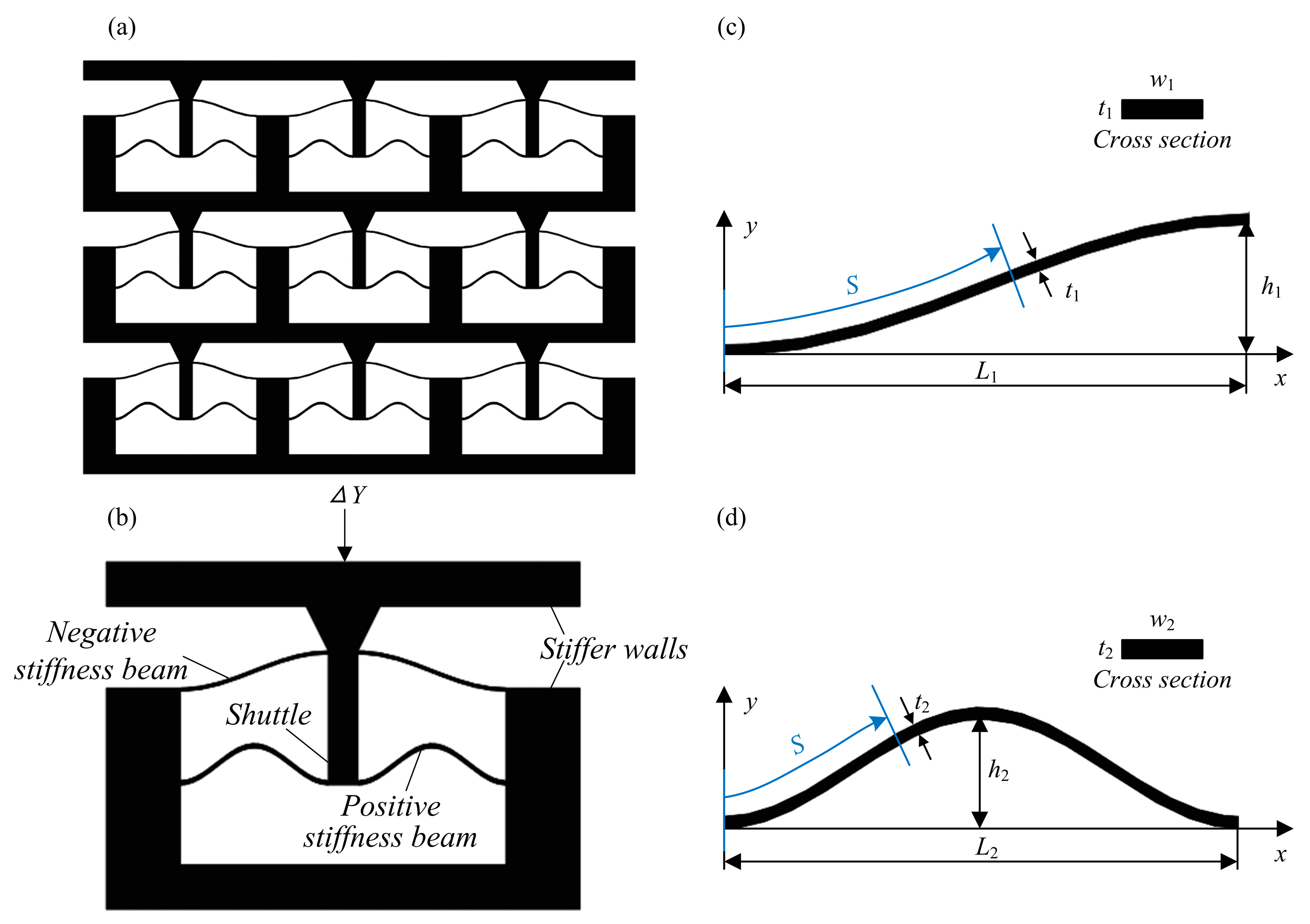
2. Design of the QZS Structure Based on Compliant Curved Beams
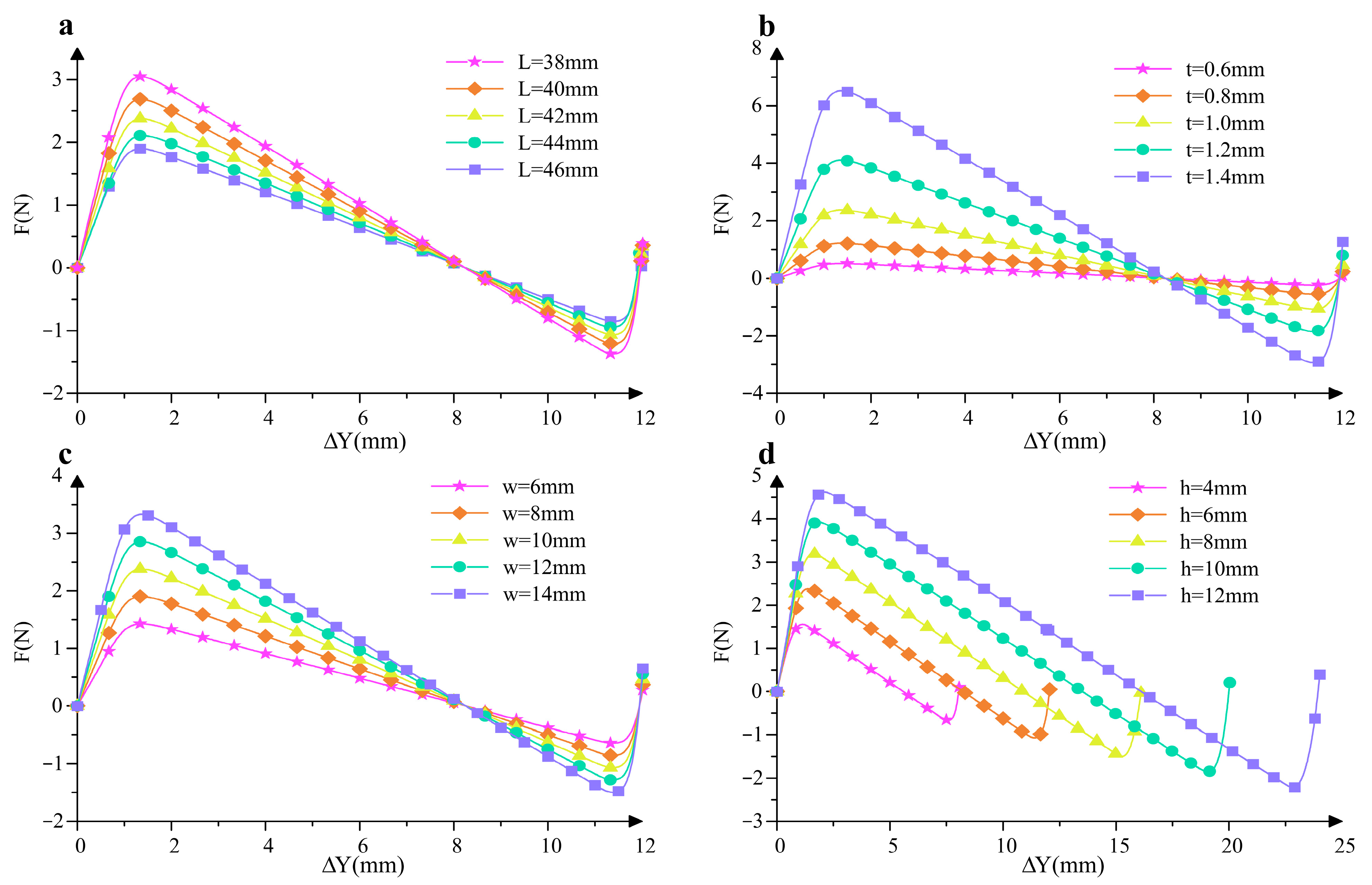
3. Parametric Analysis of the Cosine-Curve Beam
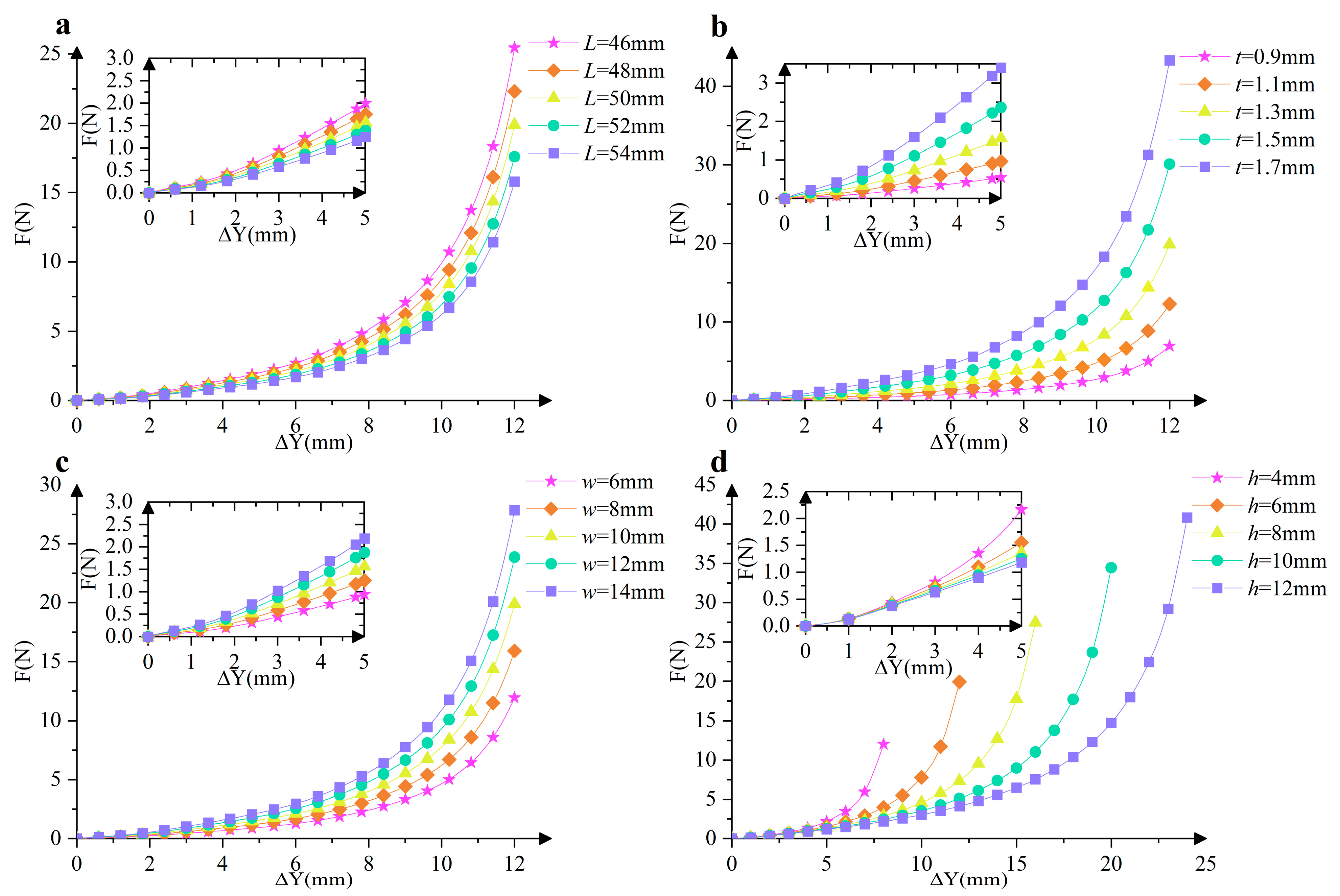
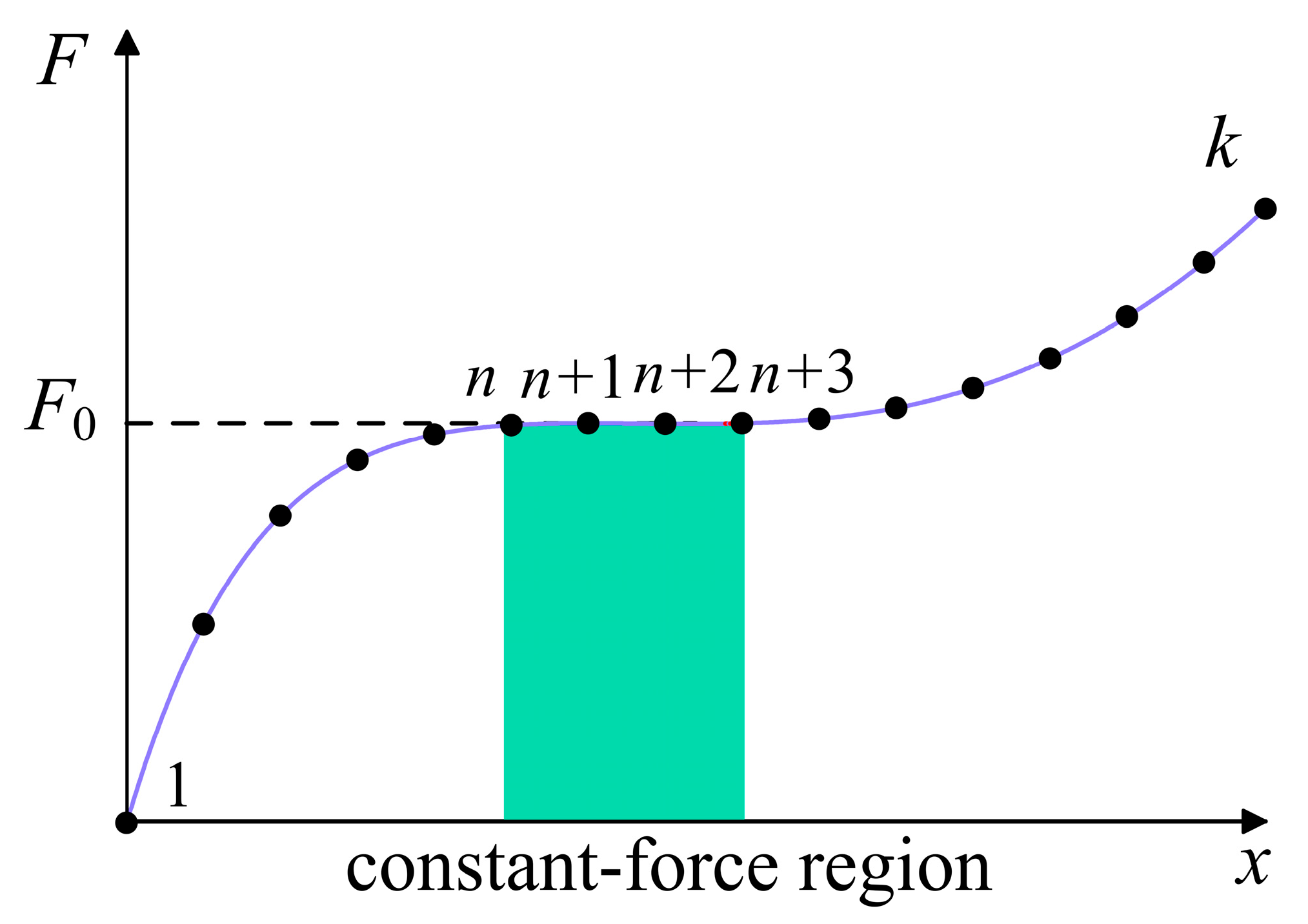
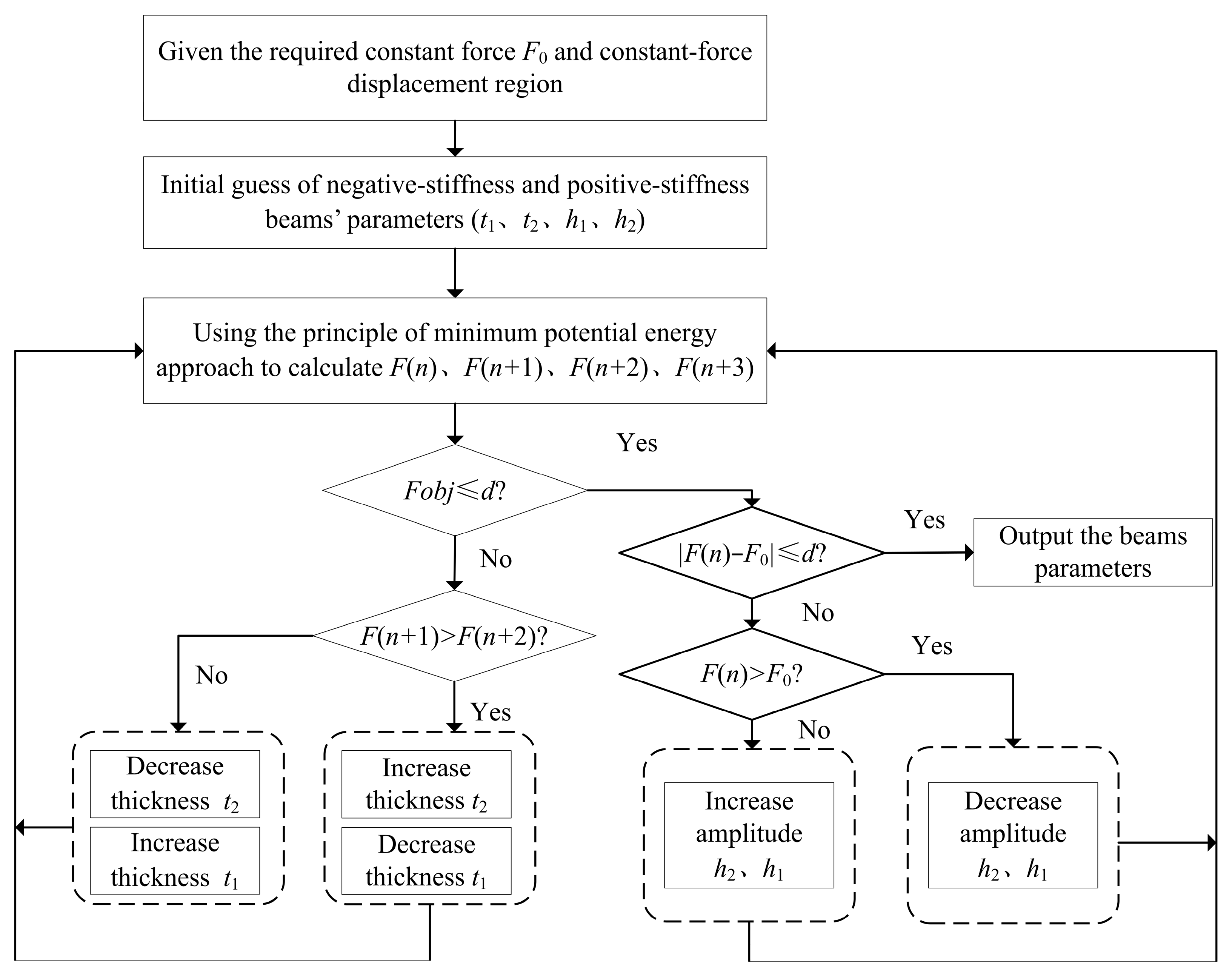
4. Parameter Optimization of QZS Structures
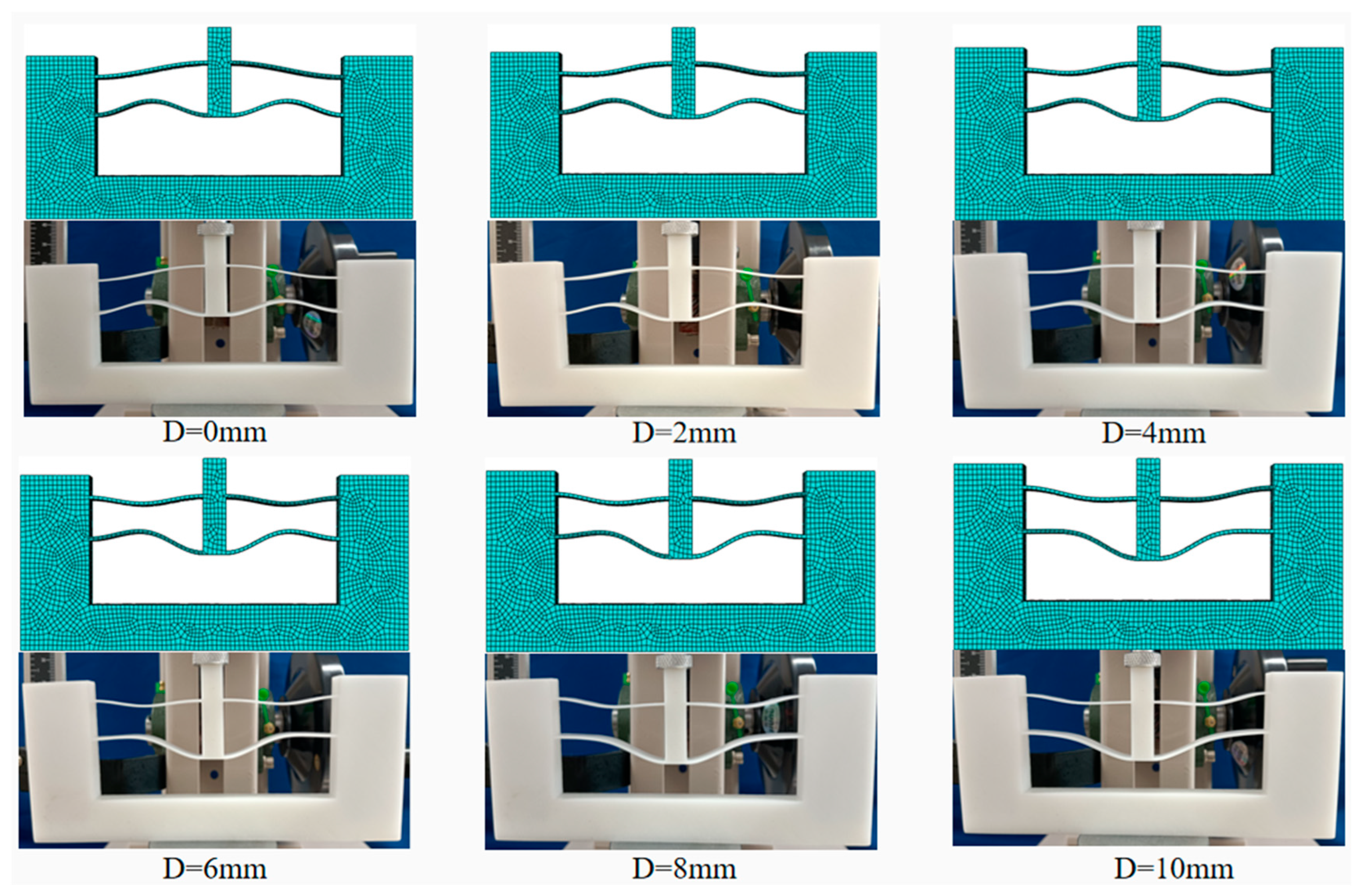
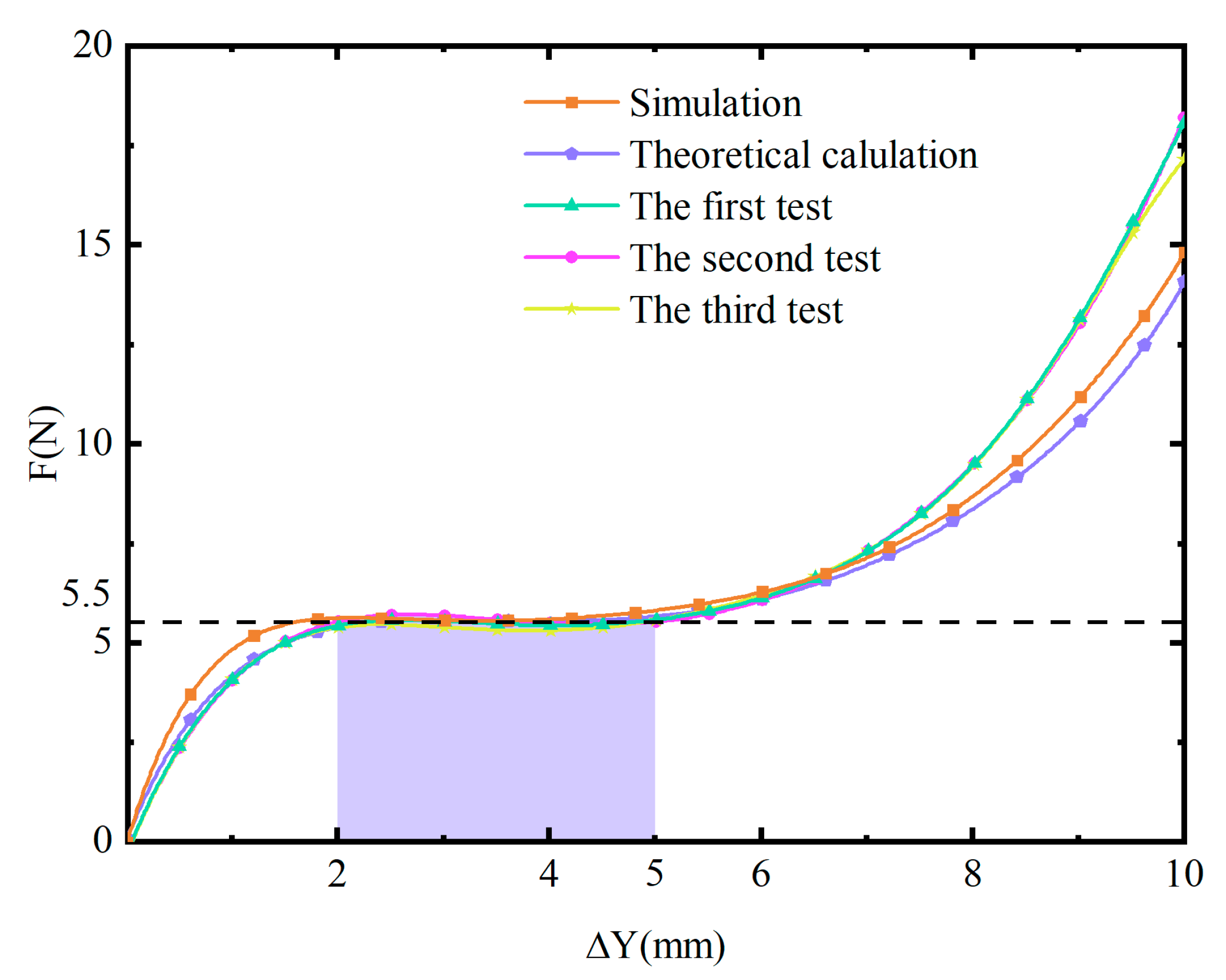
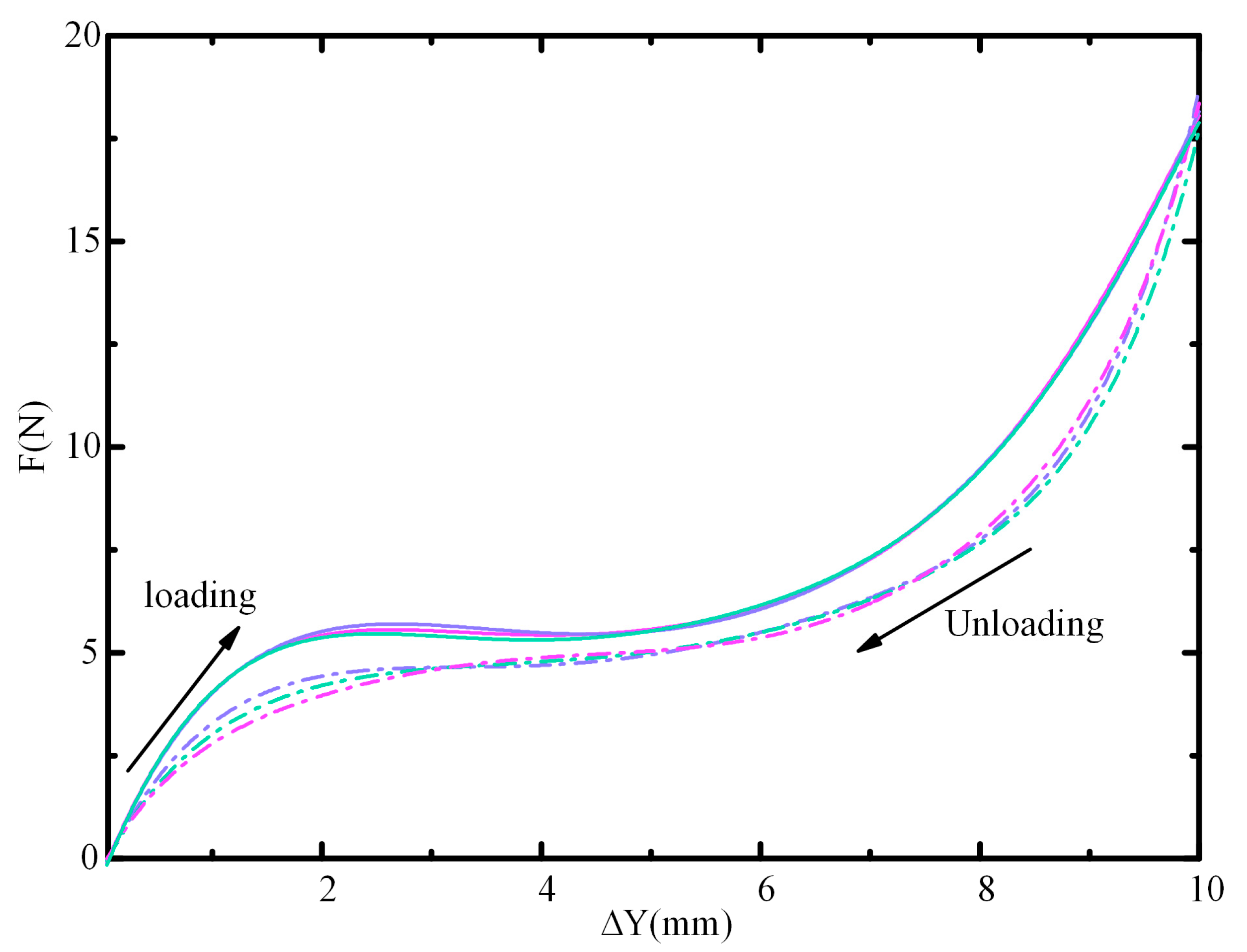
5. Simulation and Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carrella, A.; Brennan, M.J.; Waters, T.P. Waters, Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Ling, J.; Ye, T.; Feng, Z.; Zhu, Y.; Li, Y.; Xiao, X. A survey on synthesis of compliant constant force/torque mechanisms. Mech. Mach. Theory 2022, 176, 104970. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and testing of a novel 2-DOF compound constant-force parallel gripper. Precis. Eng. 2019, 56, 53–61. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and analysis of a 2-DOF compliant gripper with constant-force flexure mechanism. J. Micro-Bio Robot. 2019, 15, 31–42. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, J.; Yi, B.; Zhang, B.; Wang, K. A flexible swallowing gripper for harvesting apples and its grasping force sensing model. Comput. Electron. Agric. 2023, 204, 107489. [Google Scholar] [CrossRef]
- Ding, H.; Chen, L.-Q. Nonlinear vibration of a slightly curved beam with quasi-zero-stiffness isolators. Nonlinear Dyn. 2019, 95, 2367–2382. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.-W.; Ding, H. Vibration control combining nonlinear isolation and nonlinear absorption. Nonlinear Dyn. 2020, 100, 2121–2139. [Google Scholar] [CrossRef]
- Sun, X.; Wang, F.; Xu, J. A novel dynamic stabilization and vibration isolation structure inspired by the role of avian neck. Int. J. Mech. Sci. 2021, 193, 106166. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Xu, D.; Ouyang, H.; Duan, Y. Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness. Nonlinear Dyn. 2017, 87, 633–646. [Google Scholar] [CrossRef]
- Sun, M.; Dong, Z.; Song, G.; Sun, X.; Liu, W. A Vibration Isolation System Using the Negative Stiffness Corrector Formed by Cam-Roller Mechanisms with Quadratic Polynomial Trajectory. Appl. Sci. 2020, 10, 3573. [Google Scholar] [CrossRef]
- Chong, X.; Wu, Z.; Li, F. Vibration isolation properties of the nonlinear X-combined structure with a high-static and low-dynamic stiffness: Theory and experiment. Mech. Syst. Signal Process. 2022, 179, 109352. [Google Scholar] [CrossRef]
- Gea, H.C. Applications of regional strain energy in compliant structure design for energy absorption. Struct. Multidiscip. Optim. 2004, 26, 224–228. [Google Scholar] [CrossRef]
- Hyland, J.E.; Frecker, M.I.; Lesieutre, G.A. Optimization of Honeycomb Contact-Aided Compliant Cellular Mechanism for Strain Energy Absorption. In Proceedings of the ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 12–15 August 2012; Volume 4: 36th Mechanisms and Robotics Conference, Parts A and B. ASME: New York, NY, USA, 2013; pp. 311–320. [Google Scholar] [CrossRef]
- Jovanova, J.; Nastevska, A.; Frecker, M. Tailoring energy absorption with functional grading of a contact-aided compliant mechanism. Smart Mater. Struct. 2019, 28, 084003. [Google Scholar] [CrossRef]
- Fang, X.; Wen, J.; Cheng, L.; Yu, D.; Zhang, H.; Gumbsch, P. Programmable gear-based mechanical metamaterials. Nat. Mater. 2022, 21, 869–876. [Google Scholar] [CrossRef]
- Dalela, S.; Balaji, P.S.; Jena, D.P. A review on application of mechanical metamaterials for vibration control. Mech. Adv. Mater. Struct. 2022, 29, 3237–3262. [Google Scholar] [CrossRef]
- Yang, H.; D’Ambrosio, N.; Liu, P.; Pasini, D.; Ma, L. Shape memory mechanical metamaterials. Mater. Today 2023, 66, 36–49. [Google Scholar] [CrossRef]
- Lin, Q.; Zhou, J.; Wang, K.; Xu, D.; Wen, G.; Wang, Q.; Cai, C. Enhanced low-frequency band gap of nonlinear quasi-zero-stiffness metamaterial by lowering stiffness coupling. Nonlinear Dyn. 2024, 1–20. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Kovacic, I.; Waters, T.P. On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 2009, 322, 707–717. [Google Scholar] [CrossRef]
- Liu, T.; Li, A. Theoretical Design and Dynamic Analysis of a Quasi-Zero Stiffness Device Using Precompressed Springs as Negative Stiffness Component. J. Eng. Mech. 2024, 150, 04023116. [Google Scholar] [CrossRef]
- Yang, J.-H.; Yang, X.-D. Theoretical and experimental study of a novel nonlinear quasi-zero Stiffness vibration isolator based on a symmetric link-rod-type structure. Eng. Struct. 2024, 301, 117284. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Xu, D.; Bishop, S. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam–roller–spring mechanisms. J. Sound Vib. 2015, 346, 53–69. [Google Scholar] [CrossRef]
- Wang, S.; Yu, L.; Zhang, Q.; Xiang, R. Design and analysis of a novel horizontal large-amplitude and low-frequency vibration isolator. J. Vib. Eng. Technol. 2024, 12, 6155–6167. [Google Scholar] [CrossRef]
- Zou, D.; Liu, G.; Rao, Z.; Tan, T.; Zhang, W.; Liao, W.H. A device capable of customizing nonlinear forces for vibration energy harvesting, vibration isolation, and nonlinear energy sink. Mech. Syst. Signal Process. 2021, 147, 107101. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Lan, C.-C. An Adjustable Constant-Force Mechanism for Adaptive End-Effector Operations. J. Mech. Des. 2012, 134, 031005. [Google Scholar] [CrossRef]
- Fan, H.; Yang, L.; Tian, Y.; Wang, Z. Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Compos. Struct. 2020, 243, 112244. [Google Scholar] [CrossRef]
- Winterflood, J.; Blair, D.G.; Slagmolen, B. High performance vibration isolation using springs in Euler column buckling mode. Phys. Lett. A 2002, 300, 122–130. [Google Scholar] [CrossRef]
- Sui, G.; Zhang, X.; Hou, S.; Shan, X.; Hou, W.; Li, J. Quasi-Zero Stiffness Isolator Suitable for Low-Frequency Vibration. Machines 2023, 11, 512. [Google Scholar] [CrossRef]
- Ding, B.; Li, X.; Chen, S.-C. Modular quasi-zero-stiffness isolator based on compliant constant-force mechanisms for low-frequency vibration isolation. J. Vib. Control 2023, 30, 3006–3020. [Google Scholar] [CrossRef]
- Yu, B.; Liu, H.; Fan, D.; Xie, X. Design of quasi-zero stiffness compliant shock isolator under strong shock excitation. Precis. Eng. 2022, 78, 47–59. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Mei, Y. Characteristic analysis of a quasi-zero-stiffness vibration isolator. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 397, p. 012045. [Google Scholar] [CrossRef]
- Zhang, C.; He, J.; Zhou, G.; Wang, K.; Xu, D.; Zhou, J. Compliant quasi-zero-stiffness isolator for low-frequency torsional vibration isolation. Mech. Mach. Theory 2023, 181, 105213. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X.; Sun, J.; Zhang, Z.; Hua, H. Effect of the system imperfections on the dynamic response of a high-static-low-dynamic stiffness vibration isolator. Nonlinear Dyn. 2014, 76, 1157–1167. [Google Scholar] [CrossRef]
- Chen, R.; Li, X.; Yang, Z.; Xu, J.; Yang, H. A variable positive-negative stiffness joint with low frequency vibration isolation performance. Measurement 2021, 185, 110046. [Google Scholar] [CrossRef]
- Zhou, C.; Sui, G.; Chen, Y.; Shan, X. A nonlinear low frequency quasi zero stiffness vibration isolator using double-arc flexible beams. Int. J. Mech. Sci. 2024, 276, 109378. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Yang, S.; Sun, T.; Yang, M.; Niu, W. Customized quasi-zero-stiffness metamaterials for ultra-low frequency broadband vibration isolation. Int. J. Mech. Sci. 2024, 269, 108958. [Google Scholar] [CrossRef]
- Huo, K.; Yuan, Z.; Zhou, G.; Mu, R.; Wang, K.; Zhao, H. Modeling of programmable low-frequency isolator with quasi-zero stiffness metamaterials. Acta Mech. 2024, 235, 2919–2944. [Google Scholar] [CrossRef]
- Zheng, Y.M.J. Optimization design of compliant constant-force mechanism for apple picking actuator. Comput. Electron. Agric. 2020, 170, 105232. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, D.; Hu, G. Tailored Mechanical Metamaterials with Programmable Quasi-Zero-Stiffness Features for Full-Band Vibration Isolation. Adv. Funct. Mater. 2021, 31, 2101428. [Google Scholar] [CrossRef]
- Lin, Q.; Zhou, J.; Wang, K.; Xu, D.; Wen, G.; Wang, Q.; Cai, C. Low-frequency locally resonant band gap of the two-dimensional quasi-zero-stiffness metamaterials. Int. J. Mech. Sci. 2022, 222, 107230. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Li, L.; Ma, F.; Chen, G. Design of Passive Constant-Force End-Effector for Robotic Polishing of Optical Reflective Mirrors. Chin. J. Mech. Eng. 2022, 35, 141. [Google Scholar] [CrossRef]
- Tong, Z.; Zhang, X.; Wang, G. Automatic Optimization for Compliant Constant Force Mechanisms. Actuators 2023, 12, 61. [Google Scholar] [CrossRef]
- Xiang, L.X.Z. Compliant quasi-zero stiffness device for vibration energy harvesting and isolation. Sens. Actuators A Phys. 2022, 347, 113964. [Google Scholar] [CrossRef]
- Wei, S.H.J. A quasi-zero stiffness mechanism with monolithic flexible beams for low-frequency vibration isolation. Mech. Syst. Signal Process. 2024, 210, 111154. [Google Scholar] [CrossRef]
- Feng, X.; Feng, J.; An, E.; Wang, H.; Wu, S.; Qi, L. Palm petiole inspired nonlinear anti-vibration ring with deformable crescent-shaped cross-section. Nonlinear Dyn. 2024, 112, 6919–6945. [Google Scholar] [CrossRef]
- Rosenberg, E.J.; Radaelli, G.; Herder, J.L. An Energy Approach to a 2DOF Compliant Parallel Mechanism With Self-Guiding Statically-Balanced Straight-Line Behavior. In Proceedings of the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15–18 August 2010; ASME: New York, NY, USA, 2011; pp. 455–464. [Google Scholar] [CrossRef]
- Radaelli, G.; Herder, J.L. A potential energy field (PEF) approach to the design of a compliant self-guiding statically-balanced straight-line mechanism. Mech. Mach. Theory 2017, 114, 141–155. [Google Scholar] [CrossRef]
- Radaelli, G.; Gallego, J.A.; Herder, J.L. An Energy Approach to Static Balancing of Systems with Torsion Stiffness. J. Mech. Des. 2011, 133, 091006. [Google Scholar] [CrossRef]
- Su, O.A.T.H.-J. A general and efficient multiple segment method for kinetostatic analysis of planar compliant mechanisms. Mech. Mach. Theory 2017, 112, 205–217. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Euler-Bernoulli beam theory. In Structural Analysis; Springer: Dordrecht, The Netherlands, 2009; Volume 163, pp. 173–221. [Google Scholar] [CrossRef]
- Fahroo, F.; Ross, I.M. Costate Estimation by a Legendre Pseudospectral Method. J. Guid. Control Dyn. 2001, 24, 270–277. [Google Scholar] [CrossRef]
- Michael, I. Direct Trajectory Optimization by a Chebyshev Pseudospectral Method. J. Guid. Control Dyn. 2002, 25, 160–166. [Google Scholar] [CrossRef]
- Wang, P.; Yang, S.; Xu, Q. Design and Optimization of a New Compliant Rotary Positioning Stage with Constant Output Torque. Int. J. Precis. Eng. Manuf. 2018, 19, 1843–1850. [Google Scholar] [CrossRef]
- Phan, T.V.; Pham, H.T. Design and Optimization of a Large-Stroke Compliant Constant-Torque Mechanism. J. Tech. Educ. Sci. 2022, 17, 93–100. [Google Scholar] [CrossRef]
| Parameters of the Half-Period Cosine-Curve Beam | Parameters of the Half-Period Cosine-Curve Beam | ||||||
|---|---|---|---|---|---|---|---|
| L1 (mm) | h1 (mm) | w1 (mm) | t1 (mm) | L2 (mm) | h2 (mm) | w2 (mm) | t2 (mm) |
| 20 | 6 | 5 | 0.4 | 20 | 3 | 5 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Hu, J.; Li, D.; Huang, L. Design and Parameter Optimization of Quasi-Zero-Stiffness Structures Based on Cosine-Curve Compliant Beams. Micromachines 2025, 16, 961. https://doi.org/10.3390/mi16080961
Sun Z, Hu J, Li D, Huang L. Design and Parameter Optimization of Quasi-Zero-Stiffness Structures Based on Cosine-Curve Compliant Beams. Micromachines. 2025; 16(8):961. https://doi.org/10.3390/mi16080961
Chicago/Turabian StyleSun, Zhuo, Jinpeng Hu, Deng Li, and Long Huang. 2025. "Design and Parameter Optimization of Quasi-Zero-Stiffness Structures Based on Cosine-Curve Compliant Beams" Micromachines 16, no. 8: 961. https://doi.org/10.3390/mi16080961
APA StyleSun, Z., Hu, J., Li, D., & Huang, L. (2025). Design and Parameter Optimization of Quasi-Zero-Stiffness Structures Based on Cosine-Curve Compliant Beams. Micromachines, 16(8), 961. https://doi.org/10.3390/mi16080961





