Cell Partitioning Design for Microfluidic ATPS Devices: A Dynamic Energy Strategy and Calculation Using Chondrocytes and Model Microparticles
Abstract
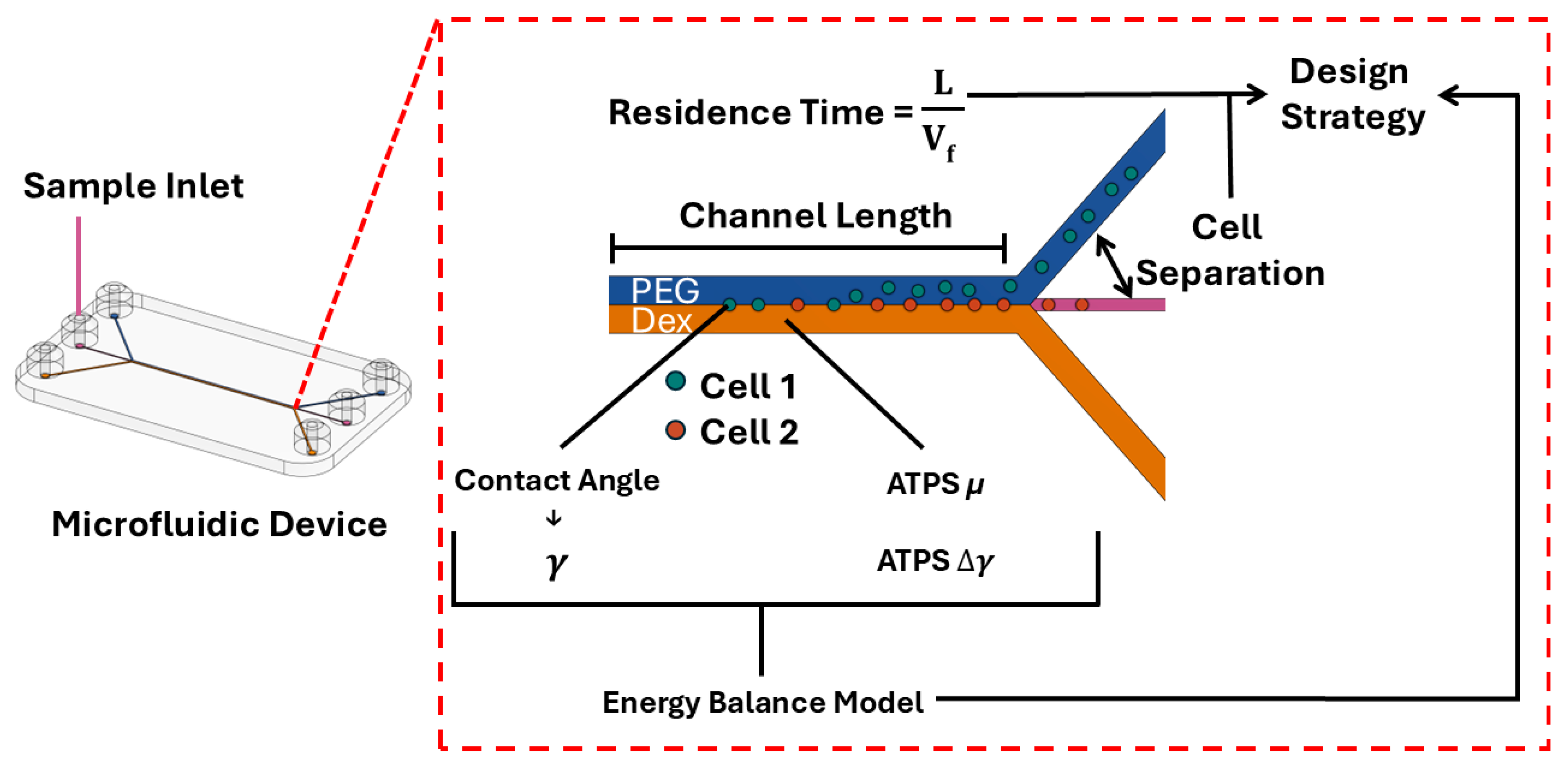
1. Introduction
2. Materials and Methods
2.1. Materials
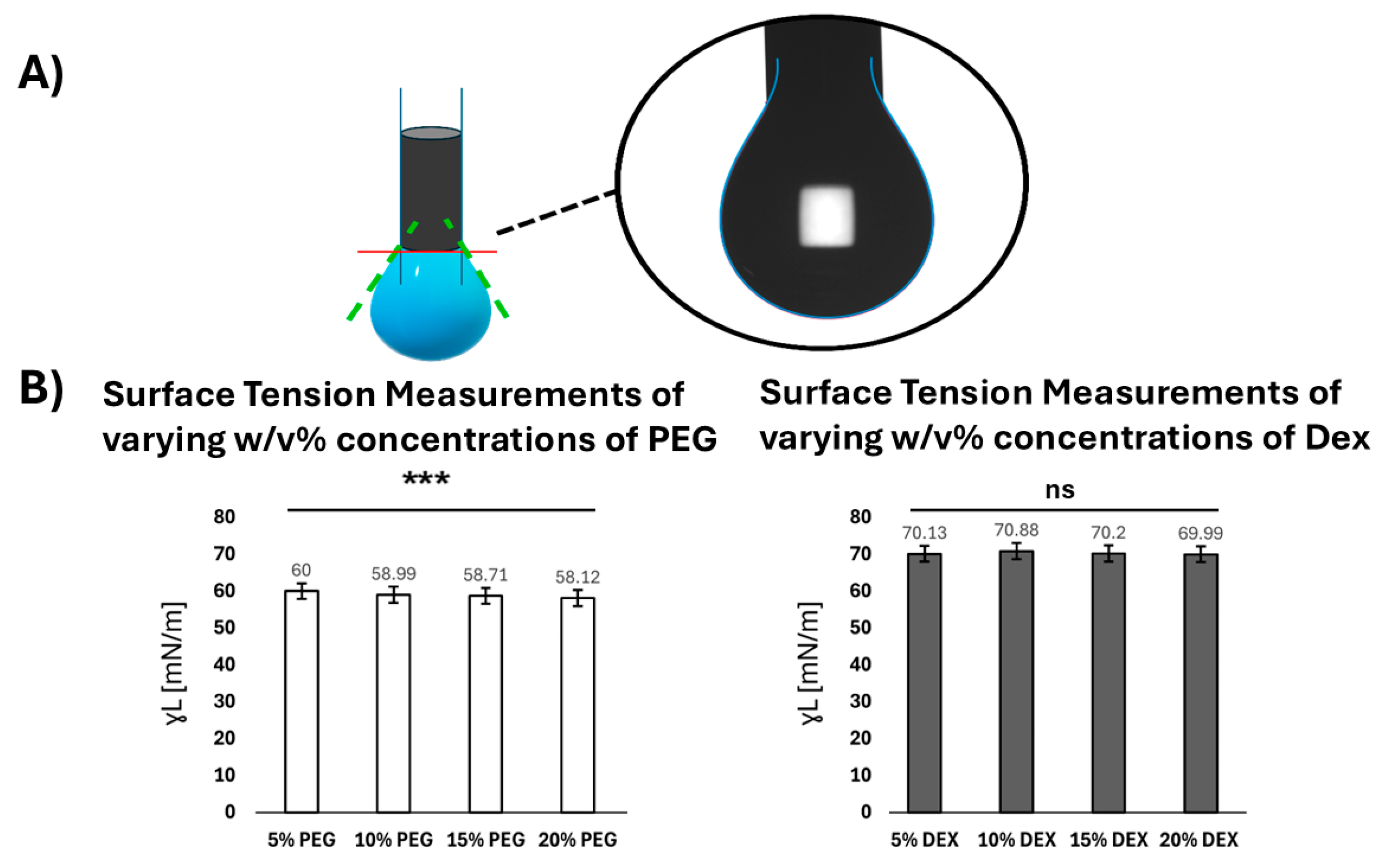
2.2. Pendent Drop Method for Surface Tension Measurements
2.3. Cell Source and Culture
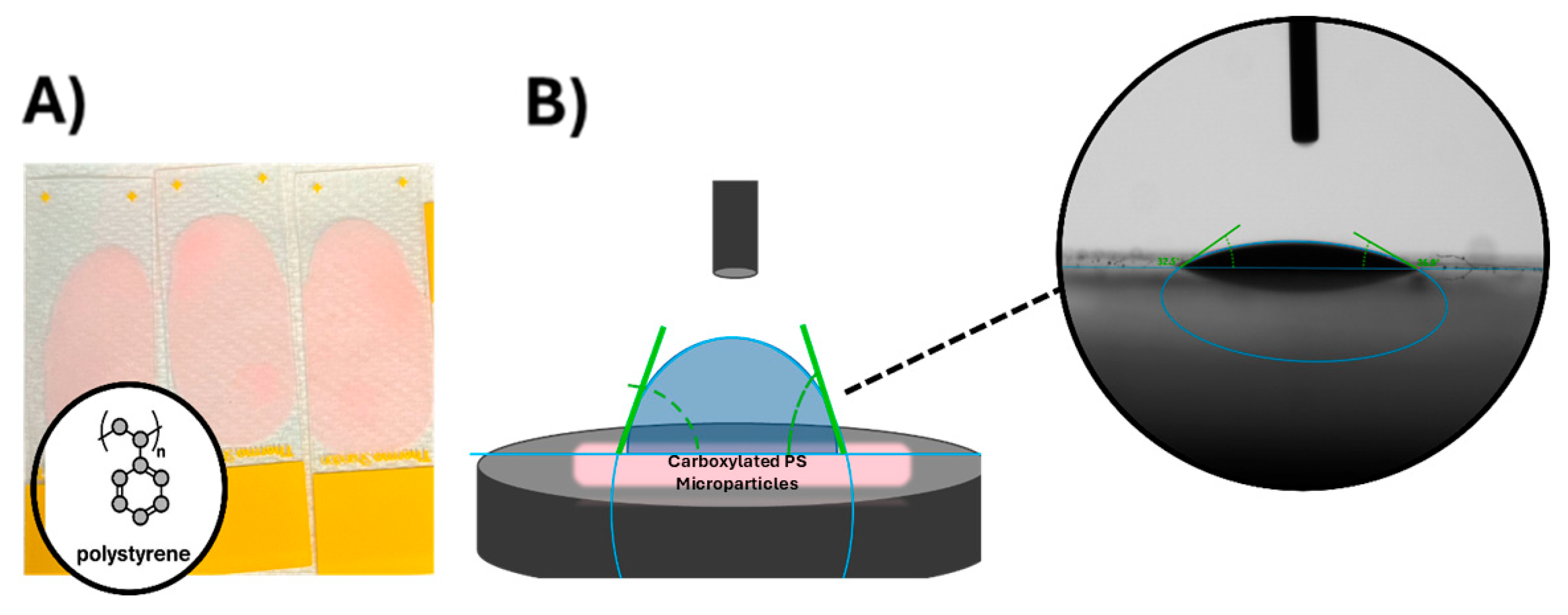
2.4. Cell Preparation for Goniometric Analysis
2.5. Polystyrene Microparticle Preparation for Goniometric Analysis
2.6. Goniometric Analysis for Contact Angle Measurements
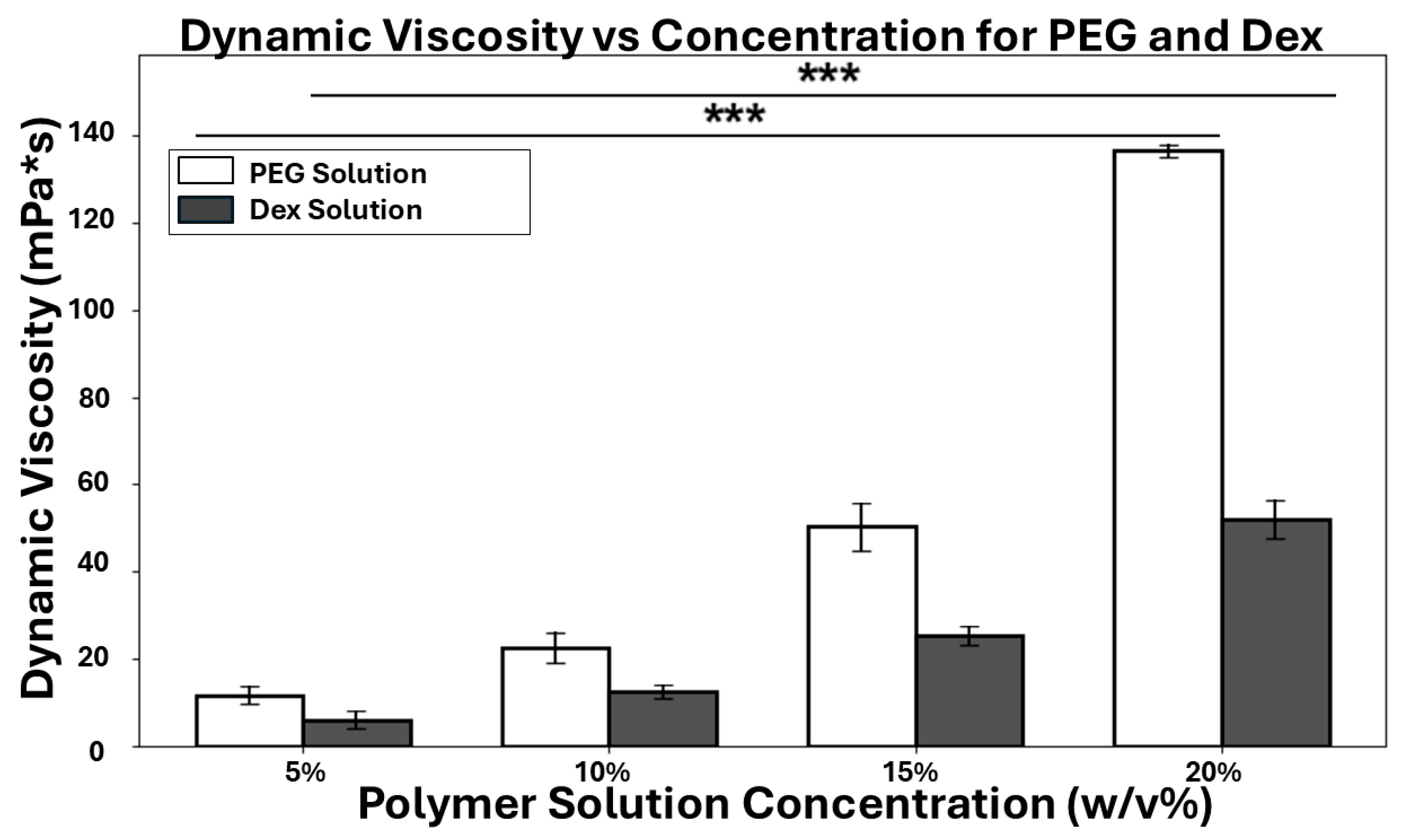
2.7. Dynamic Viscosity Measurement of Polymer Solutions
3. Results and Discussion
3.1. Surface Energy of ATPS Solutions
3.2. Dynamic Viscosity of ATPS Solutions
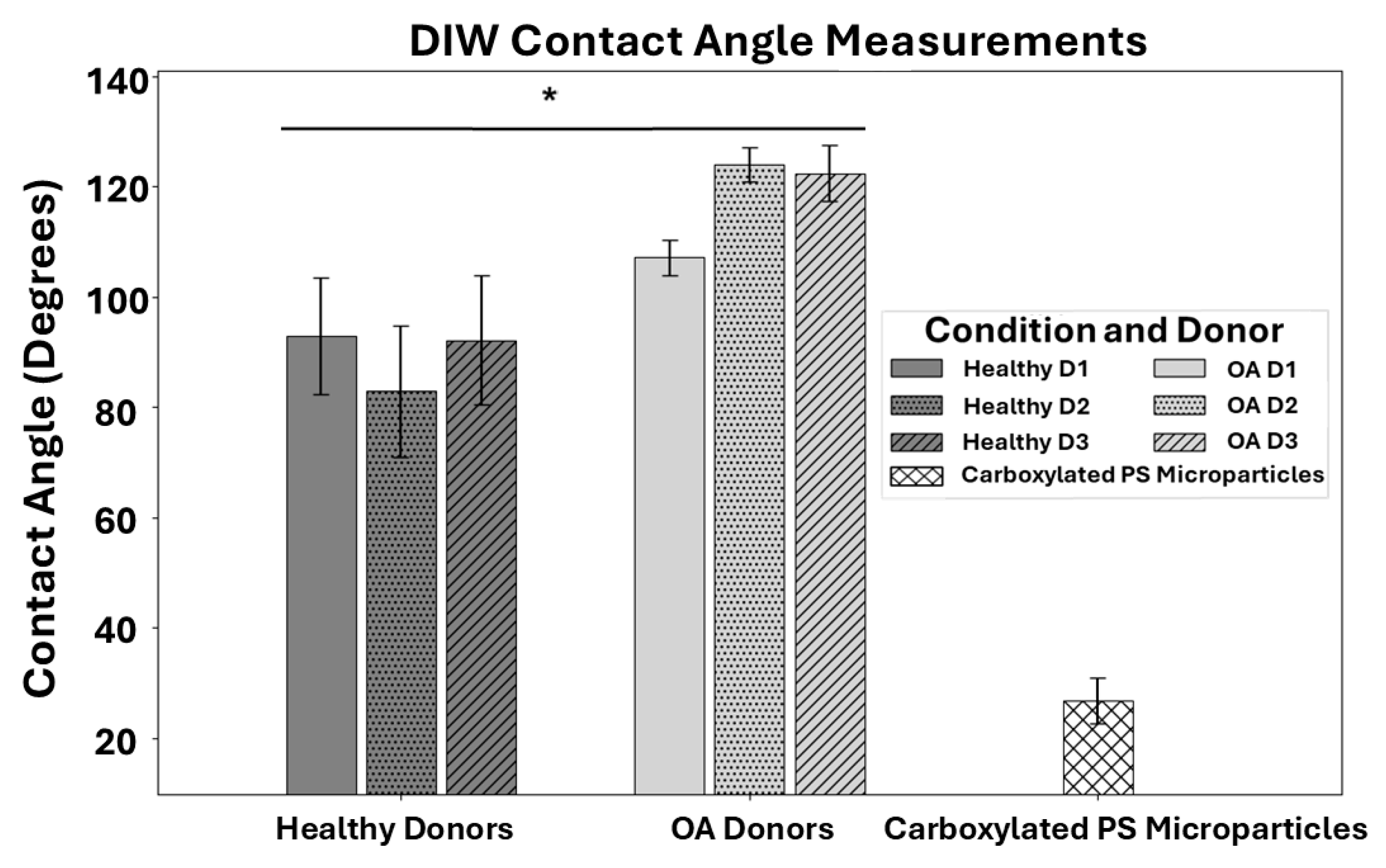
3.3. Contact Angle of Cell Models
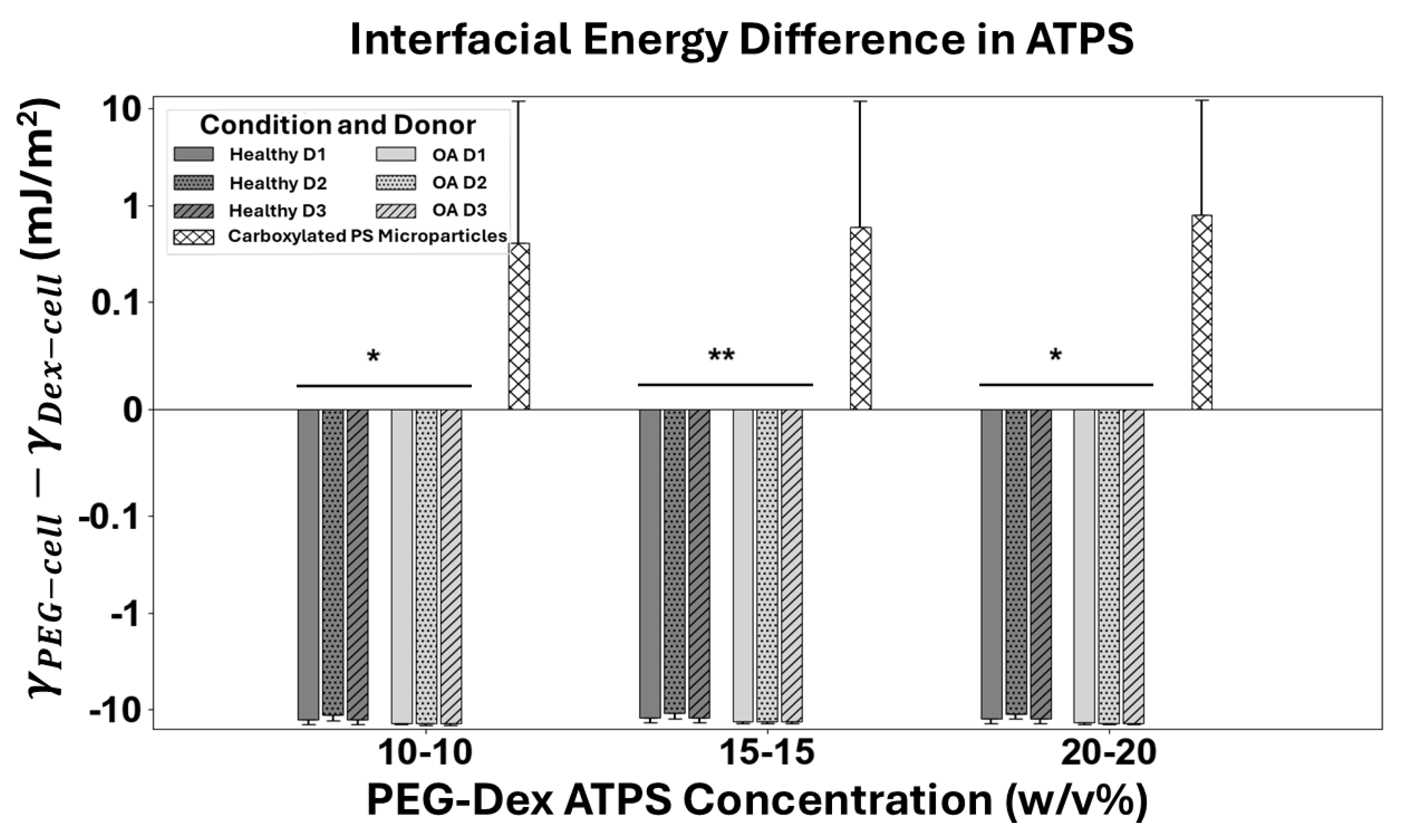
3.4. Interfacial Energy Between Cells and ATPS Solutions
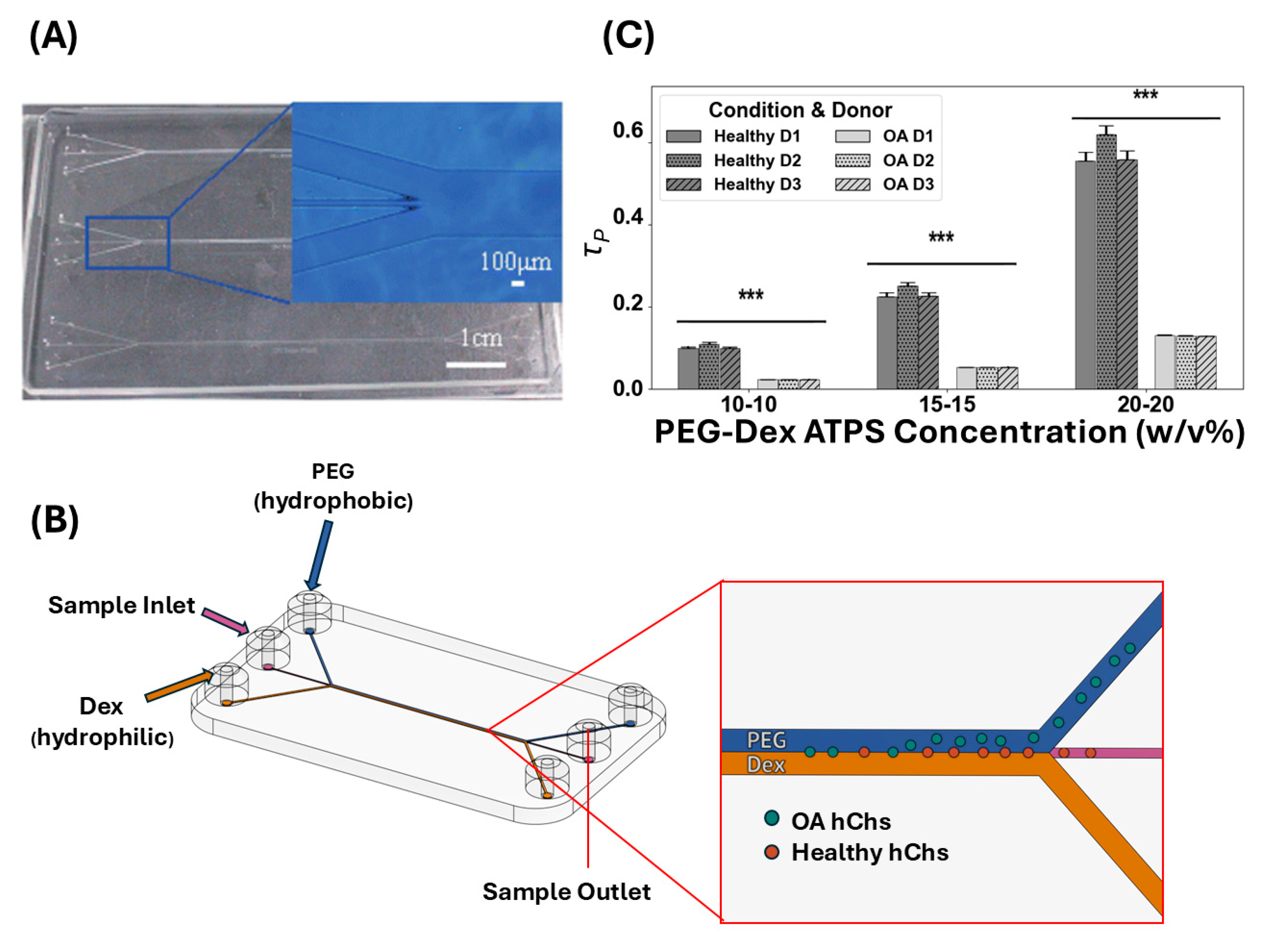
3.5. Interface Translocation Dynamics of hChs
4. Limitations and Future Studies
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| PEG | Polyethylene Glycol |
| Dex | Dextran |
| PS | Polystyrene |
| AFM | Atomic Force Microscope |
| ATPS | Aqueous Two-Phase System |
| MACS | Magnetic Activated Cell Sorting |
| FACS | Fluorescent Activated Cell Sorting |
| OA | Osteoarthritis |
| DIW | Deionized Water |
| GAG | Glycosaminoglycan |
| DMEM | Dulbecco’s Modified Eagle Medium |
| PBS | Phosphate-Buffered Saline |
| hChs | Human Chondrocytes |
| LMM | Linear Mixed Model |
| τp | Partitioning Time |
References
- Dalili, A.; Samiei, E.; Hoorfar, M. A review of sorting, separation and isolation of cells and microbeads for biomedical applications: Microfluidic approaches. Analyst 2019, 144, 87–113. [Google Scholar] [CrossRef]
- Wang, H.-Y.; Bharti, D.; Levental, I. Membrane Heterogeneity Beyond the Plasma Membrane. Front. Cell Dev. Biol. 2020, 8, 580814. [Google Scholar] [CrossRef] [PubMed]
- Miwa, H.; Dimatteo, R.; de Rutte, J.; Ghosh, R.; Di Carlo, D. Single-cell sorting based on secreted products for functionally defined cell therapies. Microsyst. Nanoeng. 2022, 8, 84. [Google Scholar] [CrossRef]
- Witek, M.A.; Freed, I.M.; Soper, S.A. Cell Separations and Sorting. Anal. Chem. 2020, 92, 105–131. [Google Scholar] [CrossRef]
- Bacon, K.; Lavoie, A.; Rao, B.M.; Daniele, M.; Menegatti, S. Past, Present, and Future of Affinity-based Cell Separation Technologies. Acta Biomater. 2020, 112, 29–51. [Google Scholar] [CrossRef]
- Sutermaster, B.A.; Darling, E.M. Considerations for high-yield, high-throughput cell enrichment: Fluorescence versus magnetic sorting. Sci. Rep. 2019, 9, 227. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.-J.; Olsthoorn, R.C.; Zeng, Y.; Bakkum, T.; Kros, A.; Boyle, A.L. Magnetic-Activated Cell Sorting Using Coiled-Coil Peptides: An Alternative Strategy for Isolating Cells with High Efficiency and Specificity. ACS Appl. Mater. Interfaces 2021, 13, 11621–11630. [Google Scholar] [CrossRef]
- Civelekoglu, O.; Frazier, A.B.; Sarioglu, A.F. The Origins and the Current Applications of Microfluidics-Based Magnetic Cell Separation Technologies. Magnetochemistry 2022, 8, 10. [Google Scholar] [CrossRef]
- Duong, P.; Chung, A.; Bouchareychas, L.; Raffai, R.L.; Hancock, R. Cushioned-Density Gradient Ultracentrifugation (C-DGUC) improves the isolation efficiency of extracellular vesicles. PLoS ONE 2019, 14, e0215324. [Google Scholar] [CrossRef]
- Graham, J. Biological Centrifugation; Taylor & Francis: London, UK, 2001. [Google Scholar]
- Singla, M.; Sit, N. Theoretical Aspects and Applications of Aqueous Two-Phase Systems. ChemBioEng Rev. 2023, 10, 65–80. [Google Scholar] [CrossRef]
- Zhang, X.; Han, M.; Han, S.; Zong, W. Aqueous two-phase system (ATPS): From basic science to applications. RSC Adv. 2025, 15, 9041–9054. [Google Scholar] [CrossRef] [PubMed]
- Segaran, A.; Chua, L.S. Review of recent applications and modifications of aqueous two-phase system for the separation of biomolecules. Int. J. Biol. Macromol. 2024, 276, 133856. [Google Scholar] [CrossRef]
- Gerson, D.F. Cell surface energy, contact angles and phase partition. I. Lymphocytic Cell Lines Biphasic Aqueous mixtures. Biochim. Biophys. Acta (BBA)—Biomembr. 1980, 602, 269–280. [Google Scholar] [CrossRef]
- Han, C.; Takayama, S.; Park, J. Formation and manipulation of cell spheroids using a density adjusted PEG/DEX aqueous two phase system. Sci. Rep. 2015, 5, 11891. [Google Scholar] [CrossRef]
- Ahmed, T.; Yamanishi, C.; Kojima, T.; Takayama, S. Aqueous Two-Phase Systems and Microfluidics for Microscale Assays and Analytical Measurements. Annu. Rev. Anal. Chem. 2021, 14, 231–255. [Google Scholar] [CrossRef]
- Yamada, M.; Kasim, V.; Nakashima, M.; Edahiro, J.; Seki, M. Continuous cell partitioning using an aqueous two-phase flow system in microfluidic devices. Biotechnol. Bioeng. 2004, 88, 489–494. [Google Scholar] [CrossRef]
- Soohoo, J.R.; Walker, G.M. Microfluidic aqueous two phase system for leukocyte concentration from whole blood. Biomed. Microdevices 2009, 11, 323–329. [Google Scholar] [CrossRef]
- Nam, K.-H.; Chang, W.-J.; Hong, H.; Lim, S.-M.; Kim, D.-I.; Koo, Y.-M. Continuous-Flow Fractionation of Animal Cells in Microfluidic Device Using Aqueous Two-Phase Extraction. Biomed. Microdevices 2005, 7, 189–195. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Fu, L.; Duan, Y.; Bai, Y.; Wang, X.; Sun, X.; Liu, C.; Zhang, B.; Di, Z. Effect of organic solvents on the conductivity of polyethylene glycol-based deep eutectic solvents. J. Mol. Liq. 2022, 346, 117038. [Google Scholar] [CrossRef]
- Hoorfar, M.; Kurz, M.A.; Policova, Z.; Hair, M.L.; Neumann, A.W. Do Polysaccharides Such as Dextran and Their Monomers Really Increase the Surface Tension of Water? Langmuir 2006, 22, 52–56. [Google Scholar] [CrossRef] [PubMed]
- Kanduč, M.; Schneck, E.; Netz, R.R. Understanding the “Berg limit”: The 65° contact angle as the universal adhesion threshold of biomatter. Phys. Chem. Chem. Phys. 2024, 26, 713–723. [Google Scholar] [CrossRef]
- Matta, C.; Zhang, X.; Liddell, S.; Smith, J.R.; Mobasheri, A. Label-free proteomic analysis of the hydrophobic membrane protein complement in articular chondrocytes: A technique for identification of membrane biomarkers. Biomarkers 2015, 20, 572–589. [Google Scholar] [CrossRef]
- Li, D.; Neumann, A.W. Equation of state for interfacial tensions of solid-liquid systems. Adv. Colloid Interface Sci. 1992, 39, 299–345. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Szymczyk, K.; Krawczyk, J.; Jańczuk, B. Components and parameters of solid/surfactant layer surface tension. Colloids Surf. A: Physicochem. Eng. Asp. 2017, 522, 461–469. [Google Scholar] [CrossRef]
- Drelich, J.; Miller, J.D. Examination of Neumann’s Equation-of-State for Interfacial Tensions. J. Colloid Interface Sci. 1994, 167, 217–220. [Google Scholar] [CrossRef]
- Byun, C.K. Partitional Behavior of Janus Dumbbell Microparticles in a Polyethylene Glycol (PEG)-Dextran (DEX) Aqueous Two-Phase System (ATPS). Coatings 2022, 12, 415. [Google Scholar] [CrossRef]
- Singh, K.K.; Bart, H.-J. Passage of a Single Bubble through a Liquid–Liquid Interface. Ind. Eng. Chem. Res. 2015, 54, 9478–9493. [Google Scholar] [CrossRef]
- Sinha, A.; Mollah, A.K.; Hardt, S.; Ganguly, R. Particle dynamics and separation at liquid–liquid interfaces. Soft Matter 2013, 9, 5438. [Google Scholar] [CrossRef]
- Tsukamoto, M.; Taira, S.; Yamamura, S.; Morita, Y.; Nagatani, N.; Takamura, Y.; Tamiya, E. Cell separation by an aqueous two-phase system in a microfluidic device. Anal. 2009, 134, 1994. [Google Scholar] [CrossRef]
- Mege, J.L.; Capo, C.; Benoliel, A.M.; Foa, C.; Bongrand, P. Nonspecific Cell Surface Properties: Contact Angle of Water on Dried Cell Monolayers. Immunol. Commun. 1984, 13, 211–227. [Google Scholar] [CrossRef]
- Majhy, B.; Priyadarshini, P.; Sen, A.K. Effect of surface energy and roughness on cell adhesion and growth—Facile surface modification for enhanced cell culture. RSC Adv. 2021, 11, 15467–15476. [Google Scholar] [CrossRef] [PubMed]
| Group | Surface Energy (mJ/m2) |
|---|---|
| Healthy hChs Donor 1 | 26.75 |
| Healthy hChs Donor 2 | 33.06 |
| Healthy hChs Donor 3 | 27.22 |
| OA hChs Donor 1 | 18.06 |
| OA hChs Donor 2 | 9.01 |
| OA hChs Donor 3 | 9.78 |
| Carboxylated PS Microparticles | 65.93 |
| Group | Concentration (w/v%) | Average | Standard Deviation |
|---|---|---|---|
| PEG—Healthy | 10% | 13.48 | 2.67 |
| 15% | 13.23 | 2.60 | |
| 20% | 12.72 | 2.56 | |
| PEG—OA | 10% | 29.67 | 5.67 |
| 15% | 29.37 | 5.58 | |
| 20% | 28.73 | 5.45 | |
| Dex—Healthy | 10% | 25.79 | 3.46 |
| 15% | 24.99 | 3.46 | |
| 20% | 24.74 | 3.45 | |
| Dex—OA | 10% | 43.58 | 5.71 |
| 15% | 42.74 | 5.70 | |
| 20% | 42.48 | 5.69 | |
| PEG—Carboxylated PS Microparticle | 10% | 0.88 | |
| 15% | 0.95 | ||
| 20% | 1.11 | ||
| Dex—Carboxylated PS Microparticle | 10% | 0.48 | |
| 15% | 0.35 | ||
| 20% | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garibaldi, G.; Alegria, J.; Shayan, A.; Stannert, R.; Abu-Lail, N.I.; Sun, G. Cell Partitioning Design for Microfluidic ATPS Devices: A Dynamic Energy Strategy and Calculation Using Chondrocytes and Model Microparticles. Micromachines 2025, 16, 926. https://doi.org/10.3390/mi16080926
Garibaldi G, Alegria J, Shayan A, Stannert R, Abu-Lail NI, Sun G. Cell Partitioning Design for Microfluidic ATPS Devices: A Dynamic Energy Strategy and Calculation Using Chondrocytes and Model Microparticles. Micromachines. 2025; 16(8):926. https://doi.org/10.3390/mi16080926
Chicago/Turabian StyleGaribaldi, Gabriel, Jimena Alegria, Anita Shayan, Robert Stannert, Nehal I. Abu-Lail, and Gongchen Sun. 2025. "Cell Partitioning Design for Microfluidic ATPS Devices: A Dynamic Energy Strategy and Calculation Using Chondrocytes and Model Microparticles" Micromachines 16, no. 8: 926. https://doi.org/10.3390/mi16080926
APA StyleGaribaldi, G., Alegria, J., Shayan, A., Stannert, R., Abu-Lail, N. I., & Sun, G. (2025). Cell Partitioning Design for Microfluidic ATPS Devices: A Dynamic Energy Strategy and Calculation Using Chondrocytes and Model Microparticles. Micromachines, 16(8), 926. https://doi.org/10.3390/mi16080926






