Configuration Synthesis and Performance Analysis of 1T2R Decoupled Wheel-Legged Reconfigurable Mechanism
Abstract
1. Introduction
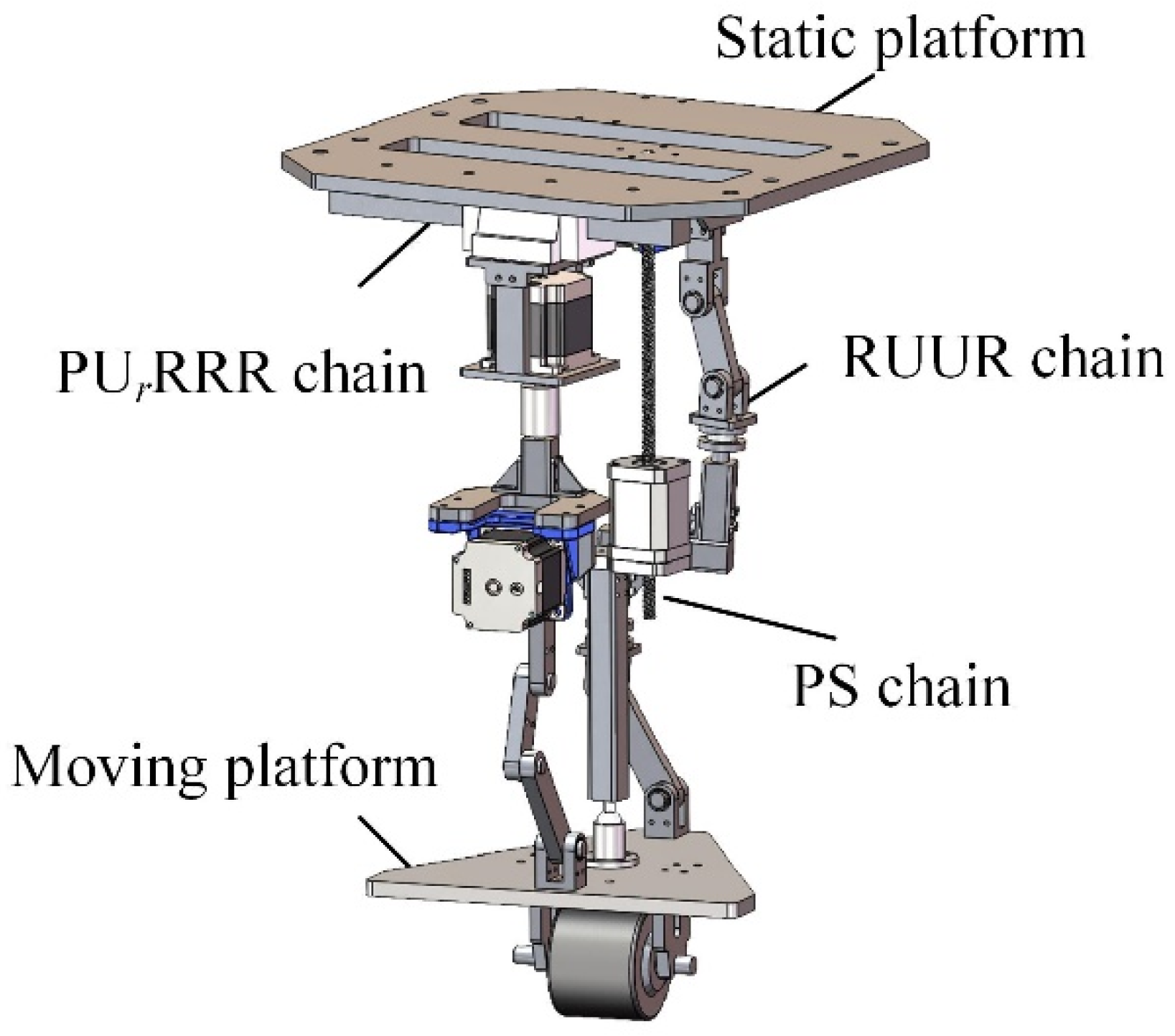
2. Configuration Synthesis of the Reconfigurable Decoupled Mechanical Leg
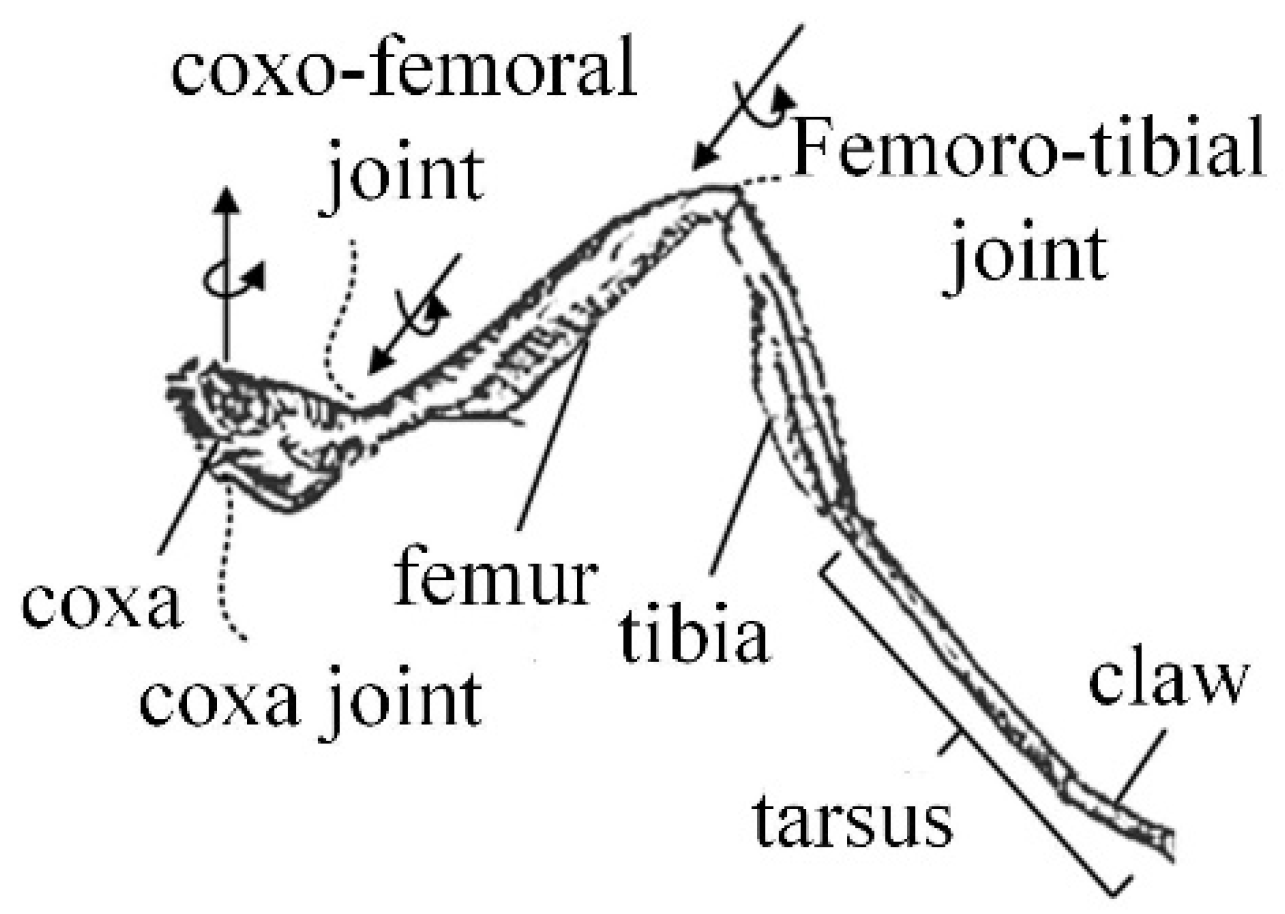
2.1. Analysis of Biological Limbs’ Motion Characteristics
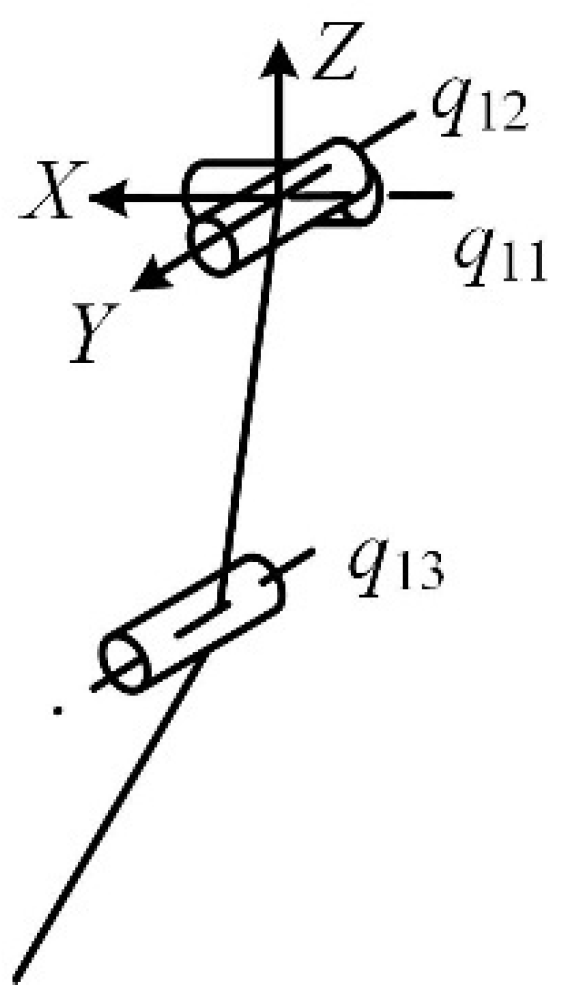
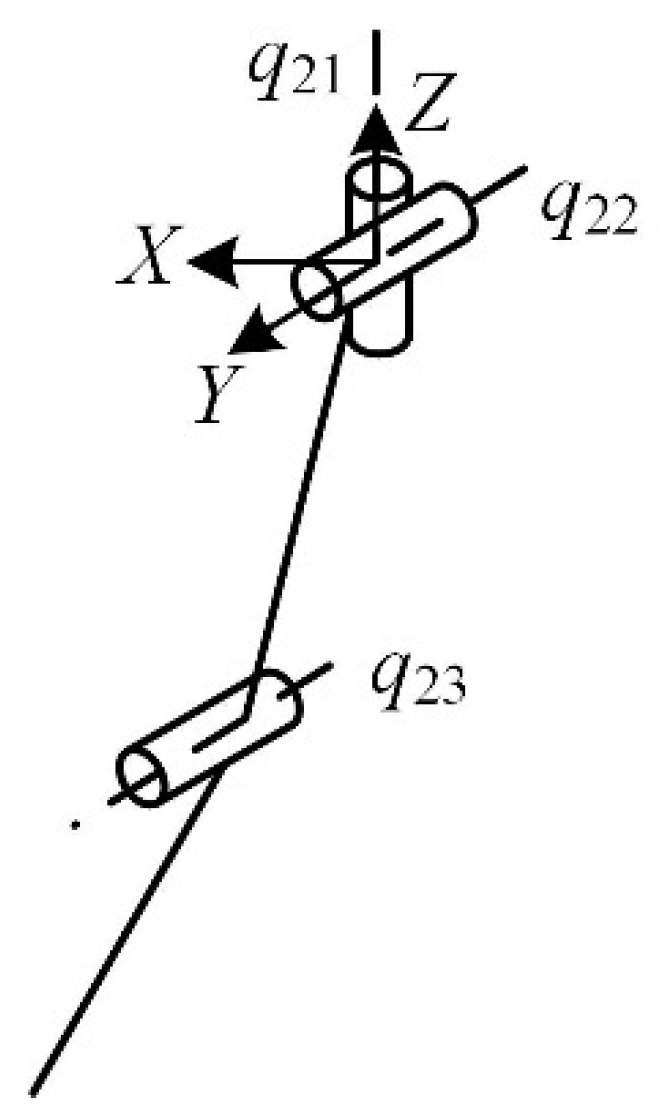
2.2. Input–Output Analysis of 1T2R Decoupled Parallel Mechanism
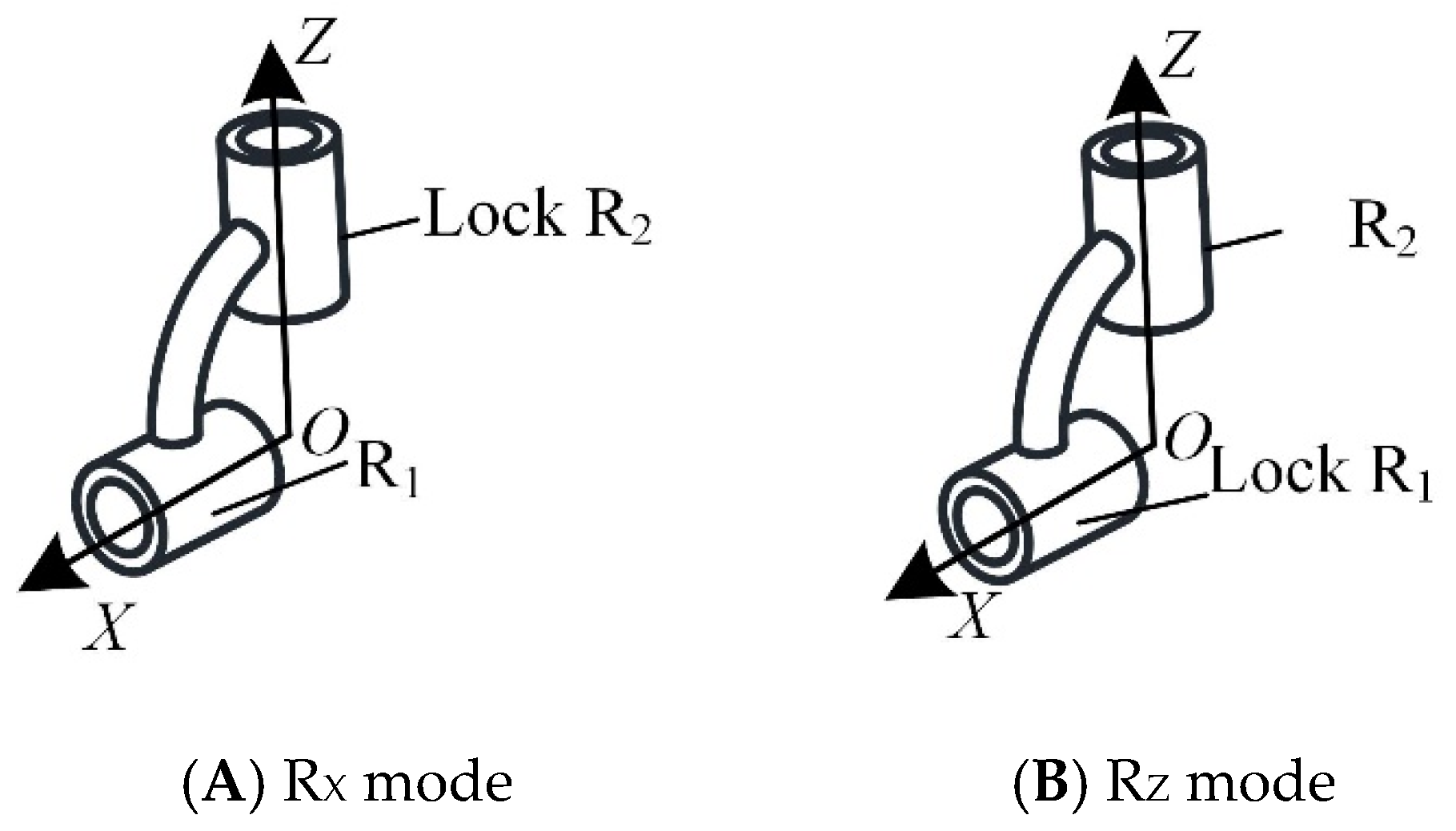
2.3. Reconfiguration Principle of Mechanical Leg
3. Chain Type Synthesis Process of Mechanism
3.1. Configuration Synthesis of Chain I
3.1.1. The First Case
3.1.2. The Second Case
3.1.3. The Third Case
3.2. Configuration Synthesis of Chain II
3.3. Configuration Synthesis of Chain III
- (1)
- The motion characteristics of the constraint chain do not include rotation around the X-axis and Z-axis, but they must include rotation around the Y-axis.
- (2)
- The intersection between the motion characteristics of the constrained chain and those of chains I and II is the translation along the Z-axis.
3.4. Feasible Constraint Model
3.5. Selection of Feasible Constraint Mode
3.5.1. Motion Characteristics of Moving Platform in ABC Constraint Mode
3.5.2. Motion Characteristics of Moving Platform in CDH Constraint Mode
3.5.3. Motion Characteristics of Moving Platform in AEH Constraint Mode
3.5.4. Motion Characteristics of Moving Platform in GHH Constraint Mode
3.6. Extension of Chain Structure Type
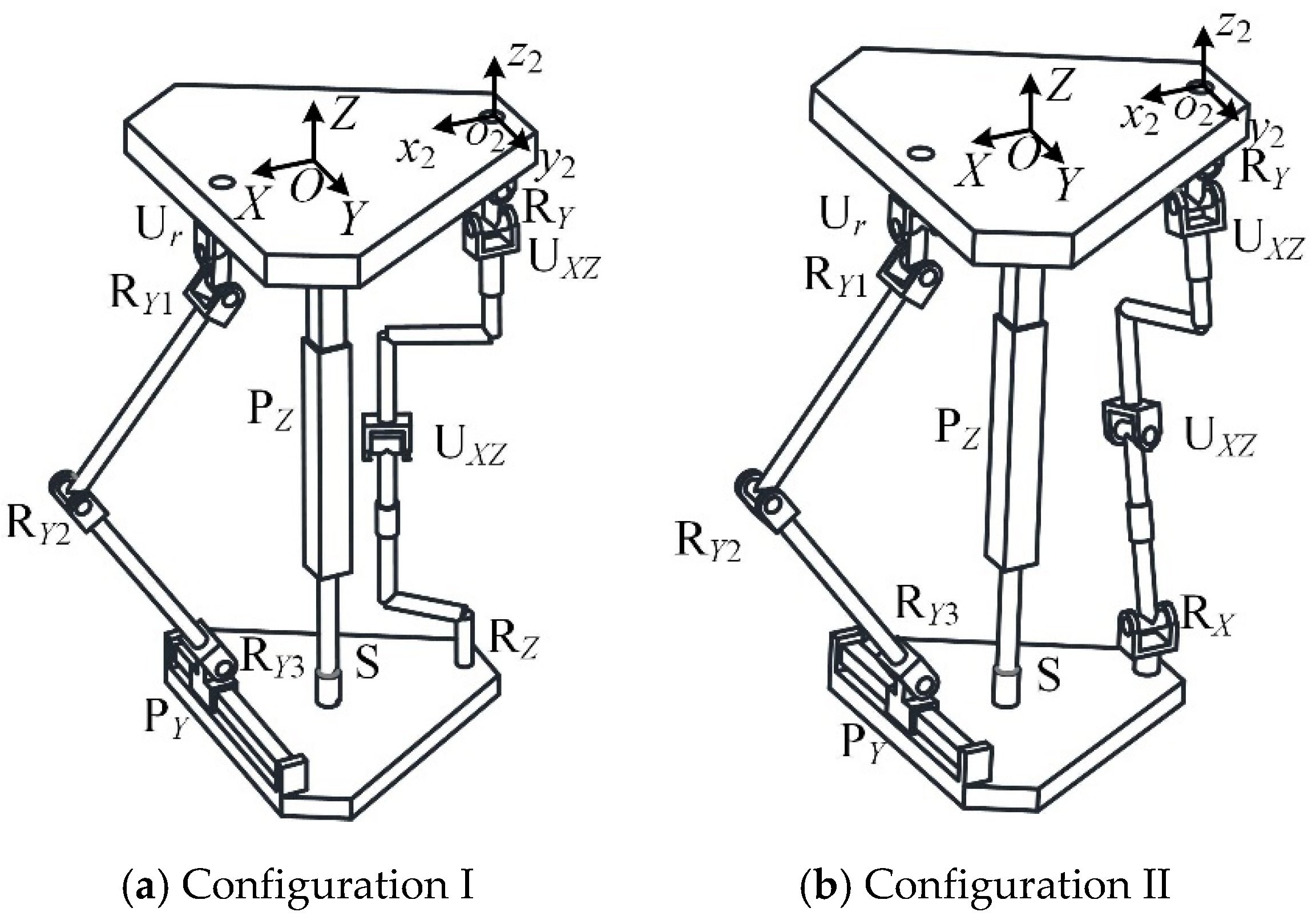
4. Evaluation of Mechanical Leg Mechanism Configuration
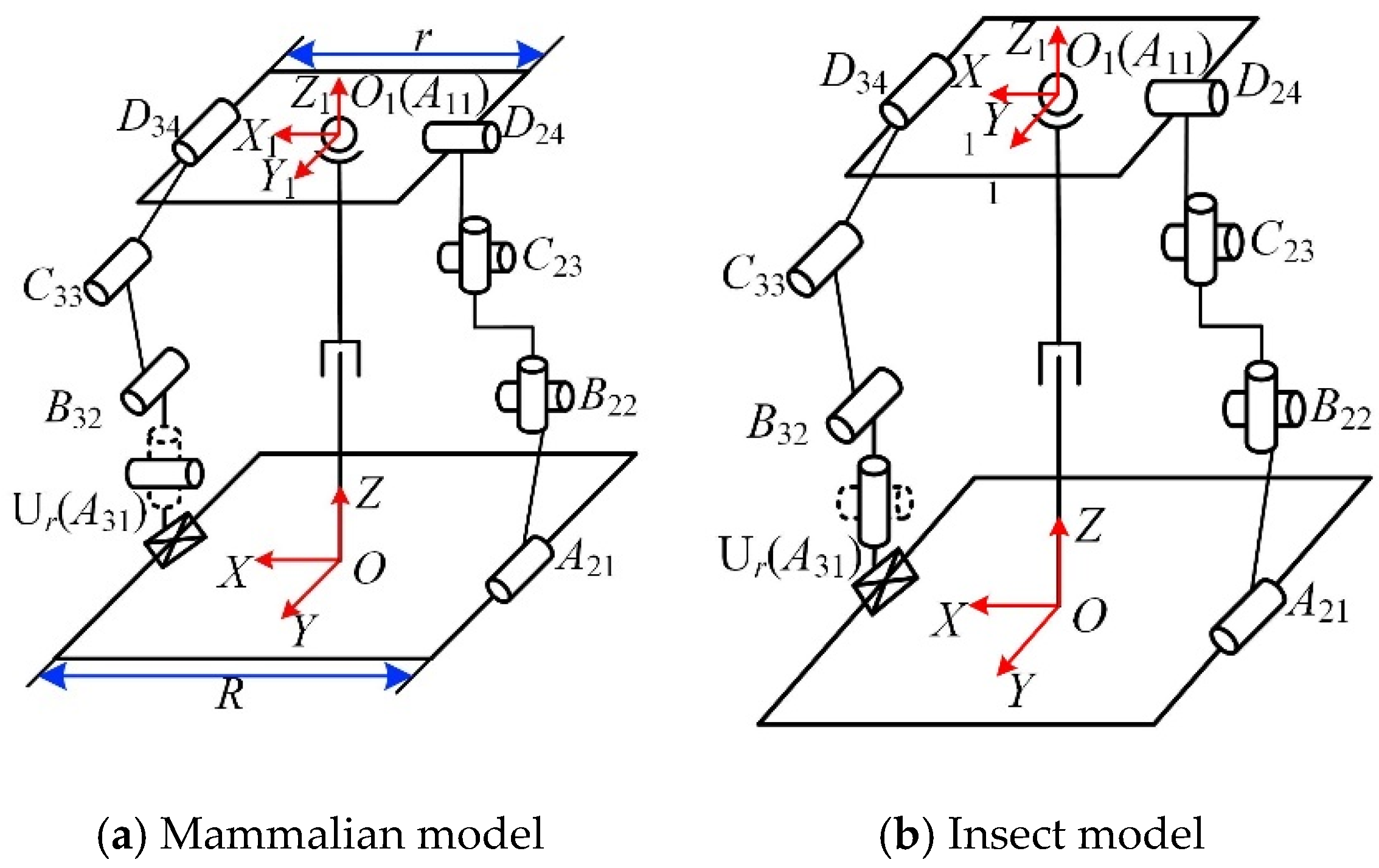
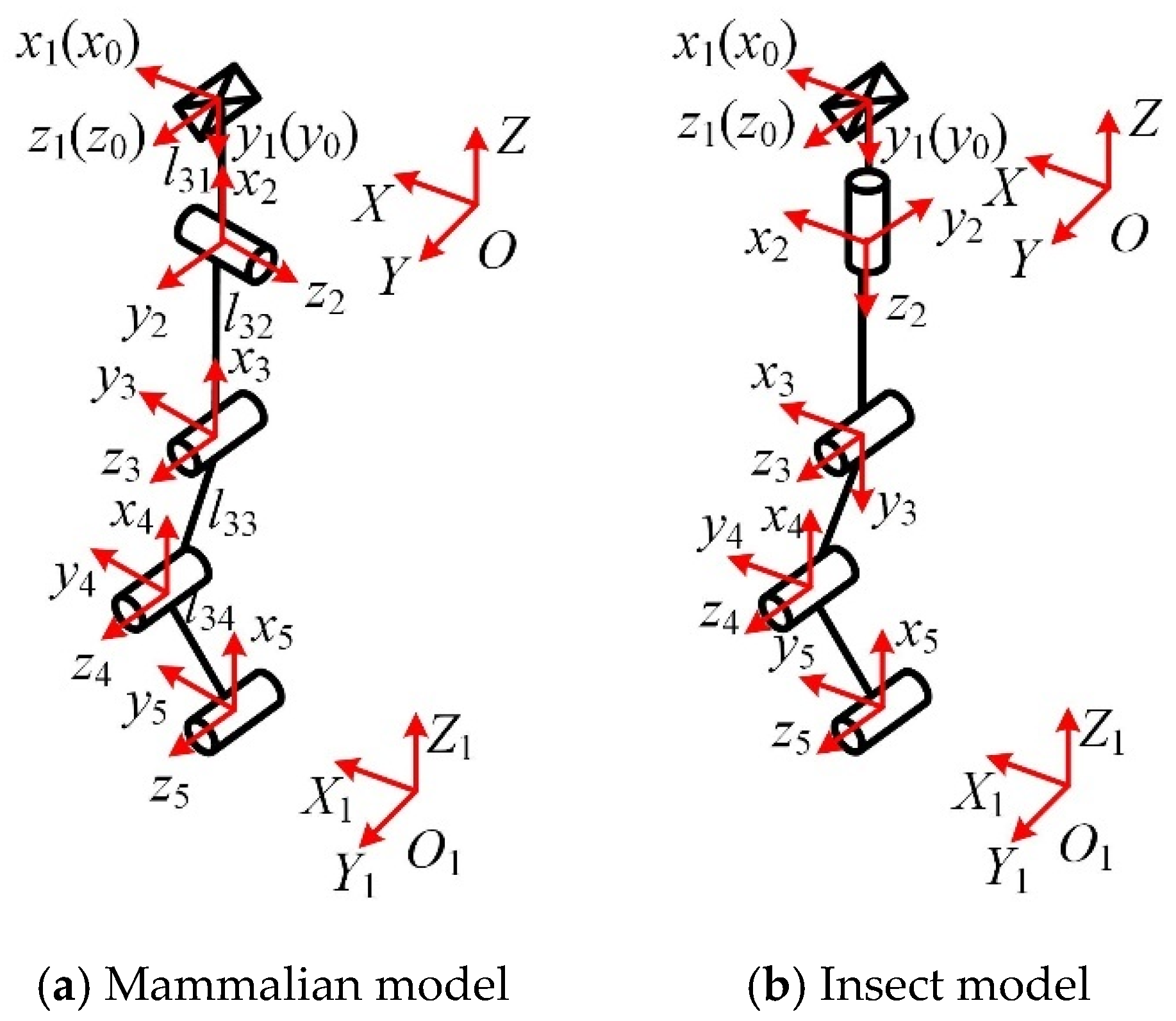
5. Kinematic Analysis of the Reconfigurable Mechanical Leg
5.1. Inverse Position Solution
5.2. Velocity Analysis
6. Performance Analysis and Optimization Design of the Reconfigurable Mechanical Leg
6.1. Workspace Analysis
6.2. Motion/Force Transmission Performance Analysis
6.3. Optimized Design
6.3.1. Design Variables
6.3.2. Objective Function
6.3.3. Constraints
6.3.4. Optimization Examples
6.3.5. Comparison of Results
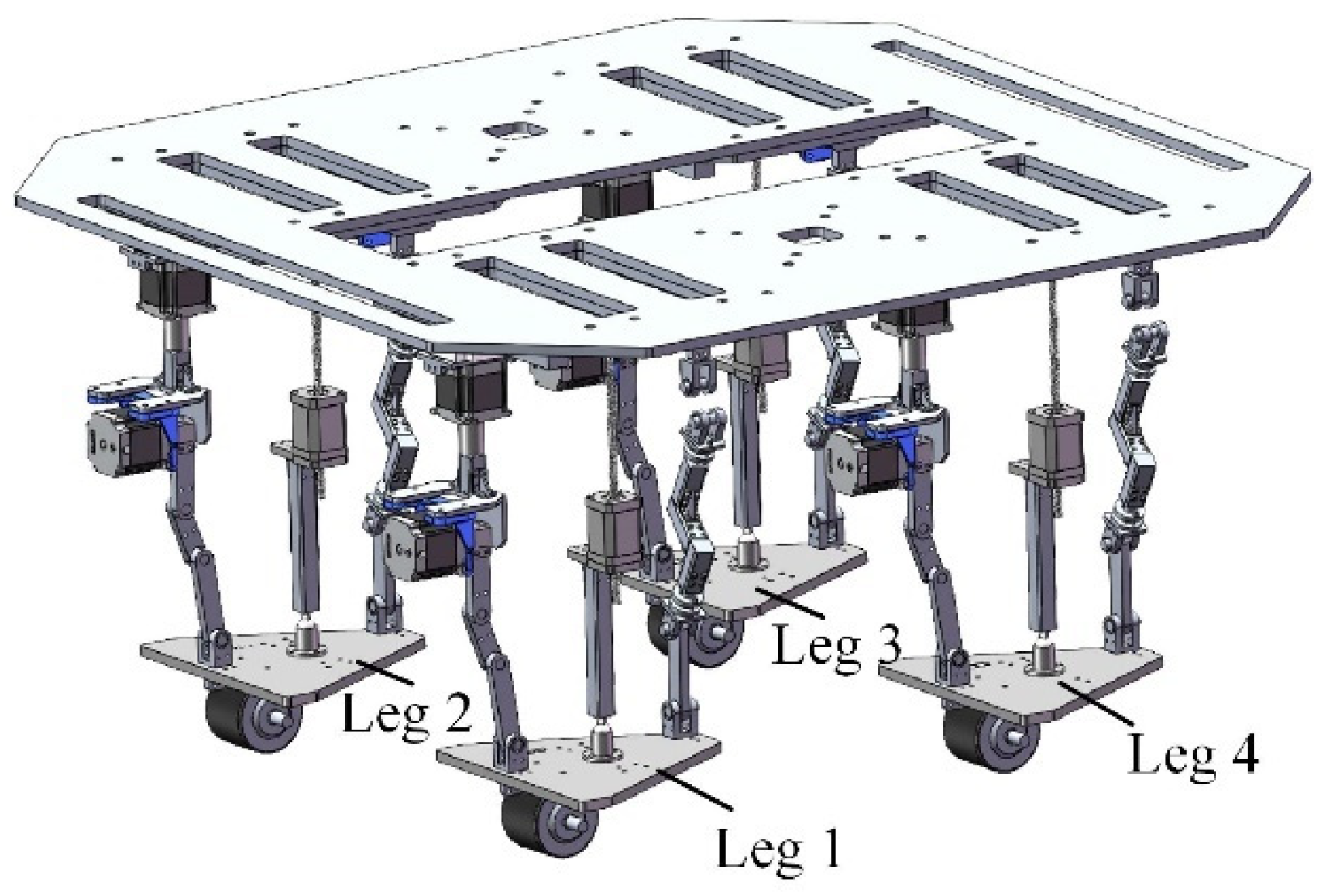
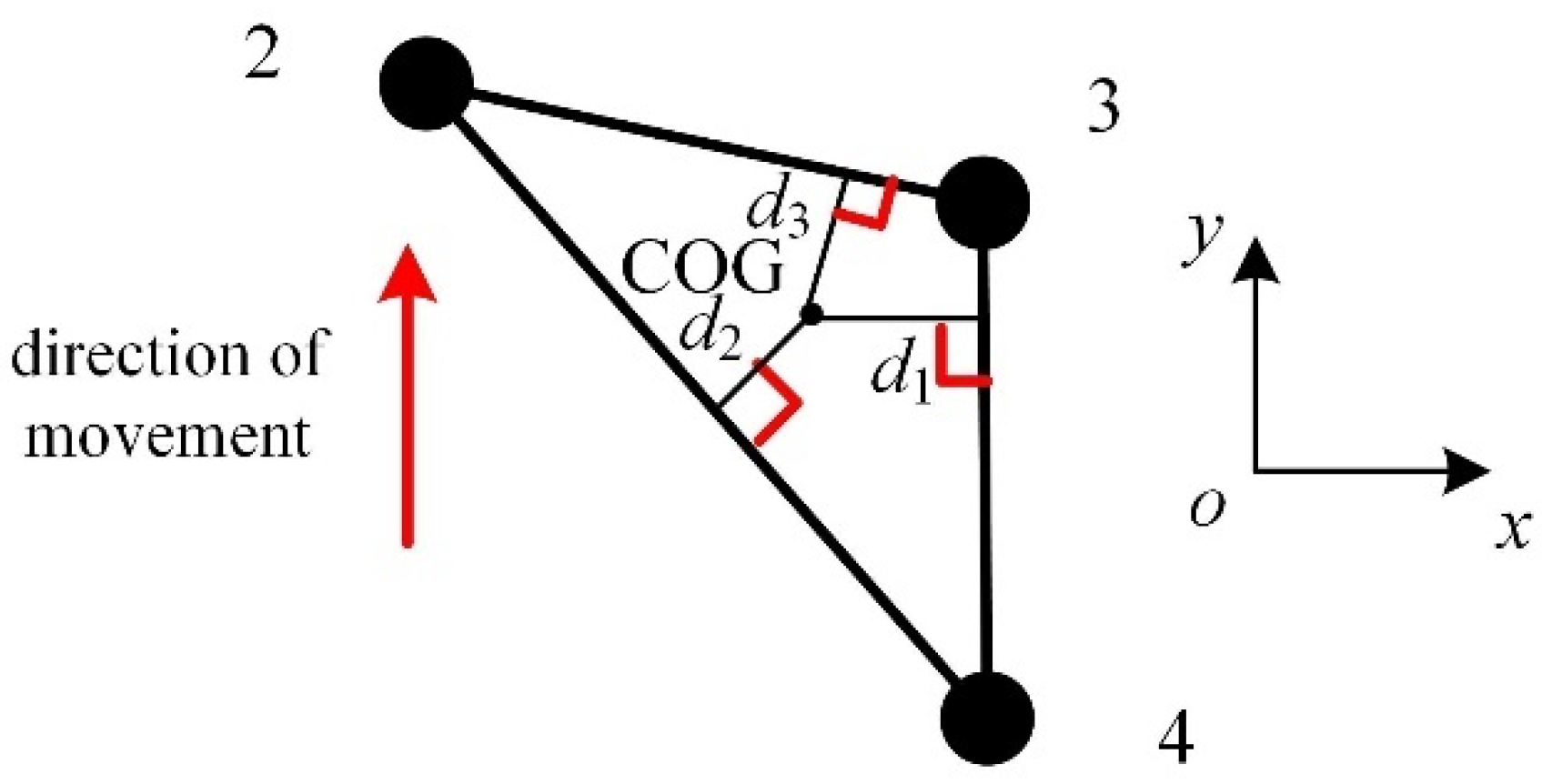
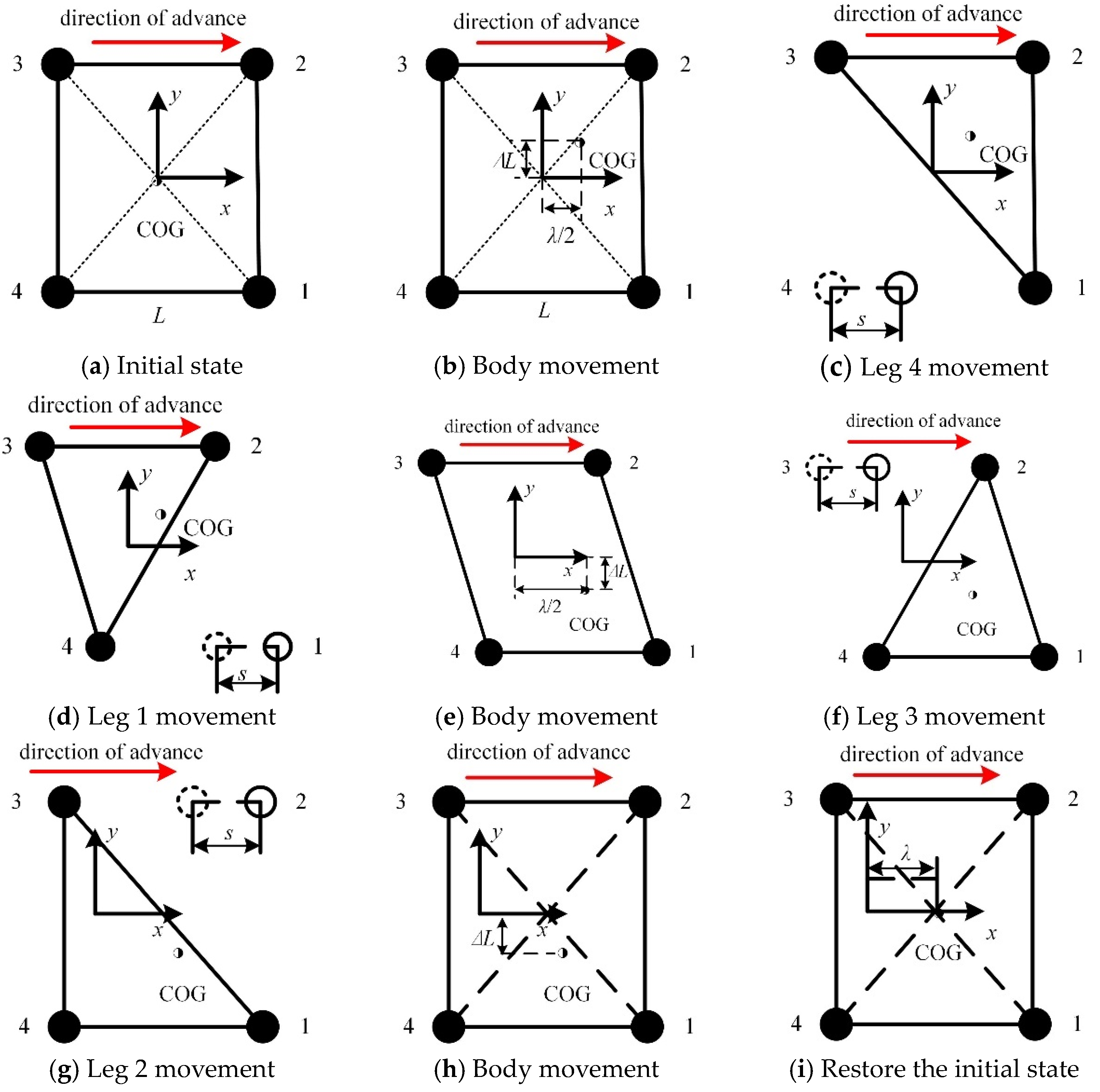
7. Research on Stability of Reconfigurable Four-Wheel-Legged Robot
8. Conclusions
- (1)
- Based on bionic principles and configuration synthesis theory for a decoupled parallel mechanism, a method for configuration synthesis of a reconfigurable decoupled mechanical leg was proposed. The mechanical leg switches between mammalian and insect modes through a change in the lockable universal pair rotating shaft.
- (2)
- Based on the difficulty of fabricating and protecting the chain, as well as its compactness, an evaluation index for the complexity of the chain of the reconfigurable mechanical leg was proposed, and a series of synthesized chain configurations were evaluated. Then, the configuration of each chain of the reconfigurable mechanical leg was determined.
- (3)
- Based on the weighted standard deviation of motion/force transmission performance, a global performance fluctuation index of the motion/force transmission of the mechanical leg was proposed. The proposed index can reflect the fluctuation of the mechanism’s motion performance in the workspace and evaluate its stability.
- (4)
- When the robot is in the walking operation mode, the insect mode is used as the configuration of the reconfigurable mechanical leg. The static stability criterion is used to plan the robot’s gait such that it can meet the needs of the task environment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ni, L.W.; Wu, L.; Zhang, H.S. Parameters uncertainty analysis of posture control of a four-wheel-legged robot with series slow active suspension system. Mech. Mach. Theory 2022, 175, 104966. [Google Scholar] [CrossRef]
- Grand, C.; Benamar, F.; Plumet, F.; Bidaud, P. Stability and traction optimization of a reconfigurable wheel-legged robot. Int. J. Rob. Res. 2014, 23, 1041–1058. [Google Scholar] [CrossRef]
- Grand, C.; Benamar, F.; Plumet, F. Motion kinematics analysis of wheeled-legged rover over 3D surface with posture adaptation. Mech. Mach. Theory 2010, 45, 477–495. [Google Scholar] [CrossRef]
- Klemm, V.; Morra, A.; Salzmann, C.; Tschopp, F.; Bodie, K.; Gulich, L.; Kung, N.; Mannhart, D.; Pfister, C.; Vierneisel, M.; et al. Ascento: A two-wheeled jumping robot. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7515–7521. [Google Scholar]
- Tedeschi, F.; Carbone, G. Design of a novel leg-wheel hexapod walking robot. Robotics 2017, 6, 40. [Google Scholar] [CrossRef]
- Hutter, M.; Gehring, C.; Lauber, A.; Gunther, F.; Bellicoso, C.D.; Tsounis, V.; Fankhauser, P.; Diethelm, R.; Bachmann, S.; Bloesch, M.; et al. ANYmal-toward legged robots for harsh environments. Adv. Rob. 2017, 31, 918–931. [Google Scholar] [CrossRef]
- Hutter, M.; Gehring, C.; Jud, D.; Lauber, A.; Bellicoso, C.D.; Tsounis, V.; Hwangbo, J.; Bodie, K.; Fankhauser, P.; Bloesch, M.; et al. ANYmal a highly mobile and dynamic quadrupedal robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots And Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 38–44. [Google Scholar]
- Niu, J.Y.; Wang, H.B.; Shi, H.M.; Pop, N.; Li, D.; Li, S.S.; Wu, S.Z. Study on structural modeling and kinematics analysis of a novel wheel-legged rescue robot. Int. J. Adv. Rob. Syst. 2018, 15, 1729881417752758. [Google Scholar] [CrossRef]
- Xu, K.; Ding, X.L. Typical gait analysis of a six-legged robot in the context of metamorphic mechanism theory. Chin. J. Mech. Eng. 2013, 26, 771–783. [Google Scholar] [CrossRef]
- Zeng, D.X.; Jing, G.N.; Su, Y.L.; Wang, Y.; Hou, Y.L. A novel decoupled parallel mechanism with two translational and one rotational degree of freedom and its performance indices analysis. Adv. Mech. Eng. 2016, 8, 1687814016646936. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, H.; Qin, Y.L.; Liu, K.; Ge, S.Y.; Zhu, J.Y.; Wang, K.; Yu, J.H.; Ji, W.X.; Zhou, H. Type synthesis of fully-decoupled three-rotational and one-translational parallel mechanisms. Int. J. Adv. Rob. Syst. 2016, 13, 79. [Google Scholar] [CrossRef]
- Xu, Y.D.; Wang, B.; Wang, Z.F.; Zhao, Y.; Liu, W.L.; Yao, J.T.; Zhao, Y.S. Investigations on the principle of full decoupling and type synthesis of 2R1T and 2R parallel mechanisms. Trans. Can. Soc. Mech. Eng. 2019, 43, 263–271. [Google Scholar] [CrossRef]
- Qu, S.W.; Li, R.Q.; Ma, C.S.; Li, H. Type synthesis for lower-mobility decoupled parallel mechanism with redundant constraints. J. Mech. Sci. Technol. 2021, 35, 2657–2666. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Wei, X.M.; Zhang, S.; Chang, Z.Z.; Li, Y.G. Type synthesis of the fully-decoupled two-rotational and one-translational parallel mechanism. J. Mech. Sci. Technol. 2023, 37, 6669–6678. [Google Scholar] [CrossRef]
- Li, S.H.; Wang, S.; Li, H.R.; Wang, Y.J.; Chen, S. Type synthesis of fully decoupled three translational parallel mechanism with closed-loop units and high stiffness. Chin. J. Mech. Eng. 2023, 36, 113. [Google Scholar] [CrossRef]
- Wang, S.; Li, S.H.; Li, H.R.; Zhou, Y.J.; Wang, Y.J.; Wang, X.Y. Type synthesis of 3T2R decoupled hybrid mechanisms with large bearing capacity. J. Mech. Sci. Technol. 2022, 36, 2053–2067. [Google Scholar] [CrossRef]
- Wang, R.Q.; Song, Y.Q.; Dai, J.S. Reconfigurability of the origami-inspired integrated 8R kinematotropic metamorphic mechanism and its evolved 6R and 4R mechanisms. Mech. Mach. Theory 2021, 161, 104245. [Google Scholar] [CrossRef]
- Hu, X.Y.; Liu, H.Z. Design and analysis of full-configuration decoupled actuating reconfigurable parallel spherical joint. J. Mech. Sci. Technol. 2022, 36, 933–945. [Google Scholar] [CrossRef]
- Palpacelli, M.C.; Carbonari, L.; Palmieri, G. Details on the design of a lockable spherical joint for robotic applications. J. Intell. Robot. Syst. 2016, 81, 169–179. [Google Scholar] [CrossRef]
- Ye, W.; Chai, X.X.; Zhang, K.T. Kinematic modeling and optimization of a new reconfigurable parallel mechanism. Mech. Mach. Theory 2020, 149, 103850. [Google Scholar] [CrossRef]
- Yuan, Y.T.; Li, D.L.; Zhang, D.H. Configuration change and kinematics analysis of a novel reconfigurable parallel mechanism with metamorphic joint. In Proceedings of the 2024 6th International Conference on Reconfigurable Mechanisms and Robots, Chicago, IL, USA, 23–26 June 2024; pp. 231–238. [Google Scholar]
- Kuang, Y.L.; Qu, H.B.; Li, X.; Wang, X.L.; Guo, S. Design and singularity analysis of a parallel mechanism with origami-inspired reconfigurable 5R closed-loop linkages. Robotica 2024, 42, 1861–1884. [Google Scholar] [CrossRef]
- Zhong, Y.H.; Wang, R.X.; Feng, H.S.; Chen, Y.S. Analysis and research of quadruped robot’s legs: A comprehensive review. Int. J. Adv. Rob. Syst. 2019, 16, 1729881419844148. [Google Scholar] [CrossRef]
- Zeng, D.X.; Hou, Y.L.; Lu, W.J.; Chang, W.; Huang, Z. Type synthesis method for the translational decoupled parallel mechanism based on screw theory. J. Harbin Inst. Technol. (New Ser.) 2014, 21, 84–91. [Google Scholar]
- Ding, H.F.; Cao, W.A.; Cai, C.W.; Kecskeméthy, A. Computer-aided structural synthesis of 5-DOF parallel mechanisms and the establishment of kinematic structure databases. Mech. Mach. Theory 2015, 83, 14–30. [Google Scholar] [CrossRef]
- Shen, H.P.; Tang, Y.; Wu, G.L.; Li, J.; Li, T.; Yang, T.L. Design and analysis of a class of two-limb non-parasitic 2T1R parallel mechanism with decoupled motion and symbolic forward position solution-influence of optimal arrangement of limbs onto the kinematics, dynamics and stiffness. Mech. Mach. Theory 2021, 161, 104245. [Google Scholar] [CrossRef]
- He, J.; Gao, F.; Meng, X.D.; Guo, W.Z. Type synthesis for 4-DOF parallel press mechanism using GF set theory. Chin. J. Mech. Eng. 2015, 28, 851–859. [Google Scholar] [CrossRef]
- Caro, S.; Khan, W.A.; Pasini, D.; Angeles, J. The rule-based conceptual design of the architecture of serial Schönflies-motion generators. Mech. Mach. Theory 2010, 45, 251–260. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Jin, Z.L.; Feng, H.B. Type synthesis of a 3-mixed-DOF protectable leg mechanism of a firefighting multi-legged robot based on GF set theory. Mech. Mach. Theory 2018, 130, 567–584. [Google Scholar] [CrossRef]
- Wang, J.S.; Wu, C.; Liu, X.J. Performance evaluation of parallel manipulators: Motion/force transmissibility and its index. Mech. Mach. Theory 2010, 45, 1462–1476. [Google Scholar] [CrossRef]
- Meng, Q.Z.; Xie, F.G.; Liu, X.J. Motion-force interaction performance analyses of redundantly actuated and overconstrained parallel robots with closed-loop subchains. Mech. Mach. Theory 2020, 142, 103304. [Google Scholar] [CrossRef]
- Mcghee, R.B.; Frank, A.A. On stability properties of quadruped creeping gaits. Math. Biosci. 1968, 3, 331–351. [Google Scholar] [CrossRef]
- de Santos, P.G.; Garcia, E.; Estremera, J. Quadrupedal Locomotion: An Introduction to the Control of Four-legged Robots; Springer: London, UK, 2007; pp. 59–60. [Google Scholar]




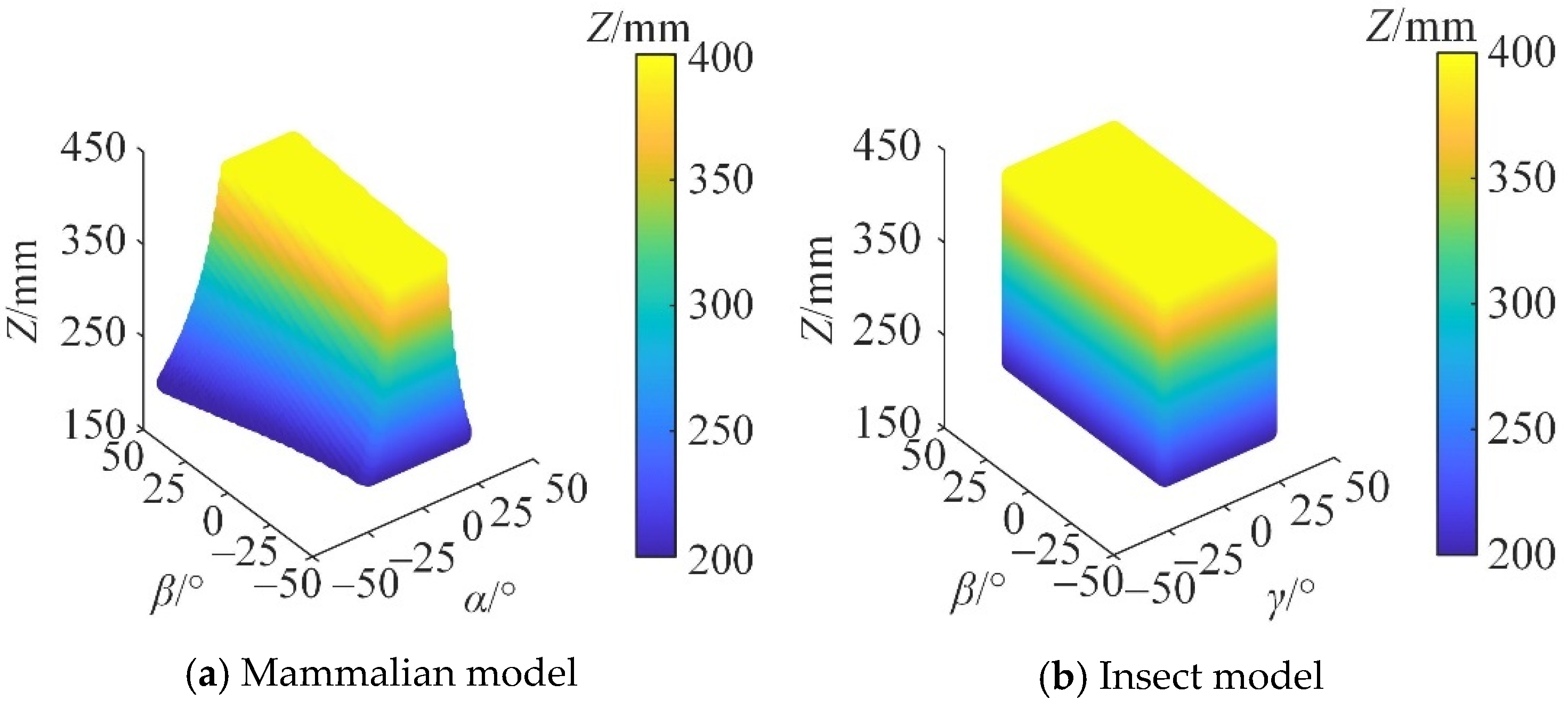
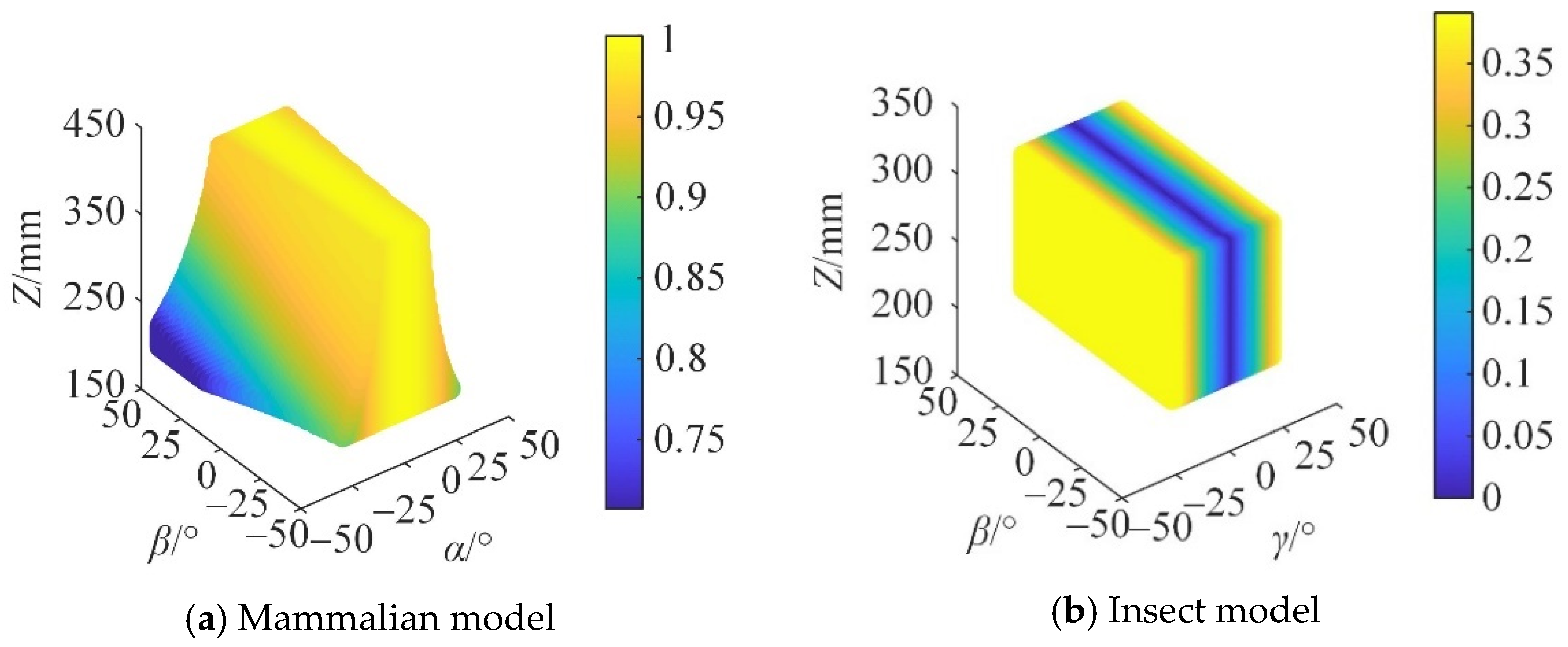
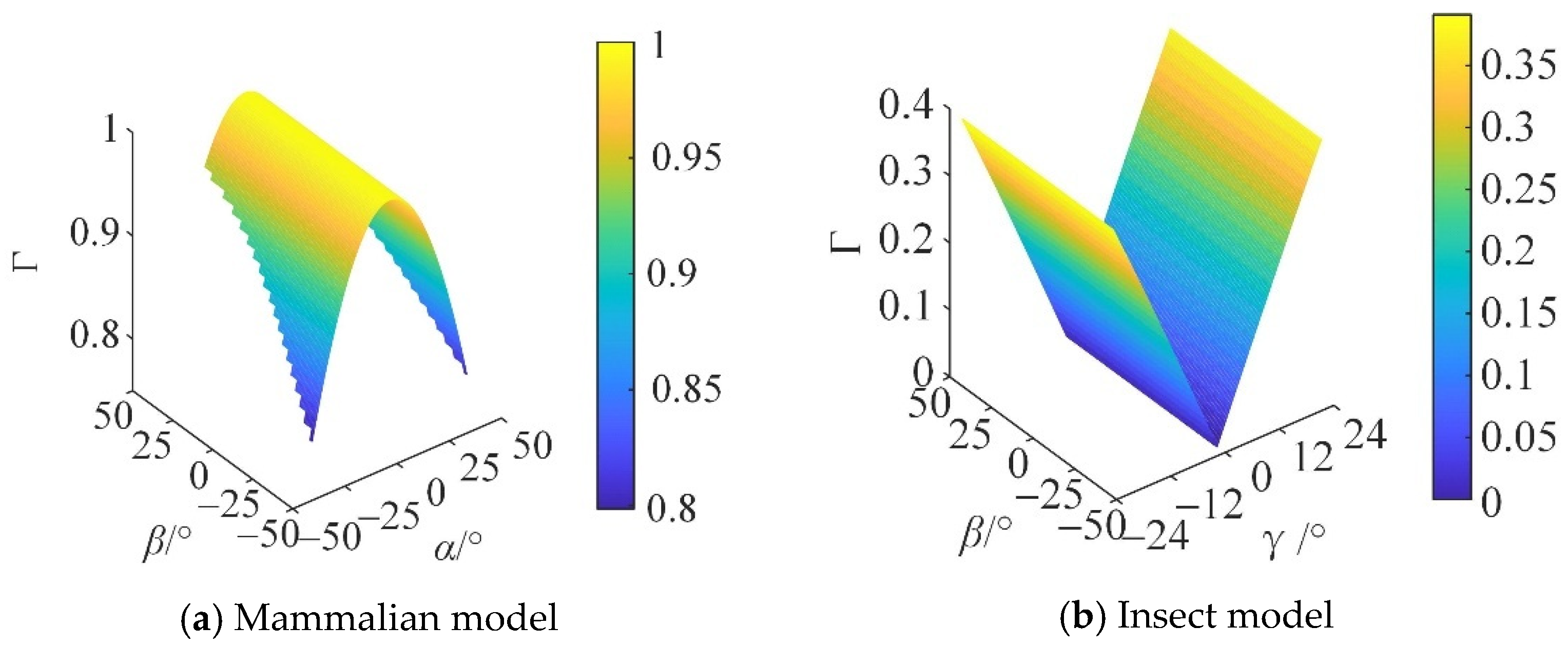
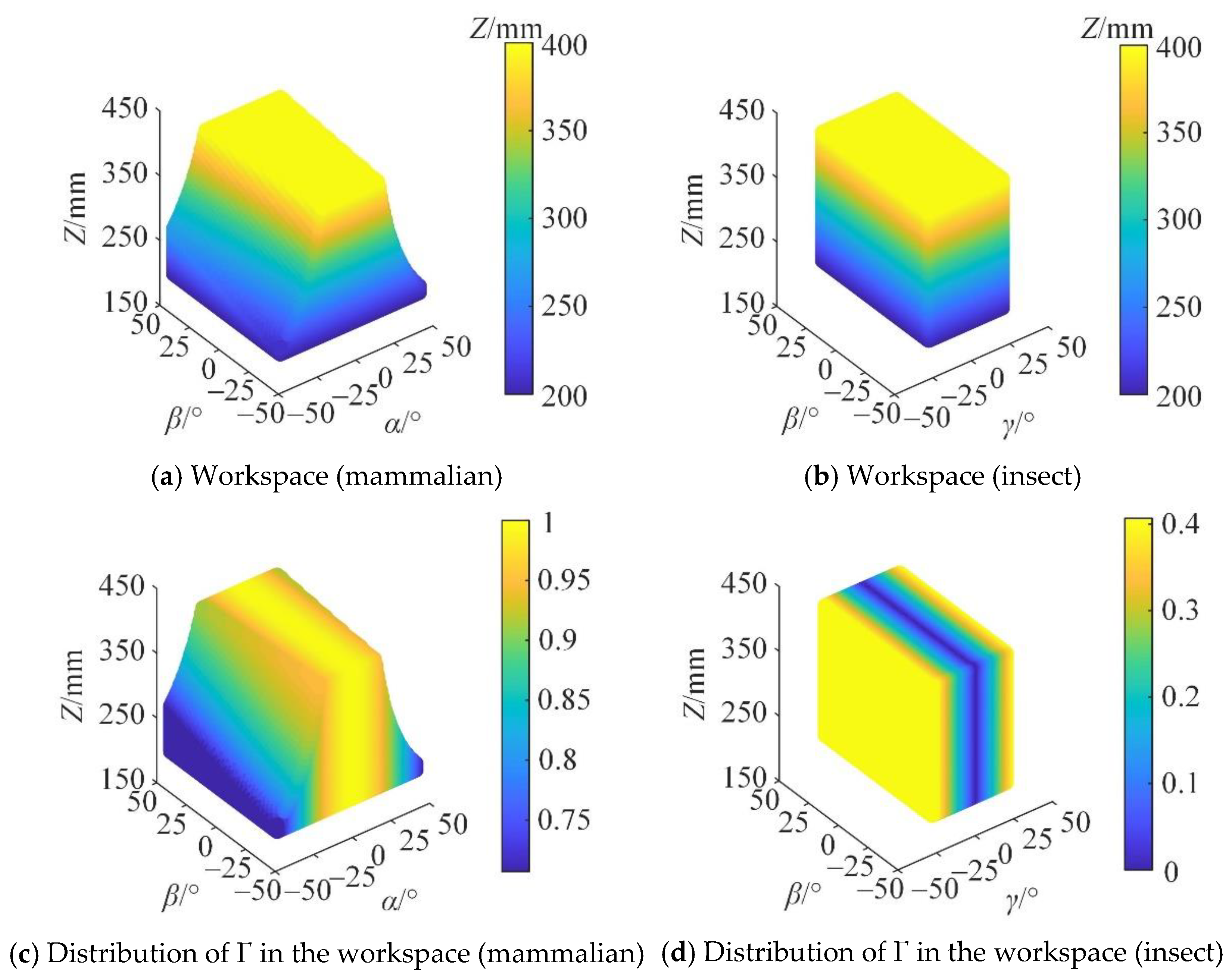
| Driving Category | Characteristics of Degrees of Freedom | Kinematic Pair Type | Chain Type |
|---|---|---|---|
| The first case | 1T3R | 1P3R | PZRXRYRZ |
| 2T3R | 2P3R | PZRXRYRZPX; PZRXRYRZPY | |
| 1P4R | PZRXRYRZ1RZ2 | ||
| 3T3R | 3P3R | PZPXPYRXRYRZ | |
| 2P4R | PZPXRXRYRZ1RZ2; PZPYRXRYRZ1RZ2 | ||
| 1P5R | PZRXRYRZ1RZ2RZ3; | ||
| The second case | 2T3R | 4R1P | RX1RX2RYRZPY |
| 5R | RX1RX2RX3RYRZ | ||
| 3T3R | 4R2P | RX1RX2RYRZPXPY | |
| 5R1P | RX1RX2RX3RYRZPX; RX1RX2RY1RY2RZPY RX1RX2RYRZ1RZ2PY; RX1RX2RYRZ1RZ2PX | ||
| 6R | RX1RX2RYRZ1RZ2RZ3; RX1RX2RX3RYRZ1RZ2 RX1RX2RY1RY2RZ1RZ2; RX1RX2RX3RY1RY2RZ | ||
| The third case | 2T3R | 4R1P | RY1RY2RXRZPX |
| 5R | RY1RY2RXRZ1RZ2 | ||
| 3T3R | 4R2P | RY1RY2RXRZPXPY | |
| 5R1P | RY1RY2RXRZ1RZ2PY; RY1RY2RXRZ1RZ2PX | ||
| 6R | RY1RY2RXRZ1RZ2RZ3 |
| Connectivity | Characteristics of Degrees of Freedom | Kinematic Pair Type | Chain Type |
|---|---|---|---|
| 4 | 1T3R | 3R1P | RYPZRXRZ |
| 5 | 2T3R | 3R2P | RYPYPZRXRZ; RYPXPZRXRZ |
| 4R1P | RYPYRX1RX2RZ; RYPZRX1RX2RZ | ||
| 5R | RYRX1RX2RX3RZ | ||
| 6 | 3T3R | 3R3P | RYPXPYPZRXRZ |
| 4R2P | RYPYPXRX1RX2RZ; RYPZPXRX1RX2RZ; RYPYPZRXRZ1RZ2; RYPXPZRXRZ1RZ2 | ||
| 5R1P | RYPYRX1RX2RZ1RZ2; RYPXRX1RX2RX3RZ; RYPXRX1RX2RZ1RZ2; RYPZRX1RX2RZ1RZ2; RYPZRXRZ1RZ2RZ3 | ||
| 6R | RY1RX1RX2RZ1RZ2RZ3; RYRX1RX2RX3RZ1RZ2 |
| Connectivity | Characteristics of Degrees of Freedom | Kinematic Pair Type | Chain Type |
|---|---|---|---|
| 2 | 1T1R | 1P1R | PZRY |
| 3 | 2T1R | 2P1R | PXPZRY; PZPXRY; PZPYRY |
| 1P2R | PXRY1RY2; PZRY1RY2; RY1PYRY2 | ||
| 3R | RY1RY2RY3 | ||
| 4 | 3T1R | 3P1R | PXPYPZRY |
| 2P2R | PYPXRY1RY2; PYPZRY1RY2 | ||
| 3R1P | PYRY1RY2RY3 |
| Feasible Constraint Pattern | Chain | Degree-of-Freedom Type | Constraint Type |
|---|---|---|---|
| ABC | 1 | 2T3R | A/B |
| 2 | 2T3R | B/A | |
| 3 | 3T2R | C | |
| CDH | 1 | 1T3R/3T3R | D/H |
| 2 | 3T3R/1T3R | H/D | |
| 3 | 3T2R | C | |
| AEH | 1 | 2T3R/3T3R | A/H |
| 2 | 3T3R/2T3R | H/A | |
| 3 | 2T2R | E | |
| GHH | 1 | 3T3R | H |
| 2 | 3T3R | H | |
| 3 | 1T2R | G |
| Chain | Basic Chain Structure | Chain Structure with Multi-Degree-of-Freedom Kinematic Pair | Chain Structure Containing Closed-Loop Structures |
|---|---|---|---|
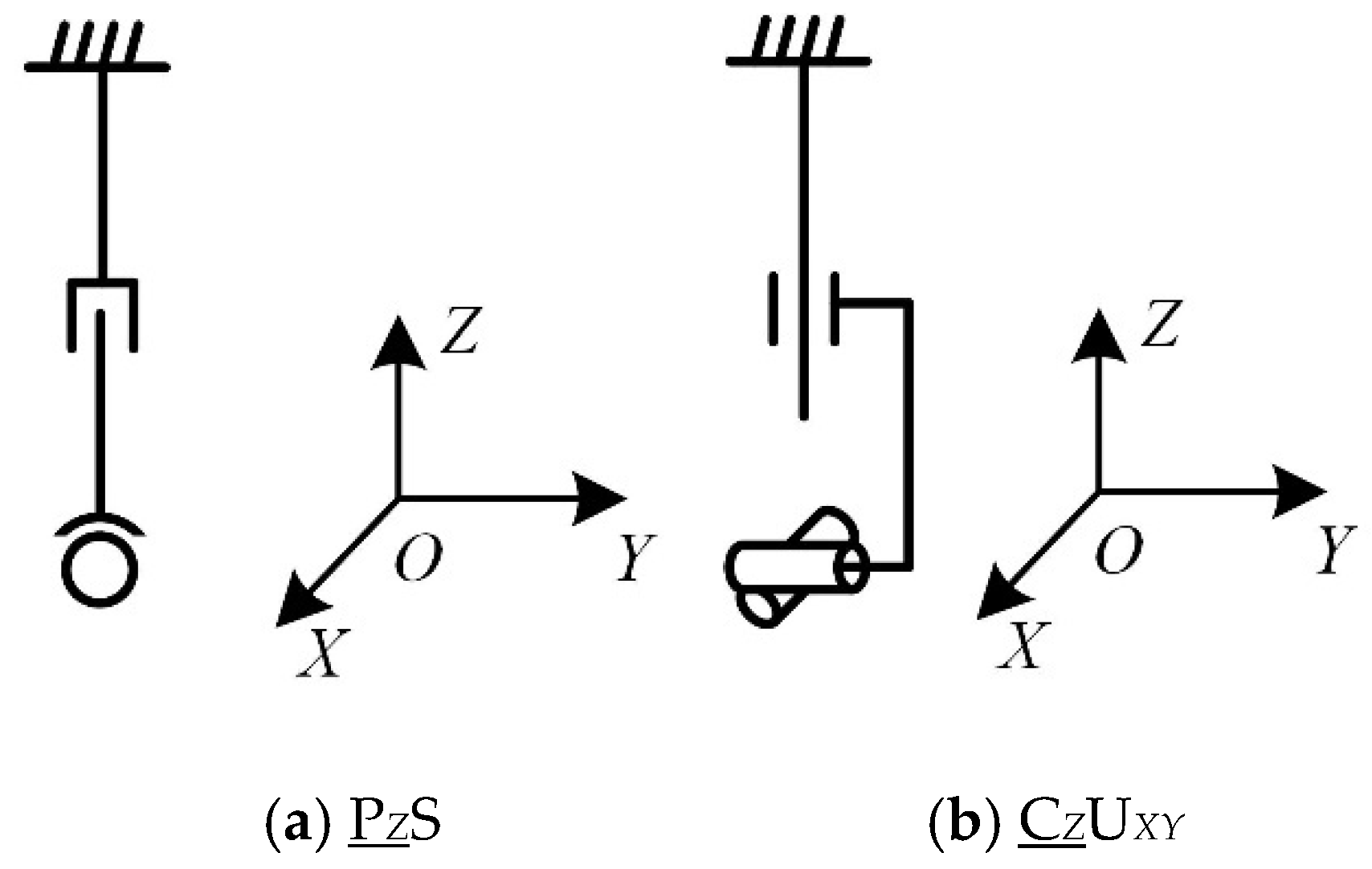
| Chain I | PZRXRYRZ | PZS; CZUXY | — |
| Chain | Basic Chain Structure | Chain Structure with Multi-Degree-of-Freedom Kinematic Pair | Chain Structure Containing Closed-Loop Structures |
|---|---|---|---|
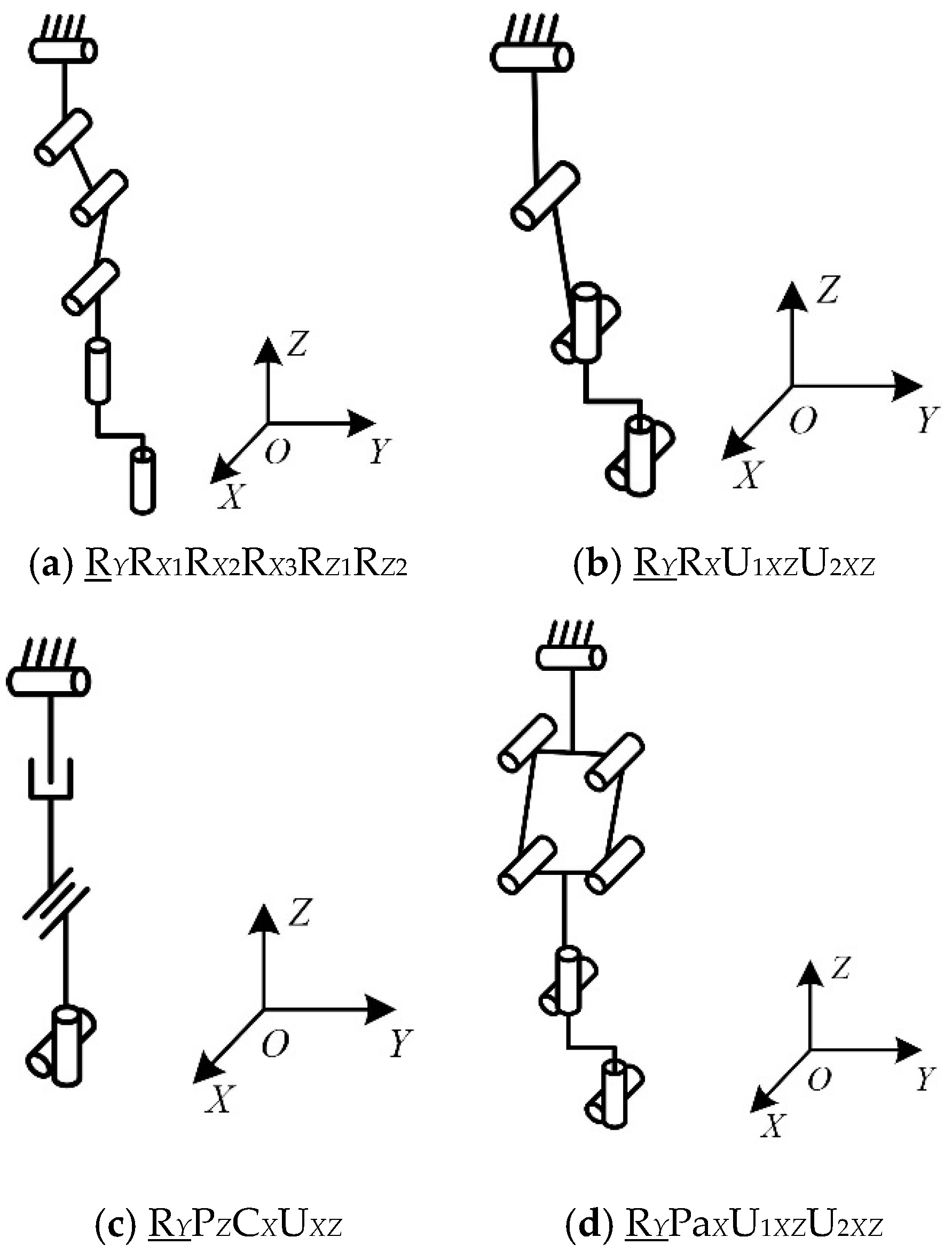
| Chain II | RYPXPYPZRXRZ | RYPXPYPZUXZ | RYPXPYPaYUXZ; RYPX/YPaX/YPaX/YUXZ; RYPaY/XPaX/YPaX/YUXZ |
| RYPXPYPZRXRZ | CYPXPZUXZ; CYCZCX | CYPX/ZPaYUXZ; CYPaYPaYUXZ | |
| RYPYPXRX1RX2RZ | RYPXPYRXUXZ; RYPYCXUXZ; CYCXUXZ | RYPXPaZRXUXZ; RYPaZPaZRXUXZ; RYPaZCXUXZ | |
| RYPZPXRX1RX2RZ | RYPZPXRXUXZ; RYPZCXUXZ; RYRXCZCX | RYPZPaYRXUXZ; RYPaYPaYRXUXZ; RYPaYCXUXZ | |
| RYPYPZRXRZ1RZ2 | RYPYPZRZUXZ; RYPYCZUXZ; CYCZUXZ | RYPYPaXRZUXZ; RYPaXPaXRZUXZ; RYPaXCZUXZ | |
| RYPXPZRXRZ1RZ2 | RYPXPZRZUXZ; RYPXCZUXZ; RYRZCXCZ | RYPXPaYRZUXZ; RYPaYPaYRZUXZ; RYPaYCZUXZ | |
| RYPYRX1RX2RZ1RZ2 | RYPYRXRZUXZ; RYPYU1XZU2XZ; CYPYU1XZU2XZ | RYPaX/ZRXRZUXZ; RYPaX/ZU1XZU2XZ; | |
| RYPXRX1RX2RX3RZ | RYPXRX1RX2UXZ; RYRXCXUXZ; | RYPaY/ZRX1RX2UXZ | |
| RYPXRX1RX2RZ1RZ2 | RYPXRXRZUXZ; RYPXU1XZU2XZ; RYRZCXUXZ | RYPaY/ZRXRZUXZ; RYPaY/ZU1XZU2XZ; | |
| RYPZRX1RX2RZ1RZ2 | RYPZRXRZUXZ; RYPZU1XZU2XZ; RYRXCZUXZ | RYPaY/XRXRZUXZ; RYPaY/XU1XZU2XZ | |
| RYPZRXRZ1RZ2RZ3 | RYPZRZ1RZ2UXZ; RYCZRZUXZ | RYPaY/XRZ1RZ2UXZ | |
| RYRX1RX2RZ1RZ2RZ3 | RYRXRZ1RZ2UXZ; RYRZU1XZU2XZ | — | |
| RYRX1RX2RX3RZ1RZ2 | RYRZRX1RX2UXZ; RYRXU1XZU2XZ | — |
| Chain | Basic Chain Structure | Chain Structure with Multi-Degree-of-Freedom Kinematic Pair | Chain Structure Containing Closed-Loop Structures |
|---|---|---|---|
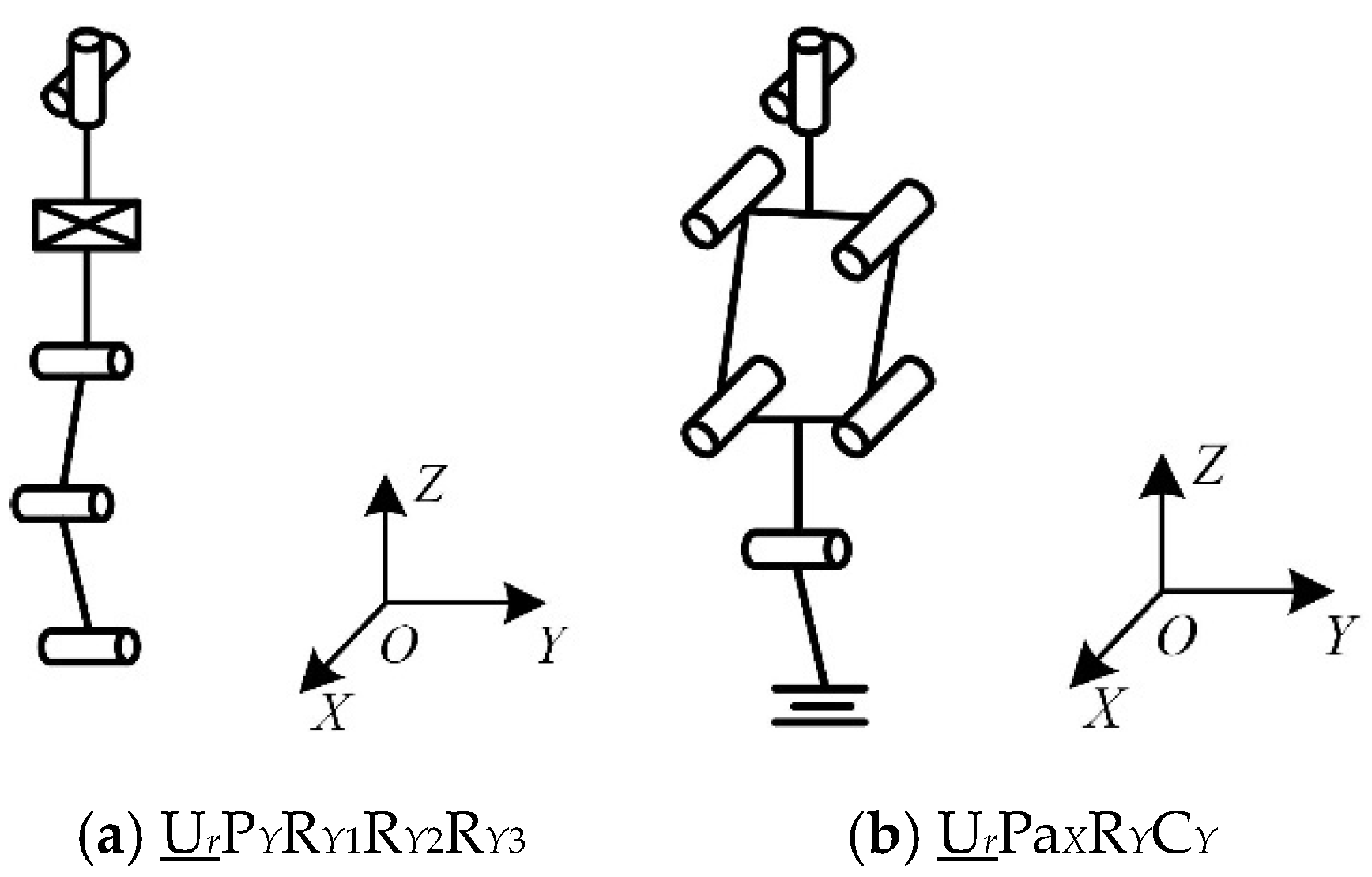
| Chain III | UrPXPYPZRY | UrPXPZCY | UrPXPaYCY; UrPaXPaYCY; UrPaXPaYPaZRY |
| UrPYPXRY1RY2 | UrPXRYCY | UrRYPaZCY; UrPX/YPaZRY1RY2; UrPaZPaZRY1RY2 | |
| UrPYPZRY1RY2 | UrPZRYCY | UrRYPaXCY; UrPYPaXRY1RY2; UrPaXPaXRY1RY2 | |
| UrPYRY1RY2RY3 | UrRY1RY2CY | UrPaXRY1RY2RY3 |
| Chain Type | Kinematic Pair Type | Complexity |
|---|---|---|
| Chain structure containing multi-degree-of-freedom kinematic pair | PZS | 1.7 |
| CZUXY | 1.95 |
| Chain Structure | Complexity | Chain Structure Containing Multi-Degree-of-Freedom Kinematic Pair | Complexity |
|---|---|---|---|
| RYPXPYPZRXRZ | 1.75 | RYPXPYPZUXZ; CYPXPZUXZ; CYCZCX | 1.8 2.03 2.6 |
| RYPYPXRX1RX2RZ | 1.63 | RYPXPYRXUXZ; RYPYCXUXZ; CYCXUXZ | 1.66 1.85 2.167 |
| RYPZPXRX1RX2RZ | 1.63 | RYPZPXRXUXZ; RYPZCXUXZ; RYRXCZCX | 1.66 1.85 2 |
| RYPYPZRXRZ1RZ2 | 1.63 | RYPYPZRZUXZ; RYPYCZUXZ; CYCZUXZ | 1.66 1.85 2.167 |
| RYPXPZRXRZ1RZ2 | 1.63 | RYPXPZRZUXZ; RYPXCZUXZ; RYRZCXCZ | 1.66 1.85 2 |
| RYPYRX1RX2RZ1RZ2 | 1.52 | RYPYRXRZUXZ; RYPYU1XZU2XZ; CYU1XZU2XZ | 1.52 1.525 1.733 |
| RYPXRX1RX2RX3RZ | 1.52 | RYPXRX1RX2UXZ; RYRXCXUXZ | 1.52 1.675 |
| RYPXRX1RX2RZ1RZ2 | 1.52 | RYPXRXRZUXZ; RYPXU1XZU2XZ; RYRZCXUXZ | 1.52 1.525 1.675 |
| RYPZRX1RX2RZ1RZ2 | 1.52 | RYPZRXRZUXZ; RYPZU1XZU2XZ; RYRXCZUXZ | 1.52 1.525 1.675 |
| RYPZRXRZ1RZ2RZ3 | 1.52 | RYPZRZ1RZ2UXZ; RYCZRZUXZ | 1.52 1.675 |
| RYRX1RX2RZ1RZ2RZ3 | 1.4 | RYRXRZ1RZ2UXZ; RYRZU1XZU2XZ | 1.38 1.35 |
| RYRX1RX2RX3RZ1RZ2 | 1.4 | RYRZRX1RX2UXZ; RYRXU1XZU2XZ | 1.38 1.35 |
| Chain II Structure Containing Closed-Loop Structures | Complexity |
|---|---|
| RYPXPYPaYUXZ | 1.92 |
| RYPX/YPaX/YPaX/YUXZ | 2.04 |
| RYPaY/XPaX/YPaX/YUXZ | 2.16 |
| CYPX/ZPaYUXZ | 2.175 |
| CYPaYPaYUXZ | 2.325 |
| RYPXPaZRXUXZ; RYPZPaYRXUXZ; RYPYPaXRZUXZ; RYPXPaYRZUXZ | 1.78 |
| RYPaZPaZRXUXZ; RYPaYPaYRXUXZ; RYPaXPaXRZUXZ; RYPaYPaYRZUXZ | 1.9 |
| RYPaZCXUXZ; RYPaYCXUXZ; RYPaXCZUXZ; RYPaYCZUXZ | 2 |
| RYPaX/ZRXRZUXZ; RYPaY/ZRX1RX2UXZ; RYPaY/ZRXRZUXZ; RYPaY/XRZ1RZ2UXZ; RYPaY/XRXRZUXZ | 1.64 |
| RYPaX/ZU1XZU2XZ; RYPaY/ZU1XZU2XZ; RYPaY/XU1XZU2XZ | 1.675 |
| Chain Structure | Complexity | Chain Structure Containing Multi-Degree-of-Freedom Kinematic Pair | Complexity | Chain Structure Containing a Closed-Loop Structure | Complexity |
|---|---|---|---|---|---|
| UrPXPYPZRY | 1.82 | UrPXPZCY | 2.05 | UrPXPaYCY; UrPaXPaYCY; UrPaXPaYPaZRY | 2.2 2.35 2.18 |
| UrPYPXRY1RY2 | 1.68 | UrPXRYCY | 1.875 | UrRYPaZCY; UrPX/YPaZRY1RY2; UrPaZPaZRY1RY2 | 2.025 1.8 1.92 |
| UrPYPZRY1RY2 | 1.68 | UrPZRYCY | 1.875 | UrRYPaXCY; UrPYPaXRY1RY2; UrPaXPaXRY1RY2 | 2.025 1.8 1.92 |
| UrPYRY1RY2RY3 | 1.54 | UrRY1RY2CY | 1.7 | UrPaXRY1RY2RY3 | 1.66 |
| i | αi−1/(°) | ai−1/mm | θi/(°) | di/mm |
|---|---|---|---|---|
| 1 | 0 | 0 | θ21 | 0 |
| 2 | −90 | l21 | θ22 + 90 | 0 |
| 3 | −90 | 0 | θ23 + 90 | 0 |
| 4 | 0 | a24 | θ24 | l24 |
| 5 | −90 | 0 | θ25 | 0 |
| 6 | 0 | l25 | θ26 | 0 |
| i | αi−1/(°) | ai−1/mm | θi/(°) | di/mm |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | d31 |
| 2 | 90 | l31 | θ32 − 90 | 0 |
| 3 | −90 | l32 | θ33 | 0 |
| 4 | 0 | l33 | θ34 | 0 |
| 5 | 0 | l34 | θ35 | 0 |
| i | αi−1/(°) | ai−1/mm | θi/(°) | di/mm |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | d31 |
| 2 | 90 | 0 | θ32 | l31 |
| 3 | −90 | 0 | θ33 | l32 |
| 4 | 0 | l33 | θ34 − 90 | 0 |
| 5 | 0 | l34 | θ35 | 0 |
| Design Variables | Constraint Range |
|---|---|
| R (mm) | [250, 450] |
| l31 (mm) | [50, 150] |
| r (mm) | [100, 220] |
| Parameter | Population Size | Number of Iterations | Social Learning Factor | Inertia Weight |
|---|---|---|---|---|
| Numerical value | 50 | 80 | 2.0 | 0.99 |
| Structural Parameters | R/mm | l31/mm | r/mm |
|---|---|---|---|
| Before optimization | 300 | 90 | 160 |
| After optimization | 441.4536 | 143.5765 | 122.2757 |
| Mode | Performance Indicators | WV | ζ |
|---|---|---|---|
| Mammalian mode | Before optimization | 0.4144 | 0.9332 |
| After optimization | 0.7310 | 0.8870 | |
| Insect mode | Before optimization | 0.5165 | 0.1981 |
| After optimization | 0.5385 | 0.2059 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Li, R.; Guo, W. Configuration Synthesis and Performance Analysis of 1T2R Decoupled Wheel-Legged Reconfigurable Mechanism. Micromachines 2025, 16, 903. https://doi.org/10.3390/mi16080903
Shi J, Li R, Guo W. Configuration Synthesis and Performance Analysis of 1T2R Decoupled Wheel-Legged Reconfigurable Mechanism. Micromachines. 2025; 16(8):903. https://doi.org/10.3390/mi16080903
Chicago/Turabian StyleShi, Jingjing, Ruiqin Li, and Wenxiao Guo. 2025. "Configuration Synthesis and Performance Analysis of 1T2R Decoupled Wheel-Legged Reconfigurable Mechanism" Micromachines 16, no. 8: 903. https://doi.org/10.3390/mi16080903
APA StyleShi, J., Li, R., & Guo, W. (2025). Configuration Synthesis and Performance Analysis of 1T2R Decoupled Wheel-Legged Reconfigurable Mechanism. Micromachines, 16(8), 903. https://doi.org/10.3390/mi16080903









