An N-Shaped Beam Symmetrical Vibration Energy Harvester for Structural Health Monitoring of Aviation Pipelines
Abstract
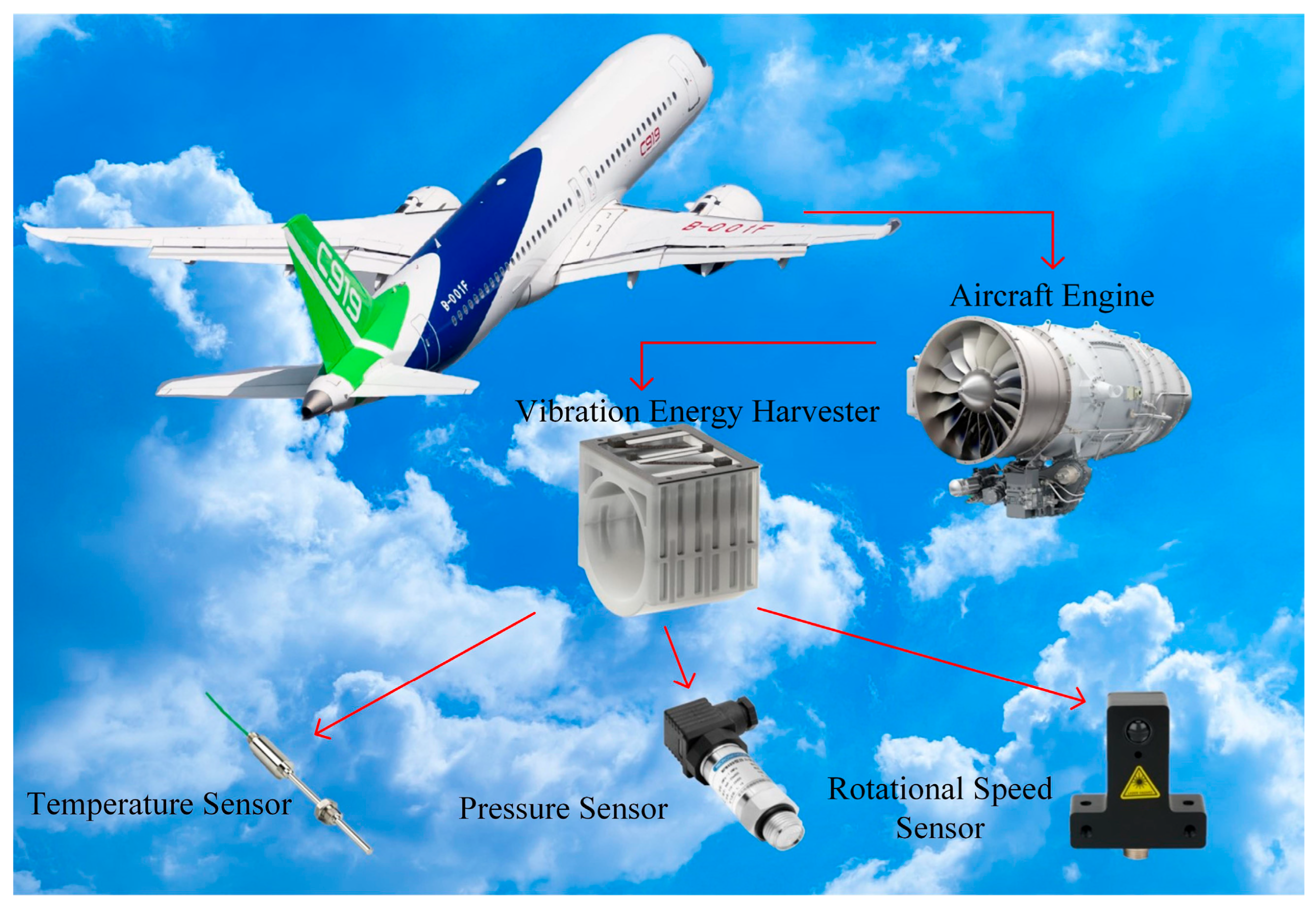
1. Introduction
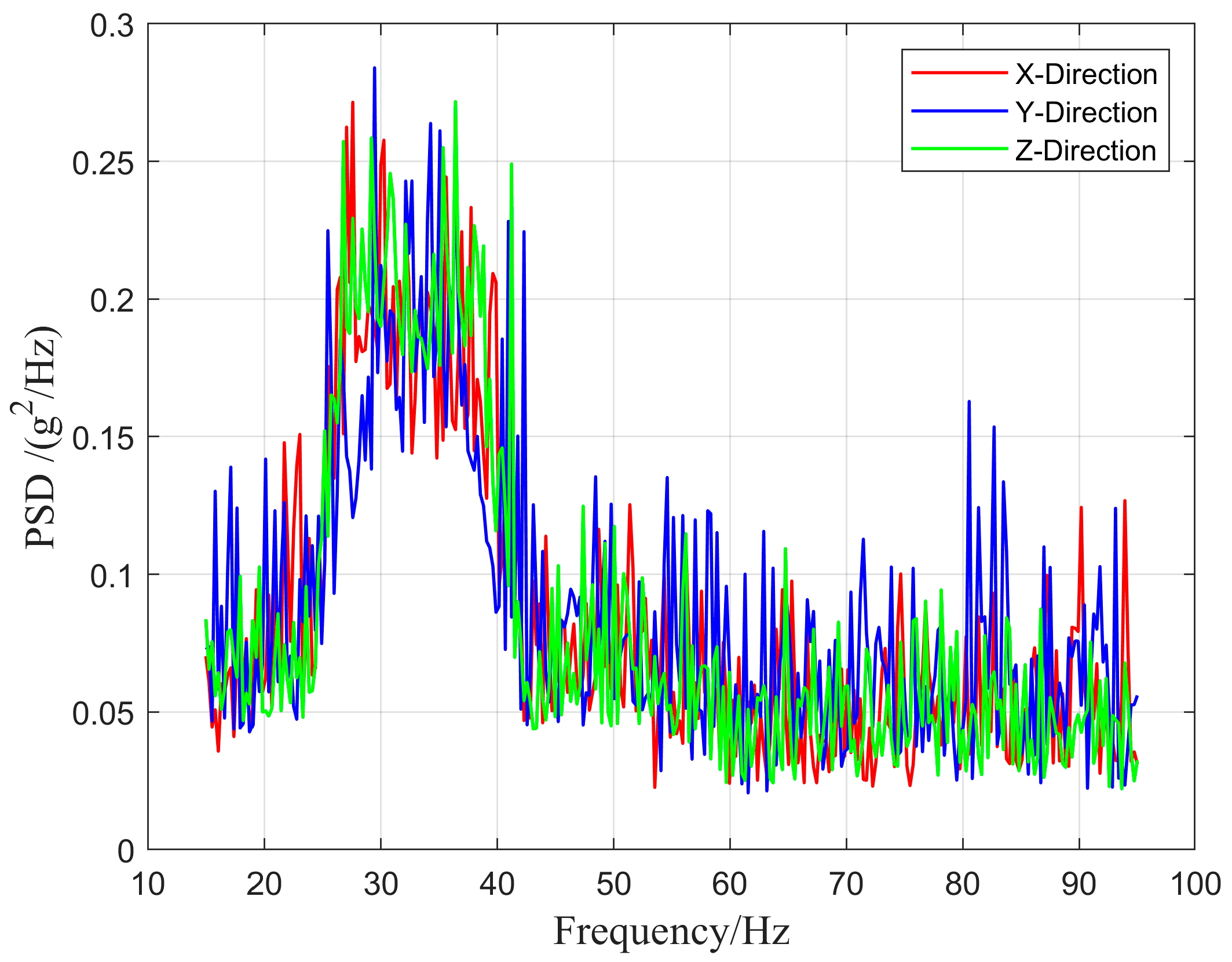
2. Analysis of Vibration Characteristics of Aviation Pipelines
3. N-Shaped Symmetrical Vibration Energy Harvester Model
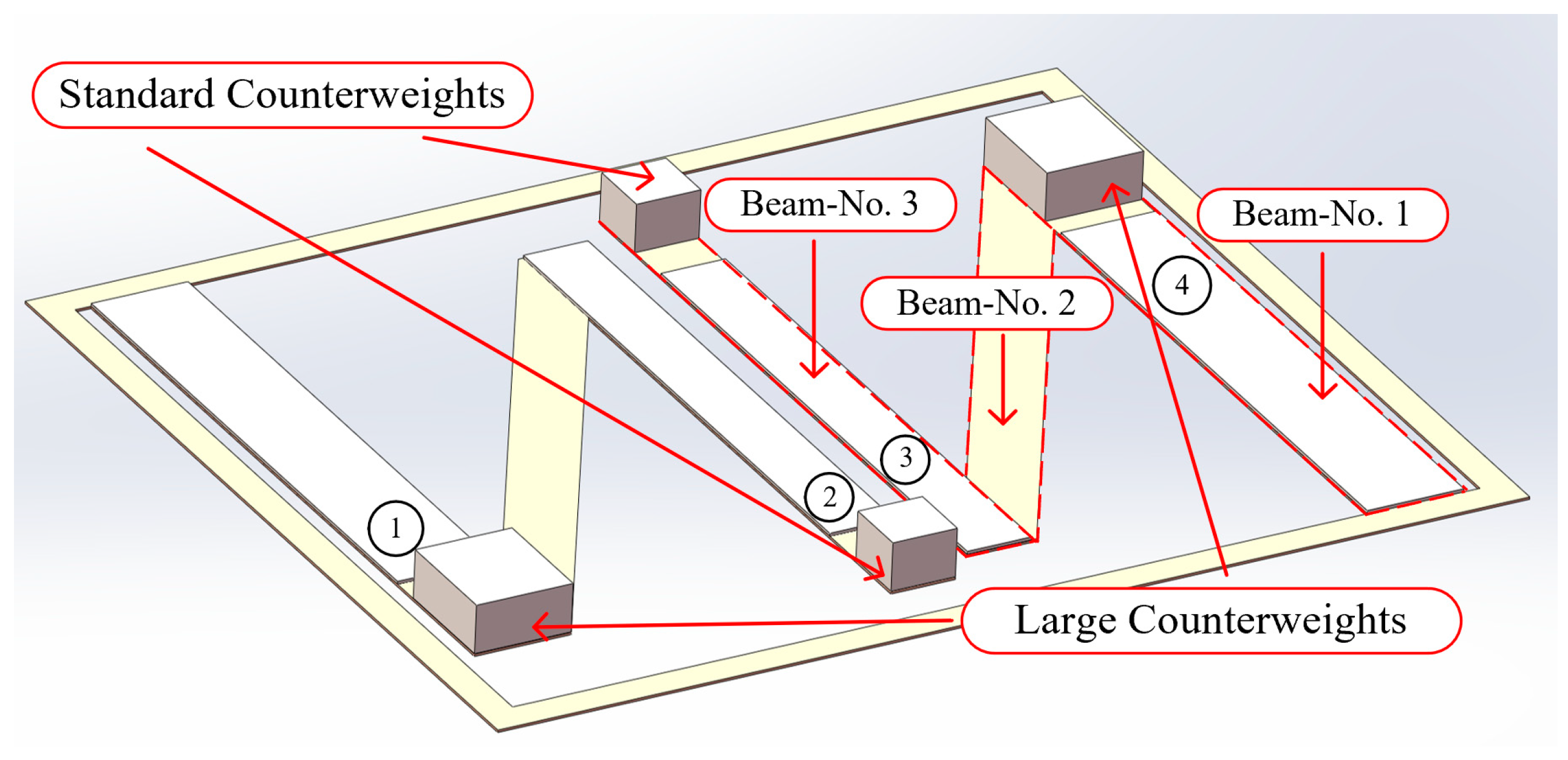
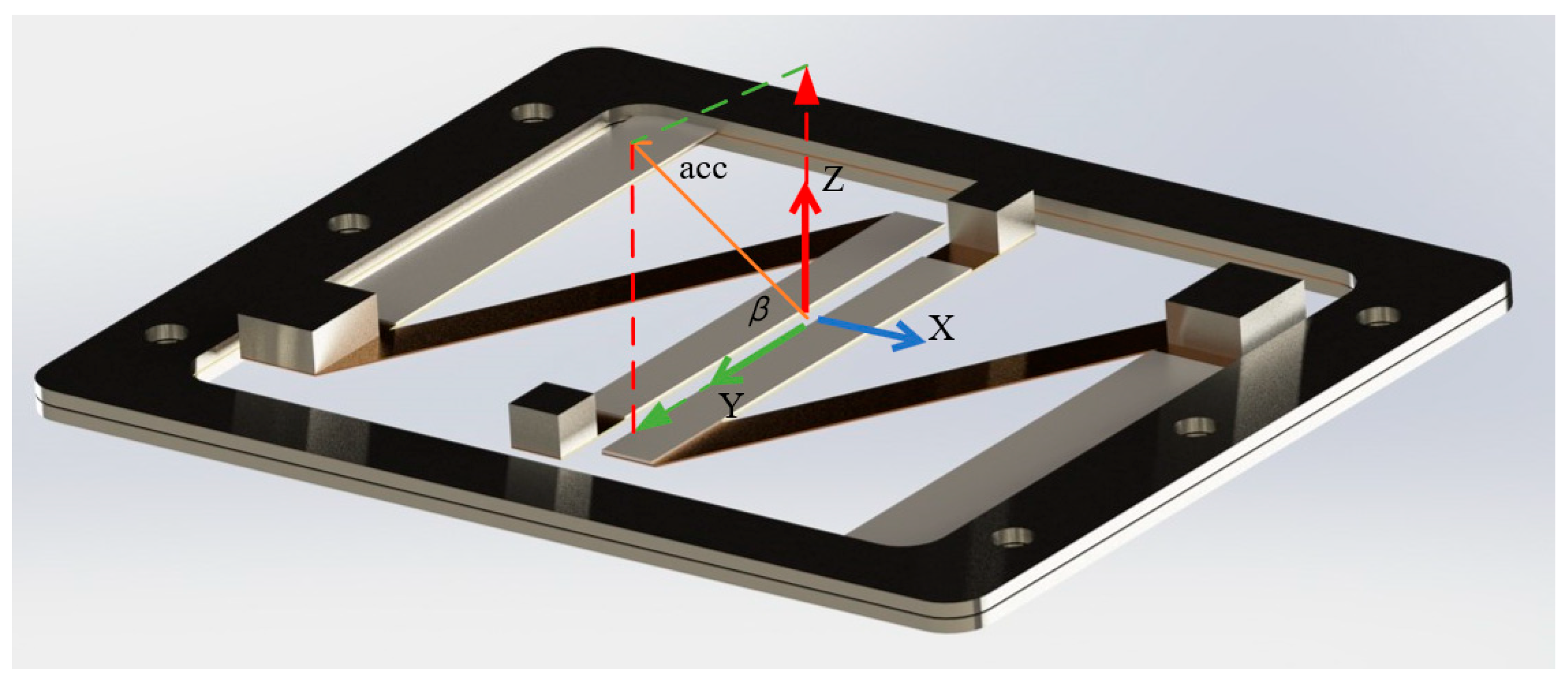
3.1. Structural Design of Energy Harvesting Device
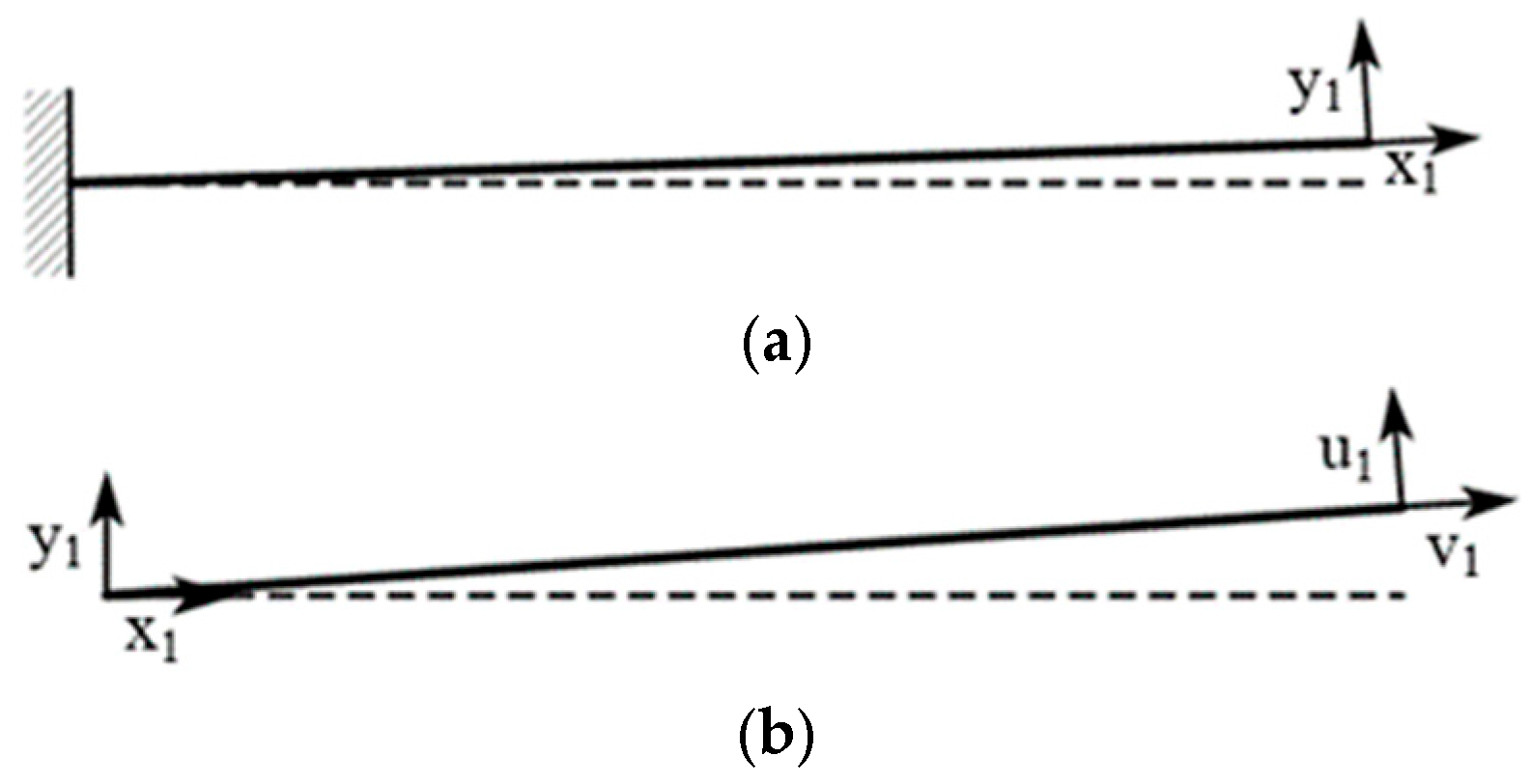
3.2. The Mechanical Model of the Device
4. Energy Harvester Simulation and Parameter Optimization
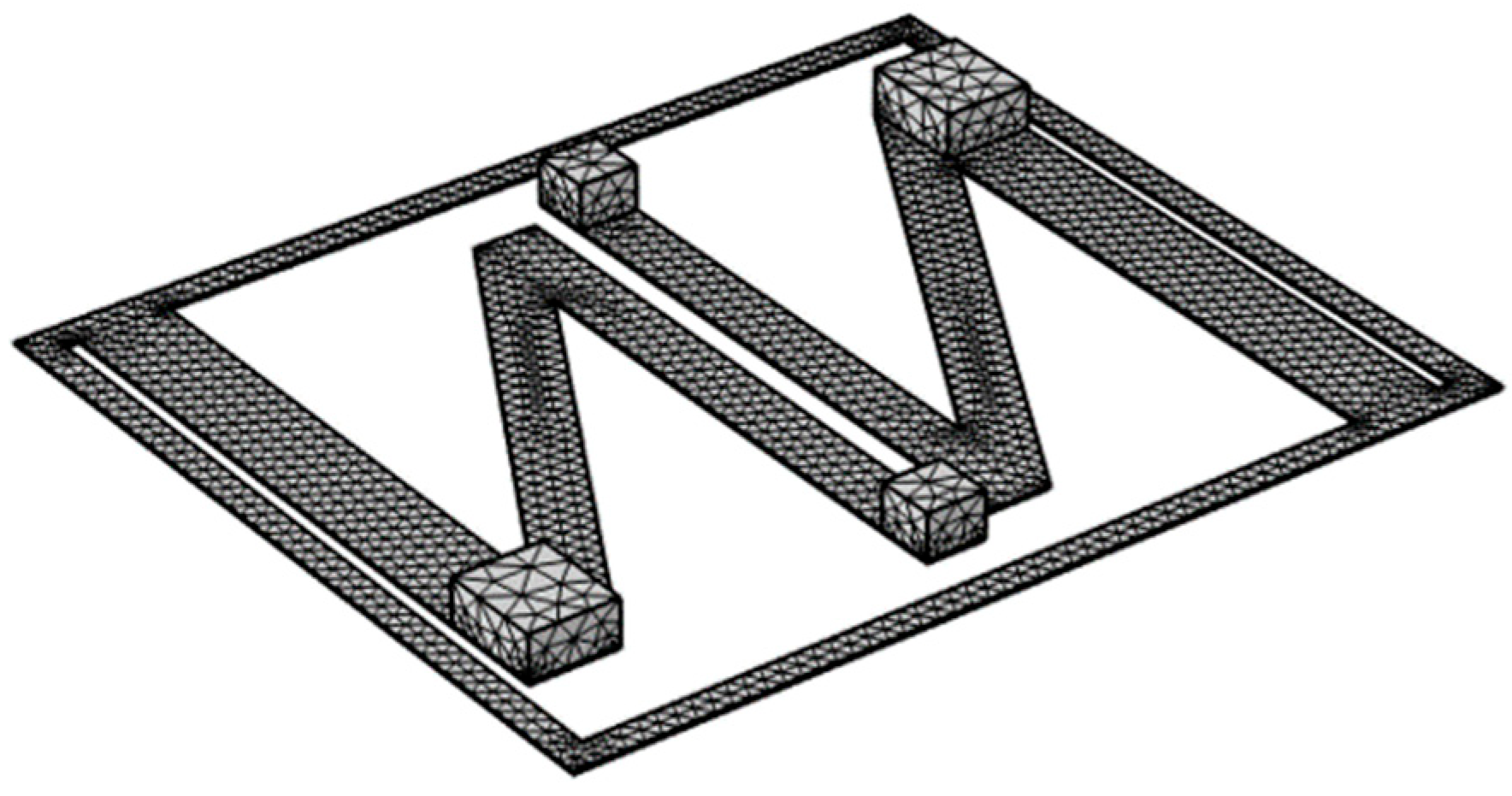
4.1. Finite Element Modeling
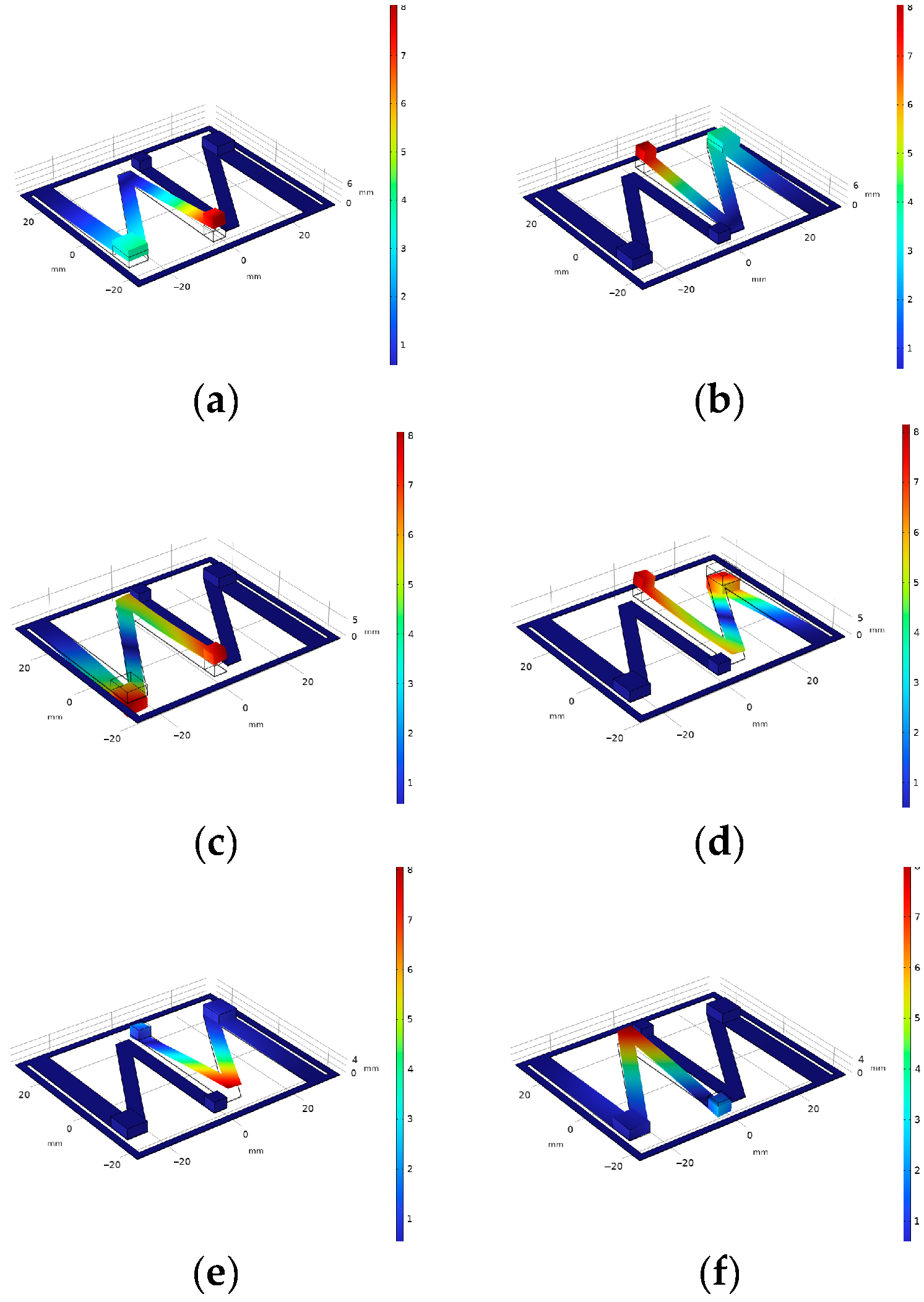
4.2. Modal Analysis of the Vibration Energy Harvester
4.3. Parameter Optimization for Vibration Energy Harvester
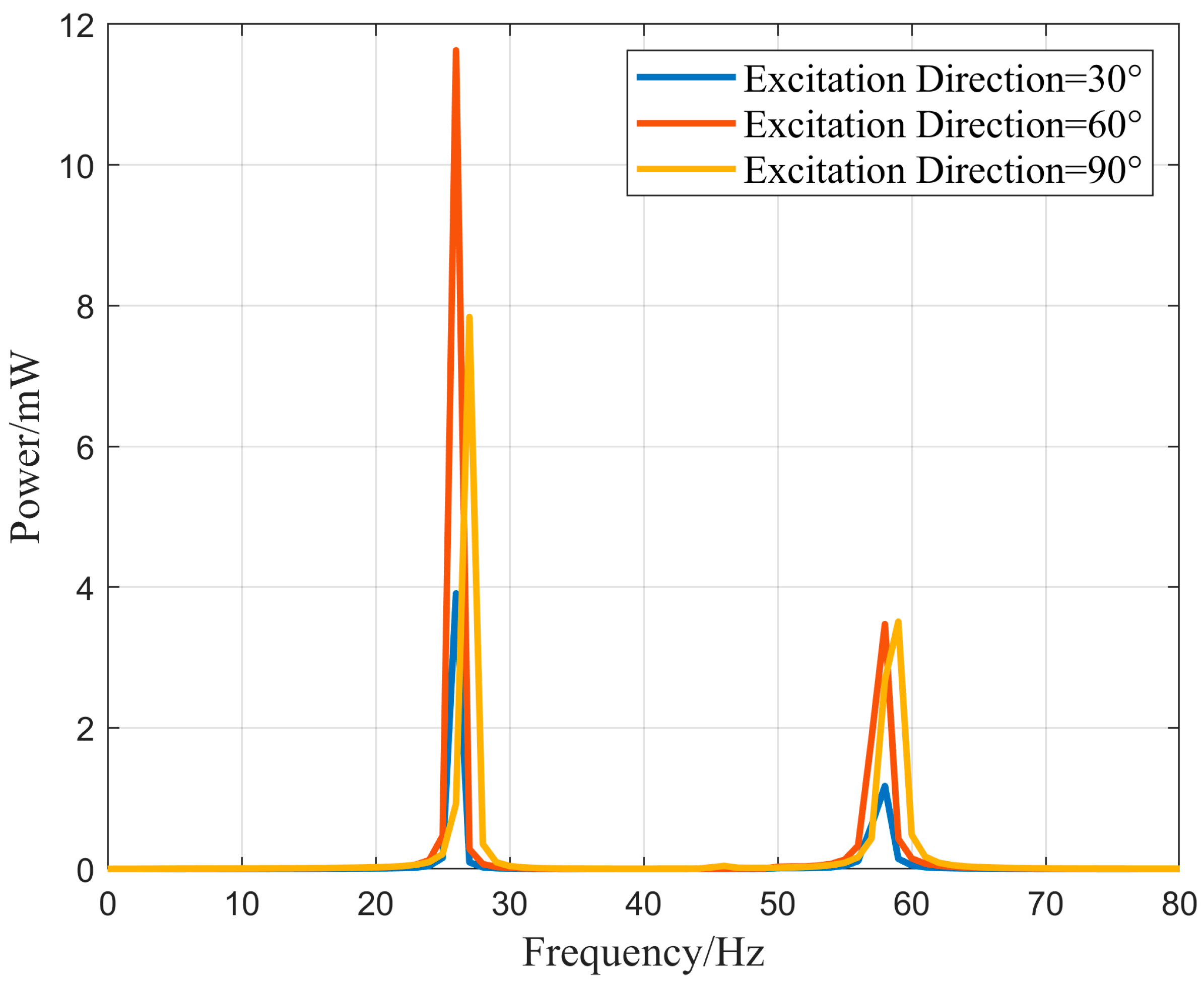
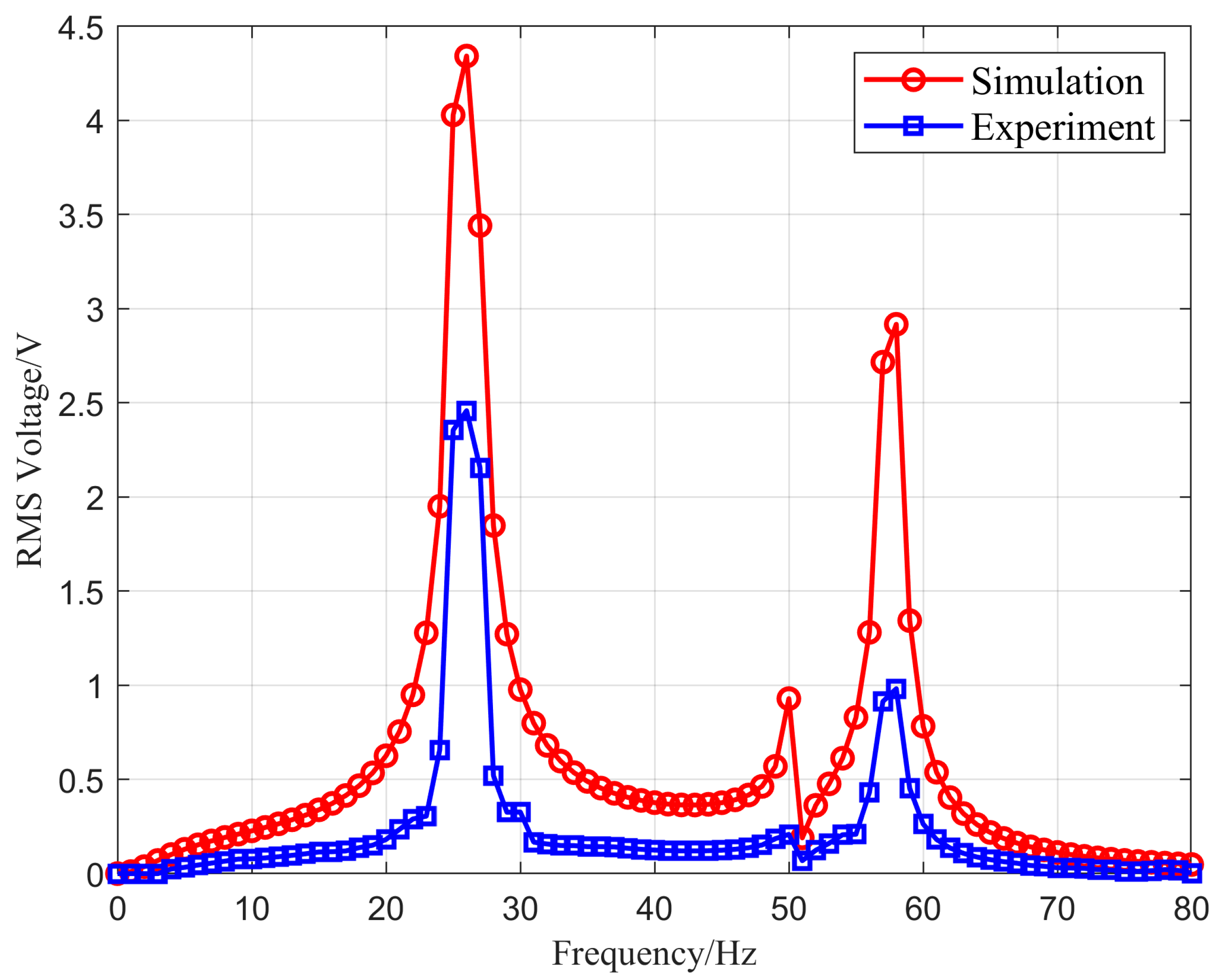
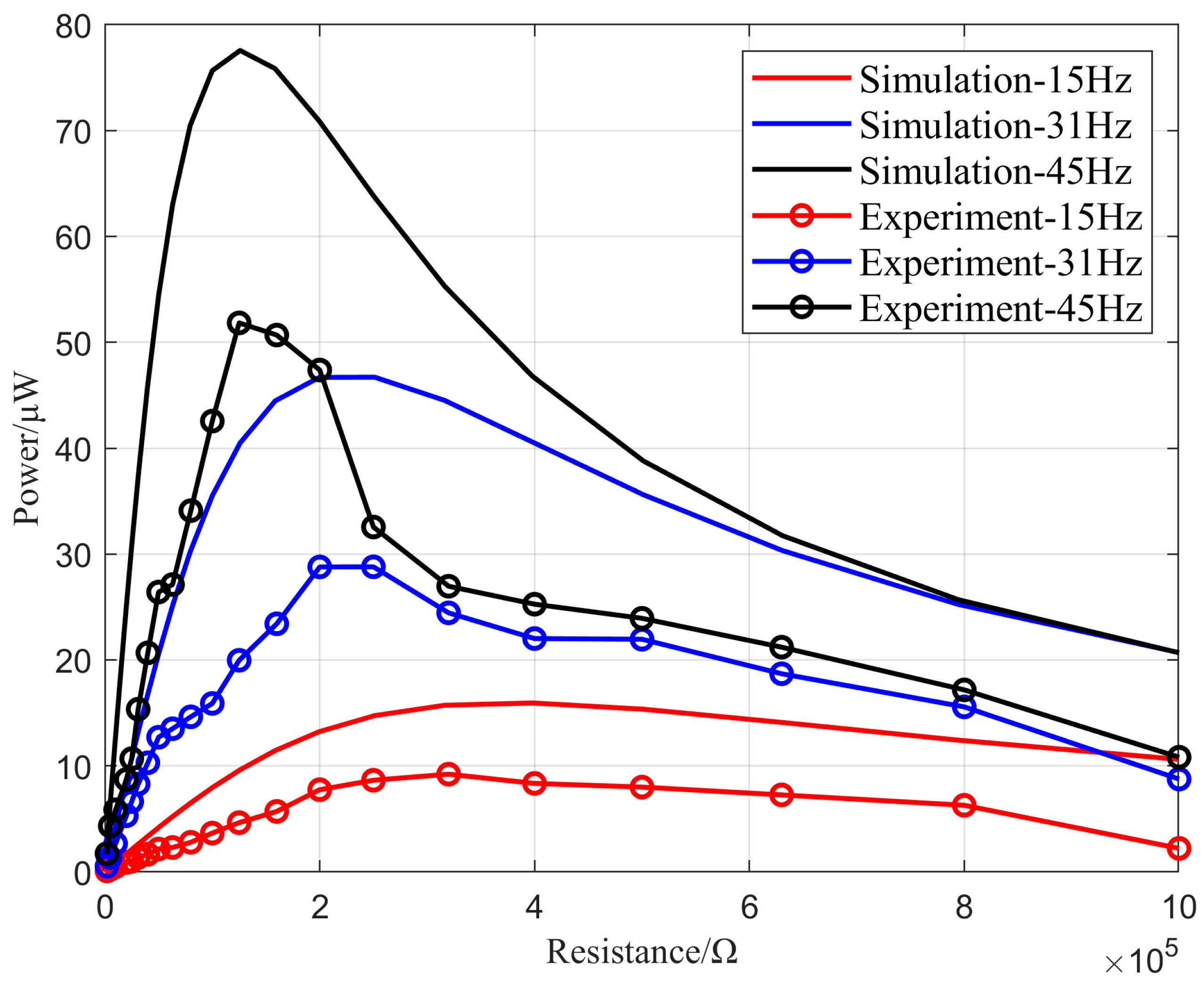
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, P.X.; Tao, Y.; Zhang, Y.; Wang, J.; Zhai, J.Y. Vibration analysis and control technologies of hydraulic pipeline system in aircraft: A review. Chin. J. Aeronaut. 2021, 34, 83–114. [Google Scholar] [CrossRef]
- Tiassou, K.; Kanoun, K.; Kaâniche, M.; Seguin, C.; Papadopoulos, C. Aircraft operational reliability—A model-based approach and a case study. Reliab. Eng. Syst. Saf. 2013, 120, 163–176. [Google Scholar] [CrossRef]
- Hausamann, D.; Zirnig, W.; Schreier, G.; Strobl, P. Monitoring of gas pipelines—A civil UAV application. Aircr. Eng. Aerosp. Technol. 2005, 77, 352–360. [Google Scholar] [CrossRef]
- Zhu, H.-H.; Liu, W.; Wang, T.; Su, J.-W.; Shi, B. Distributed acoustic sensing for monitoring linear infrastructures: Current status and trends. Sensors 2022, 22, 7550. [Google Scholar] [CrossRef]
- Śliwa, R.E.; Dymora, P.; Mazurek, M.; Kowal, B.; Jurek, M.; Kordos, D.; Rogalski, T.; Flaszynski, P.; Doerffer, P.; Doerffer, K. The latest advances in wireless communication in aviation, wind turbines and bridges. Inventions 2022, 7, 18. [Google Scholar] [CrossRef]
- Spandonidis, C.; Theodoropoulos, P.; Giannopoulos, F.; Galiatsatos, N.; Petsa, A. Evaluation of deep learning approaches for oil & gas pipeline leak detection using wireless sensor networks. Eng. Appl. Artif. Intell. 2022, 113, 104890. [Google Scholar] [CrossRef]
- Rashid, B.; Rehmani, M.H. Applications of wireless sensor networks for urban areas: A survey. J. Netw. Comput. Appl. 2016, 60, 192–219. [Google Scholar] [CrossRef]
- Prauzek, M.; Konecny, J.; Borova, M.; Janosova, K.; Hlavica, J.; Musilek, P. Energy harvesting sources, storage devices and system topologies for environmental wireless sensor networks: A review. Sensors 2018, 18, 2446. [Google Scholar] [CrossRef]
- Ye, L.; Wang, Z.; Liu, Y.; Chen, P.; Li, H.; Zhang, H.; Wu, M.; He, W.; Shen, L.; Zhang, Y. The challenges and emerging technologies for low-power artificial intelligence IoT systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4821–4834. [Google Scholar] [CrossRef]
- Li, Y.; Tao, K.; George, B.; Tan, Z. Harvesting vibration energy: Technologies and challenges. IEEE Ind. Electron. Mag. 2020, 15, 30–39. [Google Scholar] [CrossRef]
- Wang, J.; Yurchenko, D.; Hu, G.; Zhao, L.; Tang, L.; Yang, Y. Perspectives in flow-induced vibration energy harvesting. Appl. Phys. Lett. 2021, 119. [Google Scholar] [CrossRef]
- Yang, T.; Zhou, S.; Fang, S.; Qin, W.; Inman, D.J. Nonlinear vibration energy harvesting and vibration suppression technologies: Designs, analysis, and applications. Appl. Phys. Rev. 2021, 8. [Google Scholar] [CrossRef]
- Ahmad, I.; Hee, L.M.; Abdelrhman, A.M.; Imam, S.A.; Leong, M. Scopes, challenges and approaches of energy harvesting for wireless sensor nodes in machine condition monitoring systems: A review. Measurement 2021, 183, 109856. [Google Scholar] [CrossRef]
- Rubes, O.; Chalupa, J.; Ksica, F.; Hadas, Z. Development and experimental validation of self-powered wireless vibration sensor node using vibration energy harvester. Mech. Syst. Signal Process. 2021, 160, 107890. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.-W.; Lin, L. A comprehensive review on piezoelectric energy harvesting technology: Materials, mechanisms, and applications. Appl. Phys. Rev. 2018, 5. [Google Scholar] [CrossRef]
- He, M.; Zhang, X.; dos Santos Fernandez, L.; Molter, A.; Xia, L.; Shi, T. Multi-material topology optimization of piezoelectric composite structures for energy harvesting. Compos. Struct. 2021, 265, 113783. [Google Scholar] [CrossRef]
- Liu, Z.; Ding, G.; Wang, J.; Cai, G.; Qin, X.; Shi, K. Fabrication and performance of Tile transducers for piezoelectric energy harvesting. AIP Adv. 2020, 10. [Google Scholar] [CrossRef]
- Wakshume, D.G.; Płaczek, M.Ł. Optimizing Piezoelectric Energy Harvesting from Mechanical Vibration for Electrical Efficiency: A Comprehensive Review. Electronics 2024, 13, 987. [Google Scholar] [CrossRef]
- Wu, N.; Bao, B.; Wang, Q. Review on engineering structural designs for efficient piezoelectric energy harvesting to obtain high power output. Eng. Struct. 2021, 235, 112068. [Google Scholar] [CrossRef]
- Fu, Y.; Huang, M.; Wu, R.; Huang, F.; Zhou, M.; Chen, S.; Wang, Q.; Li, Q. Piezoelectric vibration energy harvesting device based on water sloshing-inspired extensions. AIP Adv. 2021, 11. [Google Scholar] [CrossRef]
- Han, P.; Huang, Q.; Pan, G.; Wang, W.; Zhang, T.; Qin, D. Energy harvesting from flow-induced vibration of a low-mass square cylinder with different incidence angles. AIP Adv. 2021, 11. [Google Scholar] [CrossRef]
- Kabashkin, I.; Perekrestov, V. Ecosystem of Aviation Maintenance: Transition from Aircraft Health Monitoring to Health Management Based on IoT and AI Synergy. Appl. Sci. 2024, 14, 4394. [Google Scholar] [CrossRef]
- Schmitz, M.; Schmitz, G. Experimental study on the accretion and release of ice in aviation jet fuel. Aerosp. Sci. Technol. 2018, 82, 294–303. [Google Scholar] [CrossRef]
- Legros, S.; Brunet, C.; Domingo-Alvarez, P.; Malbois, P.; Salaun, E.; Godard, G.; Caceres, M.; Barviau, B.; Cabot, G.; Renou, B. Combustion for aircraft propulsion: Progress in advanced laser-based diagnostics on high-pressure kerosene/air flames produced with low-NOx fuel injection systems. Combust. Flame 2021, 224, 273–294. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, X.; Qian, L.; Yuan, Y.; Ma, S.; Guo, M. A review of aviation spline research. Lubricants 2022, 11, 6. [Google Scholar] [CrossRef]
- Ramezanpour, R.; Nahvi, H.; Ziaei-Rad, S. A vibration-based energy harvester suitable for low-frequency, high-amplitude environments: Theoretical and experimental investigations. J. Intell. Mater. Syst. Struct. 2016, 27, 642–665. [Google Scholar] [CrossRef]
- Xiangjian, L.; Renwen, C.; Liya, Z. Energy conversion efficiency of rainbow shape piezoelectric transducer. Chin. J. Aeronaut. 2012, 25, 691–697. [Google Scholar] [CrossRef]
- Sriramdas, R.; Chiplunkar, S.; Cuduvally, R.M.; Pratap, R. Performance enhancement of piezoelectric energy harvesters using multilayer and multistep beam configurations. IEEE Sens. J. 2015, 15, 3338–3348. [Google Scholar] [CrossRef]
- Eshtehardiha, R.; Tikani, R.; Ziaei-Rad, S. Experimental and numerical investigation of energy harvesting from double cantilever beams with internal resonance. J. Sound Vib. 2021, 500, 116022. [Google Scholar] [CrossRef]
- Gibus, D.; Gasnier, P.; Morel, A.; Formosa, F.; Charleux, L.; Boisseau, S.; Pillonnet, G.; Berlitz, C.A.; Quelen, A.; Badel, A. Strongly coupled piezoelectric cantilevers for broadband vibration energy harvesting. Appl. Energy 2020, 277, 115518. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Tseng, C.-T.; Chen, Y.-S. Analysis and experiment of self-frequency-tuning piezoelectric energy harvesters for rotational motion. Smart Mater. Struct. 2014, 23, 075013. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Y.; Cheng, G.; He, S.; Yang, Z.; Ding, J. An enhanced galloping-based piezoelectric energy harvester with non-rotational bluff body. Appl. Phys. Lett. 2022, 121. [Google Scholar] [CrossRef]
- van Heerden, A.S.; Judt, D.M.; Jafari, S.; Lawson, C.P.; Nikolaidis, T.; Bosak, D. Aircraft thermal management: Practices, technology, system architectures, future challenges, and opportunities. Prog. Aerosp. Sci. 2022, 128, 100767. [Google Scholar] [CrossRef]
- Xin, L.; Weihao, L.; Jian, S.; Qiang, L.; Shaoping, W. Pipelines vibration analysis and control based on clamps’ locations optimization of multi-pump system. Chin. J. Aeronaut. 2022, 35, 352–366. [Google Scholar] [CrossRef]
- He, L.; Yu, G.; Han, Y.; Liu, L.; Hu, D.; Cheng, G. Research on nonlinear isometric L-shaped cantilever beam type piezoelectric wind energy harvester based on magnetic coupling. Rev. Sci. Instrum. 2022, 93. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Najar, F.; Nayfeh, A.; Ayed, S.B. An energy harvester using piezoelectric cantilever beams undergoing coupled bending–torsion vibrations. Smart Mater. Struct. 2011, 20, 115007. [Google Scholar] [CrossRef]
- Jin, L.; Gao, S.; Zhou, X.; Zhang, G. The effect of different shapes of cantilever beam in piezoelectric energy harvesters on their electrical output. Microsyst. Technol. 2017, 23, 4805–4814. [Google Scholar] [CrossRef]
- Mohamed, K.; Elgamal, H.; Kouritem, S.A. An experimental validation of a new shape optimization technique for piezoelectric harvesting cantilever beams. Alex. Eng. J. 2021, 60, 1751–1766. [Google Scholar] [CrossRef]
- Wang, B.; Li, X.-F. Flexoelectric effects on the natural frequencies for free vibration of piezoelectric nanoplates. J. Appl. Phys. 2021, 129, 034102. [Google Scholar] [CrossRef]
- Raafat, A.; Al-Haik, M.Y.; Al Nuaimi, S. Numerical characterization of piezoelectric energy harvesting from an L-shaped frame. AIP Adv. 2024, 14. [Google Scholar] [CrossRef]
- Ahmadpar, M.; Hoseinzadeh, S.; Nakhaei, F.; Memon, S. Experimental modal analysis of distinguishing microstructural variations in carbon steel SA516 by Applied heat treatments, natural frequencies, and damping coefficients. J. Mater. Eng. Perform. 2021, 30, 9256–9261. [Google Scholar] [CrossRef]

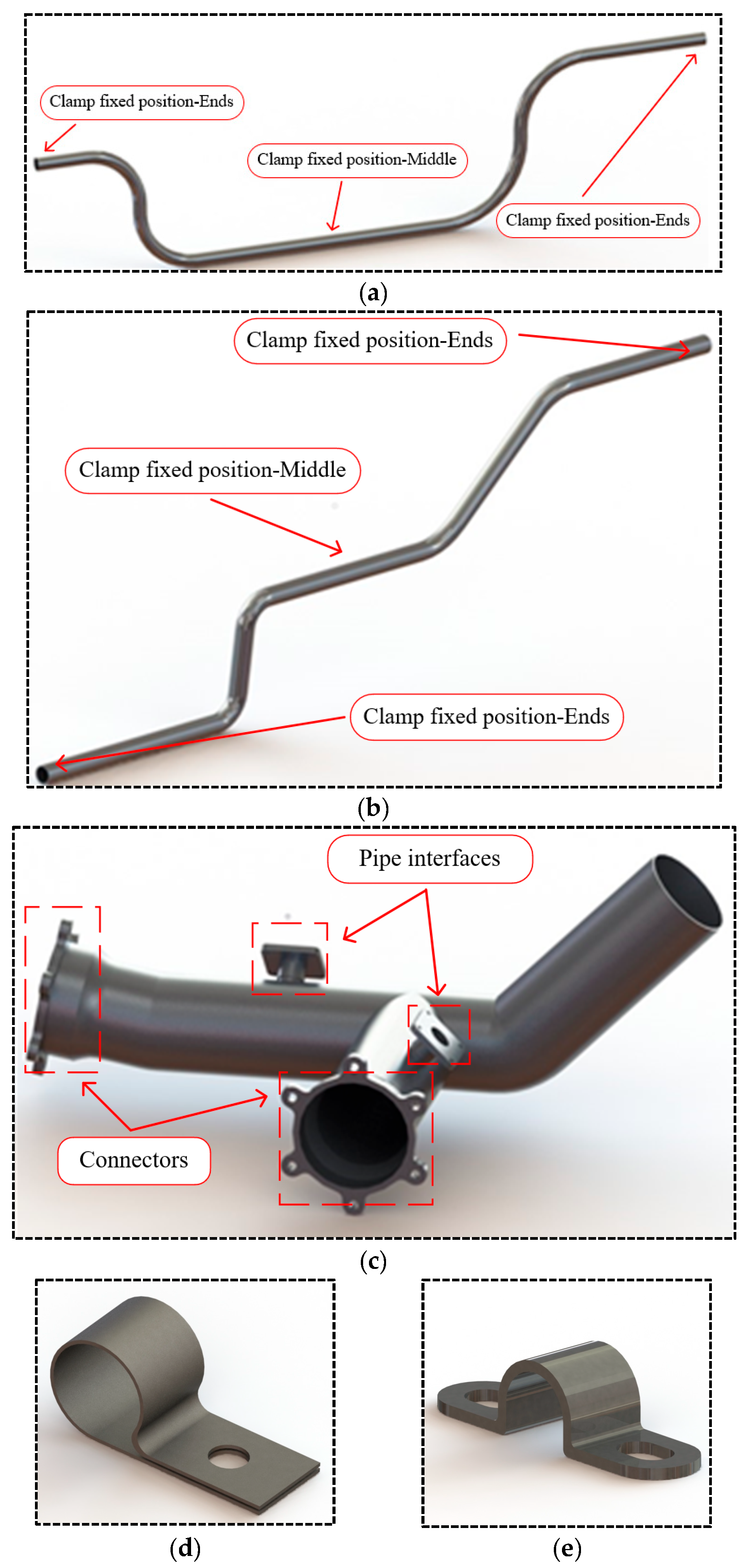

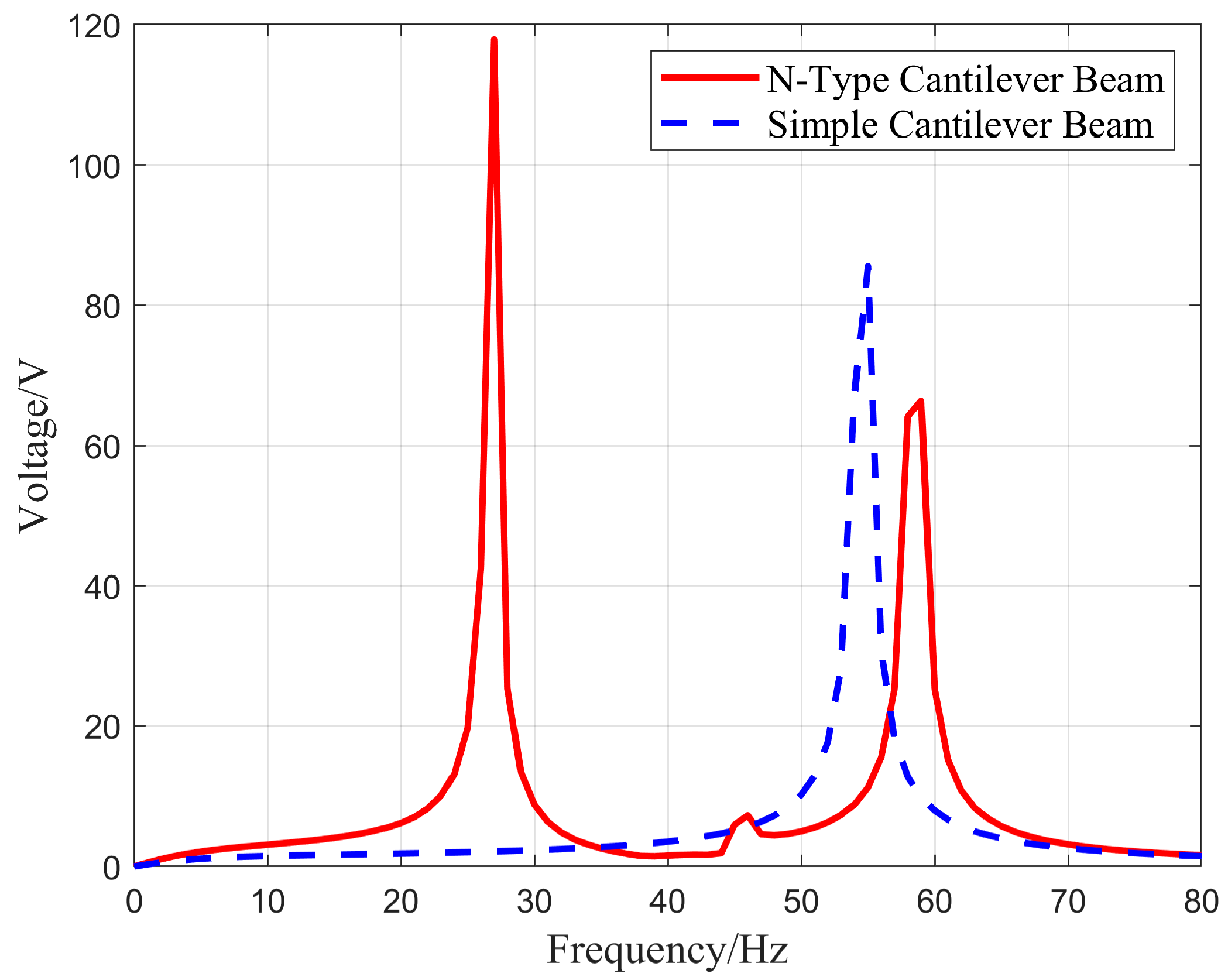
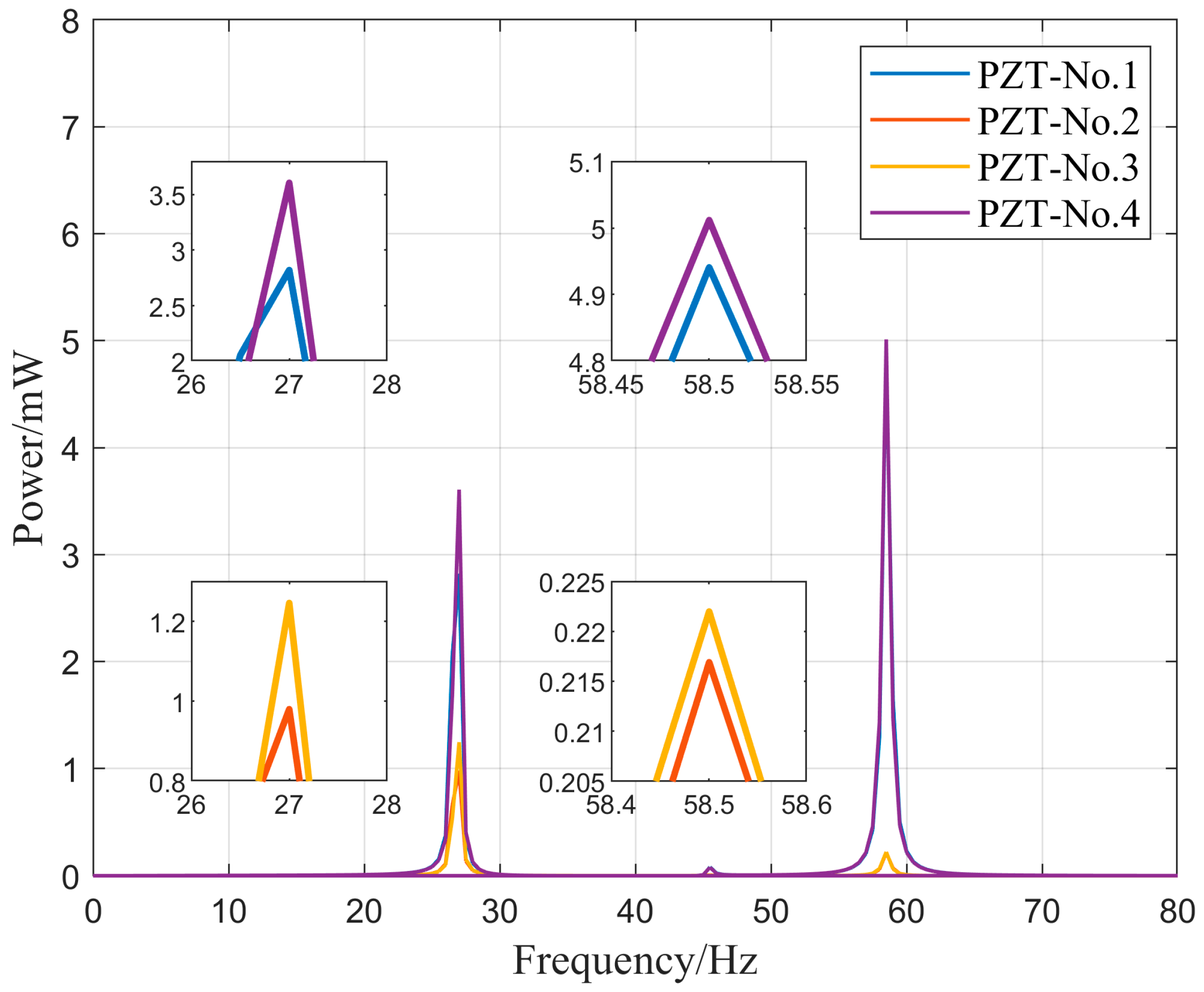
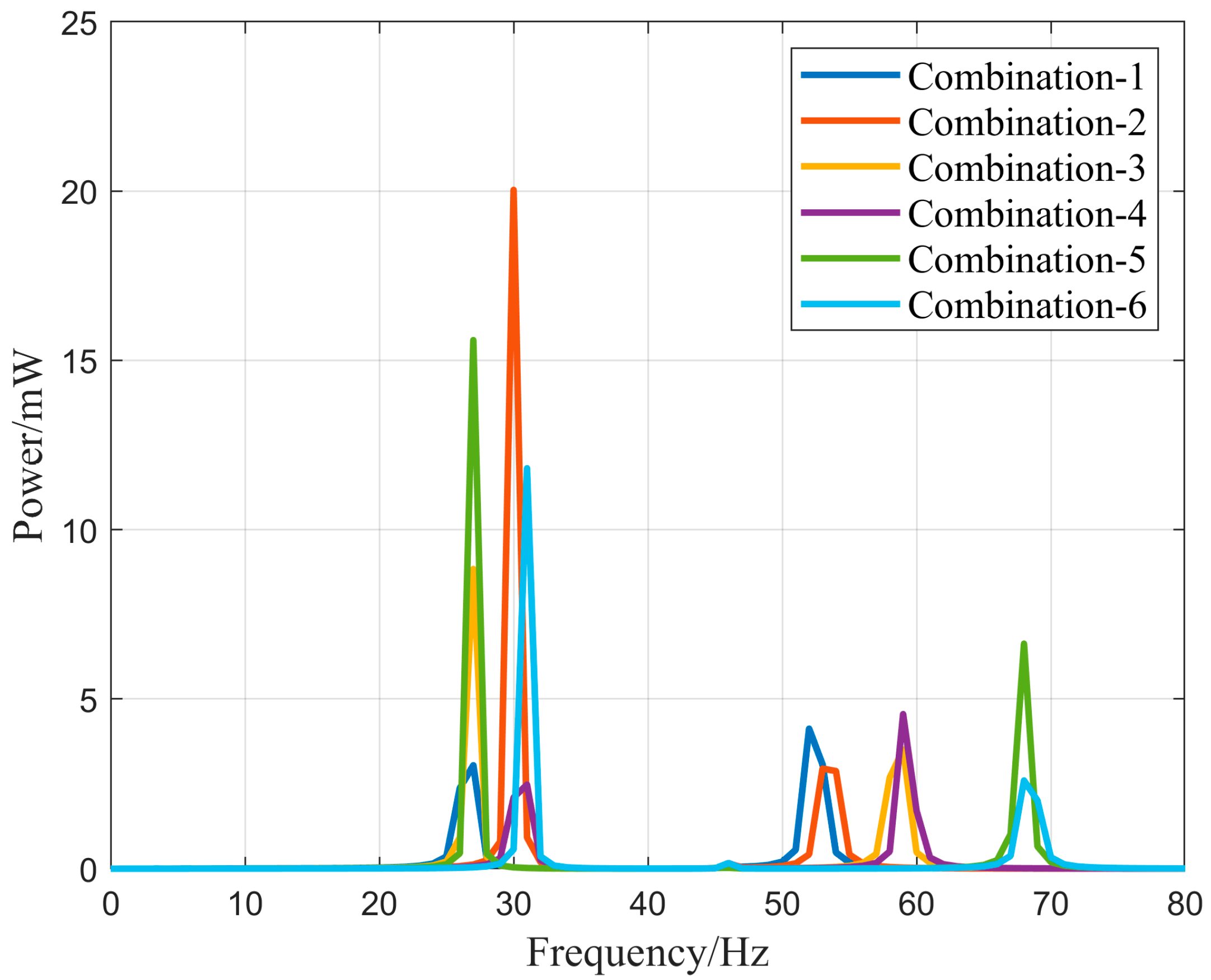
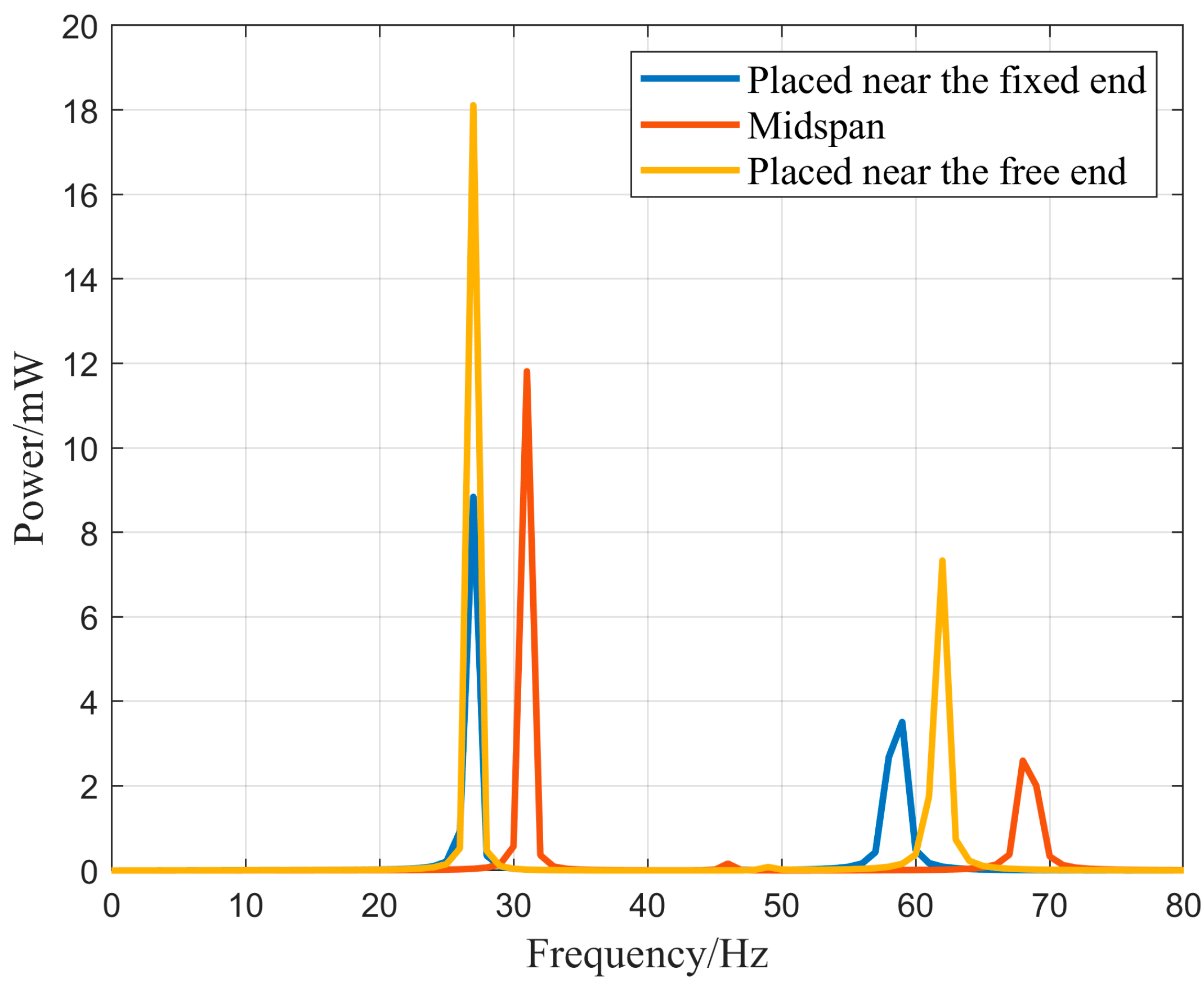



| Parameters | Transportation Pipeline 1 | Transportation Pipeline 2 | Connection Pipeline |
|---|---|---|---|
| Inner Diameter r/mm | 6 | 6 | 29 |
| Outer Diameter R/mm | 7 | 7 | 30 |
| Total Length of Pipeline L/mm | 550 | 880 | - |
| Bending Angle/rad | / | ||
| Radius of Curvature/mm | 50/70 | 20/50 | 30 |
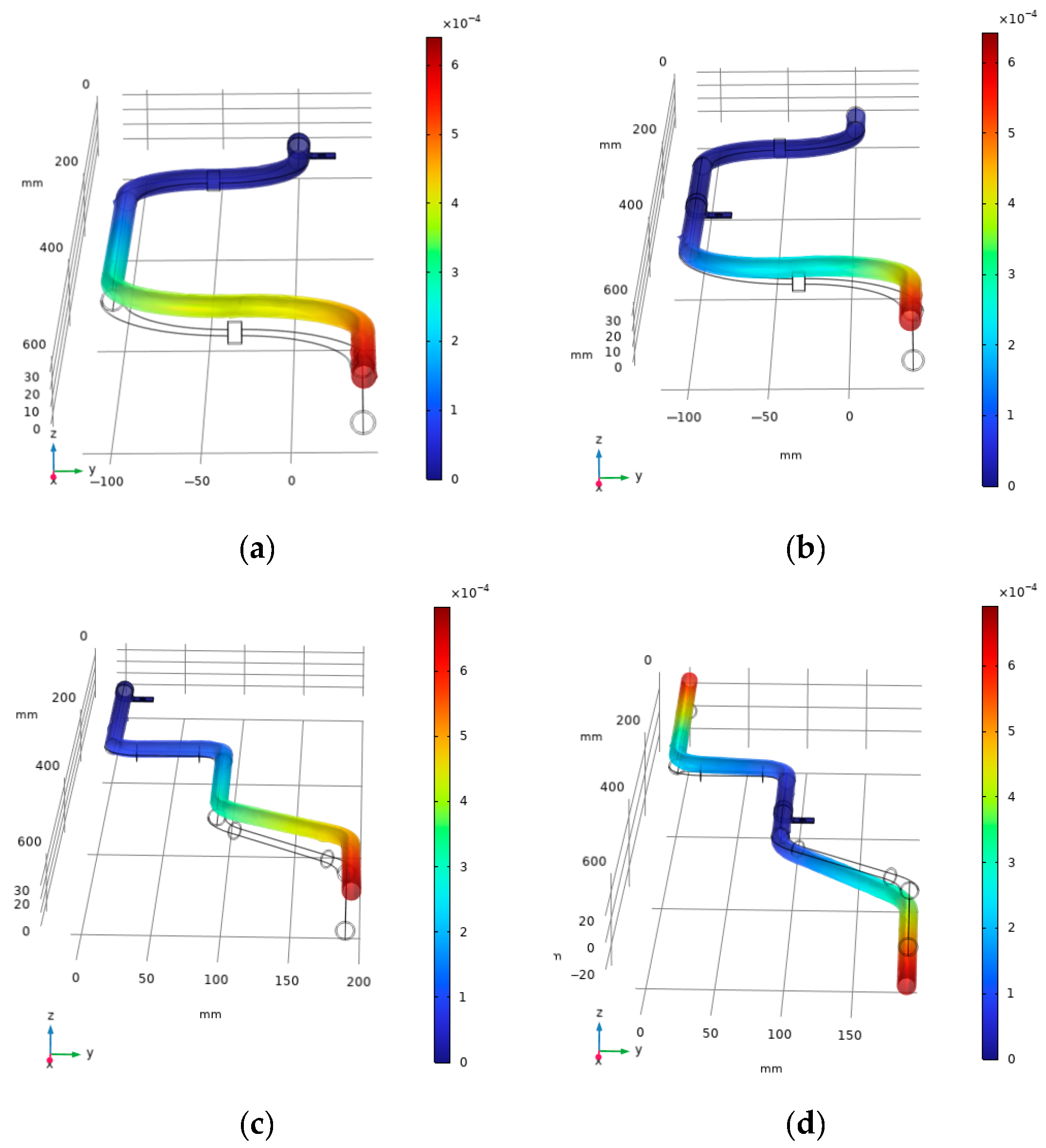
| Pipeline Type | Number and Arrangement of Clamps | First Mode/Hz | Second Mode/Hz | Third Mode/Hz | Fourth Mode/Hz | Fifth Mode/Hz | Sixth Mode/Hz |
|---|---|---|---|---|---|---|---|
| Transportation Pipeline 1 | Single clamp, placed on one side | 24.85 | 26.12 | 149.44 | 156.93 | 334.12 | 368.61 |
| Single clamp, in the middle | 69.79 | 73.01 | 125.56 | 130.2 | 362.65 | 394.66 | |
| Double clamps, on both sides | 147.09 | 158.43 | 365.41 | 394.95 | 594.13 | 602.07 | |
| Double clamps, placed in the middle and on one side | 123.06 | 128.98 | 355.28 | 387.1 | 566.38 | 645.33 | |
| Triple clamps, placed in the middle and on both sides | 364.08 | 390.95 | 631.21 | 721.01 | 1632.1 | 1811.7 | |
| Transportation Pipeline 2 | Single clamp, placed on one side | 23.42 | 24.49 | 101.22 | 101.97 | 320.18 | 334.47 |
| Single clamp, in the middle | 66.66 | 68.82 | 135.61 | 144.97 | 354.72 | 378.42 | |
| Double clamps, on both sides | 115.83 | 279.11 | 338.81 | 405.08 | 520.42 | 762.20 | |
| Double clamps, placed in the middle and on one side | 112.63 | 119.86 | 373.53 | 420.21 | 536.84 | 847.74 | |
| Triple clamps, placed in the middle and on both sides | 366.62 | 483.33 | 832.17 | 988.61 | 1112.4 | 1222.8 |
| Description | Parameter | Value |
|---|---|---|
| Beam No. 1 Width (mm) | 6 | |
| Beam No. 1 Length (mm) | 45 | |
| Beam No. 2 Width (mm) | 4 | |
| Beam No. 2 Length (mm) | 37 | |
| Beam No. 3 Width (mm) | 4 | |
| Beam No. 3 Length (mm) | 42 | |
| Thickness (mm) | 0.2 | |
| Beam Angle(rad) | ||
| Density (kg/m3) | 8250 | |
| Poisson’s Ratio | G | 0.3 |
| Young’s Modulus (GPa) | E | 128 |
| Combination | ||
|---|---|---|
| (1) | 4 mm | 3 mm |
| (2) | 4 mm | 2 mm |
| (3) | 3 mm | 3 mm |
| (4) | 3 mm | 2 mm |
| (5) | 2 mm | 3 mm |
| (6) | 2 mm | 2 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Qin, Y.; Jiang, Z.; Li, J. An N-Shaped Beam Symmetrical Vibration Energy Harvester for Structural Health Monitoring of Aviation Pipelines. Micromachines 2025, 16, 858. https://doi.org/10.3390/mi16080858
Lu X, Qin Y, Jiang Z, Li J. An N-Shaped Beam Symmetrical Vibration Energy Harvester for Structural Health Monitoring of Aviation Pipelines. Micromachines. 2025; 16(8):858. https://doi.org/10.3390/mi16080858
Chicago/Turabian StyleLu, Xutao, Yingwei Qin, Zihao Jiang, and Jing Li. 2025. "An N-Shaped Beam Symmetrical Vibration Energy Harvester for Structural Health Monitoring of Aviation Pipelines" Micromachines 16, no. 8: 858. https://doi.org/10.3390/mi16080858
APA StyleLu, X., Qin, Y., Jiang, Z., & Li, J. (2025). An N-Shaped Beam Symmetrical Vibration Energy Harvester for Structural Health Monitoring of Aviation Pipelines. Micromachines, 16(8), 858. https://doi.org/10.3390/mi16080858





