A High Dynamic Range and Fast Response Logarithmic Amplifier Employing Slope-Adjustment and Power-Down Mode
Abstract
1. Introduction
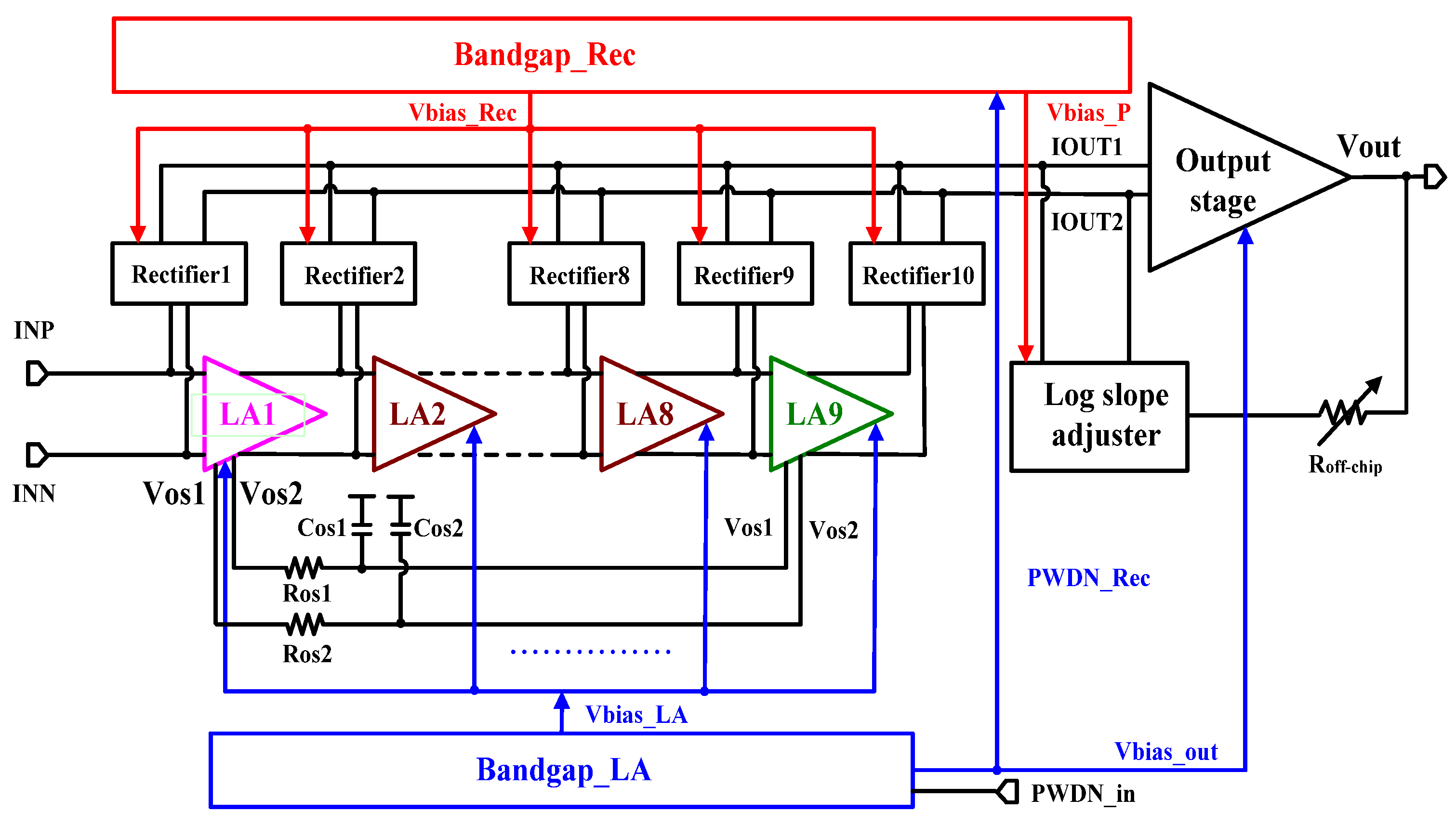
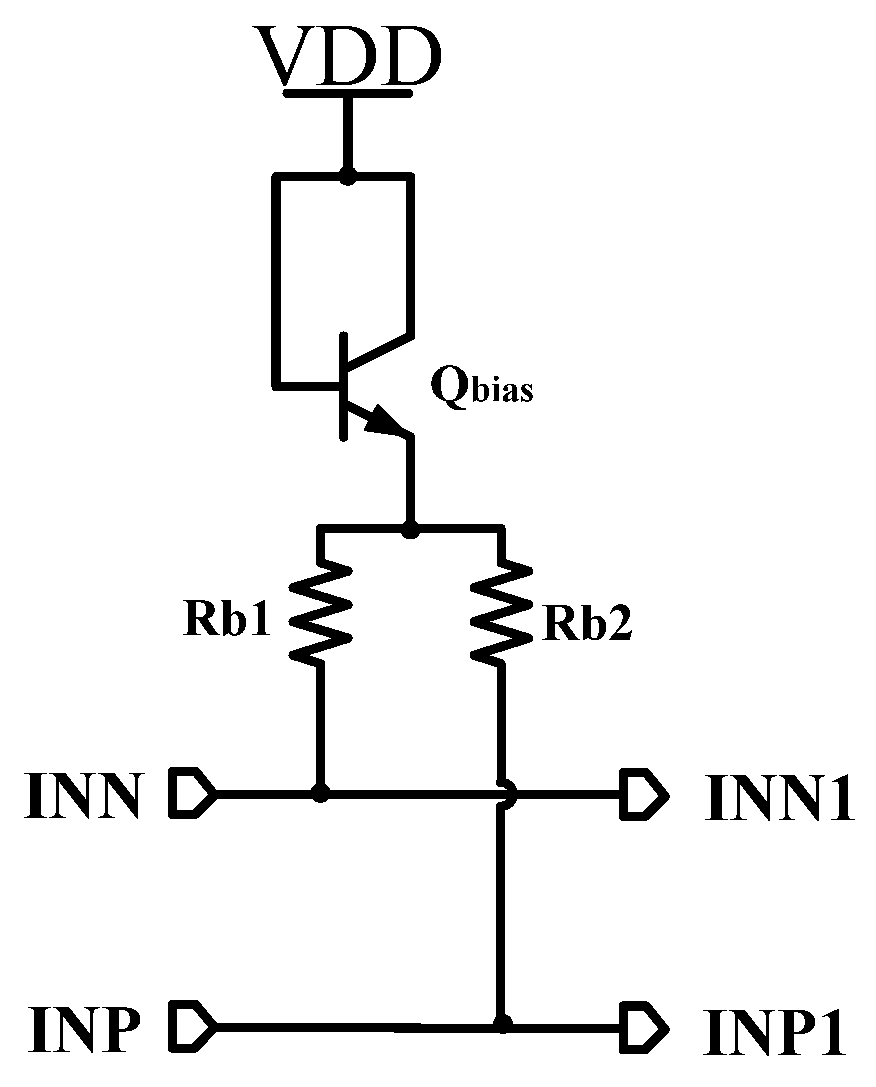
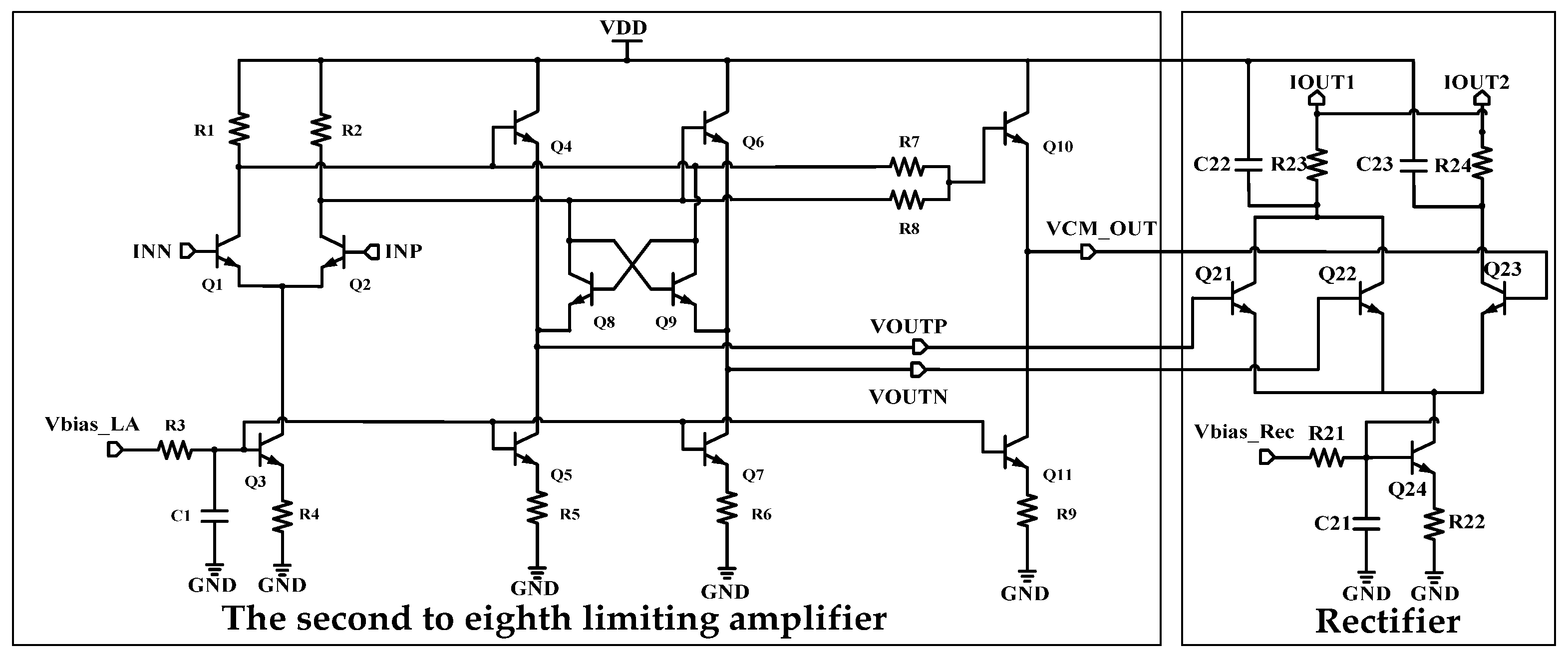
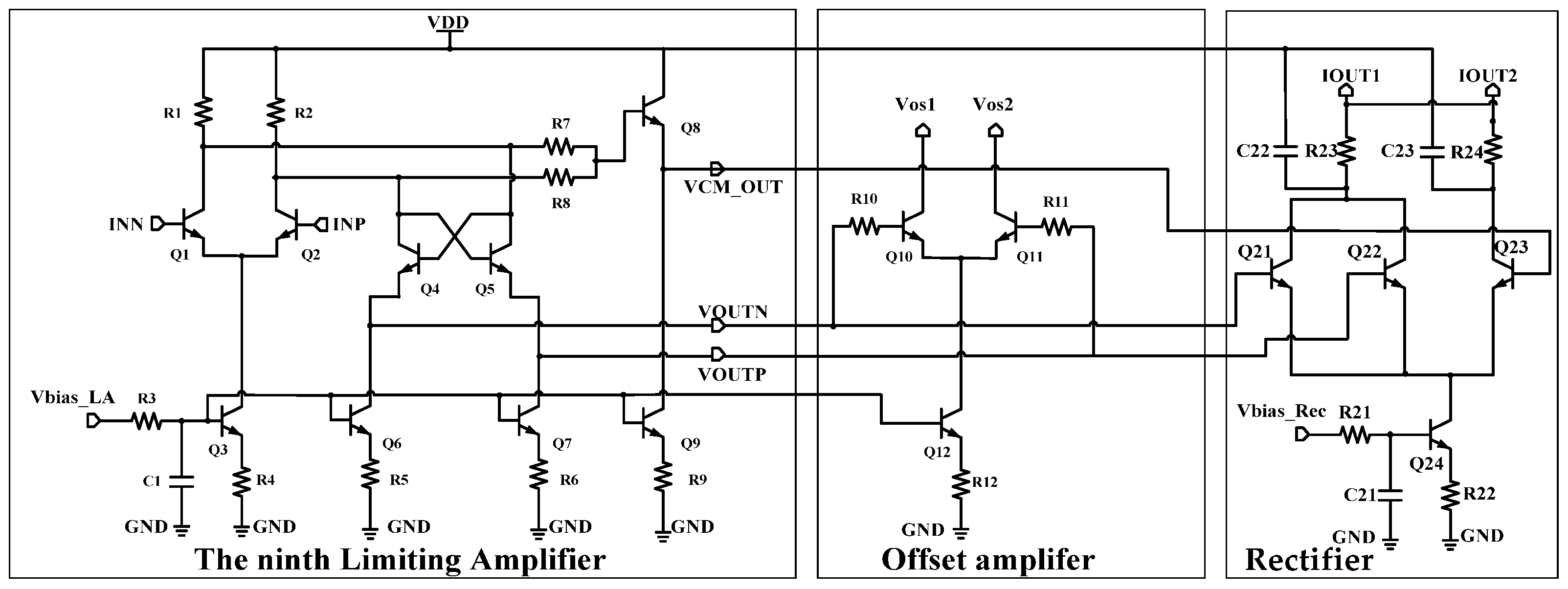
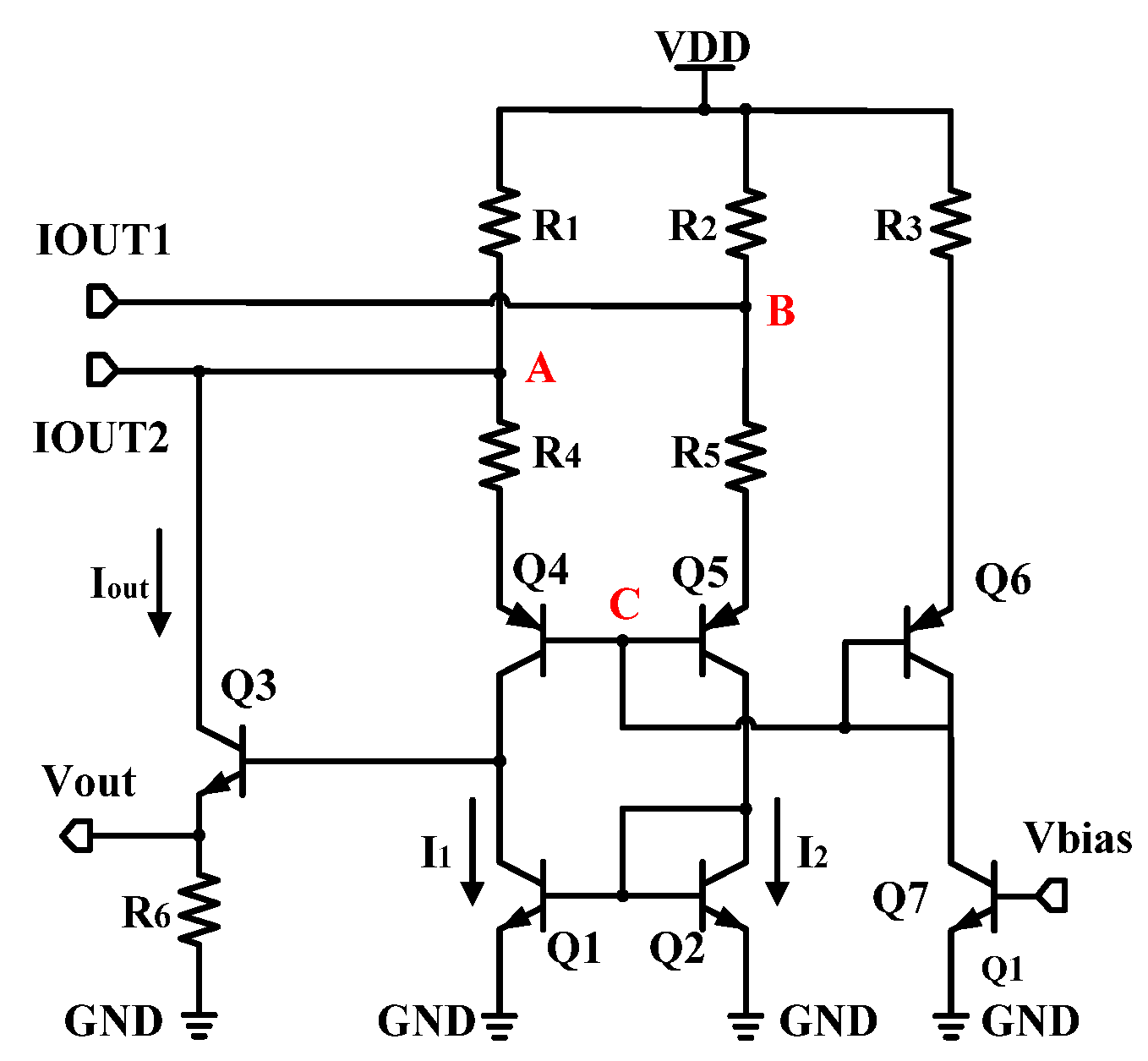
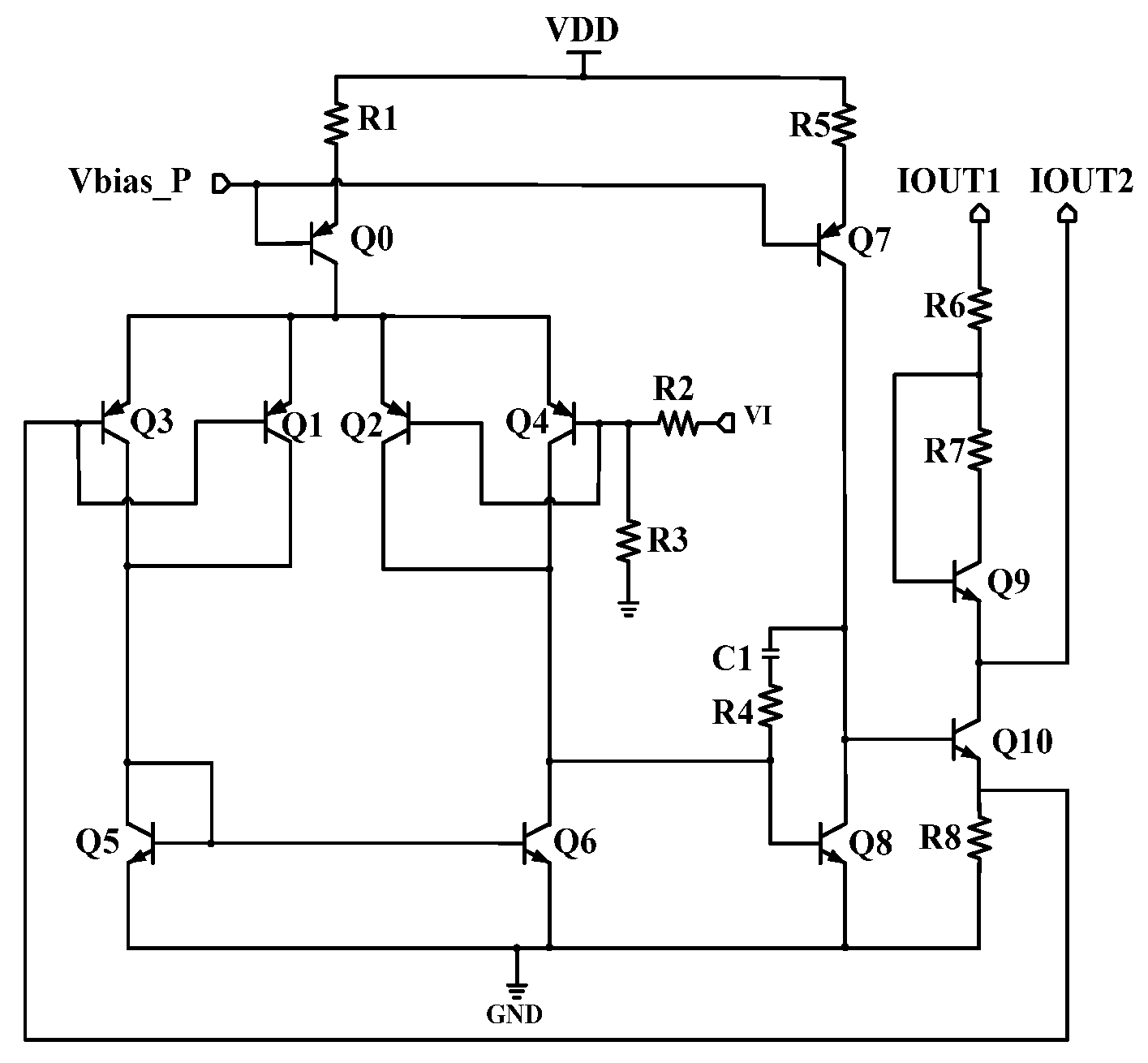
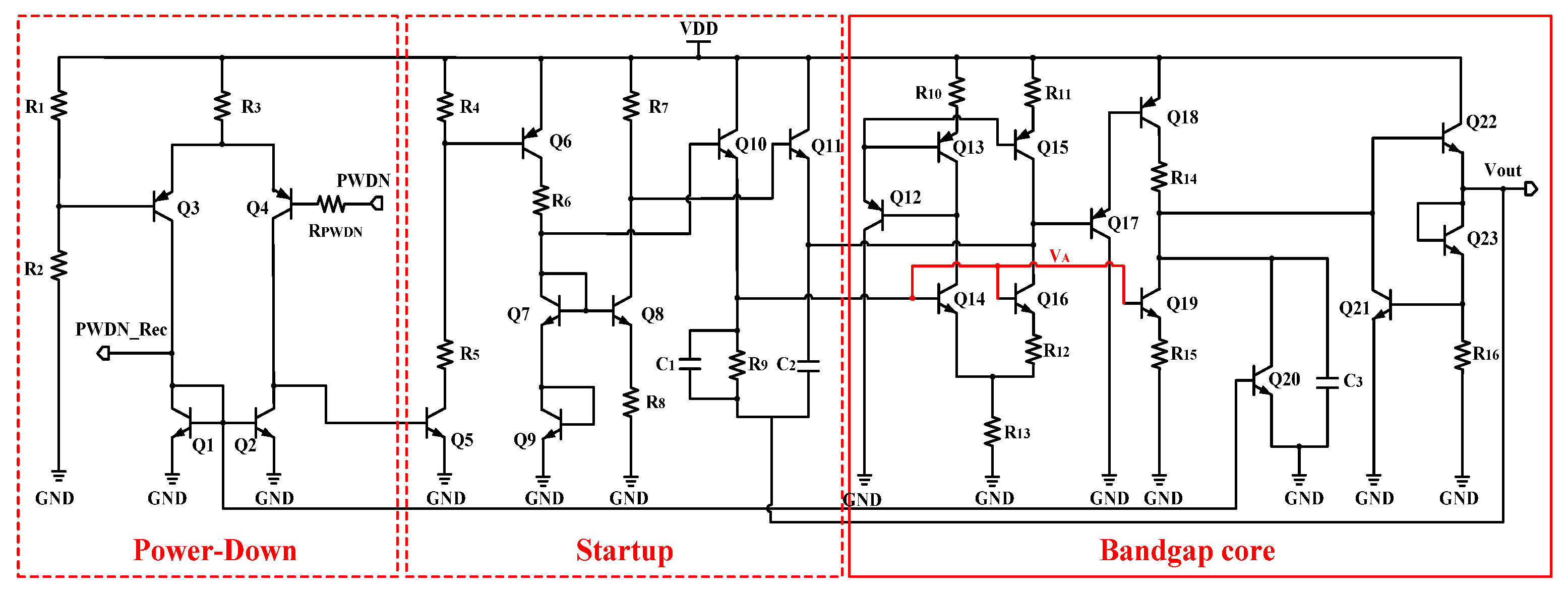
2. Circuit Architecture and Design
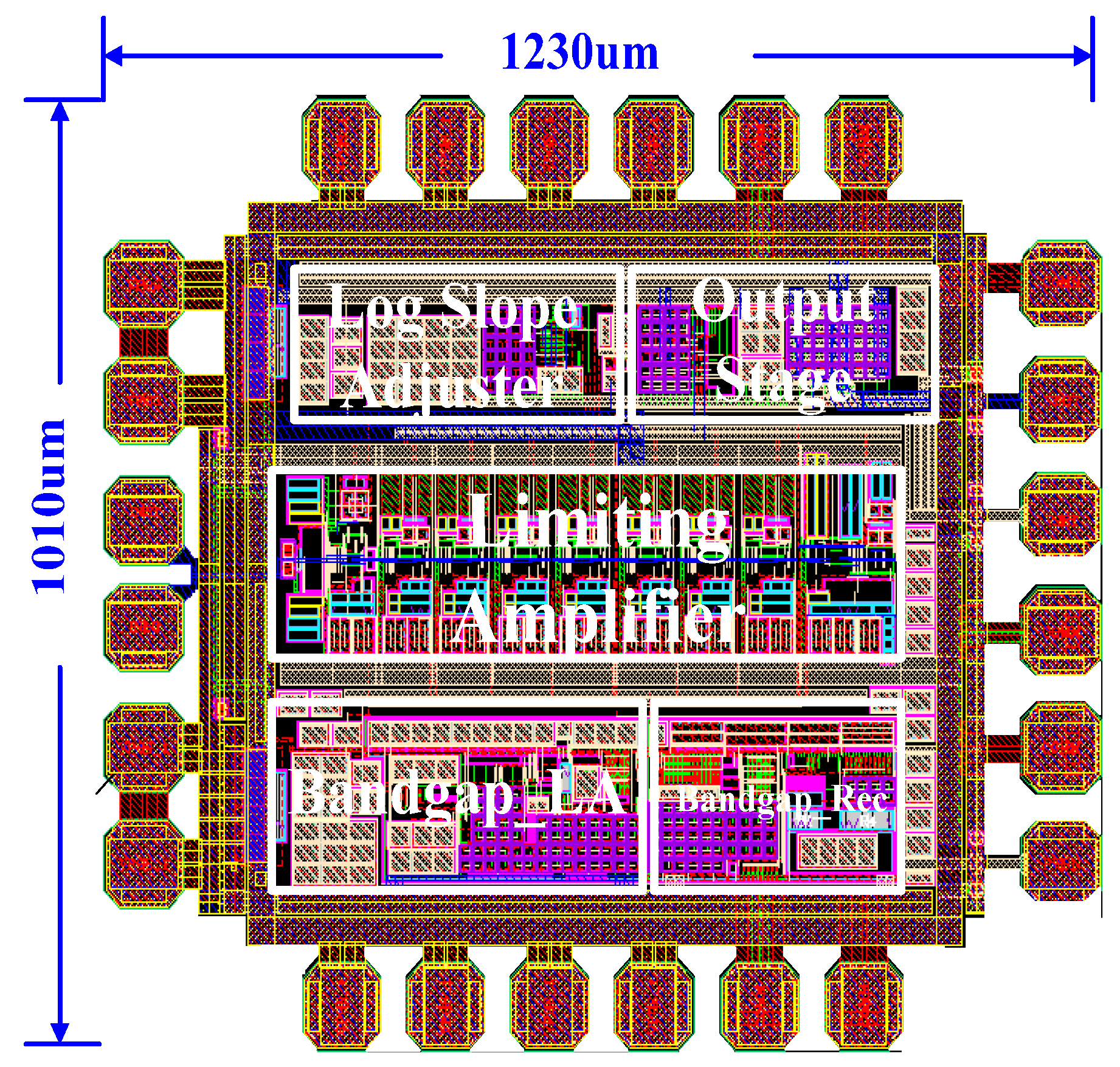
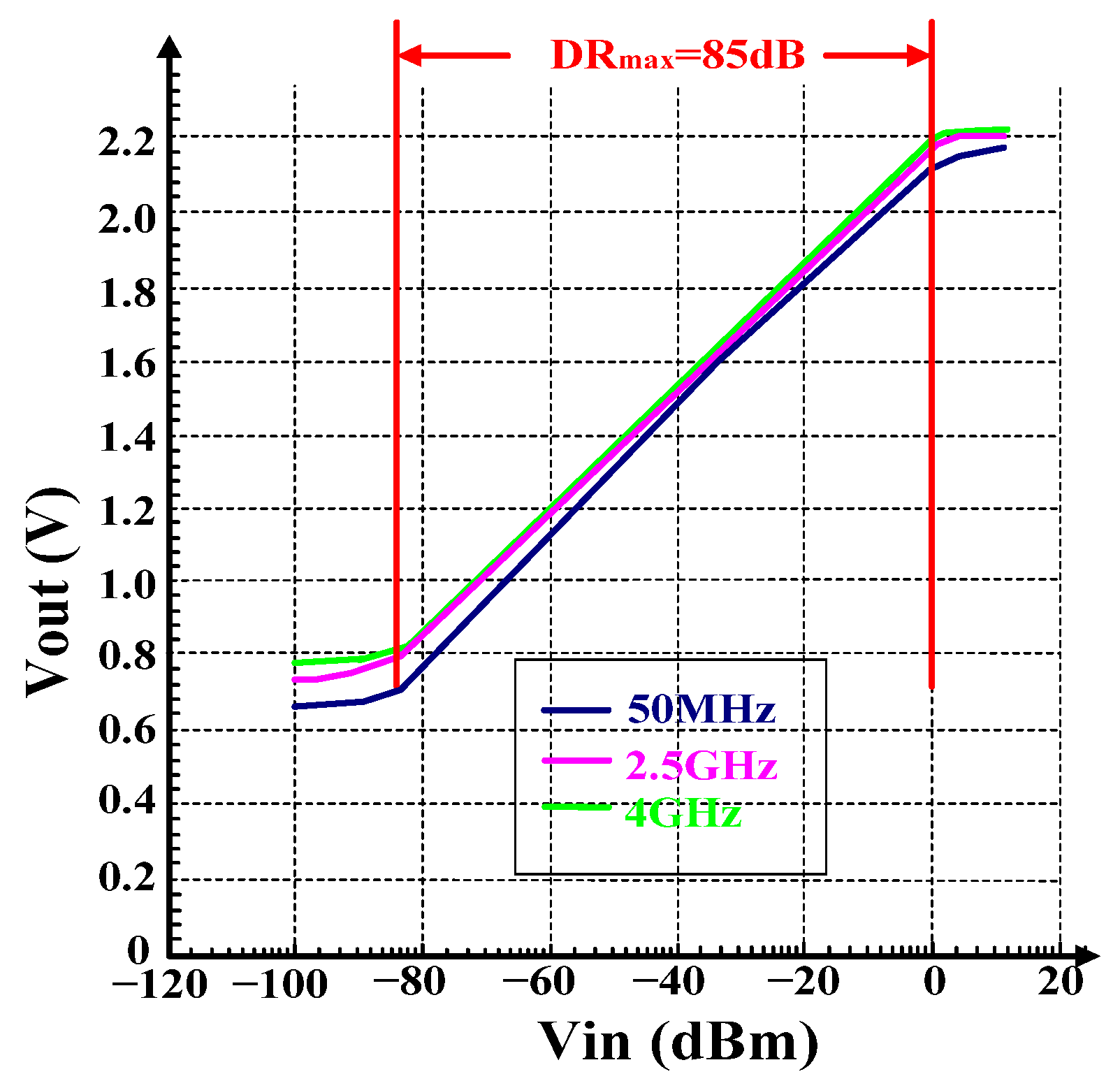
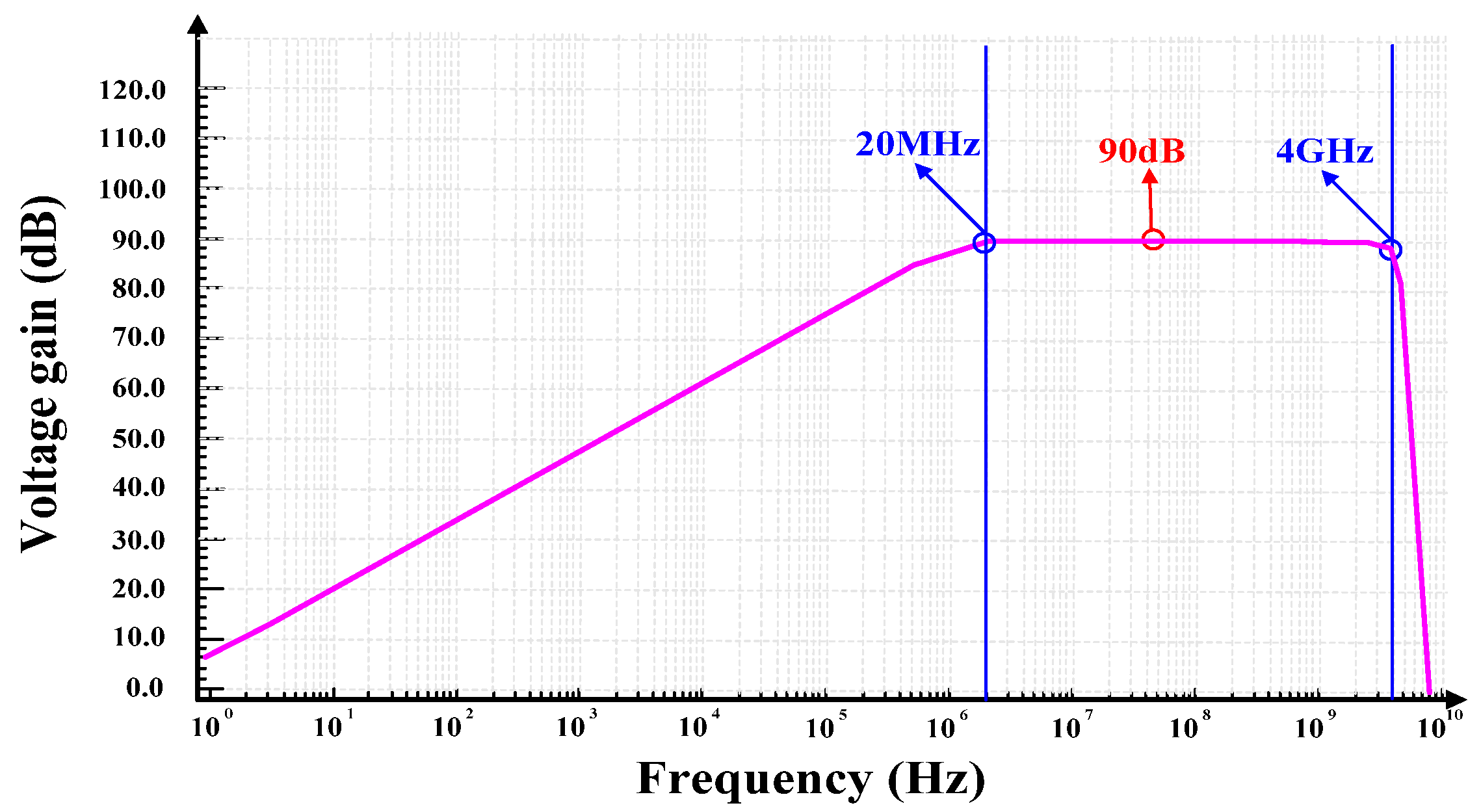
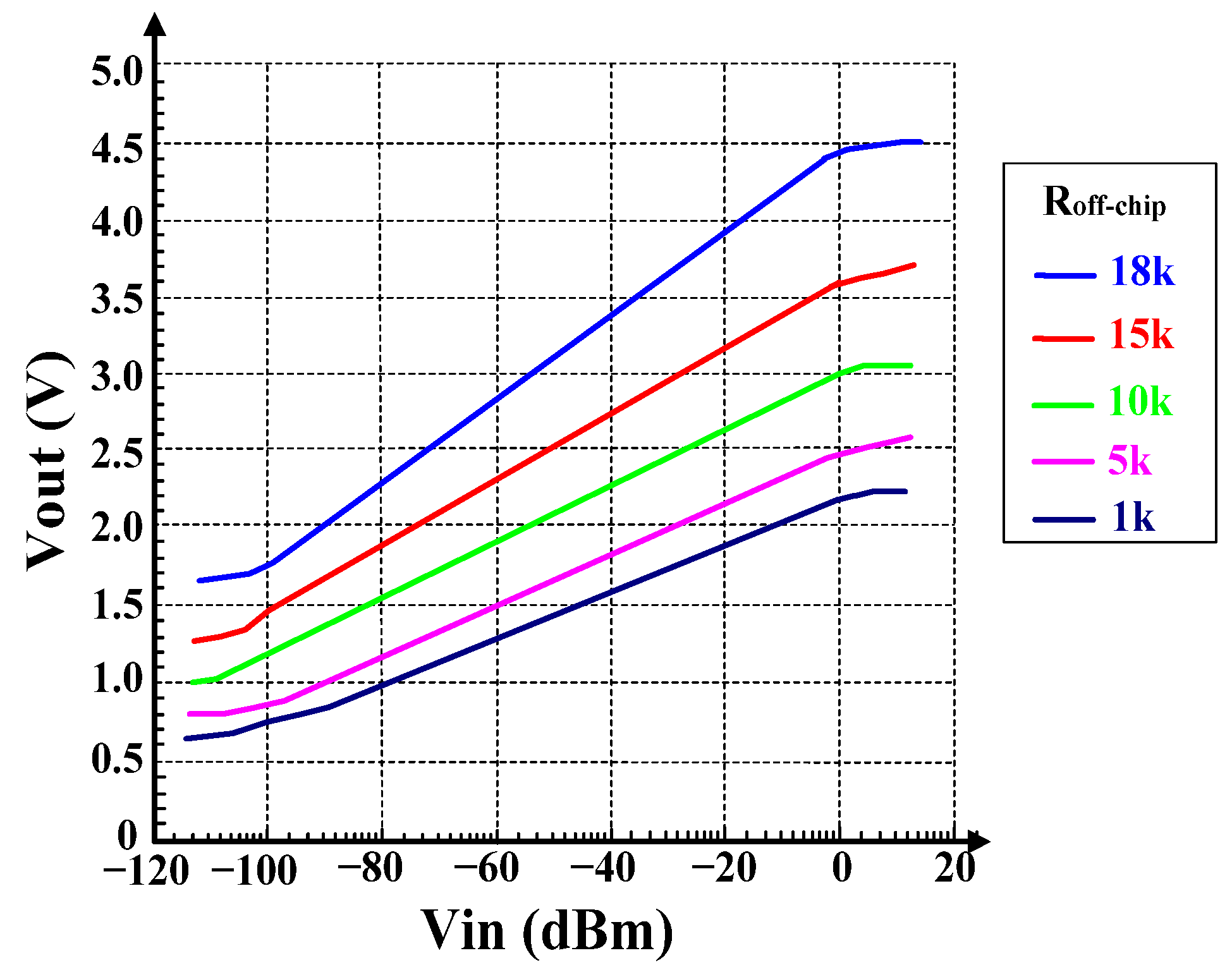
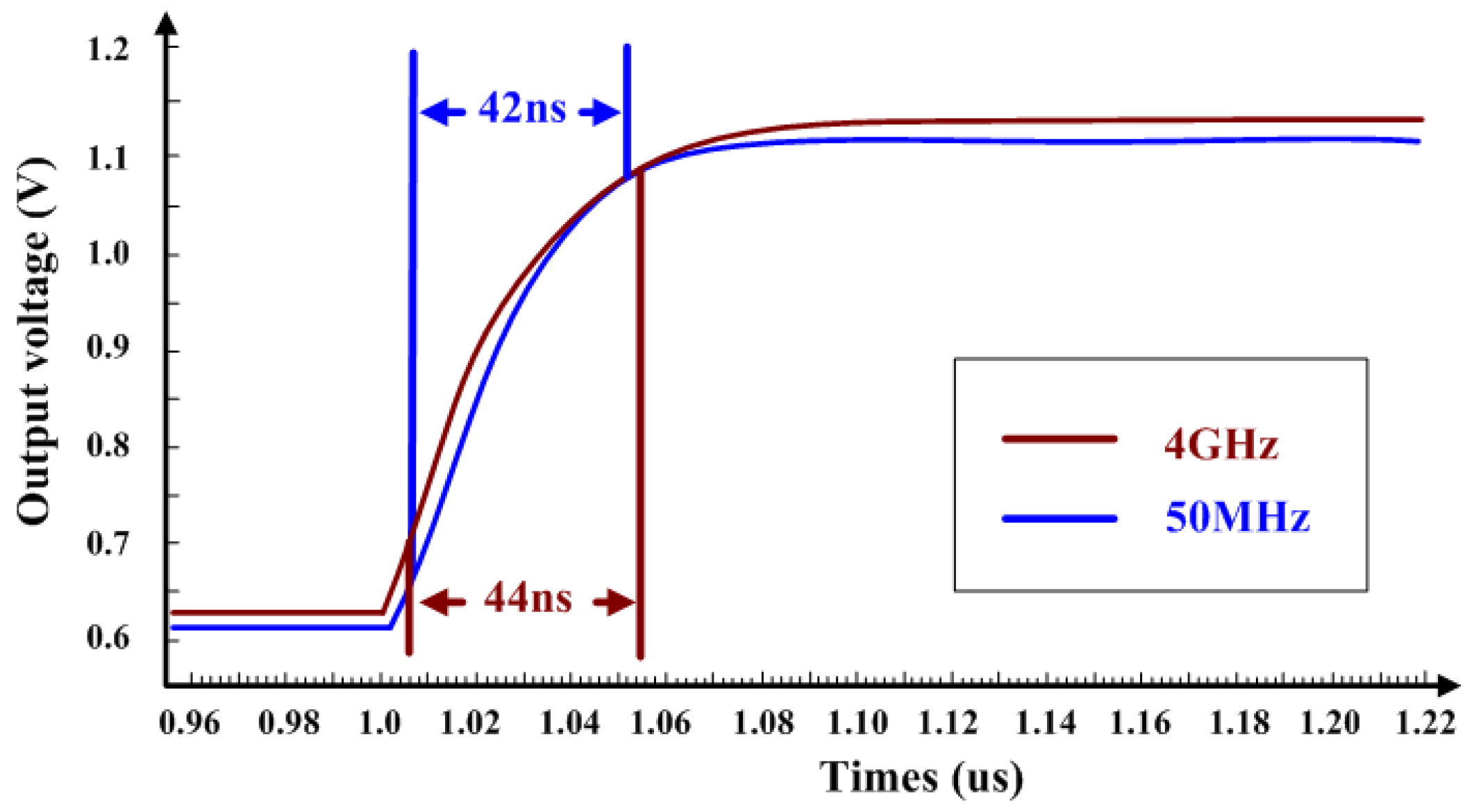
3. Post Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Li, K. A 1.3 GHz wideband successive detection logarithmic amplifier. In Proceedings of the 2007 7th International Conference on ASIC, Gulin, China, 22–25 October 2007; pp. 481–484. [Google Scholar]
- Gu, M.; Chakrabartty, S. Design of a Programmable Gain, Temperature Compensated Current-Input Current-Output CMOS Logarithmic Amplifier. IEEE Trans. Biomed. Circuit Syst. 2014, 8, 423–431. [Google Scholar]
- Cho, M.; Kenney, J. A fast accurate and digitally calibrate-able logarithmic amplifier for analog predistortion power amplifiers. In Proceedings of the Asia-Pacific Microwave Conference, Sendai, Japan, 4–7 November 2014; pp. 113–115. [Google Scholar]
- Alessandro, L.; Palomba, M.; Colangeli, S.; Limiti, E. Robust GaN Successive-Detection Logarithmic Video-Amplifier for EW Applications. In Proceedings of the Integrated Nonlinear Microwave and Millimeter wave Circuits Workshop, Taormina, Italy, 10–11 April 2015; pp. 66–68. [Google Scholar]
- Zhang, D.; Li, L.; Chen, K. Design of a 18–40 GHz Successive Detection Logarithmic Video Amplifier. In Proceedings of the Microwave circuits Radio frequency Detectors Dynamic range Noise measurement Europe Conferences, Hangzhou, China, 5–7 September 2018; pp. 4–7. [Google Scholar]
- Ravi, G.; Reddy, S.; Bharathi, A. Successive Detection Logarithmic Amplifier for ECCM features of RADAR. In Proceedings of the International Conference on Intelligent Technologies (CONIT), Karnataka, India, 23–25 June 2023; pp. 1–6. [Google Scholar]
- Miri, D.; Moezzi, M. An Ultra Wideband Low Power Detector Logarithmic Video Amplifier in 0.15 μm GaAs. In Proceedings of the Iranian Conference on Electrical Engineering (ICEE2019), Yazd, Iran, 30 April 2019; pp. 135–140. [Google Scholar]
- Holdenried, D.; Haslett, W.; McRory, G.; Beard, D.; Bergsma, J. A DC-4 GHz true logarithmic amplifier: Theory and implemenation. IEEE J. Solid-State Circuits 2002, 10, 1290–1299. [Google Scholar] [CrossRef]
- Lakshminarayanan, S.; Hofmann, K. A Wideband Large Dynamic Range Logarithmic RF Power Detector With 50 mV Input Offset Cancellation Range. In Proceedings of the 2019 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Bangkok, Thailand, 11–14 November 2019; pp. 85–88. [Google Scholar]
- Zhang, Y.; Chen, L.; Zhang, X.; Lai, Z. A parallel-amplification parallel-summation logarithmic amplifier for UHF RFID reader. In Proceedings of the 2009 IEEE 8th International Conference on ASIC, Changsha, China, 20–23 October 2009; pp. 1121–1124. [Google Scholar]
- Ahuja, A.; Mehta, D. Design and Simulation of Ultra-Low-Power Parallel Summation Logarithmic Amplifier. In Proceedings of the 2022 IEEE International Conference of Electron Devices Society Kolkata Chapter (EDKCON), 26–27 November 2022; pp. 324–327. [Google Scholar]
- Wongnamkam, S.; Thanachayanont, A.; Krairiksh, M. A 2.4-GHz 43-dB CMOS Logarithmic Amplifier for RF Signal Level Detection. In Proceedings of the 2008 5th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Krabi, Thailand, 28 February–2 March 2008; pp. 725–728. [Google Scholar]
- Chuang, Y.; Cimino, K.; Stuenkel, M.; Feng, M.; Le, M.; Milano, R. A wideband InP DHBT True Logarithmic Amplifier. IEEE Trans. Microw. Theory Tech. 2006, 11, 3843–3847. [Google Scholar] [CrossRef]
- Kim, K.; Kwon, Y. A Broadband Logarithmic Power Detector in 0.13-um CMOS. IEEE Microw. Wirel. Compon. Lett. 2013, 9, 498–500. [Google Scholar] [CrossRef]
- Ramos, J.; AUSÍN, J.; Duque-Carrillo, J.; Torelli, G. Design of limiting/logarithmic amplifier for wideband bioimpedance measuring devices. In Proceedings of the 2010 Biomedical Circuits and Systems Conference (BioCAS), Paphos, Cyprus, 3–5 November 2010; pp. 290–293. [Google Scholar]
- Zareie, M.; Hosseinnejad, M.; Azhari, J. Ultra-Low-Power, Wide Dynamic Range Front-End Logarithmic Amplifier for Biomedical Applications. In Proceedings of the Conference on Knowledge Based Engineering and Innovation (KBEI), Tehran, Iran, 28 February 2019; pp. 548–552. [Google Scholar]
- Shaterian, M.; Abrishamifar, A.; Shamsi, H. Analysis and Design of The True Piecewise Approximation Logarithmic Amplifiers. Analog Integr. Circuits Signal Process 2012, 1, 193–203. [Google Scholar] [CrossRef]
- Derafshi, Z.; Frounchi, J. Low-noise low-power front-end logarithmic amplifier for neural recording system. Int. J. Circuit Theory Appl. 2014, 5, 437–451. [Google Scholar] [CrossRef]
- Morozov, D.N.; Repin, V.V.; Mukhin, I.I. A 70 dB SiGe Adjustable True Logarithmic Amplifier. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 27–30 January 2020. [Google Scholar]
- Lin, C.; Huang, H.; Wang, K. A 15 mW 280 MHz 80 dB gain CMOS limiting/logarithmic amplifier with active cascode gain–enhancement. In Proceedings of the Solid-State Circuits Conference, Florence, Italy, 24–26 September 2002; pp. 311–314. [Google Scholar]
- Chokchalermwat, P.; Supmonchai, B. Design of a CMOS Low-Power Limiting Amplifier with RSSI Integrated Circuit for Low-Frequency Wake-Up Receivers. In Proceedings of the International Electrical Engineering Congress, Krabi, Thailand, 7–9 March 2018; pp. 1–4. [Google Scholar]
- Shieh, L.; Lai, J.; Li, S.; Chiang, L.; Wu, H.; Xsieh, C.; Tu, H.; Chen, W.; Wu, W. Linear radio frequency power detector. In Proceedings of the Asia Pacific Microwave Conference, Singapore, 7–10 December 2009; pp. 2316–2319. [Google Scholar]
- Townsend, A.; Haslett, W. A wideband power detection system optimized for the UWB spectrum. IEEE J. Solid-State Circuits 2009, 2, 371–381. [Google Scholar] [CrossRef]
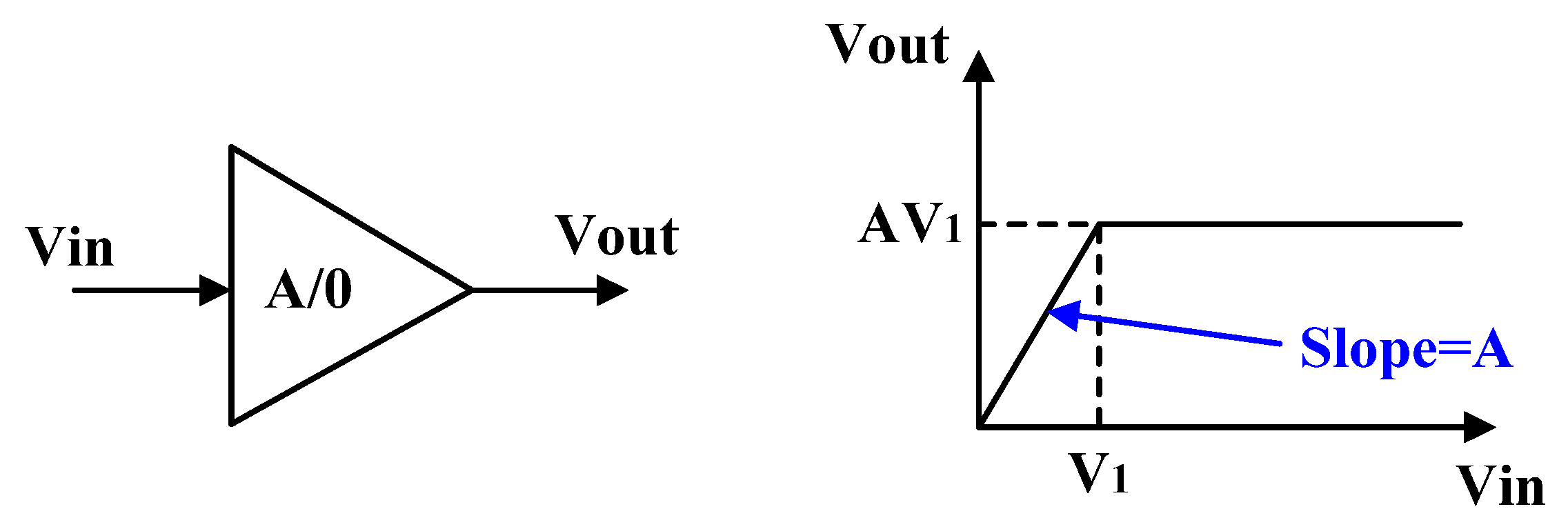


| Parameter | [10] | [12] | [14] | [22] | [23] | This Work |
|---|---|---|---|---|---|---|
| Process | 180 nm CMOS | 350 nm CMOS | 130 nm CMOS | 180 nm CMOS | 180 nm CMOS | 180 nm SiGe BiCMOS |
| Power supply (V) | 3.3 | 2.5 | 2 | 1.8 | 1.8 | 5 |
| Bandwidth (GHz) | 0.001 | 2.4 | 16 | 1.8 | 10.6 | 4 |
| Dynamic range (dB) | 70 | 43 | 43 | 29 | 20 | 85 |
| Log error (dB) | N/A * | N/A | ±1.5 | ±1 | ±2.4 | ±1 |
| Response Time (ns) | N/A | N/A | N/A | N/A | N/A | 42 |
| log slope adjustment | N/A | N/A | No | No | No | Yes |
| Pdc (mW) | 19 | 184 | 35.2 | 16 | 10.8 | 70 |
| FoM (mW/(dBm × GHz)) | 271.4 | 1.78 | 0.051 | 0.31 | 0.051 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Teng, R.; Zhou, Y.; Lu, M.; Ruan, W.; Li, J. A High Dynamic Range and Fast Response Logarithmic Amplifier Employing Slope-Adjustment and Power-Down Mode. Micromachines 2025, 16, 741. https://doi.org/10.3390/mi16070741
Wang Y, Teng R, Zhou Y, Lu M, Ruan W, Li J. A High Dynamic Range and Fast Response Logarithmic Amplifier Employing Slope-Adjustment and Power-Down Mode. Micromachines. 2025; 16(7):741. https://doi.org/10.3390/mi16070741
Chicago/Turabian StyleWang, Yanhu, Rui Teng, Yuanjie Zhou, Mengchen Lu, Wei Ruan, and Jiapeng Li. 2025. "A High Dynamic Range and Fast Response Logarithmic Amplifier Employing Slope-Adjustment and Power-Down Mode" Micromachines 16, no. 7: 741. https://doi.org/10.3390/mi16070741
APA StyleWang, Y., Teng, R., Zhou, Y., Lu, M., Ruan, W., & Li, J. (2025). A High Dynamic Range and Fast Response Logarithmic Amplifier Employing Slope-Adjustment and Power-Down Mode. Micromachines, 16(7), 741. https://doi.org/10.3390/mi16070741





