MCE-HGCN: Heterogeneous Graph Convolution Network for Analog IC Matching Constraints Extraction
Abstract
1. Introduction
- (1)
- Framework for matching constraint extraction: We propose a framework based on heterogeneous graph convolutional networks to identify matching structure types required for layout placement from analog netlists. The matching constraint extraction task is reformulated as a classification problem involving node pairs within a heterogeneous graph.
- (2)
- Mixed-domain attention mechanism: We enhance the heterogeneous graph neural network with a mixed-domain attention mechanism that considers both nodes and edges. This improvement facilitates more effective message passing between different node and edge types, maximizes the utility of small datasets, and strengthens the identification of matching structures in netlists.
- (3)
- Matching classifier and filter: A matching classifier based on support vector machines is proposed to identify matching structures within circuits. Additionally, matching filters are implemented to further improve recognition accuracy.
- (4)
- Experimental validation: Experimental results confirm the effectiveness of the proposed method in extracting matching constraints across various ICs and processes. This approach provides layout engineers with valuable support in determining device matching relationships.
2. Problem Description and Graph Construction
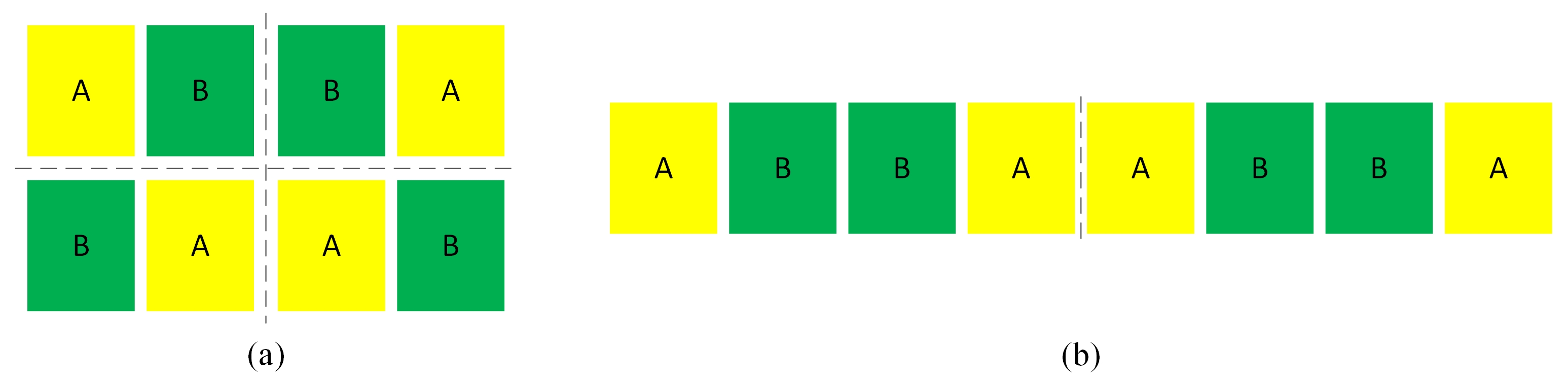
2.1. Problem Description
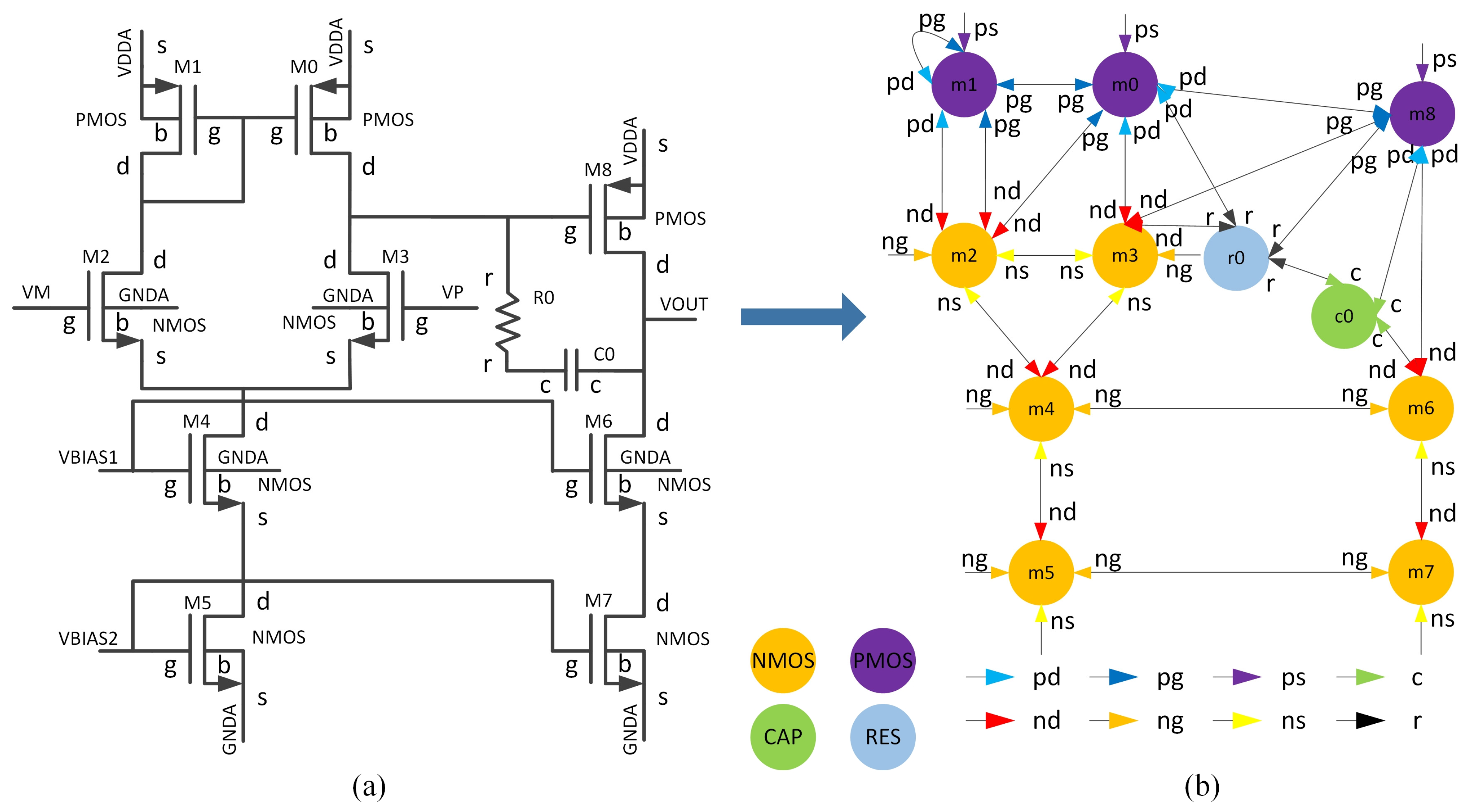
2.2. Heterogeneous Attribute Multi-Graph
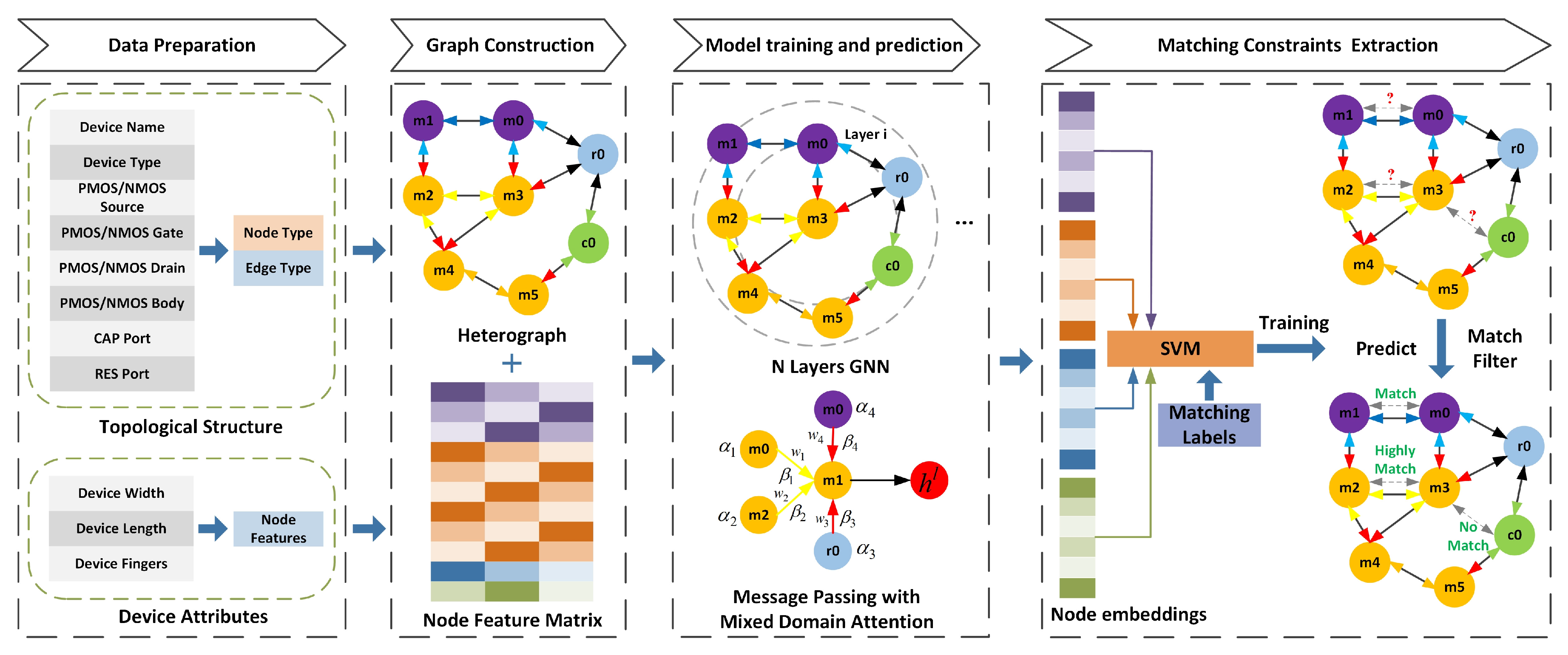
3. MCE-HGCN Framework
3.1. MCE-HGCN Network
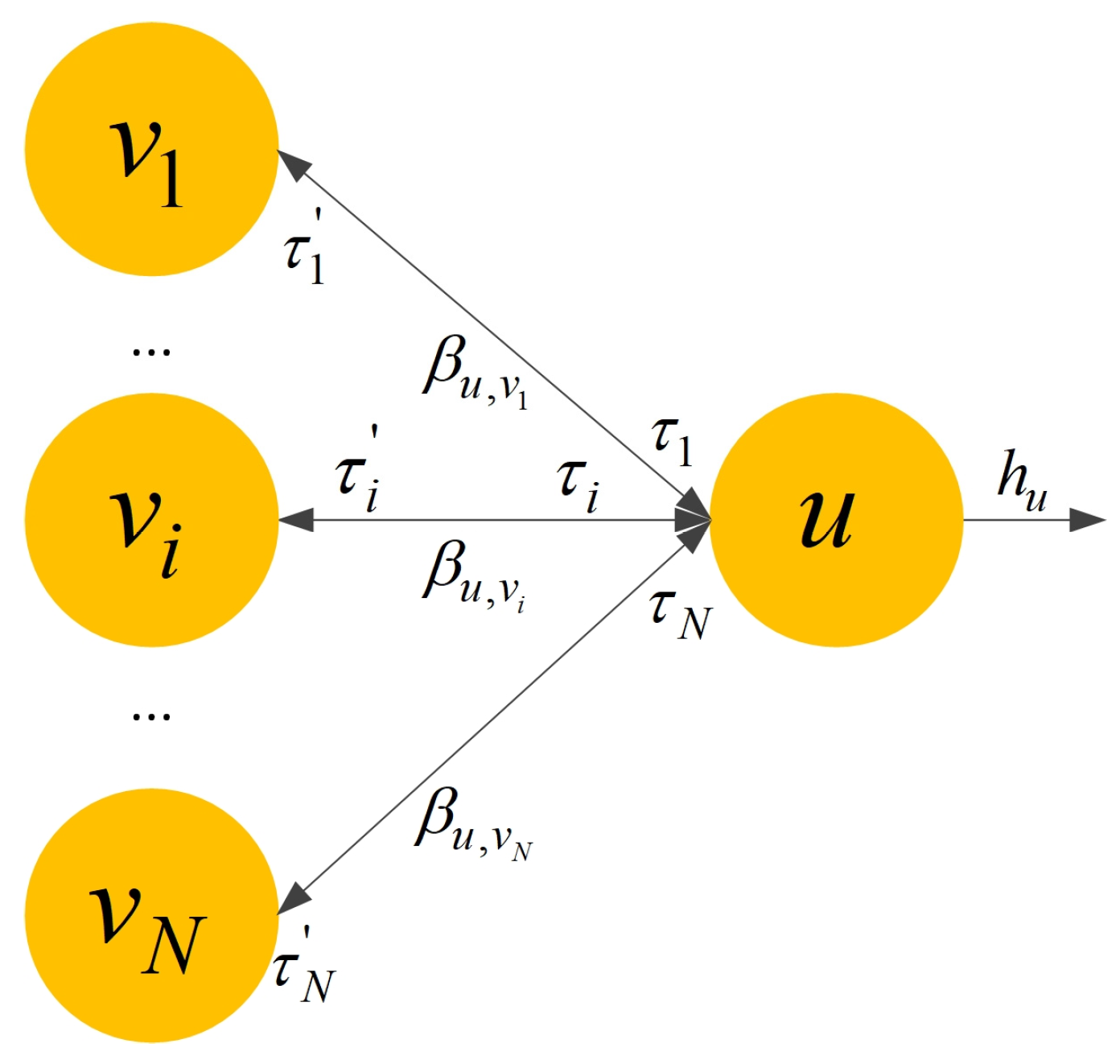
3.2. Mixed-Domain Attention Mechanism
3.2.1. Node Attention
3.2.2. Edge Attention
3.3. Matching Constraint Extraction Methods
3.3.1. Matched Classifier
| Algorithm 1 Matchings Predict Model Training |
| Input: Heterogeneous attribute multi-graph datasets , Annotated matching relationship . Output: Matching predict model . 1. Initialize the MCE-HGCN net; 2. for each graph in do 3. predict graph embedding ; 4. for each node in graph do 5. for each node in graph do 6. Compute the Euclidean distance between node and node by nodes’ embedding; 7. Add to Euclidean distance set between node pairs; , is the number of nodes in the graph; 8. Support vector machine training ; 9. return . |
3.3.2. Matched Filter
| Algorithm 2 Matching Constraints Extraction |
| Input: An analog circuit netlist . Output: Matching pairs in the netlist. 1. Construct the heterogeneous attribute multi-graph form the netlist ; 2. MCE-HGCN predicts nodes’ embedding in ; 3. Predicting matching node pairs p by ; 4. for each node pair do 5. if then 6. Add to ; 7. return . |
4. Experiment
4.1. Experimental Data
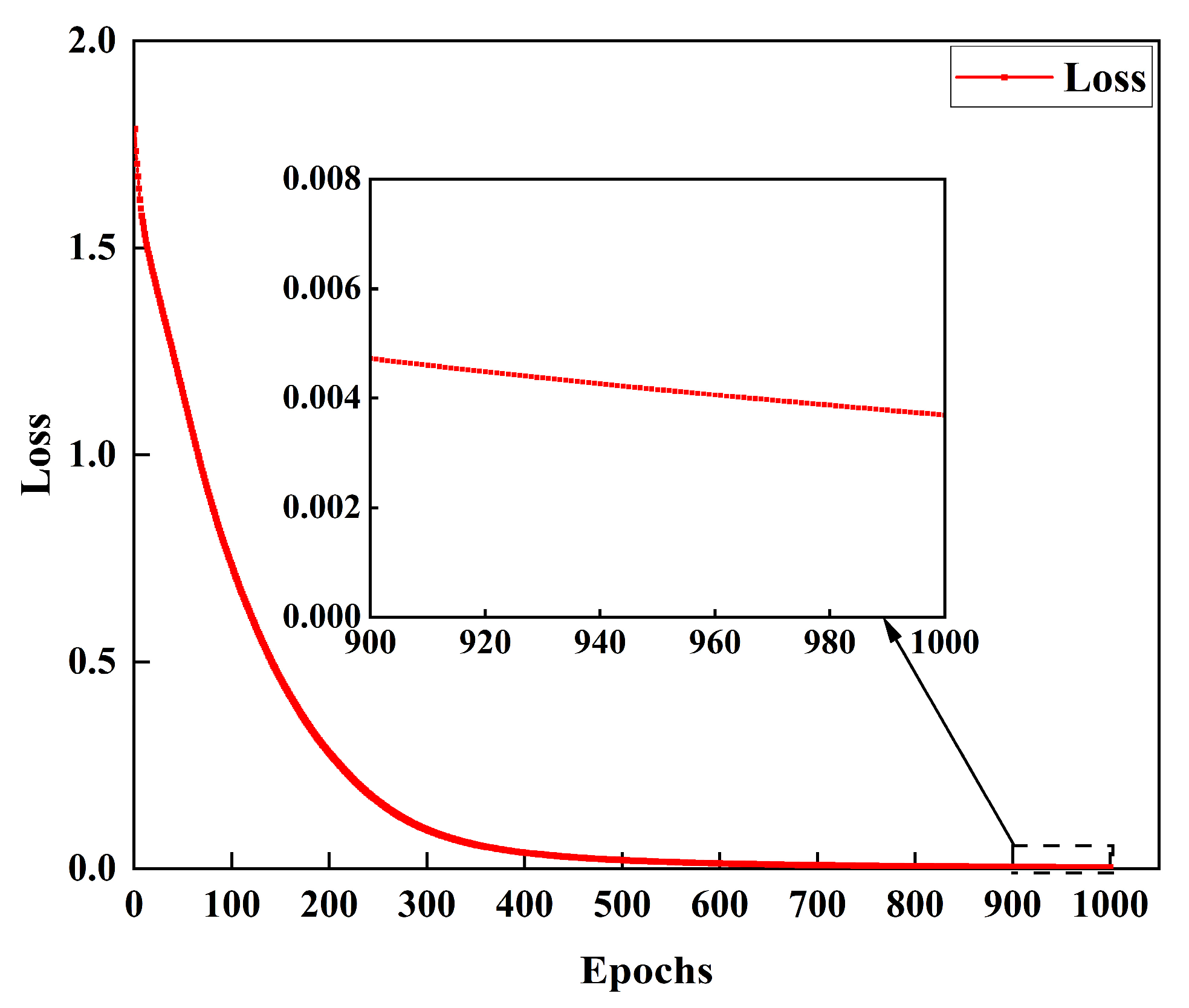
4.2. Model Training
4.3. Experimental Analysis
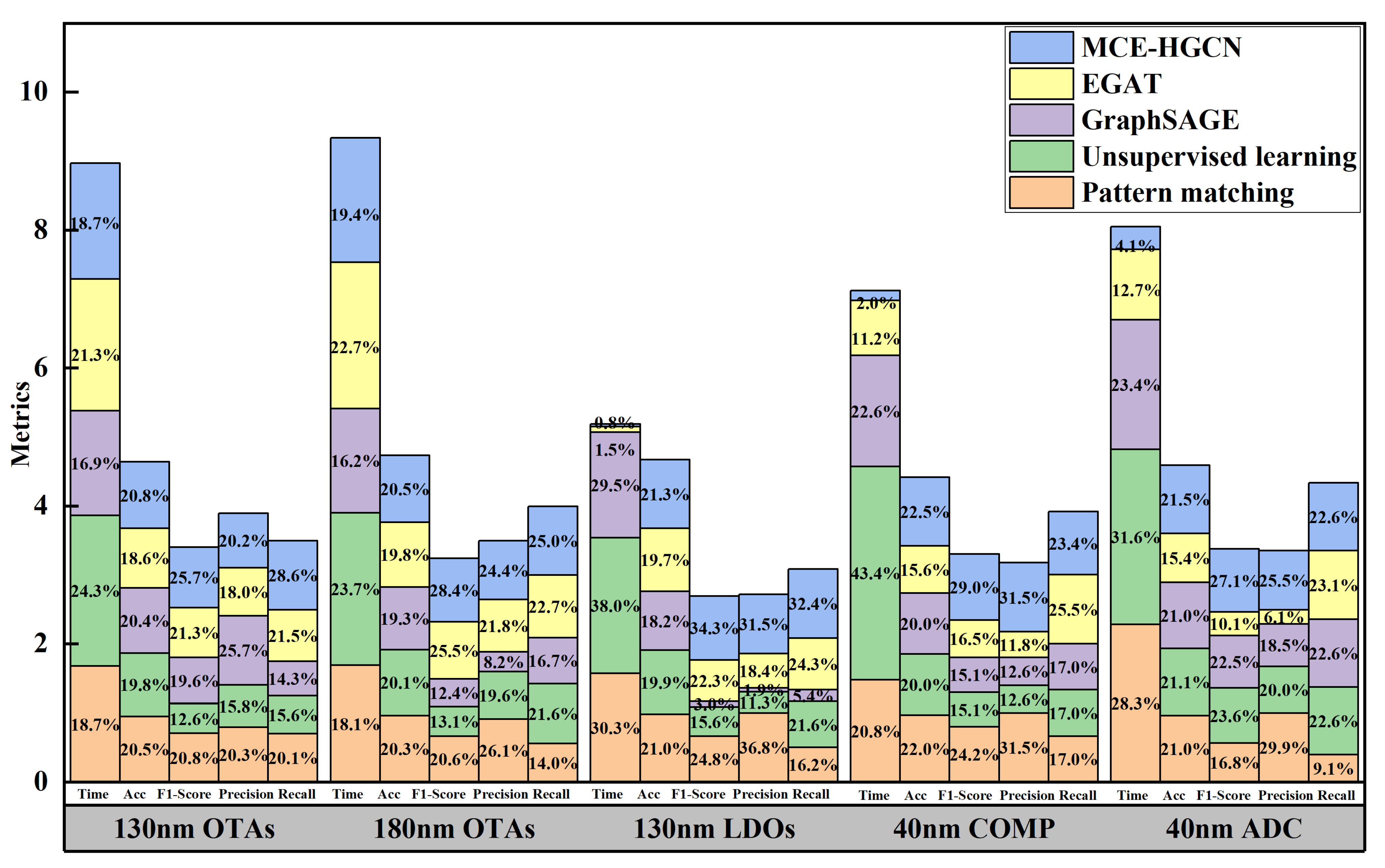
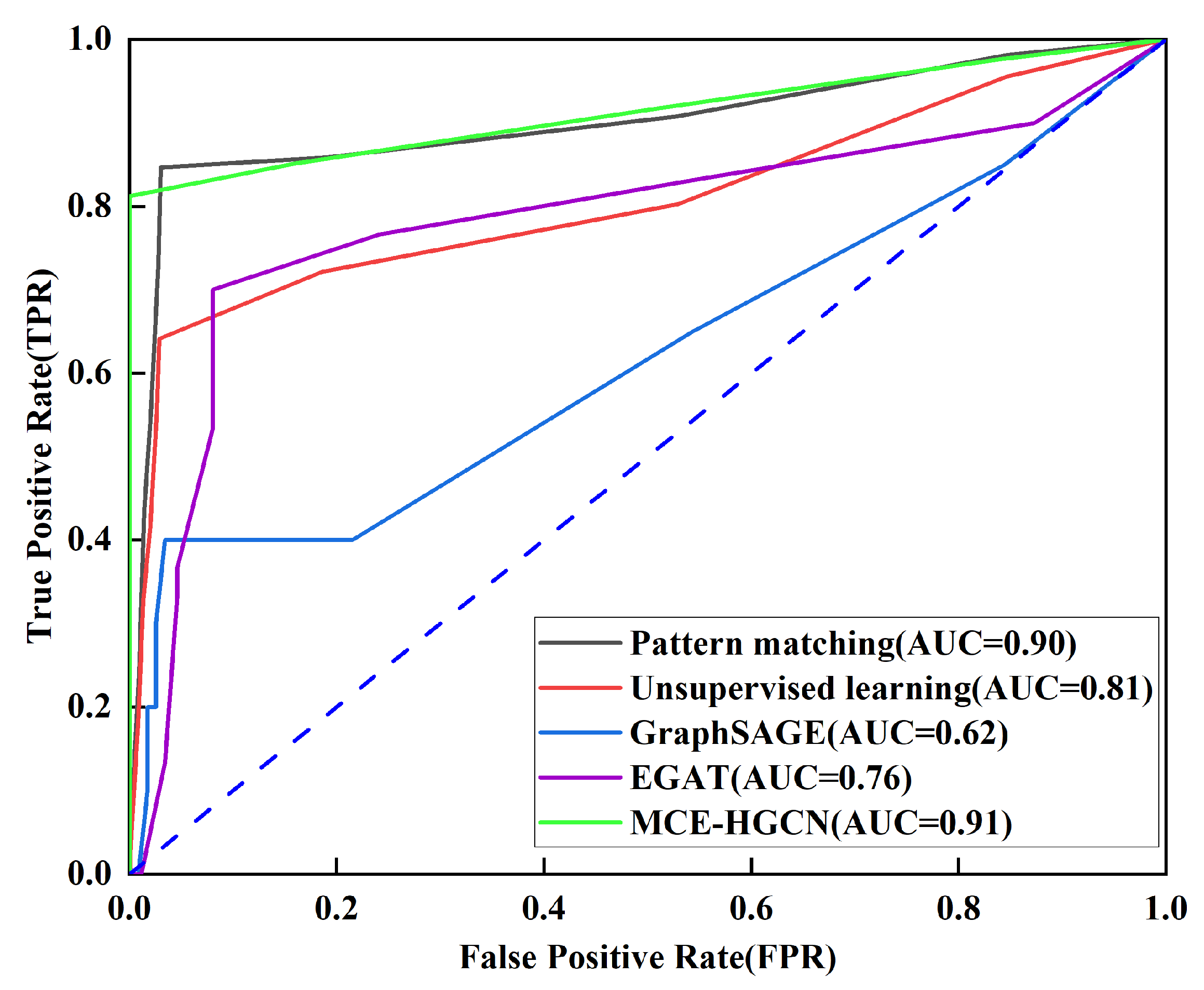
4.3.1. Comparison Experiments
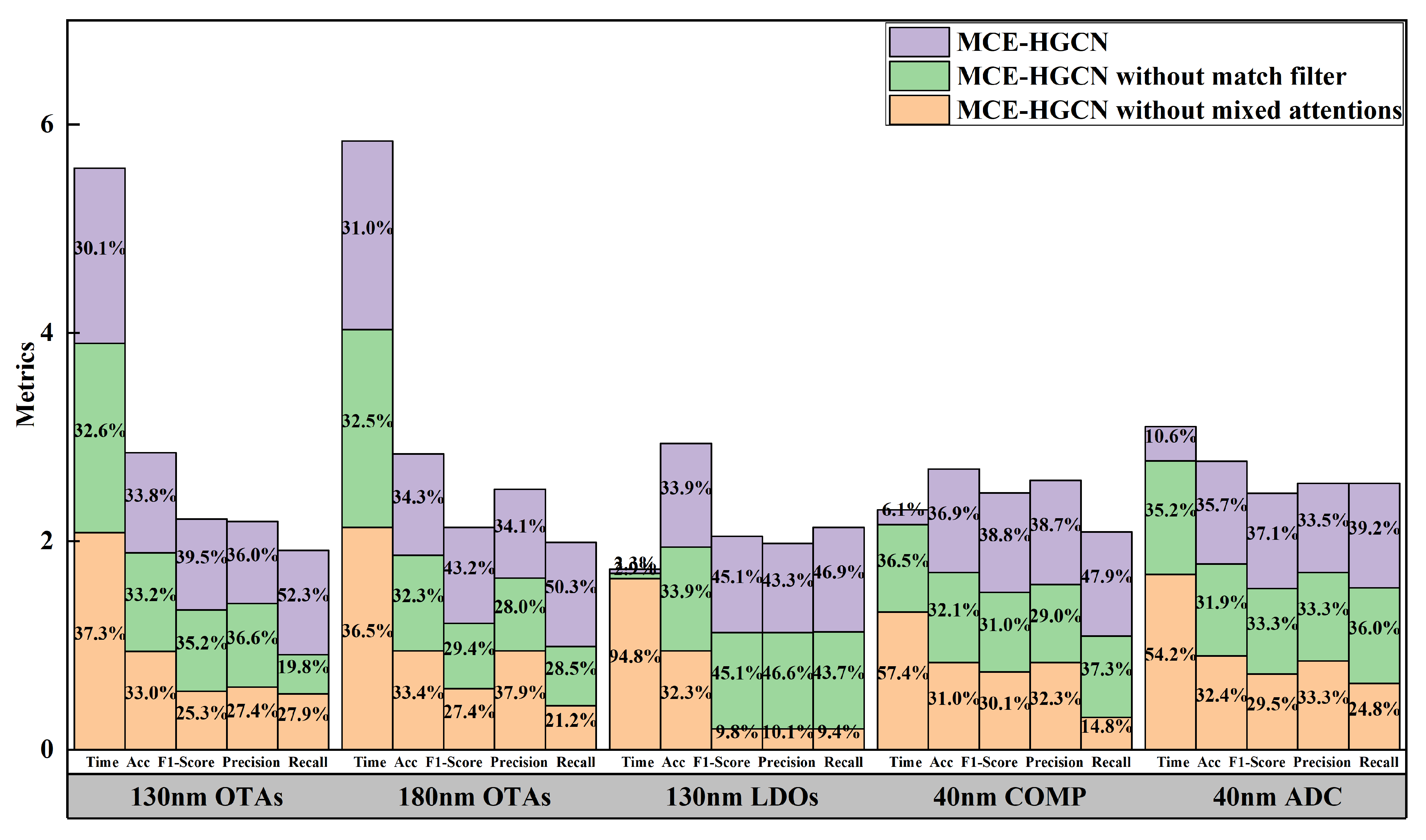
4.3.2. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dhar, T.; Kunal, K.; Li, Y.; Madhusudan, M.; Poojary, J.; Sharma, A.K.; Xu, W.; Burns, S.M.; Harjani, R.; Hu, J.; et al. ALIGN: A system for automating analog layout. IEEE Des. Test 2020, 38, 8–18. [Google Scholar] [CrossRef]
- Martins, R.; Lourenço, N.; Horta, N. Analog Integrated Circuit Design Automation; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Malavasi, E.; Charbon, E.; Felt, E.; Sangiovanni Vincentelli, A. Automation of IC layout with analog constraints. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1996, 15, 923–942. [Google Scholar] [CrossRef]
- Wu, P.H.; Lin, M.P.H.; Ho, T.Y. Analog layout synthesis with knowledge mining. In Proceedings of the 2015 European Conference on Circuit Theory and Design (ECCTD), Trondheim, Norway, 24–26 August 2015; pp. 1–4. [Google Scholar]
- Zhu, K.; Chen, H.; Liu, M.; Pan, D.Z. Automating analog constraint extraction: From heuristics to learning. In Proceedings of the 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC), Taipei, Taiwan, 17–20 January 2022; pp. 108–113. [Google Scholar]
- Chen, S.; Liu, J.; Shen, L. A Survey on Graph Neural Network Acceleration: A Hardware Perspective. Chin. J. Electron. 2024, 33, 601–622. [Google Scholar] [CrossRef]
- Gao, X.; Deng, C.; Liu, M.; Zhang, Z.; Pan, D.Z.; Lin, Y. Layout symmetry annotation for analog circuits with graph neural networks. In Proceedings of the 26th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 18–21 January 2021; pp. 152–157. [Google Scholar]
- Kunal, K.; Poojary, J.; Dhar, T.; Madhusudan, M.; Harjani, R.; Sapatnekar, S.S. A general approach for identifying hierarchical symmetry constraints for analog circuit layout. In Proceedings of the 39th International Conference on Computer-Aided Design, San Diego, CA, USA, 2–5 November 2020; pp. 1–8. [Google Scholar]
- Kunal, K.; Dhar, T.; Madhusudan, M.; Poojary, J.; Sharma, A.; Xu, W.; Sapatnekar, S.S. GANA: Graph convolutional network based automated netlist annotation for analog circuits. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 55–60. [Google Scholar]
- Bai, Y.; Ding, H.; Bian, S.; Chen, T.; Sun, Y.; Wang, W. Simgnn: A neural network approach to fast graph similarity computation. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, VIC, Australia, 11–15 February 2019; pp. 384–392. [Google Scholar]
- Zhou, Z.; Dong, S.; Hong, X.; Hao, Q.; Chen, S. Analog constraints extraction based on the signal flow analysis. In Proceedings of the 2005 6th International Conference on ASIC, Shanghai, China, 24–27 October 2005; Volume 2, pp. 825–828. [Google Scholar]
- Eick, M.; Strasser, M.; Lu, K.; Schlichtmann, U.; Graeb, H.E. Comprehensive generation of hierarchical placement rules for analog integrated circuits. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2011, 30, 180–193. [Google Scholar] [CrossRef]
- Kunal, K.; Dhar, T.; Madhusudan, M.; Poojary, J.; Sharma, A.K.; Xu, W.; Burns, S.M.; Hu, J.; Harjani, R.; Sapatnekar, S.S. GNN-based hierarchical annotation for analog circuits. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 2801–2814. [Google Scholar] [CrossRef]
- Yao, W.; Gao, X.; Lin, Y.; Li, L. Automatic layout symmetry extraction for analog constraint learning. In Proceedings of the 2023 International Symposium of Electronics Design Automation (ISEDA), Nanjing, China, 8–11 May 2023; pp. 76–81. [Google Scholar]
- Liu, M.; Li, W.; Zhu, K.; Xu, B.; Lin, Y.; Shen, L.; Tang, X.; Sun, N.; Pan, D.Z. S3det: Detecting system symmetry constraints for analog circuits with graph similarity. In Proceedings of the 2020 25th Asia and South Pacific Design Automation Conference (ASP-DAC), Beijing, China, 13–16 January 2020; pp. 193–198. [Google Scholar]
- Arnold, T.B.; Emerson, J.W. Nonparametric goodness-of-fit tests for discrete null distributions. R J. 2011, 3, 34–39. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, K.; Liu, M.; Tang, X.; Sun, N.; Pan, D.Z. Universal symmetry constraint extraction for analog and mixed-signal circuits with graph neural networks. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 1243–1248. [Google Scholar]
- Xu, Q.; Wang, L.; Wang, J.; Cheng, L.; Chen, S.; Kang, Y. Graph attention-based symmetry constraint extraction for analog circuits. IEEE Trans. Circuits Syst. I Regul. Papers. 2024, 71, 3754–3763. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Y.; Madhusudan, M.; Sharma, A.; Xu, W.; Sapatnekar, S.S.; Harjani, R.; Hu, J. A customized graph neural network model for guiding analog IC placement. In Proceedings of the 39th International Conference on Computer-Aided Design, San Diego, CA, USA, 2–5 November 2020; pp. 1–9. [Google Scholar]
- Xu, B.; Zhu, K.; Liu, M.; Lin, Y.; Li, S.; Tang, X.; Sun, N.; Pan, D.Z. Magical: Toward fully automated analog ic layout leveraging human and machine intelligence. In Proceedings of the 2019 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Westminster, CO, USA, 4–7 November 2019; pp. 1–8. [Google Scholar]
- Chen, H.; Liu, M.; Xu, B.; Zhu, K.; Tang, X.; Li, S.; Lin, Y.; Sun, N.; Pan, D.Z. MAGICAL: An open-source fully automated analog IC layout system from netlist to GDSII. IEEE Des. Test 2020, 38, 19–26. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Yun, S.; Jeong, M.; Kim, R.; Kang, J.; Kim, H.J. Graph transformer networks. Adv. Neural Inf. Process. Syst. 2019, 32, 1–11. [Google Scholar]
- Shao, K.; Zhang, Y.; Wen, Y.; Zhang, Z.; He, S.; Bo, X. DTI-HETA: Prediction of drug–target interactions based on GCN and GAT on heterogeneous graph. Brief. Bioinform. 2022, 23, bbac109. [Google Scholar] [CrossRef] [PubMed]
- Linmei, H.; Yang, T.; Shi, C.; Ji, H.; Li, X. Heterogeneous graph attention networks for semi-supervised short text classification. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; pp. 4821–4830. [Google Scholar]
- Yang, T.; Hu, L.; Shi, C.; Ji, H.; Li, X.; Nie, L. HGAT: Heterogeneous graph attention networks for semi-supervised short text classification. ACM Trans. Inf. Syst. (TOIS) 2021, 39, 1–29. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Y.; Xue, J.; Liu, Z. Fast cross-platform binary code similarity detection framework based on CFGs taking advantage of NLP and inductive GNN. Chin. J. Electron. 2024, 33, 128–138. [Google Scholar] [CrossRef]
- Bin, L.; Yi, W.; Jianjun, C.; Yaqing, C.; Xiaohu, Y. Technology Dependency of TID Response for a Custom Bandgap Voltage Reference in 65 nm to 28 nm Bulk CMOS Technologies. Chin. J. Electron. 2023, 32, 1286–1292. [Google Scholar] [CrossRef]

| Circuit Type | Number of Training Dataset | Number of Test Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| Circuits | Unmatched Pairs | Matched Pairs | Highly Matched Pairs | Circuits | Unmatched Pairs | Matched Pairs | Highly Matched Pairs | |
| 130 nm OTAs | 100 | 7914 | 407 | 92 | 8 | 265 | 20 | 8 |
| 130 nm LDOs | 4 | 588 | 18 | 6 | 1 | 147 | 6 | 0 |
| 180 nm OTAs | 43 | 1901 | 127 | 51 | 5 | 321 | 21 | 5 |
| 40 nm COMP | / | / | / | / | 1 | 125 | 8 | 3 |
| 40 nm ADC | / | / | / | / | 1 | 1464 | 77 | 19 |
| Metrics | 130 nm OTAs | 180 nm OTAs | 130 nm LDOs | 40 nm COMP | 40 nm ADC | Average | |
|---|---|---|---|---|---|---|---|
| Pattern matching [12] | Time/s | 1.68 | 1.69 | 1.57 | 1.48 | 2.28 | 1.74 |
| /% | 94.9 | 96.3 | 98.0 | 97.1 | 96.3 | 96.5 | |
| 0.706 | 0.667 | 0.667 | 0.800 | 0.567 | 0.681 | ||
| Precision | 0.792 | 0.913 | 1.000 | 1.000 | 1.000 | 0.941 | |
| Recall | 0.702 | 0.560 | 0.500 | 0.667 | 0.396 | 0.565 | |
| Unsupervised learning [15] | Time/s | 2.18 | 2.21 | 1.97 | 3.09 | 2.54 | 2.40 |
| /% | 91.8 | 94.9 | 92.8 | 88.2 | 96.9 | 92.9 | |
| 0.429 | 0.424 | 0.421 | 0.500 | 0.797 | 0.514 | ||
| Precision | 0.614 | 0.683 | 0.308 | 0.400 | 0.671 | 0.535 | |
| Recall | 0.544 | 0.863 | 0.667 | 0.667 | 0.979 | 0.744 | |
| GraphSAGE [22] | Time/s | 1.52 | 1.51 | 1.53 | 1.61 | 1.88 | 1.61 |
| /% | 94.4 | 91.2 | 85.0 | 88.2 | 96.2 | 91.0 | |
| 0.667 | 0.400 | 0.080 | 0.500 | 0.758 | 0.481 | ||
| Precision | 1.000 | 0.286 | 0.052 | 0.400 | 0.618 | 0.471 | |
| Recall | 0.500 | 0.667 | 0.167 | 0.667 | 0.979 | 0.596 | |
| EGAT [18] | Time/s | 1.91 | 2.12 | 0.08 | 0.80 | 1.02 | 1.19 |
| /% | 86.3 | 93.8 | 92.0 | 68.8 | 70.8 | 82.3 | |
| 0.724 | 0.826 | 0.600 | 0.546 | 0.340 | 0.607 | ||
| Precision | 0.700 | 0.760 | 0.500 | 0.375 | 0.205 | 0.508 | |
| Recall | 0.750 | 0.905 | 0.750 | 1.000 | 1.000 | 0.881 | |
| MCE-HGCN | Time/s | 1.68 | 1.81 | 0.04 | 0.14 | 0.33 | 0.80 |
| /% | 96.3 | 97.1 | 99.4 | 99.3 | 98.8 | 98.2 | |
| 0.874 | 0.920 | 0.923 | 0.957 | 0.913 | 0.917 | ||
| Precision | 0.787 | 0.851 | 0.857 | 1.000 | 0.855 | 0.870 | |
| Recall | 1.000 | 1.000 | 1.000 | 0.917 | 0.979 | 0.979 | |
| Metrics | 130 nm OTAs | 180 nm OTAs | 130 nm LDOs | 40 nm COMP | 40 nm ADC | Average | |
|---|---|---|---|---|---|---|---|
| MCE-HGCN without mixed attentions | Time/s | 2.08 | 2.13 | 1.64 | 1.32 | 1.68 | 1.77 |
| /% | 94.1 | 94.7 | 94.8 | 83.5 | 89.7 | 91.4 | |
| 0.560 | 0.583 | 0.200 | 0.743 | 0.726 | 0.542 | ||
| Precision | 0.600 | 0.947 | 0.200 | 0.835 | 0.850 | 0.686 | |
| Recall | 0.533 | 0.421 | 0.200 | 0.310 | 0.633 | 0.419 | |
| MCE-HGCN without match filter | Time/s | 1.82 | 1.90 | 0.05 | 0.84 | 1.09 | 1.14 |
| /% | 94.5 | 91.7 | 99.4 | 86.4 | 88.3 | 92.06 | |
| 0.778 | 0.627 | 0.923 | 0.765 | 0.820 | 0.783 | ||
| Precision | 0.801 | 0.700 | 0.921 | 0.749 | 0.850 | 0.804 | |
| Recall | 0.378 | 0.567 | 0.930 | 0.779 | 0.920 | 0.715 | |
| MCE-HGCN | Time/s | 1.68 | 1.81 | 0.04 | 0.14 | 0.33 | 0.80 |
| /% | 96.3 | 97.1 | 99.4 | 99.3 | 98.8 | 98.2 | |
| 0.874 | 0.920 | 0.923 | 0.957 | 0.913 | 0.917 | ||
| Precision | 0.787 | 0.851 | 0.857 | 1.000 | 0.855 | 0.868 | |
| Recall | 1.000 | 1.000 | 1.000 | 0.917 | 0.979 | 0.979 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yin, Y.; Xu, N.; Jia, B. MCE-HGCN: Heterogeneous Graph Convolution Network for Analog IC Matching Constraints Extraction. Micromachines 2025, 16, 677. https://doi.org/10.3390/mi16060677
Zhang Y, Yin Y, Xu N, Jia B. MCE-HGCN: Heterogeneous Graph Convolution Network for Analog IC Matching Constraints Extraction. Micromachines. 2025; 16(6):677. https://doi.org/10.3390/mi16060677
Chicago/Turabian StyleZhang, Yong, Yong Yin, Ning Xu, and Bowen Jia. 2025. "MCE-HGCN: Heterogeneous Graph Convolution Network for Analog IC Matching Constraints Extraction" Micromachines 16, no. 6: 677. https://doi.org/10.3390/mi16060677
APA StyleZhang, Y., Yin, Y., Xu, N., & Jia, B. (2025). MCE-HGCN: Heterogeneous Graph Convolution Network for Analog IC Matching Constraints Extraction. Micromachines, 16(6), 677. https://doi.org/10.3390/mi16060677






