A Characterizing Method of Carbon Nanotubes in Powder Form with Different Packing Densities
Abstract
1. Introduction
2. Methodology
2.1. Experimental Procedure
2.2. Parameters Measurement
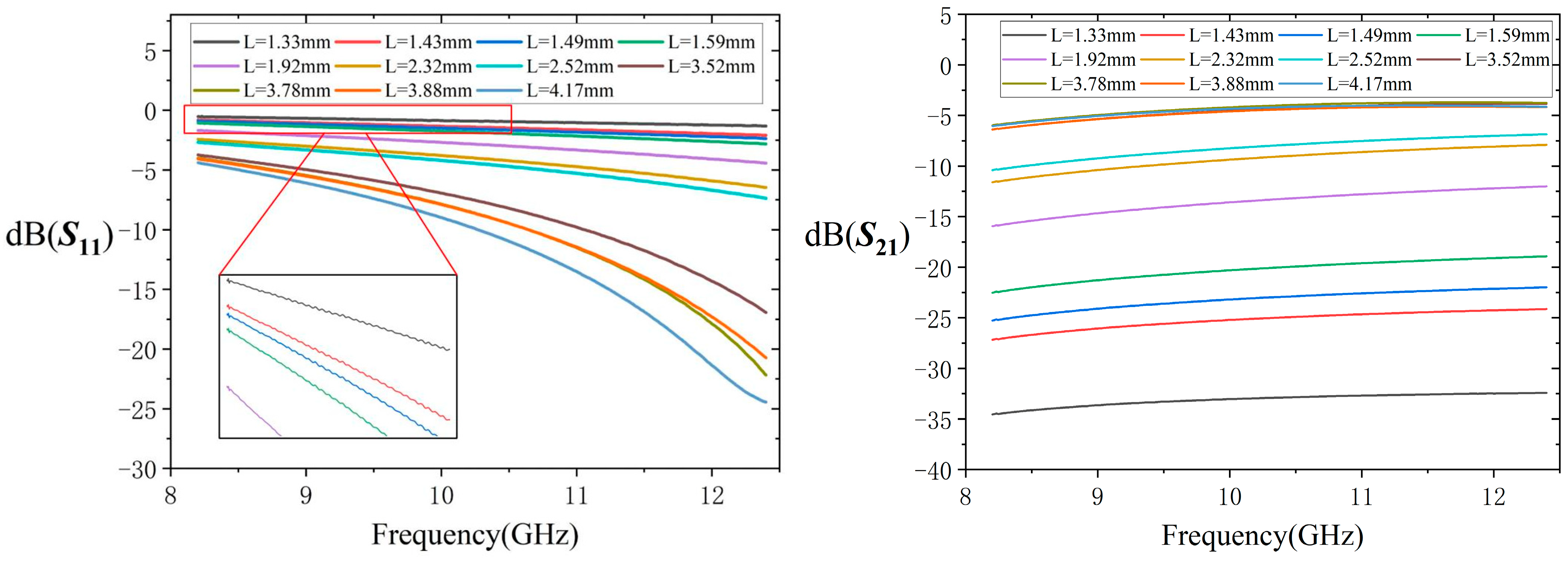
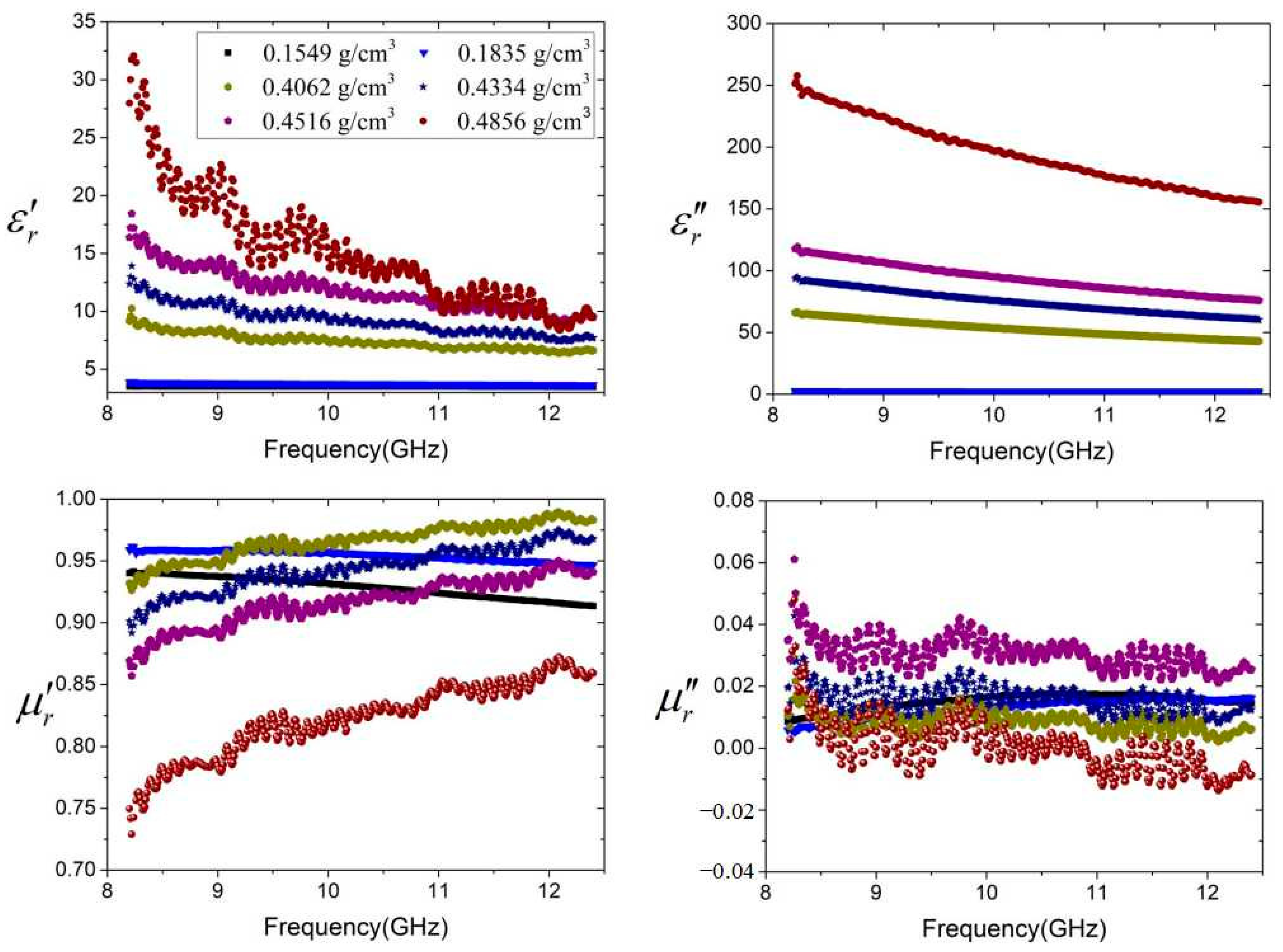
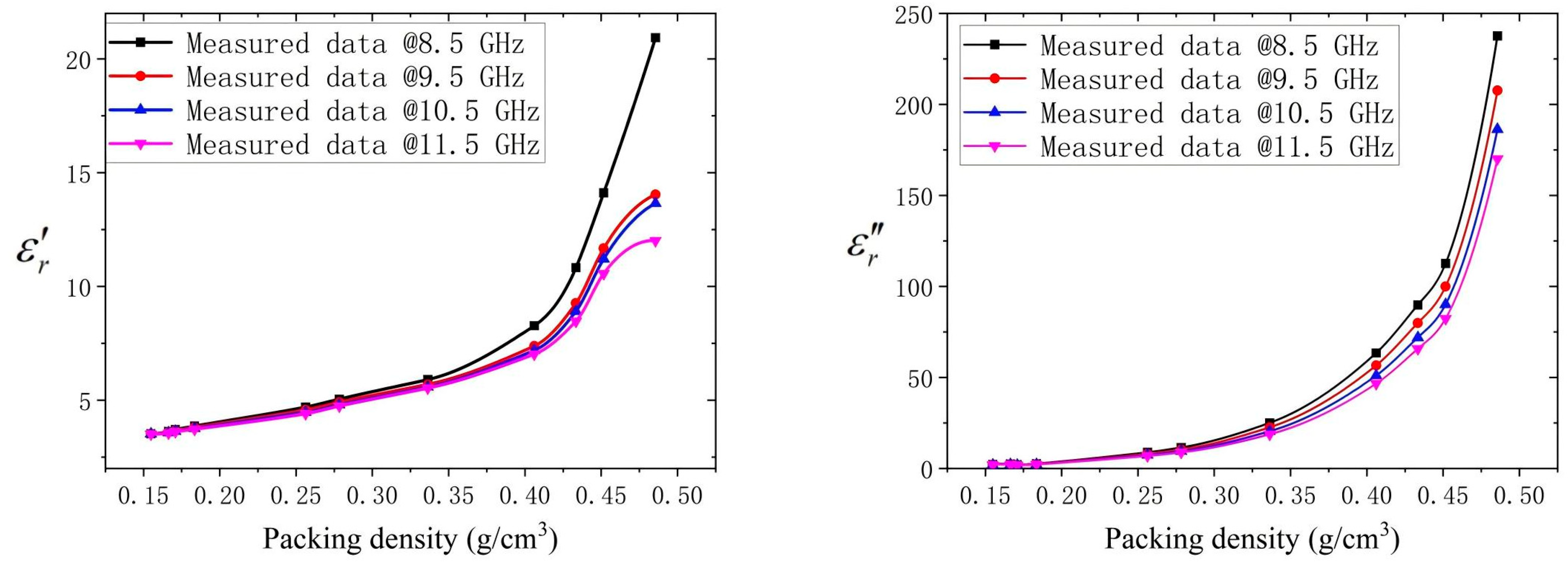
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Dragoman, M.; Grenier, K.; Dubuc, D.; Bary, L.; Fourn, E.; Plana, R.; Flahaut, E. Experimental determination of microwave attenuation and electrical permittivity of double-walled carbon nanotubes. Appl. Phys. Lett. 2006, 88, 153108. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Yi, Z.; Zhang, H.; Song, Q.; Hao, Z.; Sun, T.; Wu, P.; Zeng, Q.; Raza, R. Advanced optical reinforcement materials based on three-dimensional four-way weaving structure and metasurface technology. Appl. Phys. Lett. 2025, 126, 033503. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, S.; Zhang, H.; Yang, W.; Yi, Z.; Yi, Y.; Wang, J.; Ahmad, S.; Raza, R. Ultrathin broadband terahertz metamaterial based on single-layer nested patterned graphene. Phys. Lett. A 2025, 534, 130262. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, R.; Xin, H. Microwave (8–50 GHz) Characterization of Multiwalled Carbon Nanotube Papers Using Rectangular Waveguides. IEEE Trans. Microwave Theory Tech. 2008, 56, 499–506. [Google Scholar] [CrossRef]
- Liang, M.; Wu, Z.; Chen, L.; Song, L.; Ajayan, P.; Xin, H. Terahertz Characterization of Single-Walled Carbon Nanotube and Graphene On-Substrate Thin Films. IEEE Trans. Microwave Theory Tech. 2011, 59, 2719–2725. [Google Scholar] [CrossRef]
- Grimes, C.A.; Mungle, C.; Ong, K.; Qian, D. Effect of purification of the electrical conductivity and complex permittivity of multiwall carbon nanotubes. J. Appl. Phys. 2001, 90, 4134–4137. [Google Scholar] [CrossRef]
- Challa, R.; Kajfez, D.; Demir, V.; Gladden, J.; Elsherbeni, A. Characterization of Multiwalled Carbon Nanotube (MWCNT) Composites in a Waveguide of Square Cross Section. Microwave Wireless Compon. Lett. 2008, 18, 161–163. [Google Scholar] [CrossRef]
- Decrossas, E.; Sabbagh, M.A.E.; Hanna, V.F.; El-Ghazaly, S.M. Rigorous Characterization of Carbon Nanotube Complex Permittivity Over a Broadband of RF Frequencies. IEEE Trans. Electromagn. Compat. 2012, 54, 81–87. [Google Scholar] [CrossRef]
- Decrossas, E.; El Sabbagh, M.; El-Ghazaly, S.; Hanna, V. Engineered Carbon-Nanotubes-Based Composite Material for RF Applications. IEEE Trans. Electromagn. Compat. 2012, 54, 52–59. [Google Scholar] [CrossRef]
- Ji, Z.; Song, Y.; Gao, M.; Zhang, Q.; Liu, Y. Multimode Miniature Polarization-Sensitive Metamaterial Absorber with Ultra-Wide Bandwidth in the K Band. Micromachines 2024, 15, 1446. [Google Scholar] [CrossRef] [PubMed]
- Yang, C. Determination of unique and stable complex permittivity of granular materials from transmission and reflection measurements. Microwave Opt. Technol. Lett. 2020, 63, 753–757. [Google Scholar] [CrossRef]
- Hasar, U.C.; Westgate, C. Noniterative Permittivity Extraction of Lossy Liquid Materials From Reflection Asymmetric Amplitude-Only Microwave Measurements. Microwave Wireless Compon. Lett. 2009, 19, 419–421. [Google Scholar] [CrossRef]
- Havrilla, M.; Nyquist, D.P. Electromagnetic Characterization of Layered Materials via Direct and De-embed Methods. IEEE Trans. Instrum. Meas. 2006, 55, 158–163. [Google Scholar] [CrossRef]
- Collin, R.E. Field Theory of Guided Waves, 2nd ed.; IEEE Press: New York, NY, USA, 1991. [Google Scholar]
- Weir, W.B. Automatic Measurement of Complex Dielectric Constant and Permeability at Microwave Frequencies. Proc. IEEE 1974, 62, 33–36. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yang, C.; Ma, K.; Ma, J. A Noniterative and Efficient Technique to Extract Complex Permittivity of Low-Loss Dielectric Materials at Terahertz Frequencies. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1971–1975. [Google Scholar] [CrossRef]
- Yang, C.; Ma, J.-G. Direct Extraction of Complex Permittivity and Permeability of Materials on a Known-Substrate From Transmission/Reflection Measurements. IEEE Microwave Wireless Compon. Lett. 2019, 29, 693–695. [Google Scholar] [CrossRef]


| L (mm) | 4.17 | 3.88 | 3.78 | 3.52 | 2.52 | 2.32 | 1.92 | 1.59 | 1.49 | 1.43 | 1.33 |
| ρ (g/cm3) | 0.1549 | 0.1665 | 0.1709 | 0.1835 | 0.2563 | 0.2784 | 0.3364 | 0.4062 | 0.4334 | 0.4516 | 0.4856 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Yang, C.; Zhang, Y.; Wang, J. A Characterizing Method of Carbon Nanotubes in Powder Form with Different Packing Densities. Micromachines 2025, 16, 662. https://doi.org/10.3390/mi16060662
Li R, Yang C, Zhang Y, Wang J. A Characterizing Method of Carbon Nanotubes in Powder Form with Different Packing Densities. Micromachines. 2025; 16(6):662. https://doi.org/10.3390/mi16060662
Chicago/Turabian StyleLi, Ruiliang, Chuang Yang, Yunlong Zhang, and Jian Wang. 2025. "A Characterizing Method of Carbon Nanotubes in Powder Form with Different Packing Densities" Micromachines 16, no. 6: 662. https://doi.org/10.3390/mi16060662
APA StyleLi, R., Yang, C., Zhang, Y., & Wang, J. (2025). A Characterizing Method of Carbon Nanotubes in Powder Form with Different Packing Densities. Micromachines, 16(6), 662. https://doi.org/10.3390/mi16060662







