Abstract
In this paper, we design an ultra-thin broadband transparent absorber based on indium tin oxide (ITO) film, and we choose polymethyl methacrylate (PMMA) high-transmittance dielectric sheet instead of the traditional dielectric sheet and polyethylene glycol terephthalate (PET) as the ITO film substrate. Simulation results indicate that the absorber achieves more than 90% absorption for positively incident electromagnetic waves in the broadband range of 5–21.15 GHz with a fractional bandwidth (FBW) of 123.5% and a thickness of 6.3 mm (0.105 λL, where λL is the wavelength at the lowest frequency). Meanwhile, this paper introduces the interference theory to explain the broadband absorption mechanism of the absorber, which makes up for the defect that the equivalent circuit model (ECM) method cannot analyze the oblique incidence electromagnetic wave. This paper also compares the HFSS simulation results, ECM theoretical values, and interference theoretical values under positively incident electromagnetic waves to clarify the advantages of interference theory in the design of wave absorbers.
1. Introduction
With the rapid development of 5G technology and wireless communications, the increasingly complex electromagnetic environment has put forward higher requirements for wave-absorbing materials. As a key material for solving electromagnetic interference problems, the core application scenarios of wave absorbers include improving the electromagnetic compatibility (EMC) of electronic systems, reducing the radar cross-section (RCS), and suppressing electromagnetic pollution [1,2,3]. We can divide wave absorbers into two main types based on the differences in their material systems and mechanisms of action: One type uses traditional materials as wave absorbers, such as graphite, carbon black, ferrite, etc., through the coating or impregnation process to form a loss layer. This type relies on dielectric or magnetic loss mechanisms to convert incident electromagnetic waves into heat or other forms of energy, thereby suppressing surface electromagnetic wave reflection [4,5,6,7]. The other category is metamaterial absorber (MMA), which is based on the design of artificial periodic structure and realizes the efficient absorption in wide bandwidth through the synergy of multiple mechanisms, such as impedance matching, resonance loss, and interference phase cancellation. Compared with traditional wave-absorbing materials, MMA breaks through the “λ/4” thickness limitation and achieves strong absorption at sub-wavelength thickness through localized resonance. In addition, MMA’s ability to flexibly adjust unit structure parameters helps to optimize electromagnetic impedance matching and resonance loss characteristics. This provides a new degree of design freedom for the development of high-performance absorbers [8,9,10].
As early as 2008, Landy, N.I. et al. proposed an MMA based on metal units and FR4 dielectric plates, which achieved near-perfect absorption at an operating frequency of 11.48 GHz, and since then, MMA has attracted a lot of attention [11]. In 2009, Zadeh, A.K. et al. proposed a fast method for designing wave absorbers based on ECM [12]. In 2019, Xie, J et al. designed an all-dielectric MMA to achieve 0–45° angular domain absorption for two polarization waves [13]. In addition, the rapid development of hypersurface technology provides new ideas for MMA design [14,15]. Zheng, C.-L. et al. designed a multifunctional hypersurface for polarization multiplexing by jointly regulating the propagation phase and the geometric phase. This study demonstrated the flexible ability of the hypersurface to regulate the phase, polarization, and energy of electromagnetic waves, and its design concept is also applicable to the optimization of MMA [16]. The above designs have contributed to the development of MMA, but the use of opaque metals and dielectrics has made these designs difficult to apply where high optical transparency is required.
In recent years, with the rapid development of transparent materials, many people use transparent materials in combination with wave-absorbing materials. They have made MMA optically transparent while combining the characteristics of “thin thickness, light weight, wide bandwidth, and strong wave-absorbing ability” [17,18,19,20,21]. Xiong, Y. et al. designed a transparent absorber in the form of ITO-PMMA-ITO by utilizing ITO film instead of metal and PMMA as the dielectric plate, which can achieve more than 90% wave absorption in the frequency range of 6–17.8 GHz [22]. This transparent MMA designed based on ITO film can still be analyzed by ECM. Dong, L. et al. designed an optically transparent MMA based on ECM, which can absorb more than 90% of electromagnetic waves in the frequency range of 15.77–38.69 GHz [23]. Lai, S. et al. have also designed a transparent absorber in the form of ITO-PET-ITO based on ITO film and PET dielectric using an equivalent circuit model, which absorbs more than 90% of the wave in the frequency range of 19.9–44.6 GHz [24]. While ECM remains prevalent in MMA design, its foundational assumptions fail to account for oblique incidence scenarios. Therefore, an analytical method based on the theory of interference has been proposed, which allows obtaining reflection coefficients related to the electromagnetic parameters and the thickness of the medium [25,26]. Starting from the multiple-reflection interference model, Chen, H.-T. demonstrated that the near-field interaction or magnetic response between neighboring metal structures in MMA is negligible, and the two layers can be decoupled, with the only connection being multiple reflections between them [27]. Zeng, X. et al. designed a three-band MMA based on ECM and interference theory, which exhibits high absorption greater than 95% at 4.4 GHz, 6.05 GHz, and 13.9 GHz. Theoretical predictions and simulations, as well as experimental measurements, are in excellent agreement with each other, which also proves the feasibility of the interference theory [28].
In MMA design, the electromagnetic parameters and thickness of the medium significantly affect the propagation phase of electromagnetic waves. When the phase difference between two electromagnetic waves is an odd multiple of π, the interference phase cancellation phenomenon occurs, thus realizing efficient wave absorption. In this paper, the interference theory of monolayer dielectric is extended to the multilayer dielectric system, and a transparent absorber is designed using ITO film with PMMA and PET transparent dielectric sheets. By comparing the multilayer interference theory predictions with the HFSS full-wave simulation results, we find that there is a non-negligible weak electromagnetic coupling effect between the ITO film layers. This study also compares and analyzes the reflection coefficients obtained by three different methods (multilayer interference theory, ECM, and HFSS full-wave simulation) under positive incidence conditions and clarifies the advantages of interference theory in the design of wave absorbers. The schematic diagram of the transparent absorber in this paper is shown in Figure 1, which has an absorption rate of more than 90% for positively incident electromagnetic waves in a wide frequency range of 5–21.15 GHz. In the case of oblique incidence, it maintains a high absorption rate of more than 90% for TM-polarized waves in the range of 5.35–21 GHz and TE-polarized waves in the range of 5.8–20.65 GHz at the angle of incidence of 0–45°. The design of this absorber, which combines broadband, wide-angle domain, and optically transparent properties, provides an important solution for next-generation stealth technology and electromagnetic compatibility applications.
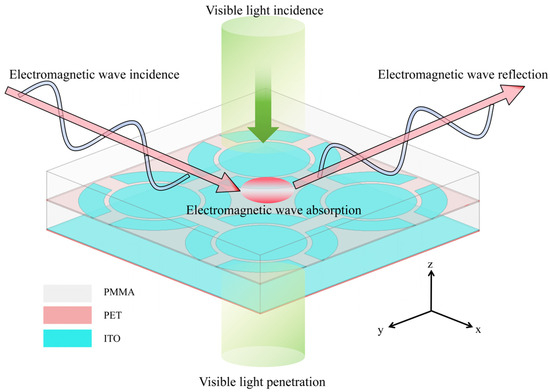
Figure 1.
Schematic diagram of transparent absorber.
2. Design and Analysis
2.1. Modular Design
Figure 2a demonstrates the four-layer symmetric-structure absorber unit designed in this study, where the symmetric nature of the unit pattern gives the structure the advantage of polarization insensitivity. In order to realize the synergistic design of broadband wave absorption and optical transparency, PMMA with dielectric constant ε1 = 3.05 − j0.0305 is selected as the transparent dielectric plate for the first and third layers. The second-layer structure is shown in Figure 2b, where an ITO thin film pattern with a surface resistance I1 = 80 Ω/sq is prepared by an etching process on a highly transparent PET substrate with a dielectric constant ε2 = 3 − j0.18 to form a lossy layer. The fourth layer adopts a highly conductive ITO film (I2 = 6 Ω/sq) to replace the traditional metal reflector plate, the top view of which is shown in Figure 2c, to ensure the electromagnetic wave reflecting performance while maintaining the optical transparency characteristics.
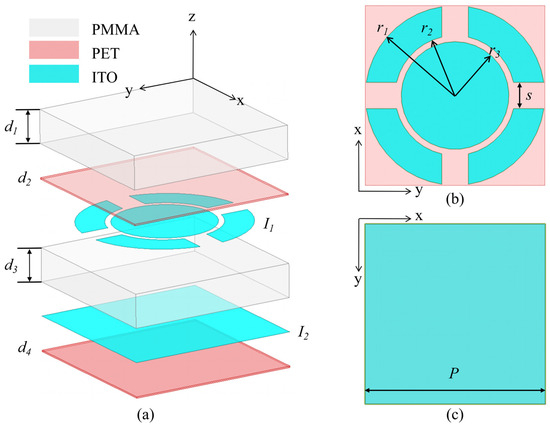
Figure 2.
Absorber unit design. P = 15 mm, r1 = 7.5 mm, r2 = 5 mm, r3 = 4.5 mm, s = 2 mm, d1 = d3 = 3 mm, d2 = 0.125 mm, d4 = 0.175 mm. (a) Unit Exploded View; (b) Elevation view of the second layer of the absorber; (c) Top view of the fourth layer of the absorber.
Figure 3a illustrates the evolution of the MMA cell, and in order to compare the reflection of electromagnetic waves by each structure, we make all the structural parameters consistent with Figure 2. Circular resonators are known to be widely used in MMA designs and exhibit excellent polarization insensitivity due to the geometrical symmetry of their structures. However, the analysis of the reflection coefficient curve in Figure 3b shows that Structure A can only cover the 7.5–20 GHz band at −10 dB operating bandwidth, with two strong resonance points at 12.2 GHz and 14.6 GHz, respectively. In order to expand the wave-absorbing bandwidth, it is necessary to realize the redistribution of resonance modes through structural optimization and to shift the double resonance point to the direction of low frequency and high frequency in a synergistic way.
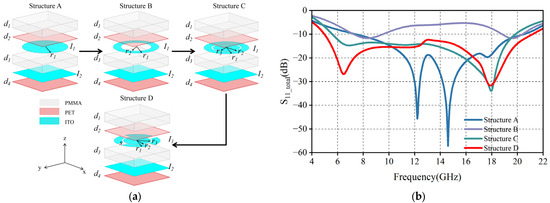
Figure 3.
(a) MMA unit evolution process; (b) Reflection coefficients for different unit structures.
After we reconfigured the initial cell into a circular resonator (Structure B), its dual resonance points were shifted to 8.1 GHz and 19.7 GHz. However, as shown in Figure 3b, the structure exhibits a significant absorption depression in the 9.5–18.8 GHz band, which is attributed to the lack of ohmic loss due to the missing ITO film in the center region of the ring and the limited electromagnetic coupling efficiency of the single ring resonator. To solve the above problem, we introduce circular patches of radius r3 in the structure C. Experimental data show that the −10 dB bandwidth of Structure C extends to 5.6–19.9 GHz, but the depth of absorption in the lower frequency band is insufficient. We finally succeeded in exciting the dual resonant modes at 6.5 GHz and 17.9 GHz by implementing a slotting design (Structure D) in the outer ring arm, and the optimized Structure D achieves highly efficient absorption (≥90% absorption) in the 5–21.15 GHz band.
In order to deeply investigate the modulation mechanism of MMA unit structure parameters on the electromagnetic wave reflection characteristics, we systematically analyzed the reflection coefficients under different parameter conditions based on ANSYS HFSS 2020R2. Figure 4a,b demonstrate the pattern of the radius parameters r2 and r3 on the reflection coefficient, respectively. As r2 gradually decreases from 6 mm to 5 mm, the width of the central annular slit decreases accordingly, leading to a significant increase in the depth of reflection at both resonance points. This phenomenon suggests that a moderate narrowing of the gap can effectively enhance the local coupling effect of the electromagnetic field. It is worth noting that an increase in r3 is physically equivalent to a decrease in r2, and thus the two are consistent in their mechanisms of modulation of MMA performance. When r2 = 4.5 mm, the intermediate gap is completely closed, at which time the structural properties are similar to those of structure A in Figure 3a, with the low-frequency resonance point gradually shifted to the high frequency and the reflection depth reduced. After comprehensive optimization, we finally selected r2 = 5 mm and r3 = 4.5 mm as the best parameter combination.
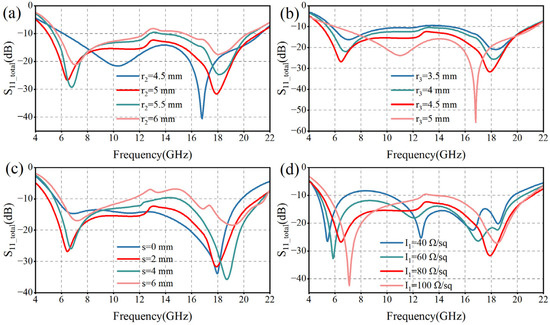
Figure 4.
Reflection coefficients corresponding to different unit parameters of MMA. (a) Reflection coefficients for different r2 conditions; (b) Reflection coefficients for different r3 conditions; (c) Reflection coefficients for different s conditions; (d) Reflection coefficients for different I1 conditions.
The effect of the spacing parameter s on the reflection coefficient is further investigated in Figure 4c. As s decreases from 6 mm to 2 mm, the circular gap gradually becomes narrower, and the wave-absorbing property is subsequently enhanced. However, when s = 0 mm (the circular gap is completely closed), the depth of reflection at the low-frequency resonance point decreases significantly, which destroys the original resonance characteristics. After weighing the bandwidth against the absorption depth, we determined that s = 2 mm is the optimal value. The above results indicate that the variation of the structural parameters of the MMA unit can significantly modulate its resonance characteristics, which is one of the key mechanisms to realize the broadband efficient absorption.
The broadband absorption mechanism of this MMA is not only dependent on the optimization of structural parameters but also closely related to the ohmic loss of the ITO film. Among them, the surface resistance value (I1) of the first ITO film has a significant modulation effect on the reflection characteristics, as shown in Figure 4d. With the increase of I1 from 40 Ω/sq to 100 Ω/sq, the low-frequency resonance point is shifted to the high-frequency direction, and the depth of the reflection coefficient is obviously increased, and the resonance effect in the high-frequency band is also enhanced. However, this variation simultaneously leads to a decrease in the absorption performance in the center band. Through comparative analysis, it is found that the −10 dB relative bandwidth of the MMA reaches the optimal value of 123.5% when I1 = 80 Ω/sq, which achieves a balance between wide bandwidth and strong absorption.
2.2. Interference Theory Analysis
Interference phase cancellation is another key mechanism to realize broadband wave absorption in this design. When the phase difference between two columns of electromagnetic waves is an odd multiple of π, the interference phase cancellation phenomenon will occur. The total reflection coefficient of a monolayer medium obtained by the interference theory is shown in Equation (1) [25]:
where , , , , c is the speed of light, f is the frequency, and d is the thickness of the medium. Table 1 shows the expressions of reflection coefficient and transmission coefficients.

Table 1.
Expression of reflection and transmission coefficients.
In this study, due to the design of multilayer dielectric structures, the above interference theory needs to be extended to multilayer systems. Figure 5 illustrates the propagation of electromagnetic waves in a multilayer medium, whose total reflection coefficient can be calculated by Equation (2):
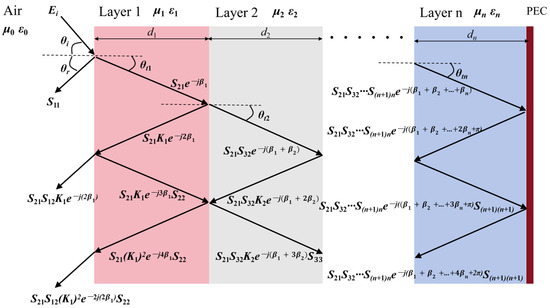
Figure 5.
Electromagnetic wave propagation patterns based on multilayer dielectric interference theory.
When an electromagnetic wave is irradiated to the surface of a medium by oblique incidence, it can be decomposed into two orthogonal polarization components: perpendicularly polarized wave (TE) and parallel polarized wave (TM), where the reflection coefficient and transmission coefficient of the perpendicularly polarized wave (TE) are, respectively, [29]:
The reflection coefficient and transmission coefficient of the parallel polarized wave (TM) are:
When an electromagnetic wave is directed obliquely to the surface of a medium at an angle of incidence , it can be shown that is , according to . The actual path of the electromagnetic wave in the first layer of the medium is and so on to obtain the angle of incidence , the angle of refraction , and the actual path dn for each layer.
To reveal the broadband absorption mechanism of the absorber, this study uses a combination of interference theory modeling and full-wave simulation for quantitative analysis. According to the findings of the literature [25], the near-field coupling effect between the ITO film pattern and the reflector plate in the absorber structure is negligible. Based on this theoretical framework, in this study, the analytical solutions of the reflection and transmission coefficients are calculated by considering the three parts of PET (d2 = 0.125 mm), ITO film (I1 = 80 Ω/sq), and PMMA (d3 = 3 mm) as a whole, which are simulated individually by HFSS software, and the analytical solutions of the reflection and transmission coefficients are substituted into the formulae of the multilayer interference theory (Equation (2)).
Figure 6 demonstrates the comparative analysis of the HFSS full-wave simulation results with the multilayer interference theory model. Among them, the yellow solid line indicates the reflection characteristics of the MMA for electromagnetic waves with different incidence angles shown in Figure 2a, while the red solid line is the result of the theoretical calculation based on the multilayer interference theory. It is shown that when a low-surface-resistance ITO reflective layer (square resistance I2 = 6 Ω/sq) is used, the simulation results show a significant trend of agreement with the theoretical predictions, but the theoretical model predicts significantly deeper reflection coefficient valleys than the simulation results at the resonance frequency point. This discrepancy stems from the fact that the theoretical model approximates the low-resistance ITO layer as an ideal electrical conductor (PEC), while the actual ITO film (6 Ω/sq) does not completely suppress electromagnetic wave transmission.
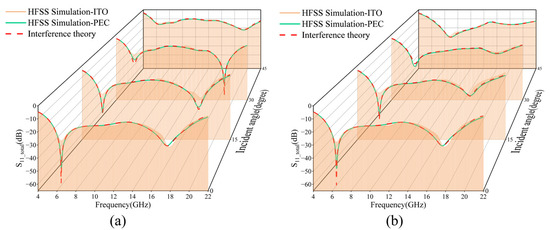
Figure 6.
Comparison of HFSS Simulation and Interference theory results. (a) TM polarized wave 0–45° reflection coefficient; (b) TE polarized wave 0–45° reflection coefficient.
To verify this mechanism, this study further replaces the underlying ITO with a PET substrate for comparative simulation. The results show that the reflection characteristics of the green solid line (PEC replacement group) and the red dashed line (theoretical value) exhibit a high degree of agreement in the two polarization bands, and this control experiment conclusively demonstrates that the non-ideal reflection due to the finite conductivity is the main reason for the difference. At the same time, this result also reveals the weak electromagnetic coupling effect between the upper and lower ITO film layers.
In order to further verify the correctness of the interference theory, we analyze it in comparison with the theoretical values of ECM. By analyzing the simulated electromagnetic field distribution on the surface of the ITO film at the resonance points (6.5 GHz and 17.9 GHz), the loss mechanism of the absorber can be deeply analyzed to construct the EMC. As shown in Figure 7, at 6.5 GHz and 17.9 GHz, the electric field energy is highly concentrated at the edge of the inner and outer rings and the slit region, indicating that the equivalent capacitance is formed here due to charge aggregation. The magnetic field is mainly concentrated in the outer annular ring arms, as well as in the center region of the inner circle, whose time-varying properties induce an equivalent inductance. The synergistic effect of the above electric and magnetic fields can be modeled as a second-order R-L-C resonant circuit. Based on the transmission line theory, the PMMA layer and the PET layer can be equated to a transmission line with characteristic impedances of ZPMMA and ZPET, and the constructed EMC is shown in Figure 8a.
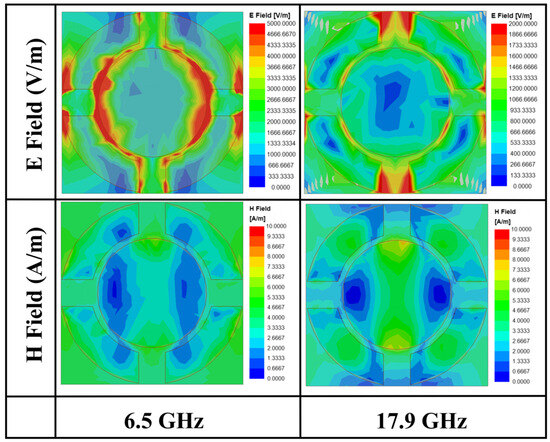
Figure 7.
Simulated electric and magnetic field distributions at 6.5 GHz and 17.9 GHz.
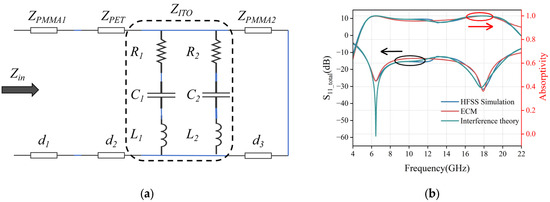
Figure 8.
(a) ECM; (b) Comparison data plots of HFSS simulation results, ECM theoretical values, and interference theory values. (The direction of the arrow indicates the Y-axis of each data reference.)
Based on the unit dimensions in Figure 1, the Advanced Design System 2024 was used to optimize the parameters of the ECM, and the final circuit component values were determined as R1 = 256.217 Ω, R2 = 222.254 Ω, C1 = 5.20518 fF, C2 = 34.0447 fF, L1 = 13.0811 nH, and L2 = 22.6156 nH.
The absorbance of the absorber is shown in Equation (7):
Figure 8b compares the HFSS simulation results, the ECM theoretical values, and the multilayer interference theory values of the MMA under positive incidence conditions of electromagnetic waves. The results show that compared to the ECM theoretical values, the interferometric theoretical values match better with the HFSS simulation results in the overall trend, but the weak coupling effect between the ITO films above and below the MMA causes the ECM theoretical values to be closer to the HFSS simulation results in terms of reflection depth.
Based on the multilayer interference theory, it is known that the dielectric constant ε and the thickness d of the dielectric layer are two key parameters affecting the performance of the absorber. Since the sub-wavelength thickness of the PET layer has less influence on the phase of electromagnetic wave propagation, we mainly analyze the influence of electromagnetic parameters and the thickness of the PMMA layer on the performance of the absorber. Based on the HFSS simulation data in Figure 9, it can be seen that the two resonance points are gradually shifted to lower frequencies as ε1 gradually increases. Based on the HFSS simulation data in Figure 10, it can be seen that, keeping d3 constant, the resonance points at high frequencies are gradually formed as d1 increases, and the two resonance points are gradually shifted to low frequencies. Keeping d1 constant, as d3 increases, the resonance point at the high frequency first forms and then disappears, and the resonance point at the low frequency is similarly shifted to the low frequency. When both d1 and d3 are 3 mm, both resonance points are formed and the −10 dB bandwidth is more desirable, which proves that at this time, the electromagnetic wave occurs many times in the internal interference phase cancellation of the absorber. Meanwhile, the high similarity between the TM polarization wave and TE polarization wave results verifies that the designed MAA is insensitive to polarization.
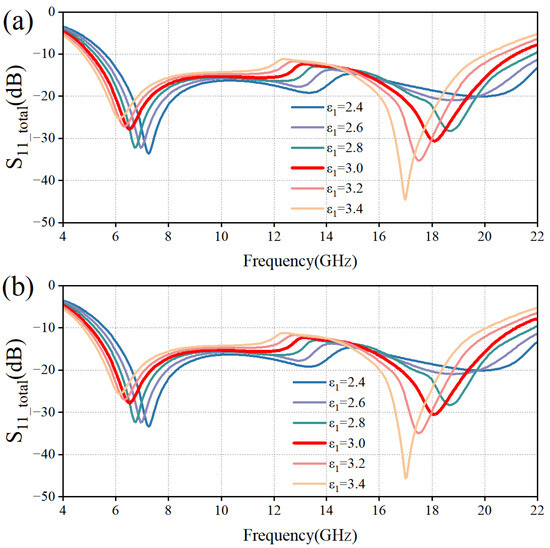
Figure 9.
Effect of variation of ε1 on reflection coefficients of two polarizations. (a) TM Polarization; (b) TE Polarization.
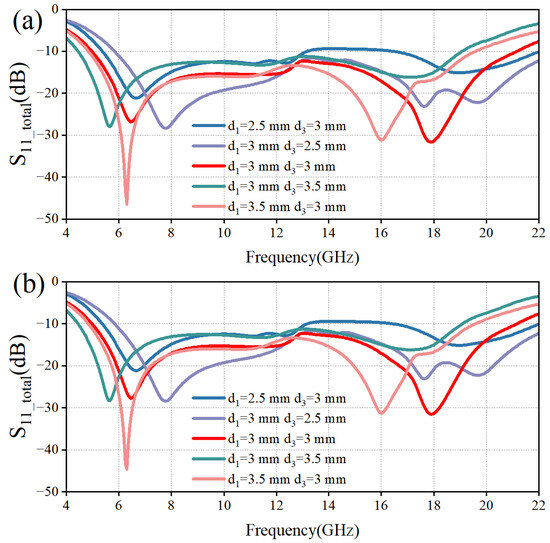
Figure 10.
Effect of d1 and d3 variations on the reflection coefficients of the two polarizations. (a) TM Polarization; (b) TE Polarization.
3. Experimental Verification
To verify the broadband absorption properties of the proposed absorber, we prepared the experimental samples shown in Figure 11a. The sample consists of a 10 × 10 array of periodic cells with an overall size of 150 mm × 150 mm × 6.3 mm. The YHT-23 transmittance tester (produced in China Guangdong Shenzhen YuanHengTong Technology Co., Shenzhen, China) was used to characterize the optical properties of the samples, and the test results are shown in Figure 11b. The average transmittance data of different wavelengths are obtained through multi-point sampling measurements: the transmittance in the UV band (365 nm) is the lowest at 6.5%; the transmittance in the visible band (530 nm) is increased to 51.3%; and the near-infrared band (940 nm) shows the best transmittance performance at 64.7%.

Figure 11.
(a) Transparent MMA samples; (b) Schematic diagram of MMA single-point light transmittance test; (c) Schematic diagram of MMA light transmittance under sunlight; (d) MMA microwave darkroom test chart (The red box is a partial enlarged image).
The experimental verification of the designed wave absorber is carried out, and the simulation and experimental results are shown in Figure 12. In the case of positive incidence, the absorber achieves more than 90% absorption in the broadband range of 5–21.15 GHz; in the case of oblique incidence, the absorber achieves more than 90% absorption in the angular domains of 0–45° for TM-polarized waves in the range of 5.35–21 GHz and in the angular domains of 0–45° for TE-polarized waves in the range of 5.8–20.65 GHz. Table 2 shows a comparison of the data from this work with MMA designs from recent years.
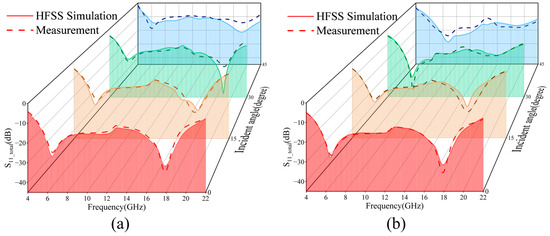
Figure 12.
Simulation and experimental results of transparent wave absorber. (a) TM polarized wave 0–45° reflection coefficient; (b) TE polarized wave 0–45° reflection coefficient.

Table 2.
Comparison of Performance.
4. Conclusions
In this paper, an ultra-thin broadband transparent absorber is designed based on ITO film and PMMA and PET transparent media, and the parameters of this absorber are analyzed based on multilayer interference theory. Simulation results indicate that the absorber achieves more than 90% absorption in the broadband range of 5–21.15 GHz for forward-incidence electromagnetic waves; for oblique-incidence electromagnetic waves, the absorber achieves 0–45° angular domain absorption for TM-polarized waves in the range of 5.35–21 GHz and TE-polarized waves in the range of 5.8–20.65 GHz, and the experimental results are in good agreement with the simulation results. This work promotes MMA’s move toward broadband and transparency.
Author Contributions
All authors have significantly contributed to the research presented in this manuscript; Conceptualization, Z.W. and Y.L.; investigation, Z.W. and Y.L.; writing, Y.L. and Y.S.; Z.W., Z.L. (Zechen Li), J.G., Z.L. (Ziming Lv) and C.L. reviewed and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data generated or analyzed during this study are included in this manuscript. There are no additional data or datasets beyond what is presented in the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fionov, A.; Kraev, I.; Yurkov, G.; Solodilov, V.; Zhukov, A.; Surgay, A.; Kuznetsova, I.; Kolesov, V. Radio-Absorbing Materials Based on Polymer Composites and Their Application to Solving the Problems of Electromagnetic Compatibility. Polymers 2022, 14, 3026. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.B.; Faruque, M.R.I.; Abdullah, S.; Islam, M.T.; Al-mugren, K.S. A Coding Based Metasurface Absorber with Triple Circular Ring Resonator for Broadband RCS Reduction and High EMI Shielding Effectiveness. Results Eng. 2024, 21, 101791. [Google Scholar] [CrossRef]
- Zheng, L.; Zuo, Y.; Song, D.; Li, X.; Lou, Z.; Wu, Y. Green Strategy for a Large-Format, Superhard, and Insulated Electromagnetic Wave Absorber Inspired by a Natural Feature of a Conch Shell. ACS Nano 2024, 18, 29457–29468. [Google Scholar] [CrossRef]
- Pang, H.; Duan, Y.; Huang, L.; Song, L.; Liu, J.; Zhang, T.; Yang, X.; Liu, J.; Ma, X.; Di, J.; et al. Research Advances in Composition, Structure and Mechanisms of Microwave Absorbing Materials. Compos. Part B Eng. 2021, 224, 109173. [Google Scholar] [CrossRef]
- Si, T.; Xie, S.; Ji, Z.; Ma, C.; Wu, Z.; Wu, J.; Wang, J. Modification of Basalt Fiber with Ni and Carbon Black Formed Synergistic Microstructure for Enhanced Electromagnetic Wave Absorption. J. Mater. Sci. Mater. Electron. 2023, 34, 1035. [Google Scholar] [CrossRef]
- Xie, A.; Ma, Z.; Xiong, Z.; Li, W.; Jiang, L.; Zhuang, Q.; Cheng, S.; Lu, W. Conjugate Ferrocene Polymer Derived Magnetic Fe/C Nanocomposites for Electromagnetic Absorption Application. J. Mater. Sci. Technol. 2024, 175, 125–131. [Google Scholar] [CrossRef]
- Javed, Z.; Rasool, R.T.; Alhummiany, H.; Majeed, A.; Gulbadan, S.; Ashraf, G.A.; Al-Anazy, M.M.; Irfan, M.; Yousef, E.S.; Akhtar, M.N.; et al. Structural, Morphological, Dielectric, and Spectral Properties of Sr-Mg-Ho X-Type Magnetic Nanomaterials Suitable for Microwave Absorption Application. Vacuum 2024, 222, 112965. [Google Scholar] [CrossRef]
- Feng, J.; Wu, L.-S.; Mao, J.-F. Switchable Broadband/Narrowband Absorber Based on a Hybrid Metasurface of Graphene and Metal Structures. Opt. Express 2023, 31, 12220–12231. [Google Scholar] [CrossRef]
- Tao, G.; Zhao, Q.; Song, Q.; Yi, Z.; Yi, Y.; Zeng, Q. A Polarization-Insensitive and Highly Sensitive THz Metamaterial Multi-Band Perfect Absorber. Micromachines 2024, 15, 1388. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Y.; Yang, S.; Li, Z.; Wang, X.; Zhang, J. Modeling of a Broadband Microwave Composite Thin Film Absorber. Micromachines 2023, 14, 2119. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, A.K.; Karlsson, A. Capacitive Circuit Method for Fast and Efficient Design of Wideband Radar Absorbers. IEEE Trans. Antennas Propag. 2009, 57, 2307–2314. [Google Scholar] [CrossRef]
- Xie, J.; Quader, S.; Xiao, F.; He, C.; Liang, X.; Geng, J.; Jin, R.; Zhu, W.; Rukhlenko, I.D. Truly All-Dielectric Ultrabroadband Metamaterial Absorber: Water-Based and Ground-Free. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 536–540. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, C.; Zhu, W.; Liu, M.; Zhang, S.; Zhang, S.; Chen, L.; Lezec, H.J.; Agrawal, A.; Lu, Y.; et al. Photonic Spin-Multiplexing Metasurface for Switchable Spiral Phase Contrast Imaging. Nano Lett. 2020, 20, 2791–2798. [Google Scholar] [CrossRef]
- Zheng, C.-L.; Ni, P.-N.; Xie, Y.-Y.; Genevet, P. On-Chip Light Control of Semiconductor Optoelectronic Devices Using Integrated Metasurfaces. Opto-Electron. Adv. 2025, 8, 240159. [Google Scholar] [CrossRef]
- Zang, H.; Zhou, X.; Yang, Z.; Yu, Q.; Zheng, C.; Yao, J. Polarization Multiplexed Multifunctional Metasurface for Generating Longitudinally Evolving Vector Vortex Beams. Phys. Lett. A 2024, 497, 129336. [Google Scholar] [CrossRef]
- Zhong, S.; Zhang, Y.; Ma, Y. Optically Transparent Frequency-Tunable Microwave Absorber Based on Patterned Graphene-ITO Structure. IEEE Trans. Antennas Propag. 2022, 70, 9959–9964. [Google Scholar] [CrossRef]
- Xi, Y.; Jiang, W.; Wei, K.; Hong, T.; Gong, S. An Optically Transparent Hybrid Mechanism Metasurface for Wideband, Wide-Angle and Omnidirectional Scattering Suppression. IEEE Trans. Antennas Propag. 2023, 71, 422–432. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Y.; Wan, Z.; Li, Y.; Li, R.; Li, H.; Cao, Q. Design and Analysis of an Optically Transparent Ultra-Wideband Absorber Covering C-, X-, Ku-, K-, Ka- Bands. Opt. Mater. Express 2022, 12, 1512–1521. [Google Scholar] [CrossRef]
- Dai, H.; Li, S.; Dong, P.; Ma, Y. Design of an Ultra-Wideband Transparent Wave Absorber. Materials 2023, 16, 5962. [Google Scholar] [CrossRef]
- Hayat, B.; Zhang, J.; Khan, A.; Abbas, S.M.; Majeed, A.; Al-Bawri, S.S. A Flexible and Optical Transparent Metasurface Absorber with Broadband RCS Reduction Characteristics. Nanomaterials 2024, 14, 1507. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Chen, F.; Cheng, Y.; Luo, H. Ultra-Thin Optically Transparent Broadband Microwave Metamaterial Absorber Based on Indium Tin Oxide. Opt. Mater. 2022, 132, 112745. [Google Scholar] [CrossRef]
- Dong, L.; Si, L.; Xu, H.; Shen, Q.; Lv, X.; Zhuang, Y.; Zhang, Q. Rapid Customized Design of a Conformal Optical Transparent Metamaterial Absorber Based on the Circuit Analog Optimization Method. Opt. Express 2022, 30, 8303–8316. [Google Scholar] [CrossRef] [PubMed]
- Lai, S.; Liu, Y.; Luo, J. Flexible and Transparent Broadband Absorber Based on Gridded ITO Ground. IEEE Photon. Technol. Lett. 2024, 36, 223–226. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Z.; Wang, G.; Huang, X.; Wang, S.; Hu, X.; Liu, M. High-Impedance Surface-Based Broadband Absorbers with Interference Theory. IEEE Trans. Antennas Propag. 2015, 63, 4367–4374. [Google Scholar] [CrossRef]
- Wanghuang, T.; Chen, W.; Huang, Y.; Wen, G. Analysis of Metamaterial Absorber in Normal and Oblique Incidence by Using Interference Theory. AIP Adv. 2013, 3, 102118. [Google Scholar] [CrossRef]
- Chen, H.-T. Interference Theory of Metamaterial Perfect Absorbers. Opt. Express 2012, 20, 7165–7172. [Google Scholar] [CrossRef]
- Zeng, X.; Gao, M.; Zhang, L.; Wan, G.; Hu, B. Design of a Triple-Band Metamaterial Absorber Using Equivalent Circuit Model and Interference Theory. Microw. Opt. Technol. Lett. 2018, 60, 1676–1681. [Google Scholar] [CrossRef]
- Zhiying, C.; Yueming, G.; Min, D. Electromagnetic Wave Transmission Characteristics on Different Tissue Boundaries for Implantable Human Body Communication. Chin. J. Radio Sci. 2017, 32, 134–143. [Google Scholar]
- Han, Y.; Zhu, L.; Chang, Y.; Li, B. Dual-Polarized Bandpass and Band-Notched Frequency-Selective Absorbers Under Multimode Resonance. IEEE Trans. Antennas Propag. 2018, 66, 7449–7454. [Google Scholar] [CrossRef]
- Ji, Z.; Song, Y.; Gao, M.; Zhang, Q.; Liu, Y. Multimode Miniature Polarization-Sensitive Metamaterial Absorber with Ultra-Wide Bandwidth in the K Band. Micromachines 2024, 15, 1446. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Ren, H.; Zhang, C.; Zhao, J.; Wu, H.; Dai, H. Optically Transparent Conformal Ultra-Broadband Metamaterial Absorber Based on ITO Conductive Film. J. Phys. D Appl. Phys. 2023, 56, 425101. [Google Scholar] [CrossRef]
- Li, T.; Chen, K.; Ding, G.; Zhao, J.; Jiang, T.; Feng, Y. Optically Transparent Metasurface Salisbury Screen with Wideband Microwave Absorption. Opt. Express 2018, 26, 34384–34395. [Google Scholar] [CrossRef]
- Zhou, Q.; Yin, X.; Ye, F.; Mo, R.; Tang, Z.; Fan, X.; Cheng, L.; Zhang, L. Optically Transparent and Flexible Broadband Microwave Metamaterial Absorber with Sandwich Structure. Appl. Phys. A 2019, 125, 131. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Singh, G.; Srivastava, K.V.; Ramkumar, J.; Ramakrishna, S.A. Polarization-Insensitive Optically Transparent Microwave Metamaterial Absorber Using a Complementary Layer. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 163–167. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).