Design and Control of the Manipulator of Magnetic Surgical Forceps with Cable Transmission
Abstract
1. Introduction
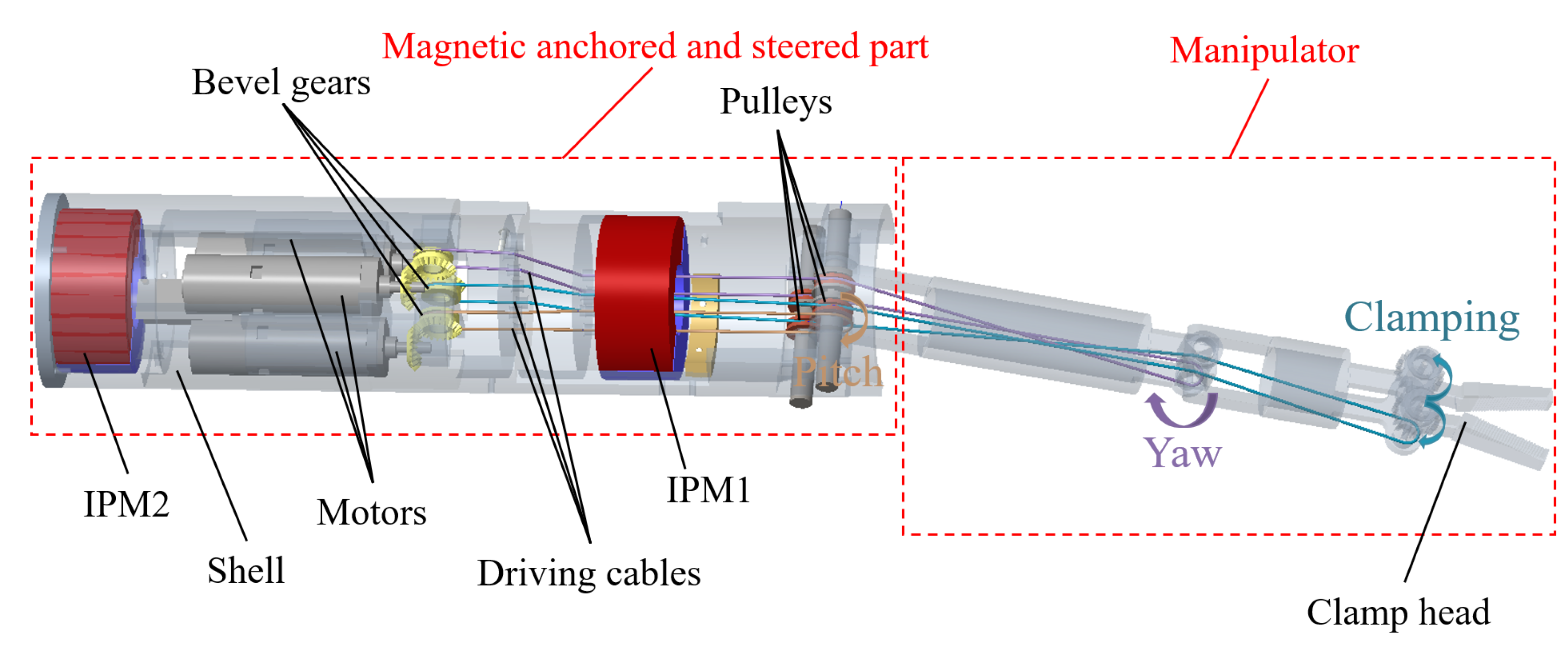
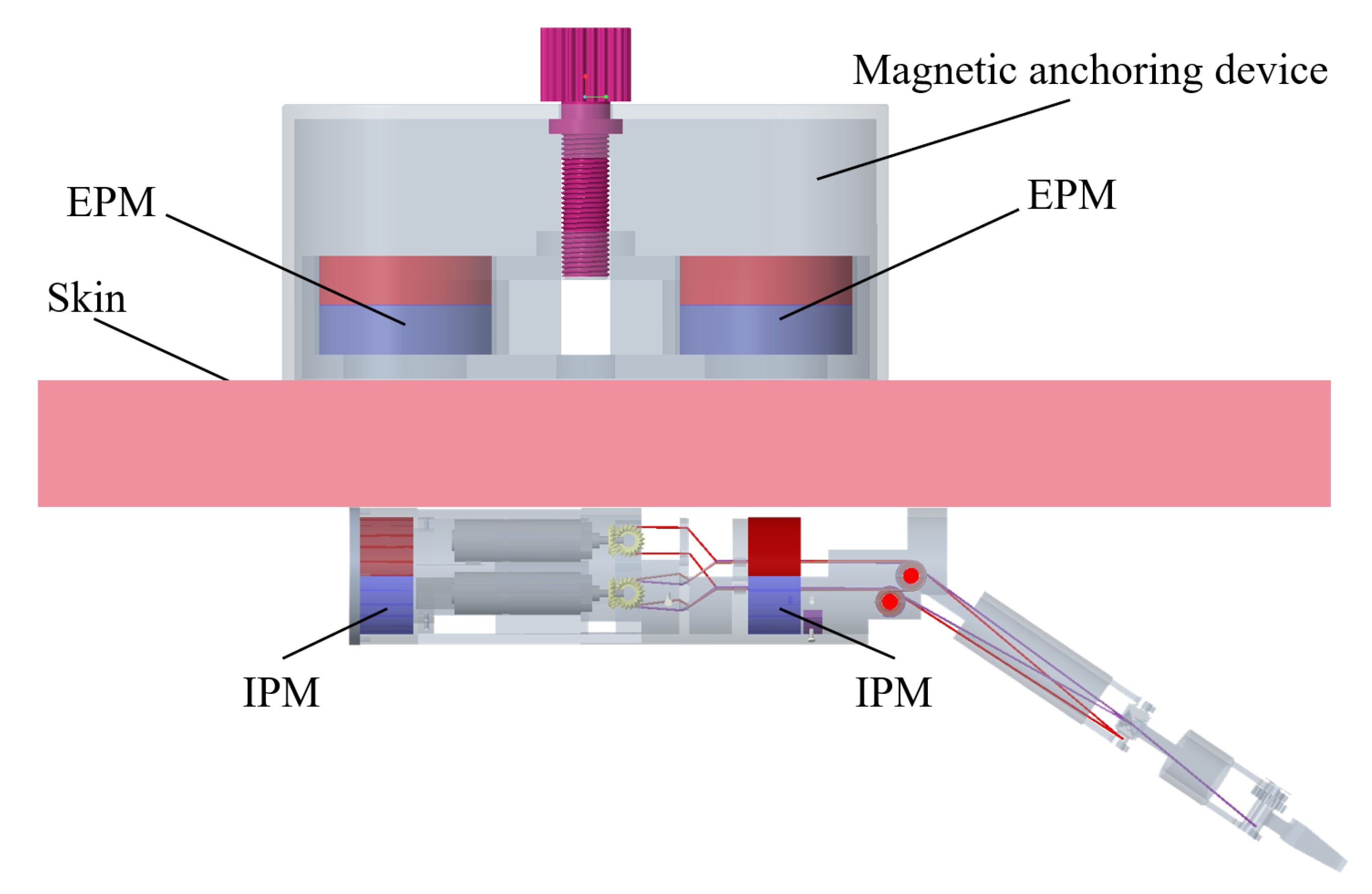
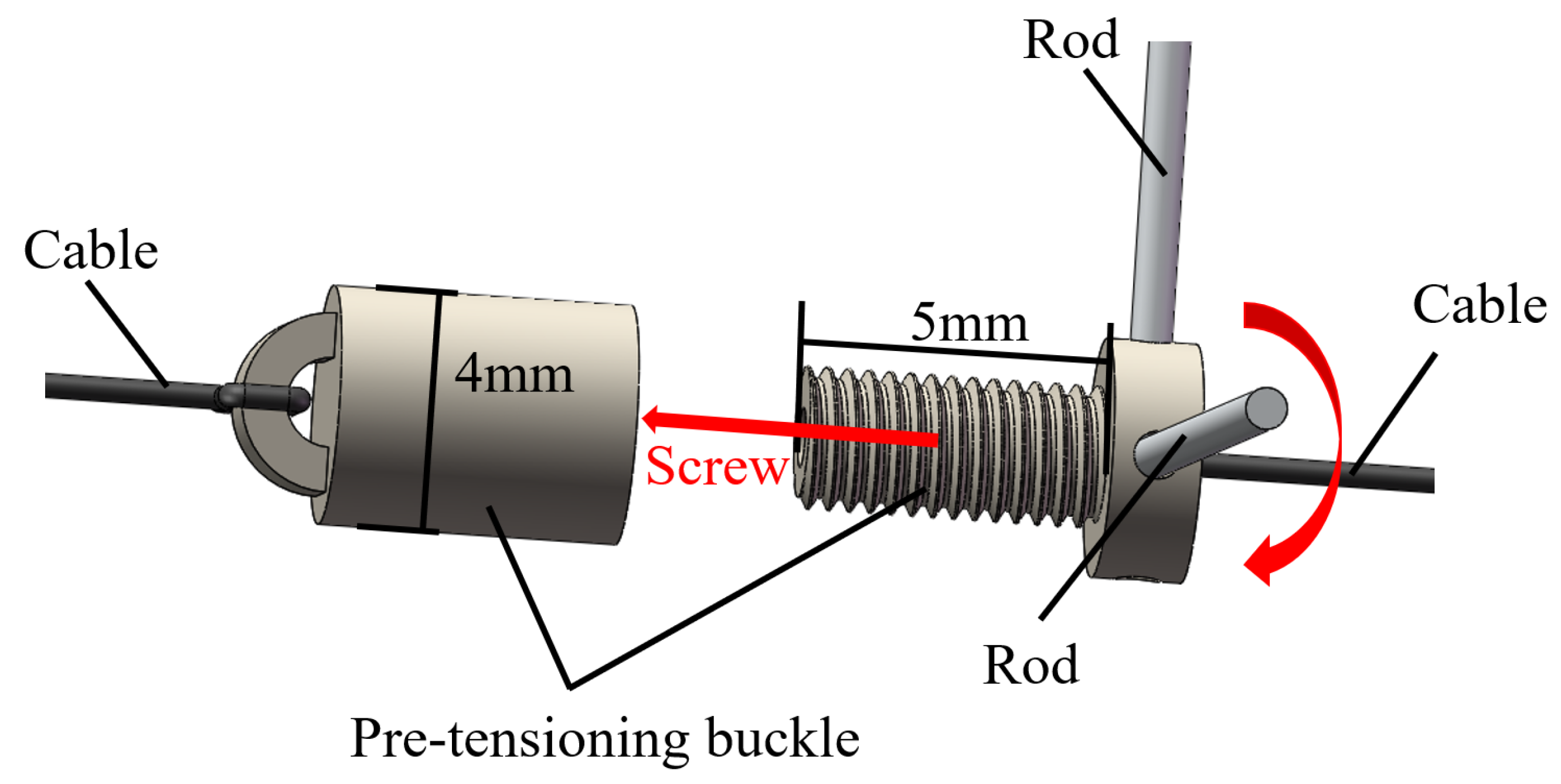
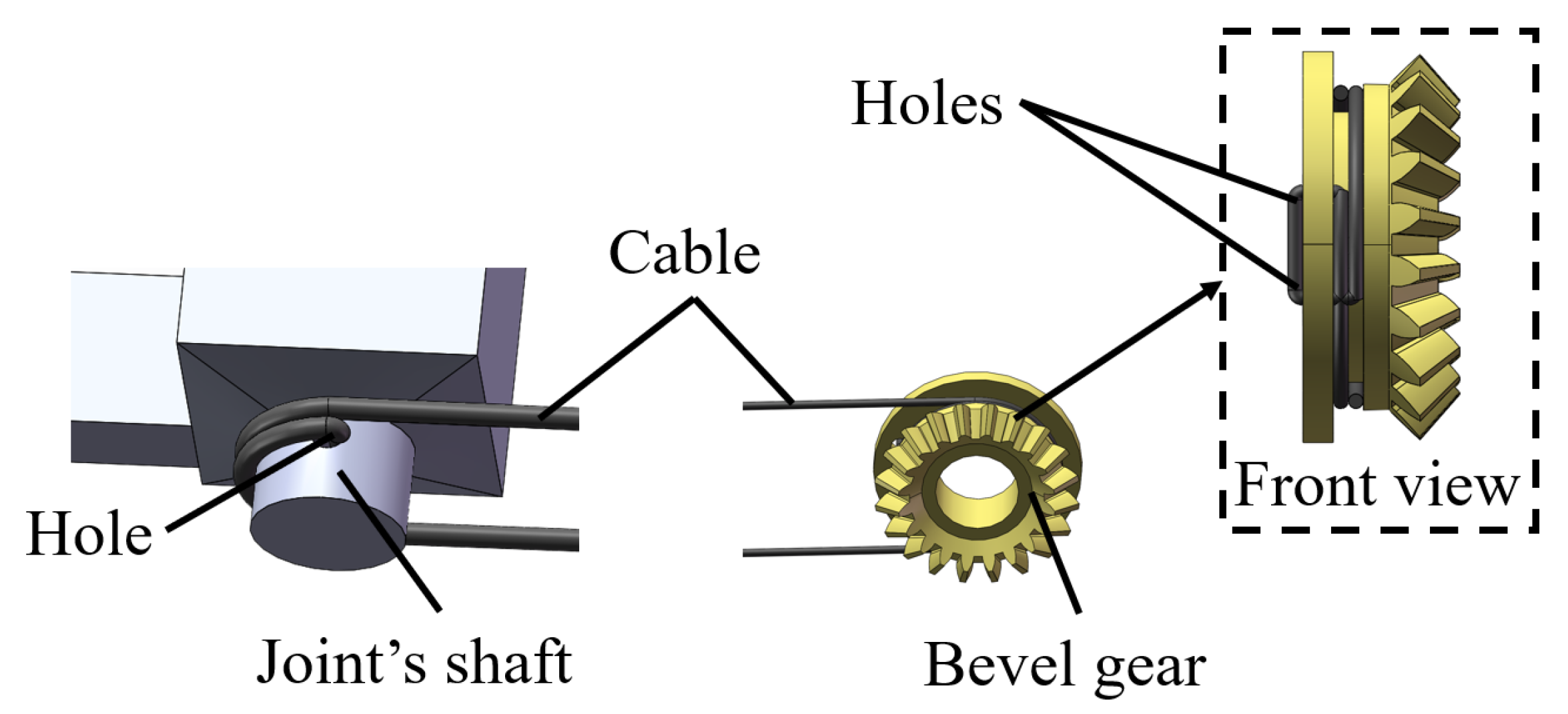
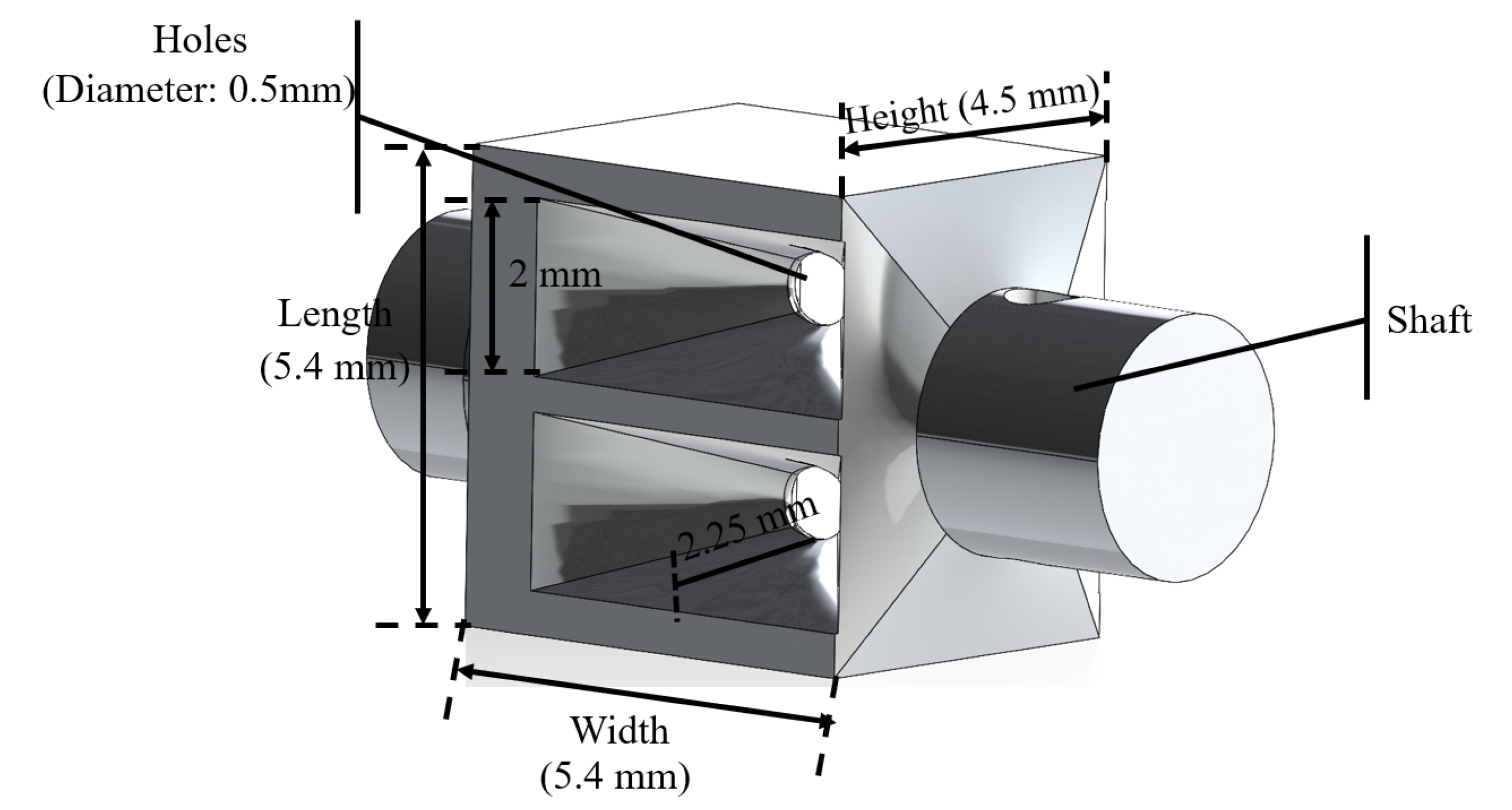
2. Structure and Manufacturing of the Magnetic Surgical Forceps
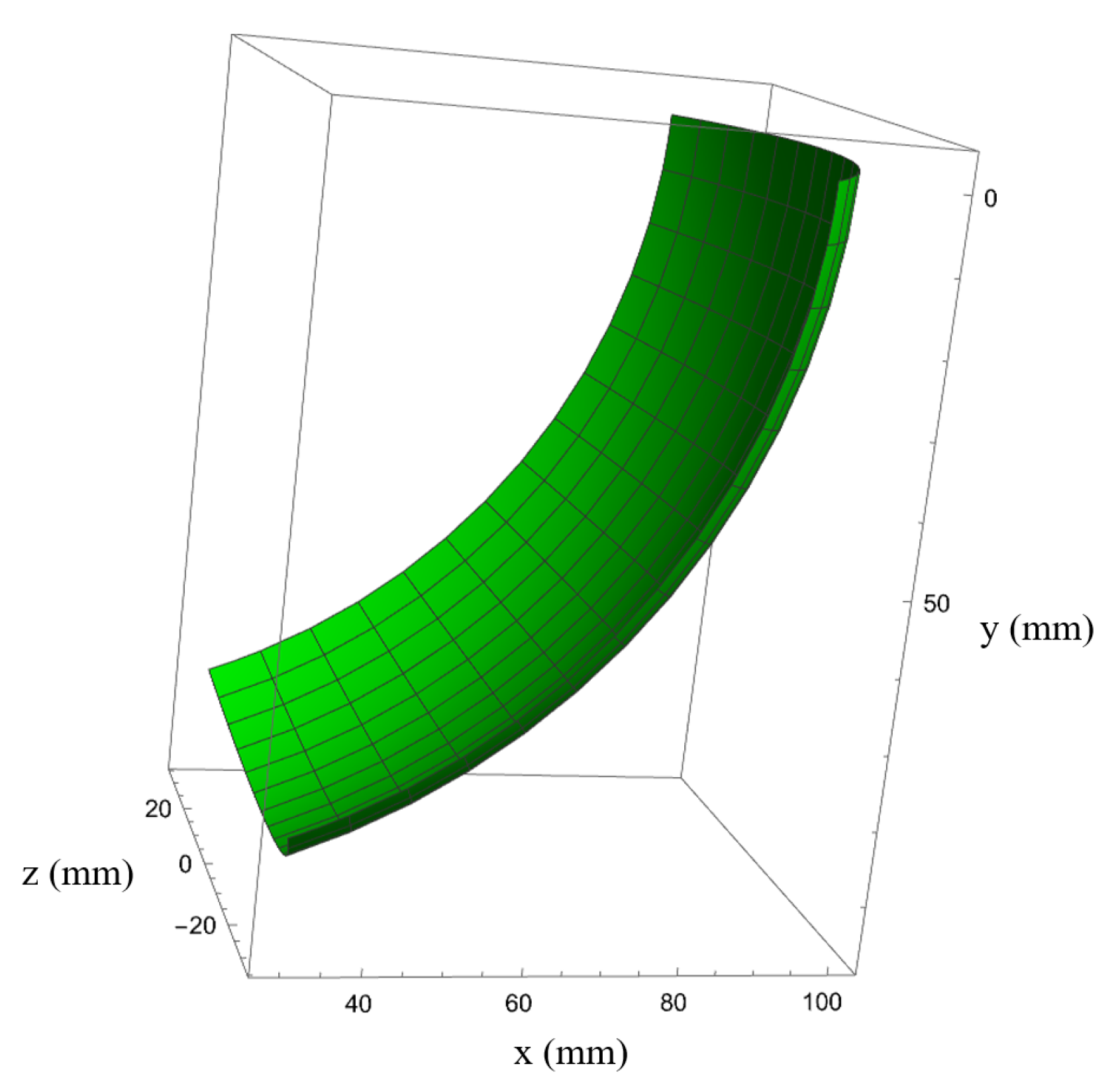
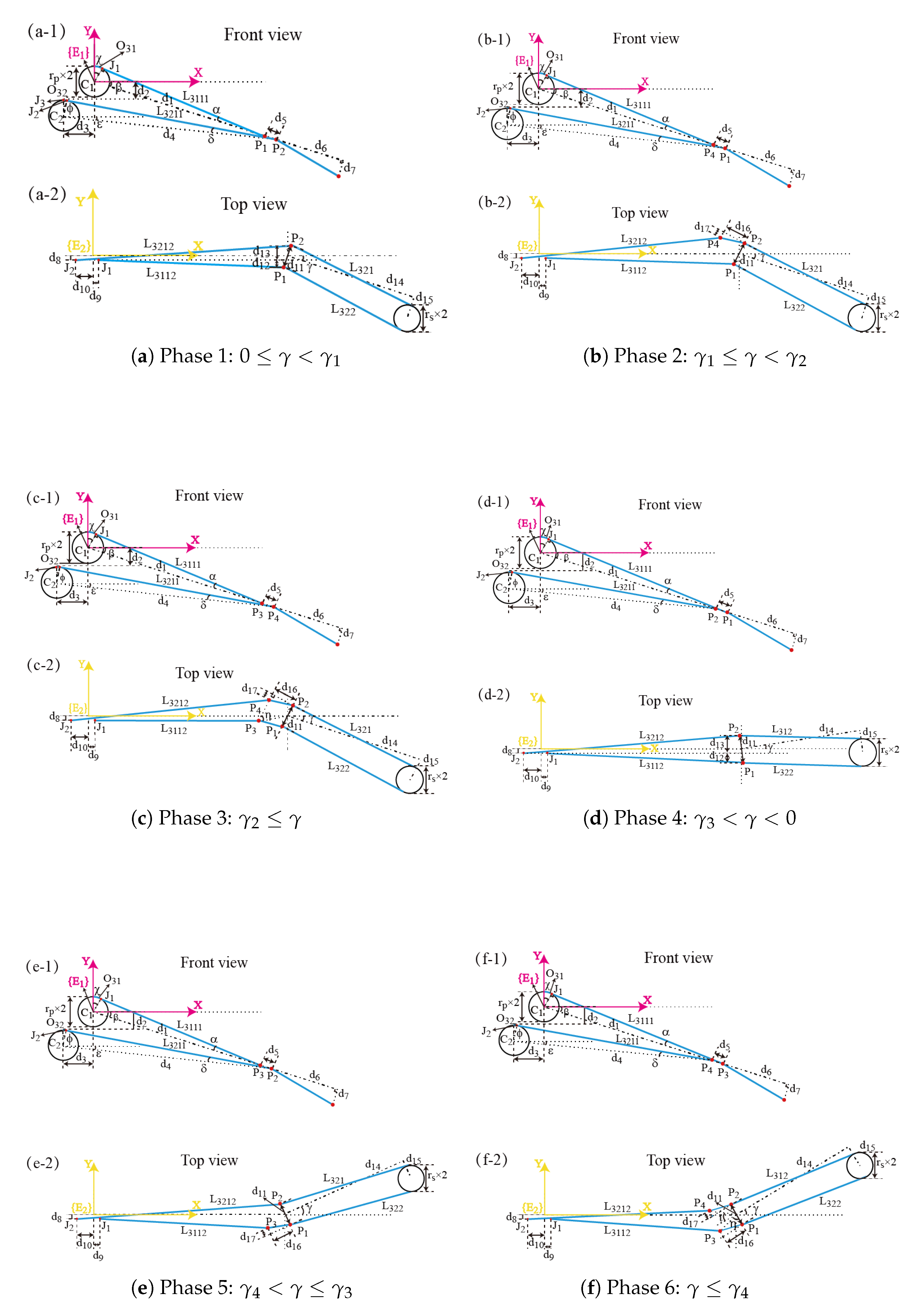
3. Kinematic Analysis of the Manipulator
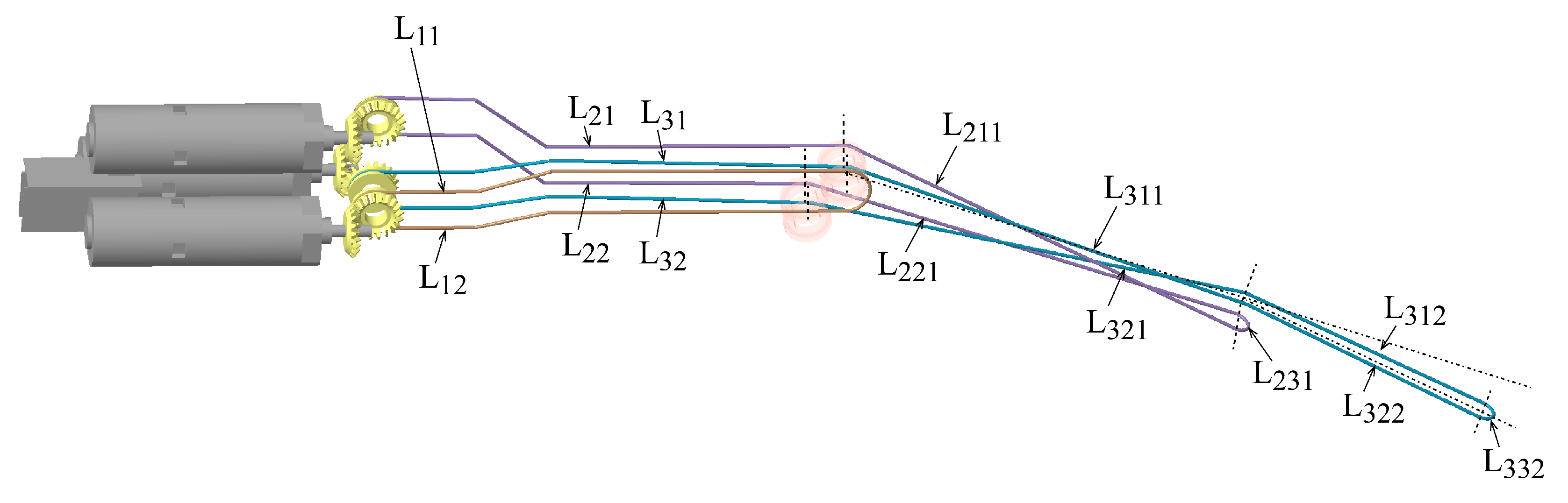
4. The Coupling Among Manipulator Joints
4.1. Motion Coupling of the Manipulator Joints
4.2. The Yaw Joint Coupling with the Pitch Joint
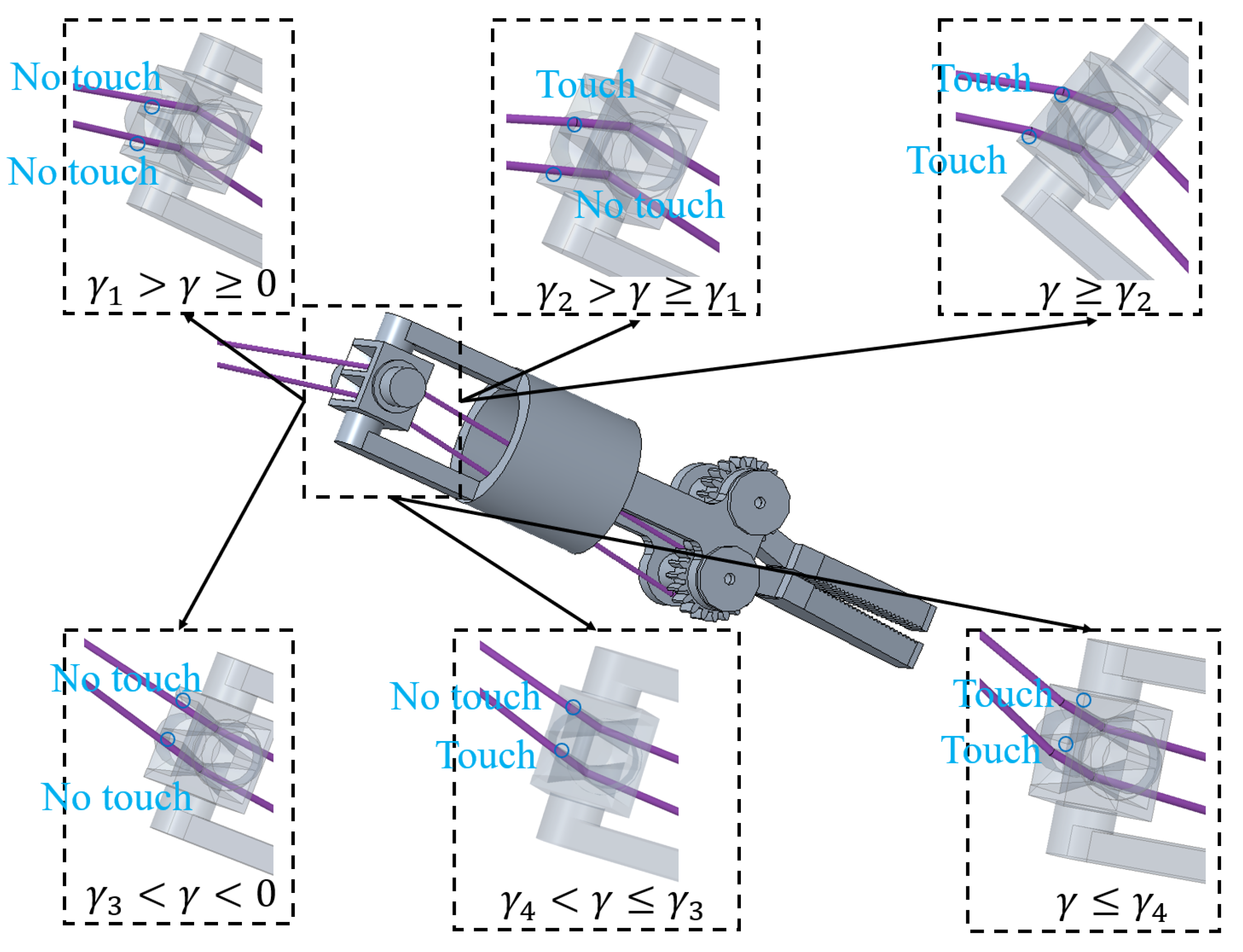
4.3. The Clamping Joint Coupling with the Pitch Joint and the Yaw Joint
5. Experimental Validation
5.1. Experiment Platform Setup
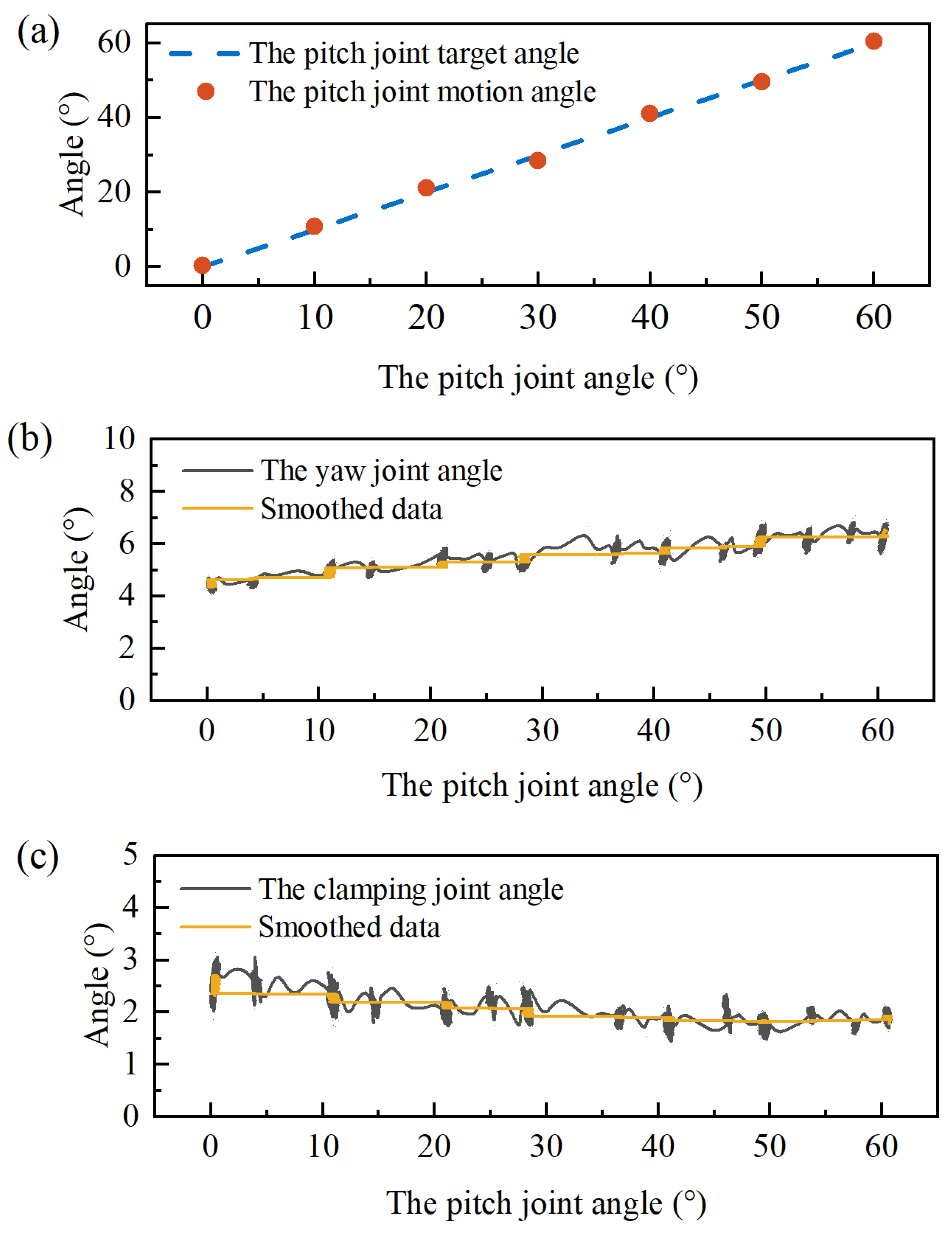
5.2. Joint Decoupling
5.3. Control Accuracy of the Manipulator
5.4. Grasping Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.Y.; Foo, D.C.C. Single-incision laparoscopic surgery: An update of current evidence. Ann. Laparosc. Endosc. Surg. 2016, 1. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, K.; Qian, K.; Hao, J.; Zhang, Z.; Shi, C. An operating stiffness controller for the medical continuum robot based on impedance control. Cyborg Bionic Syst. 2024, 5, 0110. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Song, D.; Zhang, G.; Bu, Q.; Dong, Y.; Hu, C.; Shi, C. A novel electromagnetic driving system for 5-DOF manipulation in intraocular microsurgery. Cyborg Bionic Syst. 2024, 5, 0083. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xu, Q. Multi-Section Magnetic Soft Robot with Multirobot Navigation System for Vasculature Intervention. Cyborg Bionic Syst. 2024, 5, 0188. [Google Scholar] [CrossRef]
- Brodie, A.; Vasdev, N. The future of robotic surgery. Ann. R. Coll. Surg. Engl. 2018, 100, 4–13. [Google Scholar] [CrossRef]
- Cheng, T.; Li, Z. Magnetic actuated endoscope systems for surgical applications. In Magnetic Sensors and Actuators in Medicine; Elsevier: Amsterdam, The Netherlands, 2023; pp. 81–101. [Google Scholar]
- Park, S.; Bergs, R.A.; Eberhart, R.; Baker, L.; Fernandez, R.; Cadeddu, J.A. Trocar-less instrumentation for laparoscopy: Magnetic positioning of intra-abdominal camera and retractor. Ann. Surg. 2007, 245, 379–384. [Google Scholar] [CrossRef]
- Liu, X.; Mancini, G.J.; Guan, Y.; Tan, J. Design of a magnetic actuated fully insertable robotic camera system for single-incision laparoscopic surgery. IEEE/ASME Trans. Mechatron. 2015, 21, 1966–1976. [Google Scholar] [CrossRef]
- Liu, X.; Mancini, G.J.; Tan, J. Design of a unified active locomotion mechanism for a capsule-shaped laparoscopic camera system. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2449–2456. [Google Scholar]
- Li, W.; Cheng, T.; Ye, M.; Ng, C.S.H.; Li, Z. Kinematic Modeling and Visual Servo Control of a Soft-Bodied Magnetic Anchored and Guided Endoscope. IEEE/ASME Trans. Mechatron. 2020, 25, 1531–1542. [Google Scholar] [CrossRef]
- Cheng, T.; Zhang, X.; Ng, C.S.H.; Chiu, P.W.Y.; Li, Z. A novel magnetic anchored and steered camera robot for single port access surgery. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1406–1412. [Google Scholar]
- Scaglioni, B.; Fornarelli, N.; Garbin, N.; Menciassi, A.; Valdastri, P. Independent control of multiple degrees of freedom local magnetic actuators with magnetic cross-coupling compensation. IEEE Robot. Autom. Lett. 2018, 3, 3622–3629. [Google Scholar] [CrossRef]
- Garbin, N.; Slawinski, P.R.; Aiello, G.; Karraz, C.; Valdastri, P. Laparoscopic camera based on an orthogonal magnet arrangement. IEEE Robot. Autom. Lett. 2016, 1, 924–929. [Google Scholar] [CrossRef]
- Feng, H.; Lu, Y.; Chen, D.; Ma, T.; Fu, Y. Development on a magnetic anchoring robot system based on visual servo control for laparoendoscopic single-site surgery. Int. J. Med. Robot. Comput. Assist. Surg. 2018, 14, e1904. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Abdolmalaki, R.Y.; Zuo, T.; Guan, Y.; Mancini, G.J.; Tan, J. Transformable in vivo robotic laparoscopic camera with optimized illumination system for single-port access surgery: Initial prototype. IEEE/ASME Trans. Mechatron. 2018, 23, 1585–1596. [Google Scholar] [CrossRef]
- Liu, X.; Yazdanpanah, R.A.; Zuo, T.; Guan, Y.; Mancini, G.J.; Tan, J. Design and test of an in-vivo robotic camera integrated with optimized illumination system for single-port laparoscopic surgery. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1392–1397. [Google Scholar]
- Lim, A.; Schonewille, A.; Forbrigger, C.; Looi, T.; Drake, J.; Diller, E. Design and comparison of magnetically-actuated dexterous forceps instruments for neuroendoscopy. IEEE Trans. Biomed. Eng. 2020, 68, 846–856. [Google Scholar] [CrossRef]
- Tortora, G.; Dimitracopoulos, A.; Valdastri, P.; Menciassi, A.; Dario, P. Design of miniature modular in vivo robots for dedicated tasks in minimally invasive surgery. In Proceedings of the 2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Budapest, Hungary, 3–7 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 327–332. [Google Scholar]
- da Veiga, T.; Chandler, J.H.; Lloyd, P.; Pittiglio, G.; Wilkinson, N.J.; Hoshiar, A.K.; Harris, R.A.; Valdastri, P. Challenges of continuum robots in clinical context: A review. Prog. Biomed. Eng. 2020, 2, 032003. [Google Scholar] [CrossRef]
- Orekhov, A.; Abah, C.; Simaan, N. Snake-like robots for minimally invasive, single-port, and intraluminal surgeries. Encycl. Med. Robot. 2018, 1, 203–243. [Google Scholar]
- Celotto, F.; Ramacciotti, N.; Mangano, A.; Danieli, G.; Pinto, F.; Lopez, P.; Ducas, A.; Cassiani, J.; Morelli, L.; Spolverato, G.; et al. Da Vinci single-port robotic system current application and future perspective in general surgery: A scoping review. Surg. Endosc. 2024, 38, 4814–4830. [Google Scholar] [CrossRef]
- Haidegger, T.; Speidel, S.; Stoyanov, D.; Satava, R.M. Robot-assisted minimally invasive surgery—Surgical robotics in the data age. Proc. IEEE 2022, 110, 835–846. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Zuo, S. Development of visible manipulator with multi-gear array mechanism for laparoscopic surgery. IEEE Robot. Autom. Lett. 2020, 5, 3090–3097. [Google Scholar] [CrossRef]
- Zhang, B.; Liao, Z.; Yang, P.; Liao, H. Robotic visible forceps manipulator with a novel linkage bending mechanism. J. Mech. Robot. 2019, 11, 011012. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Wang, C.; Zhang, B.; Shang, W.; Lin, Z.; Duan, L.; Wu, Z.; Fujie, M.G. System Design of A Dual-Arm Surgical Robot for Single Port Access Surgery. In Proceedings of the 2018 IEEE International Conference on Intelligence and Safety for Robotics (ISR), Shenyang, China, 24–27 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 349–354. [Google Scholar]
- Hong, M.B.; Jo, Y.H. Design of a novel 4-DOF wrist-type surgical instrument with enhanced rigidity and dexterity. IEEE/ASME Trans. Mechatron. 2013, 19, 500–511. [Google Scholar] [CrossRef]
- Li, J.; Zhang, T.; Cheng, T.; Li, Y.; Ng, C.S.H.; Chiu, P.W.Y.; Li, Z. Design, Analysis, and Preliminary Validation of Magnetic Anchored and Cable Driven Endoscope for Minimally Invasive Surgery. IEEE Trans. Med. Robot. Bionics 2024, 6, 1397–1400. [Google Scholar] [CrossRef]
- Mohammadi, A.; Samsonas, D.; Leong, F.; Tan, Y.; Thiruchelvam, D.; Valdastri, P.; Oetomo, D. Modeling and control of local electromagnetic actuation for robotic-assisted surgical devices. IEEE/ASME Trans. Mechatron. 2017, 22, 2449–2460. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, T.; Chen, J.; Xu, W.; Wei, H.; Song, Y.; Guan, Y. A modular cable-driven humanoid arm with anti-parallelogram mechanisms and Bowden cables. Front. Mech. Eng. 2023, 18, 6. [Google Scholar] [CrossRef]
- Liu, F.; Xu, W.; Huang, H.; Ning, Y.; Li, B. Design and Analysis of a High-Payload Manipulator Based On Cable-Driven Serial-Parallel Mechanism. J. Mech. Robot. 2019, 11, 051006. [Google Scholar] [CrossRef]
- Jiang, S.; Hua, D.; Wang, Y.; Ju, F.; Yin, L.; Chen, B. Design and modeling of motion-decoupling mechanism for cable-driven joints. Adv. Mech. Eng. 2018, 10, 1687814018777428. [Google Scholar] [CrossRef]
- Tsumaki, Y.; Shimanuki, S.; Ono, F.; Han, H.T. Ultra-lightweight forearm with a parallel-wire mechanism. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besacon, France, 8–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1419–1423. [Google Scholar]
- Zhao, B.; Nelson, C.A. Decoupled cable-driven grasper design based on planetary gear theory. J. Med. Devices 2013, 7, 020918. [Google Scholar] [CrossRef]
- Yang, G.; Mustafa, S.K.; Yeo, S.H.; Lin, W.; Lim, W.B. Kinematic design of an anthropomimetic 7-DOF cable-driven robotic arm. Front. Mech. Eng. China 2011, 6, 45–60. [Google Scholar] [CrossRef]
- Quigley, M.; Asbeck, A.; Ng, A. A low-cost compliant 7-DOF robotic manipulator. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 6051–6058. [Google Scholar]
- Berthet-Rayne, P.; Gras, G.; Leibrandt, K.; Wisanuvej, P.; Schmitz, A.; Seneci, C.A.; Yang, G.Z. The i2 snake robotic platform for endoscopic surgery. Ann. Biomed. Eng. 2018, 46, 1663–1675. [Google Scholar] [CrossRef]
- Hong, W.; Schmitz, A.; Bai, W.; Berthet-Rayne, P.; Xie, L.; Yang, G.Z. Design and compensation control of a flexible instrument for endoscopic surgery. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1860–1866. [Google Scholar]
- Rivas, I.; Tortora, G.; Menciassi, A.; Munoz, V.F. Control Architecture of a sensorless robotic platform for Minimally Invasive Surgery. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besancon, France, 8–11 July 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Tortora, G.; Salerno, M.; Ranzani, T.; Tognarelli, S.; Menciassi, A. A modular magnetic platform for natural orifice transluminal endoscopic surgery. In Proceedings of the Engineering in Medicine & Biology Society, Osaka, Japan, 3–7 July 2013. [Google Scholar]
- Lehman, A.C.; Wood, N.A.; Farritor, S.; Goede, M.R.; Oleynikov, D. Dexterous miniature robot for advanced minimally invasive surgery. Surg. Endosc. 2011, 25, 119–123. [Google Scholar] [CrossRef]
- Lehman, A.C.; Dumpert, J.; Wood, N.A.; Redden, L.; Visty, A.Q.; Farritor, S.; Varnell, B.; Oleynikov, D. Natural orifice cholecystectomy using a miniature robot. Surg. Endosc. 2009, 23, 260–266. [Google Scholar] [CrossRef]
- Zidane, I.F.; Khattab, Y.; Rezeka, S.; El-Habrouk, M. Robotics in laparoscopic surgery-A review. Robotica 2023, 41, 126–173. [Google Scholar] [CrossRef]
- Simi, M.; Silvestri, M.; Cavallotti, C.; Vatteroni, M.; Valdastri, P.; Menciassi, A.; Dario, P. Magnetically activated stereoscopic vision system for laparoendoscopic single-site surgery. IEEE/ASME Trans. Mechatron. 2012, 18, 1140–1151. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Wu, Z.; Yang, B.; Luo, Q.; Xu, K. Review of surgical robotic systems for keyhole and endoscopic procedures: State of the art and perspectives. Front. Med. 2020, 14, 382–403. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, Y.H.; Collins, J.; Kapoor, A.; Kwon, D.S.; Mansi, T. Non-linear hysteresis compensation of a tendon-sheath-driven robotic manipulator using motor current. IEEE Robot. Autom. Lett. 2021, 6, 1224–1231. [Google Scholar] [CrossRef]
- Khoshnam, M.; Patel, R.V. Robotics-assisted control of steerable ablation catheters based on the analysis of tendon-sheath transmission mechanisms. IEEE/ASME Trans. Mechatron. 2017, 22, 1473–1484. [Google Scholar] [CrossRef]
- Wang, X.; Bie, D.; Han, J.; Fang, Y. Active modeling and compensation for the hysteresis of a robotic flexible ureteroscopy. IEEE Access 2020, 8, 100620–100630. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Modeling, online identification, and compensation control of single tendon sheath system with time-varying configuration. Mech. Syst. Signal Process. 2019, 130, 56–73. [Google Scholar] [CrossRef]







| Symbol | Value (mm) |
|---|---|
| 50 | |
| 3.2 | |
| 2.53 | |
| 0.75 | |
| 4 | |
| 2.35 | |
| 1.6 |
| Symbol | Value (mm) |
|---|---|
| 2.35 | |
| 1.6 | |
| 50 | |
| 2.53 | |
| 4 | |
| 0.75 | |
| 3 | |
| 2.4 | |
| 30 | |
| 3.2 | |
| 2.25 | |
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Sun, Z. Design and Control of the Manipulator of Magnetic Surgical Forceps with Cable Transmission. Micromachines 2025, 16, 650. https://doi.org/10.3390/mi16060650
Li J, Sun Z. Design and Control of the Manipulator of Magnetic Surgical Forceps with Cable Transmission. Micromachines. 2025; 16(6):650. https://doi.org/10.3390/mi16060650
Chicago/Turabian StyleLi, Jingwu, and Zhijun Sun. 2025. "Design and Control of the Manipulator of Magnetic Surgical Forceps with Cable Transmission" Micromachines 16, no. 6: 650. https://doi.org/10.3390/mi16060650
APA StyleLi, J., & Sun, Z. (2025). Design and Control of the Manipulator of Magnetic Surgical Forceps with Cable Transmission. Micromachines, 16(6), 650. https://doi.org/10.3390/mi16060650






