Miniaturized BAW Filter for Wide Band Application Based on High-Q Factor Active Inductor
Abstract
1. Introduction
2. Active Inductor Design
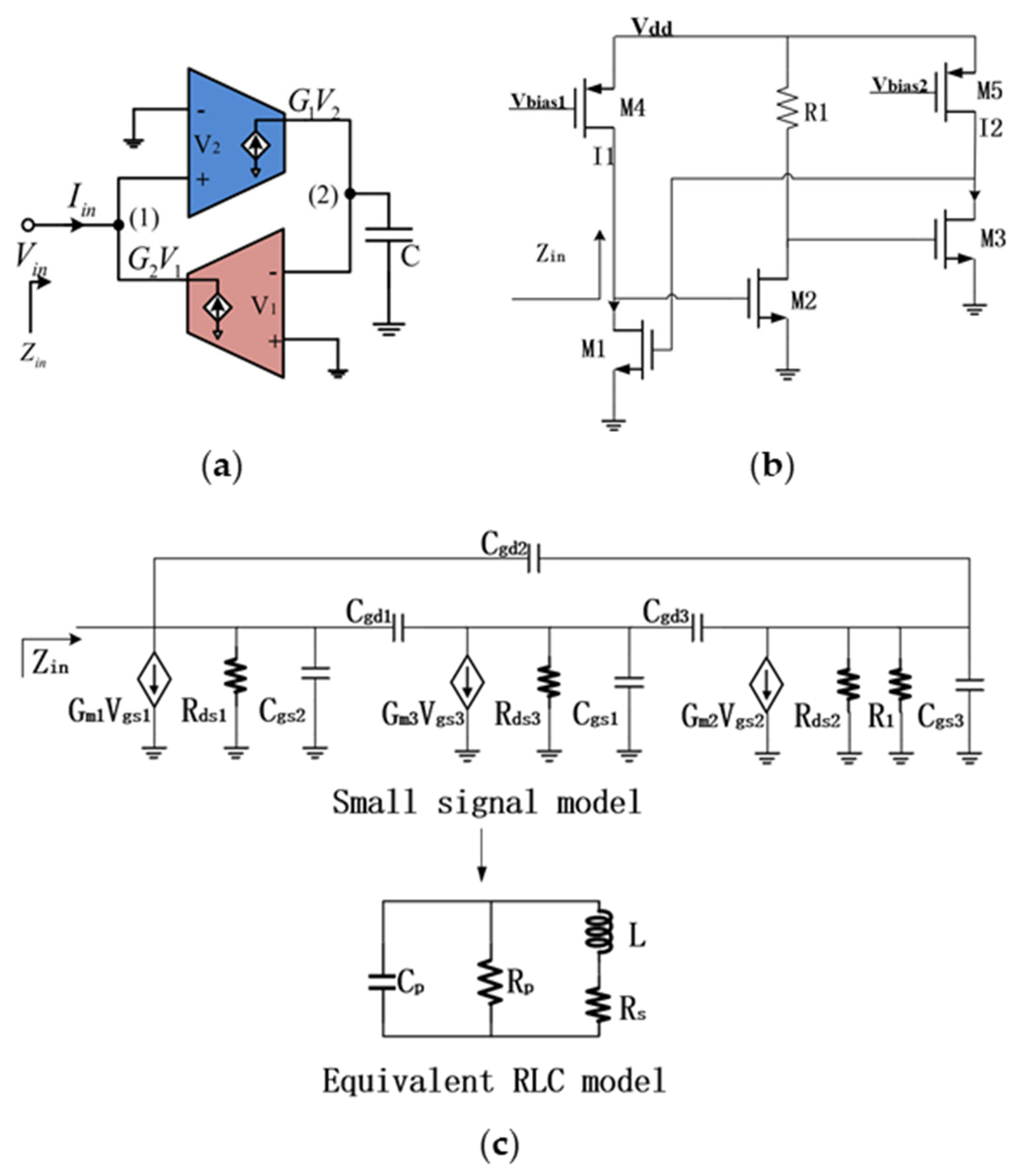
2.1. Description of Proposed Active Inductor Topology
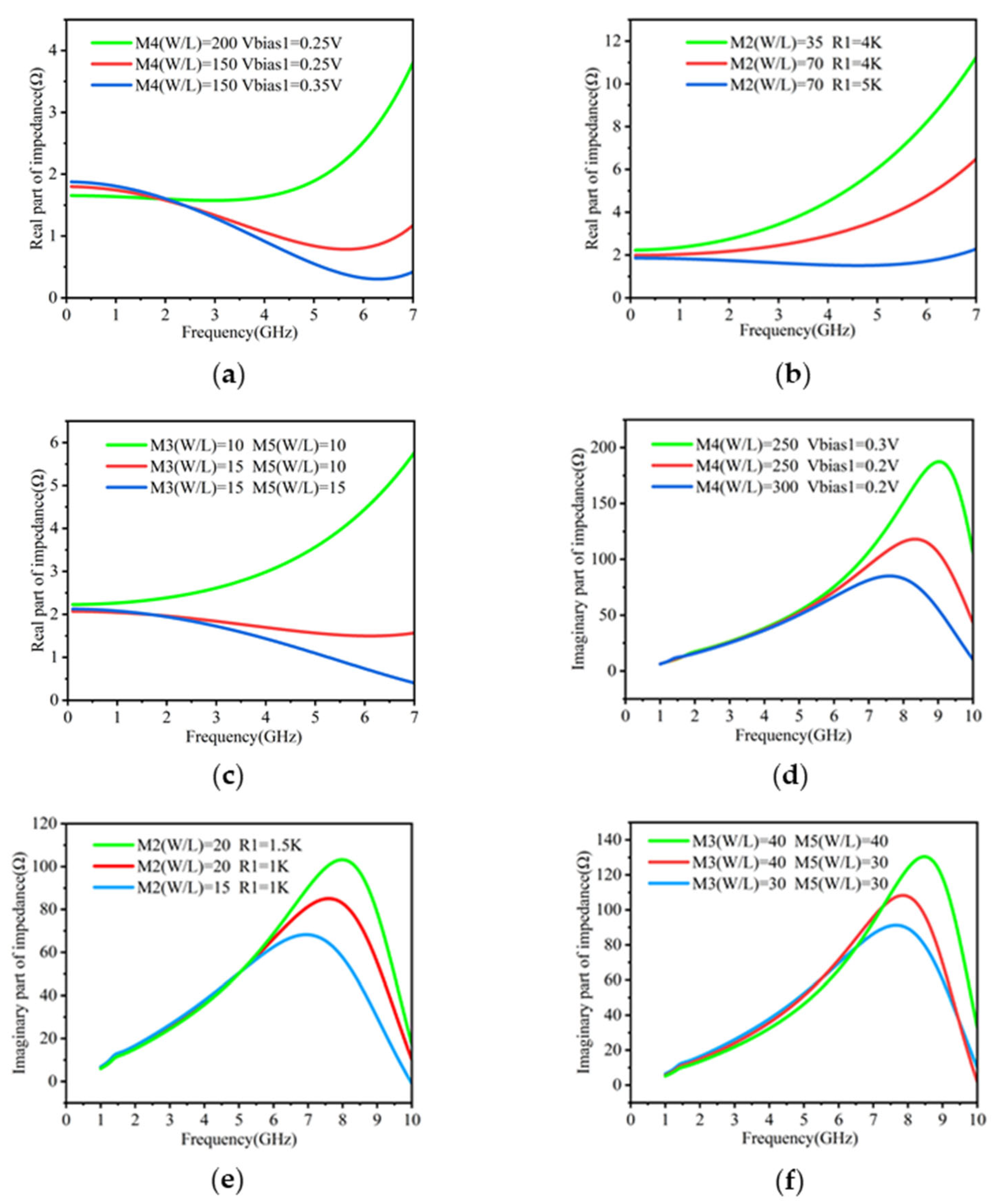
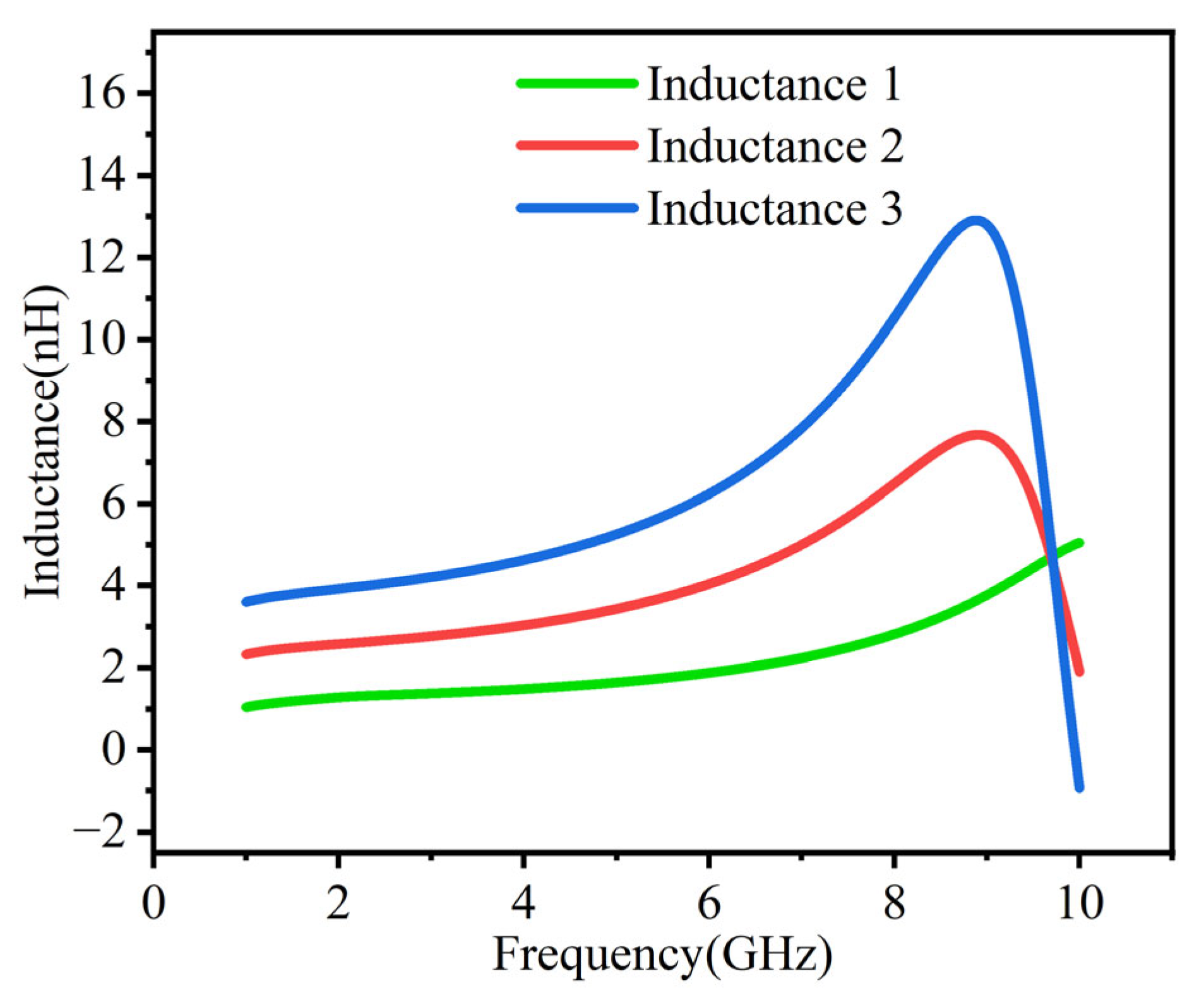
2.2. Improvement of Q Factor and Inductance Stability
2.3. Inductor Simulation Results
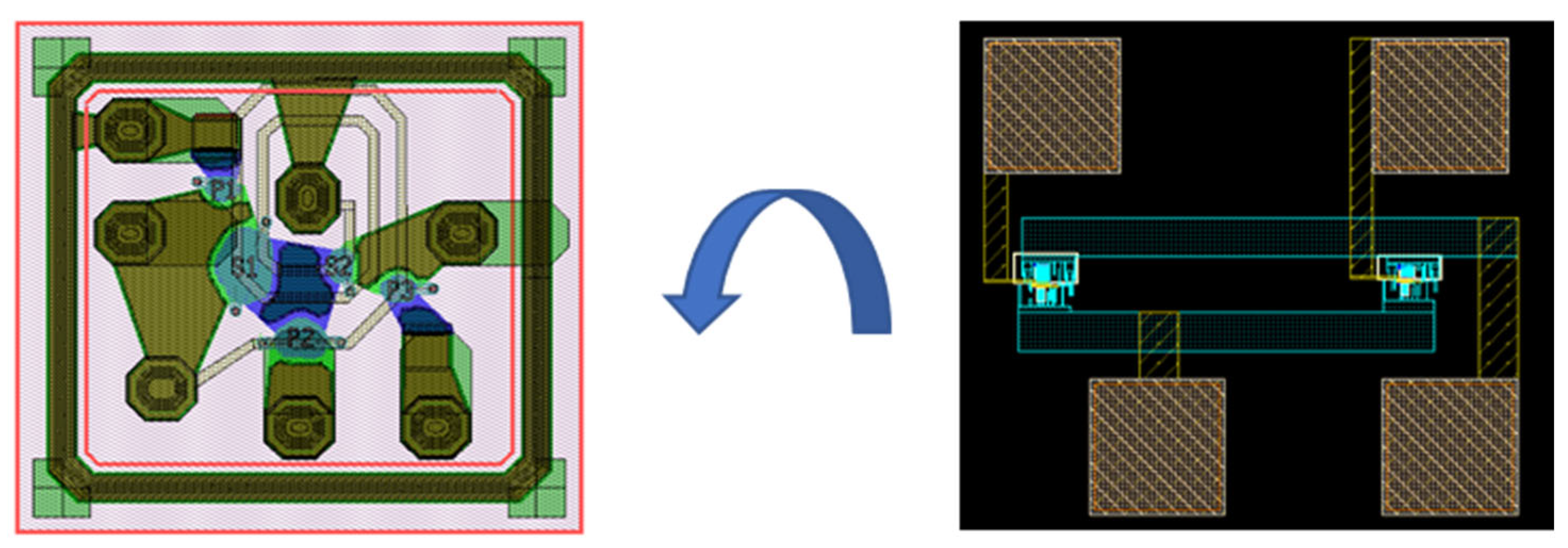
2.4. Inductor Layout
3. BAW Filter with Active Inductor Embedded
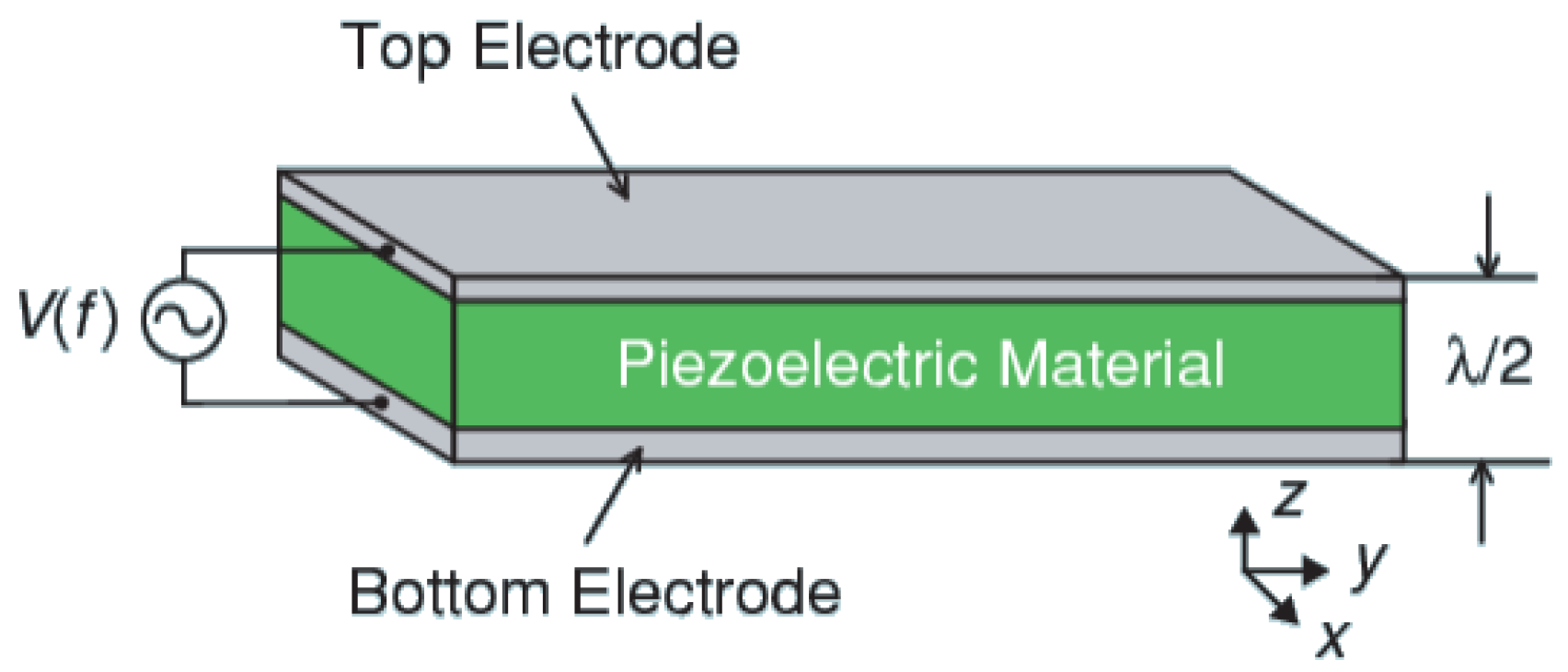
3.1. Characteristics of BAW Resonator
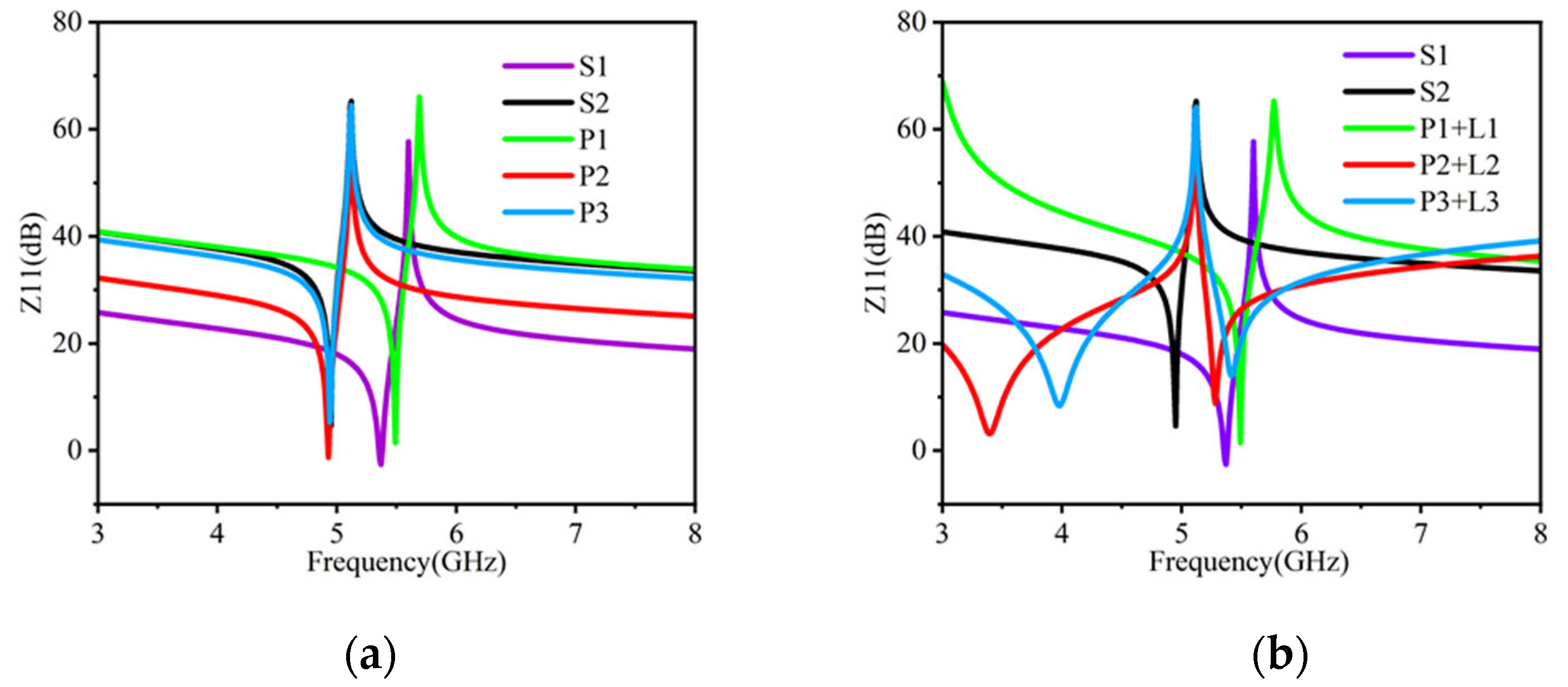
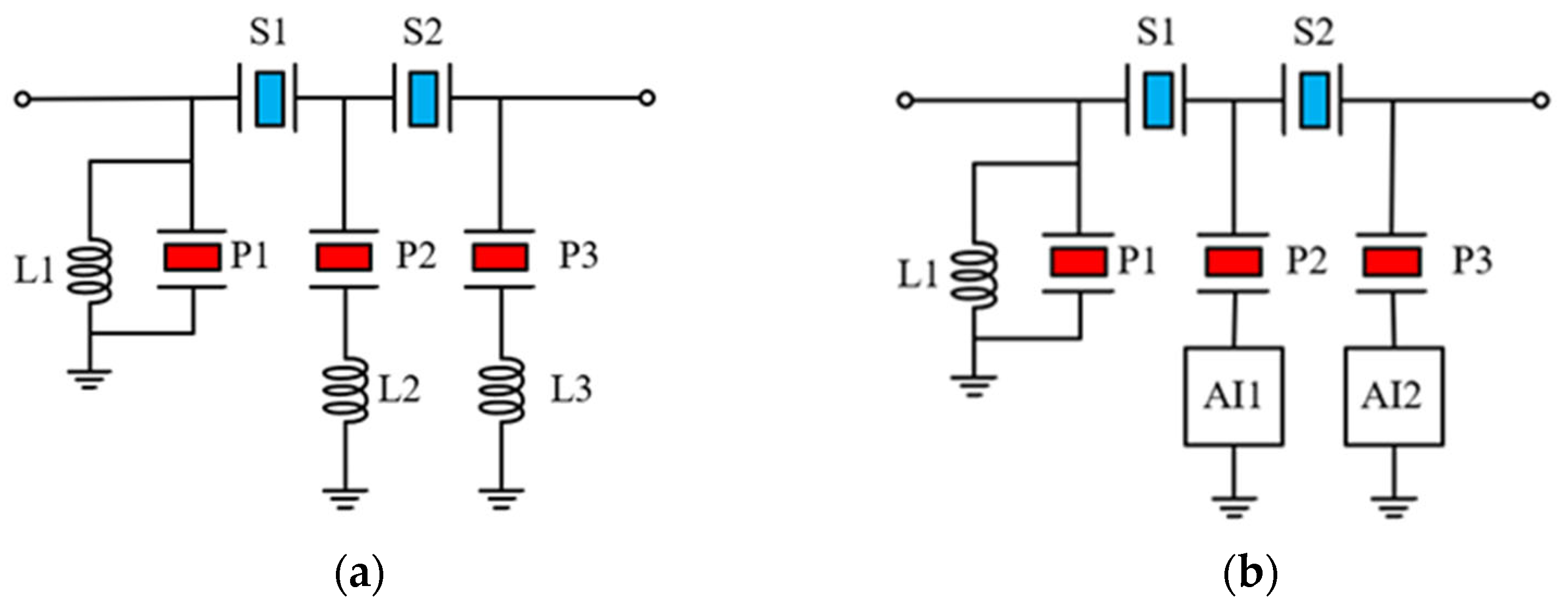
3.2. Topology of BAW Filter and Its Combination with Active Inductor
3.3. Influence of Q Factor and Inductance Stability on BAW Filter
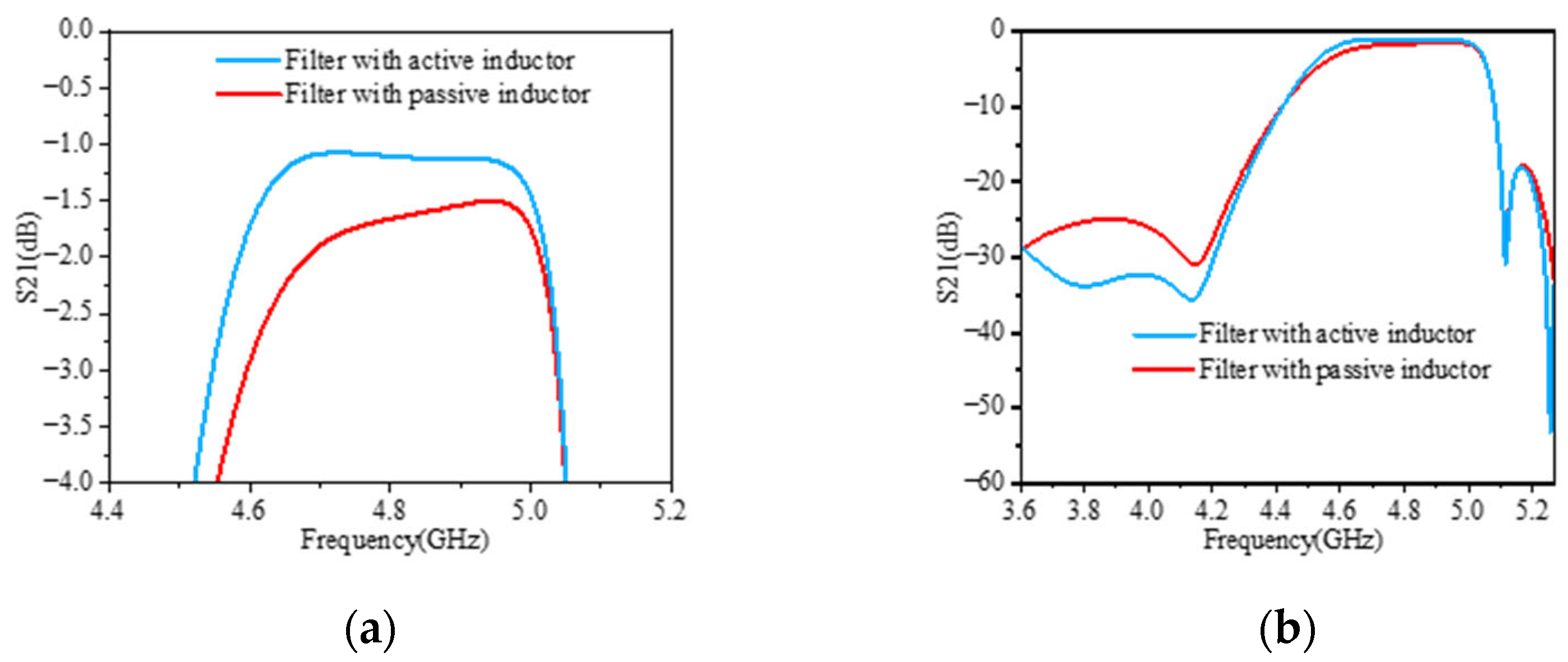
3.4. Simulation Results and Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Active inductor |
| BAW | Bulk acoustic wave |
| NMOS | N-channel Metal-Oxide-Semiconductor |
| PMOS | P-channel Metal-Oxide-Semiconductor |
| Q | Quality |
| RF | Radio Frequency |
| RLC | Resistor-Inductor-Capacitor |
| SAW | Surface acoustic wave |
| SRF | Self-resonant frequency |
References
- Ding, R.; Xuan, W.; Gao, F.; Cao, T.; Jin, H.; Luo, J.; Ma, F.; Dong, S. Key High-Performance N79 Band AlScN BAW Resonator and Filter With the Consideration of Area Effect. IEEE Trans. Electron Devices 2023, 70, 5839–5844. [Google Scholar] [CrossRef]
- Ding, R.; Xuan, W.; Gao, F.; Jiang, H.; Wang, W.; Jin, H.; Luo, J.; Dong, S. Compact and High Steep Skirts Hybrid Heterogeneous Integrated N77 Full Band BAW Filter Based on Band-Stop Theory. IEEE Electron Device Lett. 2024, 45, 793–796. [Google Scholar] [CrossRef]
- Tilhac, C.; Razafimandimby, S.; Cathelin, A.; Bila, S.; Madrangeas, V.; Belot, D. A tunable bandpass BAW-filter architecture using negative capacitance circuitry. In Proceedings of the 2008 IEEE Radio Frequency Integrated Circuits Symposium, Atlanta, GA, USA, 15–17 June 2008; pp. 605–608. [Google Scholar]
- Yang, Y.; Dejous, C.; Hallil, H. Trends and Applications of Surface and Bulk Acoustic Wave Devices: A Review. Micromachines 2023, 14, 43. [Google Scholar] [CrossRef] [PubMed]
- Lv, L.; Shuai, Y.; Bai, X.; Huang, S.; Zhu, D.; Wang, Y.; Zhao, J.; Luo, W.; Wu, C.; Zhang, W. Wide Band BAW Filter Based on Single-Crystalline LiNbO3 Thin Film with Insulating Bragg Reflector. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 1535–1541. [Google Scholar] [CrossRef] [PubMed]
- Guerrero, E.; Gimenez, A.; Heeren, W.; Al-Joumayly, M. BAW Filter Trends for 5G and Beyond. In Proceedings of the 2024 IEEE International Microwave Filter Workshop (IMFW), Cocoa Beach, FL, USA, 21–23 February 2024; pp. 75–77. [Google Scholar]
- Karnati, K.; Schaefer, M.; Yusuf, W.; Rothemund, R.; Al-Joumayly, M.; Fattinger, G. 5G C-V2X Filter Using BAW Technology. In Proceedings of the 2021 IEEE MTT-S International Microwave Filter Workshop (IMFW), Perugia, Italy, 17–19 November 2021; pp. 109–111. [Google Scholar]
- AlJoumayly, M.; Rothemund, R.; Schaefer, M.; Heeren, W. 5G BAW Technology: Challenges and Solutions. In Proceedings of the 2022 IEEE 22nd Annual Wireless and Microwave Technology Conference (WAMICON), Clearwater, FL, USA, 27–28 April 2022; pp. 1–3. [Google Scholar]
- Aliouane, S.; Kouki, A.B.; Aigner, R. RF-MEMS switchable inductors for tunable bandwidth BAW filters. In Proceedings of the 5th International Conference on Design & Technology of Integrated Systems in Nanoscale Era, Hammamet, Tunisia, 23–25 March 2010; pp. 1–6. [Google Scholar]
- Yu, H.; Wang, X.; Peng, X.; Zhang, L.; Jiang, P.; Zhao, X.; Deng, L.; Ma, J. Performance Optimization of FBAR Filters with Wafer-Level Chip-Scale Package Using Embedded Matching Inductors on Multilayer PCB. In Proceedings of the 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Guangzhou, China, 27–29 November 2022; pp. 1–3. [Google Scholar]
- Cheon, S.J.; Bang, D.H.; Park, J.Y. Miniaturization of FBAR duplexer using PCB embedded high Q spiral inductors. In Proceedings of the 2009 European Microwave Conference (EuMC), Rome, Italy, 29 September–1 October 2009; pp. 1002–1005. [Google Scholar]
- Zhou, C.; Dou, W.; Qin, R.; Lu, J.; Yang, Y.; Mu, Z.; Yu, W. Highly Doped Single Crystal Al1-xScxN Bulk Acoustic Resonators for High-Frequency and Wideband Applications. IEEE Trans. Electron Devices 2024, 71, 6329–6335. [Google Scholar] [CrossRef]
- Herbert, T.B.; Hyland, J.S.; Abdullah, S.; Wight, J.; Amaya, R.E. An Active Bandpass Filter for LTE/WLAN Applications Using Robust Active Inductors in Gallium Nitride. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2252–2256. [Google Scholar] [CrossRef]
- Oraha, J.A.; Younis, A.T. Design, Realization, and Simulation of CMOS Active Inductors for RF Applications. In Proceedings of the 2022 2nd International Conference on Advances in Engineering Science and Technology (AEST), Babil, Iraq, 24–25 October 2022; pp. 489–494. [Google Scholar]
- Momen, H.G.; Yazgi, M.; Kopru, R.; Saatlo, A.N. CMOS high-performance UWB active inductor circuit. In Proceedings of the 2016 12th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Lisbon, Portugal, 27–30 June 2016; p. 14. [Google Scholar]
- Hammadi, A.B.; Mhiri, M.; Haddad, F.; Saad, S.; Besbes, K. A 1.82–4.44 GHz reconfigurable bandpass filter based on tunable active inductor. In Proceedings of the 2016 11th International Design & Test Symposium (IDT), Hammam-et, Tunisia, 18–20 December 2016; pp. 254–259. [Google Scholar]
- Allidina, K.; Mirabbasi, S. A widely tunable active RF filter topology. In Proceedings of the 2006 IEEE International Symposium on Circuits and Systems, Kos, Greece, 21–24 May 2006; p. 4. [Google Scholar]
- Lu, H.; Hao, X.; Yang, L.; Hou, B.; Zhang, M.; Wu, M.; Dong, J.; Ma, X. Recent Advances in AlN-Based Acoustic Wave Resonators. Micromachines 2025, 16, 205. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Wang, X.; Zhang, Y.; Liu, C.; Zhu, Y. Demonstration of 8-Inch Thin-Film Sc0.3A10.7N BAW Resonator with High Electromechanical Coupling Coefficient. In Proceedings of the 2024 IEEE MTT-S International Conference on Microwave Acoustics & Mechanics (IC-MAM), Chengdu, China, 13–15 May 2024; pp. 5–8. [Google Scholar] [CrossRef]
- Gerbe, R.; Yang, Y.; Hou, D. ScAlN BAW resonator technology with coupling coefficients up to 21% for high performance filter design. In Proceedings of the 2024 IEEE Ultrasonics, Ferroelectrics, and Frequency Control Joint Symposium (UFFC-JS), Taipei, Taiwan, 22–26 September 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Zhang, Y.; Yang, W.; Qian, Y.; Liu, P.; Quek, Z.J.; Hong, Y.; Yi, E.; Woo, Z.; et al. Thin Sc0.2Al0.8N Film Based 15 GHz Wideband Filter: Towards mmWave Acoustic Filters. In Proceedings of the 2023 International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 9–13 December 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Lai, Y.-L.; Zheng, C.-Y. Electromagnetic Characteristics of a Novel Radio-Frequency Complementary Metal–Oxide–Semiconductor Active Inductor. IEEE Trans. Magn. 2011, 47, 2768–2771. [Google Scholar] [CrossRef]
- Belen, A.; Belen, M.A.; Palandöken, M.; Mahouti, P.; Tari, Ö. Design and Realization of Broadband Active Inductor Based Band Pass Filter. Chin. J. Electron. 2023, 32, 731–735. [Google Scholar] [CrossRef]



| Ref. | Frequency (GHz) | Inductance (nH) | Inductance Stability | Quality Factor |
|---|---|---|---|---|
| [14] | 0.5–4 | 8–20 | 0.6 nH per GHz | 3–10 |
| [16] | 1.76–6.18 | 3–10 | 0.45 nH per GHz | 0–400 |
| [22] | 0.1–3.8 | 1.55–4 | 0.88 nH per GHz | 10–76 |
| [23] | 0.8–2.7 | 0–5 | 2.9 nH per GHz | 0–50 |
| This work | 2–7 | 1–10 | 0.08 nH per GHz | 100–4000 |
| Ref. | Frequency (GHz) | Bandwidth (MHz) | Insertion Loss (dB) | Out-of-Band Rejection (dB) | Size (mm2) |
|---|---|---|---|---|---|
| [1] 2023 BAW | 4.73–4.97 | 240 | 0.93 | 25 | 1.1 × 0.75 |
| [5] 2022 BAW | 2.97–3.29 | 324 | 2.2 | 10 | 0.6 × 0.4 |
| [10] 2022 BAW+ passive inductor | 2.02–2.14 | 120 | 2.3 | 40 | 2.5 × 1.5 |
| This work BAW+ active inductor | 4.55–5.05 | 500 | 1.1 | 35 | 0.83 × 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Pan, J.; Gao, F.; Xuan, W.; Jin, H.; Luo, J.; Dong, S. Miniaturized BAW Filter for Wide Band Application Based on High-Q Factor Active Inductor. Micromachines 2025, 16, 616. https://doi.org/10.3390/mi16060616
Xu Z, Pan J, Gao F, Xuan W, Jin H, Luo J, Dong S. Miniaturized BAW Filter for Wide Band Application Based on High-Q Factor Active Inductor. Micromachines. 2025; 16(6):616. https://doi.org/10.3390/mi16060616
Chicago/Turabian StyleXu, Zhencheng, Jiabei Pan, Feng Gao, Weipeng Xuan, Hao Jin, Jikui Luo, and Shurong Dong. 2025. "Miniaturized BAW Filter for Wide Band Application Based on High-Q Factor Active Inductor" Micromachines 16, no. 6: 616. https://doi.org/10.3390/mi16060616
APA StyleXu, Z., Pan, J., Gao, F., Xuan, W., Jin, H., Luo, J., & Dong, S. (2025). Miniaturized BAW Filter for Wide Band Application Based on High-Q Factor Active Inductor. Micromachines, 16(6), 616. https://doi.org/10.3390/mi16060616











