Mechanical Properties of Medical Microbubbles and Echogenic Liposomes—A Review
Abstract
1. Introduction
2. Historical Overview of the Major Developments in Modeling of Microbubble Physics
3. Radial Dynamic Response
3.1. Rayleigh–Plesset Equation
- The MB is filled with a compressed ideal gas.
- The MB motion is symmetrical.
- The wavelength of the excitation wave is much longer than the MB radius.
Modified Rayleigh–Plesset Equation
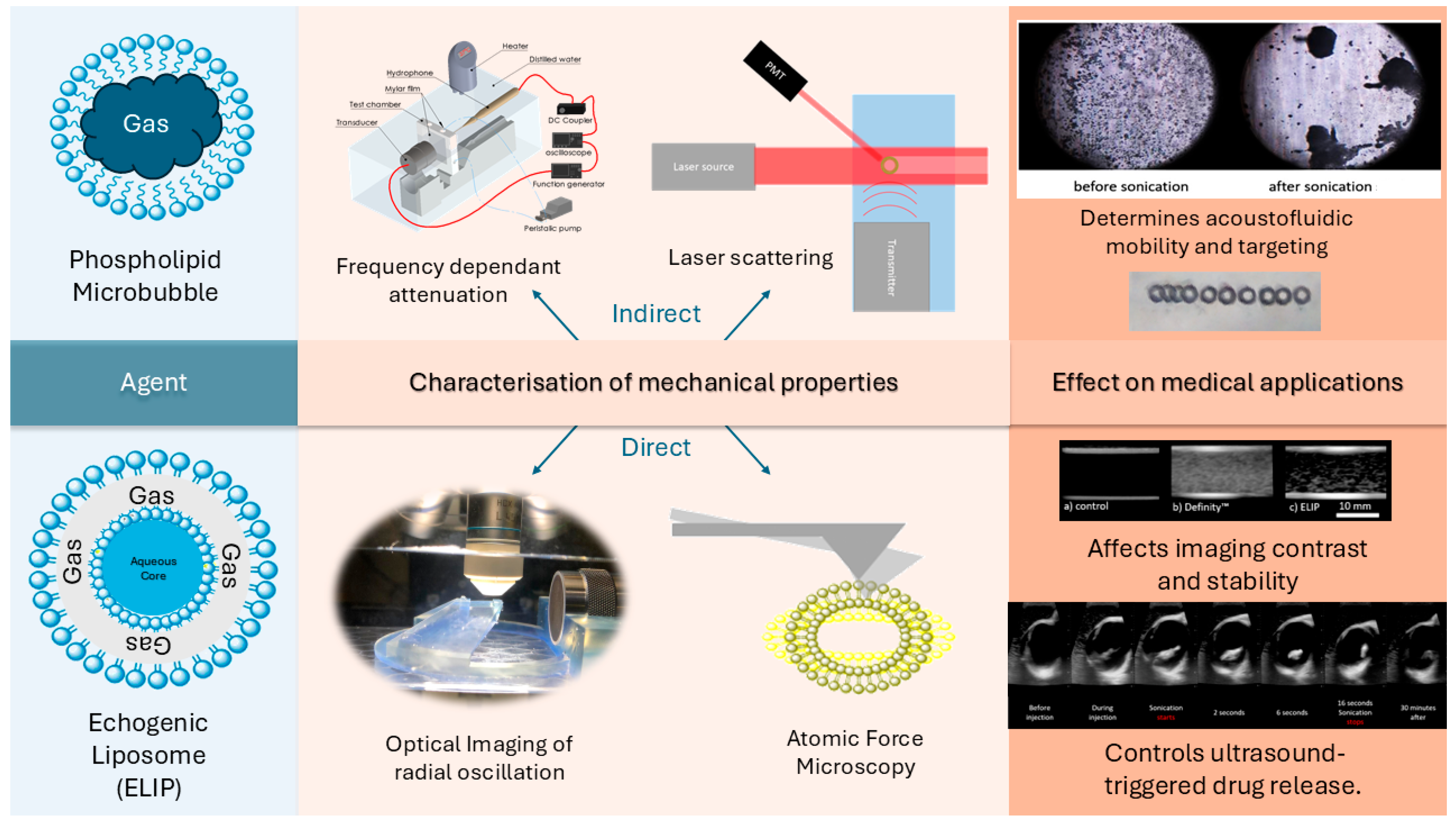
4. Characterization Methods
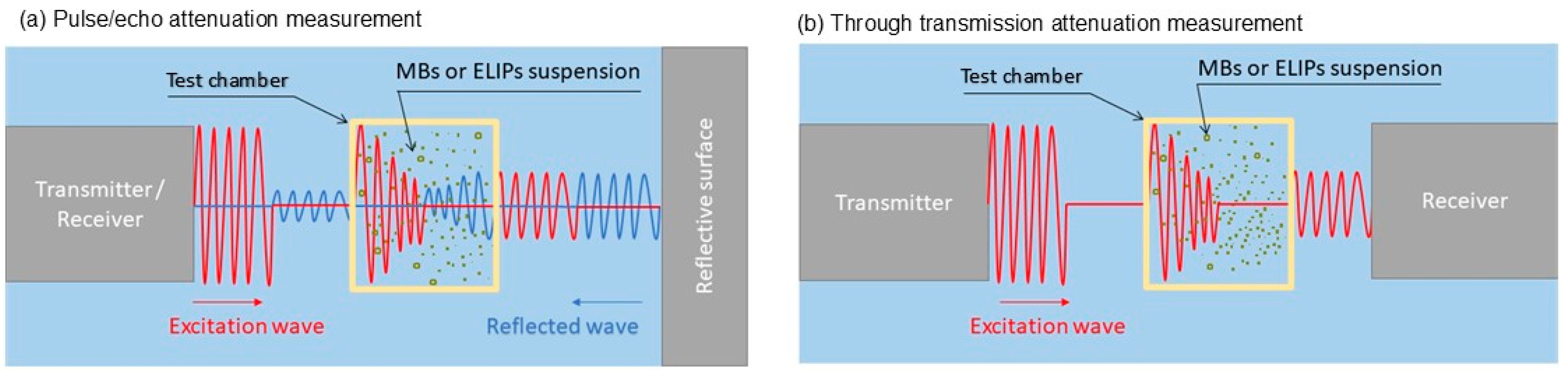
4.1. Frequency-Dependent Attenuation
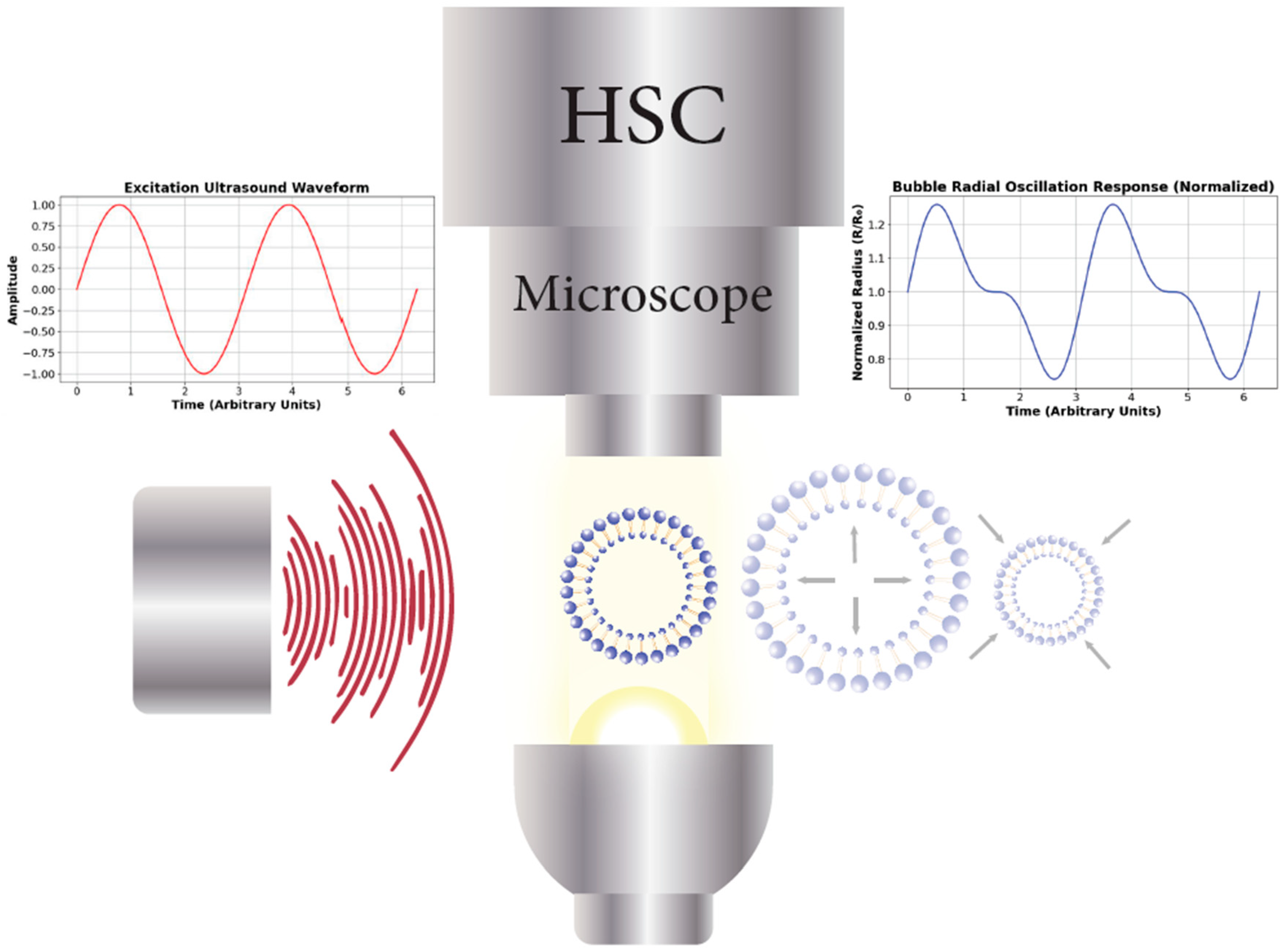
4.2. Optical Acquisition
| Study | Agents | (kPa) | (MHz) | Model | Radius (µm) | Elasticity | Viscosity |
|---|---|---|---|---|---|---|---|
| [61] | MP1950 | 310 | 2.4 | Morgan et al. | 2.6 | = 4 nm Pa s | |
| 360 | 2.4 | 2.6 | = 3.4 nm Pa s | ||||
| 360 | 2.4 | 1 | = 0.6 nm Pa s | ||||
| [68] | BR-14 | ≤40 | 2.5 | Marmottant | 1.5–5.2 | kg/s * | |
| [68] fitted by [69] | BR-14 | 40 | 2.5 | Marmottant | 1.7 | ||
| Sarkar | |||||||
| Hoff | |||||||
| [63] | EggPC:DPPC:DPPE:DPPG:CH (27:42:8:8:15)-(Air) | 250 | Marmottant | 1.5 | |||
| 4 | 2.3 | ||||||
| 3 | |||||||
| [67] | Sonovue™ | 40–80 | 0.5 | Hoff | 6.5 | ||
| 8.1 | |||||||
| 9.3 | |||||||
| 10.3 | |||||||
| 11 |
4.3. Light Scattering
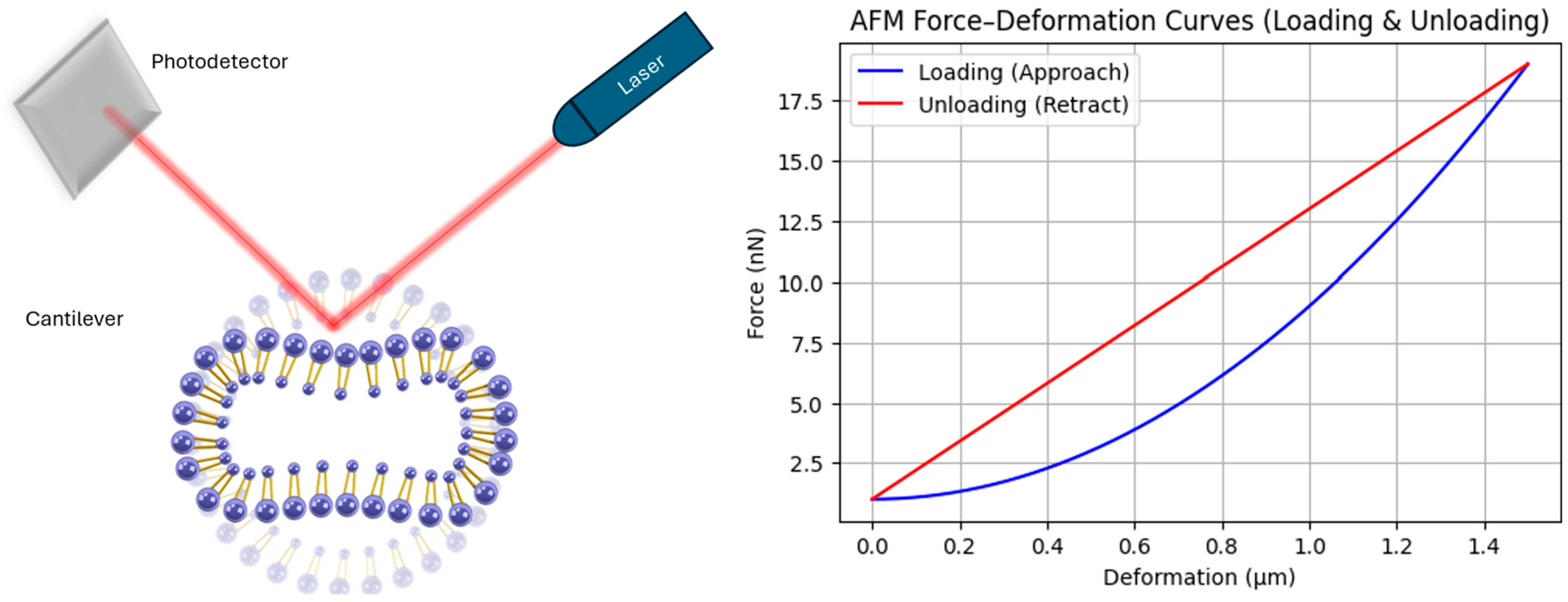
4.4. Atomic Force Microscopy
5. Effect of Temperature on Shell Elastic Properties
6. Effect of Chemical Composition on Shell Properties
6.1. Importance of a Composition-Based Predictive Model
6.2. Proposed Approach to Developing the Model
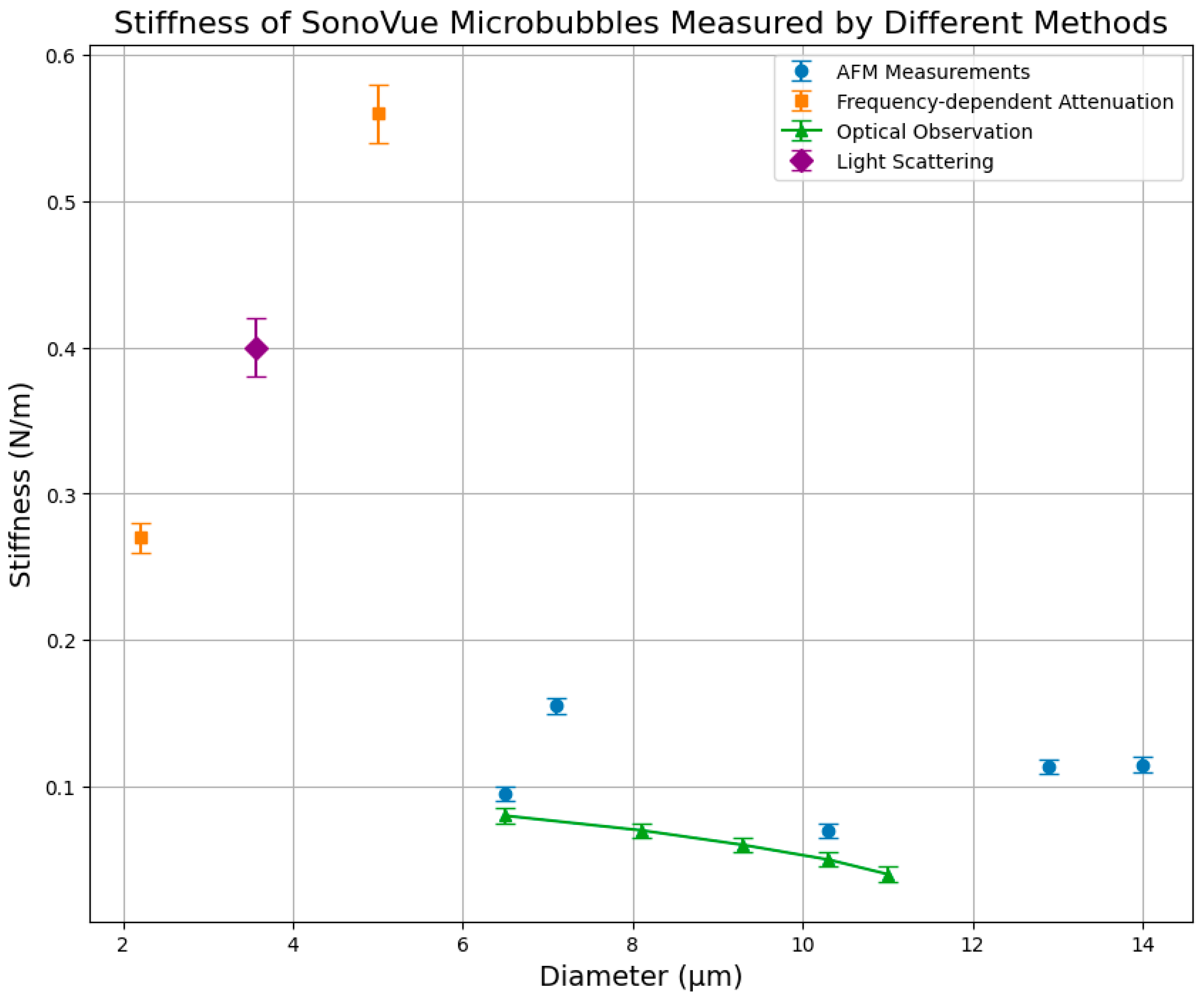
7. Correlation of Microbubble Mechanical Properties Across Studies
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, K.; Lee, J.; Park, M.-H. Microbubble Delivery Platform for Ultrasound-Mediated Therapy in Brain Cancers. Pharmaceutics 2023, 15, 698. [Google Scholar] [CrossRef] [PubMed]
- Kotopoulis, S.; Postema, M. Microfoam formation in a capillary. Ultrasonics 2010, 50, 260–268. [Google Scholar] [CrossRef]
- Hoff, L.; Sontum, P.C. Acoustic Characterization of Contrast Agents for Medical Ultrasound Imaging; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Sirsi, S.R.; Borden, M.A. Microbubble compositions, properties and biomedical applications. Bubble Sci. Eng. Technol. 2009, 1, 3–17. [Google Scholar] [CrossRef]
- Immordino, M.L.; Dosio, F.; Cattel, L. Stealth liposomes: Review of the basic science, rationale, and clinical applications, existing and potential. Int. J. Nanomed. 2006, 1, 297. [Google Scholar]
- Barnett, S.B.; Ter Haar, G.R.; Ziskin, M.C.; Rott, H.-D.; Duck, F.A.; Maeda, K. International recommendations and guidelines for the safe use of diagnostic ultrasound in medicine. Ultrasound Med. Biol. 2000, 26, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Nelson, T.R.; Fowlkes, J.B.; Abramowicz, J.S.; Church, C.C. Ultrasound biosafety considerations for the practicing sonographer and sonologist. J. Ultrasound Med. 2009, 28, 139–150. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Bouakaz, A. Review of shell models for contrast agent microbubbles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011, 58, 981–993. [Google Scholar] [CrossRef]
- Faez, T.; Emmer, M.; Kooiman, K.; Versluis, M.; van der Steen, A.F.; de Jong, N. 20 years of ultrasound contrast agent modeling. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 60, 7–20. [Google Scholar] [CrossRef]
- Paul, S.; Nahire, R.; Mallik, S.; Sarkar, K. Encapsulated microbubbles and echogenic liposomes for contrast ultrasound imaging and targeted drug delivery. Comput. Mech. 2014, 53, 413–435. [Google Scholar] [CrossRef]
- Roovers, S.; Segers, T.; Lajoinie, G.; Deprez, J.; Versluis, M.; De Smedt, S.C.; Lentacker, I. The role of ultrasound-driven microbubble dynamics in drug delivery: From microbubble fundamentals to clinical translation. Langmuir 2019, 35, 10173–10191. [Google Scholar] [CrossRef]
- El-Hammadi, M.M.; Arias, J.L. An update on liposomes in drug delivery: A patent review (2014–2018). Expert Opin. Ther. Patents 2019, 29, 891–907. [Google Scholar] [CrossRef]
- Tsutsui, J.M.; Xie, F.; Porter, R.T. The use of microbubbles to target drug delivery. Cardiovasc. Ultrasound 2004, 2, 23. [Google Scholar] [CrossRef]
- Bull, J.L. The application of microbubbles for targeted drug delivery. Expert Opin. Drug Deliv. 2007, 4, 475–493. [Google Scholar] [CrossRef]
- Dijkmans, P.; Juffermans, L.; Musters, R.; Vanwamel, A.; Tencate, F.; Vangilst, W.; Visser, C.; Dejong, N.; Kamp, O. Microbubbles and ultrasound: From diagnosis to therapy. Eur. J. Echocardiogr. 2004, 5, 245–256. [Google Scholar] [CrossRef]
- Ferrara, K.; Pollard, R.; Borden, M. Ultrasound microbubble contrast agents: Fundamentals and application to gene and drug delivery. Annu. Rev. Biomed. Eng. 2007, 9, 415–447. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Miyoshi, H.; Nakamura, M. Encapsulated ultrasound microbubbles: Therapeutic application in drug/gene delivery. J. Control. Release 2006, 114, 89–99. [Google Scholar] [CrossRef]
- Bekeredjian, R.; Grayburn, P.A.; Shohet, R.V. Use of ultrasound contrast agents for gene or drug delivery in cardiovascular medicine. J. Am. Coll. Cardiol. 2005, 45, 329–335. [Google Scholar] [CrossRef] [PubMed]
- Delalande, A.; Kotopoulis, S.; Postema, M.; Midoux, P.; Pichon, C. Sonoporation: Mechanistic insights and ongoing challenges for gene transfer. Gene 2013, 525, 191–199. [Google Scholar] [CrossRef] [PubMed]
- Fix, S.M.; Borden, M.A.; Dayton, P.A. Therapeutic gas delivery via microbubbles and liposomes. J. Control. Release 2015, 209, 139–149. [Google Scholar] [CrossRef]
- Rad, I.J.; Chapman, L.; Tupally, K.R.; Veidt, M.; Al-Sadiq, H.; Sullivan, R.; Parekh, H.S. A systematic review of ultrasound-mediated drug delivery to the eye and critical insights to facilitate a timely path to the clinic. Theranostics 2023, 13, 3582–3638. [Google Scholar] [CrossRef]
- Besant, W.H. A Treatise on Hydrostatics and Hydrodynamics; Deighton, Bell: Cambridge, UK, 1859. [Google Scholar]
- Cheeke, J.D.M. Fundamentals and Applications of Ultrasonic Waves; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Lord, R. On the pressure developed in a liquid during the collapse of a spherical cavity. Philos. Mag. 1917, 34, 94–98. [Google Scholar]
- Plesset, M.S. The dynamics of cavitation bubbles. J. Appl. Mech. 1949, 16, 277–282. [Google Scholar] [CrossRef]
- Trilling, L. The collapse and rebound of a gas bubble. J. Appl. Phys. 1952, 23, 14–17. [Google Scholar] [CrossRef]
- Gilmore, F.R. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid; California Institute of Technology: Pasadena, CA, USA, 1952. [Google Scholar]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Church, C.C. The effects of an elastic solid surface layer on the radial pulsations of gas bubbles. J. Acoust. Soc. Am. 1995, 97, 1510–1521. [Google Scholar] [CrossRef]
- Khismatullin, D.B.; Nadim, A. Radial oscillations of encapsulated microbubbles in viscoelastic liquids. Phys. Fluids 2002, 14, 3534–3557. [Google Scholar] [CrossRef]
- Gramiak, R.; Shah, P.M. Echocardiography of the aortic root. Investig. Radiol. 1968, 3, 356–366. [Google Scholar] [CrossRef]
- Roy, R.A.; Church, C.C.; Calabrese, A. Cavitation produced by short pulses of ultrasound. In Proceedings of the 12th International Symposium on Nonlinear Acoustics, Austin, TX, USA, 27–31 August 1990; pp. 476–481. [Google Scholar]
- de Jong, N.; Hoff, L. Ultrasound scattering properties of Albunex microspheres. Ultrasonics 1993, 31, 175–181. [Google Scholar] [CrossRef]
- Leighton, T. The Acoustic Bubble; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Manasseh, R. Acoustic bubbles, acoustic streaming, and cavitation microstreaming. In Handbook of Ultrasonics and Sonochemistry; Springer: Singapore, 2016; pp. 1–36. [Google Scholar]
- Alehossein, H.; Qin, Z. Numerical analysis of Rayleigh–Plesset equation for cavitating water jets. Int. J. Numer. Methods Eng. 2007, 72, 780–807. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Sinelshchikov, D.I. Analytical solutions of the Rayleigh equation for empty and gas-filled bubble. J. Phys. A Math. Theor. 2014, 47, 405202. [Google Scholar] [CrossRef]
- Leong, T.; Ashokkumar, M.; Kentish, S. The growth of bubbles in an acoustic field by rectified diffusion. In Handbook of Ultrasonics and Sonochemistry; Springer: Singapore, 2016; Volume 10, pp. 978–981. [Google Scholar]
- Chatterjee, D.; Sarkar, K. A Newtonian rheological model for the interface of microbubble contrast agents. Ultrasound Med. Biol. 2003, 29, 1749–1757. [Google Scholar] [CrossRef]
- Gorce, J.-M.; Arditi, M.; Schneider, M. Influence of bubble size distribution on the echogenicity of ultrasound contrast agents: A study of SonoVue™. Investig. Radiol. 2000, 35, 661–671. [Google Scholar] [CrossRef]
- Medwin, H. Counting bubbles acoustically: A review. Ultrasonics 1977, 15, 7–13. [Google Scholar] [CrossRef]
- Coakley, W.T.; Nyborg, W. Cavitation; dynamics of gas bubbles; applications. Ultrasound Its Appl. Med. Biol. 1978, 3, 77–159. [Google Scholar]
- de Jong, N.; Hoff, L.; Skotland, T.; Bom, N. Absorption and scatter of encapsulated gas filled microspheres: Theoretical considerations and some measurements. Ultrasonics 1992, 30, 95–103. [Google Scholar] [CrossRef]
- Faez, T.; Goertz, D.; De Jong, N. Characterization of Definity™ ultrasound contrast agent at frequency range of 5–15 MHz. Ultrasound Med. Biol. 2011, 37, 338–342. [Google Scholar] [CrossRef] [PubMed]
- Helfield, B.L.; Goertz, D.E. Nonlinear resonance behavior and linear shell estimates for Definity™ and MicroMarker™ assessed with acoustic microbubble spectroscopy. J. Acoust. Soc. Am. 2013, 133, 1158–1168. [Google Scholar] [CrossRef] [PubMed]
- Overvelde, M.; Garbin, V.; Sijl, J.; Dollet, B.; de Jong, N.; Lohse, D.; Versluis, M. Nonlinear shell behavior of phospholipid-coated microbubbles. Ultrasound Med. Biol. 2010, 36, 2080–2092. [Google Scholar] [CrossRef]
- Alsadiq, H.; Tupally, K.; Vogel, R.; Kokil, G.; Parekh, H.S.; Veidt, M. Shell properties and concentration stability of acoustofluidic delivery agents. Phys. Eng. Sci. Med. 2021, 44, 79–91. [Google Scholar] [CrossRef]
- Chen, Q.; Zagzebski, J.; Wilson, T.; Stiles, T. Pressure-dependent attenuation in ultrasound contrast agents. Ultrasound Med. Biol. 2002, 28, 1041–1051. [Google Scholar] [CrossRef]
- Tang, M.-X.; Eckersley, R.J.; Noble, J. Pressure-dependent attenuation with microbubbles at low mechanical index. Ultrasound Med. Biol. 2005, 31, 377–384. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.-X.; Eckersley, R.J. Frequency and pressure dependent attenuation and scattering by microbubbles. Ultrasound Med. Biol. 2007, 33, 164–168. [Google Scholar] [CrossRef]
- Acconcia, C.N.; Wright, A.; Goertz, D.E. Translational dynamics of individual microbubbles with millisecond scale ultrasound pulses. J. Acoust. Soc. Am. 2018, 144, 2859–2870. [Google Scholar] [CrossRef] [PubMed]
- Alsadiq, H.; Reddy, K.; Parekh, H.; Veidt, M. Influence of acoustofluidic parameters on velocity streaming of sonicated medical microbubbles. In Proceedings of the Australian Acoustical Society Annual Conference, AAS 2018, Adelaide, Australia, 6–9 November 2018. pp. 22–29.
- Goertz, D.E.; de Jong, N.; van der Steen, A.F. Attenuation and size distribution measurements of Definity™ and manipulated Definity™ populations. Ultrasound Med. Biol. 2007, 33, 1376–1388. [Google Scholar] [CrossRef] [PubMed]
- Shekhar, H.; Smith, N.J.; Raymond, J.L.; Holland, C.K. Effect of temperature on the size distribution, shell properties, and stability of Definity®. Ultrasound Med. Biol. 2018, 44, 434–446. [Google Scholar] [CrossRef]
- Raymond, J.L.; Haworth, K.J.; Bader, K.B.; Radhakrishnan, K.; Griffin, J.K.; Huang, S.-L.; McPherson, D.D.; Holland, C.K. Broadband attenuation measurements of phospholipid-shelled ultrasound contrast agents. Ultrasound Med. Biol. 2014, 40, 410–421. [Google Scholar] [CrossRef]
- Shi, W.T.; Forsberg, F.; Hall, A.L.; Chiao, R.Y.; Liu, J.-B.; Miller, S.; Thomenius, K.E.; Wheatley, M.A.; Goldberg, B.B. Subharmonic imaging with microbubble contrast agents: Initial results. Ultrason. Imaging 1999, 21, 79–94. [Google Scholar] [CrossRef]
- Frinking, P.J.; de Jong, N. Acoustic modeling of shell-encapsulated gas bubbles. Ultrasound Med. Biol. 1998, 24, 523–533. [Google Scholar] [CrossRef]
- Sarkar, K.; Shi, W.T.; Chatterjee, D.; Forsberg, F. Characterization of ultrasound contrast microbubbles using in vitro experiments and viscous and viscoelastic interface models for encapsulation. J. Acoust. Soc. Am. 2005, 118, 539–550. [Google Scholar] [CrossRef]
- Varanasi, U.; Apfel, R.E.; Malins, D.C. A novel microtechnique for the measurement of acoustic properties of lipids. Chem. Phys. Lipids 1977, 19, 179–184. [Google Scholar] [CrossRef]
- Hernandez, C.; Lilly, J.L.; Nittayacharn, P.; Hadley, J.; Coyne, R.; Kolios, M.; Exner, A.A. Ultrasound signal from sub-micron lipid-coated bubbles. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Morgan, K.; Allen, J.; Dayton, P.; Chomas, J.; Klibaov, A.; Ferrara, K. Experimental and theoretical evaluation of microbubble behavior: Effect of transmitted phase and bubble size. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2000, 47, 1494–1509. [Google Scholar] [CrossRef]
- Raymond, J.L.; Luan, Y.; Peng, T.; Huang, S.-L.; McPherson, D.D.; Versluis, M.; de Jong, N.; Holland, C.K. Loss of gas from echogenic liposomes exposed to pulsed ultrasound. Phys. Med. Biol. 2016, 61, 8321–8339. [Google Scholar] [CrossRef] [PubMed]
- Raymond, J.L.; Luan, Y.; van Rooij, T.; Kooiman, K.; Huang, S.-L.; McPherson, D.D.; Versluis, M.; de Jong, N.; Holland, C.K. Impulse response method for characterization of echogenic liposomes. J. Acoust. Soc. Am. 2015, 137, 1693–1703. [Google Scholar] [CrossRef] [PubMed]
- Chetty, K.; Stride, E.; Sennoga, C.A.; Hajnal, J.V.; Eckersley, R.J. High-speed optical observations and simulation results of SonoVue microbubbles at low-pressure insonation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2008, 55, 1333–1342. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Haac, J.F.; Dayton, P.A. Modeling of nonlinear viscous stress in encapsulating shells of lipid-coated contrast agent microbubbles. Ultrasonics 2009, 49, 269–275. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.C.; Wu, S.-Y.; Finan, J.D.; Morrison, B.; Konofagou, E.E. An experimental study on the stiffness of size-isolated microbubbles using atomic force microscopy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013, 60, 524–534. [Google Scholar] [CrossRef]
- Vos, H.; Emmer, M.; de Jong, N. Oscillation of single microbubbles at room versus body temperature. In Proceedings of the 2008 IEEE Ultrasonics Symposium (IUS), Beijing, China, 2–5 November 2008; pp. 982–984. [Google Scholar]
- Van der Meer, S.M.; Dollet, B.; Voormolen, M.M.; Chin, C.T.; Bouakaz, A.; de Jong, N.; Versluis, M.; Lohse, D. Microbubble spectroscopy of ultrasound contrast agents. J. Acoust. Soc. Am. 2007, 121, 648–656. [Google Scholar] [CrossRef] [PubMed]
- Tu, J.; Guan, J.; Qiu, Y.; Matula, T.J. Estimating the shell parameters of SonoVue® microbubbles using light scattering. J. Acoust. Soc. Am. 2009, 126, 2954–2962. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Bouakaz, A. Acoustic microstreaming around a gas bubble. J. Acoust. Soc. Am. 2010, 127, 703–709. [Google Scholar] [CrossRef]
- Guan, J.; Matula, T.J. Using light scattering to measure the response of individual ultrasound contrast microbubbles subjected to pulsed ultrasound in vitro. J. Acoust. Soc. Am. 2004, 116, 2832–2842. [Google Scholar] [CrossRef]
- Tu, J.; Swalwell, J.E.; Giraud, D.; Cui, W.; Chen, W.; Matula, T.J. Microbubble sizing and shell characterization using flow cytometry. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011, 58, 955–963. [Google Scholar] [CrossRef] [PubMed]
- Sboros, V.; Glynos, E.; Pye, S.; Moran, C.; Butler, M.; Ross, J.; Short, R.; McDicken, W.; Koutsos, V. Nanointerrogation of ultrasonic contrast agent microbubbles using atomic force microscopy. Ultrasound Med. Biol. 2006, 32, 579–585. [Google Scholar] [CrossRef] [PubMed]
- Takechi-Haraya, Y.; Goda, Y.; Sakai-Kato, K. Atomic force microscopy study on the stiffness of nanosized liposomes containing charged lipids. Langmuir 2018, 34, 7805–7812. [Google Scholar] [CrossRef]
- Shafi, A.S.; McClements, J.; Albaijan, I.; Abou-Saleh, R.H.; Moran, C.; Koutsos, V. Probing phospholipid microbubbles by atomic force microscopy to quantify bubble mechanics and nanostructural shell properties. Colloids Surf. B Biointerfaces 2019, 181, 506–515. [Google Scholar] [CrossRef]
- Mitkova, D.; Marukovich, N.; Ermakov, Y.A.; Vitkova, V. Bending rigidity of phosphatidylserine-containing lipid bilayers in acidic aqueous solutions. Colloids Surf. A Physicochem. Eng. Asp. 2014, 460, 71–78. [Google Scholar] [CrossRef]
- Borden, M.A.; Longo, M.L. Dissolution behavior of lipid monolayer-coated, air-filled microbubbles: Effect of lipid hydrophobic chain length. Langmuir 2002, 18, 9225–9233. [Google Scholar] [CrossRef]
- Borden, M.A.; Song, K.-H. Reverse engineering the ultrasound contrast agent. Adv. Colloid Interface Sci. 2018, 262, 39–49. [Google Scholar] [CrossRef]
- AlSadiq, H.; Tupally, K.; Vogel, R.; Parekh, H.S.; Veidt, M. Multi-physics study of acoustofluidic delivery agents’ clustering behavior. Phys. Med. Biol. 2022, 67, 015002. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.C.; Crist, R.M.; Clogston, J.D.; McNeil, S.E. Zeta potential: A case study of cationic, anionic, and neutral liposomes. Anal. Bioanal. Chem. 2017, 409, 5779–5787. [Google Scholar] [CrossRef]
- Vogel, R.; Pal, A.K.; Jambhrunkar, S.; Patel, P.; Thakur, S.S.; Reátegui, E.; Parekh, H.S.; Saá, P.; Stassinopoulos, A.; Broom, M.F. High-resolution single particle zeta potential characterisation of biological nanoparticles using tunable resistive pulse sensing. Sci. Rep. 2017, 7, 17479. [Google Scholar] [CrossRef]
- Ja’Afar, F.; Leow, C.H.; Garbin, V.; Sennoga, C.A.; Tang, M.-X.; Seddon, J.M. Surface charge measurement of SonoVue, Definity and Optison: A comparison of laser doppler electrophoresis and micro-electrophoresis. Ultrasound Med. Biol. 2015, 41, 2990–3000. [Google Scholar] [CrossRef] [PubMed]
- Petrache, H.I.; Tristram-Nagle, S.; Gawrisch, K.; Harries, D.; Parsegian, V.A.; Nagle, J.F. Structure and fluctuations of charged phosphatidylserine bilayers in the absence of salt. Biophys. J. 2004, 86, 1574–1586. [Google Scholar] [CrossRef] [PubMed]
- Eloy, J.O.; de Souza, M.C.; Petrilli, R.; Barcellos, J.P.A.; Lee, R.J.; Marchetti, J.M. Liposomes as carriers of hydrophilic small molecule drugs: Strategies to enhance encapsulation and delivery. Colloids Surfaces B Biointerfaces 2014, 123, 345–363. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Ferrara, K.W. Acoustic response of compliable microvessels containing ultrasound contrast agents. Phys. Med. Biol. 2006, 51, 5065–5088. [Google Scholar] [CrossRef]
- Dollet, B.; van der Meer, S.M.; Garbin, V.; de Jong, N.; Lohse, D.; Versluis, M. Nonspherical oscillations of ultrasound contrast agent microbubbles. Ultrasound Med. Biol. 2008, 34, 1465–1473. [Google Scholar] [CrossRef]
- Sijl, J.; Dollet, B.; Overvelde, M.; Garbin, V.; Rozendal, T.; de Jong, N.; Lohse, D.; Versluis, M. Subharmonic behavior of phospholipid-coated ultrasound contrast agent microbubbles. J. Acoust. Soc. Am. 2010, 128, 3239–3252. [Google Scholar] [CrossRef]

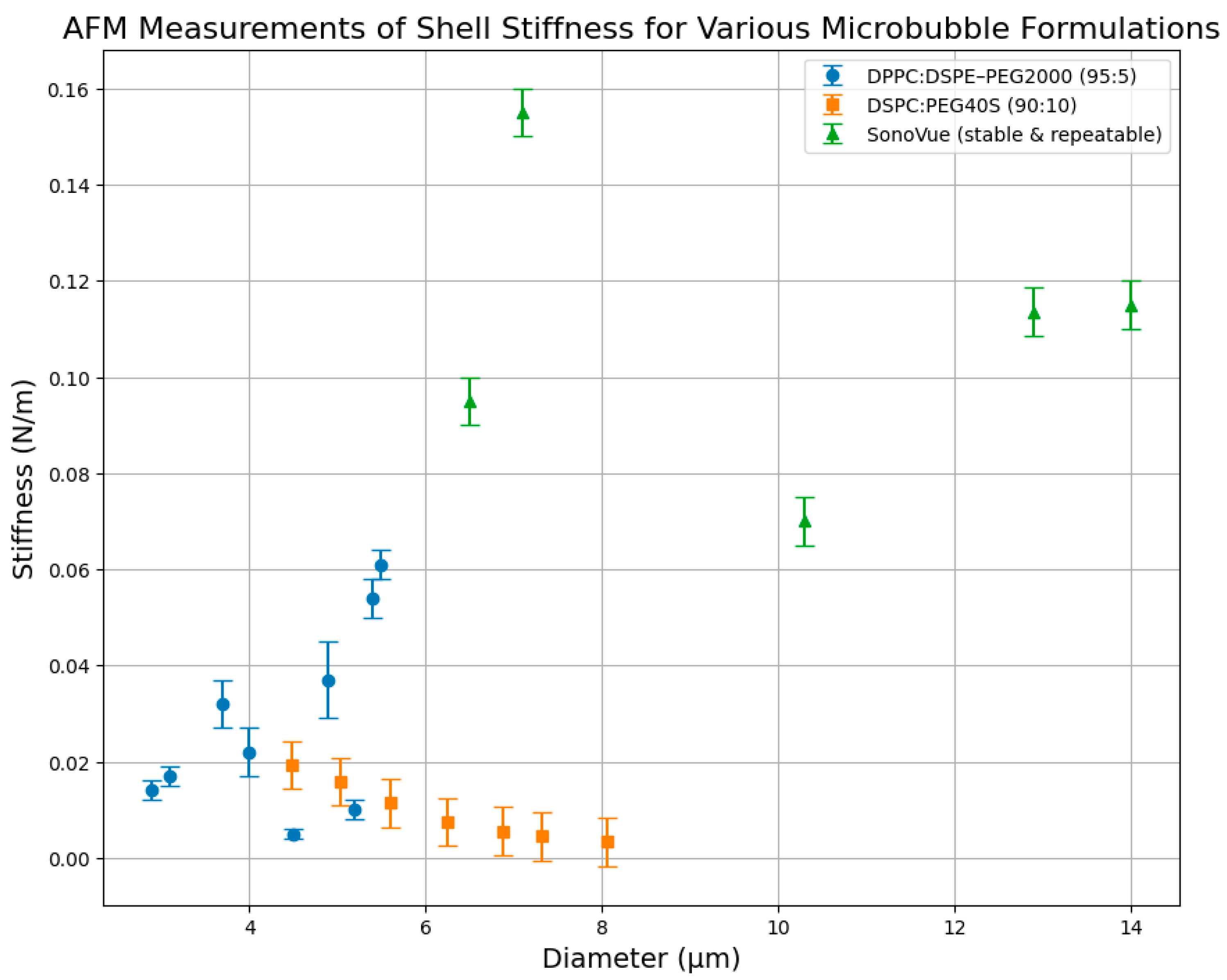
| Study | Agents | (MHz) | (kPa) | T (°C) | Method | Dilution | (N/m) | (kg/s) |
|---|---|---|---|---|---|---|---|---|
| [33] | Albunex™ (Performed on different size filtered dilutions and single average estimation is calculated.) | 0.7–12.5 | NR | RT | P/E | 1:20,000 | 8 | 4 |
| P/E 12 µm filtered | 1:10,000 | |||||||
| P/E 8 µm filtered | 1:10,000 | |||||||
| P/E 5 µm filtered | 1:3500 | |||||||
| P/E 3 µm filtered | 1:1400 | |||||||
| [53] | Definity™ | 13–29 | RT | P/E 2 µm filtered | 1:15,000 | 1.51 | 0.016 | |
| [53] | Definity™ | 12–28 | RT | P/E | 1:15,000 | 1.71 | ||
| [44] | Definity™ | 7–15 | RT | TT | 1:15,000 | 1.64 | 0.15 | |
| [44] | Definity™ | 15–25 | RT | TT | 1:15,000 | |||
| [54] | Definity™ | 2–25 | 25 | TT | 1:2000 | |||
| [54] | Definity™ | 2–25 | 37 | TT | 1:2000 | |||
| [55] | Definity™ | 2–25 | 25 | TT | 1:2000 | |||
| [55] | Definity™ | 2–25 | 37 | TT | 1:2000 | |||
| [47] | Definity™ | 2–20 | 25 | TT | 1:2000 | 1.53 ± 0.08 | 1.51 ± 0.12 | |
| [47] | Definity™ | 2–20 | 37 | TT | 1:2000 | 1.18 ± 0.16 | 1.09 ± 0.2 | |
| [40] | SonoVue™ | 0.8–3 | RT | P/E | 1:2000 | 1.1 | 0.27 | |
| [40] | SonoVue™ | 3–7 | RT | P/E (dec 10′) | 1:1000 | 1.1 | 0.56 | |
| [3] | Sonazoid™ | 1.5–8 | - | RT | P/E | - | ||
| [55] | MicroMarker™ | 2–25 | 25 | TT | 1:200 | 1.20 ± 0.06 | 0.62 ± 0.03 | |
| [55] | MicroMarker™ | 2–25 | 37 | TT | 1:200 | 1.90 ± 0.05 | 0.87 ± 0.02 | |
| [55] | EggPC:DPPE: DPPG:CH (69:8:8:15)-(Air) | 2–25 | 25 | TT | 1:200 | 1.13 ± 0.13 | 0.82 ± 0.04 | |
| [55] | EggPC:DPPE: DPPG:CH (69:8:8:15)-(Air) | 2–25 | 37 | TT | 1:200 | 1.49 ± 0.20 | 1.41 ± 0.07 | |
| [55] | EggPC:DPPC:DPPE:DPPG:CH (27:42:8:8:15)-(Air) | 2–25 | 25 | TT | 1:200 | 1.98 ± 0.10 | 0.41 ± 0.03 | |
| [55] | EggPC:DPPC:DPPE:DPPG:CH (27:42:8:8:15)-(Air) | 2–25 | 37 | TT | 1:200 | 3.10 ± 0.25 | 1.01 ± 0.07 | |
| [55] | DPPC:DOPC:DPPG:CH (46:24:24:6)-(Air) | 2–25 | 25 | TT | 1:200 | 3.69 ± 0.76 | 1.88 ± 0.23 | |
| [55] | DPPC:DOPC:DPPG:CH (46:24:24:6)-(Air) | 2–25 | 25 | TT | 1:200 | 5.16 ± 0.37 | 2.09 ± 0.10 | |
| [47] | DPPC:DSPE-PEG2000 (94:6)-(C3F8) | 2–20 | 25 | TT | 1:20 | 0.11 ± 0.02 | 0.31 ± 0.03 | |
| [47] | DPPC:DSPE-PEG2000 (94:6)-(C3F8) | 2–20 | 37 | TT | 1:20 | 0.15 ± 0.01 | 0.29 ± 0.01 |
| MBs | (ms Pa) | (N/m) |
|---|---|---|
| Albunex™ | 0.05 | 0.78 |
| Optison™ | 0.08 | 0.9 |
| Quantison™ | 4.24 | 38.34 |
| Sonazoid™ | 0.01 | 0.6 |
| Study | Agents | (kPa) | (MHz) | Radius (µm) | Model | Elasticity | Viscosity |
|---|---|---|---|---|---|---|---|
| [71] | Optison™ | 1.8 | 1.5 | Morgan et al. | Assumed | = 6 nm Pa s | |
| Sonazoid™ | 1.8 | 1.1 | Morgan et al. | = 2 nm Pa s | |||
| [69] | SonoVue™ | 150 | 2.5 | 1.78 | Marmottant | ||
| Sarkar | |||||||
| Hoff | |||||||
| [72] | Definity™ | 308 | 1 | 1.18 | Marmottant |
| Influencing Factor | Property | Frequency-Dependent Attenuation | Optical Observation | AFM | Light Scattering |
|---|---|---|---|---|---|
| Radius | Stiffness | Confirmed inverse relationship [40,44,77,82] | Confirmed inverse relationship [62,63,64] | Confirmed inverse relationship [66,73,75,76] | Confirmed inverse relationship [69] |
| Radius | Friction | Weakly explored; limited evidence [44,68,70] | Not extensively explored | Not extensively explored | Not extensively explored |
| Temperature | Stiffness | Confirmed inverse relationship [44,55] | Limited exploration, some inconsistency [62,63,80] | Not extensively explored | Not extensively explored |
| Temperature | Friction | Weak/inconclusive [44,68,70] | Not extensively explored | Not extensively explored | Not extensively explored |
| Frequency | Stiffness | Frequency-dependent increase clearly observed [40,44,77,82] | Not extensively explored | Not extensively explored | Not extensively explored |
| Frequency | Friction | Frequency-dependent increase observed [40,44,68,70] | Not extensively explored | Not extensively explored | Not extensively explored |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsadiq, H.; Alhay, Z. Mechanical Properties of Medical Microbubbles and Echogenic Liposomes—A Review. Micromachines 2025, 16, 588. https://doi.org/10.3390/mi16050588
Alsadiq H, Alhay Z. Mechanical Properties of Medical Microbubbles and Echogenic Liposomes—A Review. Micromachines. 2025; 16(5):588. https://doi.org/10.3390/mi16050588
Chicago/Turabian StyleAlsadiq, Hussain, and Zahra Alhay. 2025. "Mechanical Properties of Medical Microbubbles and Echogenic Liposomes—A Review" Micromachines 16, no. 5: 588. https://doi.org/10.3390/mi16050588
APA StyleAlsadiq, H., & Alhay, Z. (2025). Mechanical Properties of Medical Microbubbles and Echogenic Liposomes—A Review. Micromachines, 16(5), 588. https://doi.org/10.3390/mi16050588





