Modeling and Validation of Material Removal Based on Rheological Behavior Under Dynamic-Viscosity Nonlinear Coupling Effects
Abstract
1. Introduction
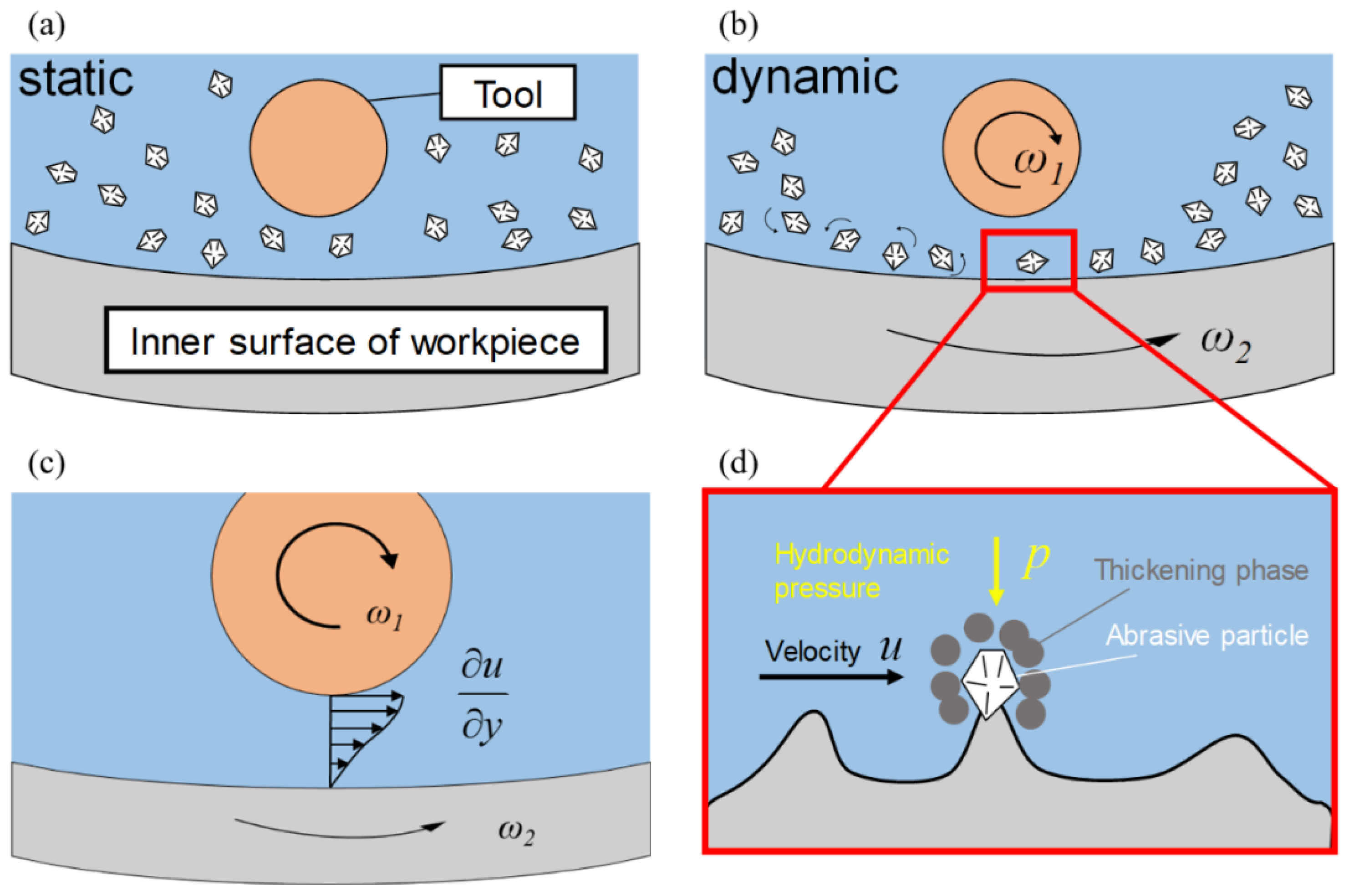
2. Principle of Dynamic-Viscous Shear-Thickening Polishing
2.1. Assumptions
- (1)
- The dispersive phase and abrasives are uniformly distributed in the liquid. The transition from one control point to another is continuous, and the analysis can be conducted using infinitesimal methods. Discontinuities only occur at the boundaries, consistent with the continuous medium model.
- (2)
- The properties of the material (including viscosity) may vary spatially, but such changes occur gradually, reflected in the spatial dependence of material properties in the continuous medium theory equations.
- (3)
- Viscous forces dominate, while inertial forces can be neglected. Additionally, there is no relative motion between the thickened and solidified dispersive phase and the abrasives.
- (4)
- The surface tension of the slurry is neglected, and due to the relatively short processing time in this experiment, temperature rise caused by friction and the evaporation of the liquid are ignored (according to a previous study) [37].
- (5)
- The slurry is incompressible and isotropic; thus, the computational fluid dynamics is based on pressure solutions.
- (6)
- Due to the high viscosity and the small thickness of the polishing film, pressure variation along the thickness direction is negligible.
2.2. Rheological Performance
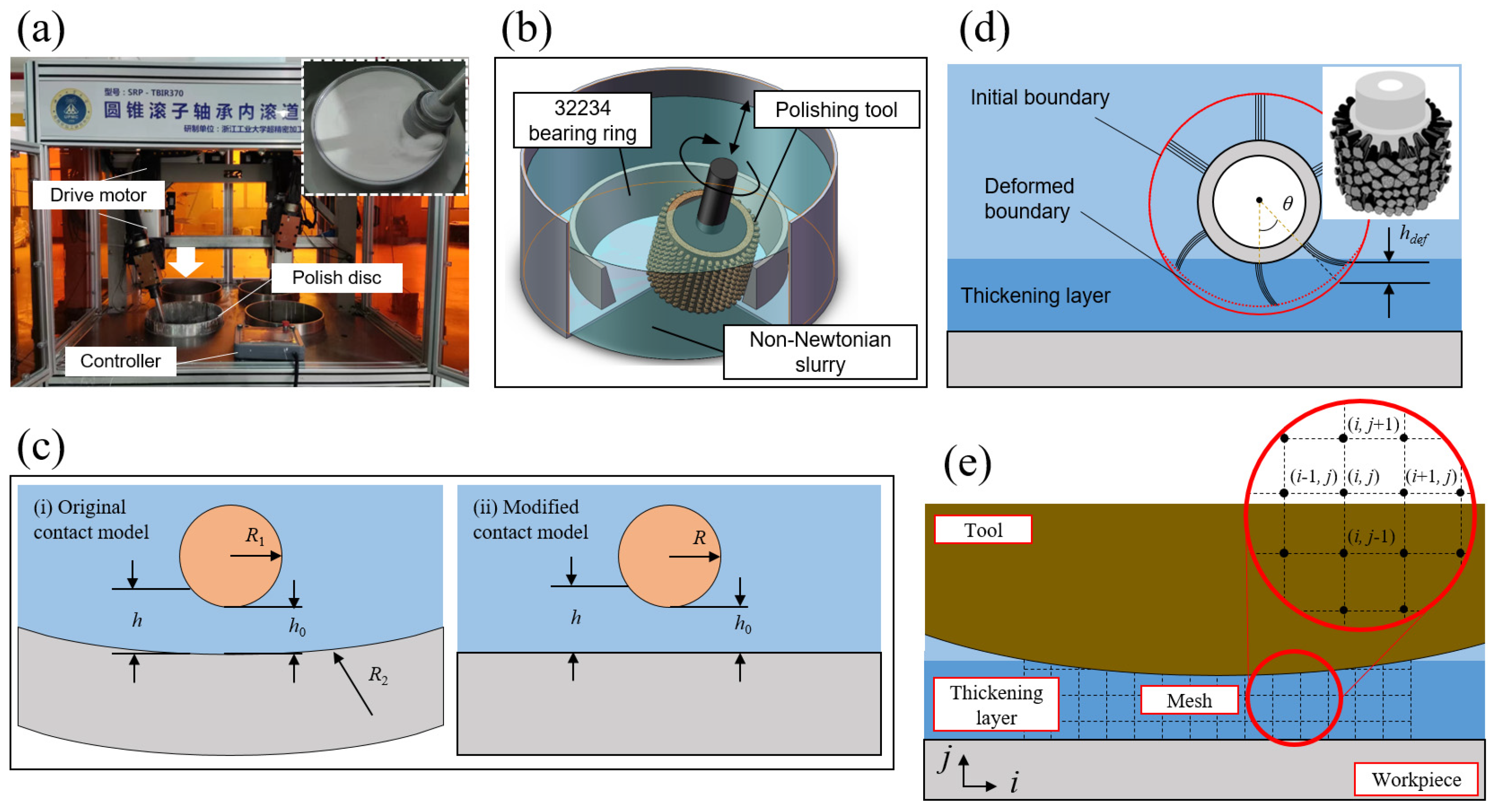
2.3. Machining System
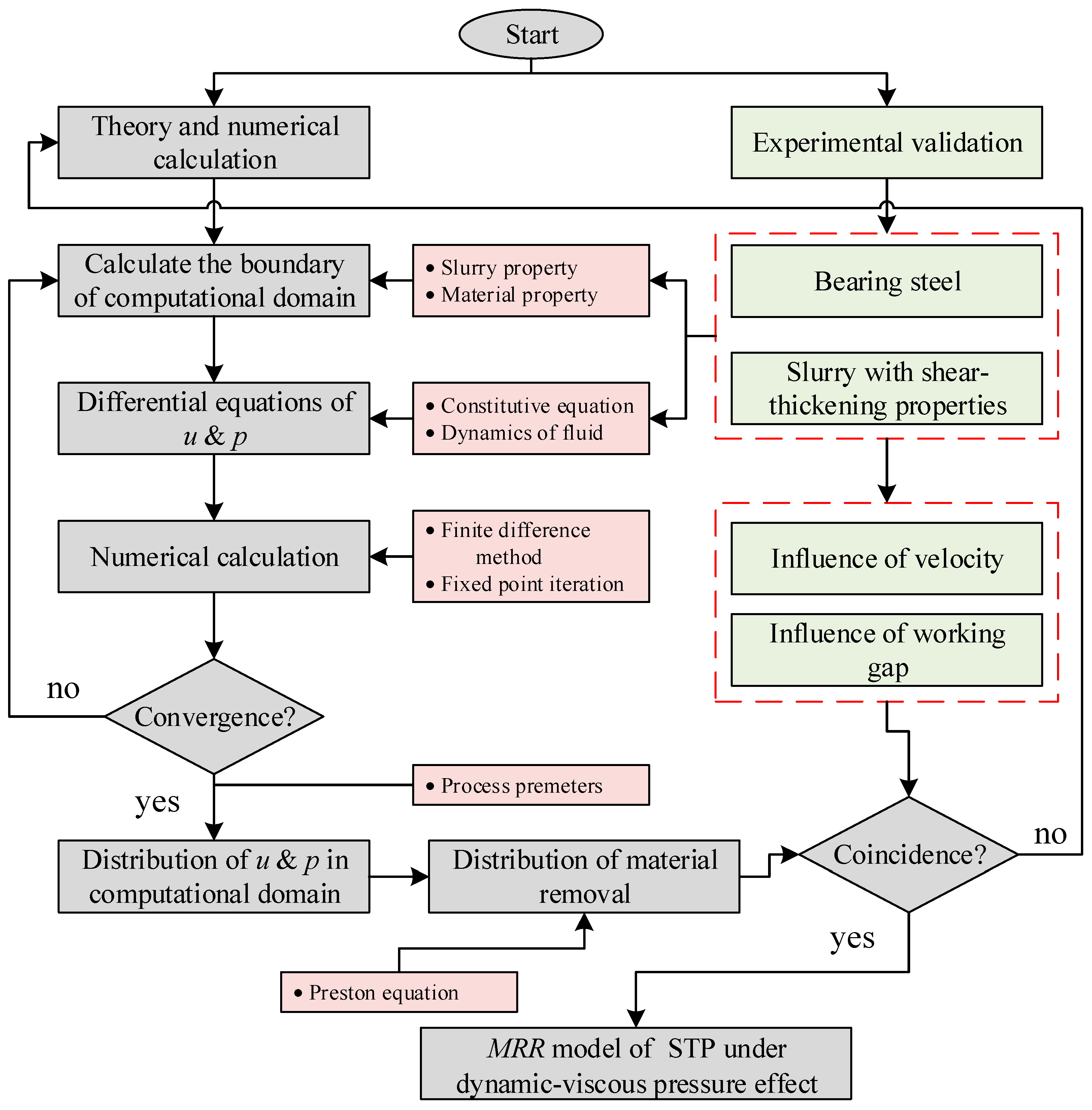
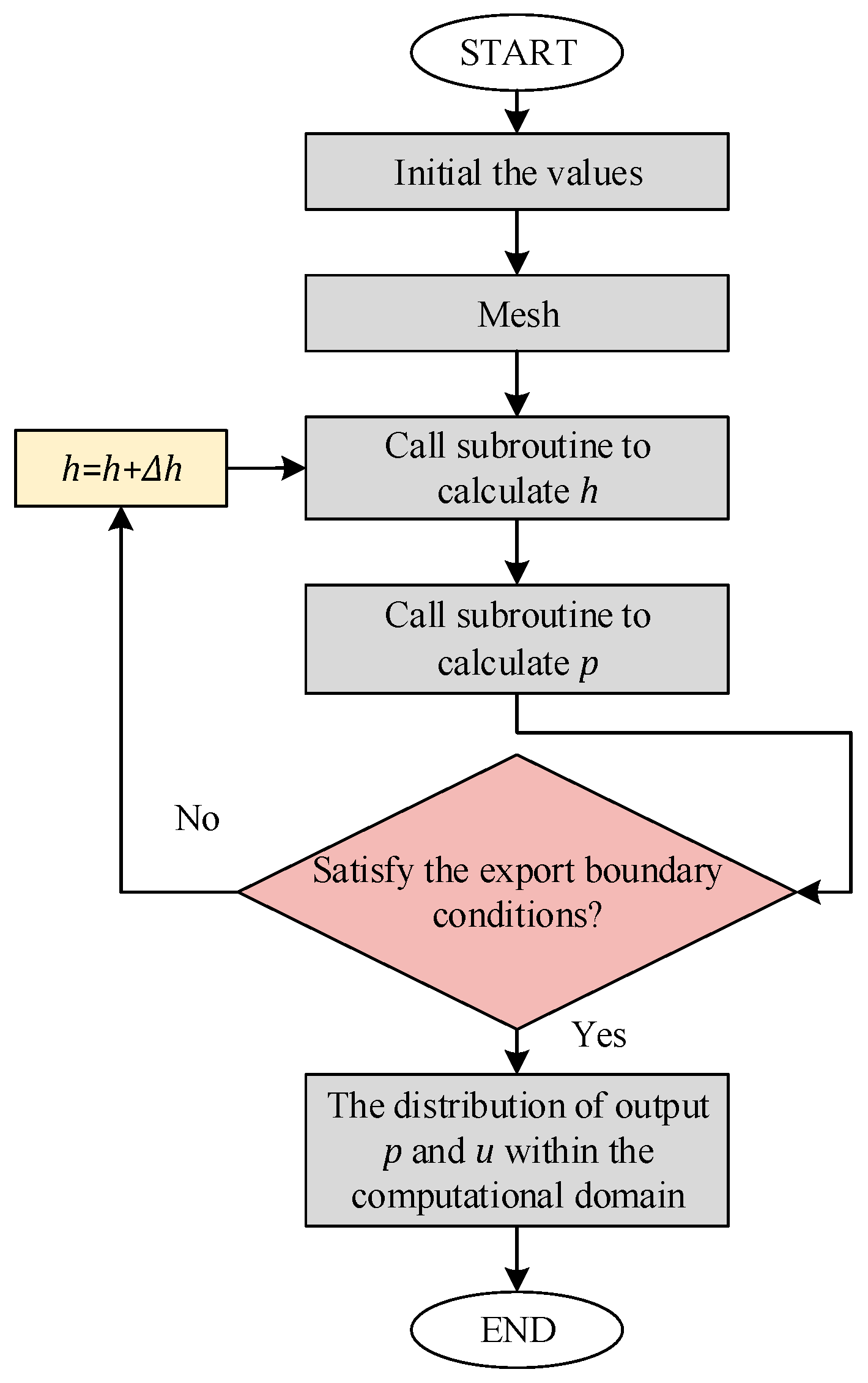
3. Simulation and Analysis
3.1. Simplification of Geometric Models
3.2. Velocity Distribution
3.3. Pressure Distribution
3.4. Removal Model of Single Abrasive
3.5. Material Removal Model
4. Validation and Analysis
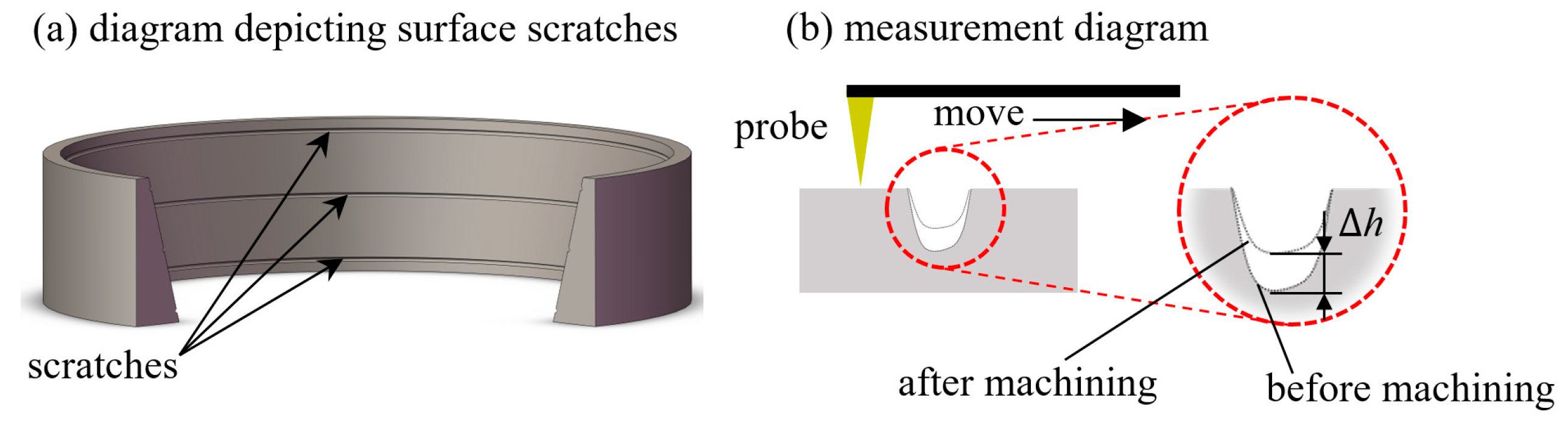
4.1. Valid Experiment Design
4.2. Validation Results and Discussion
4.2.1. Analysis of Simulation Results
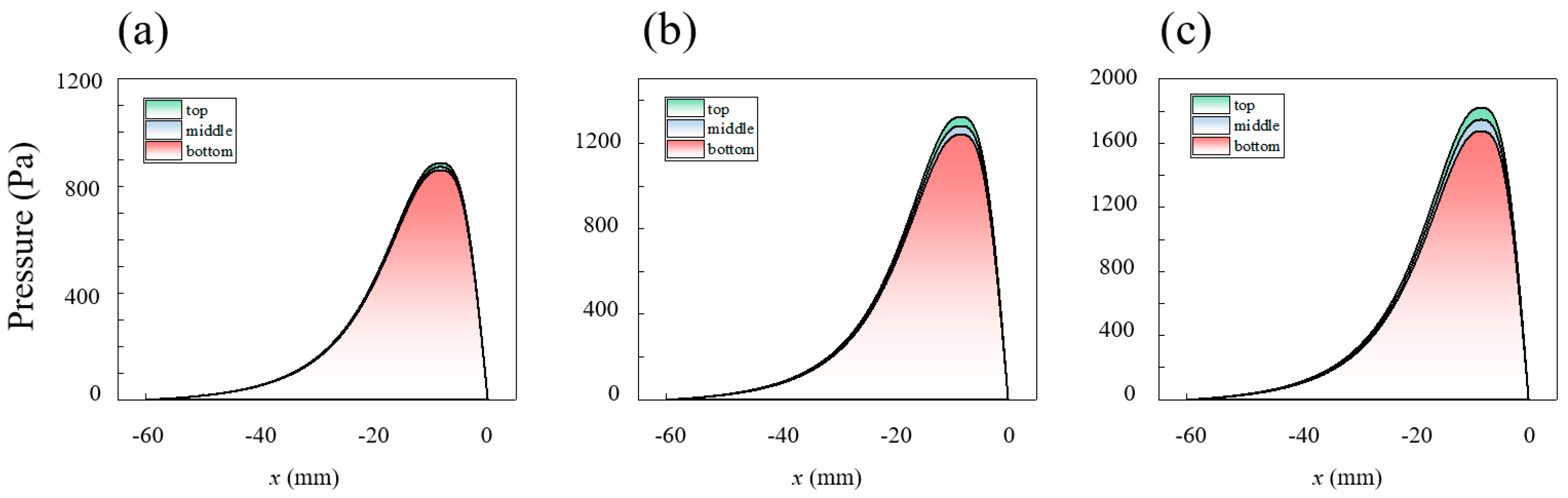
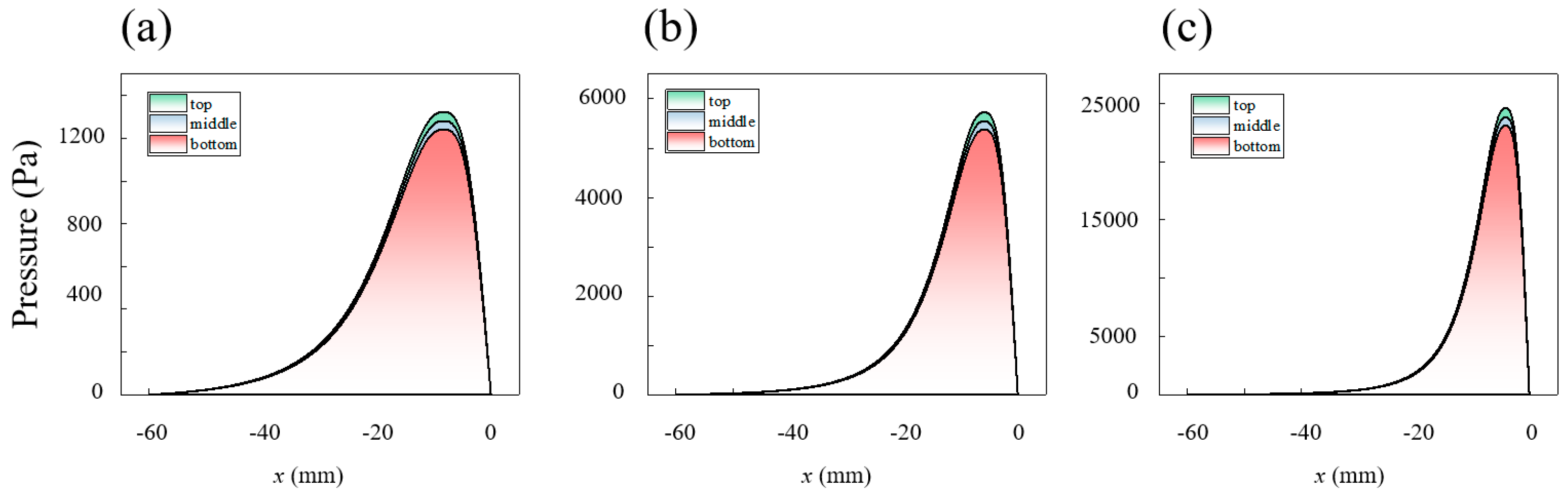
Pressure Distribution Law
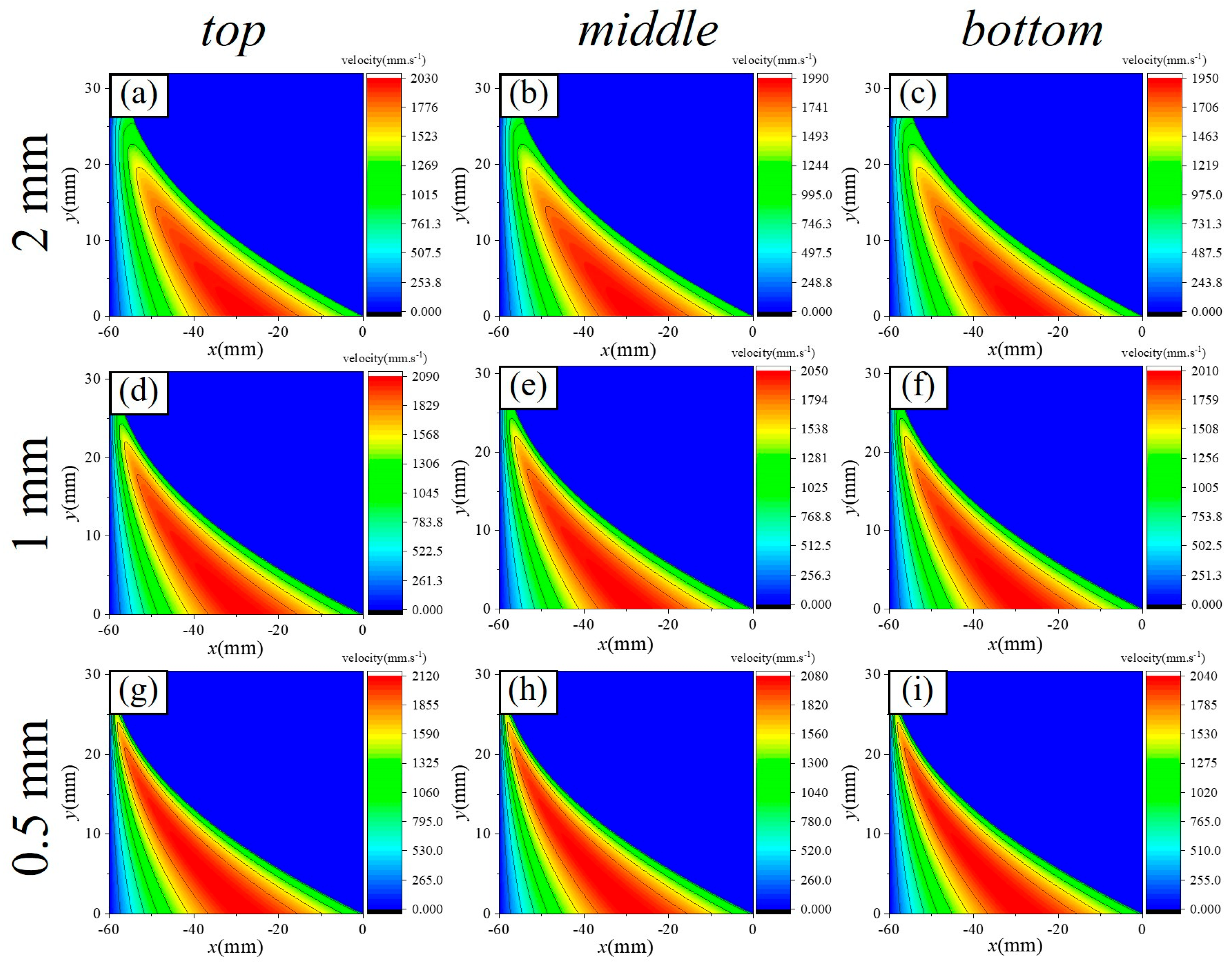
Velocity Distribution Law
- (1)
- At the same rotational speed, varying raceway radii across different regions result in different relative velocities. However, these differences are minimal, with the maximum variation being only 130 mm/s.
- (2)
- The ring rotational speed has the most significant impact on relative velocity. As the ring speed decreases from 40 rpm to 10 rpm, the peak velocity of the slurry decreases by 955 mm/s. Notably, the peak velocity does not occur at the wall but in the central region of the flow. For material removal calculations, velocity values near the wall are necessary.
- (3)
- As the gap decreases, the peak velocity increases; however, this increase is much smaller compared to the change in pressure, as the increase in viscosity hinders slurry motion. When the gap is reduced from 2 mm to 0.5 mm, the peak velocity increases from 2030 mm/s to 2120 mm/s.
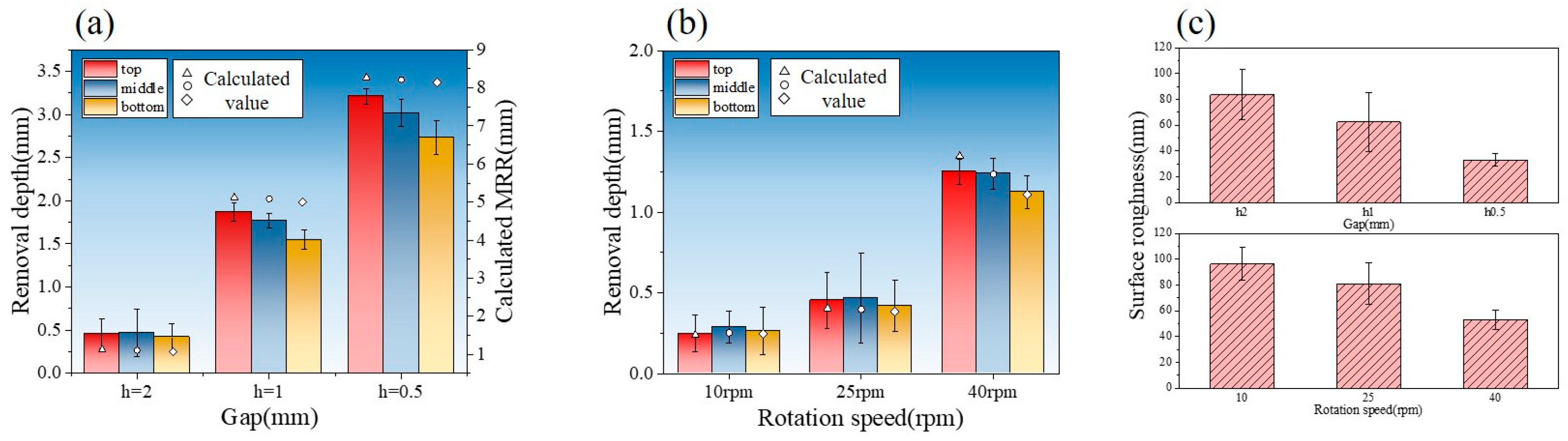
4.2.2. Validation Result
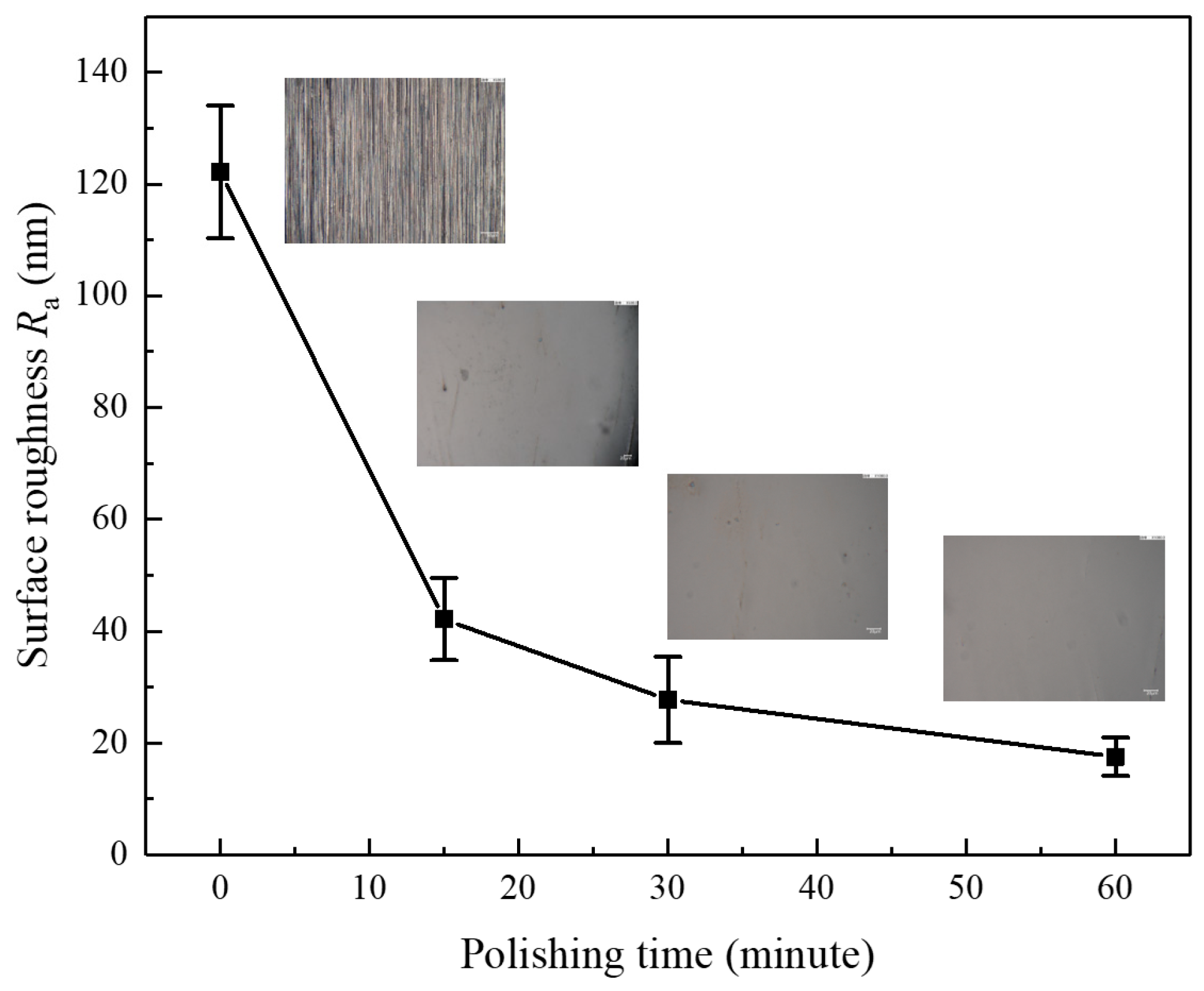
4.2.3. Optimal Experiment
5. Conclusions
- (1)
- The rheological properties of the slurry were measured, and reasonable assumptions were established based on machining conditions and relevant theory.
- (2)
- Distribution functions for pressure and velocity within the processing area were derived. The velocity distribution within the computational domain was obtained using velocity decomposition, then the pressure distribution was computed using the finite difference method.
- (3)
- A single abrasive removal function was established based on contact mechanics, and a material removal distribution function was derived using metallographic analysis.
- (4)
- Valid experiments were carried out under different process parameter levels. The results indicated that the average error of the modified theoretical model was approximately 12%, with a maximum error of 16.3%. The model demonstrated high accuracy and high reliability.
- (5)
- The surface roughness and material removal rate exhibited similar trends, allowing the removal rate to serve as an indicator for identifying the optimal process parameters for achieving the best surface quality. The optimization experiment yielded a surface with a roughness of Ra 17.59 nm and a variance of 4.42 nm2, demonstrating good processing consistency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | depth of particle penetration | ||
| actual boundary | boundary without deformance | ||
| deformation of the tool | volume concentrations | ||
| tool’s Young’s modulus | force on the tool | ||
| normal component of | tangential component of | ||
| gap size | minimum film thickness | ||
| inertia moment | correction factor | ||
| fiber length | thickening index | ||
| number of active abrasive | slurry pressure | ||
| equivalent radius | tool radius | ||
| workpiece radius | residence time | ||
| upper boundary rate | lower boundary rate | ||
| rate component in the -direction | rate component in the -direction | ||
| material removal rate | nylon deflection | ||
| film thickness | the central angle corresponding to the interval between different clusters of bristles | ||
| viscosity | apparent viscosity | ||
| density | |||
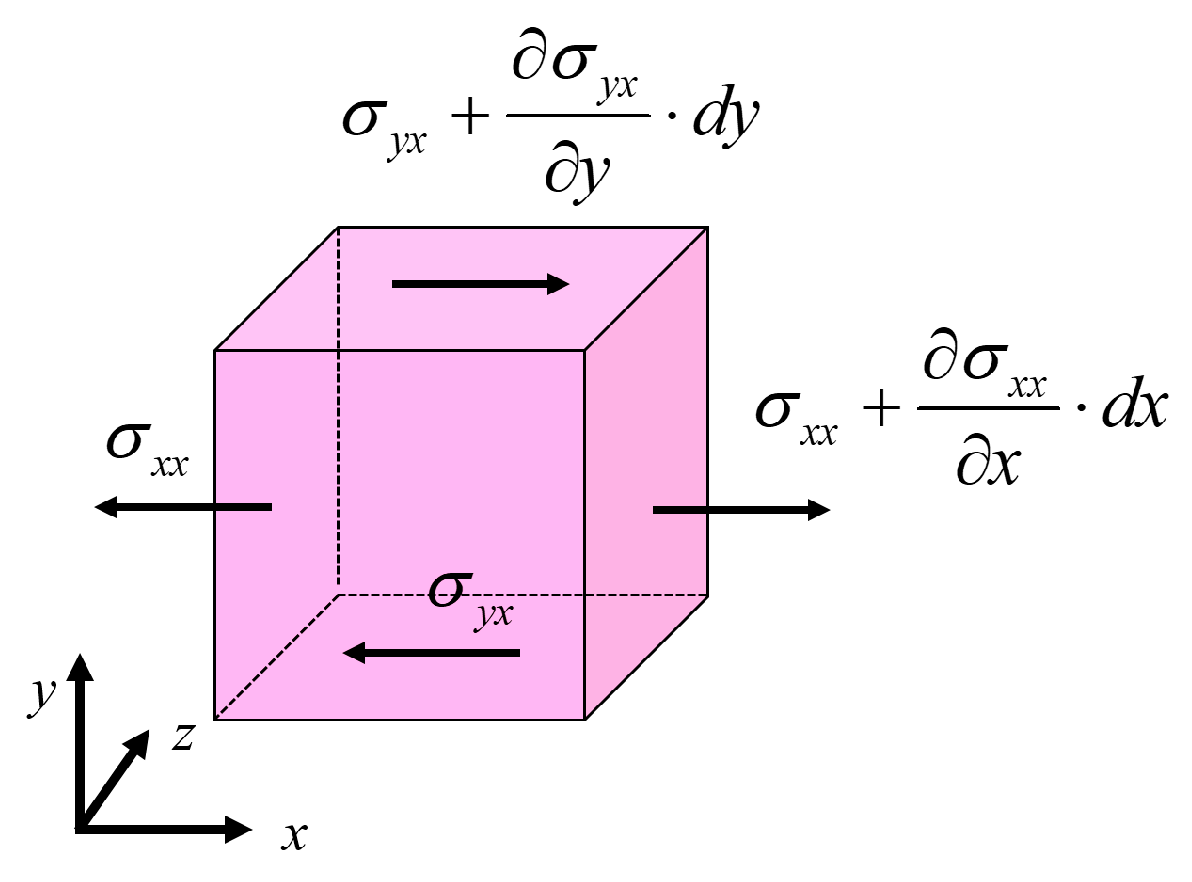
Appendix A. Euler’s Difference Method and Its Implementation
References
- Wang, L.; Wu, M.; Chen, H.; Hang, W.; Wang, X.; Han, Y.; Chen, H.; Chen, P.; Beri, T.H.; Luo, L.; et al. Damage evolution and plastic deformation mechanism of passivation layer during shear rheological polishing of polycrystalline tungsten. J. Mater. Res. Technol.-JMRT 2024, 28, 1584–1596. [Google Scholar] [CrossRef]
- Yao, W.; Chu, Q.; Lyu, B.; Wang, C.; Shao, Q.; Feng, M.; Wu, Z. Modeling of material removal based on multi-scale contact in cylindrical polishing. Int. J. Mech. Sci. 2022, 223, 19. [Google Scholar] [CrossRef]
- Wang, J.; Tang, Z.; Goel, S.; Zhou, Y.; Dai, Y.; Wang, J.; He, Q.; Yuan, J.; Lyu, B. Mechanism of material removal in tungsten carbide-cobalt alloy during chemistry enhanced shear thickening polishing. J. Mater. Res. Technol.-JMRT 2023, 25, 6865–6879. [Google Scholar] [CrossRef]
- Wang, Z.X.; Ye, L.Z.; Zhu, X.J.; Liu, Y.; Chuai, S.D.; Lv, B.Y.; Wang, D. Analysis of flow field characteristics of silicon carbide CMP under ultrasonic action. Diam. Abras. Eng. 2025, 45, 102–112. [Google Scholar]
- Cheng, F.; Wang, Z.; Zun, R.; Wang, Y.G.; Peng, Y.; Zhang, T.Y.; Zhao, D.; Fan, C. Study on dispersion of abrasive particles in electro Fenton CMP slurry and design of green polishing fluid in neutral environment. Diam. Abras. Eng. 2025, 45, 113–121. [Google Scholar]
- Lv, S.C.; Liu, Y.; Sun, X.W.; Dong, Z.X.; Yang, H.R.; Zhang, W.F. Numerical simulation of the influence of cutting parameters on the cutting process of ZrO2 ceramics. Diam. Abras. Eng. 2024, 44, 769–780. [Google Scholar]
- Huang, S.Q.; Li, X.L.; Zhao, Y.T.; Sun, Q.; Huang, H. A novel lapping process for single-crystal sapphire using hybrid nanoparticle suspensions. Int. J. Mech. Sci. 2021, 191, 12. [Google Scholar] [CrossRef]
- Huang, S.Q.; Li, X.L.; Mu, D.K.; Cui, C.C.; Huang, H.; Huang, H. Polishing performance and mechanism of a water-based nanosuspension using diamond particles and GO nanosheets as additives. Tribol. Int. 2021, 164, 13. [Google Scholar] [CrossRef]
- Qu, S.; Wei, C.; Yang, Y.; Yao, P.; Chu, D.; Gong, Y.; Zhao, D.; Zhang, X. Grinding mechanism and surface quality evaluation strategy of single crystal 4H-SiC. Tribol. Int. 2024, 194, 11. [Google Scholar] [CrossRef]
- Li, C.; Wang, K.; Piao, Y.; Cui, H.; Zakharov, O.; Duan, Z.; Zhang, F.; Yan, Y.; Geng, Y. Surface micro-morphology model involved in grinding of GaN crystals driven by strain-rate and abrasive coupling effects. Int. J. Mach. Tools Manuf. 2024, 201, 25. [Google Scholar] [CrossRef]
- Li, C.; Wang, K.; Zakharov, O.; Cui, H.; Wu, M.; Zhao, T.; Yan, Y.; Geng, Y. Damage evolution mechanism and low-damage grinding technology of silicon carbide ceramics. Int. J. Extrem. Manuf. 2025, 7, 36. [Google Scholar] [CrossRef]
- Li, C.; Liu, G.; Gao, C.; Yang, R.; Zakharov, O.; Hu, Y.; Yan, Y.; Geng, Y. Atomic-scale understanding of graphene oxide lubrication-assisted grinding of GaN crystals. Int. J. Mech. Sci. 2025, 286, 19. [Google Scholar] [CrossRef]
- Lin, B.; Jiang, X.M.; Cao, Z.C.; Huang, T. Development and theoretical analysis of novel center-inlet computer-controlled polishing process for high-efficiency polishing of optical surfaces. Robot. Comput.-Integr. Manuf. 2019, 59, 1–12. [Google Scholar] [CrossRef]
- Su, X.; Ji, P.; Liu, K.; Walker, D.; Yu, G.; Li, H.; Li, D.; Wang, B. Combined processing chain for freeform optics based on atmospheric pressure plasma processing and bonnet polishing. Opt. Express 2019, 27, 17979–17992. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chen, Z.T.; Zhang, Y. A novel polishing technology for leading and trailing edges of aero-engine blade. Int. J. Adv. Manuf. Technol. 2021, 116, 1871–1880. [Google Scholar] [CrossRef]
- Fu, Y.Z.; Gao, H.; Yan, Q.S.; Wang, X.P. A new predictive method of the finished surface profile in abrasive flow machining process. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2019, 60, 497–505. [Google Scholar] [CrossRef]
- Wu, B.; Yi, R.; Ding, X.M.; Chiu, T.; He, Q.P.; Deng, H. Surface evolution mechanism for atomic-scale smoothing of Si via atmospheric pressure plasma etching. J. Manuf. Process. 2024, 132, 353–362. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Xu, K.Z.; Gao, Y.H.; Yu, Z.N.; Zhu, F.L. Effects of oxidizer concentration and abrasive type on interfacial bonding and material removal in 4H-SiC polishing processes. Phys. Chem. Chem. Phys. 2024, 26, 27791–27806. [Google Scholar] [CrossRef]
- Zhai, Q.; Zhai, W.J.; Deng, T.H. Study on process optimization of ultrasound assisted magneto-rheological polishing of sapphire hemisphere surface based on Fe3O4/SiO2 core-shell abrasives. Tribol. Int. 2023, 181, 20. [Google Scholar] [CrossRef]
- Ye, L.; Wu, J.; Zhu, X.; Liu, Y.; Li, W.; Chuai, S.; Wang, Z. Optimization of polishing fluid composition for single crystal silicon carbide by ultrasonic assisted chemical-mechanical polishing. Sci. Rep. 2024, 14, 13. [Google Scholar] [CrossRef]
- Cheng, J.; Lv, Y.R.; Zhang, F.; Han, P.; Miao, Q.H.; Huang, Z.X. Understanding the adsorption mechanism of benzotriazole and its derivatives as effective corrosion inhibitors for cobalt in chemical mechanical polishing. Appl. Surf. Sci. 2025, 682, 11. [Google Scholar] [CrossRef]
- Lv, G.; Liu, S.S.; Cao, Y.X.; Zhang, Z.F.; Li, X.F.; Zhang, Y.F.; Liu, T.; Liu, B.S.; Wang, K.Y. Effect of synergistic CeO2/MoS2 abrasives on surface roughness and material removal rate of quartz glass. Ceram. Int. 2024, 50, 48671–48679. [Google Scholar] [CrossRef]
- Peng, C.; Gao, H.; Wang, X.P. On Characterization of Shear Viscosity and Wall Slip for Concentrated Suspension Flows in Abrasive Flow Machining. Materials 2023, 16, 6803. [Google Scholar] [CrossRef] [PubMed]
- Kum, C.W.; Wu, C.H.; Wan, S.; Kang, C.W. Prediction and compensation of material removal for abrasive flow machining of additively manufactured metal components. J. Mater. Process Technol. 2020, 282, 13. [Google Scholar] [CrossRef]
- Fu, Y.Z.; Wang, X.P.; Gao, H.; Wei, H.B.; Li, S.C. Blade surface uniformity of blisk finished by abrasive flow machining. Int. J. Adv. Manuf. Technol. 2016, 84, 1725–1735. [Google Scholar] [CrossRef]
- Guo, L.; Wang, X.; Lyu, B.; Cao, L.; Mao, Y.; Wang, J.; Chen, H.; Wang, J.; Yuan, J. Shear-thickening polishing of inner raceway surface of bearing and suppression of edge effect. Int. J. Adv. Manuf. Technol. 2022, 121, 4055–4068. [Google Scholar] [CrossRef]
- Lu, M.M.; Yang, Y.K.; Lin, J.Q.; Du, Y.S.; Zhou, X.Q. Research progress of magnetorheological polishing technology: A review. Adv. Manuf. 2024, 12, 642–678. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Yin, S.H.; Hu, T. Ultra-precision finishing of optical mold by magnetorheological polishing using a cylindrical permanent magnet. Int. J. Adv. Manuf. Technol. 2018, 97, 3583–3594. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Z.; Zhao, F.; Fan, C.; Feng, J.; Zhou, H.; Meng, F.; Zhuang, X.; Wang, J. Advanced polishing methods for atomic-scale surfaces: A review. Mater. Today Sustain. 2024, 27, 29. [Google Scholar] [CrossRef]
- Zhu, W.L.; Beaucamp, A. Generic three-dimensional model of freeform surface polishing with non-Newtonian fluids. Int. J. Mach. Tools Manuf. 2022, 172, 20. [Google Scholar] [CrossRef]
- Zhu, W.L.; Beaucamp, A. Non-Newtonian fluid based contactless sub-aperture polishing. CIRP Ann.-Manuf. Technol. 2020, 69, 293–296. [Google Scholar] [CrossRef]
- Singh, P.; Singh, L.; Singh, S. A review on magnetically assisted abrasive flow machining and abrasive material type. Proc. Inst. Mech. Eng. Part E-J. Process Mech. Eng. 2022, 236, 2765–2781. [Google Scholar] [CrossRef]
- Rajput, A.S.; Das, M.; Kapil, S. A comprehensive review of magnetorheological fluid assisted finishing processes. Mach. Sci. Technol. 2022, 26, 339–376. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Huang, C.Z. Abrasive liquid jet as a flexible polishing tool. Int. J. Mater. Prod. Technol. 2008, 31, 2–13. [Google Scholar] [CrossRef]
- Gupta, K.; Gupta, M.K. Developments in nonconventional machining for sustainable production: A state-of-the-art review. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2019, 233, 4213–4232. [Google Scholar] [CrossRef]
- Wen, S.Z.; Huang, P.; Tian, Y.; Ma, L.R. Principles of Tribology; Tsinghua University: Beijing, China, 2018. [Google Scholar]
- Guo, L.; Wang, X.; Lyu, B.; Lyu, J.; Wang, J.; Chen, H.; Zhao, W.; Yuan, J. Ultra-precision machining process of inner surface considering shear-thickening polishing method. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2024, 239, 264–277. [Google Scholar] [CrossRef]
- Guo, L.G.; Dai, Z.H.; Wang, D.F.; Wang, X.; Lyu, B.H.; Yuan, J.L. Effects of Force Rheological Polishing Processes on Surface Quality and Accuracy of Bearing Raceway. China Mech. Eng. 2025, 36, 271–279. [Google Scholar]
- Shakiba, M.; Ghomi, E.R.; Khosravi, F.; Jouybar, S.; Bigham, A.; Zare, M.; Abdouss, M.; Moaref, R.; Ramakrishna, S. Nylon-A material introduction and overview for biomedical applications. Polym. Adv. Technol. 2021, 32, 3368–3383. [Google Scholar] [CrossRef]
- Yang, Q.Q.; Huang, P.; Fang, Y.F. A novel Reynolds equation of non-Newtonian fluid for lubrication simulation. Tribol. Int. 2016, 94, 458–463. [Google Scholar] [CrossRef]
- Yang, Q.Q.; Chen, Y.J.; Huang, P. A Novel Method to Determine EHL Film Thickness with Optical Interference. Appl. Mech. Mater. 2013, 456, 549–554. [Google Scholar] [CrossRef]
- Huang, P.; Yang, Q.Q. Theory and contents of frictional mechanics. Friction 2014, 2, 27–39. [Google Scholar] [CrossRef]
- Wei, H.B.; Gao, H.; Wang, X.Y. Development of novel guar gum hydrogel based media for abrasive flow machining: Shear-thickening behavior and finishing performance. Int. J. Mech. Sci. 2019, 157, 758–772. [Google Scholar] [CrossRef]




| Tool Parameter | Value |
|---|---|
| Material | nylon fiber |
| Young’s modulus | 5 Gpa |
| Fiber diameter | 0.5 mm |
| Fiber length | 10 mm |
| Processing Parameters | Value |
|---|---|
| Rotation speed of workpiece (rpm) | 10, 25, 40 |
| Inner diameter of workpiece (mm) | 252~298 |
| Rotation speed of tool (rpm) | 100 |
| Diameter of tool (mm) | 60 |
| Gap h (mm) | 0.5, 1, 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Guo, L.; Gao, Q.; Wang, X.; Lyu, B.; Li, C. Modeling and Validation of Material Removal Based on Rheological Behavior Under Dynamic-Viscosity Nonlinear Coupling Effects. Micromachines 2025, 16, 572. https://doi.org/10.3390/mi16050572
Zhao T, Guo L, Gao Q, Wang X, Lyu B, Li C. Modeling and Validation of Material Removal Based on Rheological Behavior Under Dynamic-Viscosity Nonlinear Coupling Effects. Micromachines. 2025; 16(5):572. https://doi.org/10.3390/mi16050572
Chicago/Turabian StyleZhao, Tianchen, Luguang Guo, Qilong Gao, Xu Wang, Binghai Lyu, and Chen Li. 2025. "Modeling and Validation of Material Removal Based on Rheological Behavior Under Dynamic-Viscosity Nonlinear Coupling Effects" Micromachines 16, no. 5: 572. https://doi.org/10.3390/mi16050572
APA StyleZhao, T., Guo, L., Gao, Q., Wang, X., Lyu, B., & Li, C. (2025). Modeling and Validation of Material Removal Based on Rheological Behavior Under Dynamic-Viscosity Nonlinear Coupling Effects. Micromachines, 16(5), 572. https://doi.org/10.3390/mi16050572







