Numerical Simulation of Gravitactic Bioconvection with Nanoparticles: An Application of Solids Removal in Wastewater Using a Thermal Source
Abstract
1. Introduction
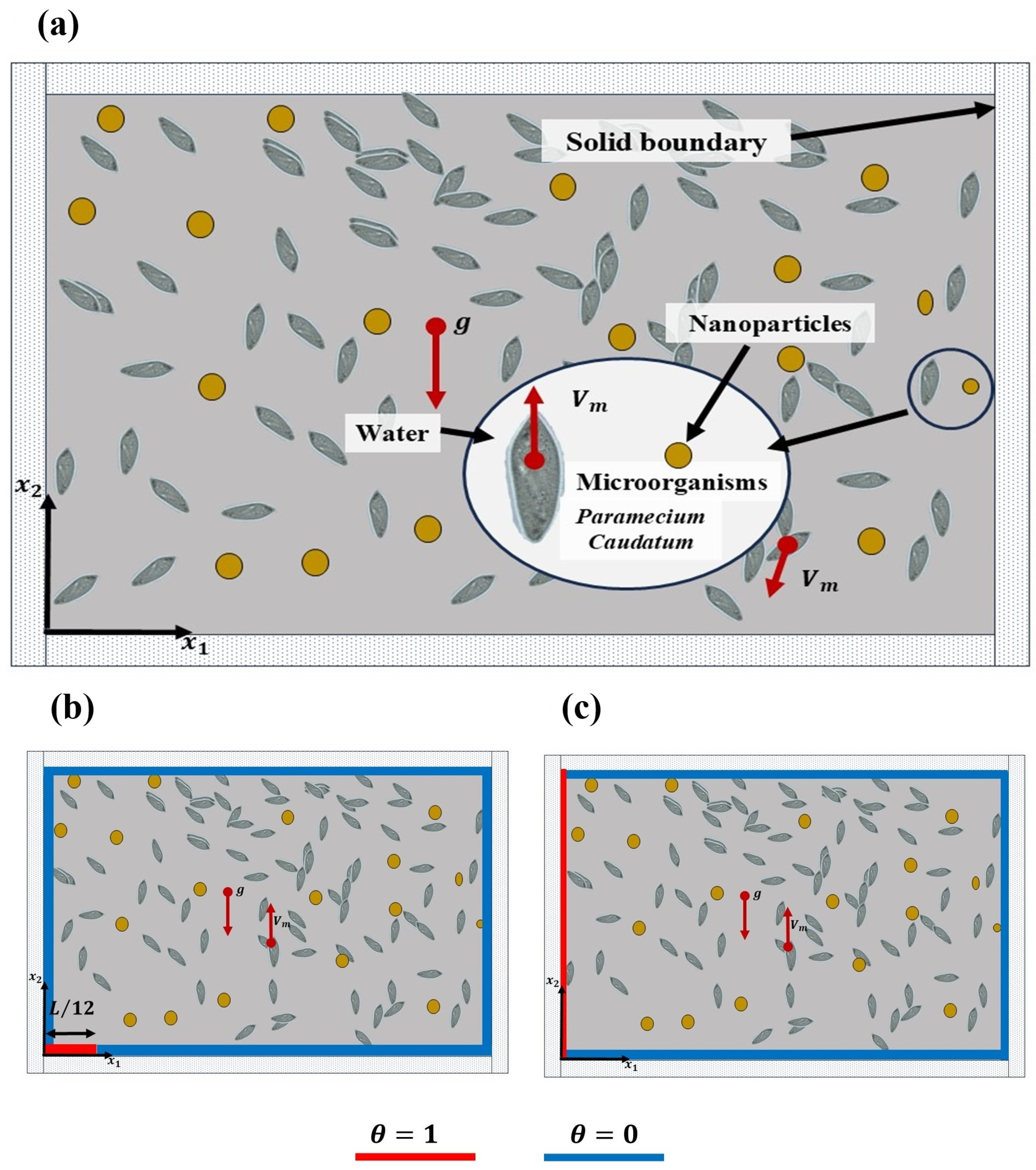
2. Problem Formulation
2.1. Dimensionless Scales
2.2. Mathematical Model
2.3. Boundary Conditions
2.4. Initial Conditions for Microorganisms, Temperature, and Nanoparticles Concentrations
3. Numerical Simulations
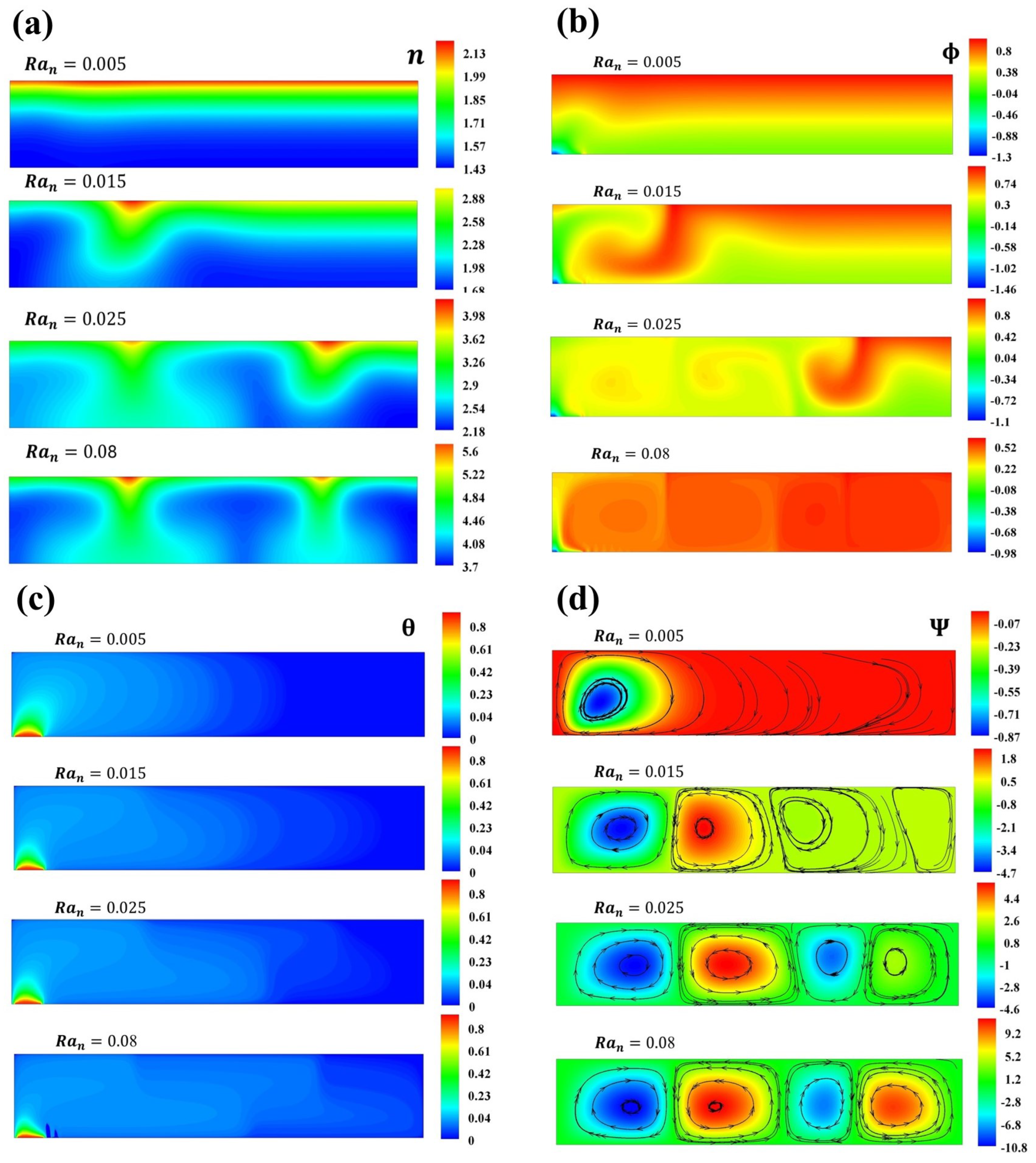
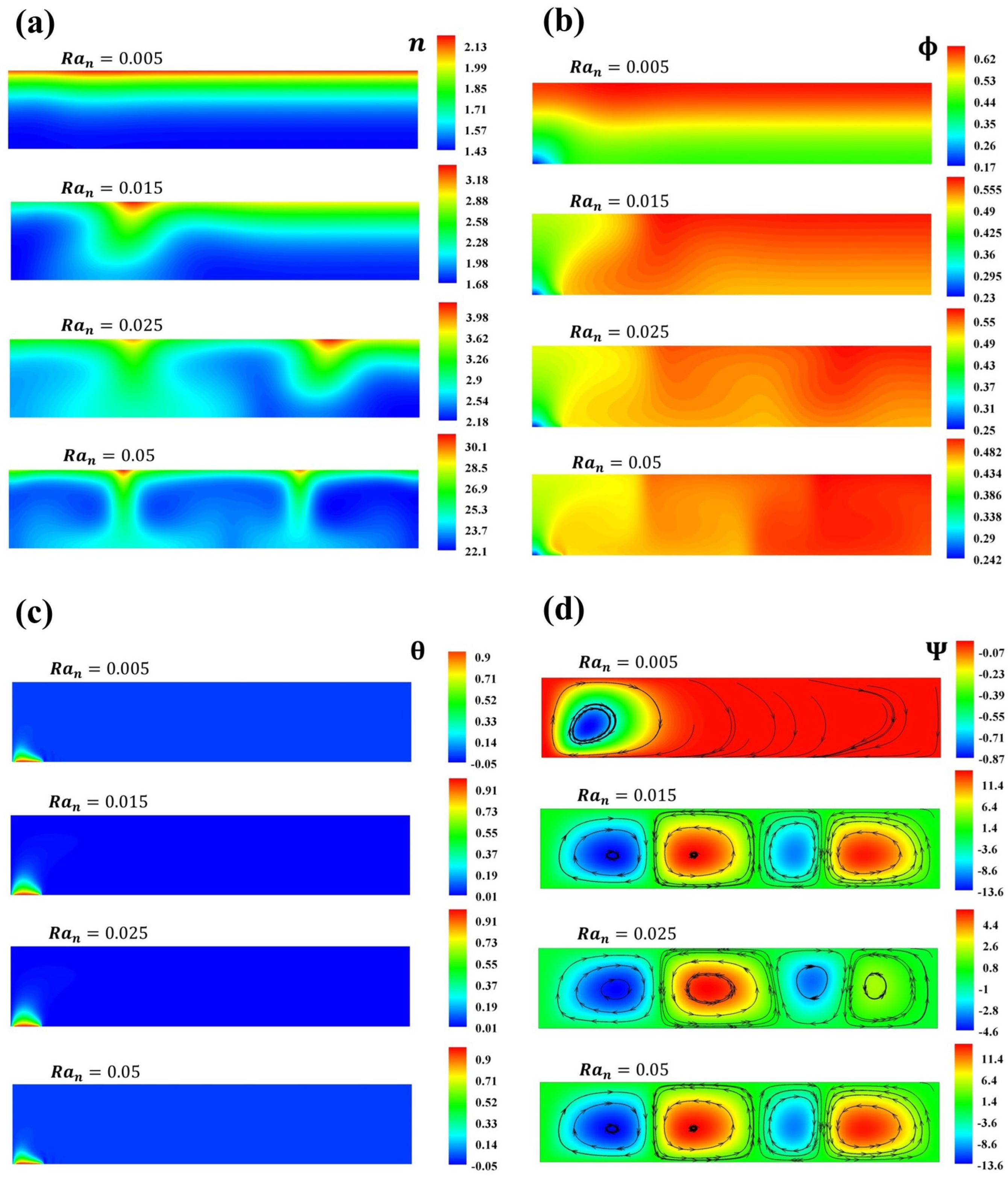
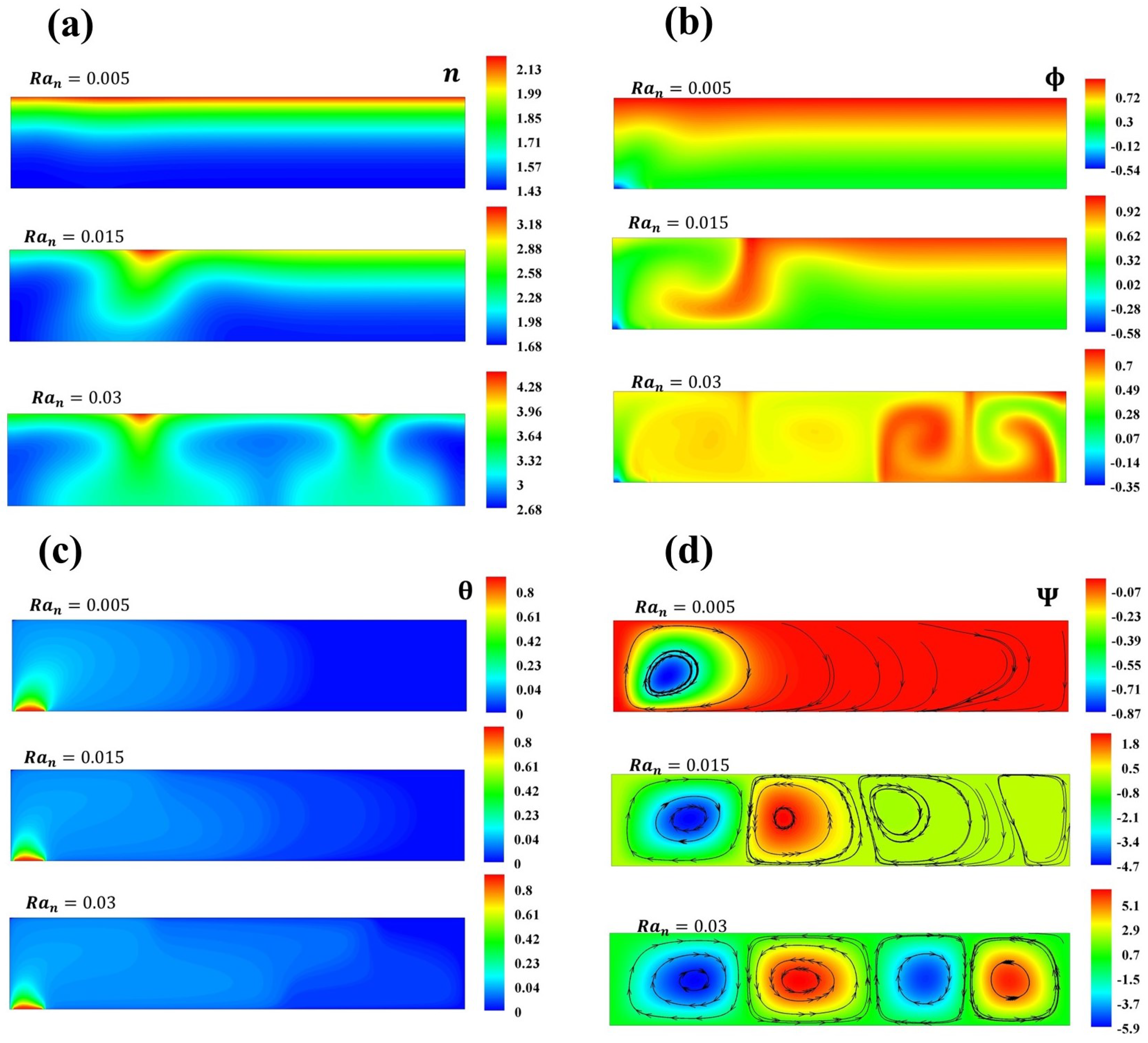
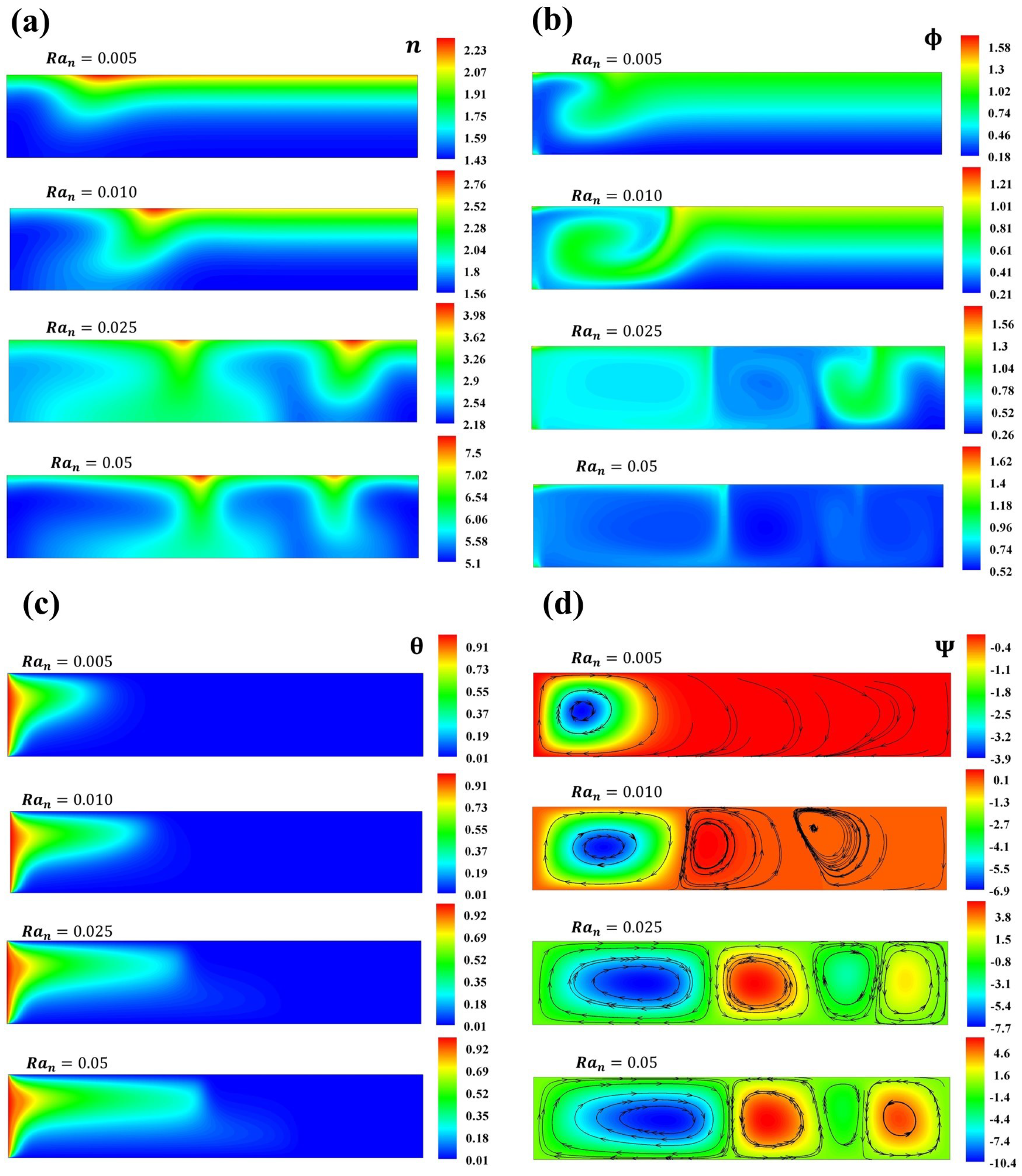
4. Results and Discussion
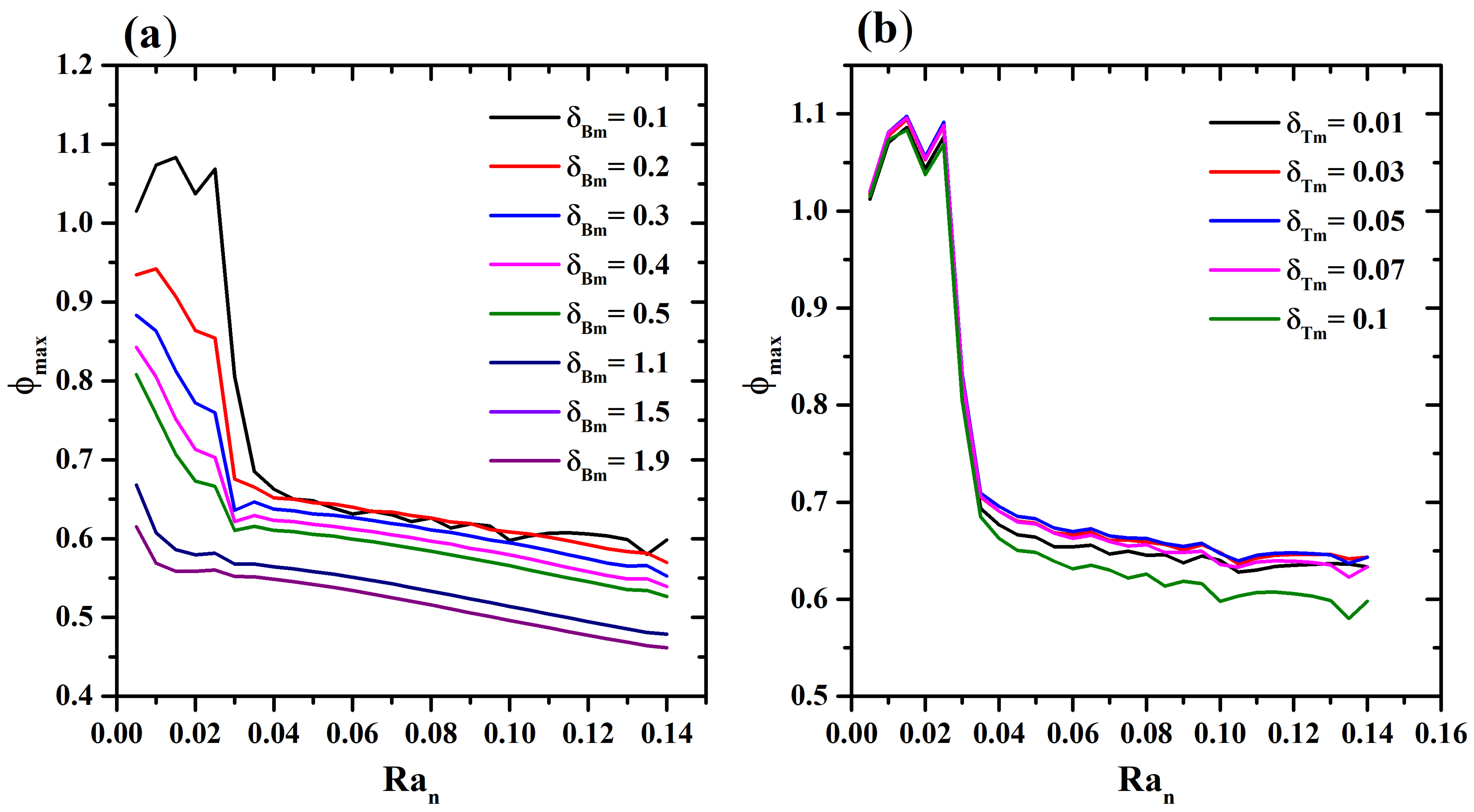
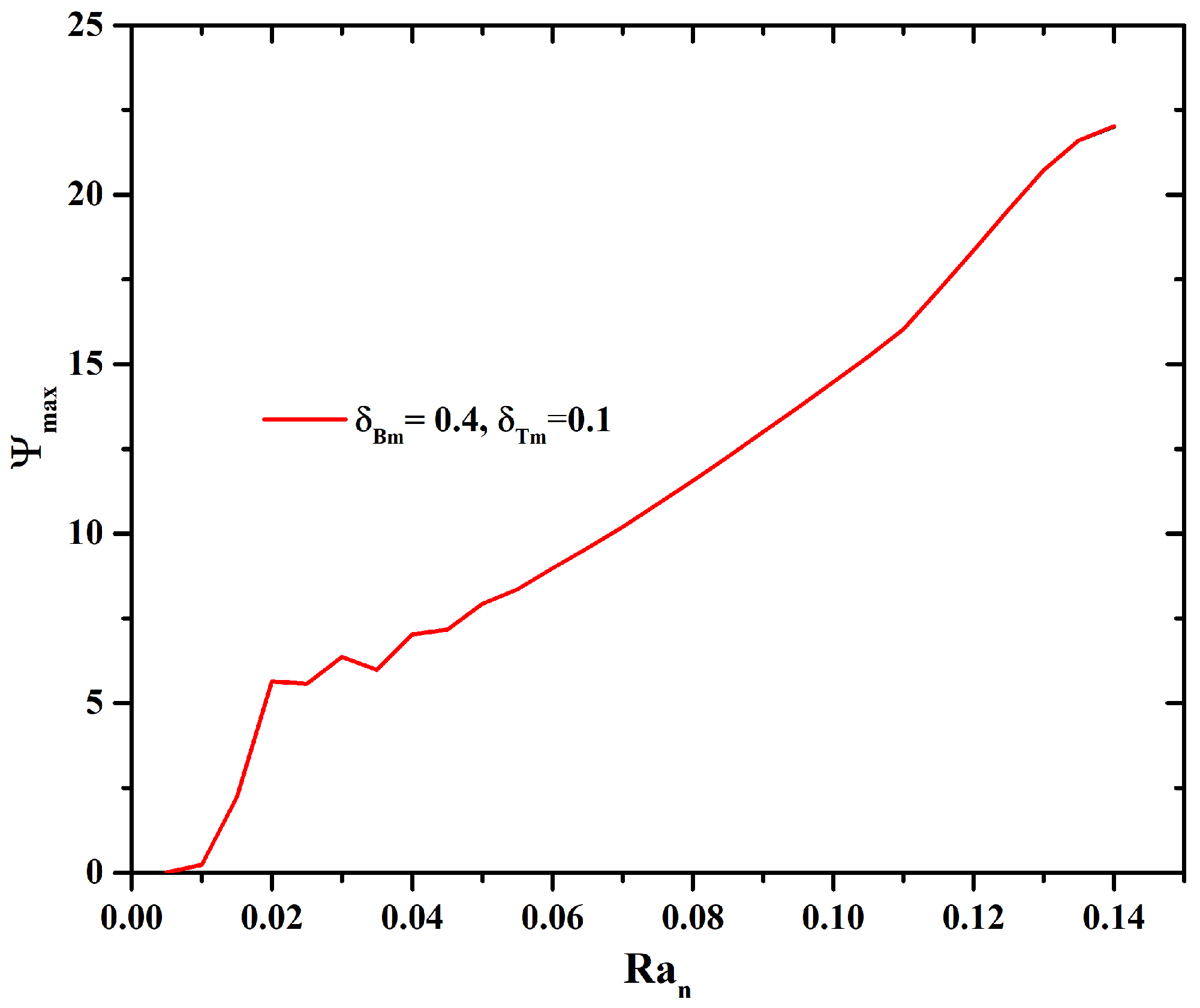
4.1. First Case, Thermal Source at Bottom Wall Side
4.2. Second Case, Thermal Source at Left Wall Side
4.3. From Theory to Real-World Setup
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Aspect ratio | - |
| Diffusivity of microorganisms | m2s−1 | |
| g | Gravity | ms−2 |
| H | Cavity height | m |
| Dimensionless flux of microorganisms | cellm−2s−1 | |
| L | Cavity width | m |
| Lewis number | - | |
| n | Microorganism concentration | cellm−3 |
| Bottom concentration of microorganisms | cellm−3 | |
| Upper concentration of microorganisms | cellm−3 | |
| Average concentration of microorganisms | cellm−3 | |
| Average dimensionless concentration of microorganisms | - | |
| Peclet number | - | |
| Rayleigh number | - | |
| Schmidt number | - | |
| t | Dimensionless time | - |
| T | Temperature | C |
| Cold wall temperature | C | |
| Hot wall temperature | C | |
| Horizontal component of dimensionless velocity | ms−1 | |
| Vertical component of dimensionless velocity | ms−1 | |
| Upward microorganisms’ velocity | ms−1 | |
| Darcy velocity | ms−1 | |
| Dimensionless coordinate system | - | |
| Greek symbols | ||
| Thermal diffusivity | m2s−1 | |
| Volume of microorganisms | m3 | |
| Unit vertical vector | - | |
| Dimensionless stream function | ||
| Nanoparticles volume fraction | ||
| Dimensionless vorticity | ||
| Subscripts | ||
| B | Brownian | |
| T | Thermal | |
| n | Nanoparticles |
References
- Nield, D.; Kuznetsov, A. Thermal instability in a porous medium layer saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5796–5801. [Google Scholar] [CrossRef]
- Kuznetsov, A. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2010, 37, 1421–1425. [Google Scholar] [CrossRef]
- Saini, S.; Sharma, Y. Numerical study of nanofluid thermo-bioconvection containing gravitactic microorganisms in porous media: Effect of vertical throughflow. Adv. Powder Technol. 2018, 29, 2725–2732. [Google Scholar] [CrossRef]
- Bisht, A.; Maheshwari, S. Thermo-Bioconvection in Nanoliquid Suspension Saturated with Thermotactic Microorganisms. Forces Mech. 2022, 9, 100128. [Google Scholar] [CrossRef]
- Akbar, Y.; Alotaibi, H.; Iqbal, J.; Nisar, K.S.; Alharbi, K.A.M. Thermodynamic analysis for bioconvection peristaltic transport of nanofluid with gyrotactic motile microorganisms and Arrhenius activation energy. Case Stud. Therm. Eng. 2022, 34, 102055. [Google Scholar] [CrossRef]
- Rashid, U.; Ullah, N.; Khalifa, H.A.E.W.; Lu, D. Bioconvection modified nanoliquid flow in crown cavity contained with the impact of gyrotactic microorganism. Case Stud. Therm. Eng. 2023, 47, 103052. [Google Scholar] [CrossRef]
- Habibishandiz, M.; Saghir, Z.; Zahmatkesh, I. Thermo-bioconvection performance of nanofluid containing oxytactic microorganisms inside a square porous cavity under constant and periodic temperature boundary conditions. Int. J. Thermofluids 2023, 17, 100269. [Google Scholar] [CrossRef]
- Li, Y.; Majeed, A.; Ijaz, N.; Barghout, K.; Mohamed, R.A.; Muhammad, T. Melting thermal transportation in bioconvection Casson nanofluid flow over a nonlinear surface with motile microorganism: Application in bioprocessing thermal engineering. Case Stud. Therm. Eng. 2023, 49, 103285. [Google Scholar] [CrossRef]
- Naveed Khan, M.; Ahmed, A.; Ahammad, N.A.; Wang, Z.; Hassan, A.M.; Elkotb, M.A. Chemotaxis bioconvection in swirling flow of Maxwell fluid with diffusion-thermo and thermal-diffusion effects. Case Stud. Therm. Eng. 2023, 49, 103334. [Google Scholar] [CrossRef]
- Mezentseva, A.; Smorodin, B.L. The influence of the marangoni effect on the onset of gravitactic bioconvection. Interfacial Phenom. Heat Transf. 2024, 12, 23–31. [Google Scholar] [CrossRef]
- Zohra, F.T.; Uddin, M.J.; Ismail, A.I.M. Magnetohydrodynamic bio-nanoconvective Naiver slip flow of micropolar fluid in a stretchable horizontal channel. Heat Transf.—Asian Res. 2019, 48, 3636–3656. [Google Scholar] [CrossRef]
- Aneja, M.; Sharma, S.; Kuharat, S.; Anwar Beg, O. Computation of electroconductive gyrotactic bioconvection under nonuniform magnetic field: Simulation of smart bio-nanopolymer coatings for solar energy. Int. J. Mod. Phys. B 2020, 34, 2050028. [Google Scholar] [CrossRef]
- Mubbashar Nazeer, S.; Saleem, F.H.; Rafiq, M.U. Numerical solution of gyrotactic microorganism flow of nanofluid over a Riga plate with the characteristic of chemical reaction and convective condition. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Siddiqa, S.; e Hina, G.; Begum, N.; Saleem, S.; Hossain, M.; Reddy Gorla, R.S. Numerical solutions of nanofluid bioconvection due to gyrotactic microorganisms along a vertical wavy cone. Int. J. Heat Mass Transf. 2016, 101, 608–613. [Google Scholar] [CrossRef]
- Mil-Martínez, R.; Ferrer, V.; Turcio, M.; López-Serrano, F.; Ortega, J.; Vargas, R. Stability analysis and numerical simulation of gravitactic bioconvection in a rectangular cavity. Comput. Math. Appl. 2019, 77, 222–236. [Google Scholar] [CrossRef]
- Pérez-Reyes, I.; Dávalos-Orozco, L.A. Bioconvective linear stability of gravitactic microorganisms. In Heat and Mass Transfer-Advances in Science and Technology Applications; IntechOpen: London, UK, 2019. [Google Scholar]
- Anjum, N.; Khan, W.; Hobiny, A.; Azam, M.; Waqas, M.; Irfan, M. Numerical analysis for thermal performance of modified Eyring Powell nanofluid flow subject to activation energy and bioconvection dynamic. Case Stud. Therm. Eng. 2022, 39, 102427. [Google Scholar] [CrossRef]
- Ghachem, K.; Ahmad, B.; Noor, S.; Abbas, T.; Khan, S.U.; Anjum, S.; Alwadai, N.; Kolsi, L. Numerical simulations for radiated bioconvection flow of nanoparticles with viscous dissipation and exponential heat source. J. Indian Chem. Soc. 2023, 100, 100828. [Google Scholar] [CrossRef]
- Garg, A.; Sharma, Y.; Jain, S.K. Stability analysis of thermo-bioconvection flow of Jeffrey fluid containing gravitactic microorganism into an anisotropic porous medium. Forces Mech. 2023, 10, 100152. [Google Scholar] [CrossRef]
- Kumar, S.; Wang, S. Thermal-bioconvection instability in a suspension of phototactic microorganisms heated from below. Therm. Sci. Eng. Prog. 2024, 53, 102691. [Google Scholar] [CrossRef]
- Avramenko, A.; Kovetska, Y.; Shevchuk, I. Lorenz approach for analysis of bioconvection instability of gyrotactic motile microorganisms. Chaos Solitons Fractals 2023, 166, 112957. [Google Scholar] [CrossRef]
- Singh, R. Microorganism as a tool of bioremediation technology for cleaning environment: A review. Proc. Int. Acad. Ecol. Environ. Sci. 2014, 4, 1. [Google Scholar]
- Karthika, V.; Sekaran, U.; Jainullabudeen, G.B.; Nagarathinam, A. Chapter 9—Advances in bioremediation of industrial wastewater containing metal pollutants. In Biological Approaches to Controlling Pollutants; Kumar, S., Hashmi, M.Z., Eds.; Advances in Pollution Research; Woodhead Publishing: Amsterdam, The Netherlands, 2022; pp. 163–177. [Google Scholar] [CrossRef]
- Rehman, A.; Shakoori, F.R.; Shakoori, A. Heavy metal uptake by Euplotes mutabilis and its possible use in bioremediation of industrial wastewater. Bull. Environ. Contam. Toxicol. 2009, 83, 130–135. [Google Scholar] [CrossRef]
- Hrynkiewicz, K.; Baum, C. Application of microorganisms in bioremediation of environment from heavy metals. In Environmental Deterioration and Human Health: Natural and Anthropogenic Determinants; Springer: Dordrech, The Netherlands, 2014; pp. 215–227. [Google Scholar]
- Abatenh, E.; Gizaw, B.; Tsegaye, Z.; Wassie, M. The role of microorganisms in bioremediation-A review. Open J. Environ. Biol. 2017, 2, 38–46. [Google Scholar] [CrossRef]
- Padhan, D.; Rout, P.P.; Kundu, R.; Adhikary, S.; Padhi, P.P. Bioremediation of heavy metals and other toxic substances by microorganisms. In Soil Bioremediation: An Approach Towards Sustainable Technology; Wiley: Hoboken, NJ, USA, 2021; pp. 285–329. [Google Scholar]
- Herman, P.; Kiss, A.; Fábián, I.; Kalmár, J.; Nagy, G. In situ remediation efficacy of hybrid aerogel adsorbent in model aquatic culture of Paramecium caudatum exposed to Hg (II). Chemosphere 2021, 275, 130019. [Google Scholar] [CrossRef]
- Zahra, I.; Liaqat, A.; Betenbaugh, M.; Ramzan, U.; Elmnasri, K.; Hedfi, A.; Ali, M.B.; Albogami, B.; Shakoori, F.R.; Shakoori, A.R. Bioremediation of heavy metals using a novel species of ciliate Paramecium multimicronucleatum isolated from industrial wastewater. Mater. Res. Express 2023, 10, 035403. [Google Scholar] [CrossRef]
- Tawada, K.; Oosawa, F. Responses of Paramecium to temperature change. J. Protozool. 1972, 19, 53–57. [Google Scholar] [CrossRef]
- Nakaoka, Y.; Oosawa, F. Temperature-sensitive behavior of Paramecium caudatum. J. Protozool. 1977, 24, 575–580. [Google Scholar] [CrossRef]
- Mil-Martínez, R.; Vargas, R.O.; Escandón, J.P.; Pérez-Reyes, I.; Turcio, M.; Gómez-López, A.; López-Serrano, F. Thermal Effect on the Bioconvection Dynamics of Gravitactic Microorganisms in a Rectangular Cavity. Fluids 2022, 7, 113. [Google Scholar] [CrossRef]
- Rapp, B.E. (Ed.) Chapter 9—fluids. In Microfluidics: Modelling, Mechanics and Mathematics, Micro and Nano Technologies; Elsevier: Oxford, UK, 2017; pp. 243–263. Available online: https://www.sciencedirect.com/science/article/pii/B9781455731411500095 (accessed on 10 March 2025). [CrossRef]
- Iqbal, M.A.; Khan, N.; Alzahrani, A.; Khan, Y. Thermophoretic particle deposition in bioconvection flow of nanofluid with microorganisms and heat source: Applications of nanoparticle and thermal radiation. J. Radiat. Res. Appl. Sci. 2025, 18, 101305. [Google Scholar] [CrossRef]
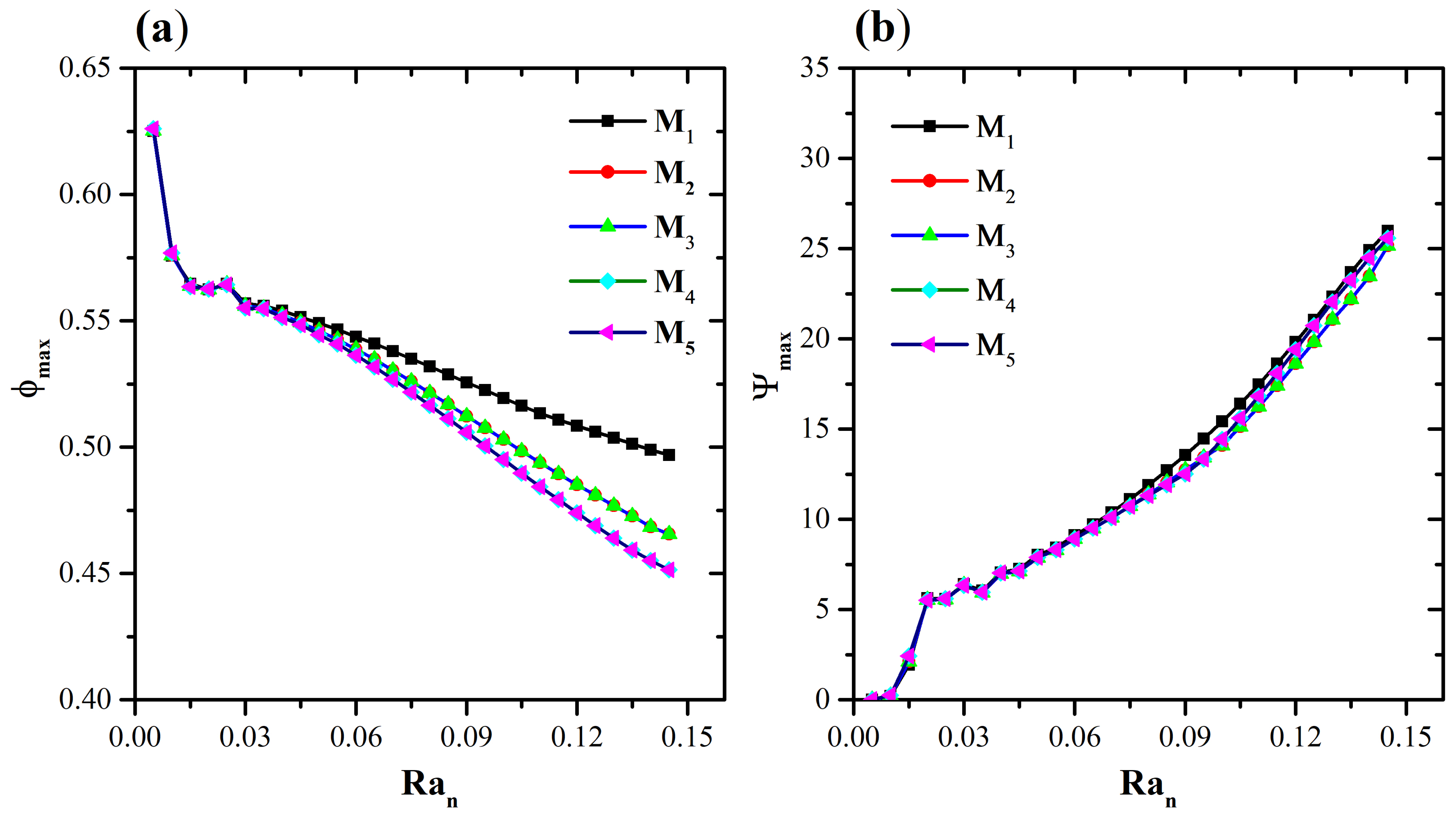

| Mesh | , | , | , | , |
|---|---|---|---|---|
| 0.52565 | 13.57062 | 0.49894 | 24.90609 | |
| 0.51224 | 12.74131 | 0.46851 | 23.48302 | |
| 0.51224 | 12.74131 | 0.46851 | 23.48302 | |
| 0.50591 | 12.51656 | 0.45513 | 24.48658 | |
| 0.50591 | 12.51656 | 0.45513 | 24.48658 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mil-Martínez, A.M.; Vargas, R.O.; Gómez-López, A.; Zacarías, A.; Escandón, J.P.; García-Leal, E.; Mil-Martínez, R. Numerical Simulation of Gravitactic Bioconvection with Nanoparticles: An Application of Solids Removal in Wastewater Using a Thermal Source. Micromachines 2025, 16, 553. https://doi.org/10.3390/mi16050553
Mil-Martínez AM, Vargas RO, Gómez-López A, Zacarías A, Escandón JP, García-Leal E, Mil-Martínez R. Numerical Simulation of Gravitactic Bioconvection with Nanoparticles: An Application of Solids Removal in Wastewater Using a Thermal Source. Micromachines. 2025; 16(5):553. https://doi.org/10.3390/mi16050553
Chicago/Turabian StyleMil-Martínez, Alejandra M., René O. Vargas, Aldo Gómez-López, Alejandro Zacarías, Juan P. Escandón, Enrique García-Leal, and Rubén Mil-Martínez. 2025. "Numerical Simulation of Gravitactic Bioconvection with Nanoparticles: An Application of Solids Removal in Wastewater Using a Thermal Source" Micromachines 16, no. 5: 553. https://doi.org/10.3390/mi16050553
APA StyleMil-Martínez, A. M., Vargas, R. O., Gómez-López, A., Zacarías, A., Escandón, J. P., García-Leal, E., & Mil-Martínez, R. (2025). Numerical Simulation of Gravitactic Bioconvection with Nanoparticles: An Application of Solids Removal in Wastewater Using a Thermal Source. Micromachines, 16(5), 553. https://doi.org/10.3390/mi16050553









