Rheological Property Changes in Polyacrylamide Aqueous Solution Flowed Through Microchannel Under Low Reynolds Number and High Shear Rate Conditions
Abstract
1. Introduction
2. Experiment
2.1. Test Fluids
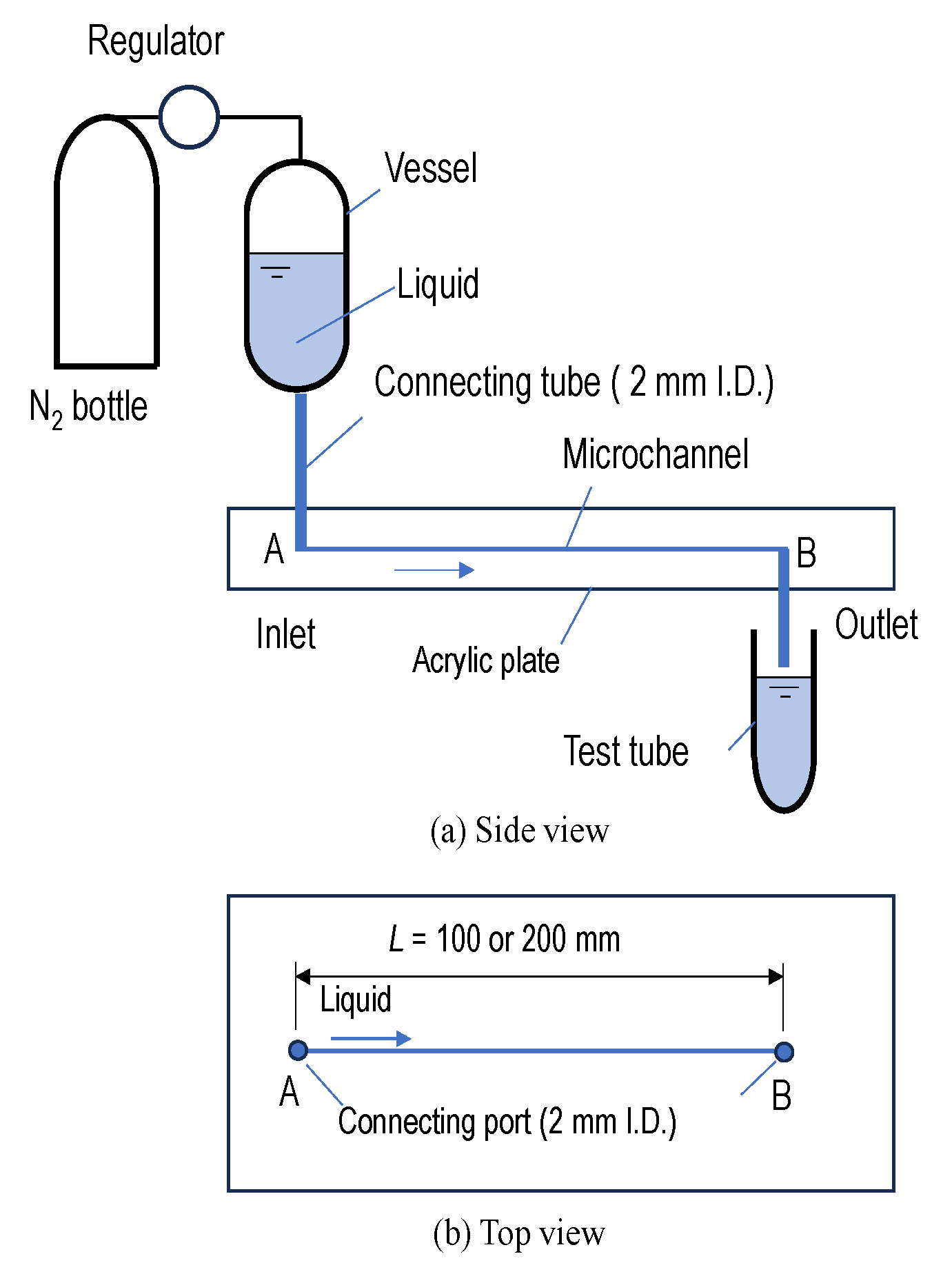
2.2. Test Apparatus and Flow Conditions
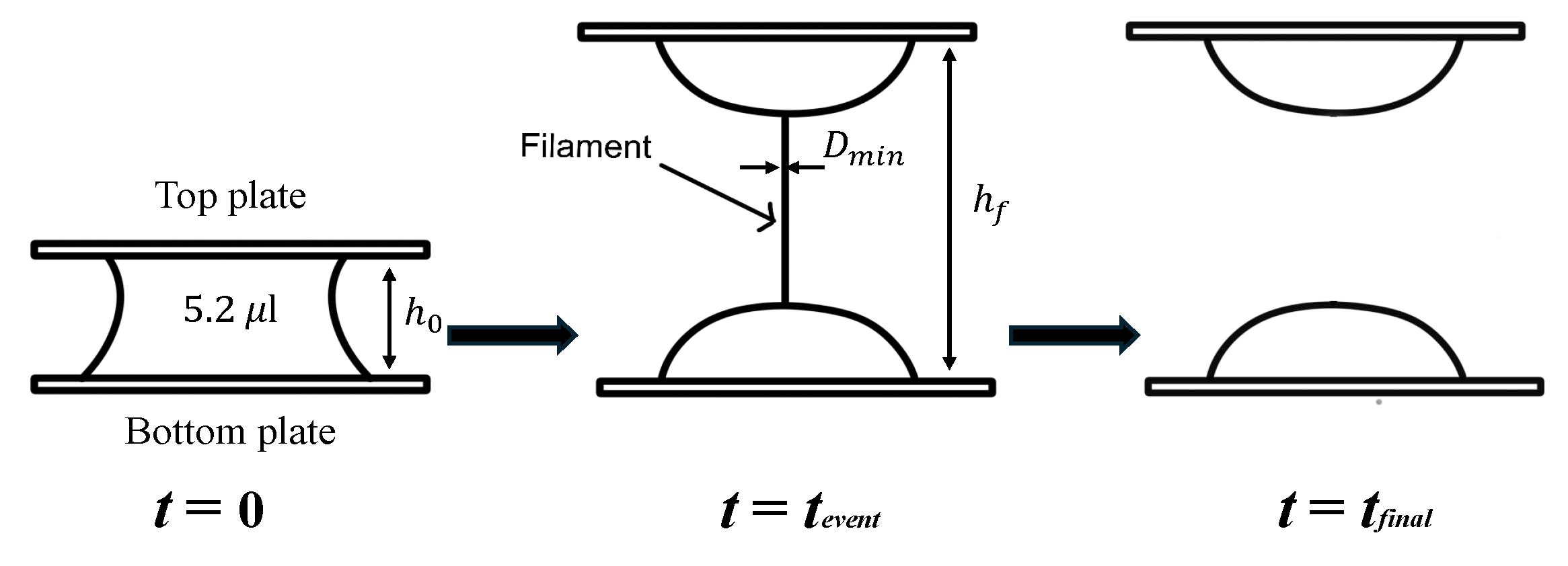
2.3. Measurement Methods for Rheological Characteristics
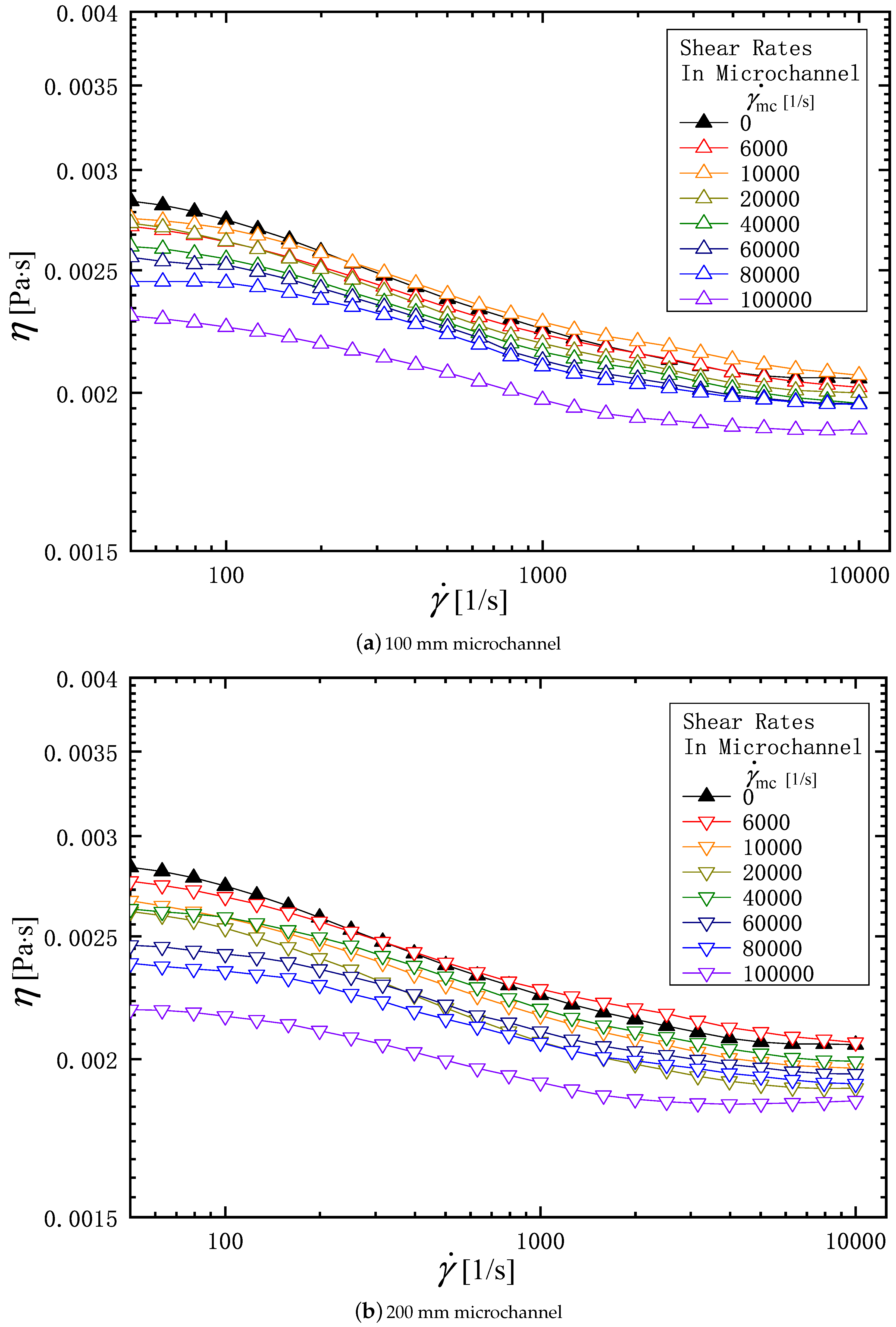
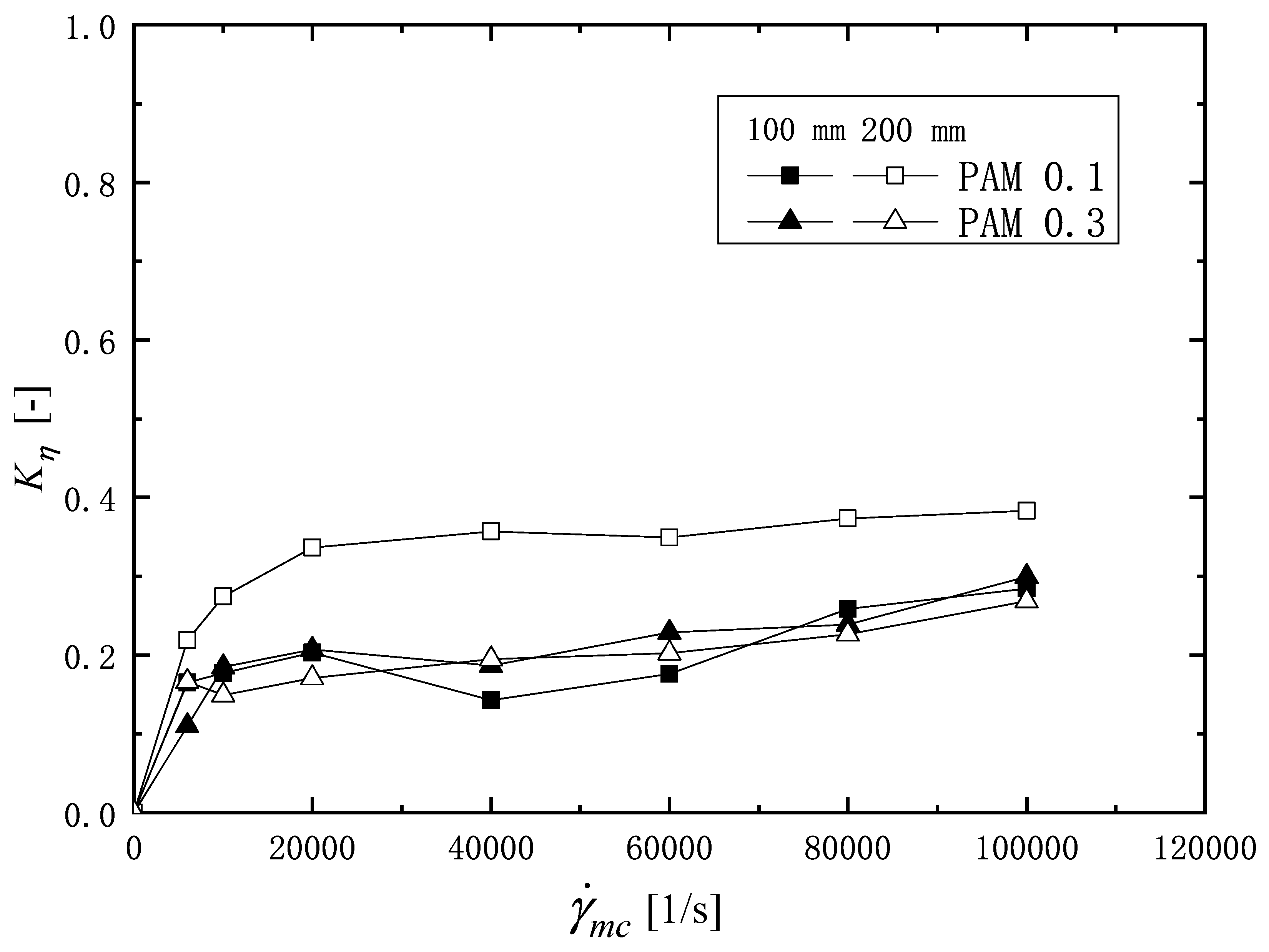
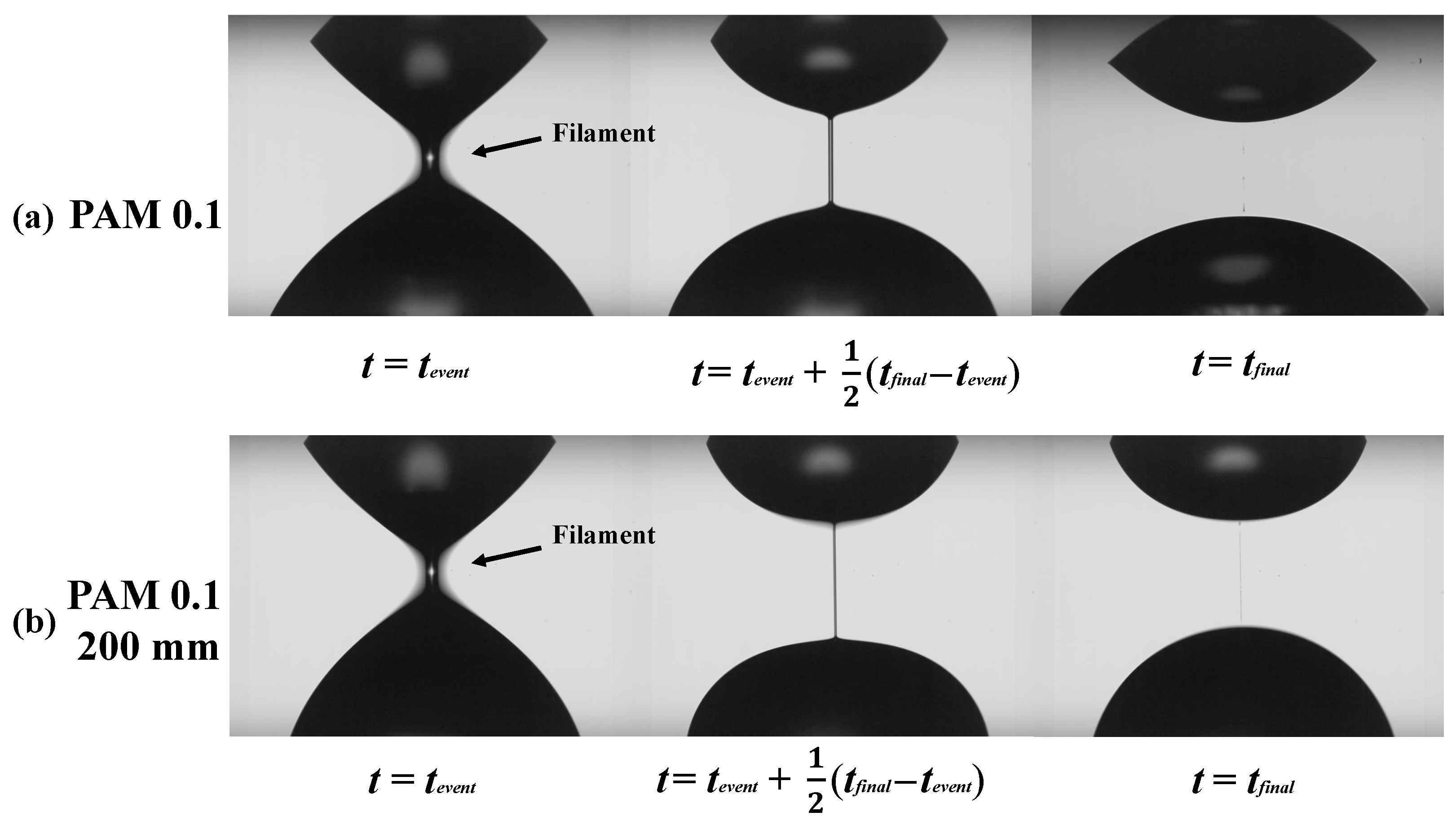
3. Result and Discussion
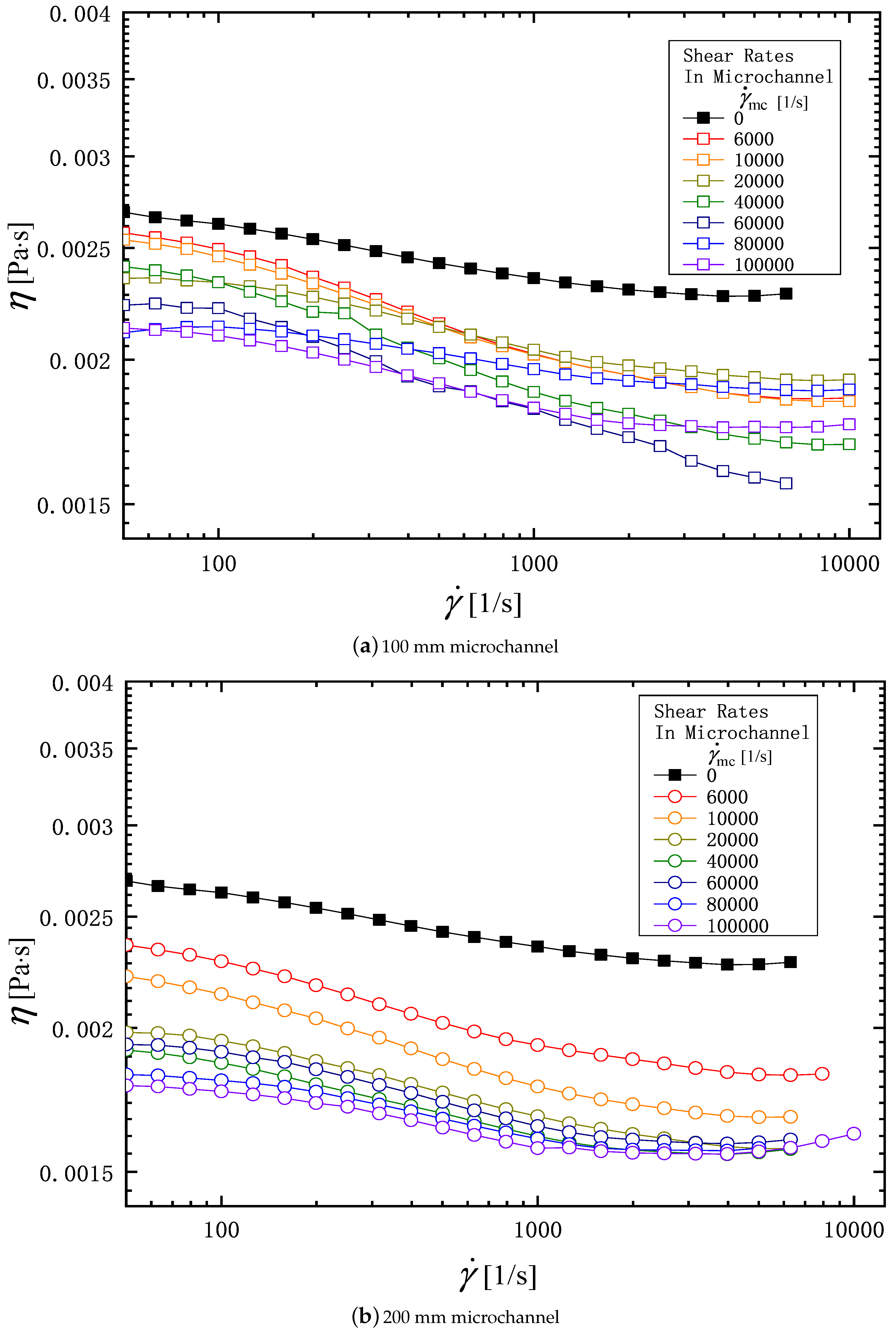
3.1. Shear Rheology
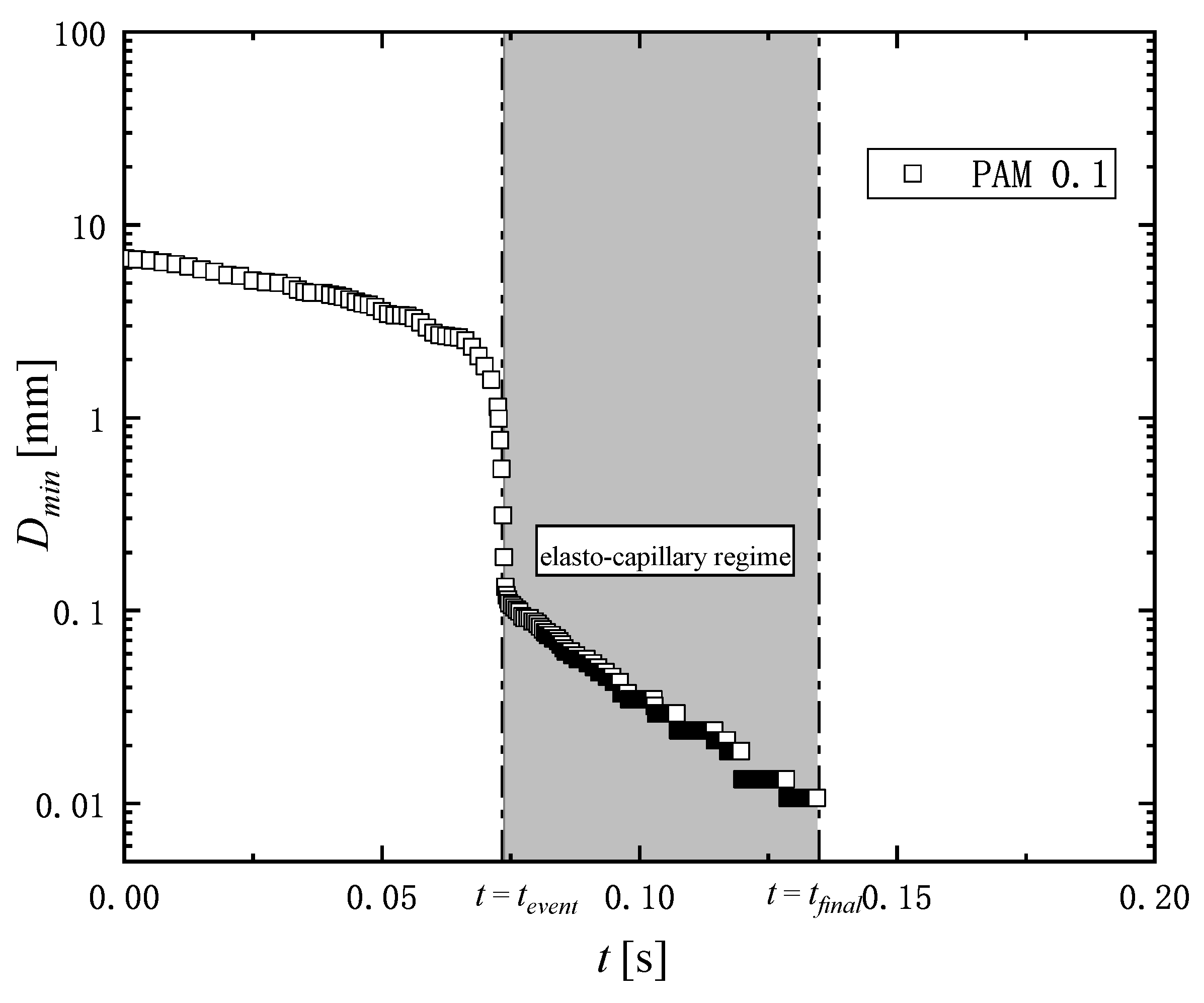
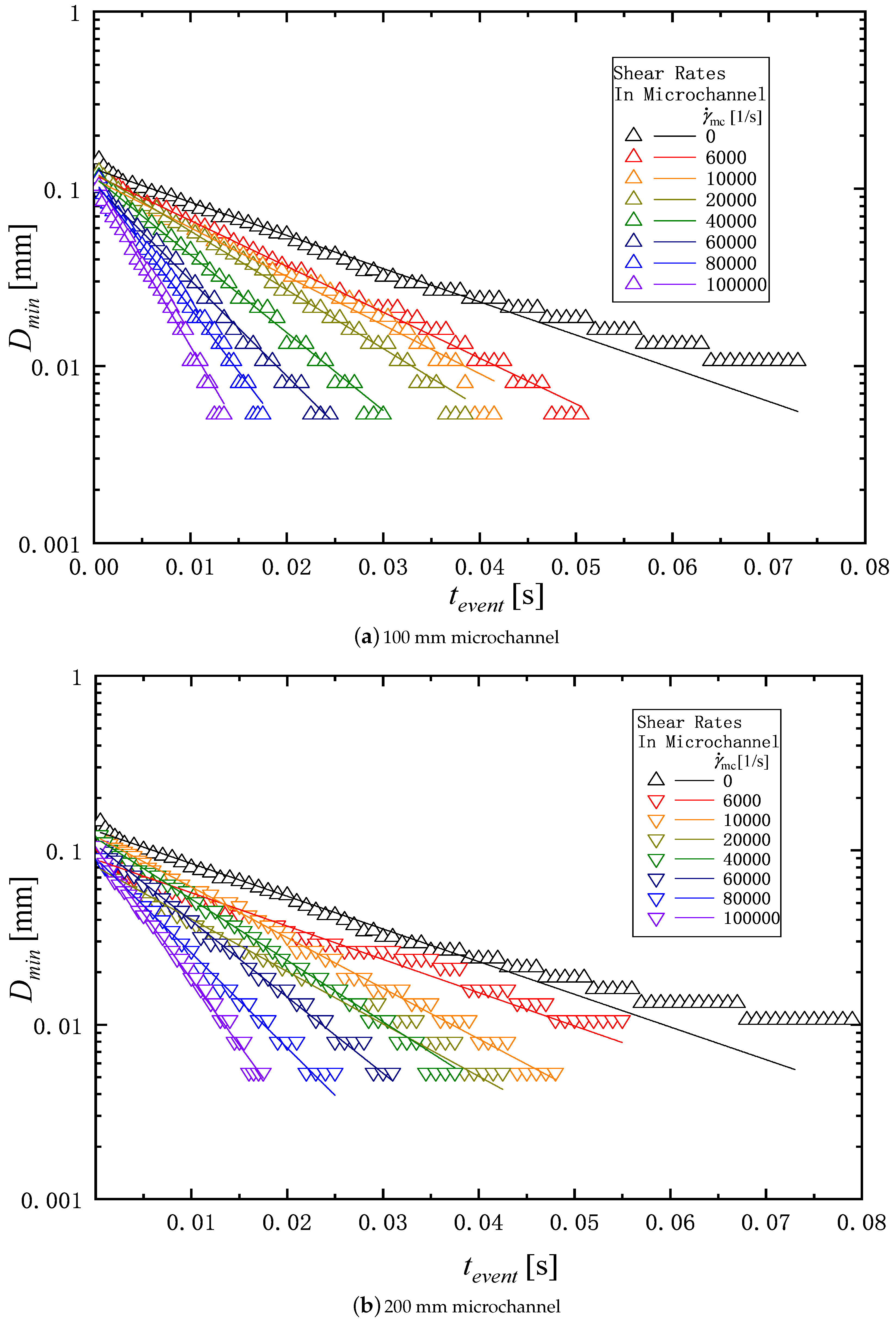
3.2. Extensional Rheology
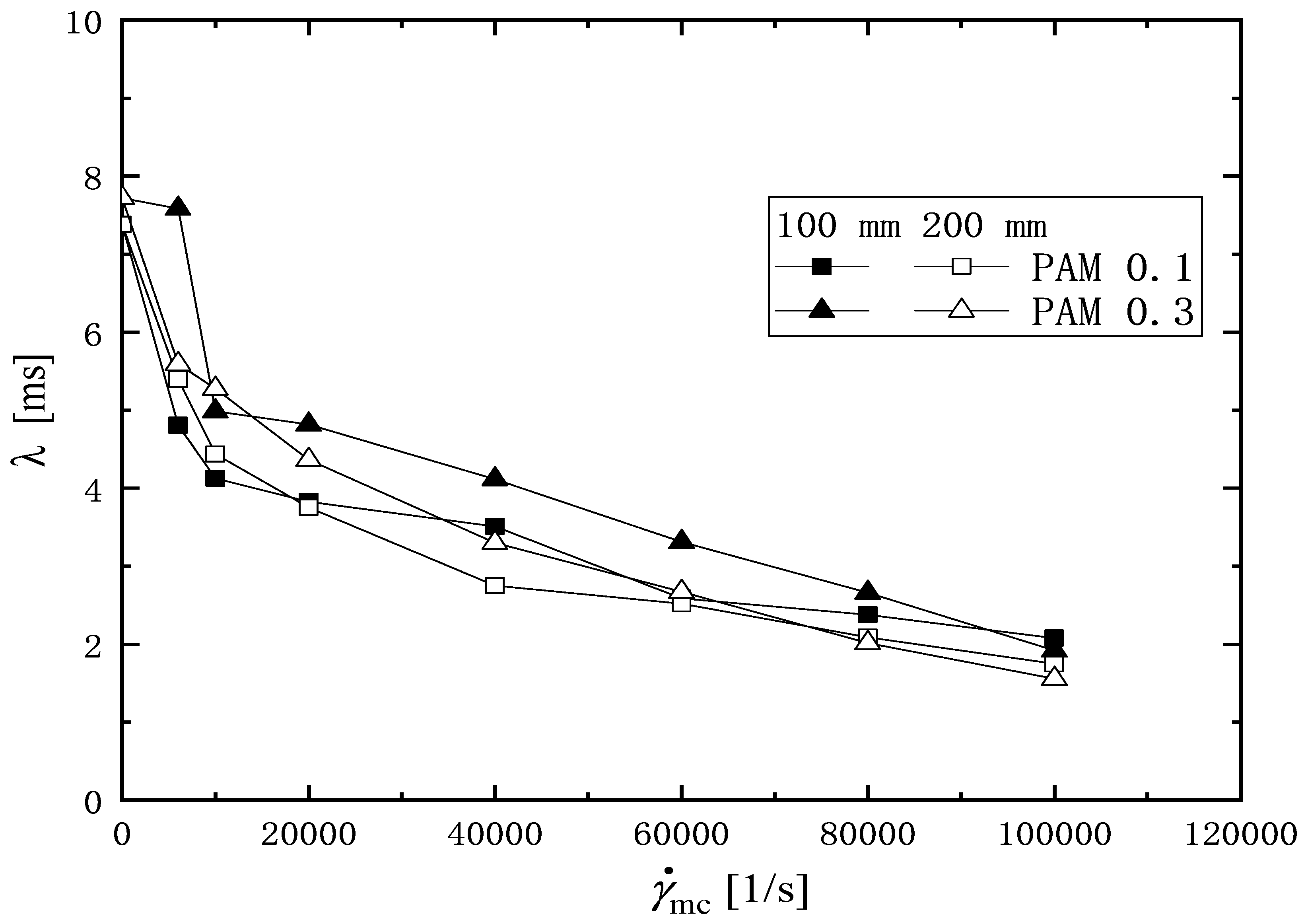
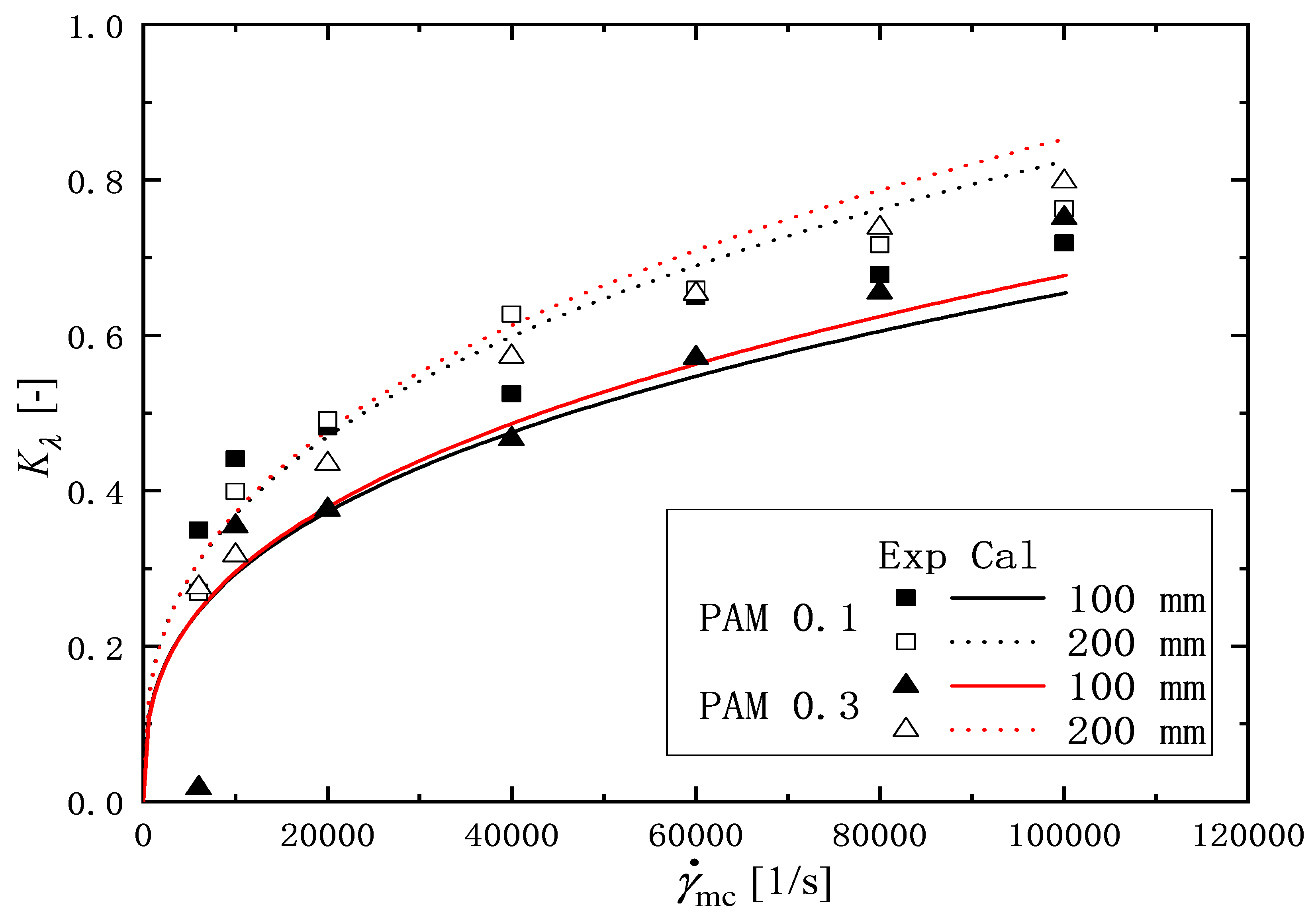
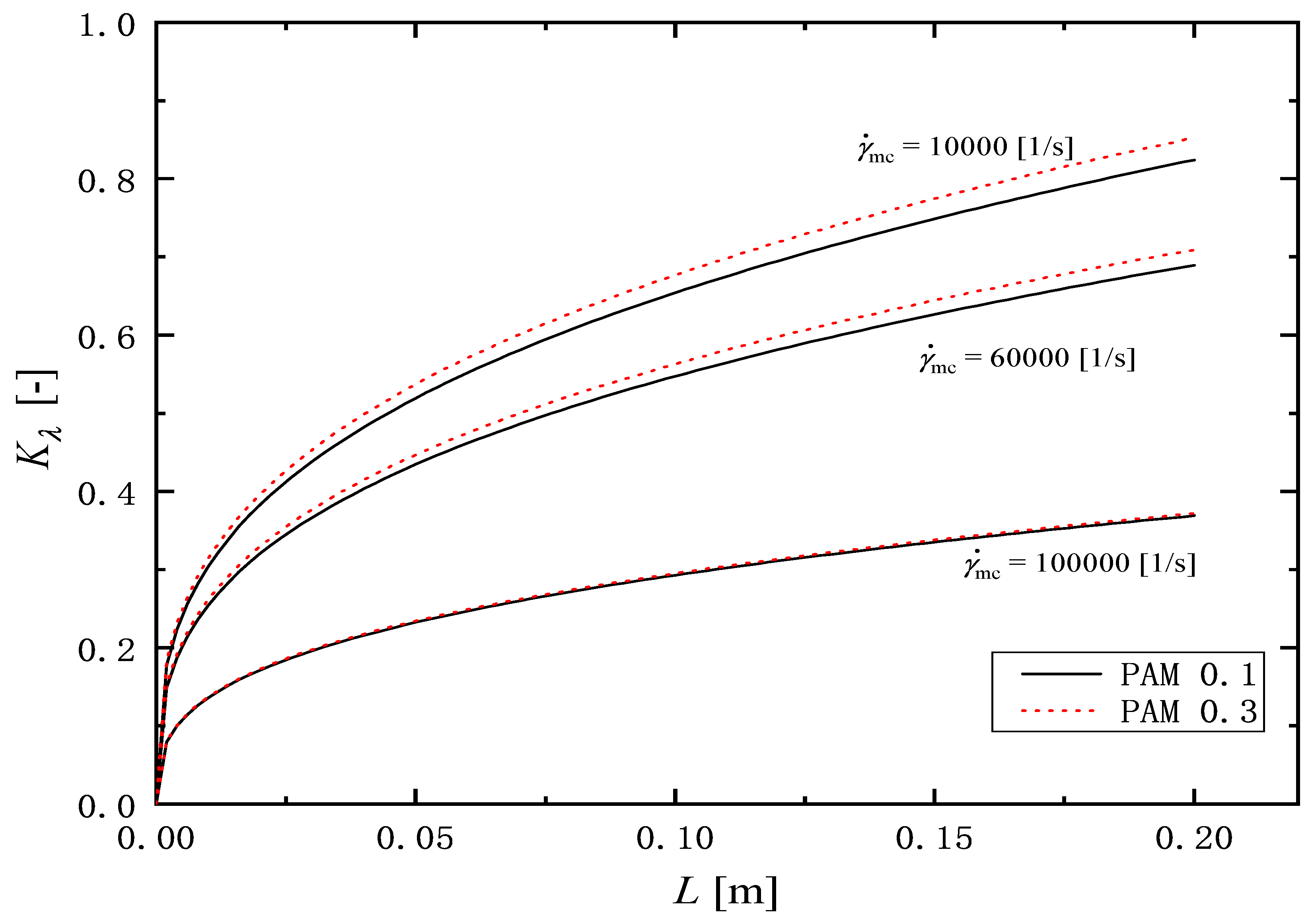
3.3. Prediction of Relaxation Time
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohamadali, M.; Ghiaseddin, A.; Irani, S.; Amirkhani, M.A.; Dahmardehei, M. Design and evaluation of a skin-on-a-chip pumpless microfluidic device. Sci. Rep. 2023, 13, 8861. [Google Scholar] [CrossRef] [PubMed]
- Fiorentini, G.; Carrandina, R.; Sarti, D.; Mulazzani, L.; Felicioli, A.; Coschiera, P.; Catalano, V.; Aliberti, C. Hepatic arterial infusion of Polythylene Glycol drug-eluting beads for Primary liver cancer therapy. Ann. Oncol. 2016, 27, iv24. [Google Scholar] [CrossRef]
- Yan, Y.; Li, J.; Bai, Y.; Peng, J. Polyethylene glycol-functionalized N, P-ligands enhance catalytic properties of cobalt complexes for the hydrosilylation reaction. Arab. J. Chem. 2023, 16, 104743. [Google Scholar] [CrossRef]
- Wen, J.; Liu, H.; Luo, J.; Schulz, J.M.; Böhm, L.; Wang, X.; Ning, P. Mass transfer characteristics of vanadium species on the high-efficient solvent extraction of vanadium in microchannels/microreactors. Sep. Purif. Technol. 2023, 315, 123638. [Google Scholar] [CrossRef]
- Gold, B.; Pyckhout-Hintzen, W.; Wischnewski, A.; Radulescu, A.; Monkenbusch, M.; Allgaier, J.; Hoffmann, I.; Parisi, D.; Vlassopoulos, D.; Richter, D. Direct assessment of tube dilation in entangled polymers. Phys. Rev. Lett. 2019, 122, 088001. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, R.; Hou, Y.; Wang, M.; Hou, X. Photochemical effect driven fluid behavior control in microscale pores and channels. Chin. Chem. Lett. 2022, 33, 3650–3656. [Google Scholar] [CrossRef]
- Wu, F.; Kong, X.; Liu, Y.; Wang, S.; Chen, Z.; Hou, X. Microfluidic-based isolation of circulating tumor cells with high-efficiency and high-purity. Chin. Chem. Lett. 2024, 35, 109754. [Google Scholar] [CrossRef]
- Ota, N.; Tanaka, N.; Sato, A.; Shen, Y.; Yalikun, Y.; Tanaka, Y. Microenvironmental Analysis and Control for Local Cells under Confluent Conditions via a Capillary-Based Microfluidic Device. Anal. Chem. 2022, 94, 16299–16307. [Google Scholar] [CrossRef]
- Xue, Q.; Xiao, Y.; Zhang, X.; Zhang, X.; Hong, W.; Yang, C. Dynamic responses of Ca-alginate/polyacrylamide hydrogels at high strain rates. Int. J. Mech. Sci. 2024, 269, 109052. [Google Scholar] [CrossRef]
- Strake, M.; Fischer-Wedi, C.V.; Khattab, M.H.; Lauermann, P.; Wollnik, C.; Stanischa, C.; Hoerauf, H.; Rehfeldt, F.; van Oterendorp, C. The influence of polyacrylamide gel substrate elasticity on primary cultures of rat retinal ganglion cells. Exp. Eye Res. 2024, 249, 110116. [Google Scholar] [CrossRef]
- Javaid, F.; Lodhi, M.S.; Khan, M.T.; Sarwar, M.; Samra, Z.Q. Comparative study on the production and immobilization of stem bromelain using polyacrylamide gel matrix and arginine coupled magnetic nanoparticles for enhanced operational stability. Biocatal. Agric. Biotechnol. 2024, 62, 103451. [Google Scholar] [CrossRef]
- Odell, J.; Keller, A. Flow-induced chain fracture of isolated linear macromolecules in solution. J. Polym. Sci. Part B Polym. Phys. 1986, 24, 1889–1916. [Google Scholar] [CrossRef]
- Odell, J.A.; Muller, A.J.; Narh, K.A.; Keller, A. Degradation of polymer solutions in extensional flows. Macromolecules 1990, 23, 3092–3103. [Google Scholar] [CrossRef]
- Buchholz, B.A.; Zahn, J.M.; Kenward, M.; Slater, G.W.; Barron, A.E. Flow-induced chain scission as a physical route to narrowly distributed, high molar mass polymers. Polymer 2004, 45, 1223–1234. [Google Scholar] [CrossRef]
- Ghoniem, S.; Chauveteau, G.; Moan, M.; Wolff, C. Mechanical degradation of semi-dilute polymer solutions in laminar flows. Can. J. Chem. Eng. 1981, 59, 450–454. [Google Scholar] [CrossRef]
- Sochi, T. Flow of non-Newtonian fluids in porous media. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 2437–2767. [Google Scholar] [CrossRef]
- Maerker, J. Shear degradation of partially hydrolyzed polyacrylamide solutions. Soc. Pet. Eng. J. 1975, 15, 311–322. [Google Scholar] [CrossRef]
- Ibezim, V.C.; Poole, R.J.; Dennis, D.J. Viscoelastic fluid flow in microporous media. J. Non-Newton. Fluid Mech. 2021, 296, 104638. [Google Scholar] [CrossRef]
- Nguyen, T.; Kausch, H.H. Influence of nozzle geometry on polystyrene degradation in convergent flow. Colloid Polym. Sci. 1991, 269, 1099–1110. [Google Scholar] [CrossRef]
- Benzi, R.; Ching, E.S. Polymers in fluid flows. Annu. Rev. Condens. Matter Phys. 2018, 9, 163–181. [Google Scholar] [CrossRef]
- Benzi, R. A short review on drag reduction by polymers in wall bounded turbulence. Phys. D Nonlinear Phenom. 2010, 239, 1338–1345. [Google Scholar]
- Lumley, J.L. Drag reduction by additives. Annu. Rev. Fluid Mech. 1969, 1, 367–384. [Google Scholar] [CrossRef]
- Dubief, Y.; White, C.M.; Terrapon, V.E.; Shaqfeh, E.S.; Moin, P.; Lele, S.K. On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 2004, 514, 271–280. [Google Scholar]
- Terrapon, V.; Dubief, Y.; Moin, P.; Shaqfeh, E.S.; Lele, S.K. Simulated polymer stretch in a turbulent flow using Brownian dynamics. J. Fluid Mech. 2004, 504, 61–71. [Google Scholar] [CrossRef]
- Pereira, A.S.; Mompean, G.; Thais, L.; Soares, E.J. Transient aspects of drag reducing plane Couette flows. J. Non-Newton. Fluid Mech. 2017, 241, 60–69. [Google Scholar]
- Pereira, A.S.; Mompean, G.; Thais, L.; Soares, E.J.; Thompson, R.L. Active and hibernating turbulence in drag-reducing plane Couette flows. Phys. Rev. Fluids 2017, 2, 084605. [Google Scholar]
- Pereira, A.S.; Mompean, G.; Thompson, R.L.; Soares, E.J. Elliptical, parabolic, and hyperbolic exchanges of energy in drag reducing plane Couette flows. Phys. Fluids 2017, 29, 115106. [Google Scholar] [CrossRef]
- Sengupta, S.; Ghosh, S.; Saha, S.; Chakraborty, S. Rotational instabilities in microchannel flows. Phys. Fluids 2019, 31, 054101. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M. Electro-elastic instabilities in cross-shaped microchannels. J. Non-Newton. Fluid Mech. 2018, 259, 61–77. [Google Scholar] [CrossRef]
- Bodiguel, H.; Beaumont, J.; Machado, A.; Martinie, L.; Kellay, H.; Colin, A. Flow enhancement due to elastic turbulence in channel flows of shear thinning fluids. Phys. Rev. Lett. 2015, 114, 028302. [Google Scholar] [CrossRef]
- Pan, L.; Morozov, A.; Wagner, C.; Arratia, P. Nonlinear elastic instability in channel flows at low Reynolds numbers. Phys. Rev. Lett. 2013, 110, 174502. [Google Scholar] [PubMed]
- Zimm, B.H. Dynamics of polymer molecules in dilute solution: Viscoelasticity, flow birefringence and dielectric loss. J. Chem. Phys. 1956, 24, 269–278. [Google Scholar]
- Bojang, A.A.; Wu, H.S. Design, fundamental principles of fabrication and applications of microreactors. Processes 2020, 8, 891. [Google Scholar] [CrossRef]
- Hakke, V.; Sonawane, S.; Anandan, S.; Sonawane, S.; Ashokkumar, M. Process intensification approach using microreactors for synthesizing nanomaterials—A critical review. Nanomaterials 2021, 11, 98. [Google Scholar] [CrossRef]
- Kulicke, W.M.; Clasen, C. Viscosimetry of Polymers and Polyelectrolytes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Mark, J.E. Polymer Data Handbook; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Binding, D. An approximate analysis for contraction and converging flows. J. Non-Newton. Fluid Mech. 1988, 27, 173–189. [Google Scholar]
- Escudier, M.; Gouldson, I.; Pereira, A.; Pinho, F.; Poole, R. On the reproducibility of the rheology of shear-thinning liquids. J. Non-Newton. Fluid Mech. 2001, 97, 99–124. [Google Scholar]
- Schramm, G. A Practical Approach to Rheology and Rheometry; Gebrueder HAAKE GmbH: Karlsruhe, Germany, 1994. [Google Scholar]
- Sridhar, T.; Tirtaatmadja, V.; Nguyen, D.; Gupta, R. Measurement of extensional viscosity of polymer solutions. J. Non-Newton. Fluid Mech. 1991, 40, 271–280. [Google Scholar] [CrossRef]
- Anna, S.L.; Rogers, C.; McKinley, G.H. On controlling the kinematics of a filament stretching rheometer using a real-time active control mechanism. J. Non-Newton. Fluid Mech. 1999, 87, 307–335. [Google Scholar]
- Clasen, C.; Phillips, P.M.; Palangetic, L.; Vermant, J. Dispensing of rheologically complex fluids: The map of misery. AIChE J. 2012, 58, 3242–3255. [Google Scholar] [CrossRef]
- McKinley, G.H. Visco-Elasto-Capillary Thinning and Break-Up of Complex Fluids; Massachusetts Institute of Technology: Cambridge, MA, USA, 2005; pp. 1–49. [Google Scholar]
- Entov, V.; Hinch, E. Effect of a spectrum of relaxation times on the capillary thinning of a filament of elastic liquid. J. Non-Newton. Fluid Mech. 1997, 72, 31–53. [Google Scholar]
- Clasen, C.; Eggers, J.; Fontelos, M.A.; Li, J.; McKinley, G.H. The beads-on-string structure of viscoelastic threads. J. Fluid Mech. 2006, 556, 283–308. [Google Scholar] [CrossRef]
- Yasuda, K.; Sugiura, Y.; Mori, N. Direct measurements of velocity profiles in flows of polymer solutions through a rectangular microchannel with a PDMS surface. Nihon Reoroji Gakkaishi 2006, 34, 41–45. [Google Scholar]
- Clasen, C.; Plog, J.; Kulicke, W.M.; Owens, M.; Macosko, C.; Scriven, L.; Verani, M.; McKinley, G.H. How dilute are dilute solutions in extensional flows? J. Rheol. 2006, 50, 849–881. [Google Scholar]
- Zell, A.; Gier, S.; Rafai, S.; Wagner, C. Is there a relation between the relaxation time measured in CaBER experiments and the first normal stress coefficient? J. Non-Newton. Fluid Mech. 2010, 165, 1265–1274. [Google Scholar]
- Vanapalli, S.A.; Islam, M.T.; Solomon, M.J. Scission-induced bounds on maximum polymer drag reduction in turbulent flow. Phys. Fluids 2005, 17, 095108. [Google Scholar]
- Mohammadtabar, M.; Sanders, R.; Ghaemi, S. Viscoelastic properties of flexible and rigid polymers for turbulent drag reduction. J. Non-Newton. Fluid Mech. 2020, 283, 104347. [Google Scholar]
- Pereira, A.S.; Andrade, R.M.; Soares, E.J. Drag reduction induced by flexible and rigid molecules in a turbulent flow into a rotating cylindrical double gap device: Comparison between Poly (ethylene oxide), Polyacrylamide, and Xanthan Gum. J. Non-Newton. Fluid Mech. 2013, 202, 72–87. [Google Scholar]
- Escudier, M.; Nickson, A.; Poole, R. Turbulent flow of viscoelastic shear-thinning liquids through a rectangular duct: Quantification of turbulence anisotropy. J. Non-Newton. Fluid Mech. 2009, 160, 2–10. [Google Scholar]
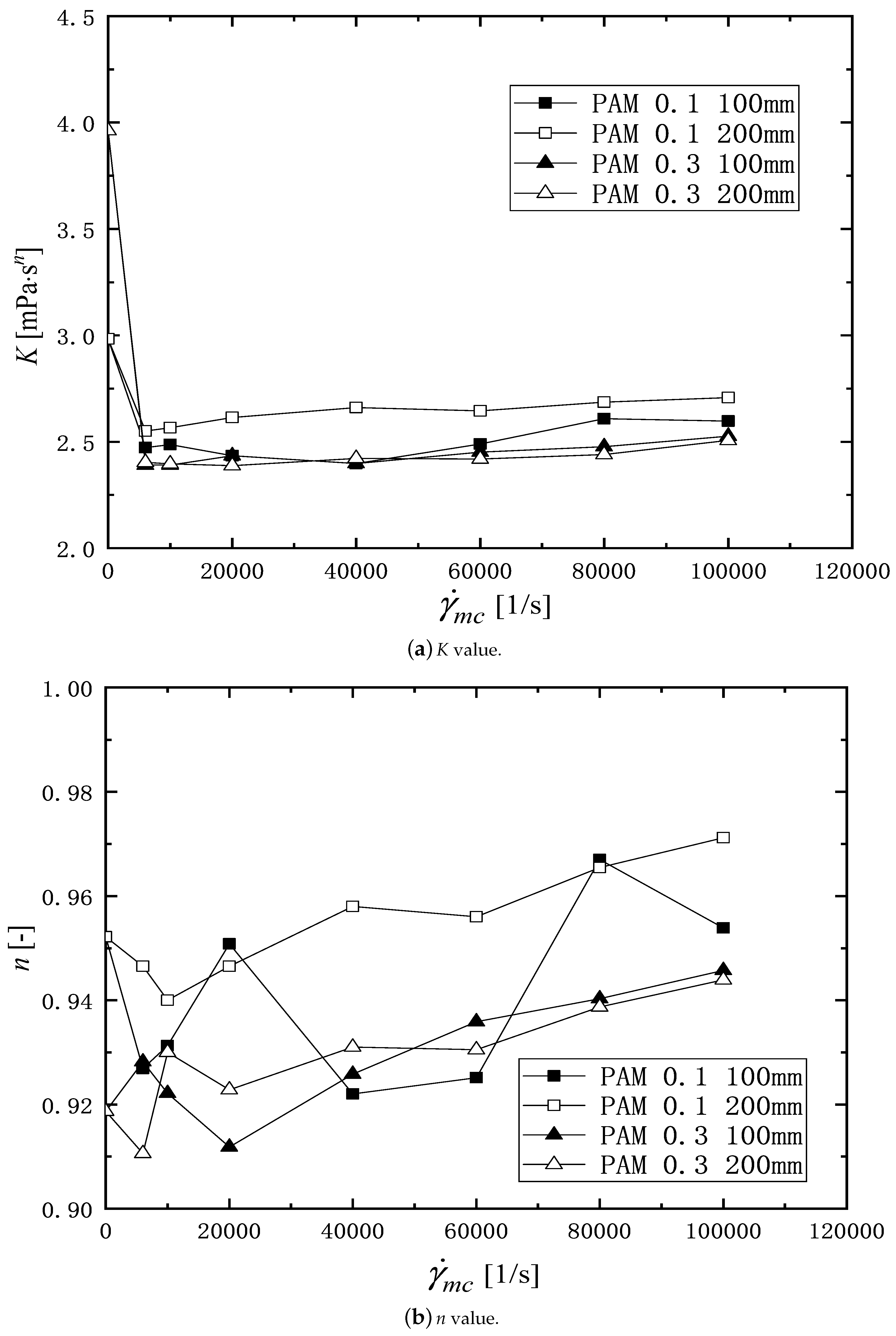

| PAM 0.1–100 mm | PAM 0.3–100 mm | PAM 0.1–200 mm | PAM 0.3–200 mm | |||||
|---|---|---|---|---|---|---|---|---|
| 1/s | [mPa· ] | [mPa· ] | [mPa· ] | [mPa· ] | ||||
| 0 | 2.98 | 0.952 | 3.96 | 0.919 | 2.98 | 0.919 | 3.96 | 0.919 |
| 6000 | 2.47 | 0.927 | 2.39 | 0.947 | 2.55 | 0.928 | 2.40 | 0.911 |
| 10,000 | 2.49 | 0.931 | 2.39 | 0.940 | 2.57 | 0.922 | 2.40 | 0.93 |
| 20,000 | 2.43 | 0.951 | 2.43 | 0.947 | 2.61 | 0.912 | 2.39 | 0.923 |
| 40,000 | 2.40 | 0.922 | 2.40 | 0.958 | 2.66 | 0.926 | 2.42 | 0.931 |
| 60,000 | 2.49 | 0.925 | 2.45 | 0.956 | 2.65 | 0.936 | 2.42 | 0.931 |
| 80,000 | 2.61 | 0.967 | 2.48 | 0.966 | 2.69 | 0.940 | 2.44 | 0.939 |
| 100,000 | 2.60 | 0.954 | 2.53 | 0.971 | 2.71 | 0.946 | 2.51 | 0.944 |
| Shear Rate (1/s) | PAM 0.1 | PAM 0.3 | ||
|---|---|---|---|---|
| 100 mm | 200 mm | 100 mm | 200 mm | |
| 0 | 7.38 | 7.38 | 7.72 | 7.72 |
| 6000 | 4.81 | 5.39 | 7.58 | 5.59 |
| 10,000 | 4.13 | 4.44 | 4.99 | 5.27 |
| 20,000 | 3.82 | 3.75 | 4.82 | 4.37 |
| 40,000 | 3.51 | 2.75 | 4.12 | 3.30 |
| 60,000 | 2.59 | 2.52 | 3.31 | 2.67 |
| 80,000 | 2.38 | 2.09 | 2.66 | 2.02 |
| 100,000 | 2.08 | 1.75 | 1.92 | 1.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yonemoto, Y.; Yamahata, Y.; Kawahara, A. Rheological Property Changes in Polyacrylamide Aqueous Solution Flowed Through Microchannel Under Low Reynolds Number and High Shear Rate Conditions. Micromachines 2025, 16, 545. https://doi.org/10.3390/mi16050545
Li Y, Yonemoto Y, Yamahata Y, Kawahara A. Rheological Property Changes in Polyacrylamide Aqueous Solution Flowed Through Microchannel Under Low Reynolds Number and High Shear Rate Conditions. Micromachines. 2025; 16(5):545. https://doi.org/10.3390/mi16050545
Chicago/Turabian StyleLi, Yishuai, Yukihiro Yonemoto, Yuki Yamahata, and Akimaro Kawahara. 2025. "Rheological Property Changes in Polyacrylamide Aqueous Solution Flowed Through Microchannel Under Low Reynolds Number and High Shear Rate Conditions" Micromachines 16, no. 5: 545. https://doi.org/10.3390/mi16050545
APA StyleLi, Y., Yonemoto, Y., Yamahata, Y., & Kawahara, A. (2025). Rheological Property Changes in Polyacrylamide Aqueous Solution Flowed Through Microchannel Under Low Reynolds Number and High Shear Rate Conditions. Micromachines, 16(5), 545. https://doi.org/10.3390/mi16050545






