Research on Valveless Piezoelectric Pump Based on Coriolis Effect
Abstract
1. Introduction
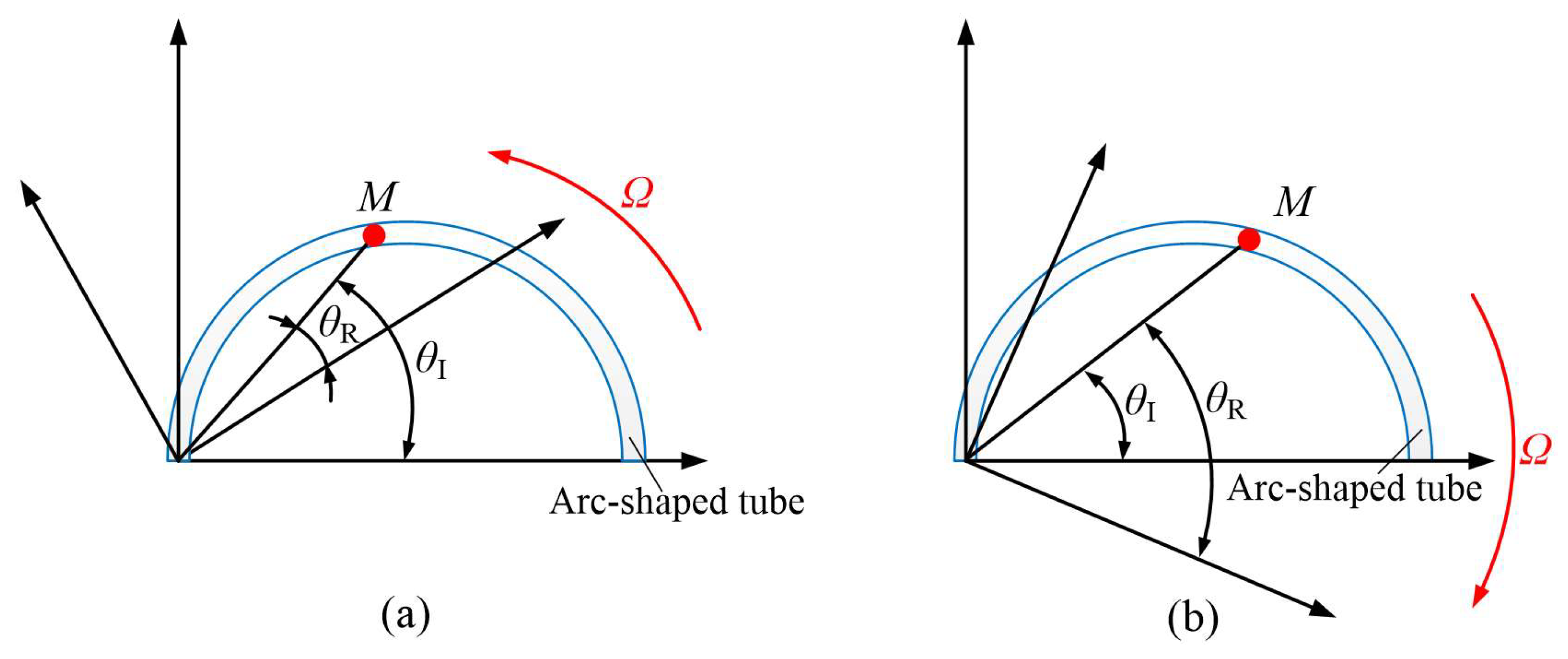
2. Internal Flow Analysis Flow Tube
3. Structure Design and Working Principle of the Pump
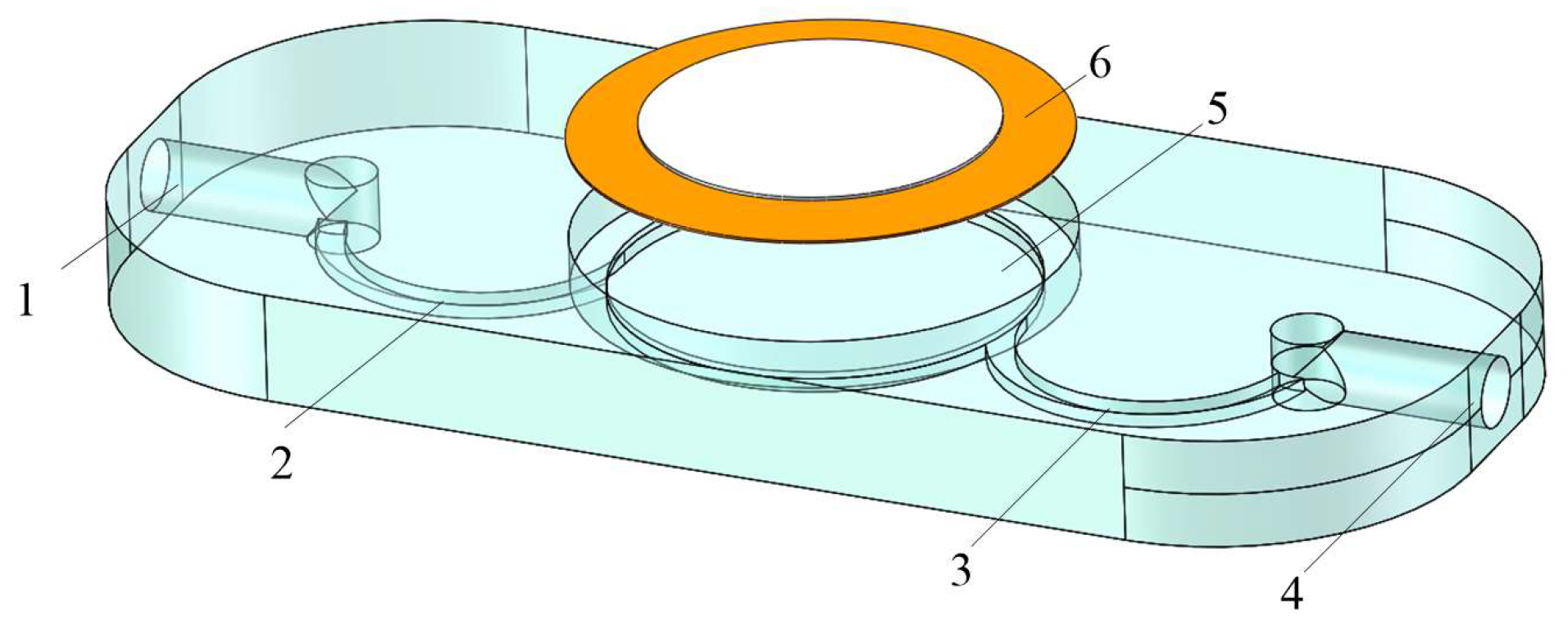
3.1. Structure Design
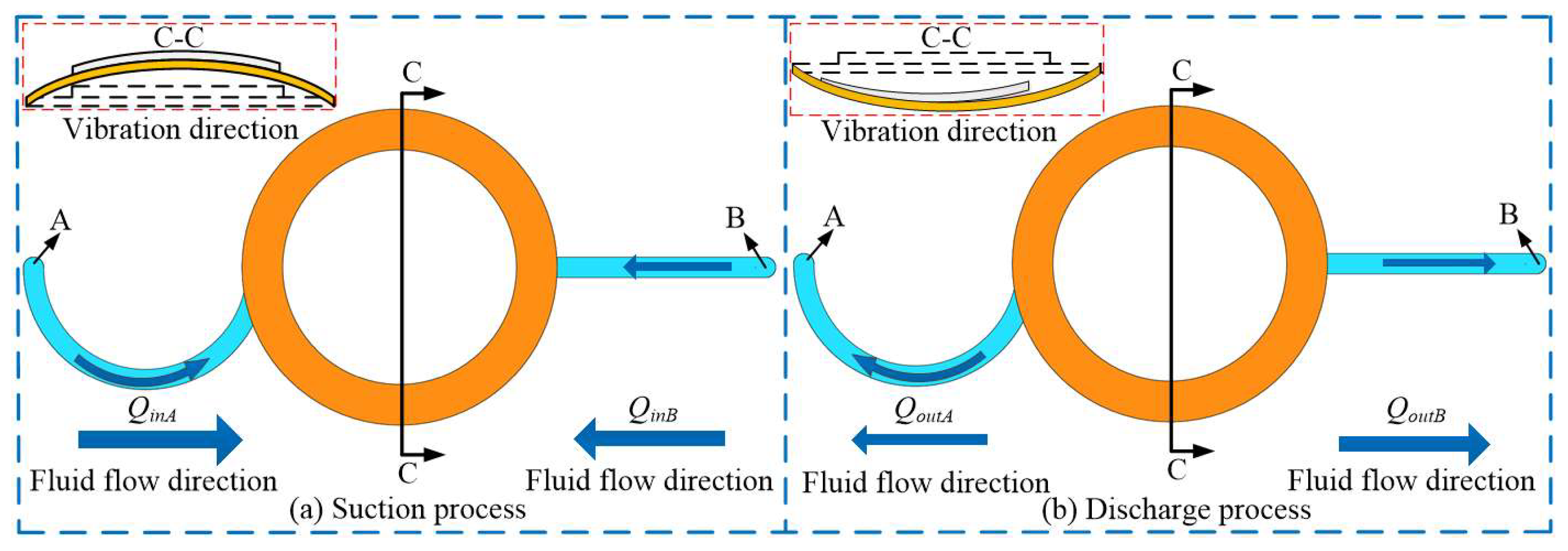
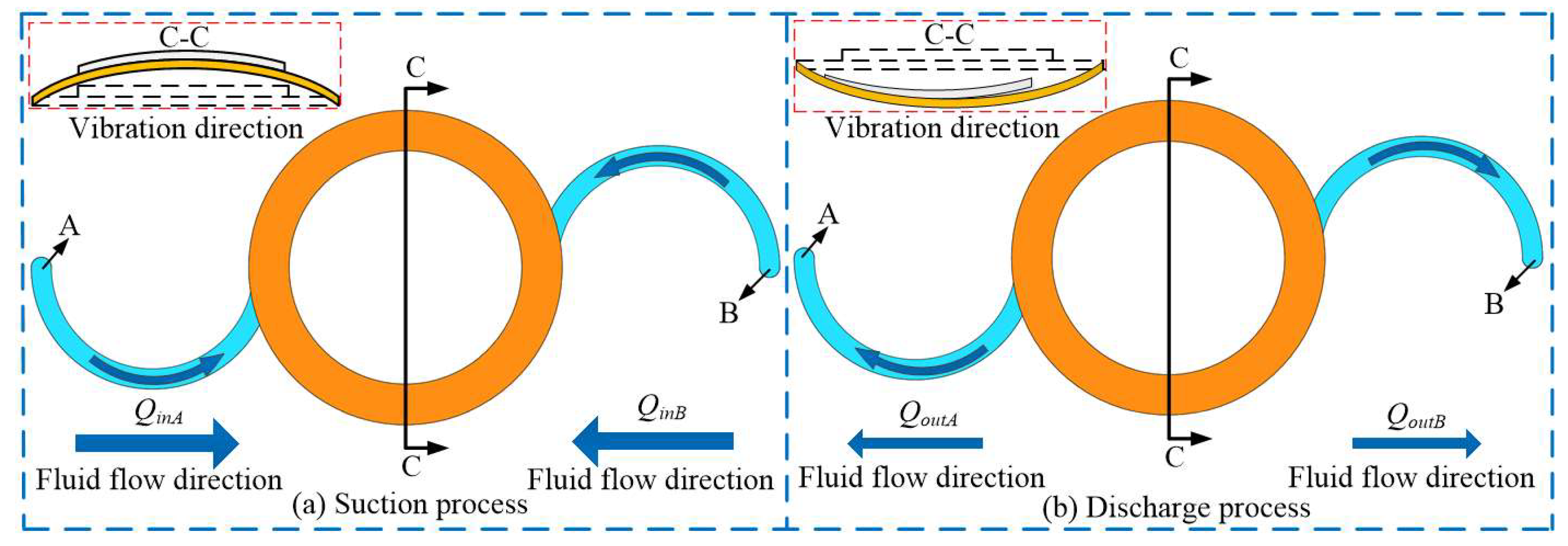
3.2. Working Principle
4. Experiments
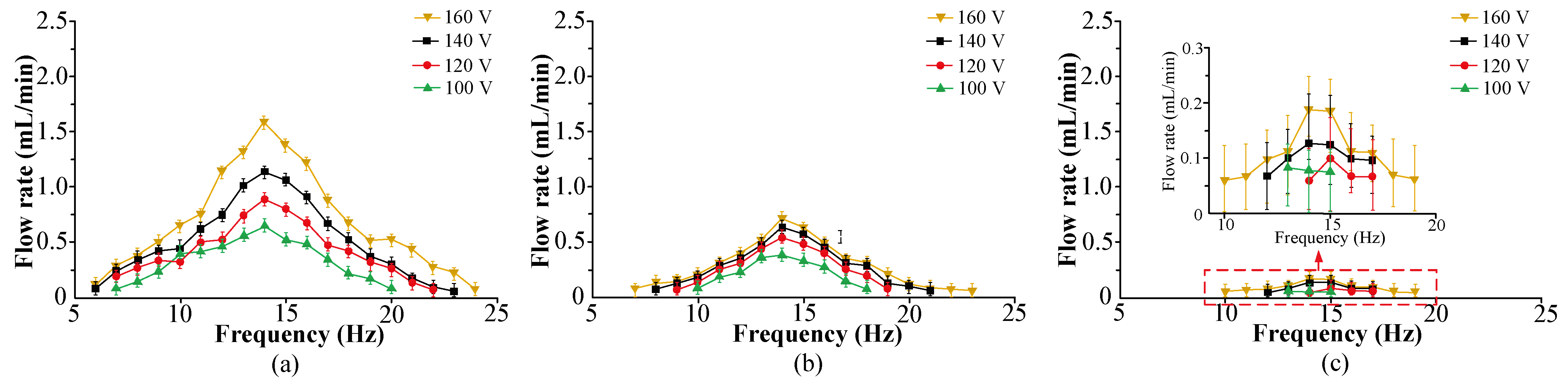
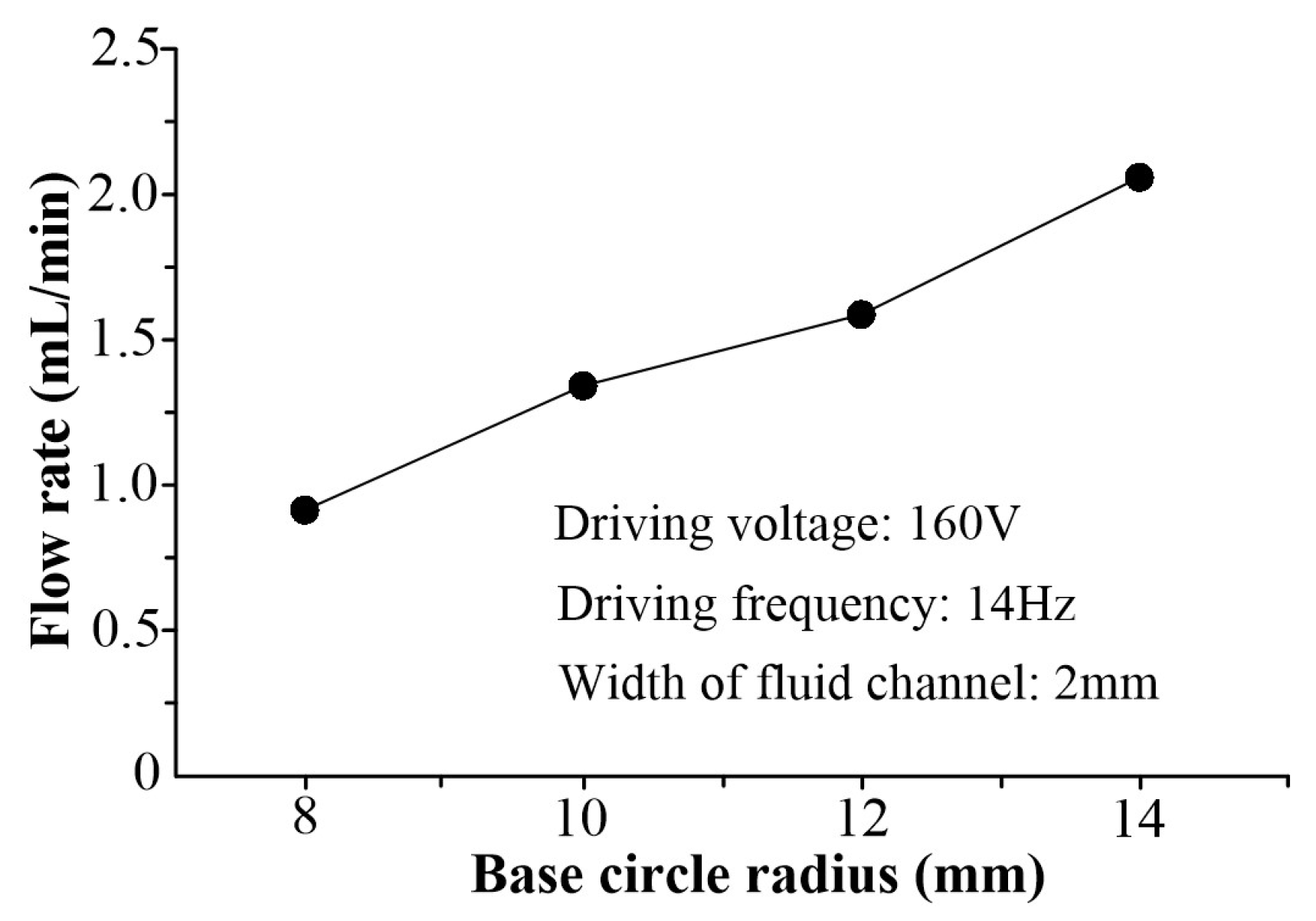
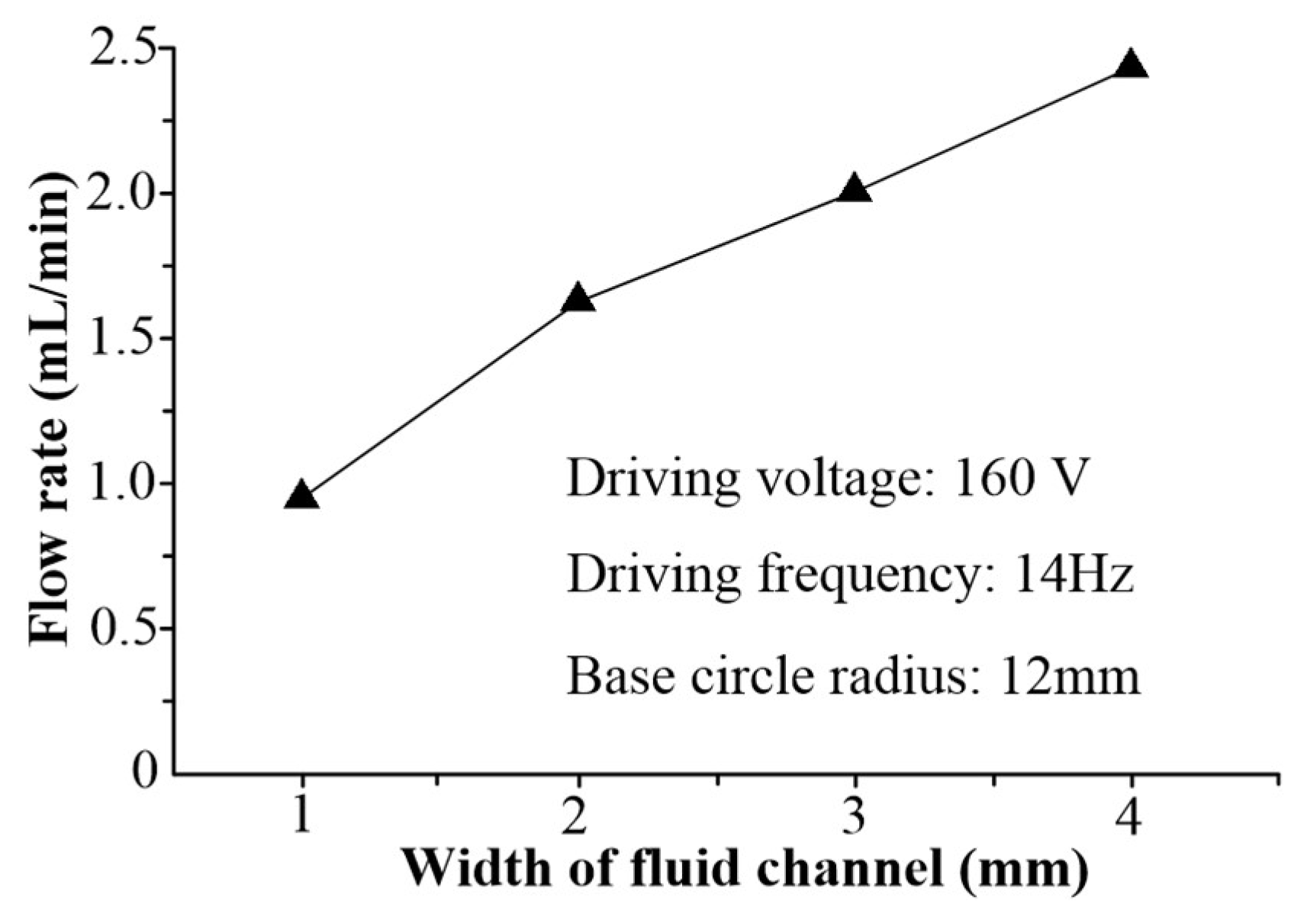
4.1. Experiment Design
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| I | quantity in the inertial frame of reference; |
| u | velocity components of the coordinate axis r; |
| v | velocity components of the coordinate axis θ; |
| w | velocity components of the coordinate axis z; |
| ρ | density of the liquid in the flow tube; |
| P | function of ρ; |
| a | base circle radius; |
| Ω | angular velocity of liquid flow; |
| vc | velocity of liquid flow clockwise; |
| va | velocity of liquid flow counterclockwise; |
| S | cross-sectional area of the flow channel; |
| t | time of liquid flow; |
| vt(in) | velocity of the liquid flows in flow tube B; |
| vt(out) | velocity of the liquid flows in tube B. |
References
- Yan, Q.F.; Yin, Y.K.; Sun, W.T.; Fu, J. Advances in Valve-less Piezoelectric Pumps. Appl. Sci. 2021, 11, 7061. [Google Scholar] [CrossRef]
- Hu, R.H.; He, L.P.; Wang, C.S.; Wang, H.X.; Sun, L.; Li, X.T.; Lin, J.Q. Performance study of external Laval tube diffusion/nozzle piezoelectric pump. Sens. Actuators A Phys. 2023, 361, 114566. [Google Scholar] [CrossRef]
- Yan, Q.F.; Sun, W.T. Research of piezoelectric pump with a vortex linear valve structure. Phys. Fluids 2023, 35, 102005. [Google Scholar] [CrossRef]
- Yan, Q.F.; Sun, W.T.; Zhang, L.; Wang, H.M.; Zhang, J.H. Effects of Vibration Characteristics on the Atomization Performance in the Medical Piezoelectric Atomization Device Induced by Intra-Hole Fluctuation. Chin. J. Mech. Eng. 2021, 34, 331–339. [Google Scholar] [CrossRef]
- Yan, Q.F.; Sun, W.T.; Zhang, J.H. Study on the formation and separation process of droplets in the medical piezoelectric atomization device induced by intra-hole fluctuation. Chin. J. Mech. Eng. 2022, 35, 285–296. [Google Scholar] [CrossRef]
- Datta, A.; Biswas, S.; Dhar, R.; Bhattacharyya, T.K. Design and development of a piezoelectric driven micropump integrated with hollow microneedles for precise insulin delivery. J. Micromech. Microeng. 2023, 33, 075003. [Google Scholar] [CrossRef]
- Ma, M.D.; Zhang, F.; Huo, Y.X.; Tan, T.; Gui, Z.Z.; Zhang, W.R.; Huang, X.; Zhou, X.S.; Zou, T.; Zhang, J.H. Pseudo-resonance phenomenon of valveless piezoelectric pump. J. Fluids Struct. 2023, 121, 103954. [Google Scholar] [CrossRef]
- Hu, R.H.; He, L.P.; Hu, D.B.; Hou, Y.; Cheng, G.M. Recent studies on the application of piezoelectric pump in different fields. Microsyst. Technol.-Micro-Nanosyst.-Inf. Storage Process. Syst. 2023, 29, 663–682. [Google Scholar] [CrossRef]
- Li, H.Y.; Liu, J.K.; Li, K.; Liu, Y.X. A review of recent studies on piezoelectric pumps and their application. Mech. Syst. Signal Process. 2021, 151, 107393. [Google Scholar] [CrossRef]
- Fan, Y.W.; Zhang, X.F.; Xiang, L.Y.; Cheng, Y.H.; Luo, X.B. A compact jet array impingement cooling system driven by integrated piezoelectric micropump. Int. J. Heat Mass Transf. 2023, 205, 123905. [Google Scholar] [CrossRef]
- Lu, S.; Yu, M.; Qian, C.P.; Deng, F.Q.; Chen, S.; Kan, J.W.; Zhang, Z.H. A Quintuple-Bimorph Tenfold-Chamber Piezoelectric Pump Used in Water-Cooling System of Electronic Chip. IEEE Access 2020, 8, 186691–186698. [Google Scholar] [CrossRef]
- Hou, Y.; He, L.P.; Hu, D.B.; Zhang, L.M.; Yu, B.J.; Cheng, G.M. Recent trends in structures and applications of valveless piezoelectric pump-a review. J. Micromech. Microeng. 2022, 32, 053002. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, H.Y.; Zhou, X.X.; Liu, B.; Chen, S.; Li, K. A Universal Piezoelectric Micropump with Capabilities of Self-Cleaning, Stable Filtration and Precise Pumping. IEEE Trans. Ind. Electron. 2024, 71, 678–687. [Google Scholar] [CrossRef]
- He, L.P.; Hu, R.H.; Wang, C.S.; Hu, D.B.; Li, X.T.; Cheng, G.M. Performance analysis of a novel flat lay-type synthetic jet pump with Y-shaped jet chamber. Rev. Sci. Instrum. 2023, 94, 105008. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.H.; Wang, D.K.; Wang, S.Y.; Akyoshi, Q. Research on piezoelectric pump-lagging of valve. Chin. J. Mech. Eng. 2003, 39, 107–110. (In Chinese) [Google Scholar] [CrossRef]
- Stemme, E.; Stemme, G. A valve-less diffuser/nozzle-based fluid pump. Sens. Actuators A Physucal 1993, 39, 159–167. [Google Scholar] [CrossRef]
- Kim, C.N. Internal pressure characteristics and performance features of the piezoelectric micropumps with the diffuser/nozzle and electromagnetic resistance. Comput. Fluids 2014, 104, 30–39. [Google Scholar] [CrossRef]
- Zhang, J.H.; Wang, S.Y. Study of Piezoelectric Valveless Diffuser/Nozzle-based Fluid Pump—One-way Flow Principle and the Pump Flow. Piezoelectr. Acoustoopt. 2001, 23, 23–25. (In Chinese) [Google Scholar]
- Jiang, L.S.; Morris, C.J.; Sharma, N.R.; Bardell, R.L.; Forster, F.K. Transport of particle-laden fluids through fixedwave micropump. Microelectromech. Syst. (MEMS) ASME 1999, 1, 503–509. [Google Scholar]
- Zhang, J.H.; Li, Y.L.; Xia, Q.X. Analysis of the pump volume flow rate and tube property of the piezoelectric valve-less pump with Y-shape tubes. Chin. J. Mech. Eng. 2007, 43, 136–141. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.H.; Xun, X.C.; Wang, S.Y. Theory and experimental verification on valve-less piezoelectric pump with multistage Y-shape treelike bifurcate tubes. Chin. J. Mech. Eng. 2013, 26, 462–468. [Google Scholar] [CrossRef]
- Huang, J.; Zou, L.; Li, Z.J.; Wang, X.; Zhang, Q.; Wang, Y. Development and performance comparison of valve-less piezoelectric pumps with asymmetrical channels. Sens. Actuators A Phys. 2020, 314, 112241. [Google Scholar] [CrossRef]
- Xia, Q.X.; Zhang, J.H.; Li, H. Valve-less piezoelectric pump with unsymmetrical slope chamber bottom. Opt. Precis. Eng. 2006, 14, 641–647. (In Chinese) [Google Scholar]
- Zhang, J.H.; Xia, Q.X.; Huang, Y.; Leng, X.F.; Huang, J.; Zhao, C.S. Theory and experimental verification of valve-less piezoelectric pump with rotatable unsymmetrical slopes. Sci. China Technol. Sci. 2011, 54, 3070–3077. [Google Scholar] [CrossRef]
- Bian, K.; Huang, Z.; Bao, Q.B.; Zhang, J.H.; Lai, L.Y.; Chen, X.S.; Chen, Z.L. Design and Experiment of Streamlined Piezoelectric Pump with Low Vortex and Large Flow Rate. Trans. Nanjing Univ. Aeronaut. Astronaut. 2020, 37, 156–163. [Google Scholar]
- Bian, K.; Huang, Z.; Dai, J.T.; Zhang, F.; Chen, X.S.; Chen, Z.L.; Lai, L.Y.; Zhang, J.H. Investigation on the Influence of Design Parameters of Streamline Flow Tubes on Pump Performance. Shock. Vib. 2021, 2021, 6640252. [Google Scholar] [CrossRef]
- Anders, P. How do we understand the Coriolis force? Bull. Am. Meteorol. Soc. 1998, 79, 1373–1385. [Google Scholar]
- Dean, W.R. Note on the motion of fluid in a curved pipe. Lond. Edinb. Dublin Philos. Mag. 1927, 4, 208–223. [Google Scholar] [CrossRef]
- Yan, Q.F.; Yin, Y.K.; Wang, L.; Wang, H.M.; Sun, W.T. Theoretical and experimental research on valve-less piezoelectric pump with arc-shaped tubes. Rev. Sci. Instrum. 2022, 93, 105004. [Google Scholar] [CrossRef]
- Yan, Q.F.; Sun, W.T.; Wang, H.M. Theoretical and Experimental Studies on Valve-less Piezoelectric Pump with Variable Cross Section Arc-shaped Tubes. J. Mech. Eng. 2023, 59, 320–327. (In Chinese) [Google Scholar]




| Title | Diameter of Piezoelectric Ceramics (mm) | Thickness of Piezoelectric Ceramics (mm) | Diameter of Brass Substrate (mm) | Thickness of Brass Substrate (mm) |
|---|---|---|---|---|
| Size | 25.0 | 0.25 | 35.0 | 0.18 |
| Pump (Number) | Base Circle Radius (mm) | Width (mm) | Depth (mm) |
|---|---|---|---|
| 1 | 8.0 | 2.0 | 1.0 |
| 2 | 10.0 | 2.0 | 1.0 |
| 3 | 12.0 | 2.0 | 1.0 |
| 4 | 14.0 | 2.0 | 1.0 |
| 5 | 12.0 | 1.0 | 1.0 |
| 6 | 12.0 | 3.0 | 1.0 |
| 7 | 12.0 | 4.0 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Liu, Z.; Sun, W.; Jiang, M. Research on Valveless Piezoelectric Pump Based on Coriolis Effect. Micromachines 2025, 16, 527. https://doi.org/10.3390/mi16050527
Yan Q, Liu Z, Sun W, Jiang M. Research on Valveless Piezoelectric Pump Based on Coriolis Effect. Micromachines. 2025; 16(5):527. https://doi.org/10.3390/mi16050527
Chicago/Turabian StyleYan, Qiufeng, Zhiling Liu, Wanting Sun, and Mengyao Jiang. 2025. "Research on Valveless Piezoelectric Pump Based on Coriolis Effect" Micromachines 16, no. 5: 527. https://doi.org/10.3390/mi16050527
APA StyleYan, Q., Liu, Z., Sun, W., & Jiang, M. (2025). Research on Valveless Piezoelectric Pump Based on Coriolis Effect. Micromachines, 16(5), 527. https://doi.org/10.3390/mi16050527






