Temperature Effects on Wicking Dynamics: Experimental and Numerical Study on Micropillar-Structured Surfaces
Abstract
1. Introduction
2. Research Methods
2.1. Experimental Methods
2.1.1. Micropillar Sample Fabrication
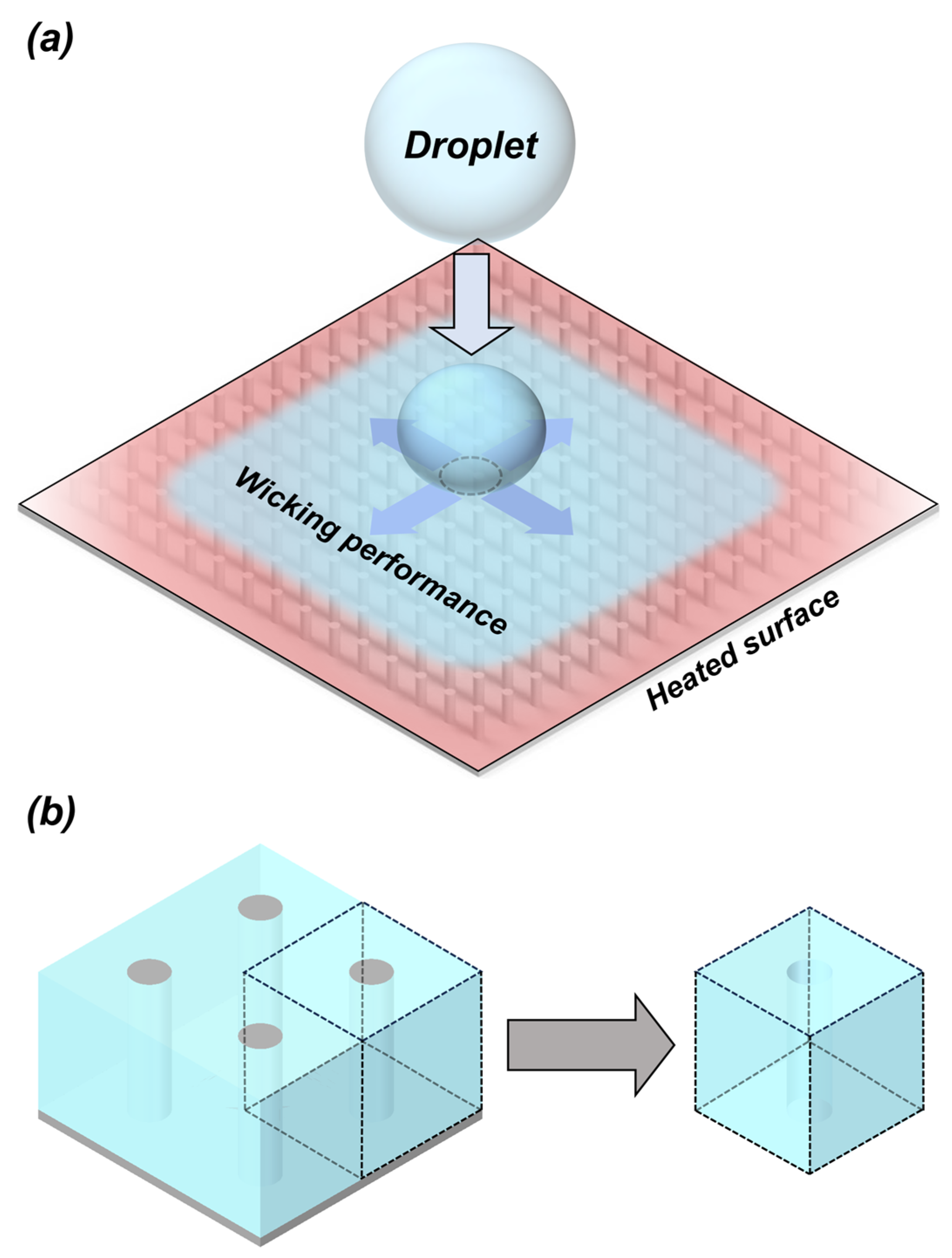
2.1.2. Wicking Measurement
2.1.3. IR Visualization
2.1.4. Uncertainty
2.2. Numerical Methods
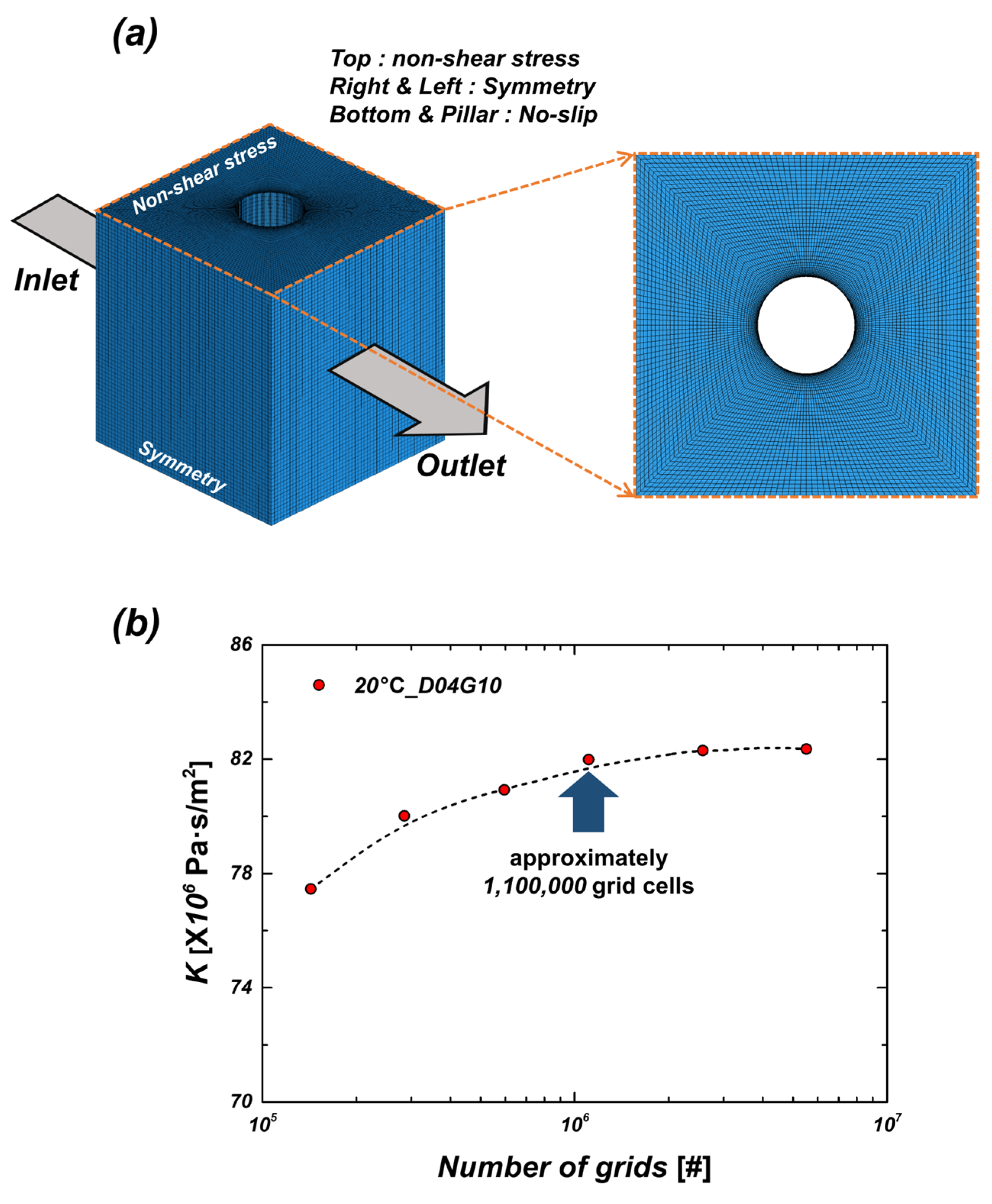
2.2.1. Physical Model and Boundary Conditions
2.2.2. Grid Independence Test
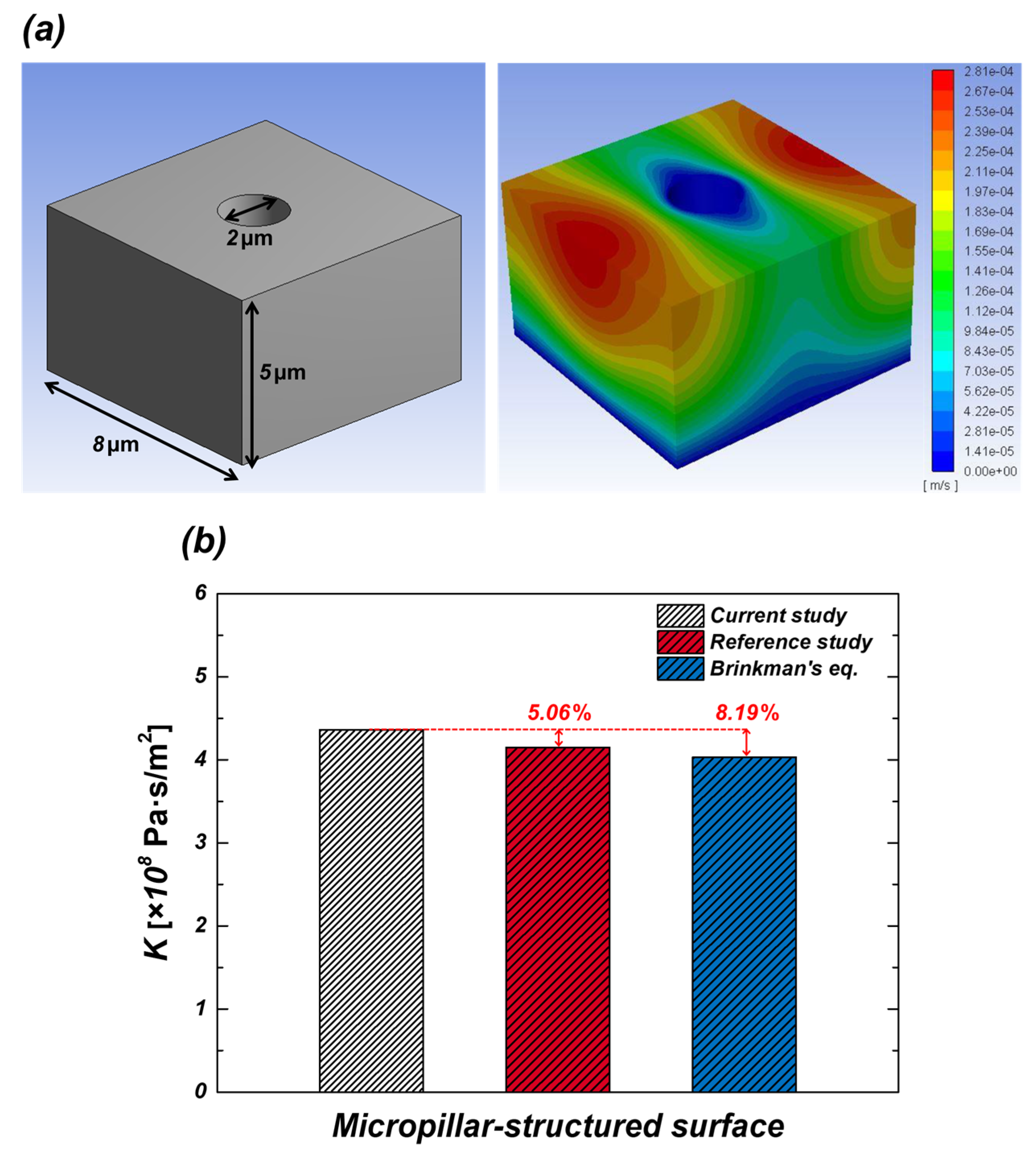
2.2.3. Model Validation
3. Results
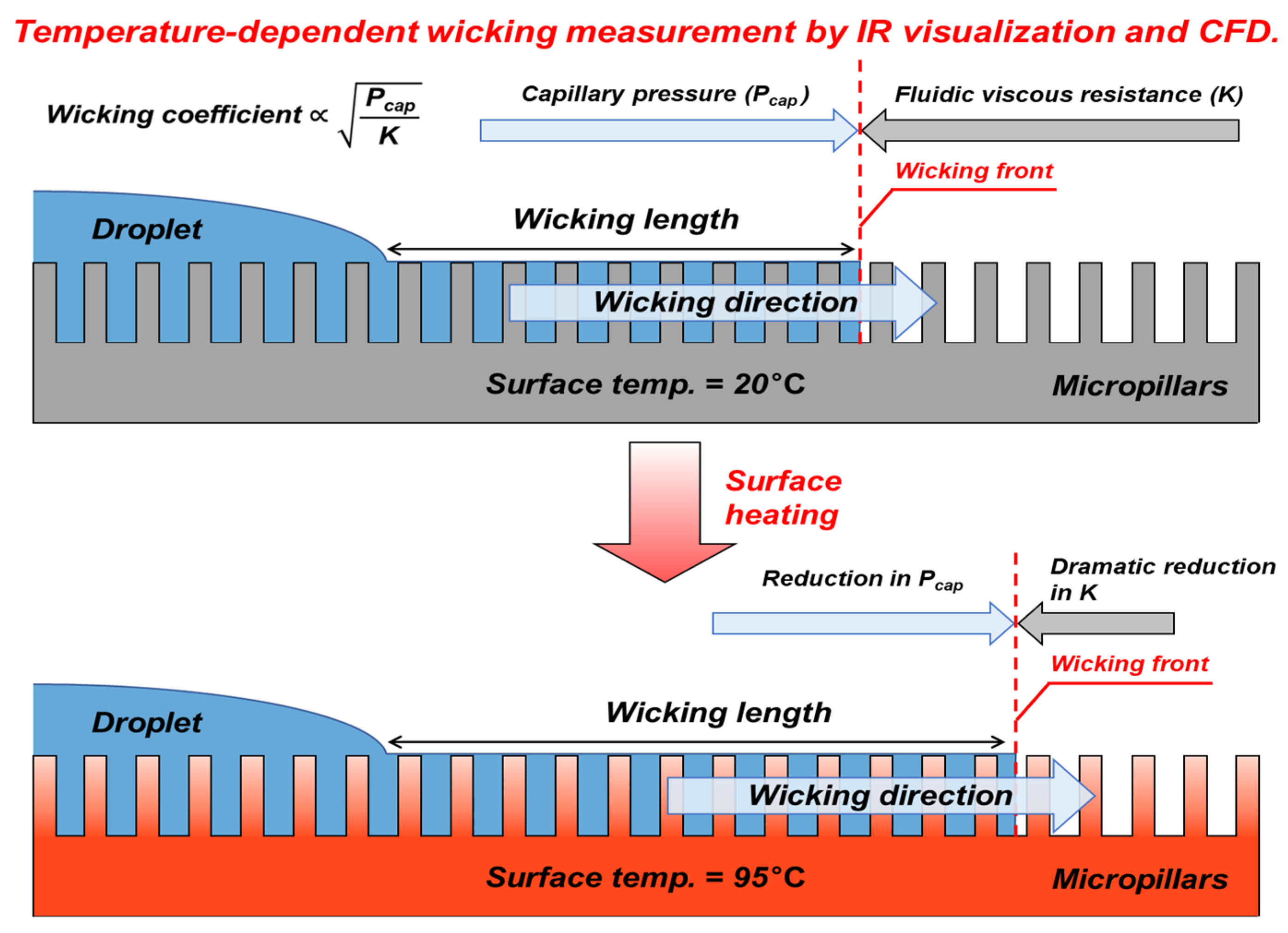
3.1. Wicking Analysis Under Temperature Variation Using IR Visualization
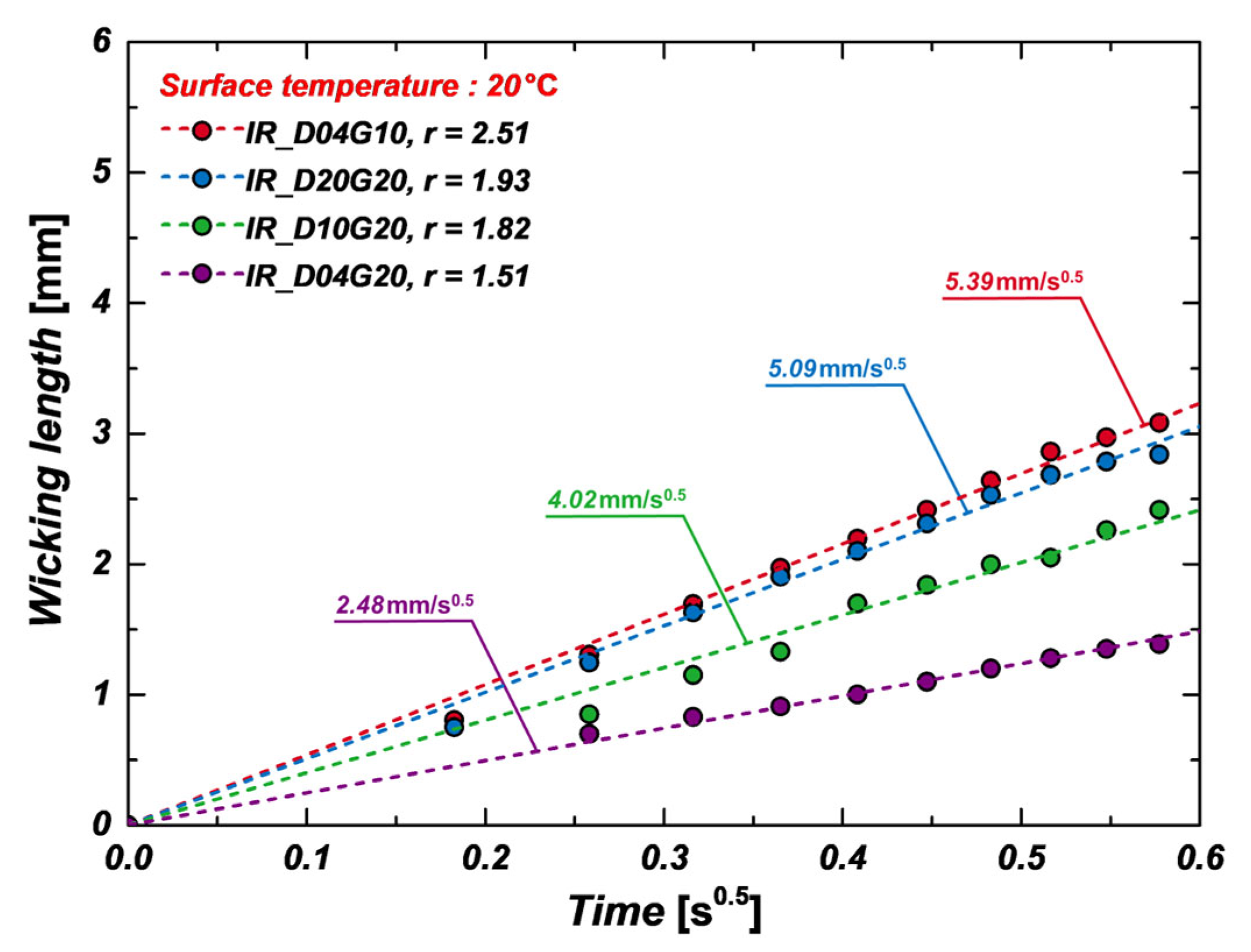
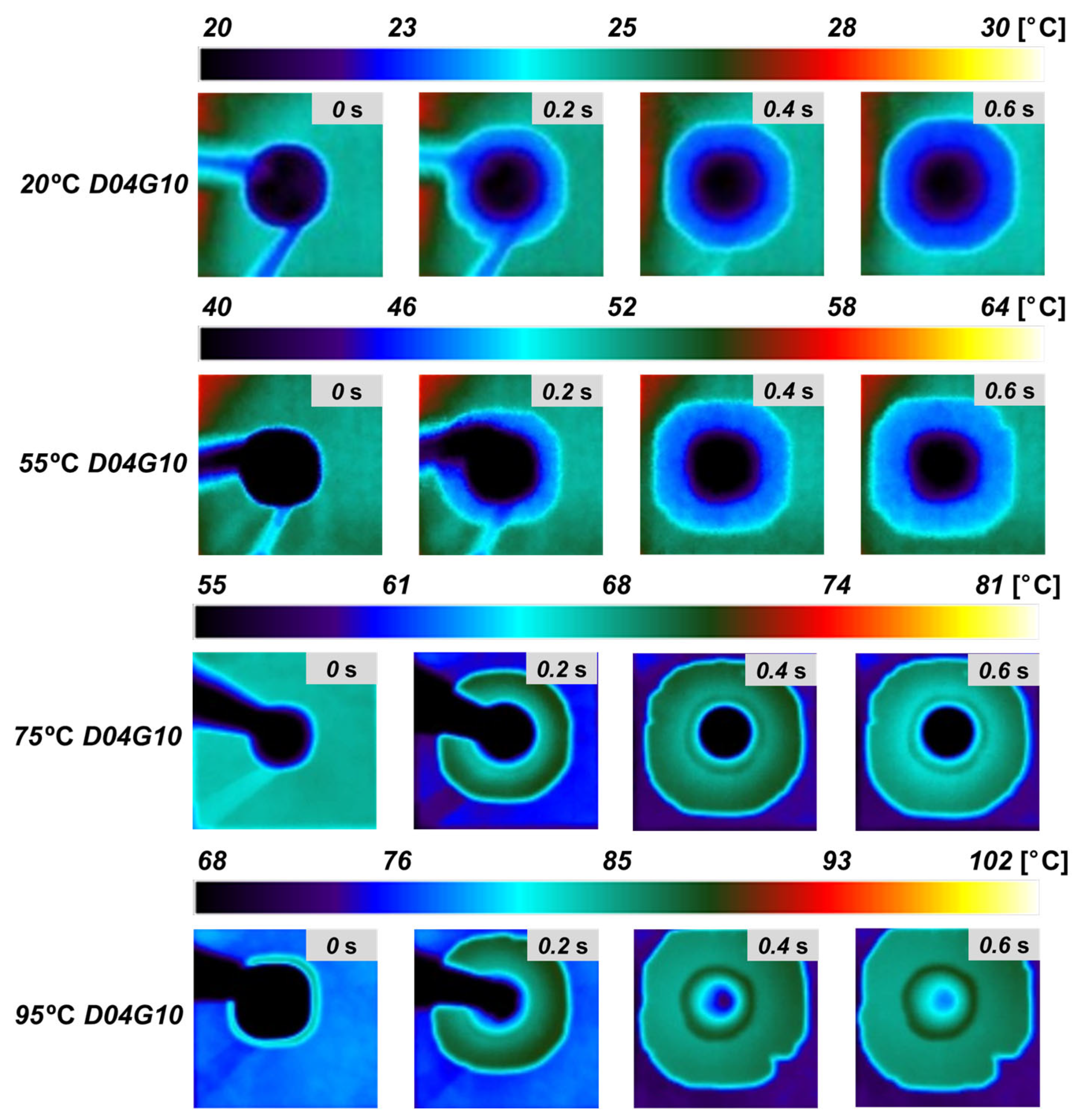
3.1.1. IR-Based Wicking Analysis at 20 °C
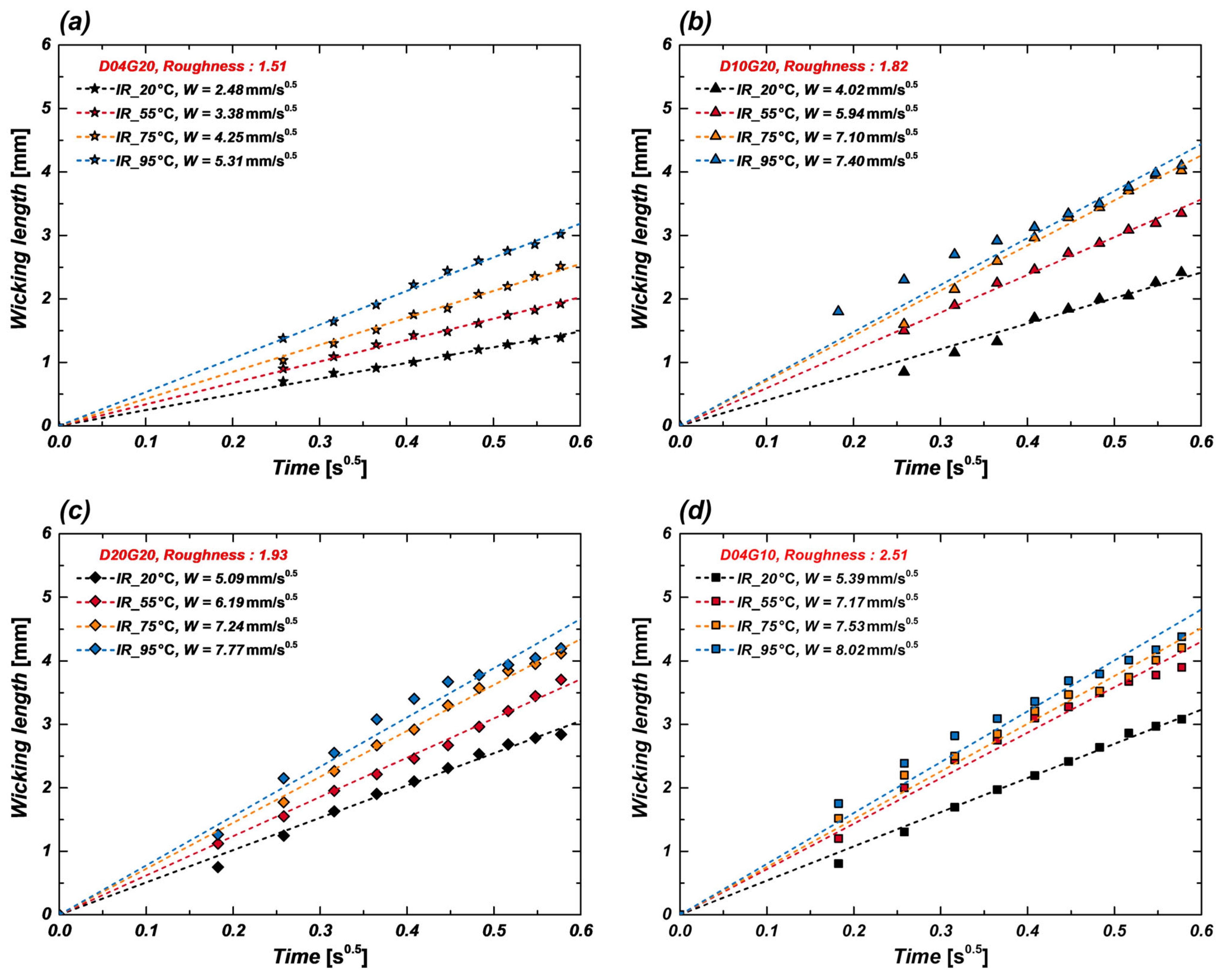
3.1.2. IR-Based Wicking Analysis Under Temperature Increase
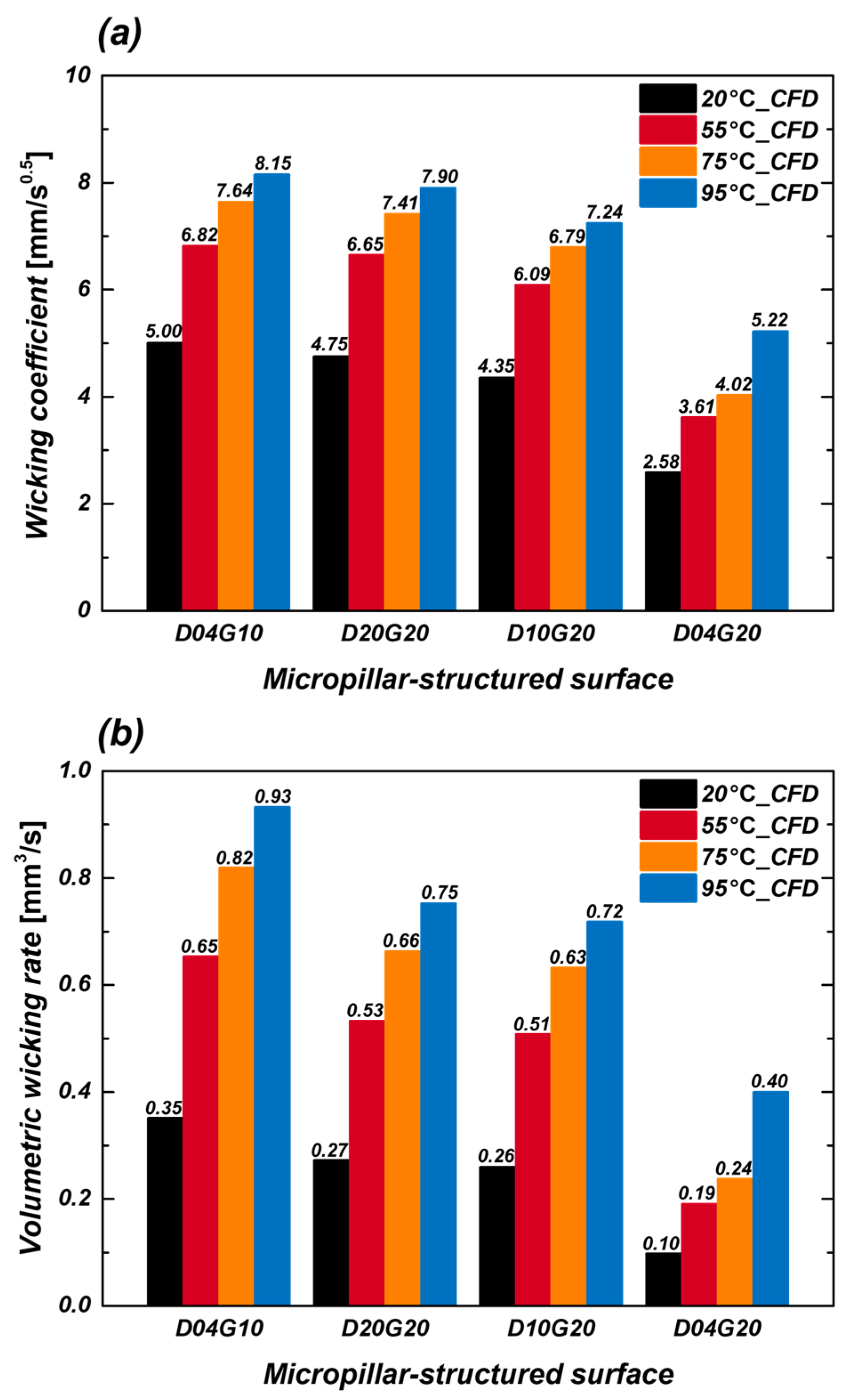
3.2. Wicking Analysis Under Temperature Variation Using CFD
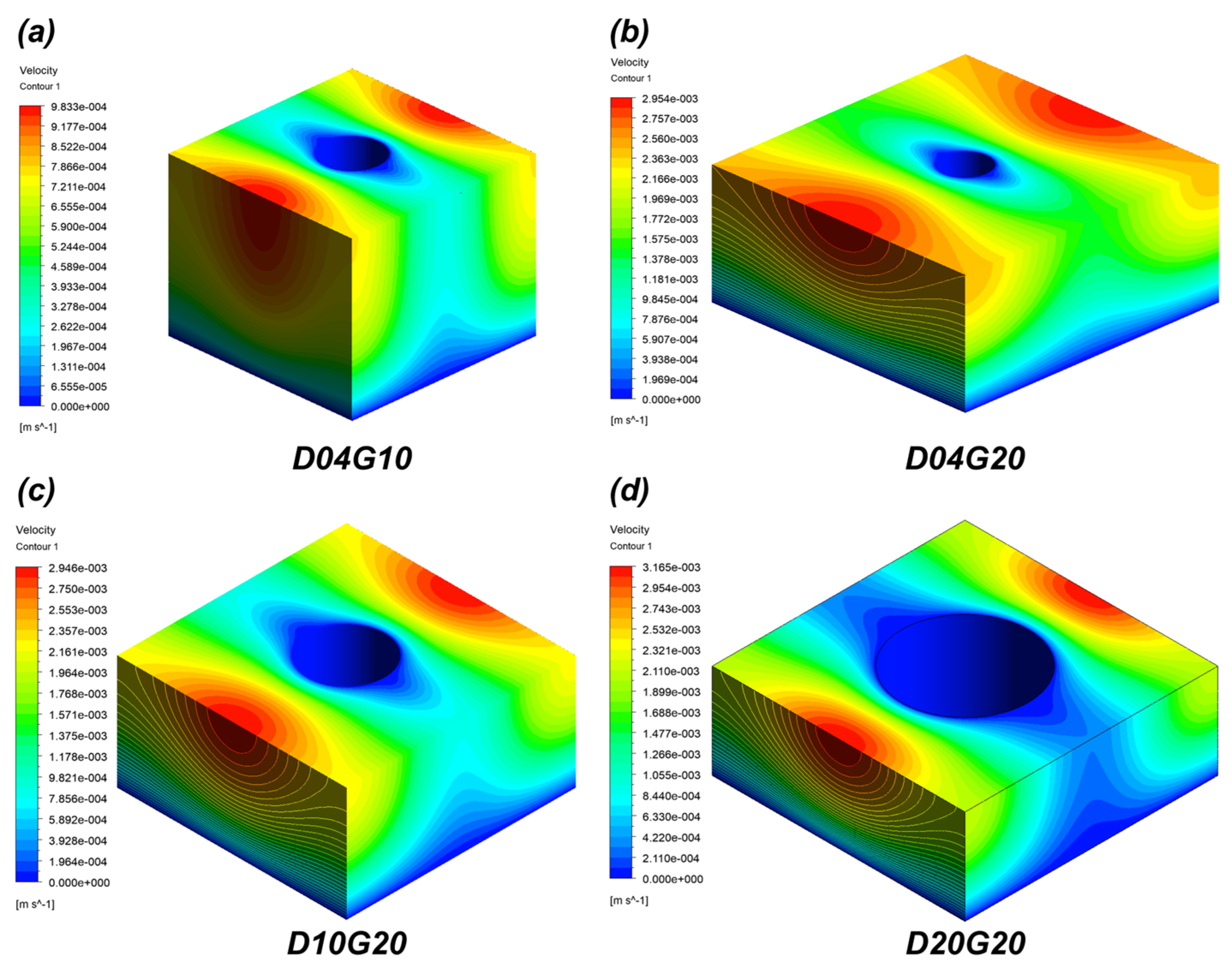
3.2.1. CFD-Based Wicking Analysis at 20 °C
3.2.2. CFD-Based Wicking Analysis Under Temperature Increase
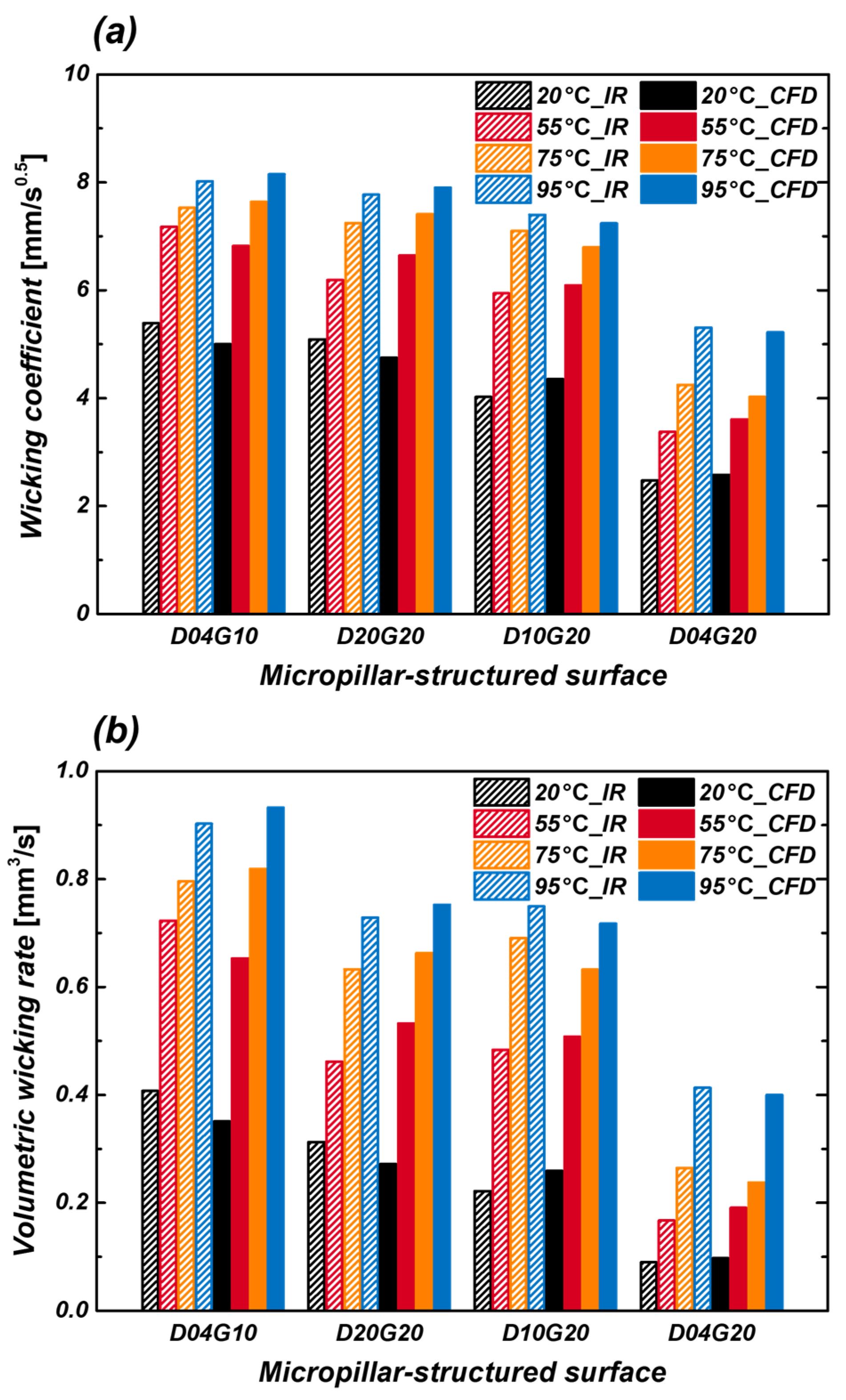
3.3. Comparison of Wicking Performance Between Experiments and CFD
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Qi, B.; Zhang, Y.; Wei, J. Pool boiling heat transfer and bubble behavior on the treelike networks with wedge-shaped channels. Int. Commun. Heat Mass Transf. 2020, 118, 104811. [Google Scholar] [CrossRef]
- Dhir, V. Boiling heat transfer. Annu. Rev. Fluid Mech. 1998, 30, 365–401. [Google Scholar] [CrossRef]
- Kim, D.E.; Yu, D.I.; Jerng, D.W.; Kim, M.H.; Ahn, H.S. Review of boiling heat transfer enhancement on micro/nanostructured surfaces. Exp. Therm. Fluid Sci. 2015, 66, 173–196. [Google Scholar] [CrossRef]
- Sarafraz, M.; Hormozi, F.; Peyghambarzadeh, S. Pool boiling heat transfer to aqueous alumina nano-fluids on the plain and concentric circular micro-structured (CCM) surfaces. Exp. Therm. Fluid Sci. 2016, 72, 125–139. [Google Scholar] [CrossRef]
- Ridwan, S.; Pollack, J.; McCarthy, M. Nanofluid boiling on micro/nano-engineered surfaces. Langmuir 2021, 37, 6107–6114. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Lim, J.-S.; Lee, N.; Cho, H.H. Enhanced thermal uniformity and stability in pool boiling heat transfer using ultrasonic actuation. Int. Commun. Heat Mass Transf. 2019, 106, 22–30. [Google Scholar] [CrossRef]
- Kim, Y.I.; Jang, K.; Park, C.; An, S.; Yarin, A.L.; Yoon, S.S. Enhanced cooling of high-power microelectronics with swing-like pool boiling. Int. Commun. Heat Mass Transf. 2021, 125, 105338. [Google Scholar] [CrossRef]
- Liu, B.; Yang, X.; Li, Q.; Chang, H.; Qiu, Y. Enhanced pool boiling on composite microstructured surfaces with microcavities on micro-pin-fins. Int. Commun. Heat Mass Transf. 2022, 138, 106350. [Google Scholar] [CrossRef]
- Zheng, D.; Choi, C.-H.; Sun, G.; Zhao, X. Superwicking on nanoporous micropillared surfaces. ACS Appl. Mater. Interfaces 2020, 12, 30925–30931. [Google Scholar] [CrossRef]
- Kim, B.S.; Lee, H.; Shin, S.; Choi, G.; Cho, H.H. Interfacial wicking dynamics and its impact on critical heat flux of boiling heat transfer. Appl. Phys. Lett. 2014, 105, 191601. [Google Scholar] [CrossRef]
- Lee, J.; Suh, Y.; Dubey, P.P.; Barako, M.T.; Won, Y. Capillary wicking in hierarchically textured copper nanowire arrays. ACS Appl. Mater. Interfaces 2018, 11, 1546–1554. [Google Scholar] [CrossRef]
- Kim, D.E.; Park, S.C.; Yu, D.I.; Kim, M.H.; Ahn, H.S. Enhanced critical heat flux by capillary driven liquid flow on the well-designed surface. Appl. Phys. Lett. 2015, 107, 023903. [Google Scholar] [CrossRef]
- Pereira, J.; Souza, R.; Moreira, A.; Moita, A. An overview of innovative surface-modification routes for pool boiling enhancement. Micromachines 2024, 15, 302. [Google Scholar] [CrossRef]
- Pereira, J.; Souza, R.; Lima, R.; Moreira, A.; Moita, A. An Overview of the Recent Advances in Pool Boiling Enhancement Materials, Structrure, and Devices. Micromachines 2024, 15, 281. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, G.C.; Kang, J.Y.; Moriyama, K.; Kim, M.H.; Park, H.S. Boiling heat transfer and critical heat flux evaluation of the pool boiling on micro structured surface. Int. J. Heat Mass Transf. 2015, 91, 1140–1147. [Google Scholar] [CrossRef]
- Choi, G.; Shim, D.I.; Lee, D.; Kim, B.S.; Cho, H.H. Enhanced nucleate boiling using a reduced graphene oxide-coated micropillar. Int. Commun. Heat Mass Transf. 2019, 109, 104331. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Chu, K.-H.; Enright, R.; Wang, E.N. Structured surfaces for enhanced pool boiling heat transfer. Appl. Phys. Lett. 2012, 100, 241603. [Google Scholar] [CrossRef]
- Nam, H.T.; Cho, H.H.; Lee, S.; Lee, D. Temperature-dependent wicking dynamics and its effects on critical heat flux on micropillar structures in pool boiling heat transfer. Int. Commun. Heat Mass Transf. 2023, 146, 106887. [Google Scholar] [CrossRef]
- Lee, D.; Lee, N.; Shim, D.I.; Kim, B.S.; Cho, H.H. Enhancing thermal stability and uniformity in boiling heat transfer using micro-nano hybrid surfaces (MNHS). Appl. Therm. Eng. 2018, 130, 710–721. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Xiao, R.; Enright, R.; Wang, E.N. Prediction and optimization of liquid propagation in micropillar arrays. Langmuir 2010, 26, 15070–15075. [Google Scholar] [CrossRef] [PubMed]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Flow Turbul. Combust. 1949, 1, 27–34. [Google Scholar] [CrossRef]



| Geometric Variables | CA | CCA | |||||
|---|---|---|---|---|---|---|---|
| Sample | |||||||
| D04G10 | 4 | 10 | 15 | 2.51 | 0.064 | 6.11 | 67.5 |
| D04G20 | 4 | 20 | 15 | 1.51 | 0.022 | 4.66 | 49.0 |
| D10G20 | 10 | 20 | 15 | 1.82 | 0.087 | 5.39 | 58.3 |
| D20G20 | 20 | 20 | 15 | 1.93 | 0.196 | 8.11 | 62.3 |
| Temp. (°C) | Sample | ||||
|---|---|---|---|---|---|
| 20 °C | D04G10 | 4687.96 | 0.61 | 82.11 | 10.69 |
| D04G20 | 559.07 | 1.36 | 36.84 | 5.51 | |
| D10G20 | 2066.46 | 1.05 | 47.77 | 9.30 | |
| D20G20 | 3141.22 | 0.82 | 60.98 | 10.15 | |
| 55 °C | D04G10 | 4262.95 | 1.25 | 40.14 | 14.57 |
| D04G20 | 508.39 | 2.92 | 17.12 | 7.71 | |
| D10G20 | 1879.11 | 2.25 | 22.19 | 13.01 | |
| D20G20 | 2856.44 | 1.77 | 28.33 | 14.20 | |
| 75 °C | D04G10 | 4031.13 | 1.65 | 30.27 | 16.32 |
| D04G20 | 480.74 | 3.84 | 13.00 | 8.60 | |
| D10G20 | 1776.93 | 2.97 | 16.86 | 14.52 | |
| D20G20 | 2701.10 | 2.32 | 21.52 | 15.84 | |
| 95 °C | D04G10 | 3850.82 | 1.97 | 25.40 | 17.41 |
| D04G20 | 459.24 | 6.78 | 7.38 | 11.16 | |
| D10G20 | 1697.45 | 3.52 | 14.19 | 15.05 | |
| D20G20 | 2580.29 | 2.76 | 18.11 | 16.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Park, H.; Nam, H.T.; Kim, Y.-H.; Ahn, J.-H.; Lee, D. Temperature Effects on Wicking Dynamics: Experimental and Numerical Study on Micropillar-Structured Surfaces. Micromachines 2025, 16, 512. https://doi.org/10.3390/mi16050512
Lee Y, Park H, Nam HT, Kim Y-H, Ahn J-H, Lee D. Temperature Effects on Wicking Dynamics: Experimental and Numerical Study on Micropillar-Structured Surfaces. Micromachines. 2025; 16(5):512. https://doi.org/10.3390/mi16050512
Chicago/Turabian StyleLee, Yoomyeong, Hyunmuk Park, Hyeon Taek Nam, Yong-Hyeon Kim, Jae-Hwan Ahn, and Donghwi Lee. 2025. "Temperature Effects on Wicking Dynamics: Experimental and Numerical Study on Micropillar-Structured Surfaces" Micromachines 16, no. 5: 512. https://doi.org/10.3390/mi16050512
APA StyleLee, Y., Park, H., Nam, H. T., Kim, Y.-H., Ahn, J.-H., & Lee, D. (2025). Temperature Effects on Wicking Dynamics: Experimental and Numerical Study on Micropillar-Structured Surfaces. Micromachines, 16(5), 512. https://doi.org/10.3390/mi16050512







